Incorporating elevation in rainfall interpolation in Tunisia using geostatistical methods

Abstract

This paper compares the performance of three geostatistical algorithms, which integrate elevation as an auxiliary variable: kriging with external drift (KED); kriging combined with regression, called regression kriging (RK) or kriging after detrending; and co-kriging (CK). These three methods differ by the way by in which the secondary information is introduced into the prediction procedure. They are applied to improve the prediction of the monthly average rainfall observations measured at 106 climatic stations in Tunisia over an area of 164 150 km² using the elevation as the auxiliary variable. The experimental sample semivariograms, residual semivariograms and cross-variograms are constructed and fitted to estimate the rainfall levels and the estimation variance at the nodes of a square grid of 20 km × 20 km resolution and to develop corresponding contour maps. Contour diagrams for KED and RK were similar and exhibited a pattern corresponding more closely to local topographic features when (a) the network is sparse and (b) the rainfall–elevation correlation is poor, while CK showed a smooth zonal pattern. Smaller prediction variances are obtained for the RK algorithm. The cross-validation showed that the RMSE obtained for CK gave better results than for KED or RK.

Editor D. Koutsoyiannis; Associate editor C. Onof

Citation Feki, H., Slimani, M., and Cudennec, C., 2012. Incorporating elevation in rainfall interpolation in Tunisia using geostatistical methods. Hydrological Sciences Journal, 57 (7), 1294–1314.

Résumé

Nous comparons les performances de trois méthodes géostatistiques qui permettent d'intégrer l'altitude comme variable auxiliaire: le krigeage avec dérive externe (KED), la régression-krigeage (RK) et le cokrigeage (CK). Ces trois méthodes se différencient par la manière avec laquelle l'information secondaire est introduite dans la procédure d'estimation. Elles sont appliquées pour améliorer l'estimation des précipitations moyennes mensuelles mesurées par 106 stations climatiques réparties sur toute la Tunisie, de superficie 164 150 km², en utilisant l'altitude comme variable auxiliaire. On a construit et ajusté les semi-variogrammes expérimentaux simples, les semi-variogrammes des résidus et les variogrammes croisés pour estimer les précipitations et la variance d'estimation au niveau des nœuds d'une grille carrée d'une résolution de 20 km × 20 km, et pour développer les cartes des isohyètes correspondantes. Les cartes de pluie obtenues par le KED et la RK sont similaires et présentent un aspect très lié aux variations topographiques lorsque (a) le réseau est peu dense et (b) la corrélation pluie–altitude est médiocre. Les cartes obtenues par CK présentent quant à elles des isohyètes lisses. Les valeurs des variances d'estimation les plus faibles sont obtenues par la RK. La validation croisée montre que la racine de l'écart quadratique moyen obtenue pour le CK est meilleure que pour le KED ou pour la RK.

Key words:

• monthly average rainfall
• semivariogram
• cross-variogram
• kriging with external drift
• regression-kriging
• co-kriging
• Tunisia

Mots clefs:

• pluie moyenne mensuelle
• semi-variogramme
• variogramme croisé
• krigeage avec dérive externe
• régression-krigeage
• cokrigeage
• Tunisie

1 INTRODUCTION

Rainfall maps have a wide range of applications, such as water resources management and hydrological simulation. Geostatistical multivariate techniques are widely used for the prediction of precipitation amounts over a given area by accounting for secondary information sampled over the same area to improve the quality of the maps.

In some studies, radar-rainfall data have been used in conjunction with measurements at raingauges to map precipitation (Creutin et al. 1988). However, the bulk of studies have made use of a cheaper, widely-available data source, the digital elevation model (DEM), in exploiting the relationship between precipitation amount and elevation.

In fact, topographic relief has marked effects on precipitation, which, generally, increases with elevation. This increase is due to the fact that hills are barriers to moist airstreams, forcing the air to rise, and they act as high-level heat sources on sunny days. The latter causes convective clouds to form over hills preferentially, resulting in showery precipitation. Weather stations tend to be sited at low elevation and may thus underestimate the regional precipitation. For these reasons, especially, in areas of high topographic relief, it will often be insufficient to use data from the nearest weather station to characterize the amount and spatial distribution of precipitation over a large-scale study area. Goovaerts (2000) reported that the techniques which used elevation data generally out-performed ordinary kriging (OK). That is, where precipitation amount and elevation are correlated linearly, estimates informed by elevation data are often more accurate than those made using the precipitation data alone. Studies have been conducted in a range of different locations and environments around the world and they suggest that incorporating elevation into the interpolation procedure will often be beneficial.

This paper builds on the work of Slimani et al. (2007), but the analysis is expanded in using multivariate geostatistical methods to assess the impact of incorporating elevation into the monthly average rainfall prediction across the whole of Tunisia by comparing three interpolation techniques: kriging with external drift (KED), regression kriging (RK) and co-kriging (CK).

2 STUDY AREA AND DATA

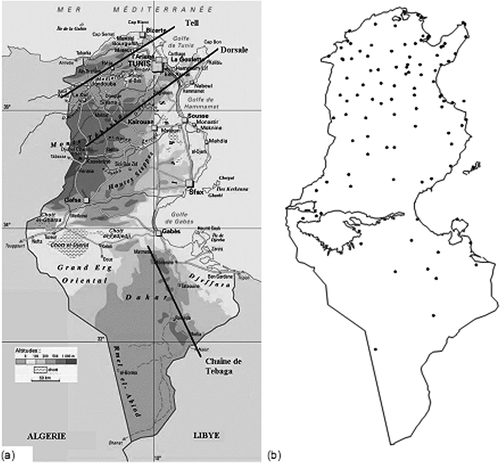
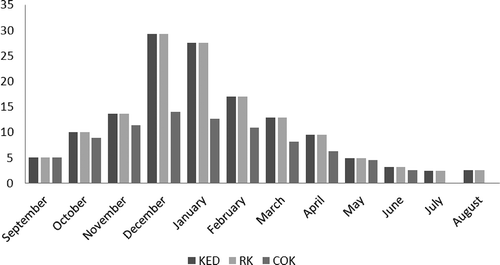
Tunisia is a Mediterranean coastal region (Cudennec et al. 2007) located in the north of Africa with an area of 164 150 km². The physical geography of the region is quite heterogeneous (Fig. 1). Mountains in the north are separated by small plains where some wadis, such as Oued Mejerda (Jebari et al. 2012), flow. The plains are progressively replaced by steppes, then by oriental coasts that stretch from Cap Bon to the Libyan border. The coasts (1300 km) are cut by deep gulfs and there are many islands. Towards the south, the mountainous chains are lower (Sahara). Climatologically, Tunisia is situated in the geographical transition zone between humid temperate climate and the arid Saharan climate. Although, the general climate is arid, we can distinguish three different climatic regions: (a) the north is characterized by a Mediterranean climate with a humid and sub-humid nuance; (b) the centre and east coast region with a semi-arid climate; and (c) the south, where the climate becomes Saharan. The precipitation is characterized by a marked north–south spatial distribution, with strong hydrological consequences (Cudennec et al. 2005, 2007). In fact, in the north, the total of the annual rainfall means is between 400 and 1000 mm and it may reach 1500 mm per year over the Kroumirie Mountains. The rainfall season extends from September to April with a rainfall maximum during the winter months. In the centre of Tunisia, the mean rainfall varies from 200 to 400 mm per year and it is characterized by a significant variability from one year to another. The south of Tunisia is characterized by a Saharan climate, where rainfall is erratic. For further details on the meteorological and physical aspects, please refer to Slimani et al. (2007), Feki (2010) and Baccour et al. (2012).

Fig. 1 (a) Map of Tunisia and (b) location of rainfall measurements.

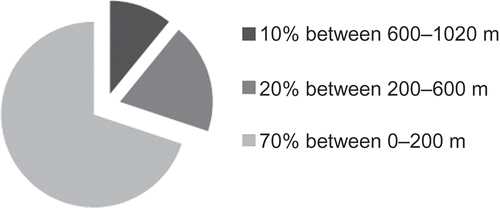
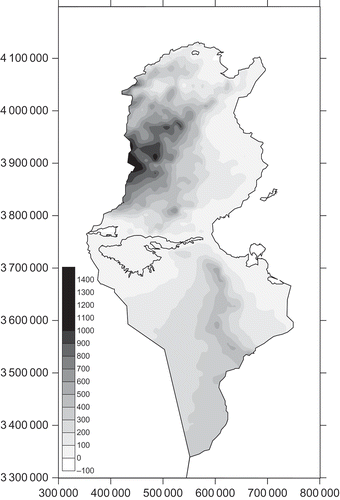
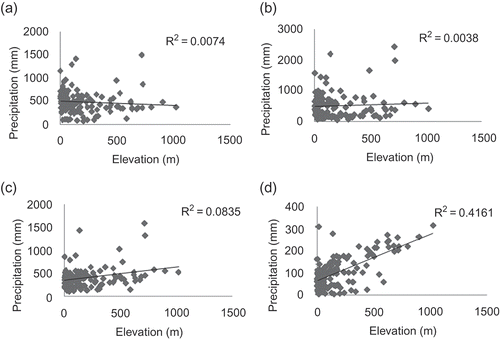
Monthly rainfall data for 106 raingauges in Tunisia for the period 1961–1990 were collected from the global directorate of water resources of the Tunisian agricultural ministry (Direction générale des resources en eau, DGRE) and the national institute of meteorology (Institut national de la meteorology, INM). Monthly average rainfall and inter-annual rainfall were calculated for a common observation period for each raingauge station and statistical analysis carried out (see Table 1). Almost all variables showed a large distribution of data around the mean value and quite high relative standard deviation (RSD). The locations of observation stations are shown in Fig. 1. Most of the raingauges are located in areas with low elevation (Fig. 2). Elevations were also available at each raingauge location and the coefficient of determination, r ², for elevation against precipitation for each month is given as the last column of Table 1. A digital elevation model (DEM) at 20 km × 20 km resolution (Fig. 3) was used as the secondary data set for KED and RK.

Table 1 Summary statistics for monthly average rainfall

Month	Minimum (mm)	Maximum (mm)	Mean (mm)	Standard deviation (mm)	r ^2 (vs elevation)	RSD
September	2.46	71.67	32.72	12.12	0.02	0.37
October	8.42	149.83	49.16	23.82	0.007	0.48
November	4.03	201.49	47.15	32.64	0.0003	0.69
December	5.50	262.51	52.60	42.20	0.002	0.80
January	6.95	243.59	51.79	39.99	0.003	0.77
February	5.82	198.72	43.22	32.04	0.008	0.74
March	11.01	159.71	40.56	21.97	0.08	0.54
April	5.35	138.90	33.75	19.70	0.09	0.58
May	3.06	86.76	22.16	12.89	0.24	0.58
June	0.56	31.58	10.73	7.07	0.41	0.65
July	0	24.88	3.34	3.20	0.25	0.95
August	0	25.42	8.93	5.70	0.29	0.63

Fig. 2 Distribution of the raingauge numbers with class of altitude.

Fig. 3 Digital elevation model of Tunisia (20 km × 20 km).

3 METHODOLOGY

The geostatistical approach is based on the theory of regionalized variables (Matheron 1970). It assumes that spatial samples are considered as the realization of a random spatial process. This allows the use of a powerful statistical instrument for spatial estimation: the semivariogram (Feki and Slimani 2006).

Let z _α(s_i ) and z _β(s_i ) represent realizations of random variables Z _α(s_i ) and Z _β(s_i ) at particular points s_i within a field S. The intrinsic hypothesis (Chauvet 1999) assumes that, for a random variable Z(s_i ): (i) the expected value of Z(s_i ) does not depend on the position s_i ; and (ii) the variance of [Z(s_i ) – Z(s_i + h )] does not depend on the position s_i in S for any separation vector h . Then the semivariogram function gives a measure of the spatial correlation of a random variable or variables as a function of separation distance. Sample semivariograms and cross-variograms were estimated by the function:

(1)

where γ_αβ is the semivariance of Z _α (when α = β), or the cross-semivariance of Z _α and Z _β (when α ≠ β) at a separation distance h; and n(h) is the number of pairs of points in a distance interval (h + Δh).

The cross-variogram must be part of a linear model of co-regionalization (LMC). A LMC requires that every structure in the cross-variogram or other model of spatial continuity be included in the spatial continuity model for primary and secondary variables. A mathematical authorized model may then be fitted to the experimental variogram and the coefficients of this model can be used for kriging. In variogram models where the semivariance reaches a finite variance and levels out, the maximum is referred to as the sill. This is termed a bounded model (spherical and exponential models). Models that do not reach a sill are termed unbounded (power model). Unbounded variograms may indicate a large-scale trend (that is, systemic increase or decrease) in the values of the property characterized across the region of study. All variogram parameters are introduced into algorithms using code written by Matlab computer programs. These algorithms concern the KED, RK and CK methods and the theory of each method is described in the Appendix.

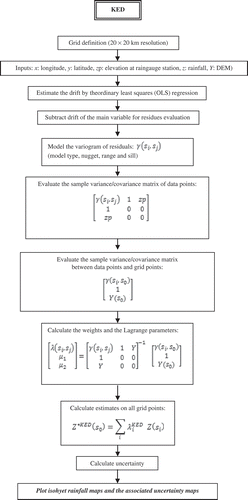
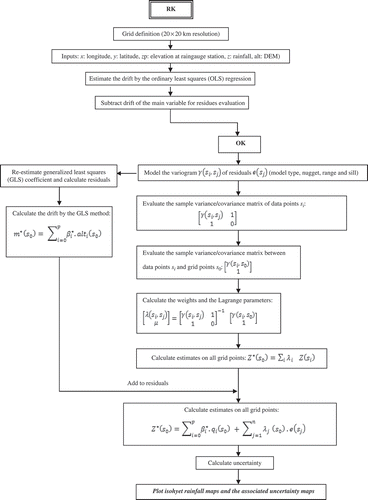
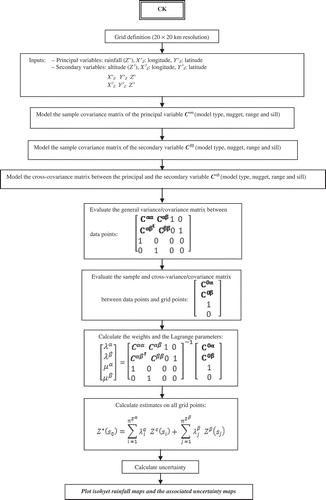
The interpolation methods differ principally by the way in which the secondary variable is introduced in the prediction procedure. In fact, for KED (Fig. 4), the following procedure is used with the data for each month: (i) ordinary least square (OLS) regression (altitude vs precipitation) is conducted around each data location (raingauge) and estimates of the drift are made at the point locations and on a regular grid; (ii) the residuals are obtained at each data location (that is, the differences in observed and estimated precipitation amount are obtained); (iii) the variogram is estimated from the residuals and a model is fitted; and (iv) estimates of precipitation are made at the locations of the DEM cells with variogram matrix extended by the elevation matrix. For RK (Fig. 5), the estimator can be decomposed as a two-stage process: a generalized least-square regression of the primary variable with the auxiliary variables followed by a simple kriging of the regression residuals (Castelier 1993, Hengl et al. 2007). This was originally suggested by Odeh et al. (1995), who named it “regression kriging”, whereas Goovaerts (2000) uses the term “kriging after detrending”. The CK (Fig. 6) is another method of multivariable geostatistics needing the determination of the cross-variogram besides the simple variogram of the principal and the secondary variable, which is often a delicate operation (Pardo-Igùzquiza et al. 2007).

Fig. 4 Explanatory diagram of the KED procedure.

Fig. 5 Explanatory diagram of the RK procedure.

Fig. 6 Explanatory diagram of the CK procedure.

The advantage of KED is that the equations are solved at once, while the advantage of RK is that there is no danger of instability as with the KED system, according to Goovaerts (2000). Some authors make different assumptions and skip some computational step(s) so that the products of RK and KED might not differ at the end. For example, Bourennane and King (2003) made an assumption that the variogram of residuals is equal to the variogram of target variable, which is a simplification. In this case, the KED prediction map will look more similar to the OK map. Other authors (e.g. Odeh et al. 1995) used only ordinary least-squares estimate of the drift, which is also sub-optimal, but is a shorter solution. Kitanidis (1997) confirms that, in practice, a single iteration for the estimation of GLS residuals can be used. In this paper, estimates of monthly precipitation in Tunisia were made using the techniques detailed above, and these were compared using: (a) a visual examination of the maps derived through estimation via a regular grid, and (b) a cross-validation procedure. The paper has several innovative components; elevation and precipitation relationships have been relatively little studied in Tunisia. One specific contribution of the paper is in illustrating how rainfall varies regionally with elevation.

4 RESULTS AND DISCUSSIONS

The analysis of the data comprised four steps: (i) a general trend surface analysis; (ii) a general and local regression analysis; (iii) structural analysis; and (iv) estimation. In step (i), the desire is to identify any large-scale trends in precipitation values across Tunisia. The estimation of the variogram for KED is based on the assumption that there is such a large-scale trend in precipitation amounts. So, if the trend surface analysis indicates a large-scale trend is present, then this suggests that the approach employed using KED is valid. In step (ii), the concern was to assess relationships between precipitation and elevation both for the whole country (use all available paired data) and locally (use only subsets of the data within a moving window). If elevation and precipitation are related locally, the KED is potentially beneficial. In step (iii), spatial variation in precipitation is characterized by estimating the variogram. Fitting a model to the variogram enables incorporation of information on spatial variation in the property into the interpolation procedure through kriging algorithms (step (iv)). The four months of October, January, March and June are used for illustrative purposes for the four seasons successively (autumn, winter, spring and summer).

4.1 Trend surface analysis

In order to assess evidence for long-range trends in precipitation amount, a general trend surface analysis was conducted. First-, second- and third-order data polynomials were fitted to the precipitation data. Precipitation amount was the dependent variable and the independent variables for a polynomial of order 1 were x and y, for order 2 they were x, y, x ², y ², xy and for order 3 they were x, y, x ², y ², xy, x ³, y ³, x ² y, xy ², with x and y the distances in the west–east and south–north directions, respectively.

In Table 2, the r ² values are given for first-, second- and third-order polynomials fitted to the point data for each month. The figures indicate that a first-order and second-order polynomial accounts for more than 40% of the variation in precipitation amount for 10 months. For a third-order polynomial, it is more than 40% for only 8 months, because February and April are exceptions. For the months of July and August, the first-, second- and third-order polynomials account for less than 40% of the variation in precipitation and, except for these two months, the r ² values indicate that there is evidence of a large-scale trend in precipitation amount for most other months. Given our knowledge of precipitation patterns in Tunisia, this is not surprising, since precipitation amount is consistently greater in the north and less in the south. If this trend is due to elevation, then the use of KDE, RK and CK informed by elevation data is likely to be beneficial.

Table 2 Precipitation amount against x and y: values of r ² for polynomials of order 1, 2 and 3

Month	Order 1	Order 2	Order 3
September	0.464	0.575	0.524
October	0.526	0.560	0.404
November	0.439	0.640	0.528
December	0.436	0.638	0.731
January	0.470	0.678	0.759
February	0.469	0.658	0.005
March	0.429	0.596	0.404
April	0.537	0.643	0.225
May	0.573	0.706	0.485
June	0.515	0.595	0.677
July	0.247	0.200	0.275
August	0.312	0.379	0.348

4.2 General and local regression: elevation vs precipitation

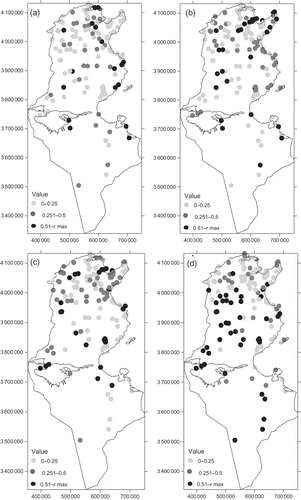
The coefficient of determination, r ², for elevation against precipitation for each month is given in Table 1. Scatter plots of elevation vs precipitation for the four illustrative months are given in Fig. 7. The smallest r ² for all months is for December (0.002) and the largest is for June (0.41). Therefore, the assumption of a (general) linear relationship between elevation and precipitation for the spring and the summer months is not unreasonable. However, KED and RK are informed by this relationship locally, and general regression analyses provide only an overview. Therefore, the relationship between elevation and precipitation was examined locally. Maps of the coefficient of determination in five data neighbourhoods (that is the nearest observations to a given station are included in the regression and the coefficients of the fitted model are attached to the station location) for the four illustrative months are given in Fig. 8. The coefficient of determination varies locally with clusters of large values visible in the north for October, January and March. Clearly, the evident patterns will vary as the data neighbourhood changes. These results suggest that using elevation as a secondary variable in estimation will increase the accuracy of estimates in some locations (that is, those locations where r ² is large). In contrast, in places where r ² is small, OK is likely to provide estimates as accurate as those provided by RK and KED. For the month of June, the large values of the coefficient of determination are visible at high altitude (the Dorsal in the north and the Dhahar toward the south).

Fig. 7 Scatter plots of monthly rainfall against elevation for: (a) October, (b) January, (c) March and (d) June.

Fig. 8 Coefficient of determination: elevation vs precipitation in five data neighborhoods (see text for explanation) for: (a) October, (b) January, (c) March and (d) June.

4.3 Structural analysis

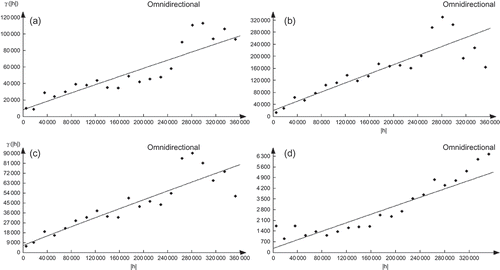
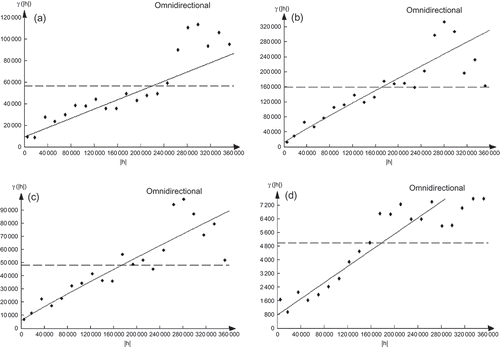
Omni-directional variograms were estimated from the precipitation data for each month and those of October, January, March and June are shown in Fig. 9. The parameters of the models fitted to the variograms of all months are detailed in Table 3. Almost all the general variations of the monthly average rainfall (11 months out of 12) are modelled by the power type of variogram, which highlights the presence of trend or drift caused by the different directional drifts. In fact, in the east–west, northwest–southeast and northeast–southwest directions, variogram models are mostly of power type. Therefore, the general drift seems to be the result of the combination of the three secondary trends caused by the east–west, northwest–southeast and northeast–southwest directions. Finally, in the north–south direction, variogram models are bounded except for the transition months (from May to August), which indicates a seasonal trend. The most important nugget effect values of the average monthly rainfall concern the northwest–southeast direction, then the east–west one. They are the most weak in the north–south direction. The general variograms present nugget effect values that vary between the directional nugget effect values for January–August. The nugget effect values are the most marked in the northwest–southeast direction in the winter months, which corresponds to the principal trend direction generating the greatest variations compared to the other directions. There is a significant spatial variation, which matches the winter season of frontal disturbances coming from the northwest encountering the mountainous chains of the Dorsal in a perpendicular direction.

Table 3 Parameters of the simple variograms

Month	Direction	Model type	Parameters			Month	Direction	Model type	Parameters
			C0	α	β				C0	α	β
Sep.	G	Power	2100	0.09	0.95	Mar.	G	Power	6240	0.5	0.94
	E–W	Spherical	1950	6449	152867		E–W	Power	1440	0.5	0.98
	NE–SW	Power	1650	0.06	1		NE–SW	Power	1920	0.5	0.91
	N–S	Exponential	0	9150	151693		N–S	Exponential	0	35520	212051
	NW–SE	Exponential	750	8400	161993		NW–SE	Power	7200	0.38	0.99
Oct.	G	Power	9688	0.215	1	Apr.	G	Power	2730	0.4	0.94
	E–W	Spherical	1140	48779	165993		E–W	Power	1950	0.35	0.98
	NE–SW	Spherical	3988	34768	147393		NE–SW	Power	4680	0.1	1
	N–S	Spherical	1710	33060	76000		N–S	Exponential	0	26749	220000
	NW–SE	Exponential	2280	47507	159339		NW–SE	Power	2730	0.35	0.98
Nov.	G	Power	24200	0.434	1	May	G	Power	850	0.14	0.96
	E–W	Spherical	3300	110000	200000		E–W	Power	0	0.136	1
	NE–SW	Spherical	0	67393	132000		NE–SW	Power	1190	0.056	1.01
	N–S	Exponential	0	92040	156200		N–S	Power	1190	0.056	1
	NW–SE	Spherical	12100	110000	163651		NW–SE	Power	0	0.121	1
Dec.	G	Power	30600	0.83	1	Jun.	G	Power	800	0.023	1
	E–W	Power	14394	1.8	0.96		E–W	Power	850	0.0035	1.2
	NE–SW	Power	9000	1.62	0.92		NE–SW	Power	550	0.027	1
	N–S	Exponential	0	146592	161693		N–S	Power	300	0.025	1
	NW–SE	Power	21588	1.54	0.99		NW–SE	Power	50	0.033	1
Jan.	G	Power	12800	1.58	0.95	Jul.	G	Power	825	0.002	0.97
	E–W	Power	12800	1.52	0.96		E–W	Pure nugget	1100	-	-
	NE–SW	Power	3200	1.6	0.92		NE–SW	Pure nugget	1012	-	-
	N–S	Exponential	0	153600	220000		N–S	Power	308	0.02	0.88
	NW–SE	Power	17600	1.504	0.98		NW–SE	Power	132	0.02	0.9
Feb.	G	Power	9900	1.1	0.94	Aug.	G	Spherical	264	3300	200000
	E–W	Power	6596	0.65	1		E–W	Power	561	0.016	1
	NE–SW	Power	4396	1.1	0.96		NE–SW	Power	561	0.013	1.02
	N–S	Exponential	0	89100	220000		N–S	Power	396	0.02	1
	NW–SE	Power	13193	1.04	0.97		NW–SE	Power	462	0.017	1.01
Note: G: general; E–W: east–west; NW–SE: northwest–southeast; NE–SW: northeast–southwest.

Fig. 9 Simple semivariograms: (a) October, (b) January, (c) March and (d) June. The experimental variogram is represented by dots (·) and the model by a solid line (––).

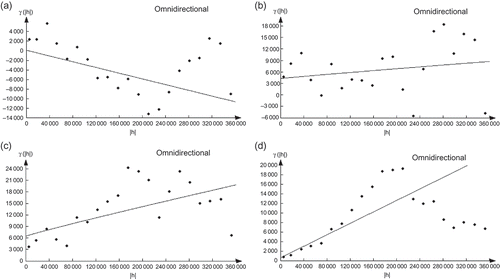
Variograms were also estimated for the residuals of the regression (between elevation and precipitation amount). It is clear that these variograms (Fig. 10) have very similar aspects to the general variograms (Fig. 9). Thus, the variogram of residuals from the regression represents variation remaining even after the trend has been removed. The relationship between rainfall and elevation is also highlighted using the cross-variograms (Table 4). Except for the winter months, represented by January, the influence of elevation on the spatial distribution of rainfall is observed in all the other seasons: autumn, spring and summer represented respectively by October, March and June (Fig. 11). In fact, the corresponding cross-variograms are well structured. For October, the rainfall gradient and elevation are inversely proportional, in contrast to March and June, where they evolve in the same direction. During the rainy season, represented by January, the cross-variogram shows rather a cloud of points. These latter confirm the absence of the influence of elevation on rainfall during this season, as the perturbations are wide-ranging and can reach thousands of kilometres. Therefore, rainfall distribution is indifferent to the orographic obstacles. For other seasons, rainfall is of convective type (especially in summer), thus in direct correlation with the relief. The variogram features of elevation for the 12 monthly average rainfalls are summarized in Table 5.

Table 4 Parameters of the cross-variogram

Month	Model type	Parameters
		C0	α	β
September	Power	1760	0.03	0.95
October	Power	0	−0.03	1
November	Power	0	−0.0064	1
December	Power	5100	0.0015	1
January	Power	4320	0.023	0.95
February	Power	3894	0.038	0.94
March	Power	6580	0.08	0.94
April	Power	4620	0.08	0.94
May	Power	3220	0.08	0.96
June	Power	700	0.06	1
July	Power	252	0.03	0.97
August	Spherical	0	6 800	200 000

Table 5 Experimental semivariogram of elevation

	Elevation
	Model	C0	α*	β**
September	Power	18 720	0.3	0.95
October	Power	4 800	0.3	1
November	Power	4 800	0.3	1
December	Power	4 800	0.3	1
January	Power	11 040	0.3	0.95
February	Power	11 040	0.3	0.94
March	Power	11 040	0.3	0.94
April	Power	11 040	0.3	0.94
May	Power	9 600	0.3	0.96
June	Power	4 800	0.3	1
July	Power	10 080	0.3	0.97
August	Spherical	6 240	48 000	2 × 10^5
Notes: C0 (1–10 mm^2) nugget effect.
α* (1–10 mm^2) sill (for the spherical model) or slope (for the power model).
β** (m) range (for the spherical model) or power coefficient (for the power model).

Fig. 10 Residual semivariograms: (a) October, (b) January, (c) March and (d) June. The experimental variogram is represented by dots (·) and the model by a solid line (––).

Fig. 11 Cross-semivariograms: (a) October, (b) January, (c) March and (d) June. The experimental variogram is represented by dots (·) and the model by a solid line (––).

4.4 Data mapping

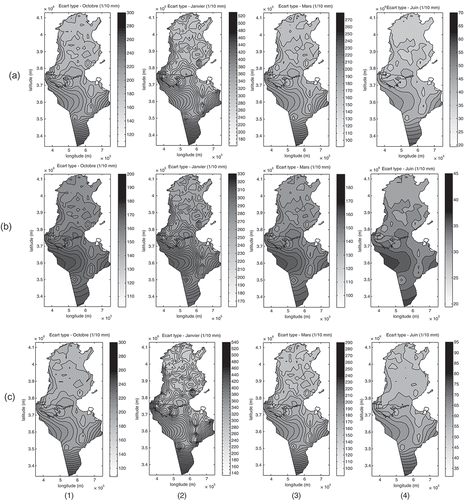
All the variogram parameters are introduced into the different kriging algorithms to obtain monthly rainfall maps and the corresponding error estimation maps. The precipitation maps (Fig. 12(a)) obtained by KED show that during the rainy months, the pattern of precipitation contours take the aspect of the bends of the DEM in the regions with very weak densities of stations: the chain of the Dhahar in the south and in the regions where rainfall and elevation are little correlated: the high altitudes of the Dorsal in the north. In fact, in these regions we notice that the KED model allows the dominance of the external drift that is the altitude. For the dry months, we rediscover the same pattern of precipitation contours as the maps obtained by OK (Slimani et al. 2007). The same result was obtained by Tapsoba et al. (2005), who indicate that, in the poorly sampled regions, the spatial organization of rain values reflects, to various degrees, that of the topography. Rossiter (2005, 2007) confirms this result while mentioning that, if the principal and the auxiliary variables are little correlated, the estimation by KED resembles the drift.

From a visual check, the plotted rainfall maps obtained by RK (Fig. 12(b)) are very similar to those obtained by KED. This result is confirmed by the studies conducted by Hengl et al. (2007). The model of RK always shows, for the rainy months (October–April), the dominance of the elevation values over precipitation in the poorly-sampled zones and the little correlated zones. In contrast to the preceding maps, those obtained by CK (Fig. 12(c)) show a smooth zonal pattern during the humid season. Goovaerts (2000) found the same result while estimating annual averaged rainfall: the CK does not improve, nor damages, the results obtained by the OK (Slimani et al. 2007); this is due to the weak correlation between the principal and secondary variables during this season. The relief introduction does not change the general aspect of the maps significantly in the well-sampled regions. The maps obtained by CK, during the spring and summer, present few differences from that obtained by OK (Slimani et al. 2007). This is the visible effect of elevation during the low-rain season found in the structural analysis.

Fig. 12 Rainfall maps obtained by Uncertainty maps obtained by (a) KED, (b) RK and (c) CK for: (1) October, (2) January, (3) March and (4) June.

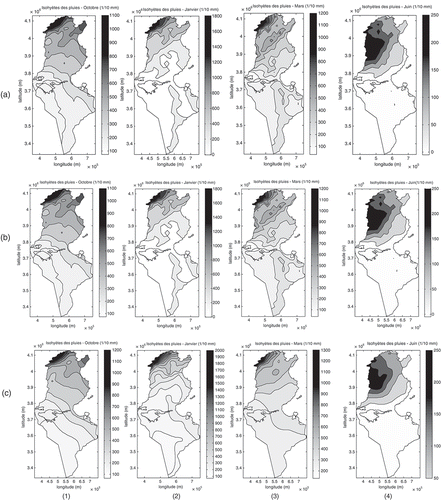
Independently of the season and of the prediction method, uncertainty associated with the rainfall estimation (Fig. 13) tends to be highest in places where there are few or no sample data (southwest and extreme south). The most notable uncertainty values concern the winter, which is illustrated by January (Fig. 13 (a-2), (b-2), (c-2)), since, during this season, the spatial variability is the most marked. In the north and centre of Tunisia, the uncertainty means reach a maximum of 22 mm, and become increasingly greater toward the south, with a maximum of 48 mm in the extreme south. To the south, we note that the RK method begins to distinguish itself from other type of kriging, while giving the weakest estimation uncertainty throughout the year.

Fig. 13 Uncertainty maps obtained by (a) KED, (b) RK and (c) CK for (1) October, (2) January, (3) March and (4) June.

5 VALIDATION PROCEDURE

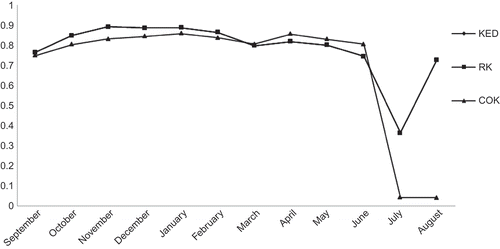
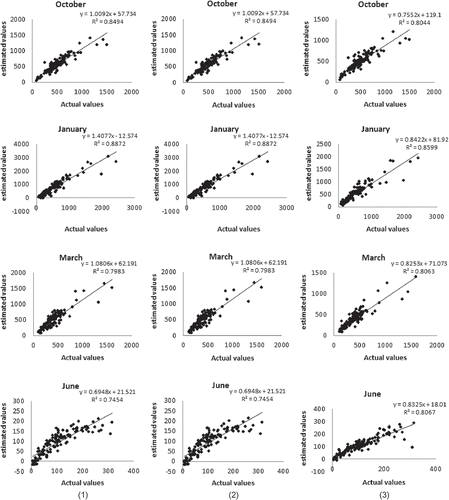
To assess the performance of each prediction method of the monthly average rainfall, cross-validation was used. This technique allows the comparison of the estimated and the true or actual values using the information available in our sample data set. The sample values are temporarily discarded from the sample data set; the value is then estimated using the remaining samples. The estimates are finally compared to the true values (Fig. 14). The KED and RK gave the same values of coefficient of determination between the actual and the estimated rainfall amounts (Fig. 15). For humid seasons (September–February), the largest coefficient of determination is given by KED and RK whereas for the less humid season (April and May), the CK method gave the largest coefficient of determination values. In terms of the RMSE (Fig. 16), CK provides the most accurate estimates for almost all months. The largest RMSE (and thus the most biased estimates) are for the winter (December and January).

Fig. 14 Correlation between actual values and estimated values obtained by cross-validation: (1) KED, (2) RK and (3) CK.

Fig. 15 Fluctuation of the coefficients of determination (actual values vs estimated values) by month and by prediction method.

Fig. 16 Cross-validation: root mean square errors varying with prediction method and with month.

6 CONCLUSION

The methodology consists of a sequence of steps which provide different information about the distribution of the considered variable. The major steps are the following: compiling a valid data base, monitoring network analysis, structural analysis including variography, interpolation using geostatistical predictors and cross-validation. The completion of these steps leads to decision-oriented maps as the final result and to relevant descriptive information provided at each step.

The coefficient of determination, r ², for elevation against precipitation for each month is low, with the largest values for the spring and the summer seasons. Therefore, the assumption of a general linear relationship between elevation and precipitation for these seasons is reasonable. However, KED and RK are informed by this relationship locally, so, the relationship between elevation and precipitation was examined locally. The coefficient of determination varies locally with seasons and regions. These results suggest that using elevation as a secondary variable in estimation will increase the accuracy of estimates in locations where r ² is large. In addition, cross-variograms show the control of elevation on the spatial distribution of rainfall for all seasons except the winter. The use of elevation as secondary information is therefore justified.

This paper indicates that, for most months, the use of elevation data to inform estimation of monthly precipitation in Tunisia is beneficial. Interpolations of an under-sampled target variable are improved by using an auxiliary variable in KED, RK and CK. Contour diagrams for KED and RK were similar and exhibited a pattern corresponding more closely to local topographic features, while CK showed a smooth zonal pattern. Smaller prediction variances are obtained for the RK algorithm.

Co-kriging provides more accurate estimates, judging by the cross-validation RMSE, than any other technique for almost all the months. We demonstrated that, using relatively simple procedures and widely available secondary data (elevation), it is possible to provide more accurate estimates of precipitation than is achievable using standard popular interpolation methods. The methods applied herein have the potential to be applied in a wide range of environments. We showed that, when elevation was used as a secondary variable, the accuracy of estimating precipitation was increased, depending on the interpolation technique.

Finally, the variograms estimated for residuals from the regressions have highly similar aspects to the general variograms. So, the variogram of residuals from the regression represents variation remaining even after the trend has been removed. This indicates that elevation is not the only factor influencing the rainfall distribution, and future work may research into the secondary information most indicative for the monthly average rainfall prediction.

Acknowledgements

We gratefully acknowledge the INM and the DGRE for providing rainfall data, and an anonymous reviewer for critical reviews of the manuscript.

APPENDIX A

Kriging with external drift (KED)

Kriging with external drift allows the prediction of a variable Z, known only at a small set of points of the study area, through another variable Y, exhaustively known in the same area. We chose to model Z with a random function Z(s) and Y as a deterministic variable Y(s) with s a particular point of a field S. The two quantities are assumed to be linearly related, i.e. it is assumed that the expected value of Z(s) is equal to Y(s) up to a constant a ₀ and a coefficient b ₁:

(A1)

We examine the case of a random function Z(s), whose prediction is to be improved by introducing the shape function Y(s) that provides detail at a smaller scale than the average sample spacing for Z(s). The estimator Z*(s ₀) at location s ₀ is a linear combination of the sample values Z(s_i ) at location s _i (i = 1, … , n):

(A2)

We look for an unbiased predictor, that is one with a prediction error that is expected to be zero, E[Z*(s₀) – Z(s₀)] = 0, so that:

(A3)

This equality can be developed into:

(A4)

This equation implies that the weights should be on average consistent with an exact interpolation of Y(s):

(A5)

The objective function (O) to minimize in this case consists of the prediction variance, σ _E ²(s ₀), and two constraints:

(A6)

where μ₁ and μ₂ are Lagrange parameters, and the prediction variance:

(A7)

with C the covariance function of Z.

The minimum of this quadratic function is found by setting the partial derivatives of the objective function O (λ _i ,μ₁,μ₂) to zero, leading to the system of equations:

(A8)

with the minimal prediction variance:

(A9)

The mixing of a second-order stationary random function with a nonstationary mean function may seem surprising. However, stationarity is a concept that depends on scale (Wackernagel 1994). Data can suggest stationarity for widely-spaced data on Z(s), while they look nonstationary when inspecting the fine detail provided by a function Y(s). Thus KED consists of incorporating into the kriging system supplementary universality conditions about one or several external drift variables Y_i (s) i = 1,  … , M measured exhaustively in the spatial domain. The functions Y_i (s) need to be known at all locations s_i of the samples Z(s_i ), as well as at the nodes of the estimation grid. In this method, we assume linear relationships between the variable of interest and the auxiliary variables at the observation points of the variable of interest. This assumption is very important in the prediction using KED method. Thus, if a nonlinear function better describes the relationships between the two variables, this function should first be used to transform the data of the auxiliary variable. The transformed data could then be used as external drift.

APPENDIX B

Regression kriging (RK)

In the case of RK, rainfall at a new, unvisited location (s ₀) is predicted by summing the predicted drift and residuals:

(B1)

where the drift m* is commonly fitted using linear regression analysis, and the residuals e* are interpolated using OK:

(B2)

with q ₀(s ₀) = 1; where β* _i are the estimated drift model coefficients, q_i (s ₀) is the ith external explanatory variable or predictor at location s ₀, p is the number of predictors, λj(s ₀) are weights determined by the covariance function, and e(s_j ) are the regression residuals. In matrix notation, the RK model is:

(B3)

where ϵ is the zero-mean regression residual. The predictions are made by:

(B4)

where q ₀ is vector of p + 1 predictors at s ₀, is vector of p + 1 estimated drift model coefficients, λ ₀ is vector of n kriging weights, and e is vector of n residuals. The drift model coefficients are preferably solved using the generalized least squares (GLS) (Hengl et al. 2007) estimation to account for spatial correlation of residuals.

(B5)

where q is the matrix of predictors at all observed locations (n × p + 1), Z is the vector of sampled observations and C is the n × n covariance matrix of residuals. The covariances between point pairs C(s_i ,s_j ), under stationarity assumptions also written as C(h), are typically estimated by modelling a variogram.

The estimation variance of RK is given by:

(B6)

where c ₀ is the vector of covariances between residuals at the unvisited and observation locations; and C ₀ and C ₁ are, respectively, the nugget effect and the sill of the variogram model.

APPENDIX C

Kriging and co-kriging

Let z ^α(s_i ) and z ^β(s_i ) represent realizations of random variables Z ^α(s_i ) and Z ^β(s_i ) at particular points s_i within a field S. It is obvious that the (co)kriging estimator is the best linear unbiased estimator, so:

The (co)kriging estimator Z*(s ₀) is a linear combination of the sample values Z ^α(s_i ) and Z ^β(s_i ):

(C1)

where Z _α*(s ₀) is the estimate of Z _α at point s₀, n _α and n _β are the number of data points of Z _α and Z _β used in estimation, and λ_αi and λ_βj are the associated weights. For ordinary kriging, Z _α(s_i ) represents the values of the monthly average rainfall at sample point s_i and the weights λ_βj are 0, since only monthly average rainfall contributes to the estimation process. For co-kriging, Z _α(s _i) and Z _β(s _j) represent the values of monthly average rainfall and elevation at sample points s _i and s _j, respectively.

the weights in equation (C1) are determined by minimizing the estimation variance:

(C2)

subject to the constraint that the estimate be unbiased:

(C3)

This yields the kriging system of equations:

(C4)

and the co-kriging system of equations:

(C5)

where γ_αβ is the semivariance of Z _α (when α = β) or cross-semi variance of Z _α and Z _β (when α ≠ β) at a separation distance h. The μ, μ_α, μ_β values are Lagrange multipliers.

When deriving the co-kriging system, there is an extra constraint of unbiasedness; therefore, the last equation in the system is required. Solving this system of equations for the weights λ and the Lagrange multipliers μ allows the calculation of the point value estimates Z _α*(s ₀) by equation (C1), and the estimation variance:

(C6)