Missing precipitation data estimation using optimal proximity metric-based imputation, nearest-neighbour classification and cluster-based interpolation methods

Abstract

New optimal proximity-based imputation, K-nearest neighbour (K-NN) classification and K-means clustering methods are proposed and developed for estimation of missing daily precipitation records. Mathematical programming formulations are developed to optimize the weighting, classification and clustering schemes used in these methods. Ten different binary and real-valued distance metrics are used as proximity measures. Two climatic regions, Kentucky and Florida, (temperate and tropical) in the USA, with different gauge density and network structure, are used as case studies to evaluate the new methods. A comprehensive exercise is undertaken to compare the performances of the new methods with those of several deterministic and stochastic spatial interpolation methods. The results from these comparisons indicate that the proposed methods performed better than existing methods. Use of optimal proximity metrics as weights, spatial clustering of observation sites and classification of precipitation data resulted in improvement of missing data estimates.

Editor D. Koutsoyiannis; Associate editor C. Onof

Résumé

Nouveau imputation basée sur la proximité optimale, voisin K plus proches (K-NN) de classification et K-means méthodes sont proposées et développées pour l’estimation de manquer des relevés quotidiens de précipitations. Les formulations de programmation mathématique sont mis au point pour optimiser les systèmes de pesage, de classification et de regroupement utilisées dans ces méthodes. Dix différentes métriques de distance binaires et valeurs réelles sont utilisés comme mesures de proximité. Deux régions climatiques, Kentucky et en Floride, (tempérées et tropicales) aux Etats-Unis, avec une structure différente de la densité de la jauge et du réseau, sont utilisés comme études de cas pour évaluer les nouvelles méthodes. Un exercice complet est effectué pour comparer les performances des nouvelles méthodes avec celles de plusieurs méthodes d’interpolation spatiale déterministes et stochastiques. Les résultats de ces comparaisons indiquent que les méthodes proposées de meilleurs résultats que les méthodes existantes. L’utilisation de mesures de proximité optimales comme poids, regroupement spatial des sites d’observation et la classification des données sur les précipitations a entraîné une amélioration des estimations de données manquantes.

Key words:

• missing precipitation records
• K-nearest neighbour imputation
• K-means clustering
• proximity metrics
• optimization
• deterministic and stochastic interpolation methods

Mots clefs:

• manquant records de précipitations
• K-plus proche voisin de l’imputation
• K-means
• mesures de proximité
• optimisation
• méthodes d’interpolation déterministes et stochastiques

INTRODUCTION

Spatial interpolation methods ranging from conceptually simple weighting techniques to methods using stochastic variance-dependent techniques are now available for estimation or imputation of missing precipitation data (Teegavarapu 2008). In this study, optimal proximity-based imputation using distance metrics derived from numerical taxonomy similarity concepts, nearest-neighbour classification and cluster-based methods are proposed and developed for estimation of missing precipitation data at a single raingauge. Weighting methods, inverse distance-based methods, nonlinear deterministic and stochastic variance-dependent interpolation methods (e.g. kriging) (Teegavarapu 2007, 2008) and regression and time series analysis methods (Tabios and Salas 1985) are among the most commonly used methods for estimating missing precipitation records. Variants of local regression models incorporating meteorological variables that change in the spatial domain (i.e. elevation) were proposed by Daly et al. (2002). The coefficient of correlation weighting method (CCWM) proposed by Teegavarapu and Chandramouli (2005) and adopted in a few recent studies (Westerberg et al. 2010) provides a method using gauge-to-gauge correlations. Optimization methods for objective selection of raingauges, optimal cluster identification and improvised traditional distance and quadrant-based methods were recently reported by Teegavarapu (2012). These methods provided improved estimates compared to those from several deterministic and stochastic interpolation methods. Grid-based transformation of precipitation estimates using geospatial interpolation methods were reported by Teegavarapu et al. (2012). The methods used grid structure, overlay of grids along with areal extents and nearest neighbours to transform multi-sensor precipitation estimates from one grid system to another.

Variants of the inverse distance weighting method (IDWM) or reciprocal distance weighting method have been provided by Teegavarapu and Chandramouli (2005) and Lu and Wong (2008). Teegavarapu (2009) used an association rule mining (ARM) approach to improve estimates of missing precipitation data. Trend surface analysis methods with polynomial equations of spatial coordinates are equally applicable for spatial interpolation of precipitation data. However, selection of the appropriate functional form to model the trend poses a major problem due to the large number of possible candidate functions. Xia et al. (2001) also reported the use of thin-plate-splines, closest-gauge and multiple linear regression techniques for estimation of daily climatological data. They indicated that the thin-splines method was the best among all the methods investigated. Variants of kriging have been used in the past to estimate missing precipitation data, as well as to interpolate precipitation from point measurements (Teegavarapu 2007). Comparative analysis of optimal spatial interpolation methods and multiple regression models was reported by Teegavarapu (2012). The study confirmed the one main disadvantage of multiple regression was negative estimates. Applications of artificial neural networks (ANNs) for estimation of missing precipitation data were documented by Teegavarapu and Chandramouli (2005) and Teegavarapu (2007). Recent work of Teegavarapu et al. (2009) has focused on the development of optimal functional forms using genetic algorithms and mathematical operators for estimating missing precipitation data. The functional forms provided better estimates compared to those by traditional geographical distance-based methods.

Limitations of spatial interpolation methods when used for estimation of missing data are documented by Teegavarapu (2008, 2009) and Teegavarapu et al. (2009). Reciprocal distances as weights in many interpolation methods may not serve as surrogate measures for spatial correlation. Numerical metrics strictly based on observations replacing Euclidean distances can be developed. If rainfall surface or field estimation is not of interest and only estimation of missing data at one single location in a region is essential, methods which rely directly on observed data are well suited for interpolation schemes. The new methods developed and investigated in this study are data-dependent and objective weighting schemes using proximity measures adopted from numerical taxonomy and conceptual ideas from K-nearest neighbour (K-NN) classification and clustering techniques. Utilization of proximity measures based only on data, classification of data into different classes and grouping of gauges to form clusters to estimate missing precipitation data was not attempted before in the literature. The contents of this paper are organized as follows. An introduction to distance metrics as proximity measures is provided first. The development of optimal K-NN classification and K-means clustering methods using nearest-neighbour techniques is discussed next. Then, applications of these methods for estimating missing precipitation data in two case study regions are presented. Finally, the results and analysis, general remarks and conclusions are presented.

PROXIMITY MEASURES FOR PRECIPITATION DATA

Proximity of two observation datasets based on real or categorical attribute values can be calculated using numerical proximity metrics. The metrics provide a measure of proximity between any two observed datasets and, in turn, can be used to assign weights in the interpolation schemes to estimate missing data. Distance metrics are calculated using pairs of observations at any two raingauges at a specific temporal scale. One of the raingauges always used in the calculations is referred to as a base raingauge, at which missing precipitation data are assumed to exist. These metrics are calculated based on historical precipitation data available at all gauges including the base raingauge. For all the metrics and formulations reported in this paper, the index n is used for time interval (i.e. day), n_s is the total number of raingauges including the gauge with missing data in a region and n_o is the total number of historical temporal observations common to any two raingauges. All the metrics are defined between any two raingauges (β,α) with observations referred to by variables θ_β,n and θ_α,n. Ling (2010) lists more than 30 distance measures that are available in the literature. However, for this study 10 commonly used real and binary distance measures are used. The Euclidean distance or L₂ norm is the simplest measure of distance between a pair of raingauge observations and is represented by equation (1). The squared Euclidean is a minor variant of the Euclidean distance and is the sum of the squares of the difference between the two raingauge observations, as given by equation (2). This metric magnifies distances between observations that are further apart.

(1)

(2)

The Manhattan distance (equation (3)) (Krause 1987), referred to as city block or taxicab distance, or L₁ norm, is less affected by outliers compared to Euclidean and squared Euclidean distances (Fielding 2007). The maximum distance metric is the maximum separation between two observations defined by their magnitudes. The absolute difference between two observations is determined and the largest difference, as defined by equation (4).

(3)

(4)

The Minkowski distance (Basilevski 1983) is a generalized measure given by equation (5). The value of λ defines a specific distance. When λ = 1, the measure is Manhattan and when λ = 2, the measure becomes Euclidean distance or L₂ norm. The Gower distance (Gower and Legendre 1986) is used for mixed variables (continuous and discrete) and is given by equation (6). The variable ω_n is the weight, which is equal to one when both observations in a given time interval, n, are available, and zero when one of them is not available. The variable τ_n is the maximum range value based on the observations.

(5)

(6)

(7)

The Cosine distance is based on a numerical measure that evaluates the similarity between two sets of observations. The distance is calculated by subtracting the similarity measure from unity and is provided by equation (8). The Canberra distance (Lance and William 1966) given by equation (9) defines the sum of the fractional differences for each variable.

(8)

(9)

The correlation distance (equation (10)) is conceptually based on similarity between observations defined by correlation coefficient or a measure of linear relationship between two datasets. The cosine distance calculated based on the transformed values of observations using z scores is the same as correlation distance. The Mahalanobis distance (Myatt and Johnson 2009) takes into account correlations within a dataset between the variables. The distance is scale independent and is calculated using equation (11). The calculated distance requires covariance ( and transformed matrices using the datasets. The variables and are vectors and not individual observations (i.e. single observation at each raingauge) and is the inverse of the covariance matrix of the data.

(10

(11)

BINARY DISTANCE MEASURES FOR PRECIPITATION DATA

Binary distance measures can be defined for observations that assume binary values (i.e. 0 and 1) and also for categorical variables when these variables can be expressed as binary variables. Similarity measures indicate how alike two observations are to each other. Lower magnitudes in the case of distance measures indicate that observations from the two series are alike. The precipitation data at any raingauge are converted into binary time series using the following expression:

(12)

The variable θ_j,n is the observed precipitation value at gauge j, in time interval n, and θ_th is the threshold value (lower limit) that helps in the assignment of binary values. The count (number) for these specific conditions is obtained from the historical data using observations at all the raingauges, including the gauge with the missing precipitation data. The countsrequired for distance metrics are calculated for each time interval, n, using conditions expressed by conditions (13)–(16). The variable θ^*_β,n is the transformed precipitation data at gauge β and θ^*_α,n is the similar transformed value at the base raingauge (i.e. the gauge with missing precipitation data referred with index m = α).

(13)

(14)

(15)

(16)

The aggregated values of these counts (,, and ) are calculated using equations (17)–(20) with all the available observations, n_o.

(17)

(18)

(19)

(20)

The values of counts given by equations (17)–(20) are used to define several different binary distance metrics. The simple matching metric calculates the similarity measure linked to the total number of times any two raingauges have conditions (17) and (18) satisfied. The distance is calculated by subtracting this similarity coefficient from the one in equation (21). The Jaccard (Jaccard 1908) distance is given by equation (22).

(21)

(22)

The Russell and Rao distance (Russell and Rao 1940) is based on a similarity coefficient that relates to the total number of times any two gauges have condition (17) satisfied compared to all conditions. The similarity coefficient is then transformed to a distance measure given by equation (23). The Dice distance (Dice 1945, Sorensen 1948) calculated by equation (24) gives more importance to common ones. This is a measure in which joint absences are excluded and matches are doubled (Fielding 2007).

(23)

(24)

The Rogers and Tanimoto distance (Rogers and Tanimoto 1960) (equation (25)) gives importance to common ones and zeros and was mainly developed for classifying plant species. The Pearson distance (Ellis et al. 1993), as defined by equation (26), was initially used to measure the degree of similarity between objects in text retrieval systems. The Yule distance (Yule 1912) given by equation (27) was developed as a method for identifying association between two attributes. The Sokal-Michener distance (Sokal and Michener 1958, Sneath and Sokal 1962) is one of the distance metrics used in numerical taxonomy for classifying organisms and building evolutionary trees, and is defined by equation (28).

(25)

(26)

(27)

(28)

Kulzinsky distance (Holliday et al. 2002) defined by equation (29) is used in ecology for finding similarity in sites with similar species and also in calculation of intermolecular similarity and dissimilarity. The Hamming distance (Hamming 1950) as given by equation (30) was originally developed to identify and correct errors in digital communication systems.

(29)

(30)

Optimal exponent weighting of proximity measures

The real and binary proximity measures discussed earlier are used to develop an optimal weighting method with the objective function and the constraints specified by equations (31), (32) and (33), respectively.

(31)

Subject to:

(32)

(33)

The formulation is solved using historical spatio-temporal precipitation data to minimize the objective function (equation (33)) and obtain optimal exponent value (k_e) using a nonlinear optimization solver.

OPTIMAL K-NEAREST NEIGHBOUR CLASSIFICATION METHOD

The optimal K-nearest neighbour (K-NN) classification method combines a classification and an optimal weighting scheme. The method classifies precipitation data into several groups to develop separate (i.e. local) optimization models. Arbitrary definitions of classes yielded inferior results in the previous study (Teegavarapu 2012). Initially, the K-NN method is used as a classifier to group spatial and temporal precipitation data into several pre-defined classes. These classes are set as the training dataset, which contains training tuples (Han and Kamber 2006), and the classification is achieved based on learning by analogy, by comparing a given test tuple with training tuples that are similar to it. When given an unknown tuple, a K-NN classifier searches the pattern space for the K training tuples that are closest to the unknown tuple. These K training tuples are the K-‘nearest neighbours’ of the unknown tuple (Fielding 2007). Closeness is defined in terms of any distance metric (e.g. Euclidean distance). The distance between two points or tuples, say, X = (θ_1,1, θ_1,2,… θ₁,_ns-1) and X_c=1 = () defined by equations (34) and (35) respectively is a function given by equation (36).

(34)

(35)

Here, X represents the n_o × n_s–1 matrix of observed precipitation values at n_s-1 gauges for n_o time intervals and X_c represents a c × n_s–1 matrix of pre-defined classes of precipitation data. The historical observations at n_s–1 gauges are evaluated for their proximity to each of the classes defined in X_c and each observation is designated to a specific class, c using a distance metric, D:

(36)

Once the precipitation data are designated to specific classes, then correlation between the observations in a specific class, c, and observations at gauge at which missing data exist are obtained. The variable n_c is the index for observation that belongs to class c and t_nc is the total number of observations that belongs to class c.

(37)

The correlation coefficients obtained from equation (37) are then used in a coefficient of correlation weighting method (CCWM) (Teegavarapu and Chandramouli 2005) for estimation of missing precipitation data at gauge, , as given by:

(38)

Alternatively, optimal weights for each class can be obtained by solving an optimization formulation given by the following objective function (equation (39)) and constraint (inequality (40)). The formulation is solved for each class, c.

(39)

where A is the n_c × j matrix of values, x is the matrix j × 1 of weight values and B is the matrix of n_c × 1 values of data at the base raingauge ( belonging to a specific cluster, c. The norm minimized is defined as the square of 2-norm, which equivalent to the sum of the squares of the differences between estimated values (Ax₎ and observed values (B).

Subject to:

(40)

The formulation minimizes the norm given by equation (39) with constraint on the weights () in inequality (40). This formulation provides non-negative optimal coefficients when solved. The missing precipitation data are then estimated by:

(41)

OPTIMAL K-MEANS CLUSTERING METHOD

Clustering of observations for analysis is common in spatial ecology (Fortin and Dale 2005), geosciences and data mining applications. In this study, clustering was used to create one ‘virtual’ gauge out of a number of gauges (i.e. cluster) where only one weight is attached to this gauge (i.e. group of gauges). Grouping (clustering) of gauges can be achieved by K-means clustering algorithms (Han and Kamber 2006) where proximity (distance-based) metrics are used to define the clusters and the members belonging to each cluster. In a previous study (Teegavarapu 2012), clustering was achieved by optimization using binary variable-mixed integer nonlinear programming (MINLP) formulation. The K-means clustering method is used in this study to identify spatial clusters of raingauges from the network of gauges in a region. Initially, the method is used to obtain a pre-specified number (i.e. K) of spatial clusters of precipitation gauges. The steps involved in the K-mean clustering method are:

1. initial spatial partitioning of precipitation gauges into K random clusters;

2. re-partitioning of the gauges by assigning each gauge to the nearest centre of cluster by using a proximity measure (e.g. a distance metric); and

3. re-calculation of the cluster centres as centroids.

Steps (b) and (c) are repeated until a stopping criterion of no change in centroid positions is reached. Once the clusters are identified, weights are assigned to them for interpolation based on two procedures discussed in the next section.

Optimal weights for selected clusters

The K-means clustering method is used to identify possible spatial clusters of raingauges and weights are assigned to these clusters using an optimization formulation. Non-negative constraint requirements to obtain positive weights are enforced using the nonlinear least square constraint formulation defined by:

(42)

Subject to:

(43)

E is the n_o × c_l matrix of values, x is the matrix c_l × 1 of weight values and F is the matrix of n_o × 1 values of data at base raingauge θ_α,n. The formulation minimizes the norm given by equation (42) with constraint on the weights (inequality (43)). This formulation provides non-negative optimal coefficients when solved. The variable is the number of gauges in a cluster c_l. The variable is based on observations at all gauges (, or one gauge in a cluster c_l, as defined by equation (44) or (45), respectively:

(44)

In equation (44), is equated to the sum of all the observations from all the gauges in a cluster c_l for time interval n, while in equation (45), is equated to observations ( at gauge, z, belonging to a specific cluster of gauges having maximum correlation with the gauge with missing data:

(45)

Using the weights obtained by solution of the optimization formulation given by equations (42)–(43), the estimation of missing precipitation data is given by equation (46), with the value of obtained by either equation (44) or (45). The variable N_cl is the number of clusters.

(46)

CASE STUDY APPLICATION AND EVALUATION OF METHODS

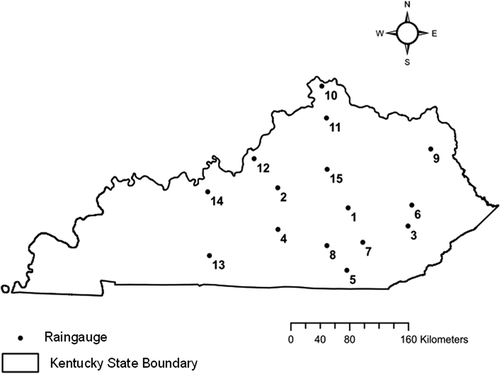
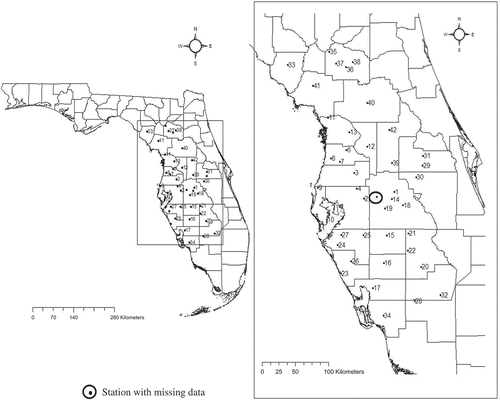
The imputation methods developed herein this study were used for estimating missing daily precipitation data at two selected gauges in two case study regions, Kentucky and Florida, referred hereafter to as Region I and Region II, respectively. Region I has a temperate climatic zone in which the storm events are mainly due to frontal precipitation, whereas Region II is predominantly tropical with convective type rainfall events. Region II has three times more raingauges than Region I and this benefits spatial interpolation. Considering the high spatial variability of precipitation in Region II in the wet season, the proximity of several gauges to the base raingauge is also crucial for accurate interpolation of precipitation data. For Region I, the methods were used to estimate missing rainfall data at gauge 15 (shown in Fig. 1). Historical daily precipitation data from the period 1971–2001 available at 15 raingauges in the state of Kentucky, USA, were used for analysis. This dataset was further filtered to obtain a time-consistent observation set of a total of 10 645 days. The locations of the gauges are shown in Fig. 1; they are numbered for convenience. The data used in this study were compiled and provided by Kentucky Agricultural Weather Center, University of Kentucky. A total of 7756 days of precipitation data (73% of data) were used to develop the methods and 2889 days (27% of data) of data were used for testing the methods. For Region II, located in southwest Florida, daily historical data from the period 1994–1999 available from 43 rainfall gauges were used. A filtered and time-consistent dataset of 2129 days was used, with data assumed to be missing at gauge 3 (shown in Fig. 2) for testing the methods.

Fig. 1 Location of raingauges in the state of Kentucky, USA (Region I).

Fig. 2 Location of raingauges and the gauge with missing data in the state of Florida, USA (Region II).

The training and testing datasets used for this region are 1419 (67% of data) and 710 days (33% of the data), respectively. The methods were applied to the test data and the performances compared using error measures such as root mean squared error (RMSE), absolute error (AE), mean absolute error (MAE) and a goodness-of-fit measure criterion, the correlation coefficient (ρ), based on actual and estimated rainfall values at the base raingauges. The Nelder-Mead Simplex method (Lagarias et al. 1998)  was used for all formulations that involve estimation of optimal exponent values. The performances of several deterministic and stochastic spatial interpolation methods were also used to compare with those of new methods developed herein. These methods include: gauge mean estimator (GME); normal ratio; inverse distance and exponential weighting; trend surface models with linear, quadratic and cubic functions; thin-plate spines; and ordinary kriging with spherical, circular and Gaussian semivariogram models. The GME, trend surface and thin-plate spline methods do not require any parameters to be estimated from historical data.

Error and performance measures were used to evaluate intuitive reasonableness of method, conceptual accuracy, simplicity of the method and objective assessment, and, finally, selection of the methods. When multiple performance measures are used in the selection of any method from a set of equally competitive methods, identification of that best method is often difficult. Linear or nonlinear weighting functions can be developed to transform the performance measures (i.e. RMSE, AE, MAE, ρ) into an accumulated dimensionless total performance measure. This total measure was used for objective comparison and selection of the best method from a set of competing methods. In this study all the performance measures were added to transform them to a score (or weight) between zero and one. The total weighted performance measure (W_total) is given by equation (51).

(47)

(48)

(49)

(50)

(51)

The variables Ω_ρ, Ω_AE, Ω_RMSE and Ω_MAE, and ρ′, AE′, RMSE′ and MAE′, are the weighting factors, and the maximum values of corresponding performance measures based on all the methods, respectively. Equations (47)–(50) define weighting functions for W_ρ (correlation coefficient), W_AE (absolute error), W_RMSE (root mean squared error) and W_MAE (mean absolute error) respectively. These functions resemble fuzzy membership functions (Teegavarapu and Elshorbagy 2005), and they transform performance measures to unitless values. The method with lowest value of overall performance measure (W_total) is the best among all the competing methods.

RESULTS AND ANALYSIS

The results from proximity-based metrics, K-NN classification and clustering are first discussed and then the results from traditional deterministic and stochastic methods along with their variants are presented and analysed. The distance metrics were obtained using historical data for both regions I and II. It is evident from the case study descriptions that the number of years of data available for Region II is much smaller than that for Region I. A threshold value (θ_th) of zero was used for binary distance measures for both the regions. Table 1 provides the performance measures for real-valued distance metrics for Region I with optimal exponents. In general, for all proximity-based methods, optimal exponents provided better performance measures compared to non-optimized versions. Therefore, the results related to performance measures from non-optimized methods are not provided. Higher variability in the performance measures is noted for optimized distance metrics compared to non-optimized metrics. The variability may be associated with non-global solutions from optimization formulations. The best two methods based on total weights before and after optimization are Minkowski and Correlation, and Cosine and Canberra, respectively. The performance measures for binary distance measures are provided in Table 2 for Region I. The two best methods with and without optimization are Kulzinksky and Jaccard, respectively. The Cosine, Kulzinsky, Jaccard and Yule distance-based methods were ranked as the top four among all the real-valued and binary distance-based methods for Region I. Tables 3 and 4 provide the performance measures for real-valued and binary distance metrics, respectively, for Region II. Higher variability in the performance measures is also noticed for optimized distance metrics compared to non-optimized distance metrics. The two best methods before and after optimization are Manhattan and Euclidean, and Cosine and squared Euclidean, respectively. The average performance values for binary distance measures were better than the real-valued distance metrics. The two best methods are Pearson and Yule, respectively. The methods Manhattan, Euclidean, Canberra and Cosine are ranked high among all the real-valued and binary metrics for Region II. Optimization of exponents attached to reciprocal distances provided substantial improvement in the performance measures for real-valued and binary distance metrics.

Table 1 Performance measures based on different real-valued distance metrics used in optimal proximity-based imputation for Region I.

Proximity measure	AE (mm)	MAE (mm)	RMSE (mm)	ρ
Euclidean	6859	2.373	5.335	0.735
Squared Euclidean	6867	2.377	5.318	0.736
Manhattan	6859	2.374	5.334	0.735
Maximum	7348	2.543	5.439	0.716
Minkowski	7226	2.501	5.342	0.722
Gower	7017	2.428	5.336	0.731
Cosine	6914	2.239	5.250	0.741
Canberra	6899	2.388	5.265	0.739
Correlation	6926	2.397	5.361	0.734
Mahalanobis	7684	2.659	5.715	0.684

Note RMSE: root mean squared error, AE: absolute error, MAE: mean absolute error, ρ: correlation coefficient.

Table 2 Performance measures based on different binary proximity measures used in optimal proximity-based imputation for Region I.

Proximity measure	AE (mm)	MAE (mm)	RMSE (mm)	ρ
Simple matching	6835	2.366	5.330	0.735
Jaccard	7661	2.652	5.618	0.693
Russell and Rao	6836	2.366	5.264	0.738
Dice	6798	2.353	5.296	0.736
Rogers and Tanimoto	6840	2.368	5.333	0.734
Pearson	6825	2.362	5.323	0.731
Yule	6826	2.363	5.237	0.742
Sokal-Mischener	6841	2.367	5.243	0.741
Kulzinksky	6776	2.341	5.279	0.738
Hamming	7573	2.621	5.570	0.700

Table 3 Performance measures based on different real-valued distance metrics used in optimal proximity-based imputation for Region II.

Proximity measure	AE (mm)	MAE (mm)	RMSE (mm)	ρ
Euclidean	2223	3.131	6.841	0.704
Squared Euclidean	2261	3.183	6.994	0.685
Manhattan	2272	3.200	6.722	0.714
Maximum	2420	3.408	7.203	0.660
Minkowski	2427	3.418	7.413	0.639
Gower	2446	3.445	6.947	0.692
Cosine	2252	3.176	6.945	0.690
Canberra	2258	3.181	6.831	0.702
Correlation	2256	3.177	7.022	0.684
Mahalanobis	2693	3.793	7.607	0.611

Table 4 Performance measures based on different binary distance metrics used in optimal proximity-based imputation for Region II.

Proximity measure	AE (mm)	MAE (mm)	RMSE (mm)	ρ
Simple matching	2334	3.286	7.171	0.667
Jaccard	2595	3.655	7.163	0.666
Russell and Rao	2356	3.318	6.888	0.696
Dice	2327	3.277	7.143	0.669
Rogers and Tanimoto	2448	3.442	6.967	0.688
Pearson	2423	3.419	6.925	0.693
Yule	2450	3.451	6.961	0.689
Sokal-Mischener	2245	3.162	6.804	0.705
Kulzinksky	2311	3.256	7.183	0.666
Hamming	2592	3.651	7.171	0.665

The threshold value (θ_th) has a significant influence on the performance of binary proximity measures in imputation of missing precipitation data. A binary distance metric defined by Sokal-Michener that performed well in both regions I and II was used to evaluate the changes in performance measures based on different threshold values. It is evident from the results provided in Table 5 that an increase in the threshold value resulted in deterioration of performance measures. Similar results were obtained for Region II also. Any increase in threshold value increases the number of observations equated to zero after binary transformation and therefore will affect the outcome of the conditions given by equations (17)–(20) and counts required for calculation of distance metrics. The length of the historical spatio-temporal precipitation data has influence on the performance of real and binary distance metrics. As the length of the data increases, the amount of information available to obtain accurate proximity measures increases thus improving the estimates. The methods are not constrained by a specific minimum data length. However, the larger the dataset the better are the proximity metrics in characterizing the inter-gauge data relationships.

Table 5 Performance measures based on different threshold values of precipitation for binary distance metric-based imputation for Region I.

Threshold value, θth (mm)	AE (mm)	MAE (mm)	RMSE (mm)	ρ
13	6878	2.381	5.220	0.743
26	6923	2.396	5.238	0.740
39	7054	2.441	5.309	0.733
52	7204	2.516	5.444	0.715
65	7417	2.566	5.508	0.709
78	7950	2.736	5.781	0.671

The K-NN classification method was used to group the available precipitation data into several pre-specified classes using maximum and minimum possible values of data. The maximum value of all observations from all gauges, except for the base raingauge, is 204 mm for Region I and 189 mm for Region II. Four classes were evaluated for regions I and II, and the classification is based on historical precipitation data (i.e. training dataset) at gauges and pre-defined classes using Euclidean distance. Once the precipitation data have been grouped into classes, coefficient of correlation weighting (Teegavarapu and Chandramouli 2005) and optimization methods are used to obtain weights for gauges for each class. The weights are then used for estimation of missing precipitation data at the base raingauge using pre-defined classes for test dataset. The results related to correlation and optimal weighting schemes for Region I are given in Table 6 and those from the application of similar schemes for Region II are given in Table 7. In general, the performance improved when the number of classes was increased for both regions I and II. The optimal weighting scheme provided better results compared to correlation weighting in both the regions. For Region I, the best performance was obtained based on the total weighted score (equation (51)), when 10 and three classes are used for correlation and optimization-based methods, respectively. For Region II, the best performance was achieved when 14 and three classes are used for correlation and optimization-based methods, respectively. In both the regions, the optimal K-NN classification with three classes provided the best performance measures. It is important to note that definition of too many classes may result in failure of any observations being assigned to a specific class. This poses difficulty in estimation of correlations and also weights.

Table 6 Performance measures based on different classes used in correlation and optimization-based K-NN classification imputation for Region I.

Number of classes	AE (mm)	MAE (mm)	RMSE (mm)	ρ
Correlation-based
14	7039	2.436	5.247	0.741
10	6945	2.404	5.300	0.736
7	7248	2.501	5.327	0.729
3	7445	2.577	5.501	0.709
Optimization-based
14	6871	2.388	5.221	0.744
10	6811	2.357	5.186	0.747
7	6787	2.349	5.184	0.747
3	6697	2.319	5.128	0.748

Table 7 Performance measures based on different classes used in correlation and optimization-based K-NN classification imputation for Region II.

Number of classes	AE (mm)	MAE (mm)	RMSE (mm)	ρ
Correlation-based
14	2449	3.449	6.895	0.697
10	2539	3.577	7.204	0.660
7	2534	3.569	7.147	0.667
3	2550	3.593	7.142	0.671
Optimization-based
14	2474	3.484	7.041	0.696
10	2557	3.604	7.608	0.628
7	2448	3.449	7.450	0.658
3	2306	3.248	6.812	0.708

The application of the K-means clustering approach required spatial partitioning of raingauges into a number of clusters using Euclidean distance as the distance metric. Different cluster sizes were experimented in this study. Two approaches described earlier indicated the use of one gauge (i.e. the gauge with maximum correlation with base gauge) in each cluster or the weighted sum of observations from all the gauges in each cluster. The results related to application of this method to regions I and II are provided in Table 8. The number of clusters used and the gauges selected in each cluster are also presented in this table. In both the regions, based on limited experiments conducted, a total of six clusters resulted in the best performance measures. The method using weighted summation of observations from clusters provided better performance measures compared to that in which the highest correlated gauge with the base gauge in each cluster is selected.

Table 8 Performance measures based on different distance metrics used in optimal K-means cluster imputation for regions I and II.

Number of clusters	Selected raingauges in cluster	AE (mm)	MAE (mm)	RMSE (mm)	ρ
Region I
2	2,4,5,8,12,13,14	6968	2.412	5.741	0.687
	1,3,6,7,9,10,11
4	1,5,7,8	6867	2.377	5.391	0.725
	2,4,12,13,14
	10,11
	3,6,9
6	3,6	6778	2.346	5.301	0.734
	1,7,8
	4,5,13
	10,11
	2,12,14
	9
Region II
2	1,2,4,5,10,14–30,32,34	2484	3.498	7.664	0.637
	3,6,7,8,9,11–13,31,33,35–42
4	15–17,20–28,32,34	2356	3.312	7.043	0.686
	1,14,18,19,29–31,39,42
	2–10,12,13
	11,33,35–38,40,41
6	6,11,12,13,40,42	2348	3.307	7.034	0.694
	10,15,23–27
	1,14,18,19,29–31,39
	33,35–38,41
	16,17,20–22,28,32,34
	2–9

The results from imputation methods using different stochastic and deterministic interpolation methods are provided in Table 9. The performance measures for gauge mean estimator (GME) using all the raingauges are substantially inferior to those when nearest neighbours are selected using the Euclidean distance criterion. Even though the performance measures improved when compared to those from the methods using all the gauges, the method provides a substantial number of under-estimations. In the case of Region II, the GME method provided the best results when eight nearest neighbours were used. The clustering of raingauges around the gauge assumed to be having missing data is higher in Region II compared to that in Region I. The best results for the normal ratio method for Region I were obtained when nine nearest neighbours based on the Euclidean distance criterion were selected. In the case of Region II, for the same method, the best performance measures were obtained when three nearest neighbours were selected based on distance. The inverse exponential method provided the best performance when nine nearest neighbours (selected by defining a pre-specified radius) were used. The trend surface and thin-spline models provided better results in Region II compared to Region I, as high gauge density provided help in generating rainfall surfaces that are representative of spatial variations of precipitation in that region. Local versions of the trend surface models were also investigated. However, these versions did not provide better results than global versions. Among the trend surface models, the global linear and cubic trend surface models provided the best performances for region I and region II, respectively. Ordinary kriging methods were developed using procedures outlined by Teegavarapu (2007) for the selection of variogram parameters (nugget and sill values) for three semi-variogram models. The effect of anisotropy on variogram parameters was neglected. The Gaussian semi-variogram model provided the best performance for Region I and the spherical semi-variogram for Region II. The best three methods among all the deterministic and stochastic methods evaluated for Region II are normal ratio (distance-based), ordinary kriging using circular semi-variogram and thin-plate splines.

Table 9 Performance measures based on different methods for regions I and II.

Method	AE (mm)	MAE (mm)	RMSE (mm)	ρ
Region I
Gauge mean estimator (distance)	7444	2.576	5.583	0.699
Normal ratio (distance)	7286	2.522	5.522	0.705
Inverse exponential (radius limited)	7758	2.685	5.737	0.679
Inverse distance	7879	2.727	5.778	0.673
Trend surface model (global, linear)	7691	2.662	5.604	0.694
Trend surface model (global, quadratic)	9410	3.257	6.894	0.584
Trend surface model (global, cubic)	9619	3.326	7.024	0.587
Thin plate spline	8581	2.971	6.541	0.609
Ordinary kriging (spherical)	8373	2.898	6.286	0.630
Ordinary kriging (Gaussian)	8086	2.799	5.935	0.656
Ordinary kriging (exponential)	8166	2.827	6.061	0.651
Region II
Gauge mean estimator (distance)	2344	3.320	6.943	0.689
Normal ratio (distance)	2378	3.351	6.956	0.689
Inverse exponential (radius limited)	2285	3.218	6.937	0.690
Inverse distance	2308	3.251	6.863	0.698
Trend surface model (global, linear)	2610	3.673	7.201	0.662
Trend surface model (global, quadratic)	2490	3.508	7.157	0.667
Trend surface model (global, cubic)	2468	3.476	7.190	0.662
Thin-plate spline	2336	3.291	7.057	0.689
Ordinary kriging (spherical)	2281	3.213	6.961	0.691
Ordinary kriging (Gaussian)	3024	4.261	8.340	0.632
Ordinary kriging (exponential)	2652	3.735	7.696	0.632

The methods developed in this study were evaluated and ranked based on total performance measure (equation (51)) with all weighting factors equal to one. The highest ranked 25 methods for regions I and II are provided in Table 10. The top 10 ranked models in Region I included several proximity metric-based optimal weighting methods and variants of optimal K-NN classification methods. In Region II, with its dense raingauge network, the ranking of models is different from that of Region I. In Region II, a conceptually simple interpolation method (i.e. inverse distance) and ordinary kriging method are also among the top 10 methods along with several proximity metric-based optimal weighting methods.

Table 10 Ranking of different imputation methods and their variants for regions I and II.

Rank	Method
	Region I		Region II
1	K-NN classification (optimization, 3 classes)		Euclidean
2	Cosine		Manhattan
3	K-NN classification (optimization, 7 classes)		Sokal-Mischener
4	K-NN classification (optimization, 10 classes)		Canberra
5	Kulzinksky		Cosine
6	Yule		K-NN classification (optimization, 3 classes)
7	Sokal-Mischener		Squared Euclidean
8	K-means cluster (optimization, 6 clusters)		Correlation
9	K-NN classification (optimization, 14 classes)		Inverse distance
10	Dice		Ordinary kriging (spherical)
11	Russell and Rao		Inverse exponential (radius limited)
12	Canberra		Russell and Rao
13	Simple matching		Gauge mean estimator (distance)
14	Pearson		K-means cluster (optimization, 6 clusters)
15	Rogers and Tanimoto		Thin-plate spline
16	Squared Euclidean		K-means cluster (optimization, 4 clusters)
17	Euclidean		Normal ratio(distance)
18	Manhattan		Kulzinksky
19	K-NN classification (correlation, 10 classes)		Dice
20	Correlation		Simple matching
21	K-NN classification (correlation, 10 classes)		Pearson
22	K-means cluster (optimization, 4 clusters)		K-NN classification (optimization, 14 classes)
23	Gower		Gower
24	K-NN classification (correlation, 7 classes)		Rogers and Tanimoto
25	Minkowski		Yule

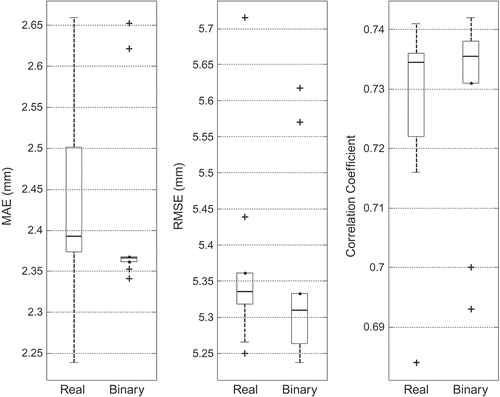
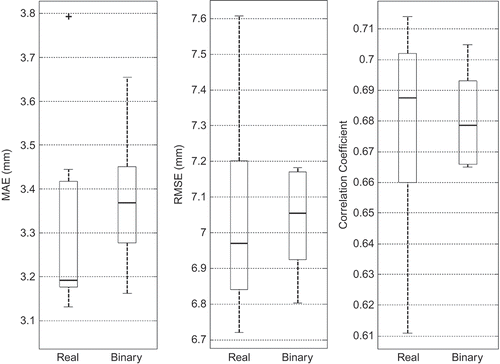
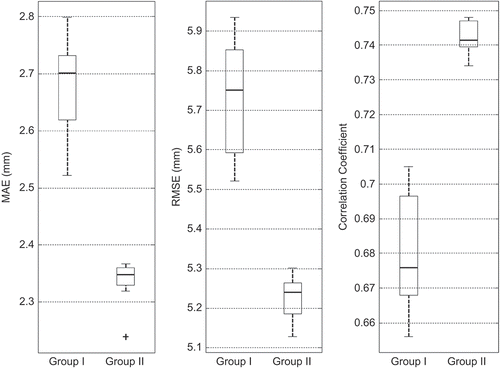
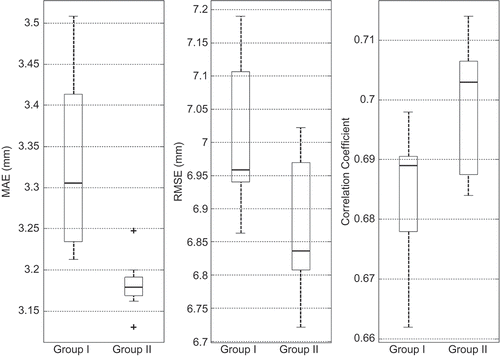
The variability of performance measures from real and binary metric-based methods are compared for regions I and II in Figs 3 and 4 respectively. Binary metrics provided better performance measures compared to those from real metrics for Region I and vice versa for Region II. The top eight imputation methods from: (a) the deterministic and stochastic interpolation methods and (b) the optimal proximity-based and K-NN classification and K-means clustering methods developed in this study were used to form two separate groups: Group 1 and Group II, respectively for comparison purposes. The average values of performance measures for Group II are better than those for Group I for both regions I and II. The deviations in performance measures among proximity-based methods within Group II are smaller compared to those from the methods in Group I. This result is no surprise, as all the methods that use distance-based metrics in Group II are conceptually similar. Variations in performance measures for group I and II methods for regions I and II are shown in Figs 5 and 6, respectively. The median values of RMSE and MAE are lower for Group II than for Group I in both the regions. Similarly, the median values of correlation coefficients are higher for Group II compared to Group I in both the regions.

Fig. 3 Variability of performance measures for real and binary metric-based methods for Region I.

Fig. 4 Variability of performance measures for real and binary metric-based methods for Region II.

Fig. 5 Variability of performance measures for two groups for Region I.

Fig. 6 Variability of performance measures for two groups for Region II.

Region II has a large number of raingauges with a higher density compared to Region I. Also, Region I has approximately five times more historical precipitation data compared to Region II. The test dataset for Region II is four times smaller than that of Region I. The influence of data length on binary-valued distance metrics is higher compared to real-valued metrics. An experiment was conducted in which the available historical data length for development of distance metrics in Region I was reduced to 1489 days (the same number of days in the test dataset used for Region I). The performance measures obtained for optimal Sokal-Michener metric (Table 2) based on this dataset were inferior when compared to those from the complete dataset used for the same metric. This result confirms the strong influence of data length on distance metrics and thereby the estimates. Cross-validation of five methods for three base raingauges was carried out for three raingauges in regions I and II. Two real-valued and binary distance-based methods were also evaluated. The results related to these cross-validation exercises are provided in Tables 11 and 12 for regions I and II, respectively. The results suggest that the binary and real-valued proximity-based weighting methods developed in this study provide better performance measures compared to those from several traditional interpolation methods.

Table 11 Performance measures based on application of different methods to different base raingauges in Region I.

Raingauge	Method	AE (mm)	ρ	RMSE (mm)	MAE (mm)
2	Inverse distance	7222.15	0.738	5.771	2.499
	GME	7707.45	0.729	5.835	2.667
	Thin-plate spline	8194.24	0.671	6.548	2.836
	Ordinary kriging (spherical)	7778.02	0.696	6.216	2.692
	Cosine	6880.90	0.757	5.527	2.381
	Kulzinsky	7084.50	0.746	5.641	2.452
4	Inverse distance	7460.21	0.730	5.803	2.582
	GME	8009.70	0.703	6.059	2.773
	Thin-plate spline	8354.66	0.675	6.557	2.891
	Ordinary kriging (spherical)	7550.97	0.715	5.982	2.614
	Cosine	7084.00	0.744	5.673	2.452
	Kulzinsky	7047.40	0.732	5.810	2.439
12	Inverse distance	8878.34	0.629	6.773	3.073
	GME	9656.15	0.581	7.062	3.343
	Thin-plate spline	10284.60	0.574	7.959	3.559
	Ordinary kriging (spherical)	8647.96	0.642	6.906	2.993
	Cosine	7237.90	0.735	5.875	2.505
	Kulzinsky	7088.70	0.727	5.954	2.453

Table 12 Performance measures based on application of different methods to different base raingauges in Region II.

Raingauge	Method	AE (mm)	ρ	RMSE (mm)	MAE (mm)
40	Inverse distance	2706.45	0.701	9.025	3.811
	GME	3026.16	0.619	9.705	4.262
	Thin-plate spline	3335.39	0.557	10.314	4.697
	Ordinary kriging (spherical)	2613.79	0.699	8.852	3.681
	Euclidean	2581.90	0.697	8.866	3.636
	Sokal-Michener	2739.60	0.630	9.628	3.858
22	Inverse distance	2278.54	0.601	6.813	3.209
	GME	2552.88	0.508	7.468	3.595
	Thin-plate spline	2469.73	0.601	7.215	3.478
	Ordinary kriging (spherical)	2345.54	0.609	6.978	3.303
	Euclidean	2219.70	0.623	6.746	3.125
	Sokal-Michener	2276.50	0.620	6.867	3.207
7	Inverse distance	2780.68	0.561	8.205	3.916
	GME	2876.86	0.591	7.825	4.052
	Thin-plate spline	2932.51	0.497	8.975	4.130
	Ordinary kriging (spherical)	2848.78	0.501	8.779	4.012
	Euclidean	2558.10	0.601	7.938	3.603
	Sokal-Michener	2500.02	0.570	8.713	3.521

The proximity measures based on distance metrics are sensitive to the length of the historical data and the threshold value used for the calculation of binary metrics. A threshold value of zero that defines rain or no rain conditions is ideal. The estimation of missing precipitation data from real-valued and binary distance metrics can be improved using data that is representative of specific storm types or a season. The proximity-based methods always provide non-negative precipitation estimates unlike several other methods such as multiple linear regression, artificial neural networks, ordinary kriging, and trend surface and thin-plate splines. The methods developed in this study are specific to a site with missing data. The parameters (weights and exponents), and number of gauges used in interpolation will be different if another site with missing data is filled. The ability of methods to preserve site and regional data statistics (Teegavarapu 2012, 2013) was not evaluated in this study. However, the methods were evaluated for precipitation estimation in temperate and tropical climate zones, and the applicability of these methods to other climatic zones needs to be thoroughly assessed.

CONCLUSIONS

New spatial interpolation methods are proposed and developed using optimal proximity-based weighting methods, K-nearest neighbour classification and K-means-clustering approaches for estimating missing precipitation records. In this study, 10 real-valued and binary distance metric-based imputation methods were evaluated and also compared with several deterministic and stochastic spatial interpolation methods. The proposed methods were evaluated for estimation of missing precipitation data at multiple raingauges in temperate and tropical climate zones. The optimal nearest neighbour classification and clustering methods provided mechanisms to identify groups of spatial precipitation data in time and space, and virtual gauges respectively that led to improved local models as opposed to global models which do not consider classification of data or clustering of observation sites. Several proximity metric-based imputation, K-NN classification and K-means clustering methods were ranked among the top 10 methods investigated for two climatic regions in this study. The new methods and optimization formulations developed in this study are objective, data-driven and generic, and they can be easily applied for estimating missing precipitation at a site in any other region.

Acknowledgements

The author thanks the Kentucky Agricultural Weather Center, University of Kentucky, USA, for providing the data required for the research study reported herein. The author sincerely thanks the anonymous reviewers and associate editor for their feedback, objective and constructive criticism that led to substantial improvement of the manuscript.