The scientific legacy of Harold Edwin Hurst (1880–1978)

ABSTRACT

Emanating from his remarkable characterization of long-term variability in geophysical records in the early 1950s, Hurst’s scientific legacy to hydrology and other disciplines is explored. A statistical explanation of the so-called “Hurst Phenomenon” did not emerge until 1968 when Mandelbrot and co-authors proposed fractional Gaussian noise based on the hypothesis of infinite memory. A vibrant hydrological literature ensued where alternative modelling representations were explored and debated, e.g. ARMA models, the Broken Line model, shifting mean models with no memory, FARIMA models, and Hurst-Kolmogorov dynamics, acknowledging a link with the work of Kolmogorov in 1940. The diffusion of Hurst’s work beyond hydrology is summarized by discipline and citations, showing that he arguably has the largest scientific footprint of any hydrologist in the last century. Its particular relevance to the modelling of long-term climatic variability in the era of climate change is discussed. Links to various long-term modes of variability in the climate system, driven by fluctuations in sea surface temperatures and ocean dynamics, are explored. Several issues related to the Hurst Phenomenon in hydrology remain as a challenge for future research.

Editor M. Acreman; Associate editor A. Carsteanu

KEYWORDS:

• Hurst
• Hurst phenomenon
• long-term persistence
• fractional Gaussian noise
• Hurst-Kolmogorov dynamics
• climatic variability

1 Introduction

In 1951, Harold Edwin Hurst published a paper in the Transactions of the American Society of Civil Engineers (Hurst 1951) that was to become one of the most influential and highly cited papers in the field of scientific hydrology; this was supplemented by two more (but less widely cited) papers: one in the Proceedings of the British Institution of Civil Engineers (Hurst 1956), and one in Nature (Hurst 1957). His unique characterization of long-term variability in Nile flow records and other geophysical time series, based on remarkable scientific insight, and years of painstaking data analysis in pre-computer days (Sutcliffe et al. 2015), revealed that hydrological and other geophysical time series exhibited statistical behaviour that could not be reconciled with the then prevailing theory (Hurst 1951). This finding, which came to be known as the Hurst Phenomenon, intrigued hydrologists and statisticians alike, and a mathematical/statistical framework that could explain it was not to emerge until some 15 years later, even though Kolmogorov (1940) had laid down its mathematical foundation, which however was totally unknown to Hurst and to the hydrological and statistical communities.

Hurst’s methodology and finding have not only continued to inspire further research by hydrologists worldwide up to the present day, but have influenced developments in many other fields of science, notably climate science, and have been cited in papers on such disparate subjects as the analysis of internet traffic and the flow of blood in human arteries. This extensive dissemination is characterized here by the knowledge tree in Figure 1, where the “branches” correspond to the broad fields of science for which Hurst’s work and references thereto have been cited; the “trunk” of the tree represents the central role that hydrology occupies in this dissemination process. It is a further mark of distinction that the large-scale “export” from hydrology to other fields represented in Figure 1 has characterized Hurst’s research, as hydrology is so often an importer of statistical/stochastic methods from other fields.

Figure 1. The proliferation of Hurst’s work in different scientific fields.

Here, we chronicle the research that has evolved from Hurst’s remarkable finding, dealing firstly with the early search for a statistical explanation of the Hurst Phenomenon in the period from 1951 up to 1968, when Mandelbrot and Van Ness (1968) unveiled fractional Brownian motion and demonstrated that its increments, fractional Gaussian noise (fGn), had the necessary attributes to account for the Hurst Phenomenon (Mandelbrot and Wallis 1968) (Section 2). An upsurge in research followed in which the statistical properties of fGn were explored further, and where alternative hypotheses and models were proposed and explored. New insights and advances have resulted from more recent research into the properties of Hurst-Kolmogorov dynamics (Section 3). Physical mechanisms that could give rise to the Hurst Phenomenon are explored in Section 4, with the climate system being the main physical context. Hurst’s legacy to other scientific disciplines is summarized in Section 5, while the case for basing climate risk assessments on the stochastic modelling tools spawned by Hurst’s original finding is articulated in Section 6. Some conclusions are added in Section 7, followed by a tribute and epilogue.

2 The early era of the Hurst Phenomenon

2.1 Hurst’s Law and the Hurst Phenomenon

Hurst’s extensive studies of long-term fluctuations in the annual flows of the River Nile and various climatic and geophysical records have been reviewed in detail in a companion paper by Sutcliffe et al. (2015). For some 900 annual time series comprising streamflow and precipitation records, stream and lake levels, Hurst established the following relationship, referred to as Hurst’s Law:

(1)

where is referred to as the adjusted range of cumulative departures of a time series of n values (Table 1), is the standard deviation, / is referred to as the rescaled range of cumulative departures, and H is a parameter, henceforth referred to as the Hurst coefficient (the use of H to represent the Hurst coefficient has become standard practice in the literature, although Hurst himself never used H). Hurst’s interest in estimating long-term reservoir storage on the River Nile led to his focus on the range as a statistic that could provide the basis of a measure of long-term variability in geophysical time series.

Table 1. Definitions of Population Range and Adjusted Range.

Denote a series of n random variables as , , …, with sample mean and with E.

Population Range of cumulative departures:

= max – min

Adjusted Range of cumulative departures:

= max – min

To estimate the coefficient H in Equation (1), Hurst used the following relationship:

(2)

where K denotes the resulting estimate of the (population) coefficient H, whereupon,

(3)

This estimate is the slope of a line in log-space with a fixed intercept of −K log 2; the choice of (n/2) in Equation (3) is discussed below. The estimates ranged from 0.46 to 0.96 with a mean of 0.729 and a standard deviation of 0.092 for record lengths ranging from 30 to 2000 years.

Hurst (1951) employed some simple coin-tossing experiments to derive the expected value of for a normal independent process as:

(4)

Independently, Feller (1951) used the theory of Brownian motion to derive Equation (4), which is an asymptotic result, but without the assumption of normality. The form of Equation (3), which was used by Hurst to estimate H, was apparently suggested by Equation (4) wherein the term (n/2) appears. Lloyd (1967) subsequently coined the term “Hurst Phenomenon” to describe the discrepancy between Hurst’s average value of 0.73 for H and the theoretical value of 0.5 deduced from classical statistical theory.

2.2 Early attempts to explain the Hurst Phenomenon

The discrepancy between Hurst’s extraordinarily well-documented finding from data analysis and his and Feller’s theoretical result puzzled many statisticians and engineers alike at the time, and a number of possible explanations were suggested. Hurst (1951) himself conjectured that non-randomness/long-term persistence, as evidenced by the tendency in geophysical time series for high values to follow high values and low values to follow low values, might be a possible explanation. In a notable contribution, Langbein and Hurst (1956), in a discussion of Hurst’s (1956) paper, reinforced Hurst’s work with the observation that the variance of the sample mean for Hurst’s data was larger than if the data were independent random, and could be approximated by the relationship:

(5)

where is the standard deviation of subsample means. This implied:

(6)

Note that the mean value of the exponent K, 0.729, derived by Hurst (1951), and Langbein’s estimate of H = 0.72, derived from Equations (5) and (6), are slightly inconsistent; this is probably due to the different estimation procedures they used. Langbein also deduced that skewness was an unlikely explanation, as was autocorrelation of a Markovian nature. He suggested that the persistence in Hurst’s data was of a more complex nature.

Feller (1951) suggested that the discrepancy might be accounted for by autocorrelation of a Markovian nature, but Barnard (1956) disputed this suggestion, commenting that no simple set of correlations could account for Hurst’s result. In a further notable contribution, Hurst (1957) reported on some card sampling experiments in which he generated time series of varying lengths, the longest of which contained 4000 values and had a mean value of H = 0.72. Hurst’s sampling procedure was subsequently interpreted by Klemeš (1974) as a form of “shifting mean” model in which the mean of the process was sampled randomly for random periods in which values were sampled independently.

Theoretical studies of the different definitions of the range (Table 1) were pursued by a number of statisticians. Anis and Lloyd (1953) derived the expected value of (the superscript p denotes population, as the definition of implies knowledge of the population mean) for finite n and independent variates with a common distribution, while Solari and Anis (1957) derived the same result for for a normal independent process. However, H = 0.5 was inherent in all of these analyses. This continued to challenge statisticians such as Moran (1959), who wrote reinforcing Barnard’s earlier (1956) contention:

… the exponent 0.73 could not occur unless the serial dependence was of a very peculiar kind because with all of the plausible models of serial dependence, the series of partial sums is approximated by a Bachelier-Wiener process when the time scale or economic horizon is sufficiently large.

However, Moran (1964), working with the population range , deduced that, for moderate n, Hurst’s result could after all be explained by skewness, and used highly skewed distributions with large but finite second moments about the mean (such as a truncated Cauchy distribution) to justify his argument. He did, however, note that such distributions were unlikely to provide a good fit to Hurst’s data, and his inferences did not extend to the rescaled range that was the basis for Hurst’s finding.

In a lucid summary of the work that had been carried out up to that time, Lloyd (1967) commented as follows:

We are then in one of those situations, so salutary for theoreticians, in which empirical discoveries stubbornly refuse to accord with theory. All of the researches described above lead to the conclusion that in the long run, should increase like , whereas Hurst’s extraordinarily well documented empirical law shows an increase like where K is about 0.7. We are forced to the conclusion that either the theorists interpretation of their own work is inadequate or their theories are falsely based: possibly both conclusions apply.

Leading stochastic hydrologists of the era fared no better than the theoreticians in explaining the Hurst Phenomenon. Monte Carlo (MC) simulation studies of the behaviour of R_n/S_n were carried out by Matalas and Huzzen (1967) for a lag-one autoregressive (Markov) process. While extended transients in R_n/S_n could be obtained as the lag-one autocorrelation coefficient increased, the simulated values were locally unrealistically smooth for annual streamflow, reflecting large lag-one autocorrelation coefficients, and they concluded that their results did not offer a satisfactory explanation. Fiering (1967) came to a similar conclusion based on simulation experiments with higher-order autoregressive models.

2.3 Fractional Brownian motion and fractional Gaussian noise

The foundations for an explanation of the Hurst Phenomenon were laid by Mandelbrot (1965), and the theoretical framework was developed fully by Mandelbrot and Van Ness (1968), who acknowledged that Kolmogorov (1940) had earlier introduced a mathematical process with such behaviour. By analogy with Brownian motion, they defined fractional Brownian motion (fBm) as a process in which past, independent increments of Brownian motion from time -∞ to t are weighted by time lag raised to the power , where H is the Hurst exponent satisfying is a continuous time stochastic process with self-similar increments such that, if the time scale is changed in the ratio T, where the functions and are governed by the same probability law (Mandelbrot and Wallis 1968). It follows from this property that

(7)

where is a constant.

A further consequence of self-similarity is that the population range and adjusted range of the continuous function obey Hurst’s law asymptotically:

(8)

(9)

where and are constants.

The increments:

(10a)

(10b)

with the kernel function described by:

(11a)

(11b)

were defined by Mandelbrot and Wallis (1969a) as discrete-time fractional Gaussian noise. With the assumption that Equation (9) holds for the discrete case, and that implies then the increments of fBm provide the necessary basis for modelling Hurst’s Law. The process is stationary for , and self-similar such that:

(12)

which means that {} and {} have the same joint distribution functions apart from the scaling constant . Noting that the concept of self-similarity had originated in the theory of turbulence, Mandelbrot and Wallis (1968) observed that it had become useful in studying a range of phenomena (Mandelbrot 1963, 1966, 1967), and suggested that self-similar models might supersede the current models, which could not account for the Hurst Phenomenon.

The autocovariance function of is (Mandelbrot and Wallis 1968):

(13)

which, for a large lag k, can be approximated as:

(14)

where is the variance of The summation of does not converge, whereas the corresponding summation for all autoregressive and autoregressive moving average models based on the increments of Brownian motion (i.e. white Gaussian noise) is finite. This has been interpreted as reflecting “infinite memory”, which is in line with the definition of fBm as a weighted integral of past increments of Brownian motion from to t, with distant past events having a small but significant influence on current behaviour. Long-term memory gives rise to long-term persistence (LTP), but LTP can also arise from models with no memory that are based on equation (13) (Sections 3.3 and 3.5). A consequence of the power-law form of is that realizations of fGn will exhibit a wealth of random low-frequency swings and cycles, similar to the behaviour observed by Hurst in the long-term records that he analysed. This is also reflected in the spectrum, which has the form:

(15)

where and .

From Equation (7), the variance of the partial sums of discrete time fGn:

(16)

is

(17)

whence,

(18)

or

(19)

This relationship, as noted above, was derived by Langbein (1956) from Hurst’s data, and referred to as Langbein’s corollary of Hurst’s law by Mandelbrot and Wallis (1968).

2.4 Fractional Gaussian noise approximations

Computer-based discrete-time approximations of fGN require (a) the integral in Equation (10) to be replaced by a weighted sum of a discrete-time white-noise process , and (b) the interval to be replaced by a finite span where M is a large enough constant. Mandelbrot and Wallis (1969a) proposed two approximations, which they labelled Type 1 and Type 2. The Type 2 approximation is written as:

(20)

which is a moving average of M Gaussian independent random increments. The Type 1 approximation employed a finer integration grid and was therefore more accurate but more computationally intensive.

Mandelbrot and Wallis (1969a, b, c) carried out a series of computer experiments in which they demonstrated that their fGn approximations obeyed Hurst’s Law (1) with the slope of a trend line on a log-log plot of against for selected in the range (referred to as a “pox diagram”) shown to correspond to the value of H used in the fGn generator. Moreover, they generated highly skewed fGn series and showed that the slopes of trend lines remained unchanged relative to the Gaussian case, demonstrating the importance of standardization by in making Hurst’s Law robust to skewness, and demonstrating that earlier attempts to explain the Hurst Phenomenon in terms of skewness, and based only on , had been fallacious (Mandelbrot and Wallis 1969d). This finding was later reinforced by O’Connell (1976). Moreover, they showed that the presence of a periodic component, such as the annual cycle in sub-annual time series, distorted the against plot, and inhibited the reliable estimation of H. They also reaffirmed Hurst’s law for long geophysical records, which extended to thousands of years in the case of tree ring data (Mandelbrot and Wallis 1969e).

3 From fractional Brownian motion to Hurst-Kolmogorov dynamics

Fractional Gaussian noise (fGn) and its associated power-law covariance function provided a new framework for stochastic hydrology, which led to an upsurge in research into different ways of approximating fGn and a renewed search for alternative, and possibly simpler statistical explanations, of the Hurst Phenomenon. But all of these endeavours were constrained by the need for (a) a stationary model and (b) one that could approximate Hurst’s Law at least for long transients and, by implication, a power law or hyperbolic covariance function.

3.1 Various methods of generating fGn

In response to criticisms of the initial Type 1 and Type 2 fGn approximations, Mandelbrot (1971) developed a “fast” fractional noise generator for 0.5 < H < 1. He approximated the covariance function of fGn using a summation of suitably weighted and independent Gauss-Markov processes, with the weights and parameters being a function of H. He incorporated a high-frequency Gauss-Markov process that would allow the fitting of the high-frequency characteristics of an observed series as well as the Hurst coefficient.

Recognizing that the initial Type 2 approximation yielded values of the lag-one autocorrelation coefficient that were too high to approximate that of fGn as well as observed annual streamflow, Matalas and Wallis (1971) developed a filtered fGn approximation by sampling every pth value (i.e. at times p, p > 1). As p increases, the lag-one autocorrelation decreases, thus giving a better fGn approximation and the flexibility to fit an estimated for an observed series. Matalas and Wallis (1971) also developed a multi-site extension of the single-site filtered fGn model.

Rodriguez-Iturbe et al. (1972) and Mejia et al. (1972) proposed the Broken Line (BL) model as a summation of simple BL processes, and showed how it could serve as an approximation to fGn. By focusing on a link between the second derivative of the autocorrelation function of the BL process at lag zero and its crossing properties, they suggested an alternative approach to estimating the long-run properties of geophysical time series. They suggested that generated synthetic time series should preserve a “memory” of a historic time series, and demonstrated a procedure for doing this using the BL model (Garcia et al. 1972).

Hipel and McLeod (1978a) proposed an exact method of generating an fGn sample of specified length n based on generating multivariate fGn random variables having an (n × n) correlation matrix with elements , the autocorrelation function of fGn based on Equation (13). They used a standard Cholesky decomposition of the correlation matrix to provide the coefficients needed to generate fGn. Here, the span of dependence is n, so it needs to be suitably large to reproduce the Hurst Phenomenon over a long time span.

3.2 ARMA models

The book by Box and Jenkins (1970) stimulated widespread interest in the use of autoregressive moving average (ARMA) models to represent hydrological time series. Heretofore, only autoregressive models had been used, and ARMA models offered additional flexibility. O’Connell (1971, 1974a) showed that a simple ARMA(1,1) model:

(21)

with autocorrelation function:

(22a)

(22b)

could provide an alternative representation of the Hurst Phenomenon in comparison to fGn. For values of close to the stationarity boundary of +1, long transients showing good agreement with Hurst’s Law were obtained (up to n = 10 000), with slopes varying as a function of the parameters, while the parameter could be used to control the value of . The ARMA(1,1) model represents a simple approximation to fGn that reproduces the main scales of fluctuation underlying Hurst’s Law, although asymptotically, H = 0.5, as is the case for all fGn approximations. However, formal fGn approximations have the advantage that H can be prescribed a priori as a model parameter, whereas, for the ARMA (1,1) model, it has to be estimated a posteriori from simulation experiments.

O’Connell (1974b, 1977) investigated the properties of the moment and maximum likelihood (ML) fitting procedures presented in Box and Jenkins (B&J) (1970) using extensive MC simulation experiments, and found the resulting estimates to be biased and highly variable for the parameter ranges explored by O’Connell (1971, 1974a) and for the sample sizes typically available for annual streamflow. As moment fitting used low lag correlations, and as the likelihood function was based on one-step-ahead innovations, B&J fitting procedures were designed primarily for short-term forecasting rather than long-term prediction. Moreover, the information content of small samples is low in the presence of LTP. In an effort to overcome these problems, O’Connell (1974b, 1977) used MC simulation to derive tables relating the ARMA(1,1) model parameters to estimated mean values of K (the estimate of the Hurst coefficient given by Equation (2)) and of , for sample sizes of 25, 50 and 100. For a practical application, values of and would then be chosen based on matching the observed K and estimates with their respective mean values in the tables, interpolating where necessary. However, sampling variability can mean that getting a unique match may not be easy.

Wallis and O’Connell (1973) explored the question of whether hydrological records were long enough to identify, with any degree of confidence, an appropriate model for use in MC simulation studies of firm reservoir yield. They used MC simulation to show that statistical tests based on and lacked power in distinguishing between different generating models, particularly when LTP was present.

Hipel and McLeod (1978b) fitted ARMA models to 23 annual geophysical time series, ranging in length from n = 96 to 1164 years using their improved methods of model identification, parameter estimation and diagnostic checking (Hipel et al. 1977). Using MC simulation and a goodness of fit test, they showed that the fitted models preserved the historic series estimates of K and , and argued that an fGn model was not needed in these cases. The series they used were generally much longer than those typically available in hydrology, thus avoiding the small-sample estimation problems discussed above.

3.3 Shifting mean models

In a penetrating discourse on the Hurst Phenomenon, Klemeš (1974) argued that the concept of infinite memory invoked by fGn was not physically realistic, and posed the question of what memory length might be plausible for hydrological systems. He first formulated a shifting mean model based on Gaussian independent synthetic series, whose mean value was allowed to assume two different values, alternating regularly after constant intervals of different lengths called epochs; this is very similar to the playing card experiment performed by Hurst (1957) and to one subsequently developed by Potter (1975). He then proceeded to show that, by choosing a suitable distribution for epoch lengths, and sampling the fluctuations in the mean from a Gaussian distribution with different standard deviations, he was able to reproduce agreement with Hurst’s Law, with slopes varying as a function of the model parameters. Although he referred to nonstationarity in the mean throughout the paper, he deduced that his model was stationary, as he stated that although “it was nonstationary by definition, can well be considered stationary in the sense that its probability laws do not change through time”. He also showed that transients with Hurst exponents greater than 0.5 could be produced through repeated cycling of white noise through a semi-infinite storage reservoir. He left open the question of what physical mechanisms in nature might account for the Hurst Phenomenon.

Boes and Salas (1978) derived the theoretical properties of a class of stationary shifting mean models, and showed that one member of the class had an autocorrelation function identical to that of the ARMA (1,1) model; they derived the relations between the parameters of the two models. Although a shifting mean model has no memory, its autocorrelation function reflects the apparent dependence introduced through fluctuations in the mean that alternate, producing pseudo-trends. Therefore, an autocorrelation function with a long tail does not necessarily imply long-term memory; it can arise from a stationary stochastic process with no memory. Based on some simulation experiments with ARMA (1,1) and shifting mean models, Salas et al. (1979) suggested the Hurst Phenomenon might be interpreted as a pre-asymptotic behaviour, since long transients could be simulated. In addition, Ballerini and Boes (1985) showed that certain shifting mean processes have autocorrelation structures exhibiting long-term dependence, giving rise to Hurst behaviour.

Bhattacharya et al. (1983) have shown that the Hurst Phenomenon can arise when a deterministic trend is incorporated into a short-memory stochastic process. However, this is a nonstationary process with a mean that grows indefinitely, and for which there may be no physical justification.

3.4 FARIMA models

Hosking (1981) and, independently, Granger (1980) and Granger and Joyeaux (1980), introduced fractionally differenced autoregressive integrated moving average FARIMA (p,d,q) models with an asymptotic covariance function:

(23)

where d is a fractional differencing parameter satisfying, and p and q are the orders of the autoregressive and moving average components. By comparing the exponents in Equations (14) and (23), The FARIMA (0,d,0) process is written as:

(24)

where B is the backward difference operator. This leads to an AR process of infinite order:

(25)

where

(26)

which offers a very convenient method of generating fractional noise with a finite upper limit in (25); a moving average representation can also be used. Hosking (1981) then generalized the FARIMA (0,d,0) model to the FARIMA (p,d,q) case. Once the parameter d has been estimated (e.g. through one of the methods used to estimate H), the well-developed ARMA estimation methodology can then be applied to the fractionally differenced series = to estimate the autoregressive and moving average parameters. This flexible approach has the advantage that it can be used to estimate explicitly both the short-term and long-term properties of a time series, whereas ARMA models can only do this implicitly, and asymptotically have H = 0.5 (Hosking 1984). An application of the FARIMA approach has been described by Montanari et al. (1997).

Granger (1980) showed that a process defined as the aggregation of a number of lag-one Markov processes with parameters sampled from a Beta distribution has the covariance function (13); this aggregation process is analogous to Mandelbrot’s (1971) fast fractional Gaussian noise generator.

3.5 Hurst-Kolmogorov dynamics

This alternative title to fractional Gaussian noise is justified to give prominence to the work of Hurst, and to that of Kolmogorov (1940) who, as already mentioned, first proposed the mathematical form of the process. It signifies further developments related to the Hurst Phenomenon that appeared more recently, in the 21st century. In a series of papers, Koutsoyiannis (2002, 2003, 2006a, 2006b, 2011) and Koutsoyiannis and Montanari (2007) have brought a fresh perspective to the Hurst Phenomenon and scaling behaviour, with a particular focus on interpreting and modelling “change”. Koutsoyiannis (2002) demystified the previous complex mathematics behind fGn by presenting its essential properties in a few equations. Firstly, he derived the variance and autocorrelation of a stochastic process on multiple temporal scales. In particular, he showed that if a Markov (AR(1)) process is aggregated to higher time scales, it has precisely the same form of autocorrelation function as an ARMA(1,1) process, while as the time scale increases, this ARMA(1,1) process becomes indistinguishable from white noise. Moreover, he showed that if fGN is aggregated to a level j, i.e. j values are summed to give the aggregated process, the autocorrelation function is independent of j, and is identical to Equation (13) when standardized by the variance. This derives from the self-similarity of fGn. He advocated the use of Equation (18) as a more reliable estimator of H than one based on the rescaled range, which is essentially the approach employed by Langbein (1956) on Hurst’s data. He then suggested that the modelling of a climate that “changes irregularly, for unknown reasons, on all timescales” (National Research Council 1991), should be undertaken using a process with multiple scales of fluctuation and no memory, and showed that such a shifting mean process can be used to approximate fGn. He then presented three algorithms for generating approximations to fGn based on (a) a multiple time-scale fluctuation approach; (b) a disaggregation approach; and (c) a symmetric moving average approach.

Koutsoyiannis (2003) focused on the problem of modelling a highly variable climate with indistinguishable contributions from natural climatic variability and greenhouse gas emissions, and advocated a stochastic modelling approach that respects the Hurst Phenomenon. Noting that classical statistics are deficient when used to characterize a highly variable climate, he developed a method of jointly estimating the unknown variance and Hurst coefficient of a time series. Starting from the relationship (18), the estimation of σ and H is based on the following relationships:

(27)

where j is the time scale (ranging from 1 to a maximum value [n/10], with n being the sample size), and represents a correction to achieve an approximately unbiased estimator of the standard deviation . A possible approach to estimating H is to use a regression of ln s^(j) on ln j to begin with, and then to use the correction iteratively until convergence is achieved. Koutsoyiannis (2003) advocated a more systematic approach involving the minimization of an error function:

(28)

where the weight 1/j^p, p = 1, 2, … allows decreasing weights to be assigned to increasing scales where the sample size is smaller. He demonstrated that, for synthetic data generated with H = 0.8, the new method gave estimates of the variance and H that were unbiased and with smaller sampling variances than conventional estimators (e.g. Equation (2)). He applied the method to three hydrometeorological time series with lengths ranging from 91 to 992 years, and showed that they were consistent with the assumed scaling hypothesis for the variance, and Hurst’s Law. Moreover, he demonstrated how appropriate hypothesis testing (e.g. testing for a trend) should be undertaken when the underlying process exhibits scaling behaviour.

In a further paper, Koutsoyiannis (2006a) argues that long-term trends in hydrological time series should not be regarded as deterministic components of a hydrological times series, and therefore indicating nonstationarity, unless there is a clear physical explanation. Otherwise, such trends are best regarded as parts of irregular long-term fluctuations that underlie the Hurst Phenomenon, and stationary stochastic models obeying Hurst’s Law offer the best means of quantifying the large hydrological uncertainty for water resources planning under a highly variable climate.

To gain insight into how the scaling behaviour synonymous with the Hurst Phenomenon might be generated, Koutsoyiannis (2006b) constructed a toy model that gives traces that can resemble historical climatic time series. The model is based on a simple dynamical system representation with feedbacks, as feedbacks are known to exist in the climate system (Rial et al., 2004); however, the model feedbacks have no physical basis, and simply act upon the previous value of the process through a transformation to generate the next value. The model is deterministic and has few parameters, and no inputs or random components; given suitable values of its parameters and initial conditions, it can mimic the time evolution of historical climatic series, and their scaling behaviour. However, it is shown to have no predictive power (except for short lead times), because the dynamics, despite being simple, is chaotic, a property also found in the climate (Rial et al. 2004).

Koutsoyiannis and Montanari (2007) discuss various approaches to detecting the presence and intensity of LTP in hydroclimatic time series, which they distinguish from self-similar scaling which is a model property, and advocate the use of the climacogram (standard deviation as a function of time scale) over other methods, i.e. based on Equation (18) applied at different time scales. Moreover, they derive measures of the information content for a simple scaling stochastic process (essentially fGn) with parameter H as:

(29)

where n^′ is the equivalent or effective sample size in the classical IID sense. Based on this result, and a sample of 1979 values for the longest temperature record for which they estimated H, the effective sample is 3 based on Equation (29). This startling result is a reminder that, in an LTP world, the typical lengths of flow record available are inadequate for such applications as reservoir yield estimation (Wallis and O’Connell 1973). Koutsoyiannis and Montanari (2007) also discuss hypothesis testing for LTP associated with natural climatic variability and anthropogenic climate change, and demonstrate, for the series that they analysed, the difficulty of detecting and attributing “change”. They cite the case where Rybski et al. (2006) and Cohn and Lins (2005) focused on the detection and attribution of climate change, but arrived at essentially opposite conclusions concerning the relative roles of natural dynamics and anthropogenic effects in explaining recent warming. They conclude that the available statistical methodologies are not wholly fit for purpose; indeed, Cohn and Lins (2005) suggest: “From a practical standpoint … it may be preferable to acknowledge that the concept of statistical significance is meaningless when discussing poorly understood systems.”

Koutsoyiannis (2011) focused initially on the use and misuse of the terms “climate change” and “nonstationarity”, and argued that the former is redundant and non-scientific, since the climate has always undergone change, while the latter, and the alternative, and infinitely more tractable, concept of stationarity, is frequently misunderstood. He used realizations from a stationary shifting mean model to make the point that, while an individual realization may appear nonstationary, the underlying stochastic process is stationary, and there is no justification for invoking nonstationarity unless there is a clear association with a deterministic forcing function. He used a case study of the water supply system for Athens to demonstrate how the uncertainty over future water availability was quantified using Hurst-Kolmogorov (HK) dynamics, in the absence of credible predictions from general circulation models (GCMs). Interestingly, Sveinsson et al. (2003) have also shown that shifting mean models can be used to model climatic indices describing atmospheric circulation (e.g. the Pacific Decadal Oscillation). In the event that credible predictions of future changes (e.g. associated with known features such as El Niño or greenhouse gas emissions) are available, then they can be incorporated into the HK approach.

Lins and Cohn (2011) express similar sentiments over stationarity and nonstationarity, but point out that, if we do not understand the long-term characteristics of hydroclimatic processes, finding a prudent course of action in water management is difficult. They discuss three aspects of this problem: HK dynamics, the complications that LTP introduces with respect to statistical understanding, and the dependence of statistical trend-testing on arbitrary sampling choices. In these circumstances, they suggest that, since we are ignorant about some aspects of the future, a prudent approach may be to proceed under well-established principles of risk aversion and adaptation, and in the absence of a viable alternative, to keep stationarity alive, rather than consider it “dead” (Milly et al. 2008). This is advocated by a couple of more recent studies by Koutsoyiannis and Montanari (2015) and Montanari and Koutsoyiannis (2014); notably, the latter study claims that “stationarity is immortal”.

4 In search of a physical explanation for the Hurst Phenomenon in hydroclimatic time series

In seeking a physical explanation of the Hurst Phenomenon, it is necessary to draw a distinction between mathematical/statistical constructs that can reproduce the required behaviour in the rescaled range and the climacogram (variance at aggregate time scales), and an understanding of the physical mechanisms giving rise to the long-term fluctuations/long-term persistence in hydroclimatic time series. Klemeš (1974) clearly recognized the distinction between inferring a physical explanation from the structure of a stochastic model and seeking to understand the causal physical mechanisms that could give rise to the Hurst Phenomenon when he wrote in his conclusions:

It also is only natural and perfectly in order for the mathematician to concentrate on the formal geometric structure of a hydrologic series, to treat it as a series of numbers and view it in the context of a set of mathematically consistent assumptions unbiased by the peculiarities of physical causation. It is, however, disturbing if the hydrologist adopts the mathematician’s attitude and fails to see that his mission is to view the series in its physical context, to seek explanations of its peculiarities in the underlying physical mechanism rather than to postulate the physical mechanism from a mathematical description of these peculiarities.

Here, we review the various explanations/mechanisms that have been proposed from the two standpoints in Klemeš’ quote. We confine ourselves to the hydrological context only, as each field in which the Hurst Phenomenon has been observed has its own specific context and possible explanations that are a function of that context.

4.1 Inferring explanatory mechanisms from data and stochastic models

The fGn model was the first stochastic model proposed in the hydrological literature that could reproduce the Hurst Phenomenon. Its kernel function (11) implies an infinite memory which, as already noted, was challenged by Klemeš (1974) as physically unreasonable. As already discussed, long transients can be generated by finite-memory ARMA models (e.g. O’Connell 1971, 1974a) and shifting mean models (e.g. Sveinsson et al. 2003) before convergence to H = 0.5. However, no convergence towards H = 0.5 has been reported in the hydroclimatic literature. Markonis and Koutsoyiannis (2013) have demonstrated that the Earth’s temperature is consistent with Hurst behaviour (with H > 0.90) throughout the entire time window on which the available reconstructions provide information i.e. up to 500 million years. Therefore, more and more variability emerges as the time window/time scale for data analysis increases. To model this multi-scale variability, one can either use a memory-based approach (e.g. the fast fGn generator (Mandelbrot 1971), or a FARIMA model (Hosking 1981), or a shifting mean model with no memory (Koutsoyiannis 2002). These represent opposite ends of the spectrum in terms of what might be plausible in physical terms, but both can arguably do the same job in terms of encapsulating the uncertainty implied by the Hurst Phenomenon when it comes to assessing the reliability of water resource systems.

It is not possible to infer which of these two assumptions (or interpretations) might be most plausible, based on the available data; however, it is important to recognise that long-term memory cannot be inferred from long-term autocorrelation, or Hurst behaviour in the rescaled range/aggregated variance; the latter can arise from a shifting mean process that has no memory. Long-term autocorrelation/Hurst behaviour can only be interpreted as evidence of increasing variability with time scale; the existence of memory in hydroclimatic systems, or not, is an open issue which we discuss in Section 4.2 below. The superposition of processes representing different time scales of variability is a common feature of fGn and shifting mean models; in the case of the fast fGn model (Mandelbrot 1971), lag-one Markov processes with different lag-one correlations/memories, and shifting means on different time scales in a process with no memory (Koutsoyiannis 2002). They can be thought of as representing a hierarchy of variable regimes.

It can be argued that the existence of various storages (soil moisture/groundwater/lakes) in river basins must lead to some memory in streamflow, which might be expected to grow with increasing basin scale. While a simple storage mechanism cannot give rise to the Hurst Phenomenon, the combination of several storage mechanisms operating at different time scales may indeed induce the presence of LTP. In this respect, it is important to point out that a Markovian process may induce pre-asymptotic behaviour that may erroneously be interpreted as LTP, when dealing with time series that cover the typical observation period of hydrological records. Therefore, the presence of important storages in large basins may indeed be related to the estimation of H values that exceed 0.5 (Montanari 2003, Mudelsee 2007).

An overarching characteristic of Hurst behaviour is the magnification of uncertainty. It is now generally recognized that the quantified measure of uncertainty is entropy, as defined by Boltzmann and Gibbs and later generalized and formalized in probabilistic terms by Shannon. Given the general tendency of entropy to reach a maximum value in irreversible systems, could the principle of maximum entropy provide an explanation for the Hurst Phenomenon? Koutsoyiannis (2011, 2014) studied this question in relation to statistical thermodynamics. He was able to reproduce Hurst behaviour by maximizing entropy production, defined to be the time derivative of entropy, at asymptotic times (tending to infinity). Interestingly, he showed that the Hurst coefficient is precisely equal to the entropy production in logarithmic time, which, for a stochastic process with Hurst behaviour, is constant at all time scales.

4.2 Possible physical causal mechanisms within the climate system

The long-term behaviour of the hydrological cycle, and its driving forces within, and exterior to, the climate system provide the context for exploring possible physical causal mechanisms of the Hurst Phenomenon within the climate system. Apparently, the climate system is a hugely complex spatially and temporally variable system that is not yet fully understood. While the main focus of the climate science community has been on trying to improve the representation of climate processes within GCMs, a number of climate scientists have, since the 1970s, been exploring long-term variability in the climate system, and possible causal mechanisms; their methods of data analysis have been strongly influenced by the work of Hurst.

The concept of long-term memory in the climate system is now well established in the climate science literature, and has been deduced from a combination of data analysis and simple modelling of the climate system’s energy balance. In the 1970s, a Brownian motion analogue was advanced for stochastic climate fluctuations (Hasselman 1976), implying H = 1. Around the same time, flicker noise (spectrum) and other power-law scaling regimes and explanatory modelling based on the climate system’s energy balance emerged (e.g. Voss and Clark, 1976, Van Vliet et al. 1980). Fraedrich (2002) carried out detrended fluctuation analysis (DFA) of high resolution near surface air and deep soil temperatures for Potsdam station (1893–2001) and found a DFA exponent of α = 0.7 over a time span from less than 1 month to about 10 000 days (or 30 years). Under the assumption that the underlying process is fGn, then α = H. Similar results were obtained from the analysis of troposphere temperatures simulated by a 1000 year GCM simulation. He then investigated a relatively simple conceptual model of the climate system’s energy balance based on (i) a Fickian diffusion plus white noise parameterization of meridional heat fluxes in the troposphere and (ii) Newtonian cooling of the near-surface soil towards the equilibrium deep-soil temperature. Analysis of the temporal fluctuations of the model’s temperature anomalies showed a long-term memory regime characterized by over a similar time span to the observed and GCM datasets, which was regarded as sufficiently close agreement, considering their standard deviations. Beyond this time span, the long-term memory regime subsides into a regime with , when low frequencies exceed the damping time of Newtonian cooling (Fraedrich 2002).

Fraedrich and Blender (2003) have analysed power-law scaling of near-surface air temperature fluctuations and its geographical distribution in up to 100 year observational records (gridded over parts of the globe for which sufficient data were available), and in a 1000 year simulation of the present-day climate with a complex atmosphere–ocean model (ECHA4/HOPE). DFA analysis of daily temperature data anomalies (defined as deviations from the annual cycle) and climate model simulations, both yielded DFA exponents of over the oceans, over the inner continents, and in transition regions. However, one can hardly explain such a huge difference in LTP in the oceans and continents; normally one would expect that the oceans, because of their huge thermal capacity, would determine, in the long run, the climatic fluctuations also in the continents and hence the high α and H in the oceans would be reflected also in the inner continents. The observational data exponents were derived in the range 1–15 years from the DFA plot. To analyse the controls on the scaling exponents and implied memories over different time scales, three levels of ocean coupling were employed for the model simulations: (i) climatological sea surface temperature (SST) represented by an annual cycle only; (ii) coupling to a simple mixed-layer ocean model, and (iii) coupling to a complex dynamic ocean model (HOPE). The simulations with (i) showed no memory at all, while the power law in the decadal range could be reproduced by (ii). To produce centennial scaling/memory, (iii) was required. This indicates that the origins of long-term memory in surface temperatures can be traced back to the internal long-term ocean dynamics (Fraedrich and Blender 2003).

The mechanism for the nonstationary H = 1 or “flicker noise” behaviour of ocean surface temperature in the Atlantic and Pacific mid-latitudes has been explained by a vertical two-layer diffusion energy balance ocean model with extremely different diffusivities, representing a shallow mixed layer on top of a deep abysmal ocean, forced by an atmospheric surface flux of white noise (Fraedrich et al. 2004). To explore millennial variability and to identify the limit of the memory, Blender et al. (2006) have analysed an ultra-long 10 000 year simulation with a CSIRO coupled atmosphere–ocean model and compared the results with those from Greenland ice core data during the Holocene. Both show scaling behaviour/long-term memory up to 1000 years with a spectral exponent (Equation (15)) of β = 0.75 (Η = 0.875). The long-term memory of the surface temperature is coupled to the intense low-frequency variability of the Atlantic meridional overturning circulation. In the Pacific and Antarctic oceans, long-term memory was not simulated, which agreed with Antarctic proxy ice core data during the Holocene.

Fraedrich et al. (2009) have discussed the spectrum of Earth’s temperature, which exhibits a range of scales of variability; scaling with β = 0.3 (H = 0.65) is indicated up to centennial time scales. Huybers and Curry (2006) demonstrate that climate variability exists at all time scales, with climate processes being closely coupled, so that understanding of variability at one time scale requires understanding of the whole. Their characterization of overall land and sea surface temperature exponents agrees with that of Fraedrich and Blender (2003) above, with β ≈ 1 (H ≈ 1) over the oceans and β ≈ 0 (H ≈ 0.5) over the inner continents. There is also a latitudinal contrast, with β larger near the equator. The existence of two separate scaling regimes, with time spans from 1 to 100 years (short) and from 100 to years (long) suggests distinct modes of climatic variability. For high-latitude continental records, the estimated spectral exponents for short and long time spans are β = 0.37 and 1.64, respectively, and similarly β = 0.56 and 1.29 for tropical sea surface temperature records. Here, nonstationarity is implied for the longer time scales with β > 1. For longer than centennial time scales, one might conjecture (Huybers and Curry 2006) that low-frequency Milankovitch forcing cascades towards higher frequencies which is analogous to turbulence (Kolmogorov 1962).

Markonis and Koutsoyiannis (2013) have analysed two instrumental series of global temperature and eight proxy series with varying lengths from 2 thousand to 500 million years. Using the climacogram based on the log-log plot of standard deviation against time span (based on Equation (18)), they have shown that climatic variability over a time span of 1 month to 50 million years can be characterized in terms of HK dynamics with H > 0.92. This implies stationarity over a very long time scale, indicating that Earth’s climate is self-correcting and stable, albeit with a huge range of variability. The orbital forcing (Milankovitch cycles) is also evident in the combined climacogram at time scales between 10 and 100 thousand years, which provides an element of predictability over this time span. This overall characterization contrasts with the separate scaling regimes identified by Huybers and Curry (2006). The extent to which this implies memory, and over what time span, remains an open question; as already noted, HK scaling behaviour does not necessarily imply memory, which on the basis of the evidence provided above, could be taken to exist up to a thousand years. Beyond this, theories and models have been advanced that variously interpret observed fluctuations in terms of insolation variations due to changes in the Earth’s orbit eccentricity, tilt and precession (Ghil and Childress 1987, Paillard 2001). These models incorporate, in one form or another, nonlinear feedback, thresholds, rectification or modulation of signals as explained by Rial et al. (2004). An alternative view is that the observed fluctuations can be explained by stochastic resonance or chaotic mechanisms (e.g. Benzi et al. 1982, Meyers and Hinnov 2010).

Mesa et al. (2012) employed a dynamical systems approach to exploring the Hurst Phenomenon in simple climate models. As non-uniformly mixing systems pass bifurcations, they can exhibit the characteristics of tipping points and critical transitions that are observed in many complex dynamical systems, ranging from ecosystems to financial markets and the climate. Bifurcations play a central role in the low-frequency dynamics of the large-scale ocean circulation (Dijkstra and Ghil 2005). Mesa et al. (2012) analysed a simple zero-dimension energy balance climate model exhibiting Hopf bifurcation, which was forced by a time-dependent dimensionless measure of solar luminosity with and without added noise. Model simulations over years exhibited complex nonstationary behaviour that inhibited consistent interpretation of the Hurst exponent using three estimation methods: the pox diagram, the spectrum and DFA. Nonetheless, understanding the possibility of a sudden, critical transition in the climate system using simple climate models within a dynamical systems framework merits further research.

All of the preceding commentary relates to long-term temperature fluctuations; we now turn to precipitation and runoff. Fraedrich et al. (2009) comment that pressure and precipitation show much less memory than surface temperature and runoff. This view is based on a 250 year high-resolution simulation of the present-day climate for eastern Asia with a coupled atmosphere–ocean model, and comparison with results for observational data (Blender et al. 2006). DFA analysis of the simulated annual precipitation and atmospheric near-surface temperature fields showed no long-term memory for most areas of eastern Asia (β ≈ 0.0; Η ≈ 0.5); based on this and other global analyses (not shown), they state that this result is found everywhere on the globe. Based on the same climate model simulations, Blender et al. (2006) found β ≈ 0.3–0.4, Η ≈ 0.65–0.7 for simulated runoff in the Yangtse and Huang He basins, which agreed with observations.

Potter (1979) looked for evidence of long-term memory in 100 annual precipitation series from the northeast United States, and found that for those series that appeared to be homogeneous, the estimated autocorrelation functions and Hurst coefficients were remarkably consistent with a Markov process, indicating that annual precipitation in the northeast United States is a short-memory process. Montanari et al. (1996) analysed six daily rainfall time series from Italy and found evidence of a linear trend in all, but of long-term memory in only two. Kantelhardt (2006) have explored LTP and multifractality in daily precipitation and runoff records. For 99 daily precipitation records (average length 86 years), they found that the average estimate of H was 0.53 (st. dev. 0.04), while for the 42 daily river runoff records, the average estimate of H was 0.72 (st. dev. 0.11); the estimates were derived using DFA (average record length 86 years). These findings for precipitation appear to support the claim of Blender et al. (2006) that precipitation is close to white noise.

On the other hand, Koutsoyiannis and Langousis (2011) found evidence for Hurst behaviour in the globally averaged monthly precipitation in the 30-year period 1979–2008 (H = 0.70), in two of the longest annual precipitation time series (Seoul, Korea, 1770s–today: H = 0.76; Charleston City, USA, 1830s–today: H = 0.74), in high-resolution (10-second) precipitation time series in Iowa (H = 0.96) and in spatially averaged daily rainfall over the Indian Ocean (H = 0.94). Also Koutsoyiannis et al. (2007) analysed annual precipitation, runoff and temperature records for the Boeoticos Kephisos basin (Greece) for the period 1907–2003, and found H = 0.64 for precipitation, H = 0.79 for runoff and H = 0.72 for temperature. This suggests an amplification in long-term runoff variability which may vary across different climatic zones.

As part of an analysis of the ability of GCMs to reproduce long-term inter-annual variability in monthly precipitation, Rocheta et al. (2014) have mapped Hurst coefficients across the globe for monthly rainfall data anomalies for the period 1951–1997; the mapping shows that, while there are large areas where Η ≈ 0.5 (e.g. eastern and mid China, which agrees with the results of Blender et al. (2006)), there are smaller continental zones with much higher values of H.

In the case of the Nile, there is a well-known link between SST fluctuations in the Pacific Ocean (and El Niño), and monsoon rainfall over the Ethiopian plateau, and, consequently, annual runoff fluctuations in the Blue Nile basin. Blue Nile runoff can account for up to 80% of the Nile flood/annual runoff, so it can be deduced that the long-term variability of Ethiopian plateau rainfall is a major driver of long-term variability in annual Nile runoff. Eltahir (1996) has found a linear relationship between a SST El Niño index for the months of September, October and November and annual Nile runoff at Aswan, which explains 25% of the variance.

At the transition from the 19th to the 20th century, a sharp decline in annual Nile runoff occurred, which initially was attributed erroneously to the impact of the building of the old Aswan Dam on the discharge rating curve. However, Todini and O’Connell (1979) showed that this decline was linked with a sudden widespread failure of the monsoon in the tropical regions (Kraus 1956). This may reflect some sort of tipping point in the climate system whereby a sudden and largely unexplained transition to a new climatic regime occurs, which can be taken to correspond to a stochastic shifting mean representation of change. In commenting on Hurst’s findings on the variability of the River Nile flows, Lamb (1965) (cited in Salas and Boes 1980) provided the underlying physical concepts such as the variability of atmospheric and oceanic processes. He commented that the first half of the 20th century had seen unusual large-scale atmospheric circulation patterns, and that the distribution of ocean sea surface temperatures had by then (the 1960s) returned to what it had been in the period 1780–1850.

The upward shift that occurred in the Equatorial Lake levels (e.g. Lake Victoria) in the early 1960s, and consequently in the White Nile flows, has been discussed extensively by Salas and Boes (1980) in the context of shifting level modelling. Based on data on lake outflows, net basin supply and precipitation, and on modelling, Salas et al. (1981) argued that the upward shift occurred due to extreme high precipitation and decreasing lake evaporation in the years 1961–1964. Based on a number of water balance studies (Piper et al. 1986, Sene and Plinston 1994), Sutcliffe and Parks (1999) attributed the upward shift largely to unusual variation in rainfall. Lamb (1966) also reviewed the various attempts made to explain and forecast the variations of the Equatorial Lakes by cycles of fixed periods and the sunspot cycle, pointing out the lack of success in such forecasting. In relation to long-term fluctuations in the River Nile flows, Fraedrich (2002) notes that periods of drought that affected the Nile in the Middle Ages were widespread, reflecting the existence of teleconnections in the climate system, but also indicating LTP in precipitation.

Using trend analysis and DFA, Jiang et al. (2005) have analysed time series of indices of floods and droughts compiled from historical documents for the period 1000–1950, supplemented by instrumental records for 1950–2003. Eight periods where higher floods had occurred were identified, coinciding with climate changes in China; droughts were found to occur in the same years as higher floods. Long-term memory up to centuries in these series was deduced from DFA, with Η ≈ 0.76 for floods and Η ≈ 0.69 for droughts, and it was suggested that this could be attributed to SSTs in the adjacent East China Sea.

Flow in the Colorado River has varied significantly since 1900, and fluctuations have been attributed to both climatic fluctuations and consumptive water use (USGS, 2004). Analysis of the basin precipitation record since 1900 has revealed some fluctuations/shifts in precipitation that operate on two time scales (Hereford et al. 2002). Short-term climatic variation, with a period of 4–7 years, is associated with El Niño and La Niña activity as expressed by several indicators, including the Southern Oscillation Index (SOI) and equatorial SST. Multidecadal climate variation follows a pattern best expressed by the Pacific Decadal Oscillation (PDO), a phenomenon of the northern Pacific Ocean. The PDO varies or oscillates on a decadal scale of 30–50 years for the total cycle; that is, much of the North Pacific Ocean will be predominantly, though not uniformly, warm (or cool) for periods of about 15 to 25 years, which was modelled by Sveinsson et al. (2003) using two different shifting mean models. In addition, the PDO is partly related to SST and atmospheric pressure of the northern Pacific Ocean (Mantua and Hare 2002). Changes in these indicators apparently trigger sharp transitions from one climate regime to another, altering the climate of North America for periods of two to three decades (Zhang et al. 1997, Hereford et al. 2002).

Enfield et al. (2001) have explored the relationship between the Atlantic Multidecadal Oscillation (AMO) in SSTs and rainfall and river flows in the continental United States. North Atlantic SSTs for 1856–1999 were found to contain a 65–80 year cycle with a 0.4°C range, while AMO warm phases were found to have occurred during 1860–1880 and 1940–1960, and cool phases during 1905–1925 and 1970–1990. The AMO signal is global in scope, with a positively correlated co-oscillation in parts of the North Pacific, but it is most intense and spatially extensive in the North Atlantic. During AMO warm events, most of the United States receives less than normal rainfall, including Midwest droughts in the 1930s and 1950s. Koutsoyiannis (2011) has found an estimate of for the monthly times series of the AMO (1856–2009); this is close to the deduced by Fraedrich and Blender (2003) for ocean SSTs.

The Atlantic Ocean Meridional Overturning Circulation (AMOC) consists of a near-surface, warm northward flow, compensated by a colder southward return flow at depth (Srokosz et al. 2012). Heat loss to the atmosphere at high latitudes in the North Atlantic makes the northward-flowing surface waters denser, causing them to sink to considerable depths. These waters constitute the deep return flow of the overturning circulation. Changes in this circulation can have a profound impact on the global climate system, as indicated by palaeoclimatic records. These include, for example, changes in African and Indian monsoon rainfall, atmospheric circulation of relevance to hurricanes, and climate over North America and Western Europe. Wang and Zhang (2013) have explored the relationship between AMOC variability and multidecadal North Atlantic sea surface temperature fluctuations characterized by the AMO in climate model simulations. A speed up (slow down) of the AMOC favours the generation of a warm (cool) phase of the AMO by anomalous northward (southward) heat transport in the upper ocean, which conversely leads to a weakening (strengthening) of the AMOC through changes in the meridional density gradient after a delayed period of ocean adjustment. This suggests that, on multidecadal time scales, the AMO and AMOC are related and interact with each other, as also observed by Blender et al. (2006).

In the North Atlantic basin, shorter-term (inter-annual to decadal) climatic fluctuations are associated with the North Atlantic Oscillation (NAO). This is driven primarily by the fluctuations in the difference of atmospheric pressure at sea level between the Icelandic low and the Azores high, which control the strength and direction of westerly winds and storm tracks across the North Atlantic. Since 1980, the NAO has tended to remain in one extreme phase and has accounted for a substantial part of the observed wintertime surface warming over Europe and downstream over Eurasia and cooling in the northwest Atlantic (Hurrell and Van Loon 1997). Anomalies in precipitation, including dry wintertime conditions over southern Europe and the Mediterranean and wetter-than-normal conditions over northern Europe and Scandinavia since 1980, are also linked to the behaviour of the NAO.

Taken together with historical analyses of the impacts of droughts going back over centuries and millennia, the above examples provide considerable evidence that precipitation has exhibited long-term fluctuations that are not consistent with Η ≈ 0.5 overall across the continents. As already noted, the evidence presented by Rocheta et al. (2014) shows some zones with Η > 0.5, but their analysis was based on just 47 years of data, which inhibits the detection of LTP, and averaging over large grid squares may disguise some of the fluctuations. Nonetheless, analysis of many time series as reported above supports the hypothesis of little or no LTP. However, results for different time intervals, and different methods of analysis/estimation of H, make comparisons difficult. Moreover, gridded data may disguise some of the fluctuations in observed time series at individual sites.

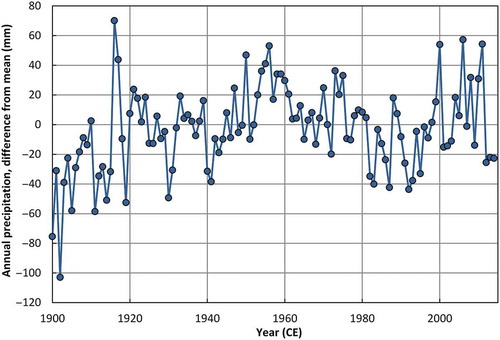
In a recent analysis of annual globally averaged, gridded precipitation data for the period 1900–2014, Koutsoyiannis and Papalexiou (2016) have found remarkably strong evidence of LTP, as evidenced by visual inspection of Figure 2 and a Hurst coefficient of 0.85. This raises a number of interesting questions. Firstly, given the different modes of variability in the climate system that would be expected to affect the inter-annual variability of precipitation in different ways, and not to be necessarily in phase with each other, it is remarkable that there is such a strong and coherent LTP signal in globally averaged precipitation. Secondly, as precipitation exhibits large spatial variability across the globe, it is likely that the local LTP signal is disguised by this variability, and is stronger/weaker in some regions as suggested by some of the above analyses. An LTP analysis of the annual gridded data averaged over different climatic zones should provide new insight into how the LTP signal varies regionally across the globe, and into how the signal apparently becomes reinforced at the global scale of averaging.

Figure 2. Globally averaged annual precipitation calculated from 5° × 5° GHCN (version 2) monthly precipitation dataset for the period 1900–2014 (http://www.ncdc.noaa.gov/temp-and-precip/ghcn-gridded-products/).

The issue of how LTP can be generated/amplified in runoff remains, even when it appears to be weak in some point and regional rainfall records. Mudelsee (2007) has done some interesting data analysis and modelling to explore how the aggregation of monthly runoff in the channel network of a river basin might lead to increasing values of the fractional differencing parameter d = Η − 0.5 with increasing area. This was investigated for six river basins with internal gauging stations, five of which showed monotonically increasing d with area. Using the analogy of a cascade of linear reservoirs within the channel network (Klemeš 1978) with precipitation inputs from 20 km × 20 km grid areas that were treated as spatially and temporarily independent, the grid areas were modelled by Markov processes with a spectrum of lag-one autocorrelation coefficients, the aggregation of which produced a process with monotonically increasing d with area, as for five of the six basins. This is analogous to the modelling of LTP by weighting and aggregating Markov processes (Mandelbrot 1971, Granger 1980, Koutsoyiannis 2002). Losses due to evaporation and infiltration were neglected. Despite the simplifying assumption, these results suggest that a river basin can induce/amplify LTP in runoff. However, it is not clear that LTP associated with extended droughts can be attributed to this aggregation process; such droughts must have their origins in the precipitation process, even if the LTP signal is weak.

5 Hurst’s legacy to other disciplines

The discipline of hydrology has commonly been an “importer” of ideas, techniques and theories developed in other scientific disciplines. The insights of Hurst, however, are a rare exception as Hurst’s work has been seminal in many areas of science and technology, as represented in Figure 1.

Figure 3. Number of citations per year of Hurst’s original paper (bars; adding up to 3752 citations) and papers in which one or more of the phrases “Hurst coefficient”, “Hurst exponent”, “Hurst parameter”, “Hurst effect” or “Hurst Phenomenon” appear (solid line; summing to 22 755 citations). Data from Google Scholar as of March 2014. Notice the logarithmic scale of the vertical axis.

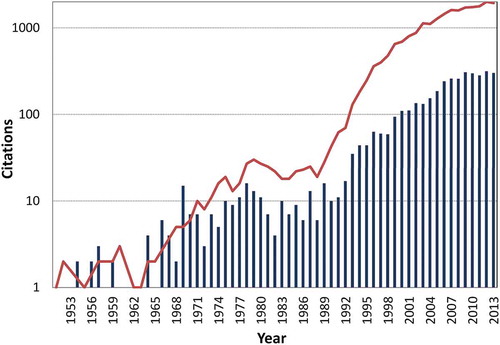
It is possible to trace the dissemination of Hurst’s findings in fields outside hydrology by studying bibliographic databases. A simple search of the scientific citations of the original 1951 paper in the Google Scholar database indicates that the dissemination of Hurst’s work occurred in four distinct periods (Fig. 3). The first was a rather quiescent period of approximately 20 years when only about 20 citations appeared, with most being self-citations or references appearing in conference proceedings within hydrology.

This dissemination period ended dramatically with the work of Mandelbrot, initially with van Ness (1968) and then with Wallis (Mandelbrot and Wallis 1968, Mandelbrot and Wallis 1969a, b, c, d, e), which expanded the awareness of the Hurst Phenomenon within the hydrological community, and also promoted it beyond hydrology. As already mentioned, the groundbreaking paper of Mandelbrot and Van Ness (1968), which introduced the fBm, clearly acknowledged that Kolmogorov (1940) and later some others (see references in Mandelbrot and Van Ness (1968)) had already recognized this process. This highly cited paper (Table 2) has played an important role in the dissemination of Hurst’s work to multiple scientific communities. Mandelbrot’s (1977) book The Fractal Geometry of Nature exploded the field of fractals, which also owes something to Hurst.

Table 2. Top-cited papers (from journals) with reference to Hurst’s work in different scientific fields (two from each one) and their impact in terms of citations (data from Google Scholar as of March 2014).

Field	Reference	Subject	Citations
Statistics and stochastics
	Mandelbrot and Van Ness (1968) Hosking (1981)	Fractional Brownian motion	5005
		FARIMA model	541
Geophysical sciences
	Mandelbrot and Wallis (1969e) Sadler (1981)^‡	Geophysical records	863
		Sediment accumulation rate	572
Physics
	Voss and Clarke (1975)	Acoustics	414
	Borland (1998)^‡	Diffusion	309
Economics and finance
	Greene and Fielitz (1977) Baillie (1996)	Stock market prices	346
		Econometrics	1282
Medical sciences
	Ellaway (1978)	Neurophysiology	377
	Kobayashi and Musha (1982)	Heartbeat period	656
Biology
	Peng et al. (1992)^‡	Nucleotide sequences	1159
	Arneodo et al. (1996)^‡	DNA sequences	174
Information sciences
	Leland et al. (1993, 1994)	Ethernet traffic	7316*
	Frost and Melamed (1994)	Traffic in telecommunication networks	667
Climate science
	Koutsoyiannis (2003)	Climatic variability	191
	Cohn and Lins (2005)	Trends in climate	202

*This is the sum of the citations of Leland et al. (1993, 1994), referring to two versions of the same paper.

^‡There is no citation to Hurst (1951), but there is a reference to Hurst Coefficient/Phenomenon in the paper.

In his original paper, Hurst (1951) noted that other geophysical time series, e.g. rainfall, temperature, pressure, tree-ring widths, lake varves and sunspot numbers, have similar behaviour to Nile runoff by estimating H for each one of them. Mandelbrot and Wallis (1969e) took his analysis one step further by applying the rescaled range (R/S) method to the time series of the above-mentioned variables (except sunspot numbers, which is unique), as well as to earthquake frequency. They confirmed Hurst’s findings, and demonstrated that the Hurst Phenomenon is a characteristic feature of different geophysical records.

Voss and Clarke (1975) showed that Hurst behaviour, in the form of 1/f noise, is found in different types of music (classical, jazz, etc.). They produced random music compositions based on three distinct stochastic models (white, 1/f and 1/f² noise) and evaluated the response of a wide range of listeners to hearing the compositions. They found that random music from the 1/f noise model was regarded as being quite close to manmade compositions.

Greene and Fielitz (1977) introduced Hurst’s work to economics, and more specifically to common stock returns. Using the R/S technique, they estimated the Hurst coefficient for 200 daily stock return series and found that the majority exhibited Hurst behaviour. However, the mean of H was close to 0.6; thus, a debate about the results ensued. The most widely recognized paper challenging Greene and Fielitz’s findings was that of Lo (1991), which reached 1700 citations and, despite representing an opposing perspective, made Hurst’s finding well known beyond the boundaries of hydrology.

During the late 1970s there were also some references to Hurst’s paper, though not to his finding. The works of Ellaway (1978) and Sadler (1981) fall into this category. As in Hurst’s original work, Ellaway used a cumulative sums procedure in neurophysiology to detect a change in the mean of peristimulus time histograms associated with neuron responses to stimulus. He asserted that the use of the cumulative sums technique decreased the number of clinical trials required to investigate the behaviour of nerve cells. Sadler (1981) presented a compilation of 25 000 records of sediment accumulation rates suggesting that the accumulation rate is time dependent and hinted that this might be reflective of the Hurst Phenomenon. Although he never quantified this supposition, he introduced Hurst’s work to the field of geology, with references also to the works of Mandelbrot and Wallis (1969e) and Klemeš (1974).

In the field of statistics, Hosking (1981) and Beran (1994) are the key researchers who further developed Hurst’s work. The former introduced the FARIMA model (see Section 3.4) to generate synthetic time series exhibiting Hurst behaviour; the latter, with his book Statistics for Long Memory Processes, offered a robust statistical framework for further analysis and development in other fields of research.

Finally, during the latter half of the second dissemination period, the Hurst Phenomenon was introduced to medical science through the work of Kobayashi and Musha (1982), who examined the spectrum of the heartbeat interval of healthy subjects. Their findings indicated that the heartbeat spectrum has a 1/f-like shape, suggesting Hurst behaviour. Notably, during the early 1980s, many researchers used the power spectrum to detect the Hurst Phenomenon. Peng et al. (1992) investigated Hurst behaviour in DNA sequences, comparing coding and non-coding DNA. In their later work, Peng et al. (1994), they introduced detrended fluctuation analysis (DFA), an alternative method to identify and quantify Hurst behaviour with some advantages over spectrum-based methods.

The third period of dissemination of Hurst’s work comes with the publications of Leland et al. (1993, 1994), who found evidence of Hurst behaviour in Ethernet LAN traffic. They analysed records with hundreds of millions of data points and determined the Hurst coefficient using Whittle’s maximum likelihood estimation approach to be near 0.8. Their results had a significant impact on the field of informatics and the modelling of network traffic, which is reflected in the number of citations that have appeared in the scientific literature (7316). During this period, the number of annual references to Hurst’s original paper, or to his theory, increased exponentially. Other disciplines contributing to this tally include transport engineering (Nagatani 1993), astrophysics (Ruzmaikin et al. 1994), ecology (Halley 1996) and, more recently, climate science and climatology (see Sections 4 and 6). An overview of the key papers in each field and their impact as quantified in terms of citations appears in Table 2.

Some of the key papers noted in Table 2 do not explicitly cite Hurst (1951). In fact, as shown in Figure 3, the papers citing Hurst’s original paper per year are fewer than those containing terms such as “Hurst coefficient”, “Hurst Phenomenon” etc., by about one order of magnitude. This may indicate that, after receiving such broad exposure, the Hurst Phenomenon has become so familiar that continued reference to the original paper is deemed unnecessary. Perhaps for the same reason, the number of citations to the Hurst paper stabilized after 2004, signalling the start of the last (fourth) period that is evident in Figure 3. It could also be that, despite the use of the Hurst coefficient in numerous applications of fractal theory, the continuing lack of reference to Hurst (1951) is leading to it being forgotten as the primary source by the fractal community. Interestingly, there are also some papers, such as the recent study by Magi et al. (2010) on DNA sequences, where even though no specific reference is made to either Hurst or the Hurst Phenomenon, they use methods that were inspired by the work of Hurst, e.g. a shifting mean model.

In addition, there are a number of publications disputing the behaviour discovered by Hurst. Indeed, for typical sample sizes, it is difficult to verify the Hurst behaviour and to distinguish it from processes without LTP. This dispute has even appeared in the hydrological literature, where the nature of the Hurst Phenomenon has been the subject of debate, as discussed by Bras and Rodriguez-Iturbe (1985, p. 214). For example, Vogel et al. (1998) examined time series of annual streamflow at 1544 gauging stations and concluded that the LTP structure of historical annual streamflow series is indistinguishable from the structure of either an AR(1) or ARMA(1,1) process. However, this may well be because it is very difficult to detect LTP in the relatively short streamflow series that are typically available due to the low information content (Wallis and O’Connell 1973, Koutsoyiannis and Montanari 2007).

6 Climate variability and change

Naturally, climatic processes strongly influence hydrological processes and the Hurst behaviour in the latter is no more than a manifestation of the same behaviour in climate. However, the climatological community has been, and continues to be, quite resistant to the idea that climate exhibits LTP. Typically, climatic variables are modelled as Markov processes, as proposed by Leith (1973), who introduced the Markov model aiming to “avoid the statistical complexity of the real atmosphere”. Astonishingly, subsequent publications interpreted this justification as evidence that climatic processes behave as Markov processes. However, Markovian behaviour is totally different from Hurst behaviour in all aspects.

For example, in a Markov process, by definition the future does not depend on the past when the present is known (Papoulis 1991), while in an HK process the entire past influences the future. Furthermore, a Markov model produces a relatively static climate while an HK model produces a highly varying climate (Koutsoyiannis 2011). In other words, the popularity of a Markovian climate view harmonizes with a perception of a static climate. With such strong conviction for a static climate, it is not difficult to explain the dominance of the current hypothesis that climate change can only be driven by external, non-natural factors, namely by anthropogenic CO₂ emissions. This is the basis for the modern prevailing theory of climate change.

Unavoidably, this has also affected hydrology, as expressed quite vividly in the Guidelines for Determining Flood Flow Frequency (U.S. Water Resources Council 1981). The resistance to recognize change, which is the conceptual basis of HK behaviour in nature, is reflected in this statement:

Available evidence indicates that major changes occur in time scales involving thousands of years. In hydrological analysis it is conventional to assume flood flows are not affected by trends or cycles. Climatic time invariance was assumed when developing this guide.

Interestingly, the same document indicates a strong conviction that natural processes should be independent in time as manifested in the following statement:

In general, an array of annual maximum peak flow rates may be considered a sample of random independent events. Even when statistical tests of the serial correlation coefficients indicate a significant deviation from this assumption, the annual peak data may define an unbiased estimation of future flood activity if other assumptions are attained.

The dominance of change in nature, and the close connection of the perpetually changing climate with HK behaviour were pointed out several years ago, even though such behaviour was identified in meteorological time series at an annual scale or finer. Bloomfield (1992) showed the significance of the selection of the statistical model in the determination of confidence intervals when modelling global air temperature. Although he did not mention the Hurst Phenomenon in his work, he was the first to introduce the use of a FARIMA process for temperature. A similar case, in which Hurst’s work was not explicitly referenced, was the work of Koscielny-Bunde et al. (1998). They examined daily data from 14 meteorological stations across the world and found that autocorrelation of all temperatures follows a similar power-law decay. They concluded that this could indicate the existence of a universal law describing atmospheric variability.

It was Koutsoyiannis (2003) that made a clear link between the Hurst behaviour and climate, presenting not only the mathematical framework, but also a conceptual background of the finding and its application. Moreover, by implementing a consistent method for estimating H that takes statistical biases into account, he found H to be near 0.88 for the Jones et al. (1998) proxy temperature record of the last 1000 years. He also showed that use of the Kendall test in trend significance estimation may be misleading unless the proper statistical model is used, and that the implied uncertainty of the natural variability of the climate system will be dramatically higher (see also Koutsoyiannis and Montanari 2007). Cohn and Lins (2005) further developed this idea by presenting an alternative test for trend detection based on Hosking’s approach (1984). They also showed that if the more realistic LTP model is used, then the p-value for the observed trend in global air temperature is near 0.07, which implies considerably less significance in comparison to the 1.8 × 10^–27 or 5.2 × 10^–11 for the white noise model and the AR model assumptions, respectively. Furthermore, recent studies examining very long instrumental and proxy time series have concluded that these time series are consistent with HK behaviour for time scales up to 50 million years (Koutsoyiannis 2013, Markonis and Koutsoyiannis 2013).

Until recently, the climatology community and the IPCC refused to recognize the connection between HK behaviour and climate. Ironically, it was only after the so-called “pause”, i.e. the rather stable global temperature of the 21st century, that the IPCC in its Fifth Assessment Report acknowledged the importance of natural climatic variability and its statistical implications. Yet this acknowledgment is indirect, as indicated in the following statements in Hartmann et al. (2013):

No attempt has been undertaken to further describe and interpret the observed changes in terms of multidecadal oscillatory (or low-frequency) variations, (long-term) persistence and/or secular trends (e.g., as in Cohn and Lins 2005, Koutsoyiannis and Montanari 2007, Zorita et al. 2008, Lennartz and Bunde 2009, Mills 2010, Mann 2011, Wu et al. 2011, Tung and Zhou 2013,Zhou and Tung 2013).

As well as in Bindoff et al. (2013):

Trends that appear significant when tested against an AR(1) model may not be significant when tested against a process which supports this ‘long-range dependence’ (Franzke 2010).

However, the Summary for Policymakers (IPCC 2013) does not mention LTP, although it speaks about internal climate variability, e.g.:

Internal variability will continue to be a major influence on climate, particularly in the near-term and at the regional scale.

7 Conclusions and unresolved issues

In this paper, we have concentrated on the main hydrological “trunk” of the knowledge tree depicted in Figure 1, whilst also giving the reader a flavour of the impact of Hurst’s work on the development of the multiple “branches”. Whilst intended more as a historical narrative of how all this has happened (with the exception of Section 4), rather than an exhaustive review (which in any case is beyond the scope of this paper), there are a number of conclusions that emerge which can be summarized as follows:

(i) The stochastic modelling of long-term persistence that reproduces Hurst’s Law for the rescaled range and the corresponding behaviour for the climacogram has been the subject of ongoing research for more than 50 years. The modelling approaches that have emerged include fractional Gaussian noise and FARIMA models based on long-term memory, as well as simpler models that do not interpret the HK dynamics as due to memory, but to changes across a range of time scales that do not have memory. The modelling tools and estimation procedures to implement any of these approaches in water resources planning are well developed and readily available.

(ii) The argument initiated by Klemeš in 1974 over the competing hypotheses of fGn with infinite memory or HK dynamics with no memory has not been resolved, as both are built upon the same foundation, the power law covariance function, and both reproduce Hurst behaviour in the rescaled range and the aggregated variance, so there is no obvious uniqueness about either hypothesis that can be tested statistically. Moreover, a power law covariance function does not in itself allow the interpretation of memory; it merely implies dependence that can arise from shifting means, or alternating random trends/broken lines, or long-term memory. However, what has emerged in Section 4 is evidence that the climate system and, in particular, ocean dynamics have long-term memory that is manifested in quasi-periodic oscillations in SSTs such as the AO, the AMOC, the PDO etc. However, with a possible exception in the case of El Niño, all of these phenomena have zero predictability in the deterministic sense, and are buried in a large amount of unexplained fluctuations and noise. Moreover, they interact in complex and possibly unknown ways, and their aggregate impact in the climate system is to make the detection of the impacts of anthropogenic warming on the frequency and intensity of floods and droughts extremely difficult.

(iii) Therefore, it is most likely that LTP in observed time series is attributable partially to memory and partially to unexplained shifts/changes.

(iv) There is inconsistent evidence over the existence, or not, of LTP in precipitation records. Regional/global scale analyses of gridded precipitation data suggest that LTP is absent across large areas. However, when the gridded data are averaged across the globe, there is strong evidence for LTP, so it may be that the LTP signal is weak in gridded data due to spatial variability across the globe. Analyses of individual precipitation records have also shown inconsistent results. This may be because the records were relatively short, and that different algorithms and data time intervals were used for estimating spectral exponents and the Hurst coefficient. Another reason for no detection could be the homogenization procedures used in the pre-processing of precipitation data: long-term fluctuations could be deemed as inhomogeneities that are usually removed, thus incorrectly removing the Hurst behaviour too. It may also be that, in many cases, the long-term signature is too weak to detect in relatively short records. Historical evidence of periods of severe and widespread droughts lasting over centuries can be found in the literature that can only be associated with prolonged periods of below average precipitation, and this is reinforced by the clear evidence for LTP in globally averaged precipitation.

(v) The amplification of the Hurst coefficient that results from the rainfall–runoff transformation is not fully understood and merits further investigation. The aggregation of runoff in the river channel network has been offered as one explanation; however, the influence of the physical processes associated with soil moisture, aquifer and lake storage in river basins with increasing scale needs to be explored within a stochastic-physical modelling framework.

(vi) Finally, the extraordinary scientific footprint of Hurst’s work must surely make him the most influential scientific hydrologist of the 20th century, particularly through his impact on developments in so many diverse fields.

So what should the water resource system analyst do when facing the problem of designing/upgrading water resource systems to meet future demand under high climatic uncertainty? It is clear that, in the absence of any long-term climatic predictability in the deterministic sense, and with the acknowledged inability of GCMs to reproduce long-term inter-annual variability, the only option is to employ a stochastic modelling approach that can encapsulate the envelope of uncertainty implied by the Hurst coefficient, estimated using a combination of an instrumental record and historical/palaeo information. With regard to whether a long-memory or no memory model should be used, the prudent approach would appear to be to use both to test the sensitivity of system response/reliability to the full range of uncertainty, and to use the precautionary principle with the outcomes. If there is a credible signal from GCMs (or any other type of deterministic model) on the additional variability that can be expected as a result of greenhouse gases (or other forcings) over and above long-term natural variability, then this can be incorporated into this approach.

Tribute and epilogue

All of the authors of this paper are so very fortunate that their careers and lives have been shaped to a greater or lesser degree by the finding of Harold Edwin Hurst. That his work should still inspire such interest, enthusiasm and inspiration across the hydroclimatic science community and beyond is a measure of the stature of the man. His extraordinary work has not only stood the test of time and multiple disciplines, executed as it was in pre-computer days, but as the citations in Figure 3 show, its sphere of influence continues to grow. And we should also remember the stellar contribution of another outstanding hydrologist of that generation, Walter Langbein, who first recognized that the behaviour of the variance of the time-averaged process (expressed as the variance of the mean) was a corollary of Hurst’s Law, and which was largely ignored until recently, when its significance and potential was recognized through the climacogram.

Several issues related to the Hurst Phenomenon, including its physical genesis in hydrological processes, remain as a stimulating challenge for the upcoming generation of scientific hydrologists. Relevant topics in other fields of science also merit exploration. The Hurst Phenomenon lives on, as vital and inspiring as it was more than 60 years ago.

Disclosure statement

No potential conflict of interest was reported by the authors.