Impact of fractal characteristics on evaporation and infiltration in unsaturated heterogeneous soils

ABSTRACT

In this study, an approach is developed to investigate the impact of fractal characteristics of unsaturated soil between the water table and land surface on the steady-state evaporation and infiltration across a heterogeneous landscape. The soil domain is conceptualized as a collection of stream tubes of soils and the particle diameters in various stream tubes follow a fractal distribution. The saturated hydraulic conductivity of each stream tube is related to the representative particle diameter in the tube. The effective specific discharge is then integrated from the specific discharge for each stream tube and the fractal distribution. The effective evaporation and infiltration in unsaturated soils increase with the fractal dimension. The ratio of minimum over maximum diameters does not significantly affect the specific discharge in the fractal soil. The specific discharge in unsaturated fractal soils calculated by using the simple average particle diameter mostly over-predicts the actual effective specific discharge.

KEYWORDS:

• fractal distribution
• unsaturated soils
• evaporation
• infiltration
• steady state

Editor A. Fiori; Associate editor I. Battiato

1 Introduction

Moisture flux across the land surface through the soil is a key component of large-scale hydroclimatic processes and a primary variable in soil–vegetation–atmospheric transfer models (Mohanty and Zhu 2007). Soil hydraulic property is quantified by the soil water characteristic function and the unsaturated hydraulic conductivity function, which are indispensable to describe flow and transport in unsaturated soils (Gardner 1958, Mualem 1976, van Genuchten 1980, Russo 1988).

Since the microstructures of soils are usually disordered and complicated, it is difficult to quantify the flow, especially for unsaturated soils. Fractal distribution is commonly used to characterize porous media due to its capability to describe a wide range of problems and soil textures (Yu 2008, Wang et al. 2019). Fractal-based approaches are increasingly used for describing the hydraulic property functions since soils have been shown to be fractal. Many studies tried to incorporate fractal characteristics into unsaturated soil hydraulic property and soil structure models.

For the soil hydraulic properties, Rieu and Sposito (1991) used pore-size self-similarity to develop a soil water characteristic curve model to reflect the relationship between soil pore structure and soil water retention characteristics. Xu (2004) derived the soil water characteristic curve and hydraulic conductivity function of unsaturated soils from the fractal model for the pore-size distribution, which included only two independently physical parameters, the fractal dimension and the air-entry value. Huang et al. (2006) developed a fractal model for the soil water retention curve and established relationships among the fractal dimension of soil water retention curve, the fractal dimension of soil mass, and soil texture. Cihan et al. (2009) presented an approach for predicting unsaturated hydraulic conductivity based on a probabilistic fractal approach, which was in series form as a function of suction. Hunt et al. (2013) applied a bimodal pore-size distribution to generate the soil water retention and the unsaturated hydraulic conductivity incorporating two fractal regimes. The developed water retention and unsaturated hydraulic conductivity models described the measured data well and demonstrated that the bimodal distribution provided more realistic predictions than the unimodal one. Bartolo et al. (2014) presented a fractal analysis of the soil retention and hydraulic conductivity curves by two fractal regimes, one for the high water content values and the other for the low water content data. The two-regime fractal approach significantly improved the physical insight of the retention process. Soldi et al. (2017) presented simple mathematical expressions for both water content and hydraulic conductivity curves by assuming that the porous media can be represented by a bundle of capillary tubes and a fractal pore-size distribution. Soto et al. (2017) developed models of hydraulic conductivity and fractal dimension based on fractal geometry for modeling the pore structure of a soil, which agreed closely with observed data. More recently, Tao et al. (2019a) derived a fractal-form of soil water characteristic curve from the fractal theory. Based on the soil water characteristic curve, the classical models for unsaturated soil hydraulic conductivity models were converted to the fractal forms. A unified fractal model for the hydraulic conductivity was proposed with only two parameters (i.e. fractal dimension and air-entry value). Based on the fractal theory, Tao et al. (2019b) presented an approach to predict the relative hydraulic conductivity under deformation condition and demonstrated that the relative hydraulic conductivity at the deformed state could be predicted using the fractal model.

For soil structure, Filgueira et al. (2006) proposed a method for characterizing soil fractal characteristics of particle-size distribution to examine the relationship between soil particle-size distribution and the corresponding mass distribution. Zolfaghari et al. (2016) used the concept of the fractal dimension of soil particle volume to evaluate the soil fractal characteristics and investigated the effect of land-use treatments and the feasibility of fractal dimension to quantify soil aggregate stability by comparing the non-linear fractal dimension, linear fractal dimension, and the mean weight diameter of aggregates.

Compared to the studies of fractal characteristics and their relation to the hydraulic characteristics and properties, there have been few studies on the quantitative relationships between the flow processes and the fractal characteristics of porous media. Among these studies, Jiang et al. (2005) analyzed the spatial variability of soil infiltration properties on a naturally sloped watershed and discussed the results using the fractal theory combined with the geostatistical method in order to improve the accuracy of the watershed hydrological model. Wang and Wang (2007) expressed the soil structure with fractal dimensions of particle-size distribution, aggregate size distribution, and soil pore-size distribution and investigated the effect of soil fractal features on the soil infiltration velocity and process. The soil infiltration process was influenced comprehensively by the soil particle-size distribution, aggregate size distribution, and soil pore-size distribution and their fractal characteristics. Li et al. (2018) proposed an approach to predict the relative permeability and its effect on the flow in a fractal porous medium based on the fractal approximation that the porous medium consists of a bundle of tortuous capillaries. The influence of tortuosity fractal dimension, pore fractal dimension, ratio of minimum-maximum capillary diameters, and threshold pressure gradient on the relative permeability was discussed. More recently, Wang et al. (2019) studied the infiltration and fractal mechanisms in relation to soil fraction and soil water retention curves. The results demonstrated that there was a significant negative correlation between the soil infiltration rate, soil fractal dimensions, and pore fractal dimensions.

The fractal theory relates the unsaturated hydraulic properties to the characterization of soil structure, which provides a powerful tool to indirectly predict the hydraulic properties. As discussed above, most previous studies tried to incorporate fractal characteristics into soil fracture and unsaturated soil hydraulic properties. Few studies have attempted to directly incorporate fractal characteristics into flow processes in unsaturated soils. In this study, an approach is developed to investigate both evaporation and infiltration through unsaturated fractal soils between the water table and land surface. The unsaturated domain is conceptualized as a collection of stream tubes of soils. In each stream tube, the soils are represented by soil particles with a representative diameter. The particle diameters in various stream tubes follow a fractal distribution. The steady-state specific discharge of both evaporation and infiltration in each stream tube is calculated from the mass conservation and Darcy’s laws. The effective specific discharge for evaporation and infiltration is then integrated from the specific discharge for each stream tube and the fractal distribution. The influence of the fractal dimension of soil particles, particle-size range, and water table depth on the evaporation and infiltration fluxes is then calculated and discussed.

2 Methods and materials

2.1 Fractal distribution of soil particle size

The fractal distribution of soil particles is combined with the stream-tube concept to examine the effect of fracture nature of unsaturated soil on steady-state evaporation and infiltration. It has been shown that the particle size and pore size of natural porous media follows the fractal distribution, which can be expressed as (Yu and Cheng 2002, Yu et al. 2009, Qin et al. 2019):

(1) $N\left(\mathrm{\Lambda }\ge \lambda \right)={\left(\frac{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\lambda }\right)}^{D_f}$(1)

where N is the total number of particles with diameter Λ greater than λ, D_f is the fractal dimension of soil particle diameters (D_f < 2), λ_max is the maximum particle diameter. The lower and upper limits of the particle diameter of fractal distribution are λ_min and λ_max, respectively.

The total number of particles can be obtained by substituting λ_min into Equation (1)(1) $N\left(\mathrm{\Lambda }\ge \lambda \right)={\left(\frac{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\lambda }\right)}^{D_f}$(1) as:

(2) $N_t(\wedge \ge {\lambda }_{min})={\left(\frac{{\lambda }_{max}}{{\lambda }_{min}}\right)}^{D_f}$(2)

For a truly fractal medium, N_t → ∞ as λ_max/λ_min → ∞. For an approximately fractal medium in the real world, such as the unsaturated soil considered in this study, λ_max/λ_min should be a large number. The number of particles within the range of diameter from λ to λ + dλ can be then determined from Equation (1)(1) $N\left(\mathrm{\Lambda }\ge \lambda \right)={\left(\frac{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\lambda }\right)}^{D_f}$(1) :

(3) $-dN=D_f{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{D_f}{\lambda }^{-\left(D_f+1\right)}d\lambda$(3)

The negative sign in Equation (3)(3) $-dN=D_f{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{D_f}{\lambda }^{-\left(D_f+1\right)}d\lambda$(3) means that the particle number decreases with increasing diameter.

The average particle diameter can be determined by the following integration using the expression of dN in Equation (3)(3) $-dN=D_f{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{D_f}{\lambda }^{-\left(D_f+1\right)}d\lambda$(3) :

(4) $\bar{\lambda }=-\frac{1}{N_t}\underset{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{\overset{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\int }}\lambda dN=\frac{D_f{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{D_f-1}\left[1-{\left(\frac{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)}^{D_f-1}\right]$(4)

2.2 Evaporation and infiltration in unsaturated stream tubes

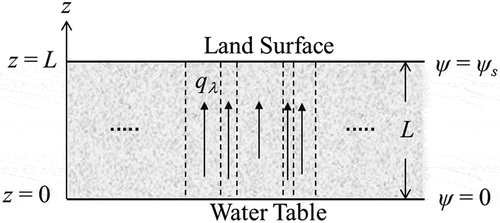
The unsaturated soil domain between the water table and the land surface shown in Fig. 1 is conceptualized as a collection of stream tubes. In each stream tube, the particle diameters are represented by an effective diameter λ, which follows the fractal distribution expressed in Equation (1)(1) $N\left(\mathrm{\Lambda }\ge \lambda \right)={\left(\frac{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\lambda }\right)}^{D_f}$(1) . Since the focus of this study is on the impact of fractal characteristics on the evaporation and infiltration, the simple exponential function for the unsaturated hydraulic conductivity K_λ (Gardner 1958) is used for each stream tube represented by λ:

(5) $K_{\lambda }\left(\psi \right)=K_{s\lambda }\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }\psi \right)$(5)

Figure 1. Schematic diagram of steady-state evaporation (upward) and infiltration (downward) in fractal soil domain between the water table and land surface.

where ψ is the suction head in the unsaturated soil, K_sλ is the saturated hydraulic conductivity, and α_λ is the pore-size distribution parameter.

If the depth from the water table to the land surface is L and the suction head at the land surface is ψ_s (Fig. 1), then the specific discharge q_λ (either evaporation or infiltration) in the unsaturated soil can be obtained from the mass conservation equation and Darcy’s law as follows (Warrick and Yeh 1990, Zhu and Mohanty 2002):

(6) $q_{\lambda }=K_{s\lambda }\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }{\psi }_s\right)}{1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)}$(6)

If ψ_s > L, q_λ is positive, which means evaporation. On the other hand, if ψ_s < L, q_λ is negative, which indicates infiltration. In the case of infiltration, however, it is more convenient to present the results as absolute values (i.e. the negative specific discharge). Introducing a dimensionless suction head relative to the water table depth L, ϕ = ψ_s/L, the expression of specific discharge in the stream tube with a representative particle diameter of λ can be determined by replacing ψ_s in Equation (6)(6) $q_{\lambda }=K_{s\lambda }\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }{\psi }_s\right)}{1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)}$(6) with Lϕ:

(7) $q_{\lambda }=K_{s\lambda }\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\varphi \right)}{1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)}$(7)

2.3 Correlation of hydraulic parameters

For the stream tube of soil represented by an effective diameter λ, the saturated hydraulic conductivity K_sλ is approximated using the US Bureau of Reclamation (USBR) formula (Cheng and Chen 2007):

(8) $K_{s\lambda }=4.8\times {10}^{-4}\left(\frac{g}{\nu }\right){\lambda }^{0.3}{\lambda }^2$(8)

where ν is the kinematic viscosity of water, and g is the gravitational acceleration. The first λ needs to be in mm in Equation (8)(8) $K_{s\lambda }=4.8\times {10}^{-4}\left(\frac{g}{\nu }\right){\lambda }^{0.3}{\lambda }^2$(8) . Note that while Equation (8)(8) $K_{s\lambda }=4.8\times {10}^{-4}\left(\frac{g}{\nu }\right){\lambda }^{0.3}{\lambda }^2$(8) for the saturated hydraulic conductivity is adopted in this study without the loss of generality, other formulas of hydraulic conductivity in relation to particle diameter can also be used. In the USBR model, the effective particle diameter is the particle diameter with 20% cumulative weight of the sample from the particle-size distribution curve.

Using the kinematic viscosity of water at 16ºC of ν = 1.12 × 10⁻⁶ m²/s, one can simplify the expression of saturated hydraulic conductivity, Equation (8)(8) $K_{s\lambda }=4.8\times {10}^{-4}\left(\frac{g}{\nu }\right){\lambda }^{0.3}{\lambda }^2$(8) , as follows:

(9) $K_{s\lambda }=33394{\lambda }^{2.3}$(9)

where λ is in m and K_sλ is in m/s.

The Gardner model in Equation (5)(5) $K_{\lambda }\left(\psi \right)=K_{s\lambda }\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }\psi \right)$(5) is used since it is simple and contains only two hydraulic parameters. While the saturated hydraulic conductivity K_sλ can be related to the particle diameter in Equation (9)(9) $K_{s\lambda }=33394{\lambda }^{2.3}$(9) , there is another important pore-size distribution parameter α_λ in the hydraulic conductivity model. Similar to K_sλ, α_λ could also be related to the effective particle diameter in the stream tube. However, there are limited data of Gardner α_λ that can be used to develop a reliable regression relationship. The other widely used hydraulic conductivity model (van Genuchten 1980) is therefore used to link α_λ and K_sλ, as described in the following. The van Genuchten model of hydraulic conductivity has the following form (van Genuchten 1980):

(10) $K_{\lambda }\left(\psi \right)=\frac{K_{s\lambda }{\left\{1-{\left({\alpha }_{\lambda vG}\psi \right)}^{mn}{\left[1+{\left({\alpha }_{\lambda vG}\psi \right)}^n\right]}^{-m}\right\}}^2}{{\left[1+{\left({\alpha }_{\lambda vG}\psi \right)}^n\right]}^{\frac{m}{2}}}$(10)

where α_λvG is the pore-size distribution parameter in the van Genuchten model, n and m are the parameters that determine the shape of the soil water retention curve.

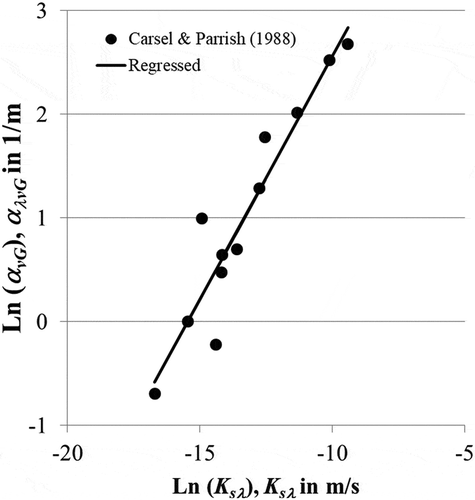
From the van Genuchten (1980) hydraulic parameters for 12 major soil textural groups according to the study by Carsel and Parrish (1988), a regression relationship can first be established between K_sλ and α_λvG. Figure 2 shows the scatterplot of ln(K_sλ) and ln(α_λvG) based on these 12 major soil groups from Carsel and Parrish (1988). The linear regression relation between ln(K_sλ) and ln(α_λvG) could be developed as:

(11) $\mathrm{l}\mathrm{n}\left({\alpha }_{\lambda vG}\right)=0.468\mathrm{l}\mathrm{n}\left(K_{s\lambda }\right)+7.236$(11)

Figure 2. Scatter plot of ln(α_λvG) and ln(K_sλ) and the regressed relationship.

where α_λvG is in 1/m, and K_sλ is in m/s. Equation (11)(11) $\mathrm{l}\mathrm{n}\left({\alpha }_{\lambda vG}\right)=0.468\mathrm{l}\mathrm{n}\left(K_{s\lambda }\right)+7.236$(11) is also plotted in Fig. 2. The correlation coefficient between the actual ln(α_λvG) and regressed ln(α_λvG) is 0.948. The linear correlation in Equation (11)(11) $\mathrm{l}\mathrm{n}\left({\alpha }_{\lambda vG}\right)=0.468\mathrm{l}\mathrm{n}\left(K_{s\lambda }\right)+7.236$(11) can be transformed into a power-law relation between α_λvG and K_sλ as follows:

(12) ${\alpha }_{\lambda vG}=1388K_{s\lambda }^{0.468}$(12)

The correlation coefficient between the actual α_λvG and regressed α_λvG is found to be 0.979.

Based on the study of Zhu et al. (2004) for upscaling evaporation in a heterogeneous landscape, the best correspondence between the Garnder α_λ and van Genuchten α_λvG could be approximately related as α_λ = 1.25α_λvG, which can be translated as follows for each stream tube (Zhu et al. 2004):

(13) ${ }_{\lambda }=227183{\lambda }^{1.08}$(13)

Therefore, both hydraulic parameters in Equations (5)(5) $K_{\lambda }\left(\psi \right)=K_{s\lambda }\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }\psi \right)$(5) and (6(6) $q_{\lambda }=K_{s\lambda }\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }{\psi }_s\right)}{1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)}$(6) ), i.e. K_sλ and α_λ, are now related to the particle diameter λ through Equations (9)(9) $K_{s\lambda }=33394{\lambda }^{2.3}$(9) and (13(13) ${ }_{\lambda }=227183{\lambda }^{1.08}$(13) ), which follows a fractal distribution. Based on the specific discharge formula in Equation (7)(7) $q_{\lambda }=K_{s\lambda }\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\varphi \right)}{1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)}$(7) and the fractal distribution of λ in Equation (1)(1) $N\left(\mathrm{\Lambda }\ge \lambda \right)={\left(\frac{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\lambda }\right)}^{D_f}$(1) , the effective (average) specific discharge through the fractal unsaturated domain can be determined, which is described in the following section.

2.4 Effective specific discharge in fractal unsaturated soils

For each stream tube, the cross-sectional area perpendicular to flow is assumed to be proportional to λ², A_λ = Bλ², where B is a proportionality constant. This assumption is made due to the fact that the pore size is directly proportional to the particle diameter and the stream-tube area is proportional to the square of pore size. The total cross-sectional area can be then determined by using the following equation and substituting Equation (3)(3) $-dN=D_f{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{D_f}{\lambda }^{-\left(D_f+1\right)}d\lambda$(3) into the integration:

(14) $A_t=-\underset{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{\overset{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\int }}{A}_{\lambda }dN=\frac{B{D}_f{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{2-D_f}\left[1-{\left(\frac{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)}^{\left(2-D_f\right)}\right]$(14)

The total volumetric flowrate through the unsaturated fractal soil domain can then be determined based on the fact that the volumetric flowrate in an individual stream tube is q_λA_λ, which leads to:

(15) $Q_t=-\underset{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{\overset{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\int }}{q}_{\lambda }{A}_{\lambda }dN=B{D}_f{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{D_f}\underset{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{\overset{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\int }}{q}_{\lambda }{\lambda }^{\left(1-D_f\right)}d\lambda$(15)

Then effective specific discharge can then be determined by the average specific discharge from the entire unsaturated zone between the water table and the land surface:

(16) $q_{\mathrm{e}\mathrm{f}\mathrm{f}}=\frac{Q_t}{A_t}=\frac{\left(2-D_f\right){\int }_{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}^{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{q}_{\lambda }{\lambda }^{\left(1-D_f\right)}d\lambda }{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\left(2-D_f\right)}\left[1-{\left(\frac{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)}^{\left(2-D_f\right)}\right]}$(16)

The integration term in the numerator in Equation (16)(16) $q_{\mathrm{e}\mathrm{f}\mathrm{f}}=\frac{Q_t}{A_t}=\frac{\left(2-D_f\right){\int }_{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}^{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{q}_{\lambda }{\lambda }^{\left(1-D_f\right)}d\lambda }{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\left(2-D_f\right)}\left[1-{\left(\frac{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)}^{\left(2-D_f\right)}\right]}$(16) is carried out numerically.

One convenient and often adopted approach to approximate specific discharge (evaporation or infiltration) is to use the average particle diameter. The calculation of the approximate average flux, q_app, is expressed as follows:

(17) $K_{s\mathrm{a}\mathrm{p}\mathrm{p}}=33394{\left(\bar{\lambda }\right)}^{2.3}$(17)

(18) ${\alpha }_{\mathrm{a}\mathrm{p}\mathrm{p}}=227183{\left(\bar{\lambda }\right)}^{1.08}$(18)

(19) $q_{\mathrm{a}\mathrm{p}\mathrm{p}}=K_{s\mathrm{a}\mathrm{p}\mathrm{p}}\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\mathrm{a}\mathrm{p}\mathrm{p}}L\right)-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\mathrm{a}\mathrm{p}\mathrm{p}}L\varphi \right)}{1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\mathrm{a}\mathrm{p}\mathrm{p}}L\right)}$(19)

Note that the approximate saturated hydraulic conductivity and pore-size distribution parameter in Equations (17)(17) $K_{s\mathrm{a}\mathrm{p}\mathrm{p}}=33394{\left(\bar{\lambda }\right)}^{2.3}$(17) and (18(18) ${\alpha }_{\mathrm{a}\mathrm{p}\mathrm{p}}=227183{\left(\bar{\lambda }\right)}^{1.08}$(18) ) are obtained by substituting average λ (i.e. $\bar{\lambda }$) into Equations (9)(9) $K_{s\lambda }=33394{\lambda }^{2.3}$(9) and (13(13) ${ }_{\lambda }=227183{\lambda }^{1.08}$(13) ), respectively.

The ratio of the approximate specific discharge over the effective specific discharge is determined as:

(20) $r=\frac{q_{\mathrm{a}\mathrm{p}\mathrm{p}}}{q_{\mathrm{e}\mathrm{f}\mathrm{f}}}$(20)

The simple approximate approach under-estimates the specific discharge if r < 1 and over-estimates it if r > 1. In the following section, the specific discharge in Equation (16)(16) $q_{\mathrm{e}\mathrm{f}\mathrm{f}}=\frac{Q_t}{A_t}=\frac{\left(2-D_f\right){\int }_{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}^{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{q}_{\lambda }{\lambda }^{\left(1-D_f\right)}d\lambda }{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\left(2-D_f\right)}\left[1-{\left(\frac{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)}^{\left(2-D_f\right)}\right]}$(16) and the specific discharge ratio in Equation (20)(20) $r=\frac{q_{\mathrm{a}\mathrm{p}\mathrm{p}}}{q_{\mathrm{e}\mathrm{f}\mathrm{f}}}$(20) are calculated in relation to the fractal dimension D_f, the ratio of minimum over maximum particle diameters λ_min/λ_max, the ratio of water table depth over the maximum particle diameter L/λ_max, and the dimensionless suction head, ϕ = ψ_s/L. The calculated results are then analyzed and discussed.

3 Results and discussion

From Equation (7)(7) $q_{\lambda }=K_{s\lambda }\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\varphi \right)}{1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)}$(7) , it can be determined that the specific discharge generally increases with increasing particle diameter then decreases quickly as the particle diameter further increases for both evaporation and infiltration. Due to the strong non-linear nature of flow in the unsaturated soil, the specific discharge linearly increases with the saturated hydraulic conductivity but decreases exponentially with the pore-size distribution parameter. The saturated hydraulic conductivity increases with the particle diameter seen in Equation (9)(9) $K_{s\lambda }=33394{\lambda }^{2.3}$(9) . On the other hand, the decay exponent also increases with the particle diameter from the combination of Equation (7)(7) $q_{\lambda }=K_{s\lambda }\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\varphi \right)}{1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\lambda }L\right)}$(7) and Equation (13)(13) ${ }_{\lambda }=227183{\lambda }^{1.08}$(13) . This competing interplay of increasing the saturated hydraulic conductivity and increasing decay exponent with the particle diameter results in the non-monotonic relation between the specific discharge and particle diameter. At certain particle diameter, the specific discharge reaches a maximum. The particle diameter when the specific discharge reaches a maximum is related to the depth to water table L and the suction head at the land surface.

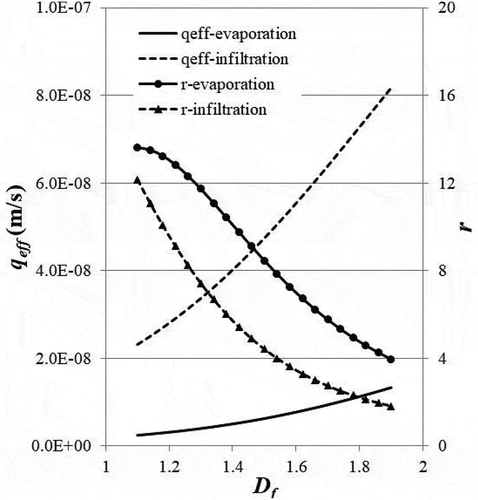
Figure 3 shows the results of effective discharge and the ratio of the approximate specific discharge over the effective specific discharge as functions of the fractal dimension. The effective specific discharge increases with the fractal dimension for both evaporation and infiltration. For a fractal distribution, the total number of stream tubes increases with the fractal dimension indicated by the power-law relation in Equation (2)(2) $N_t(\wedge \ge {\lambda }_{min})={\left(\frac{{\lambda }_{max}}{{\lambda }_{min}}\right)}^{D_f}$(2) with the given value of λ_max/λ_min. On the other hand, the total area of these stream tubes also increases with the fractal dimension D_f seen in Equation (14)(14) $A_t=-\underset{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{\overset{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\int }}{A}_{\lambda }dN=\frac{B{D}_f{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{2-D_f}\left[1-{\left(\frac{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)}^{\left(2-D_f\right)}\right]$(14) . However, the power-law increase in the total number of stream tubes is faster than the total area increase with the fractal dimension, which leads to the increase of specific discharge with the fractal dimension. The specific discharge based on the average particle diameter of fractal soil varies in a much smaller range compared to the effective specific discharge. As a result, the ratio of the specific discharge based on the average particle diameter over the effective specific discharge decreases with increasing fractal dimension. The specific discharge based on the average diameter in general over-estimates the effective specific discharge since the ratio shown in Fig. 3 is larger than 1.

Figure 3. The influence of fractal dimension of particle diameter, D_f, on the effective specific discharge, q_eff, and the specific discharge ratio, r, for both evaporation (ϕ = 1.5) and infiltration (ϕ = 0.5). Other parameters include: λ_max = 0.001 m, λ_min/λ_max = 0.01, and L/λ_max = 1000.

The results in Fig. 4 show that the effective specific discharge decreases with increasing maximum diameter λ_max, while the specific discharge ratio increases with λ_max. In general, the specific discharge for both evaporation and infiltration decreases when the particle diameter increases. While the total number of stream tubes increases at the rate of ${\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{D_f}$ from Equation (2)(2) $N_t(\wedge \ge {\lambda }_{min})={\left(\frac{{\lambda }_{max}}{{\lambda }_{min}}\right)}^{D_f}$(2) , the increase of total area is at the rate of ${\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^2$, which means the number of stream tubes increases at a slower rate than the total area since D_f is smaller than 2. This difference in the rate of increases in the total number of stream tubes and the area available for flow is the main reason that the specific discharge for both evaporation and infiltration decreases with the maximum particle diameter. The average diameter increases linearly with λ_max, which results in decreasing specific discharge with increasing λ_max. However, the effective discharge decreases at a faster pace compared to the specific discharge based on the average particle diameter of fractal unsaturated soil domain. As a result, the ratio of specific discharge based on the average diameter over the effective specific discharge increases with the maximum diameter λ_max, as shown in Fig. 4.

Figure 4. The influence of maximum particle diameter, λ_max, on the effective specific discharge, q_eff, and the specific discharge ratio, r, for both evaporation (ϕ = 1.5) and infiltration (ϕ = 0.5). Other parameters include: D_f = 1.5, λ_min = 0.0001 m, and L = 1 m.

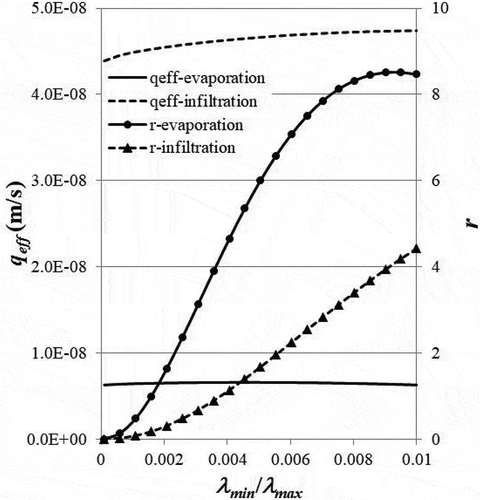
The results shown in Fig. 5 demonstrate that the effective specific discharge slightly increases with increasing particle diameter ratio, λ_min/λ_max. In this case, both the evaporation and infiltration specific discharge increases with increasing diameter ratio. Increasing the diameter ratio while keeping the maximum diameter a constant shifts the diameter distribution to the high values. Since the average diameter for the fractal distribution is near the low end of the distribution range, the increase in the diameter ratio increases the average diameter in the low range. Since the specific discharge increases with the diameter at the low range of diameter distribution, the specific discharge increases with the increasing diameter ratio. The increase in the specific discharge based on the average diameter is at a faster pace than the effective specific discharge. Therefore, the specific discharge ratio is mostly larger than one and increases with λ_min/λ_max, shown in Fig. 5.

Figure 5. The influence of particle diameter ratio, λ_min/λ_max, on the effective specific discharge, q_eff, and the specific discharge ratio, r, for both evaporation (ϕ = 1.5) and infiltration (ϕ = 0.5). Other parameters include: D_f = 1.5, λ_max = 0.001 m, and L/λ_max = 1000.

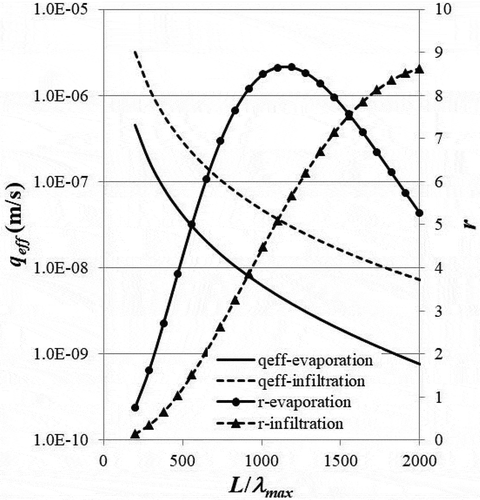
Figure 6 shows the results of effective specific discharge and the specific discharge ratio as a function of the depth to the water table. In general, as the water table becomes deep, the specific discharge for both evaporation and infiltration under otherwise same conditions decreases quickly. For evaporation, the effective discharge decreases at a higher rate than that based on the average diameter when water table depth is shallow. However, when water table depth is deep, its decrease slows down and results in the decrease in the specific discharge ratio, shown in Fig. 6. For infiltration, the specific discharge based on the average diameter is generally higher than the effective specific discharge. For a medium with the diameter having a fractal distribution, the majority of the stream tubes are smaller than the average diameter with only a few stream tubes with very large diameters. Since the flowrate generally increases with the diameter as discussed earlier, the flowrate based on the average diameter is generally larger than the flowrate in the fractal medium, which means the specific discharge ratio is generally larger than 1, shown in Fig. 6.

Figure 6. The influence of water table depth ratio, L/λ_max, on the effective specific discharge, q_eff, and the specific discharge ratio, r, for both evaporation (ϕ = 1.5) and infiltration (ϕ = 0.5). Other parameters include: D_f = 1.5, λ_max = 0.001 m, and λ_min/λ_max = 0.01.

The evaporation and infiltration in unsaturated fractal soil are complex non-linear physical processes due to the strong non-linear hydraulic property functions and fractal soil characteristics. The coupling effect of these two strong non-linear behaviors makes the prediction of evaporation and infiltration in the unsaturated soil between the land surface and water table challenging. In this study, only the steady-state case is considered, a scenario likely encountered between precipitation events in real-world scenarios. Exploring the unsteady state evaporation and infiltration in fractal soils could be achieved in future studies.

Although this study has identified important factors that affect the evaporation and infiltration in a fractal unsaturated zone, the flow process between the land surface and the water table is a complicated process affected by a wide range of factors. Currently, experimental and field studies with proper characterizations of required input parameters such as fractal dimension along with large-scale evaporation and infiltration at a heterogeneous landscape are scant; if augmented, they could significantly improve prediction of flux through the interface of atmosphere and subsurface. This study has demonstrated the importance of the identified factors that call for more concerted scientific efforts and provide guidance for future studies.

4 Conclusions

In this study, an approach is developed to quantify the impact of fractal characteristics of unsaturated soil between the land surface and water table on the steady-state evaporation and infiltration behaviors. The unsaturated soil domain is conceptualized as a collection of stream tubes of soils. The soils are represented by particles with a representative diameter in each stream tube. The particle diameters in various stream tubes follow a fractal distribution. The soil saturated hydraulic conductivity and the pore-size distribution parameter are related by a power-law relationship. The saturated hydraulic conductivity of each stream tube is a quadratic function of effective particle diameter. The steady-state specific discharge in each stream tube is calculated based on the mass conservation and Darcy’s laws. The effective specific discharge for both evaporation and infiltration is then integrated from the specific discharge for each stream tube and the fractal distribution.

It is demonstrated that the effective specific discharge for both evaporation and infiltration in unsaturated fractal soils increases with the fractal dimension. The ratio of minimum over maximum diameters in the fractal soil does not significantly affect the specific discharge in the fractal soil. Coarse fractal medium and deep water table decrease both evaporation and infiltration significantly. The specific discharge predicted by using the average particle diameter largely over-predicts the actual effective specific discharge in the unsaturated fractal soils. This is because the average diameter of the fractal medium is significantly skewed toward the low end and small diameter medium has high specific discharge.

Disclosure statement

No potential conflict of interest was reported by the author.