Thermal characteristics of microwave ablation in the vicinity of an arterial bifurcation

Abstract

Purpose: The objective of this research was to reveal the thermal characteristics of microwave ablations in the vicinity of an arterial bifurcation.

Methods: The temperature distribution after microwave heating of a liver-like material in the close proximity of an arterial bifurcation was simulated using the finite element method. Coupled fluid flow and solid heat transfer were taken into consideration and a three-dimensional analysis was performed. An experimentally determined SAR (specific absorption rate) generated by the absorption of microwaves in liver-like material was used in the analysis instead of utilizing electromagnetic calculations. Several different tests of time-controlled ablations with varying distances between the microwave antenna and the bifurcation were performed and detailed temperature distributions near the bifurcation were obtained.

Results: The interaction between the recirculation flow in the bifurcation and the heat transfer in the surrounding tissue makes the temperature distribution near the bifurcation complicated. Most importantly, after a period of continuous heating with constant microwave output power, the maximum temperatures caused by the ablation did not always increase with the distance between the antenna and the bifurcation.

Conclusion: It can be concluded that inadequate ablations can be the result not only from a close proximity between the antenna and the blood vessel, but also from a complicated blood flow in large vessels whose structure causes recirculation flow.

• Microwave ablation therapy
• temperature field
• arterial bifurcation

Introduction

In recent years, focal thermal ablation has been developing as an important oncology therapeutic approach because it is minimally invasive. It aims at increasing the temperature of malignant tissues to above 54° in order to destroy the tumour by energy blasts. A major problem in the quality assurance of thermal ablations is temperature distribution control, in which the impact of blood flow, especially flow in large arterial vessels, has to be accounted for because cold blood enters the locally heated volume, applies cooling, removes heat and by doing so can severely affect the temperature distribution [1]. Successful thermal ablation is often impeded by blood flow in the vicinity of the tumour that tends to cool the tissue.

Fractal branching is the most important feature of vessel networks. The flow pattern is significantly disturbed at the bifurcation, which may result in complicated flow patterns such as recirculation. This complicated blood flow may affect the adjacent temperature distribution in the area of a thermal ablation. So studying the bio-heat transformation near an arterial bifurcation can provide a basis for understanding the impact of complicated vasculature on thermal ablation.

Many thermal models have been developed to describe the influence of blood flow on the temperature distribution due to thermal ablation. Basically two approaches can be distinguished, the continuum model and the discrete vessel model. The most commonly used continuum model is the Pennes bio-heat or heat-sink model [2] in which the thermal impact of blood is described by introducing an energy drain that is proportional to the volumetric blood perfusion level and the temperature elevation of the local tissue. This type of model is often employed to explain the thermal effects of capillary blood perfusion. In the discrete vessel model [3], [4], the thermal impact of many large vessel segments within a complex vasculature must be taken into account individually. The thermal impact of blood flow on temperature distribution can be calculated analytically only for very basic vessel configurations, as was done for single vessels by Chen and Holmes [5], and for counter-current vessels by Baish et al. [6]. However, modeling the thermal impact of such a complex, detailed, discrete vasculature has to be done numerically. The first numerical model could only cope with straight vessels [7], [8] or branching networks with only perpendicular vessel connections [9]. Tungjitkusolmun et al. [8] simulated the temperature distribution near a bifurcated blood vessel, but the model was two-dimensional. Mooibroek and Lagendijk [10] presented a more versatile model that could cope with curved vessel networks. However, the vessel description in their model was directly coupled with the resolution of the discretized tissue, which made it cumbersome to describe extensive and curved vasculature. A very flexible and versatile discrete vasculature model, in which the vessel description was done geometrically and was completely independent of the tissue description, was developed by Kotte et al. [3], [4]. This model can be used to calculate the thermal impact of very detailed vessel networks. Recently, an excellent work was done by Sheu et al. [11] to investigate the heat sink effect of blood perfusion in radio-frequency ablation. They considered a simplified two-dimensional bifurcated blood vessel and coupled the thermal-electric effects with haemodynamics to simulate the temperature distribution, but as is often the case in a discrete vessel model, they introduced the convective coefficient as a lumped parameter to reflect the blood perfusion effect on ablation. Thus, the detailed thermal characteristics at any specific arterial segment such as at a bifurcation could not be revealed.

The objective of this research was to reveal the detailed thermal characteristics of microwave ablation in the vicinity of an arterial bifurcation. The temperature distribution in liver-like material heated by microwaves was simulated using the finite element method. Coupled fluid flow and solid heat transfer were taken into consideration and the analysis was three-dimensional. This study focused on the detailed interaction of complicated blood flow in the bifurcation with the heat transfer in the adjacent tissue by simultaneously treating the coupled blood flow and heat transfer, so that the energy balance between the blood and the solid tissue could be attained automatically and accurately. Several examples of time-controlled ablation with different distances between the microwave antenna and the bifurcation were modeled and detailed temperature distributions near the bifurcation were obtained.

Mathematical model for microwave ablation therapy

Thermal diffusion and conduction in biological tissue can be described by the Pennes bio-heat equation [2],where ρ and ρ_b are the density of tissue and blood, respectively (kg m⁻³), c and c_b are the specific heat of tissue and blood, respectively (J kg⁻¹ K⁻¹), λ is the thermal conductivity of tissue (W m⁻¹ K⁻¹), ω_b is the blood perfusion rate (kg s⁻¹m⁻³), q_m is the excess heat energy generated by metabolism (W m⁻³) (which is so small that it can be neglected in the analysis [8]) and q_r is the microwave energy that is absorbed by tissue per unit volume per unit time (W m⁻³ s⁻¹). Thus, the thermal distribution in tissue during microwave ablation therapy is correlated with the parameters involved in Equation (1), such as thermal properties, blood perfusion rate and specific thermal absorption rate of tissue for microwaves.

Thermal properties and blood perfusion rate of liver tissue

Generally speaking, it is difficult to measure tissue thermal properties because they are spatially, temporally and even temperature dependent. The thermal properties of pig liver used in this study are shown in Table I [12].

Table I.  Thermal properties of liver tissue [12].

	Temperature range
Parameters	20–70°C	80–100°C	110–120°C
Thermal conductivity (W m^−1 K^−1)	0.465	0.867	1.460
Density (kg m^−3)	1.020	1.020	1.020
Specific heat (J kg^−1 K^−1)	3.628	3.858	3.986

The blood perfusion rates in liver are shown in Figure 1, which is a modified temperature dependency curve from the literature [13]. The solid line denotes the blood perfusion rate from the literature [13]; the broken line shows the assumption that the blood perfusion rate will drop to zero when the tissue temperature exceeds 54°C.

Figure 1. Blood perfusion rate for health liver tissue [13].

Specific absorption rate

The specific absorption rate (SAR) distribution for microwaves in a treated domain can be calculated theoretically by the energy of radiated electromagnetic waves using Maxwell's equation [14]. Actually, it is impossible to compute the SAR distribution accurately [15] for complicated electromagnetic energy distributions near the antenna in microwave therapeutic systems, so the SAR distribution is often determined in practice using experimental data.

Other researchers have investigated a coaxial microwave antenna (Figure 2) [16], [17] and obtained optimal preferences for percutaneous microwave ablation therapy, namely that the inner conductor length of the forepart of the microwave antenna should be one quarter of the radiated microwave wavelength. Under this condition, the impedance between the antenna and the tissue matches well, and the shape of the ablation zone is approximately spherical.

Figure 2. Diagram of microwave electrode.

In the present study, the microwave antenna was operated at a frequency of 2450 MHz with a diameter of 1.4 mm. Preliminary experiments in the homogeneous phantom demonstrated that the thermal distribution was axially symmetric. In the r direction, SAR was fitted to an exponential decay. In the z direction, a least-squares residual method was used to fit the experimental data. However, in the z direction (along the antenna), the power deposition was asymmetric, so SAR was divided into front and back areas. Therefore, the distribution function of SAR can be described aswhere α and x_i (i = 1, 2, 3) can be determined experimentally, as shown in Table II, r and z are in cm and SAR is in W cm⁻³. It is important to note that these SAR distribution functions only fit the specified condition of the microwave antenna and its corresponding output power.

Table II.  Distribution functions of SAR/(ρc) from [17].

Numerical model and methodology

Geometric model

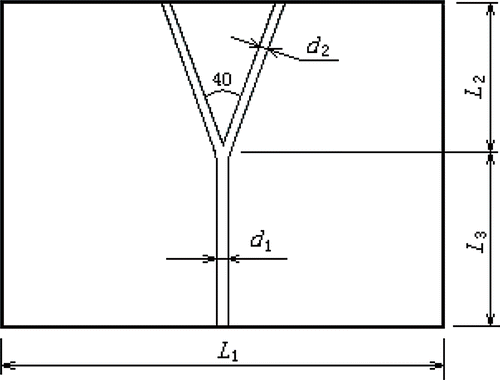
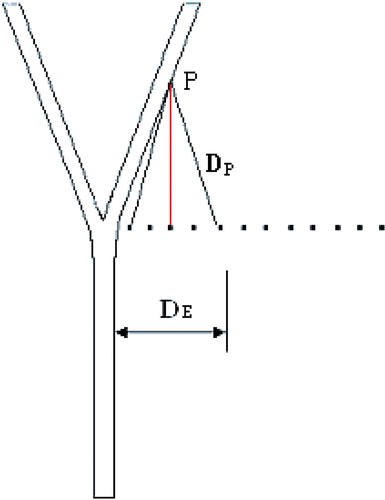
The present geometric model consists of a symmetric arterial bifurcation and a liver-like material with a sufficiently large volume surrounding the vessels (Figure 3). The dimensions can be seen in Figure 3, where d₁ = 0.4 cm, d₂ = 0.28 cm, L₁ = 10 cm, L₂ = 5 cm and L₃ = 5 cm.

Figure 3. Dimensions of the numerical model.

The microwave antenna was inserted into the liver-like material beside the bifurcation at different positions. For simplification and convenience, the antenna was placed in the plane perpendicular to the vessel's plane (Figure 4). The different positions of the microwave antenna are shown in Figure 4, in which the dots denote different positions of the antenna and the distance between two neighbouring positions was 0.5 cm.

Figure 4. Positions of the microwave antenna.

Finite element model

The vessel wall was assumed to be thin and was neglected to avoid clustering of elements. The finite element model consisted of ∼110 000 fluid elements and 310 000 solid heat transfer elements and the total nodes were ∼72 000, which ensured that the numerical results were independent of the finite element mesh. The mesh of fluid near the arterial wall was refined to suit the boundary flow and the solid mesh near the antenna was also refined to capture the rapid temperature variation in the vicinity of the antenna.

Boundary conditions

The boundary conditions for the simulation were as follows. The inlet velocity of the main artery was uniform at 50 cm s⁻¹. At the outlets of the arterial bifurcations the reference pressure was set as zero. As far as the heat was concerned, a constant temperature of 37°C was set at the outer walls of the cubic volume, based on the assumption that the volume was large enough for the outer wall temperature to be unaffected by the ablation. The microwave output power used here was 60 W and the corresponding SAR distribution in Table II was used as the heat generation rate in the simulation.

The blood flow was assumed to be steady and laminar and the blood was taken as an incompressible Newtonian fluid with constant density of 1.06 g cm⁻³, viscosity of 4.24 × 10⁻² g cm⁻¹ s⁻¹, conductivity of 0.00465 W cm⁻¹ K⁻¹ and specific heat of 3.858 J kg⁻¹ K⁻¹.

Methodology

The temperature distribution in liver-like material heated by microwave was simulated using a finite element package of ANSYS9.0 (ANSYS Inc. Houston, PA). Although a thermal ablation is usually temperature-controlled, so as to keep the maximum temperature at a specific value for a period of time, this study performed a time-controlled ablation with continuous heating at constant microwave output power in order to observe the temperature near the bifurcation, since this therapy is also widely employed in clinical practice. A transient heat transfer process with 600 s continuous heating duration was simulated after the development of steady laminar blood flow, which implies that the flow in the bifurcation was independent of the heat transfer. When solving the blood flow equations, the SIMPLEF algorithm, which has been extensively validated, was used for velocity-pressure coupling. A Tri-Diagonal Matrix Algorithm (TDMA) solver was adopted for the discretized momentum Navier-Stokes equations; whereas a Pre-Conditioned Conjugate Residual (PCCR) solver was used for the pressure equation. It took about half an hour to get a converged flow field on a DELL Precision 670 workstation. After the convergence of the flow field calculation, a transient conjugate heat transfer process in both solid and fluid was simulated with a PCCR solver. A small time increment of 0.1 s was adopted to ensure computational accuracy.

Although different positions of antenna location from the bifurcation were simulated, for brevity one has been chosen to provide the detailed thermal characteristics when the microwave antenna was placed 1.0 cm away from the bifurcation.

Numerical results

The numerical results given here include velocity and temperature in the arterial bifurcation, temperature distribution near the bifurcation, ablation zone and thermal characteristics in the vicinity of the bifurcation.

Velocity in the arterial bifurcation

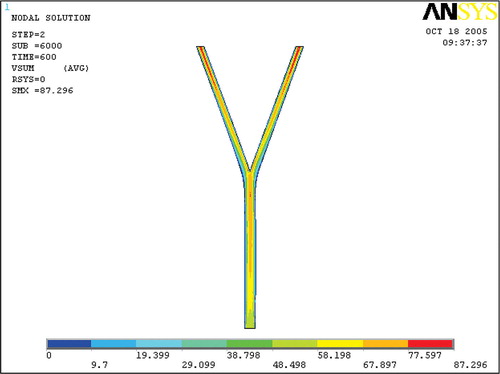
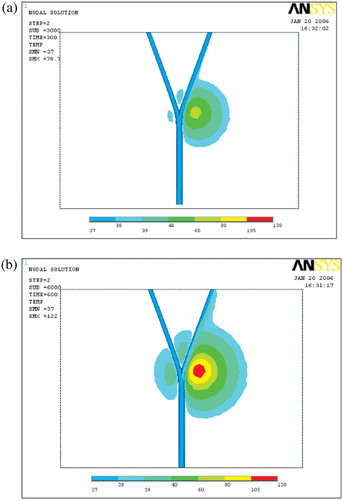
The velocity in the arterial bifurcation is shown in Figure 5. It was expected to find the common features of branching flow. In the inlet segment vessel, the flow developed from uniform flow to fully developed laminar flow, which was indicated by a velocity increase near the centre-line of the main vessel and a velocity decrease near the vessel wall due to boundary layer friction. After the bifurcation, the flow was divided into two branching flows and a region of recirculation flow, where the flow velocity was very low, developed at the outer wall of each daughter branch.

Figure 5. Velocity in the arterial bifurcation.

Temperature in the arterial bifurcation

The temperature in the blood flow at the end of the heating is depicted in Figure 6. It shows that the blood temperature in the right branch increased noticeably. This region of increased temperature was coincident with the flow recirculation zone and was located where the velocity was low. The temperature increase in the left branch was not as large as in the right one; however the temperature increase in the left recirculation zone was also noticeable.

Figure 6. Temperature in the arterial blood flow.

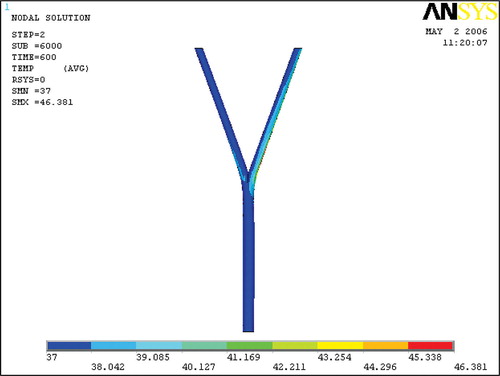
Temperature distributions in the vicinity of the bifurcation

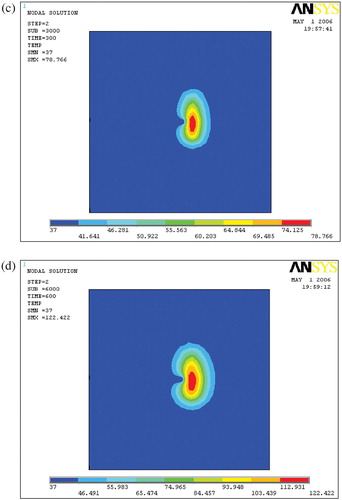
Figure 7 shows the temperature distribution in the vicinity of the bifurcation at different times during heating. From Figure 7(a) and (b), it is obvious that in the right branch the heat was transferred significantly by advection to the outlet. From Figure 7(c) and (d) it can be seen that the temperature field was attenuated by the cooling effect of blood flow. This temperature field attenuation can cause low temperatures, causing the thermal ablation to fail.

Figure 7. Temperature near the bifurcation. (a) Front View, T = 300 s; (b) Front View, T = 600 s; (c) Bottom View, T = 300 s; (d) Bottom View, T = 600 s.

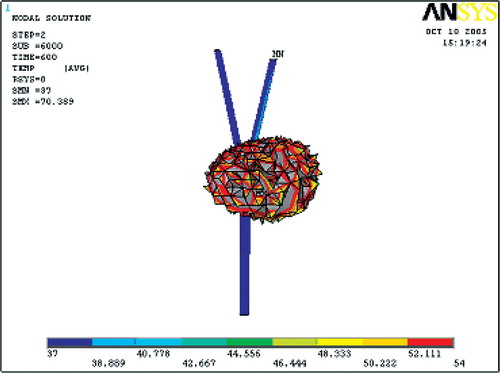
Ablation lesion

Figures 8 and 9 show the ablation lesions at different times during the thermal ablation. The ablation lesion was defined as the volume having a temperature above 54°C. At the beginning, the blood vessel had less cooling impact on the temperature field. With time increasing, the heated region gradually expanded to the blood vessel, so increased cooling impact of the blood flow was exerted on the temperature field. Thus, the ablation lesion was increasingly reduced throughout the ablation process.

Figure 8. Ablation lesions at different times. (a) T = 300 s; (b) T = 600 s.

Figure 9. Ablation lesion in 3D view.

Thermal characteristics in the vicinity of the bifurcation

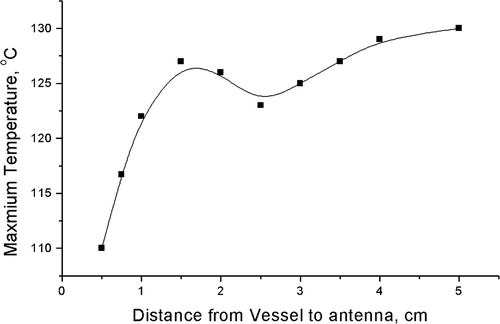
Figure 10 shows the ablation temperature distribution when the antenna was placed at different locations with respect to the bifurcation. Comparing the maximum temperatures produced during the ablation, when the antenna was located at different positions with respect to the bifurcation, it is interesting to note that the maximum temperatures of the ablation did not always increase with the distance between the antenna and the bifurcation (Figure 11).

Figure 10. Temperature distribution with different D_E. (a) D_E = 0.5 cm; (b) D_E = 1.0 cm; (c) D_E = 1.5 cm; (d) D_E = 2.0 cm; (e) D_E = 2.5 cm.

Figure 11. Thermal characteristics in vicinity of bifurcation.

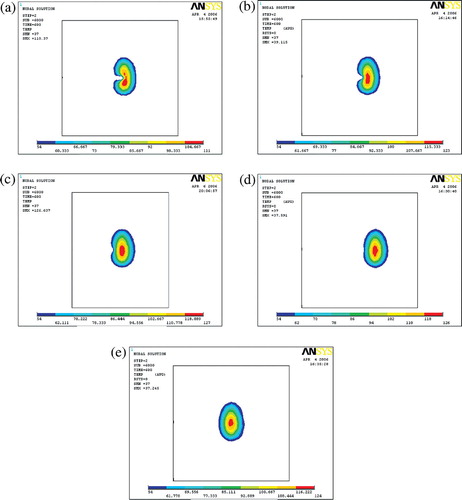
One should note two different distances: one was the distance between the antenna and the bifurcation D_E in Figure 12. The other was the distance between the antenna and the point P, D_P, where P represents the end of the recirculation zone. With increase in distance D_E, the influence of the blood flow in the main vessel on the temperature field decreased and the main vessel had less and less advective impact. At the same time, the distance of D_P decreased, so the daughter vessel had more and more advective impact on the temperature field in the vicinity of the bifurcation. When the distance D_E reached 1.5 cm, these two converse effects were balanced and the highest maximum temperature was obtained. After that, the convective effect of the daughter branches played the more important role, so the maximum temperature decreased. When the distance reached ∼2.5 cm, the right daughter branch had the strongest advective cooling effect, so the maximum temperature was the lowest. Later on, both the main and daughter vessels provided less advective cooling effects because of the greater distance, thus the maximum temperature increased.

Figure 12. Two different distances.

Discussion and conclusions

The thermal features of a microwave ablation in the vicinity of an arterial bifurcation were numerically studied as a representative of vessel networks. The velocity in the arterial bifurcation, the temperature in the arterial bifurcation, the temperature distributions in the vicinity of the bifurcation and the ablation lesion were explored and analysed. It was found that the blood flow in the bifurcation had a strong convective cooling effect on the surrounding temperature field and that the maximum temperatures of the time-controlled continuous constant power ablation did not always increase with the distance between the antenna and the bifurcation. This is because of interactions between the blood flow and the temperature field, especially the recirculation flow in the two daughter branch vessels. This observation implies that inadequate ablation results not only from close distances between the antenna and the blood vessel, but also from complicated blood flow in large vessels whose structure causes recirculation flow.

What is the physical mechanism behind this phenomenon? First, it should be noted that a recirculation region existed in the daughter branch vessels immediately after the bifurcation. The recirculation zone has a very weak convective effect on the temperature field because of the low blood velocity and the recirculation zone actually acted as a thermal insulating layer between the tissue and the blood because of the lower conductivity of blood compared with that of liver material when temperature was above 70°. This implies that the part of the right branch vessel segment with the recirculation zone had a very weak advective effect while the other portion of the right branch, except for the recirculation zone, could continue to have a strong convective effect. Secondly, the distance D_P decreased first and increased later along with the constant increase of distance D_E, therefore, the advective effect of the right branch of the bifurcation on the temperature field experienced an increasing and decreasing process and the balance between the two arms of the bifurcation resulted in the highest maximum ablation temperature.

Although the detailed three-dimensional thermal characteristics of a microwave ablation in the vicinity of an arterial bifurcation were revealed, there were some limitations in this study. Firstly, the SAR distribution obtained from experimental data was used as a heat generation rate instead of coupling the electromagnetic calculation. So the present study has limited application and is only valid for the specific microwave antenna used here. Secondly, the antenna was placed in the plane perpendicular to the vessel plane for convenience. An antenna in parallel configuration should be included in future studies. Thirdly, interesting parameter variations based on the presented flow and heat model, such as changing vessel diameter, blood velocity etc, should be done to obtain the optimal heating for a certain blood flow. This would allow the temperature field to be as uniform as possible or to have a pre-defined distribution. Finally, the exact thermal balance between the two arms of the bifurcation is highly determined by the typical geometry and experiments are essential in order to verify the present numerical results.

Acknowledgements

This research is sponsored by National Science Foundation of China under grant No. 30470450. The authors express appreciation to Drs Rhoda E. and Edmund F. Perozzi for editing and English language assistance.