Hepatic radiofrequency ablation at low frequencies preferentially heats tumour tissue

Abstract

Purpose: Radiofrequency ablation is a clinically accepted treatment modality for liver cancer. There are significant differences in dielectric properties between normal and cancer tissue in the liver, which are particularly pronounced at frequencies below 100 kHz. This study performed computer simulations to determine whether radiofrequency (RF) ablation at lower frequencies than currently employed (450–500 kHz) can take advantage of this difference to preferentially deposit energy within the tumour.

Materials and methods: Finite Element Method computer models were created for a cooled needle electrode and a multi-tine RF electrode inserted into a 2 cm diameter tumour. RF ablation was simulated and current density as well as tissue temperature distribution determined. In vivo data were used on electrical conductivity of normal and cancer tissue in the models to simulate RF ablation in liver at the currently used frequency of 500 kHz and at 10 kHz.

Results: At 500 kHz there was little difference in RF current density and final tissue temperature between normal and cancer tissue. Due to the more pronounced differences in electrical conductivity at 10 kHz, cancer tissue was heated preferentially at this frequency. Depending on power control algorithm, this resulted in either higher intra-tumour temperatures or lower temperatures outside the tumour at 10 kHz compared to 500 kHz.

Conclusion: Radiofrequency ablation at lower frequencies than currently used may preferentially heat the tumour and preserve normal tissue. A targeted device for selective tumour destruction may be designed to make use of this principle.

• Radiofrequency ablation
• RF ablation
• thermal therapy
• cancer
• tumour ablation

Introduction

Thermal ablation therapies such as radiofrequency (RF) and microwave ablation are commonly used clinical treatment modalities for tumours not amenable to traditional surgery [1]. While mostly applied towards primary and metastatic liver cancer, ablation is increasingly employed for other cancer types such as lung, bone, kidney, breast and adrenal gland [2–5]. A number of different modalities are employed to heat tissue during tumour ablation including laser, microwaves, ultrasound and radiofrequency heating, with the latter one being used most widely worldwide.

During RF ablation, an electrode (typically 14–17 gauge diameter) is first inserted into a tumour percutaneously (i.e. through a small incision), laparoscopically or during open surgery. Alternating electric current in the radiofrequency spectrum (typically 450–500 kHz) is then applied to the electrode, resulting in resistive heating of the tissue around the electrode. Over the course of a typical procedure, a volume of tissue between 3–6 cm in diameter, spherically, elliptically or disc-like shaped—depending on electrode type—is heated above 50°C for several minutes, resulting in coagulation necrosis. The main reason frequencies ∼500 kHz are used is that this frequency range has been traditionally utilized for electrosurgery devices, which served as predicate devices for RF ablation systems.

Several studies that investigated dielectric properties of cancer tissue at radiofrequencies have shown a significant difference compared to normal tissue. Swarup et al. [6] measured fibrosarcoma in mice between 10 kHz and 100 MHz ex vivo and found electrical conductivity increasing with advancing tumour stages. Smith et al. [7] measured liver carcinoma ex vivo between 1 kHz and 13 MHz from a rabbit model and found 6–7.5 times higher electrical conductivity at low frequencies, but 2–5 times lower permittivity compared to normal liver tissue. Lu et al. [8] measured human glioma and surrounding tissue ex vivo between 5–500 MHz and found 30% higher permittivity and conductivity in tumours compared to surrounding tissue. They also calculated power absorption between tumour and normal tissue and found that—depending on the direction of the electromagnetic wave—power was absorbed preferentially by either tumour or normal tissue. The difference between normal and cancer tissue is especially pronounced in the breast due to the high fat content of breast tissue [9] and a recent modelling study suggested taking advantage of this difference to preferentially ablate breast tumours but not surrounding tissue [10]. For RF tumour ablation, two recent modelling studies have shown that differences in electrical conductivity between tumour and surrounding normal tissue significantly affect tissue heati [11], [12].

A previous study has measured electrical tissue conductivity of tumour and normal liver tissue in vivo in a rat model between 10 Hz and 1 MHz [13]. The results of all referenced studies are similar in that the difference between electrical tissue conductivity of normal and cancerous tissue becomes more pronounced at lower frequencies, with cancer tissue having higher electrical conductivity. In addition, there is organ and histology-specific variation in electrical properties, which will not be further addressed here.

This study used computer models to investigate whether this more pronounced difference at low frequencies could be used to improve efficacy of RF ablation compared to frequencies used currently by commercial devices.

Materials and methods

Electric RF field computation

During application of alternating electric fields to tissue, tissue heating results from conduction losses (i.e. resistive heating from ion movement) and from dielectric losses (due to rotation of molecules in an alternating electric field). In the frequency range relevant for RF ablation, heating due to dielectric losses is negligible. In fact, any displacement currents in tissue during RF ablation are negligible compared to conduction currents [14]. Therefore, this study only considers electrical tissue conductivity and can neglect tissue permittivity in the models.

During RF ablation a certain voltage is applied to the RF electrode. One can determine the resulting electric field in the tissue from the Laplace's equation:where σ = electrical tissue conductivity (S m⁻¹) and V = electric potential (V). The electric field intensity E (V m⁻¹) and current density J (A m⁻²) can be computed from:The local power density that results in tissue heating is the product of current density J and electric field intensity E (see equation (4), 2nd term on right side).

Tissue temperature computation

During RF ablation, tissue heating occurs due to electrically resistive heating around the electrode. Energy deposition by RF current, thermal conduction and tissue cooling by blood perfusion are described by Pennes’ Bioheat equation [15]:where ρ = tissue mass density (kg m⁻³), c = tissue specific heat (J(kg · K)⁻¹), k = tissue thermal conductivity (W(m · K)⁻¹), σ = tissue electrical conductivity (S m⁻¹), J = electric current density (A m⁻²), E = electric field intensity (V m⁻¹), T_bl = blood temperature (37°C), ρ_bl = blood mass density (kg m⁻³), c_bl = blood specific heat (J(kg · K)⁻¹) and w_bl = blood perfusion (m³(m³ · s)⁻¹).

Pennes’ Bioheat Equation [15] is the most widely used tissue perfusion model. In the Bioheat equation, the energy exchange between blood and tissue is modelled as a non-directional heat source. One major limiting assumption is that the heat transfer related to perfusion between tissue and blood occurs in the capillary bed, which turned out not to be fully correct. The main thermal equilibrium process takes place in the pre- or post-capillary vessels. Nevertheless, the Pennes model describes blood perfusion with acceptable accuracy, if no large vessels are nearby [16].

These models ignore any rise in blood flow in the liver at hyperthermic temperatures due to lack of accurate experimental data. However, blood flow changes in the liver are much less pronounced than in other tissues such as skin and muscle due to lack of thermoregulation. More crucial is that at high temperatures perfusion stops due to coagulation. This cessation of perfusion was simulated by a first order kinetic model:where E_a is the activation energy (J mol⁻¹) and A is the frequency factor (1 s⁻¹), w₀ is the baseline perfusion and w(t) is the time dependent perfusion. E_a = 6.67 · 10⁵ J mol⁻¹ and A = 1.98 · 10¹⁰⁶ s⁻¹ were used, which have been determined experimentally as parameters for micro-vascular stasis [17]. As baseline perfusion, physiological perfusion of liver was used at 1 L of blood per kg of tissue per minute [18].

Model geometry and boundary coditions

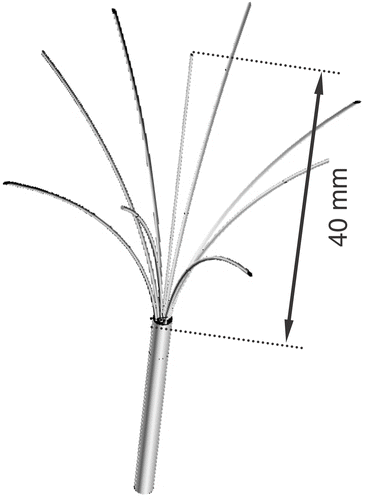
The finite element method (FEM) models were used to solve equations (1–6) and determine tissue temperature during the ablation procedure. Two commercial devices currently used clinically, a multi-prong electrode (Rita Starburst XL) and a cooled needle electrode (Valleylab Cool-Tip), were implemented. Figure 1 shows the geometry of the multi-prong electrode. The needle electrode is 1.5 mm (17 gauge) in diameter with the most distal 3 cm being electrically active. Due to symmetry, for the multi-prong electrode only a quarter of the electrode was implemented in the model and for the needle electrode an axi-symmetric 2-D model was used.

Figure 1. Multi-prong electrode (Rita Starburst XL).

In both simulations, electrodes were placed within a tumour of 20 mm diameter, with part of the electrodes in normal and parts in tumour tissue (see Figures 3 and 4). Electrodes and tumour were surrounded by a cylinder (200 mm diameter and 170 mm long) of normal liver tissue. A small mesh (0.1 mm) was used close to the electrode where electrical and thermal gradients are high and a large mesh size (5 mm) at the model boundary. Convergence tests were performed to confirm that the mesh size is sufficiently small and that the modelling domain is sufficiently large. As convergence criterion, this study used final tissue temperature and assumed sufficient mesh size and domain size when changing either by a factor of two resulted in a maximum change in temperature of less than 0.1°C.

Figure 2. Electrical conductivity of tumour and normal liver tissue. Averages of normal liver tissue and liver tumour tissue are shown from measurements performed in vivo on 17 rats (from [13], reproduced with permission from IOP Publishing).

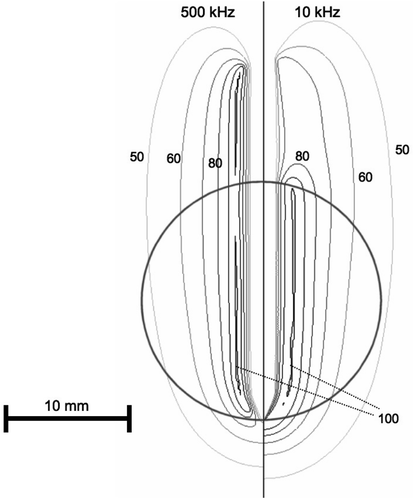
Figure 3. Electrical RF current density for cooled needle electrode, at 500 kHz (left) and 10 kHz (right) in a slice central through the electrode. At 10 kHz, current density significantly changes at tumour boundary (arrow). Current density is shown as percentage of maximum. Grey circle represents tumour boundary.

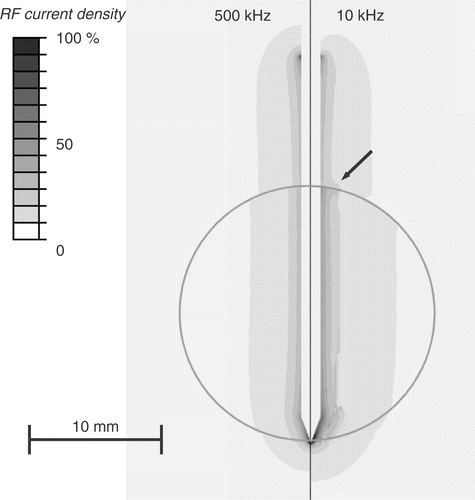
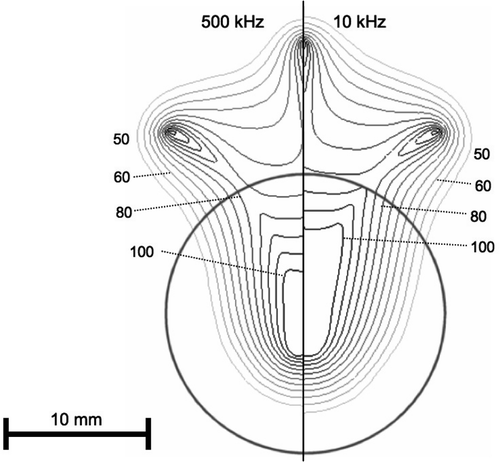
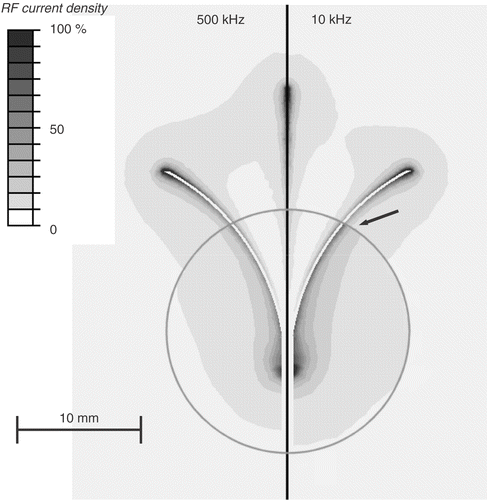
Figure 4. Electrical RF current density for multi-prong electrode, at 500 kHz (left) and 10 kHz (right) in a slice central through three of the prongs. At 10 kHz, current density significantly changes at tumour boundary (arrow). Current density is shown as percentage of maximum. Grey circle represents tumour boundary.

The two electrodes use different algorithms to control applied power delivery during the procedure [19]. The multi-prong electrode has thermocouples embedded in five of the tips and applied power is controlled as to keep average tip temperature ∼100°C for 25 min. A PI control algorithm was implemented in the computer model [20] that adjusts the voltage applied as boundary condition to the electrode surface to obtain a tip temperature of 100°C during the 25 min ablation simulation; no temperature boundary condition was applied for the multi-prong electrode. For the cooled needle electrode applied power is controlled depending on impedance measured between the electrode and the ground pad. As tissue temperature around the electrode exceeds 100°C and electrically insulating vapour forms, impedance rises; once a threshold of 20 Ω above baseline level (i.e. initial impedance) is exceeded, power is shut off for 15 s to allow for tissue to cool down and then re-applied at maximum level (200 W) for a total of 12 min [21]. In the computer model, a constant voltage was applied at the needle electrode surface as a boundary condition and impedance calculated during the simulation. This allowed one to implement the same impedance control algorithm used in the commercial device. The needle electrode is cooled by circulating chilled water. To simulate cooling, a constant temperature of 15°C was applied to the needle surface.

Both models applied 0 V electric potential at the outer model boundary. Initial tissue temperature was 37°C, which was also applied to the model boundary. RF ablation was simulated at 500 kHz and at 10 kHz by varying the electrical tissue conductivity as described below. 10 kHz was chosen, since at lower frequencies there is the possibility of stimulation of excitable tissue (i.e. muscle, nerve fibres).

Tissue and electrode properties

Thermal tissue properties were used from the literature [22–24] and it was assumed the same thermal properties for tumour as for liver tissue. Since dielectric tissue properties below 1 MHz change rapidly and considerably once tissue is removed from the body [25], data were used from an in vivo study where dielectric tissue properties of normal and cancer tissue were measured in a rat model of liver cancer [13]. Figure 2 shows the frequency dependent electrical tissue conductivity data from this study, where normal liver tissue and tumour tissue was measured in 17 rats.

A temperature coefficient of 1.5% K⁻¹ was used for electrical conductivity of liver [23] and assumed the same for tumour tissue [26]. To allow for implementation of impedance control for the cooled needle electrode, one had to implement a rapid decline in electrical tissue conductivity above 100°C. Since there is no experimental data available, a drop was assumed by a factor of 10 000 between 100–102°C, which gives impedance values that correlate well with experimental data [27].

The cooled needle electrode was made of stainless steel, the multi-prong electrode was made of Nickel–Titanium (Ni–Ti) alloy. Table I shows the tissue and electrode material properties used in the computer models. The temperature dependence of electrical and thermal conductivity is calculated from the temperature coefficients according to:The temperature T is assumed to be in °C in equations (7) and (8). Temperature dependence of specific heat was implemented according to data from a previous study [24].

Table I.  Material properties used in computer models. For temperature dependent properties, the value at 37°C is given.

	ρ (kg m^−3)	C (J(kg · K)^−1)	k (W(m · K)^−1)	αK (W(m · K^2)^−1)	σ10kHz (S m^−1)	σ500kHz (S m^−1)	ασ (1 K^−1)
Liver tissue	1060	3500	0.53	0.00116	0.17	0.36	0.015
Tumour tissue	1060	3500	0.53	0.00116	0.31	0.45	0.015
Blood	1000	4180	N/A	N/A	N/A	N/A	N/A
Stainless steel	8000	452	71	0	4·10^6	4·10^6	0
Ni–Ti	6450	840	18	0	1·10^8	1·10^8	0

Software

PATRAN Version 2003 (The MacNeal-Schwendler Co., Los Angeles, CA) was used to generate the geometric models, assign material properties, assign boundary conditions and perform meshing. After creating the model, PATRAN generates a geometry file which was imported into the ABAQUS/CAE 6.5 (Hibbitt, Karlsson & Sorensen, Inc., Pawtucket, RI) solver. A coupled thermo-electrical analysis was performed by ABAQUS. A coupled analysis is required since electrical properties change due to heating, which means that after each time step the electric field problem has to be solved to account for these changes. All analysis was performed on a PC equipped with a Pentium 4 CPU and 3 GB of memory.

Model limitations

Unlike these simplified FEM models, the liver is a very complex electrical and thermal organ due to its inhomogeneity. It is composed of three different types of blood vessels (hepatic arteries, portal veins, hepatic veins) of different diameters and flow velocities, liver parenchhyma, hepatic tumours, bile ducts and stroma, all of which have unique electrical and thermal properties. Different cell types also differ in electrical properties and tissue interfaces may complicate these simplifications. One major assumption is that perfusion is homogenous and equal in tumour and normal tissue. Constant temperature coefficients were assumed for electrical tissue conductivity of both normal and cancer tissue and any non-linear effects neglected due to irreversible tissue changes. These limitations of the model may lead to inaccurate results.

Results

Figures 3 and 4 show RF current density profile for the cooled needle and multi-tine electrodes, respectively. Figure 5 shows the current density profile for the cooled needle electrode at the beginning of ablation and after 30 s. An iso-current plot does not visualize the profile well due to the high gradient close to the electrode, which is why a shaded plot was used for RF current density. Figures 6 and 7 show temperature profile at the end of the ablation simulation for cooled needle and multi-tine electrodes, respectively.

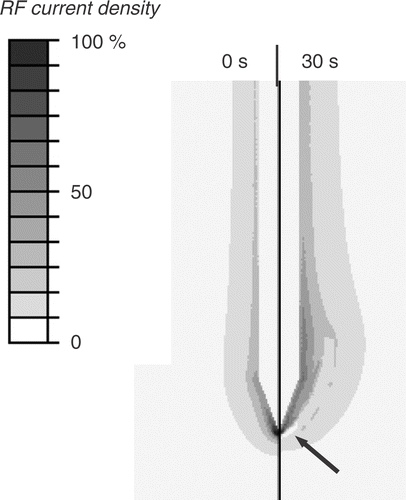
Figure 5. Electrical RF current density for cooled needle electrode at beginning of ablation (left) and after 30 s (right). Due to tissue vapourization around 100°C, current density drops after 30 s around the electrode tip (arrow), since at this location temperatures above 100°C are obtained first. Current density is shown as percentage of maximum. Grey circle represents tumour boundary.

Figure 6. Tissue temperature (°C) after 12 min RF ablation with cooled needle electrode at 500 kHz (left) and 10 kHz (right) in a slice central through the electrode. Isotherms are shown from 50–100°C in 10°C intervals. Grey circle represents tumour boundary.

Figure 7. Tissue temperature after 25 min RF ablation with multi-prong electrode at 500 kHz (left) and 10 kHz (right) in a slice central through three of the prongs. Isotherms are shown from 50–100°C in 5°C intervals. Grey circle represents tumour boundary.

Discussion

Due to historical reasons, all current commercial RF tumour ablation devices operate in the frequency range of 450–500 kHz. Several studies that measured dielectric tissue properties at radiofrequencies found significantly higher electrical conductivity of cancerous compared to normal liver tissue [6–9], [13]. This difference becomes more pronounced at lower frequencies, especially below 100 kHz (see Figure 2). This study compared in computer models RF ablation performed at 10 kHz to a frequency of 500 kHz. In preliminary models it found no significant difference in current density and tissue temperature between high and low frequencies, when the electrode was completely submerged in a large tumour. A relative difference of tissue conductivity adjacent to the electrode is required to obtain a change in the heating profile when going to the lower frequency. Therefore, the current study had the RF electrodes partially inside tumour and partially in normal tissue. While at 500 kHz tumour and normal tissue electrical conductivity are similar, at 10 kHz the difference is much more pronounced, with tumour conductivity being almost twice that of normal tissue (Figure 2). The result is preferential RF current deposition within tumour tissue at 10 kHz, compared to normal tissue outside the tumour (Figures 3 and 4). This difference in current density profile results in significantly different tissue temperatures at the end of the ablation procedure (Figures 6 and 7).

However, the effect on temperature is somewhat different between the two electrode types. For the multi-tine electrode, the intra-tumour temperature is higher at 10 kHz (Figure 7). For the cooled needle electrode the temperature inside the tumour is similar at 10 and 500 kHz (Figure 6), whereas temperatures in normal liver tissue are lower at 10 kHz compared to 500 kHz. This results from the different algorithms that the two electrodes use to control applied power, rather than from the different electrode geometry. For the multi-tined electrode applied power is controlled such that the electrode tips outside the tumour are kept at a set temperature. This results in similar temperatures in normal tissue and increased temperatures inside the tumour. For the cooled electrode, the control algorithm does not take any direct temperature measurements into account and applied power is based on tissue impedance. This results in similar temperatures inside the tumour, but lower temperatures outside the tumour at 10 kHz compared to 500 kHz (Figure 6). Note that the current density profiles shown in Figures 3 and 4 are at the beginning of the ablation and that the profile changes considerably as electrical tissue conductivity is altered due to heating and tissue vapourization during ablation. This is demonstrated in Figure 5, where current density drops around the electrode tip as this tissue region reaches temperatures of ∼100°C after 30 s.

While lower frequencies may be even more effective, one has to consider that there is an increasing possibility of stimulation of excitable tissue (i.e. muscle, nerve fibres) below ∼10 kHz [28]. However, general anaesthesia with paralytic drugs may mitigate this shortcoming if such a therapy were deemed effective.

There is currently no in vivo data available on temperature-dependent change of electrical tissue conductivity during heating of tumour vs. normal liver tissue. Depending on how the differences in electrical conductivity between normal and tumour tissue change due to heating in reality, the results may be different than presented here. Ultimately, it will have to be validated by in vivo studies whether lower frequencies provide an advantage during RF tumour ablation.

Conclusion

The use of lower frequencies than currently used during RF ablation may result in preferential heating of the tumour, which may allow for higher intra-tumour temperatures and preservation of normal tissue. This paradigm may have implications for targeted tumour destruction and device design.

Acknowledgements

This work was supported by the National Institutes of Health, Grant C06 RR018823 from the Extramural Research Facilities Program of the National Center for Research Resources. This work was supported in part by the Intramural Research Program of the National Institutes of Health, Bethesda, MD.