Simulation of different applicator positions for treatment of a presacral tumour

Abstract

Introduction: Proximally located presacral recurrences of rectal carcinomas are known to be difficult to heat due to the complex anatomy of the pelvis, which reflect, shield and diffract the power. This study is to clarify whether a change of position of the Sigma-Eye applicator in this region can improve the heating.

Material and methods: Finite element (FE) planning calculations were made for a phantom model with a proximal presacral tumour using a fixed 100 MHz radiofrequency radiation. Shifts of the applicator were simulated in 1 cm steps in x-(lateral), y-(posterior) and z-(longitudinal) direction. Computations also considered the network effects of the Sigma-Eye applicator. Optimisation of the phases and amplitudes for all positions were performed after solving the bioheat-transfer-equation. The parameters T₉₀, T₅₀, sensitivity, hot spot volume and total deposited power have been sampled for every applicator position with optimised plans and a standard plan.

Results: The ability to heat a presacral tumour clearly depends on the applicator position, for standard antenna adjustment and also for optimised steering of the Sigma-Eye applicator. The y-direction (anterior-posterior) is very sensitive. Using optimised steering for each position, in z-direction (longitudinal), we found an unexpected additional optimum at 8 cm cranial from the middle position of the phantom. The x-direction (lateral) is in a clinical setting less important and shows only smaller changes of T₉₀ with an expected optimum in the central position. A positioning of the applicator in the axial and anterior position of the mid-pubic symphysis should be avoided for treatment of the presacral region, regardless of the used adjustment. Use of amplitude and phase optimisation yields better T₉₀ values than plans optimised only by phases, but they are much more sensitive for small variations of phases and amplitudes during a treatment, and the total power of the Sigma-Eye applicator can be restricted by the treatment software.

Conclusions: Complex geometry of the human pelvis seems to be the reason for the difficulties to warm up the proximal presacral region. The assumption that every position can be balanced by a proper phase adaption, is true only in a small range. A centring of the applicator on the mid-pubic symphysis to heat this region should be avoided. From the practical point of view improved warming should be performed by optimisation of phases only.

• Planning
• 3D-steering
• Positioning effect

Introduction

Regional hyperthermia is in use for many years in multimodal treatment concepts of different human tumours. It is well known that a higher tumour temperature, especially the index temperature T₉₀, correlates with a higher response to the therapy outcom [1], [2]. Observations from heat treatments in the Sigma 60 applicator classify tumours or tumour positions as easier- or difficult-to-h [2], [3]. Suitable tumour temperatures are achieved in central parts of the pelvis. The closer the tumours are located to the pelvic bones, the more difficult is the heating procedure. Especially difficult to heat is the region just in front of the sacral bone [3]. On the other hand, this region needs special attention, since recurrences of rectal cancer are a common indication for regional hyperthermia [4]. The response of rectal recurrences is related to the degree of achieved heat and it was also found that the more distally located tumours are easier to heat [5].

In the multi antenna applicator Sigma-Eye (12 channels) the SAR distribution is improved by increasing the number of antennas [6–8]. Seebass et al. [7] performed a simulation study to analyse the most favourable position and number of antennas in a multiantenna applicator for Radio Frequency (RF) hyperthermia treatment, and evaluated a series of frequencies (100, 150 and 200 MHz) and patient models. An arrangement of three rings with four antenna pairs per ring appears to be most suitable. This is the construction plan of the Sigma-Eye applicator. The tumour model used in this study is a proximally located presacral tumour (comparable to patient 1 in [7]). No systematic evaluation of the positioning was conducted in [7]. Before we started the simulation study, we evaluated the positions of the first 20 patients treated for tumours in the pelvis inside the MRI-hyperthermia hybrid system from December 2001 to July 2002. The differences in positioning between the first and the following treatments of each of these patients have been the starting points of the actual study. The geometric parameter might be most crucial for certain tumour locations such as the presacral region because until now no striking improvement was achieved by phase adjustments alone.

Therefore, we examined whether a specific position of the Sigma-Eye applicator can improve the tumour temperatures or which positions should be avoided. In addition the question arise whether or not an unfavourable applicator position can be balanced by a phase readjustment. How much power is necessary for a further predefined increase of T₉₀ in the presacral tumour and can this power be reached by the actual available treatment system.

Methods

For this simulation study on a phantom model, we wanted to use clinically important deviations in lateral, posterior and longitudinal directions. For this reason, the typical range of position inaccuracies was estimated by evaluating heat treatments of the first 20 patients with pelvic tumours in the hybrid system, as described in Wust et al. and Gellermann et al. [5], [9]. First, an individual grid was generated for each patient from manually segmented images of the first treatment. Second, this grid was matched to the magnitude-images acquired during every heat treatment performed in the Sigma-Eye MR applicator and monitored by the MRI [9]. This matching was done by manually adjusting the grid of the pelvic bone in accordance to the dataset of the pelvic bone of the respective MR images. Then the deviation of x-(lateral direction), y-(posterior direction) and z-(longitudinal direction) within the applicator were measured in centimetre for each heat session relative to the first treatment setup.

The coordinates in the MRI were defined with positive values to the left for x-axis (L), positive values to the posterior for the y-axis (P) and positive values to the head for z-axis (H), defined as LPH-system.

For the simulation study, a model of a phantom consisting of an elliptic cylinder with PVC-walls filled with tissue-equivalent conductive material and a humanlike skeleton of the pelvis, lumbar spine and proximal lower extremities as described in Gellermann et al. [10] was used. A CT scan was made from the phantom with a slice thickness of 5 mm. The images were segmented manually. The PVC-walls were defined as fat, the inner tissue equivalent material as muscle and the skeleton as bones. In this model a presacral located tumour was defined (shown in Figure 1). From the segmented data, compartment surfaces were extracted with a marching cubes algorithm as described in [7]. On this fine surface the number of faces has been reduced to around 15 000 faces as in [7]. Next a volumetric tetrahedral mesh was created for each tissue compartment using an advancing front algorithm. Finally the mesh quality was improved by flipping interior edges and faces, for details see [7]. To calculate the E-fields, an additional grid is necessary for the applicator, bolus, antennas, parts of the surroundings and a spherical outer boundary (minimal distance to the applicator: 16 cm). This external grid was made for each applicator position separately, resulting in an extended grid (for each calculation) of about 30 000 nodes, 350 000 triangles and 174 000 tetrahedrons and a size of around 3300 KB. The maximal edge length of the bone was 2 cm (for 100 MHz wavelength, λ ∼100 cm), for fat 3 cm (for 100 MHz: λ ∼95 cm), for muscle 2.3 cm (for 100 MHz: λ ∼33.5 cm), for plastic 2.3 cm (for 100 MHz: λ ∼180 cm), and for air 5 cm (for 100 MHz: λ = 300 cm).

Figure 1. Model of the phantom used for this calculation study in sagittal and transverse direction. The central point (0, 0, 0) is marked as little orange spot and the axes in the sagittal picture show the distances in cm. The x-axis goes right–left, with positive values on left (L). The y-axis is anterior–posterior with positive values posterior (P) and the z-axis goes caudal-cranial with positive values cranial or head (H), building a L-P-H system. The presacral tumor is shown in red, located posterior from the centre of the model with its centre of gravity about 2 cm posterior to the centre of the model. Calculated fatty tissue is a small equidistant border around the elliptic phantom material. Phantom material is calculated as muscle tissue.

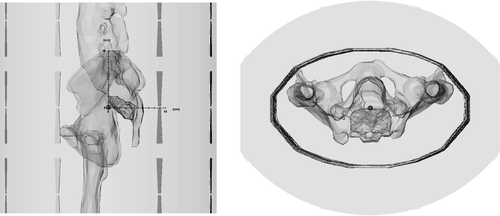
We calculated 430 different applicator positions for this model, shifting the phantom from the central position (Figure 1) with step size of 1 cm in each of the three directions of space. The deviation from the central point in x-direction was ±4 cm, in y-direction ±5 cm and in z-direction ±10 cm. For each position, a calculation time of 8 h (for 24 single antennas) on a standard computer was required.

The E-field calculations were made by the finite element (FE-) method on tetrahedral grids. All 24 antennas were calculated separately. Then the transforming network of the Sigma-Eye applicator was simulated and two antennas were put together to one channel[7], [11], [12]. The suitability of the FE-method to describe hot spots at electrical boundaries modelled by a tetrahedral grid has been validated in earlier publications [7], [13].

The parameters used for calculation, summarised in Table I, have also been published [14]. The calculation of the temperature distribution was determined in the steady state by solving the bioheat-transfer equation on the same grid. The body temperature for all calculations was set at 37°C and the bolus temperature at 25°C.

Table I.  Physical and physiological properties used for the calculations in Amira-HyperPlan [see also [14].

Tissue	Dielectric constant	Electrical conductivity (S/m)	Perfusion (ml/100g/min)	Density (g/cm^3)	Heat capacity (J kg K^−1)	Thermal conductivity (W/m K)	Max temp (°C)
Fat	10	0.04	20	900	3500	0.21	44
Muscle	80	0.8	30	1000	3500	0.642	44
Bone	9	0.02	10	1600	1000	0.436	44
Target	80	0.8	8	1000	3500	0.642	50
Bolus	78	0.001	0	1000	3500	0.642	44

First line shows the property with its unit and the first row shows the tissue used in the model. Fatty tissue is just the small equidistant layer around the phantom material, which in this study is calculated as muscle tissue.

An automatic optimisation of the calculated temperature distribution for each applicator position was performed and the following objective function as described in [7] was minimised:This objective function evaluates, if the tumour is above a therapeutic level T_ther, and the temperature in healthy tissue should not exceed a level T_health. For T_ther = 43°C and T_health = 42°C are used.

The optimisation was performed in two different procedures: In the first procedure phases and amplitudes (A plans) were optimised resulting with 23 degrees of freedom. In the second procedure with phases alone (B plans) were optimised, resulting in only 11 degrees of freedom. The total power is set variable, but restricted in order to assure a temperature of <44°C in normal tissue. Normally, the effect of the optimisation results in a reduction or a smearing of hot spots in order to increase the total power and therefore to achieve a higher T₉₀ in the tumour.

In addition, a standard adjustment with a phase delay of 50° at the channels of the middle ring and an extra delay of 70° for the dorsal channels and 20° for the lateral channels was evaluated. This standard adjustment mimics the standard setup “[0, −2]” (focussed and shifted to the back) for dorsally located tumours in the pelvic area for Sigma 60 applicator, which has been described and evaluated by Sreenivasa et al. [14].

For each position, we sampled the index temperatures T₉₀ and T₅₀, the total power, hot spot volume and sensitivity. The sensititvity has been described in Seebass [7] and gives the median change of T₉₀ for 1000 randomized samples with a variation of the amplitudes up to 10% and the phases up to 10°. This value ought to specify the effect on T₉₀ of small changes in amplitude and phase during an ongoing treatment due to fluctuations of the amplifier.

From these parameters, we additionally calculated the value “δ T₉₀”, where we looked at each applicator position separately: how much can the T₉₀ be increased from standard steering by optimisation in degrees of Celsius, so it is (T_90opt − T_90standard). In the same way we calculated “δ total power” as (total power_optimised − total power_standard), the difference of total power at a special position at optimised steering and at standard steering. From these two differences we determined the quotient (δ total power/δ T₉₀) the value “power per °C of T₉₀”, which describes the additional amount of power, which is needed to increase the T₉₀ for 1°C. A summary of all data calculated in the modelling studies is listed in Table II.

Table II.  Definition of the calculated thermal parameters T₉₀, T₅₀, hot spot volume, total power, sensitivity.

Parameter	Definition
T90	Temperature reached by at least 90% of the tumour volume
T50	Temperature reached by at least 50% of the tumour volume
Hot spot volume	Volume of normal tissue with temperature above 42°C
Total power	Power in the patient model, restricted by 44°C in normal tissue
Sensitivity of phase/amplitude adjustment	Mean deviation of the calculated T90 in°C by changing amplitudes ±10% and phases up to ±10° around this adjustment for 1000 randomized samples (corresponding to the typical variation of feedpoint characteristics)
δ T90	Difference of T90 reached by standard steering and optimised steering at the same position
δ Total power	Difference of Total power reached by standard steering and optimised steering at the same position
Power per T90	Additional amount of power needed to increase T90 for 1°C at a particular position, calculated from δ Total power/δ T90

Out of these parameters the values δ T₉₀, δ Total power and power per T₉₀ were calculated separate for each position as difference between the value (T₉₀ or Total power) reached with optimised steering minus the value reached with standard steering. The last parameter is the quotient of the difference of Total power and the difference of T₉₀.

The statistical evaluation of the data was done with the software SPSS 12.0. The test Spearman-Rho was used, a rank-order correlation coefficient which measures association at the ordinal level. This is a non-parametric version of the Pearson correlation based on the ranks of the data rather than the actual values.

If the significance level is very small (< 0.05) then the correlation is significant and the two variables are linearly related. If the significance level is relatively large (for example, 0.50) then the correlation is not significant and the two variables are not linearly related.

Results

The most critical direction for positioning patients inside the Sigma-Eye applicator was evaluated on 20 patients undergoing a series of 112 heating sessions of the pelvis. The results are shown in Table III. The greatest inaccuracies have been in z-direction, whereas the x-direction (lateral) has the best accuracy in repositioning. Note that the positioning of the patients at this time (December 2001 until July 2002) was made only visually based on the experience of the clinical staff and no specific positioning support was available. Additionally, the z-positioning was complicated by the need of moving the patient together with applicator into the MR-tomograph. During the movement of the patient inside the bore of the MRI it was possible that the applicator could collide into a small border at the entrance of the bore, so that the force of the movement could lead to a change of the relative position from the patient to the applicator. In Table III it is shown, that the z-positioning is more different for male than for female patients, because of the nearly conical form of the male body (with fat tissue at the abdomen) compared to the female body with normally more fat tissue at the hips. The conical form boosts the displacement of the applicator in z-direction.

Table III.  Mean, median and standard deviation in cm of the applicator-shifting in x-(lateral), y-(posterior) and z-(longitudinal) direction during the 112 treatment sessions of the first 10 male and 10 female patients (without positioning device) together with the numbers of treatments per patient.

	Range x (cm)	Range y (cm)	Range z (cm)	No of treatments
Mean–all	1.1	2.0	6.4	5.6
Mean–male	1.0	1.9	7.9	6.3
Mean–female	1.1	2.2	4.2	4.5
Median–all	1.0	1.9	5.5	5
Median–male	0.9	1.9	6.9	5
Median–female	1.2	2.0	4.3	4.5
SD–all	0.5	1	3.6	2.2
SD–male	0.5	0.9	3.9	2.5
SD–female	0.4	1.2	1.1	0.9

All patients were treated with a pelvic regional hyperthermia in the Sigma-Eye/MRI applicator. These ranges were retrospectively determined from the magnitude pictures of the MR thermometry measurements. The largest variation in positioning is found for z (±6 cm), followed by y (±2 cm) and x (±1 cm). The biggest difference between male and female patients is in z direction, which can be declared by the more conical form of a male pelvic region in comparison to the more elliptic form of a female pelvis (see text). Due to the conical form of a male pelvis a position deviation in z-direction is more likely.

For the numerous phantom calculations, the mean values of T₉₀, T₅₀, sensitivity, total power and hot spot volumes and their standard deviation are listed in Table IV. Clearly, the T₉₀ values differ for the different adjustments of the applicator. For the standard adjustment, the values display Gaussian distribution, whereas the values of the optimised steerings are asymmetric.

Table IV.  Mean values and standard deviation of T₉₀, T₅₀, sensitivity and hot spot volume for all different adjustments used in this study. It is clearly shown, that the plans with amplitude and phase optimisation (A plan) result in the highest temperatures, but also in the highest sensitivity to small changes of the amplifier control parameters phase and amplitude. Permitted total power is highest for the optimisation strategy with the largest number of degrees of freedom (A plans), whereas the hot spot volume decreases by optimisation. The lowest total power and the highest hot spot volumes are reached with standard steering, which have the lowest index temperatures and also the lowest sensitivity.

Opt. method		T90 (°C)	T50 (°C)	Sensitivity (°C)	Total power (W)
Mean ± SD	n	Mean ± SD	Mean ± SD	Mean ± SD	Mean ± SD	Hot Spot volume (ml)
Plan A	430	40.2 ± 0.36	40.9 ± 0.41	0.6 ± 0.11	1530 ± 6	164 ± 7
Plan B	430	39.5 ± 0.49	40.0 ± 0.58	0.3 ± 0.09	1280 ± 9	176 ± 8
Standard setup	430	38.4 ± 0.55	38.7 ± 0.65	0.04 ± 0.04	964 ± 10	260 ± 9

The standard setup has a mean T₉₀ of only 38.4°C showing that this tumour is difficult to heat. The optimisation of phases and amplitudes (A plan) achieves a mean T₉₀ of 40.2°C, 1.8° higher than the standard steering. In addition, the phase only optimisation of B plans develops a better mean T₉₀ of >1°. T₉₀ is 0.7°C higher for A plans with 0.64°C sensitivity vs. 0.32°C sensitivity for B plans (for definition, see “Methods” and Table II). This shows that optimisation with amplitudes and phases is very efficient, but also, that small changes of the amplitudes and phases can result in worse T₉₀ than the optimum. The sensitivity shows just the mean reduction of T₉₀ in °C out of 1000 randomised samples.

Optimisation permits higher power (i.e. reduces the hot spots), especially if more degrees of freedom are available, so A plan optimisation is better than B plan optimisation. The volume of the hot spots (i.e. the normal tissue volume with ≥42°C) is reduced by optimisation, and the smearing effect increases with the number of different antenna powers (amplitude optimisation). A higher T₉₀ needs a higher total power. However, the sensitivity increases with higher total power or T₉₀ with some exceptions for low T₉₀ for quite unfavourable positions. The geometric positions with the highest sensitivity are in the centre of the phantom and in close relation to the symphysis and the anterior/posterior iliacal spinae.

Table V shows that, as expected, the T₉₀ and T₅₀ values of the different steering adjustments closely correlate linearly with each other. There is also a correlation between the T₉₀ and the total power for standard steering and for B plan optimisation, but not for A plan optimisation. For standard steering there is also a correlation between total power and hot spot volume, but not for the optimised steerings. In the big number of samples there is no close linear correlation between T₉₀ and hot spot volume, hot spot volume and sensitivity and also between sensitivity and T₉₀ or total power or hot spot volume. There is only a weak linear correlation between the δ T₉₀ and the δ (total power) and a negative linear correlation between T₉₀ and the power per °C for optimised steerings, which means, the higher the T₉₀ is (at optimised steering), the lower is the power needed to raise the T₉₀ from standard steering at this position for 1°. A much closer linear correlation exists for the δ (total power) and the power per °C T₉₀, especially for A plans, showing that the greater the power difference between standard steering and optimised steering is, the higher is the power needed to raise the T₉₀ for 1°C. Figures 2–4 show the dependency of the T₉₀ on the displacement in x-, y- and z-direction. The dependency is most pronounced on shifts in y-direction (anterior-posterior), followed by the z-position (longitudinal). For standard steering also, the x-position (lateral) has nearly the same influence as the y-position on T₉₀ with an expected optimum in the centre. For optimised adjustments the influence of x-position is smaller than for y-position. After optimising the phases there is a clear optimum at z = 8 for A plans and B plans, which cannot be seen for a standard adjustment. The (optimised) T₉₀ are even lower in the central position compared with z = 8. The analysis of the total required power to yield +1°C increase of T₉₀ in a particular position shows, that positions with a high T₉₀ at standard setup need a higher amount of additional power to increase the T₉₀ for 1°C than at positions with a lower T₉₀. But in the cases with an extremly low T₉₀ at standard setup also an extra high amount of power is needed to raise the T₉₀ for 1°C (for example Y = −5). For this positions also optimisation cannot get very high T₉₀. However, using high power with the standard setup needs lower W/°C to raise the T₉₀.

Figure 2. Dependency of 430 calculated T₉₀ values on the x- (lateral) positions by optimising according A plans (with amplitude and phase optimisation, squares), B plans (only phase optimisation, triangles) and the standard setup (circles). Points show the value for y = 0 and z = 0, with bars the range of minimal and maximal T₉₀ values (for y ≠ 0 and z ≠ 0) is shown. The central x-values (x = 0) result in the best T₉₀ values after optimisation. The standard adjustments show a higher difference between the best central and the lateral positions than the optimised adjustments. The highest values are reached by A plans, which have the largest number of degrees of freedom.

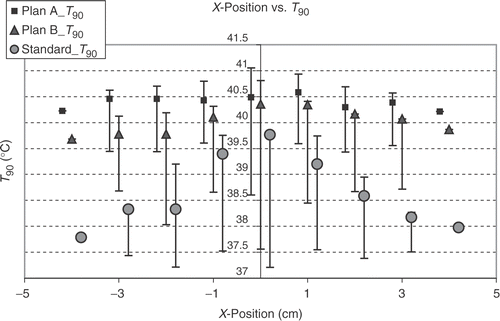
Figure 3. Dependency of 430 calculated T₉₀ values on the y-(anterior-posterior) positions by optimising according A plans (with amplitude and phase optimisation, squares), B plans (only phase optimisation, triangles) and the standard setup (circles). Points show the values for x = 0 and z = 0, with bars the range for x ≠ 0 and z ≠ 0 is shown. The optimised adjustments show a clear dependency on the y-position with the optimum around the centre. The standard adjustments show a similar dependency on the y-position. For the same number of different positions at a particular y-position the range of T₉₀ is smallest for A plans and greatest for standard steering. At the centre of gravity of the tumour at position y = 2 and also the next more posterior located position (y = 3), A plans show the best T₉₀. The lowest T₉₀ for each adjustment are at position y = −5.

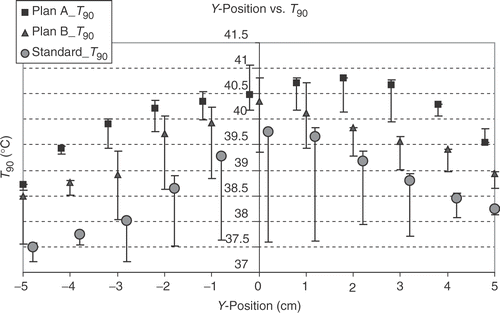
Figure 4. Dependency of 430 calculated T₉₀ values on the z-(longitudinal) positions by optimising according A plans (with amplitude and phase optimisation, squares), B plans (only phase optimisation, triangles) and the standard setup (circles). Points stand for x = 0 and y = 0, with bars the range for x ≠ 0 and y ≠ 0 is shown. (For z = 6 and z < −5 there is only one position calculated.) The optimised adjustments indicate two suitable positions to increase T₉₀: at z = 0 (especially B plans and standard adjustments) and even better for z = 8 cm (in cranial direction). For the standard adjustments the range around z = 0 shows nearly a plateau from −3 to 2 cm. At z > 6 there is no improvement of the T₉₀ values for standard adjustment. For A plans and z = 0 only positions with y ≠ 0 yield better T₉₀ than the adjacent z positions, but for z = 8 there is a clear improvement of T₉₀.

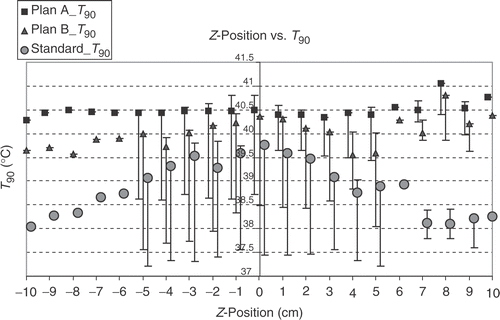
Table V.  Correlation among the thermal parameters T₉₀ and T₅₀, total power, sensitivity (to adjustment changes), hot spot volume, differences δ of T₉₀ and total power (optimised minus standard adjustment) and power needed to raise T₉₀ by 1°C (power per °C T₉₀). The correlation and significance was calculated with Spearman-Rho with the software SPSS 12.0. There exists a close linear correlation between the index temperatures T₉₀ and T₅₀. Total power has a good linear correlation with T₉₀ only for B plans and standard steering but not for A plans. Hot spot volume correlates with total power just for standard steering. A linear correlation exists for δ total power vs power per °C T₉₀, for A plans more than for B plans. There is only a weak linear correlation between δ T₉₀ vs. δ total power and a negative correlation between T₉₀ and the power per °C T₉₀. There is no close linear correlation between sensitivity and T₉₀, total power or hot spot volume.

Parameters	A plan r; p	B plan r; p	Standard plan r; p
T90 vs. T50	0.98; 0.001	0.995; 0.001	0.99; 0.001
T90 vs. total power	0.46; 0.001	0.84; 0.001	0.71; 0.001
T90 vs. Hot Spot volume	0.58; 0.001	0.47; 0.001	0.62; 0.001
T90 vs. sensitivity	0.38; 0.001	0.56; 0.001	0.43; 0.001
Total power vs. sensitivity	0.30; 0.001	0.48; 0.001	0.41; 0.001
Total power vs. Hot Spot vol.	0.25; 0.001	0.44; 0.001	0.69; 0.001
Hot Spot vol. vs. sensitivity	0.35; 0.001	0.014; n.s.	0.41; 0.001
δ T90 vs. δ total power	0.46; 0.001	0.54; 0.001	–
δ Total power vs. pow. per °C T90	0.84; 0.001	0.65; 0.001	–
T90 vs. power per °C T90	−0.24; 0.001	−0.18; 0.001	–

A linear correlation is found for “δ power” vs. “power per °C T₉₀”. The more power used for an optimised plan (in comparison to standard steering), makes more power necessary to elevate the T₉₀ for 1°C in this position by the optimisation. The positions are mainly these points, where the standard setup itself has reached a high T₉₀ value (x, y, z) = (0, −1, −2) and environment, leading to an elevation of only a few tenth part of a degrees after a large increase in total power deposition.

The additional convenient position for heating at z = 8 cm needs clearly lower power per degree of T₉₀ elevation than the central regions and the more caudal located applicator positions.

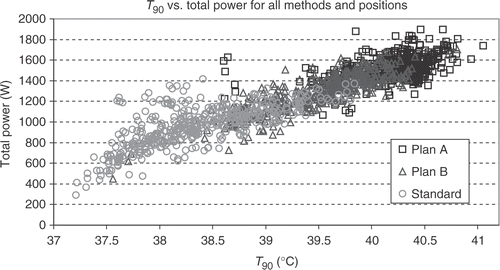
Figure 5 shows that independent of optimisation strategy, higher T₉₀ values typically need higher total power deposition. So the optimisation strategy is an attempt to smooth and reduce hot spots in order to tolerate higher total power.

Figure 5. Scatterogram of T₉₀ vs. total power. For high T₉₀'s a high total power is necessary, no matter which kind of phase control is used (there are only very few exceptions, where the power is high but T₉₀ is relatively low). Optimised phase and amplitude control reduces hot spots, so that the total power can be elevated and T₉₀ increases. The lowest T₉₀ for all adjustments is at position x = 0, y = −5 and z = −5 with the centre of the applicator just behind the mid-pubic symphysis. The power at this position is low for standard steering and B plans but quite high for A plans, adding only about 1.4°C to T₉₀ with about 1300 W additional power in comparison to standard steering and 1.05°C with about 1200 W additional power in comparison to B plan steering. One problem is permanent: only 150 W per antenna is available from the amplifier, so these calculated power levels for A plans can not be used. Amplitude optimisation is done by amplitude reduction of several antennas, and maximum power with all 12 antennas (with full power) is restricted to 1800 W.

The highest T₉₀ for A plans (41.1°C) and for B plans (40.8°C) was found at position (0, 0, 8). The next three best positions of A plans (T₉₀ between 40.9–40.8°C) have the positions z = 8 cm (1, 0, 8) and (0, 1, 8) and one z = 0 cm (in the centre of the tumour) at (0, 2, 0) yielding T₉₀ = 40.8°C. For B plans also, two of the next three best positions have a large shift in cranial direction (0, 1, 8) and (0, 0, 10) yielding T₉₀ = 40.7°C or 40.4°C. Another favourable position is (1, 0, −1) achieving T₉₀ 40.4°C. For standard setups most favourable positions were found near the centre (0, 1, −2), (0, 1, −3), (0, 0, 0) and (−1, 1, −2) with a T₉₀ of 39.8°C.

It is interesting that the positions with the lowest T₉₀ of the optimised adjustments (A and B plans) have y = −5. The position (0, −5, −5) is quite disadvantageous for every plan (A plan: 38.6°C, B plan: 37.6°C and standard: 37.2°C for T₉₀) because the centre of the applicator is directly behind the mid-pubic symphysis. Other adverse positions for standard setups are (−2, −3, 5) and (0, −5, −3). But also positions with y = −4 have very low T₉₀ resulting from lower total power due to a small distance between the posterior antennas and the sacral bone. Positions with y = 5 have also low T₉₀ with the centre of the applicator on the sacral bone and the symphysis close to the ventral antennas.

Very high power (about 1400 W) can be applied in the most beneficial positions using a standard setup, e.g. at (0, 1, −2) and (−1, 1, −2) yielding T₉₀ = 39.8°C. Here the off-centre positions with z = 8 (0, 1, 8) and (0, 0, 8) are only sufficient for T₉₀ = 38.4 and 38.1°C. This suggests, that a cranial shift of the applicator, e.g. z = 8 might be protective with respect to hot spots, but without optimisation of phases there is not enough SAR inside the tumour. In central applicator positions the tumour is better heated but more susceptible for hot spots. Only in the special position (0, 1, −2) we found favourable conditions with a low hot spot disposition. This correlates with the clinical findings when treating abdominal regions, where hot spots are distinctly less problematic in comparison to pelvic treatments, and effective temperatures may often be reached in the proximally located upper rectum.

For optimised A plans we found particularly unfavourable applicator positions with a low T₉₀ despite high power at positions with y = −5 such as (0, −5, −4), (0, −5, −5), (0, −5, −1) and (0, −5, −5) with a T₉₀ of 38,6°C. Interestingly, a slight deviation in x-direction at this position improves the T₉₀ and total power tolerated.

Discussion

We know from the treatments with the “old” Sigma 60 applicator that some tumour positions are easier to heat than other positions. Especially difficult to heat is the region just in front of the sacral bone. In clinical routine there have been clues that the positioning of the tumour inside the applicator could help to improve the temperature in this region.

First, we evaluated 20 patients treated in the MRI-hyperthermia hybrid system [9] for pelvic tumours to get an idea, which position inaccuracies are common. We found, that an inaccuracy in lateral (x) direction is rarely greater than 1 cm and in y-direction greater than 2 cm. In z-direction the inaccuracies are greater, especially for male patients. This information led us to the simulation study presented here. The phantom model implies, that the effects seen were generally caused by the form of the bones, due to the thin fat layer without complex interfaces between fat and muscle. In a real patient, the complex interface between fat and muscle (with a similar dielectric difference as bone and muscle) also would influence the positions and the strength of hot spots and therefore the result of an optimisation. But the boundaries between fat and muscle are not as fix and not as constant (during a therapy) as the boundary between bone and muscle. We used the simplified phantom model without a complex boundary between fat and muscle to learn about the effects of the fix bone structure for heating this region. In this study exactly the same parameters for the E-field and the temperature calculations were used changing only the position of the applicator to the tumour and the bones.

From the calculated temperature, the index temperatures and other treatment parameters for three different adjustments of the applicator for each particular position were determined: We used optimised antenna steerings with phase and amplitude optimisation (A plan), optimised steerings with phase-only optimisation (B plans) and a standard steering, which is focussed and shifted to the back, simulating the standard steering for dorsally located pelvic tumours, described and evaluated by Sreenivasa et al. [14].

We found that the index temperatures, especially the T₉₀, considerably depend on the position of the tumour and the bones in the applicator. The dependence is greatest for the y-direction (ventral–dorsal) for all kinds of steering. The next sensitive direction is z (caudal–cranial), where we found two optimal positions: at the centre of the tumour and for a much more cranial applicator position (z = 8). This position (z = 8) yields very good index temperatures, but only for steering with optimised plans. Obviously, in this position the hot spots formation is reduced in correlation with clinical findings during part-body hyperthermia. Here excellent temperatures in the upper rectum by positioning the applicator centred axially on the level of the navel (umbilicus) can be achieved. But with optimisation, we can also navigate the SAR in a caudally located tumour. The position dependence in x-direction is biggest for standard steering and has its optimum just in the centre. With optimised steering, there are only smaller differences between the different x-positions. From the clinical point of view, the x-direction is of minor importance, because the re-positioning in x-direction is quite accurate, whereas the z-position and the y-position are of major importance.

Some very disadvantageous positions exist, when the centre of the applicator is in the position of the mid-pubic symphysis. This position at the centre of the applicator should be avoided in y- as well as in z-direction.

For standard steering, only a well-centred position yields favourable temperatures. Small changes in position can lead to bigger hot spots and therefore to reduced applicable total power.

We found that an optimisation can yield better thermal results for each position. The degrees of freedom for the optimisation [phases-only (B) or phases and amplitudes (A)] influence the temperature that can be maximally reached. The more effective degrees of freedom are possible, the higher the temperature inside the tumour, the smaller the hot spot volumes and the higher the total power applicable. From a clinical point of view, small changes in stability of phases and amplitudes need to be avoided during a treatment. To consider this, we calculated the sensitivity, which means the mean reduction of T₉₀ out of 1000 randomised samples with changes of the amplitude of up to 10% and changes of the phases up to 10°. We see that the best optimisation strategy (A plan) also has the greatest sensitivity, and therefore the highest risk not to reach the best calculated result. Also another limitation exists: one channel cannot apply more than a total of 150 W, so the maximal power of our applicator is 12 × 150 W = 1800 W. By optimisation of amplitudes, the power of some channels will be reduced to get the optimal result. Thus for all amplitude optimised cases, the power obtainable from 11 of 12 antennas is lower than 150 W maximum, leading to a maximum system power much less than 1800 W in a clinical setting. This software-restricted total output power is often not sufficient. In general the reached T₉₀ clearly depends on the applied total power. With B plans the maximal power of 1800 W can be applied. As a rule for clinical application of the Sigma-Eye applicator, plans optimised by phases alone should be used because they can be practically realised and they are not as sensitive with respect to small amplitude and phase changes of the treatment system.

The evaluation of the increase of T₉₀ and the differences of the power between standard and optimised adjustments shows that particularly high additional amounts of power are needed to slightly elevate the T₉₀ especially at positions, where the standard adjustments are already successful, i.e. at central positions. But some positions exist, where it is quite difficult to heat the presacral region and all phase adjustments yield suboptimal temperatures (y = −5 cm and negative z values, with the centre of the applicator directly behind the mid-pubic symphysis). In some special positions, for the same or even higher T₉₀ after optimisation a lower amount of power is needed than for the standard adjustment. Generally, T₉₀ can be improved in nearly every position by optimisation.

Optimisation of phases and/or amplitudes is one strategy for increasing the total power by reducing the hot spots. Another strategy is the use of absorber structures [15], [16], but this has not been investigated in this study.

This simulation study clearly shows, that the influence of bony structures on the heatability of a difficult-to-heat tumour strongly depends on the applicator position. These bony structures are the most constant structures during a heat treatment. The influence of the fat-muscle boundary is not considered with this phantom model. This boundary may change a little bit during a treatment due to small muscle movements of the patient. Changes of perfusion, probably occuring in each patient treated with hyperthermia, are not investigated here. Also inter-individual differences in the cardiovascular potentials of the patients with higher or lower power tolerance are not considered.

Conclusion

Position of the applicator in relation to the tumour and bones influences the temperature that can be attained in the presacral region with RF-hyperthermia. Y-(anterior–posterior) and z-(longitudinal) direction offsets from the optimum position are most critical. In general a high total power is needed for a high temperature inside the tumour and an optimisation can help to reach higher power levels and therefore higher T₉₀ without overheating surrounding normal tissue.

Favourite positions for the centre of the applicator are the centre of the tumour and eight cm to the head, but the latter position requires optimised steering. Positioning on the mid-pubic symphysis should be avoided, in y- as well as z-direction. Not every unfavourable position can be improved by optimised pattern control. Therefore, a poor positioning is not always fully compensated and a careful positioning of the applicator is crucial, especially in y- and z-direction.

Even though this study shows superior heating of presacral tumours with phase and amplitude optimisation, the practical hardware limitation of 150 W per antenna lowers the total power delivered to the patient in amplitude optimised treatment plans, thus providing higher T₉₀ results for the phase optimised plans with higher total power capability.

Acknowledgements

This work has been supported by the grants of the “Deutsche Forschungsgemeinschaft (DFG)” (project WU 235/1-1) and the “Lieselotte Beutel–Stiftung”. We are grateful for the support.