Phantom experimental study on microwave ablation with a water-cooled antenna

Abstract

Microwave ablation therapy using a water-cooled antenna was studied experimentally in a phantom. The development of the heating pattern induced by the microwave antenna was determined from the thermocouple-measured temperature field, and the influence of the cooling water flow within the antenna on temperature distribution and heating pattern was investigated. The shape of the heating pattern was pear-like, and the enlarging rate of the heating pattern decreased with heating time. Because of strong cooling effect, the heating pattern in the region with Z < 0 (where Z = 0 represents the position of radiator, Z < 0 and Z > 0 represent the backward direction of the antenna with cooling water and forward direction without water, respectively) was smaller in diameter than that with Z > 0, and the heating pattern with Z < 0 was slightly reduced when the velocity of the cooling water increased. The highest ablative temperature occurred with Z > 0 decreasing. Finally, the specific absorption rate distribution was also determined and investigated analytically. The present results can be helpful in clinical ablation therapy practice and will be applicable to multiple applicators for surgical planning.

• Microwave
• thermal ablation
• temperature field
• heating pattern
• SAR

Introduction

The liver is a common location for both primary and metastatic malignancies. Annually, more than 1 million new patients around the world develop hepatocellular carcinoma [1]. Surgical resection is presently the treatment of choice for both well-localized primary and metastatic hepatic malignancies [2]. However, the majority of patients are not candidates for surgical resection owing to certain criteria, such as multifocal disease, tumour size, close location of tumour to key vessel, or coagulopathies. Thus, there is a demand for novel minimally invasive techniques to cure hepatic malignancies.

Focal ablative therapies have been developed and applied to the treatment of hepatic malignancies. Unlike surgical resection, ablative therapies are not associated with the loss of entire segments or lobes of a normal liver. The most widely investigated focal ablative techniques may be radio-frequency (RF) ablation [3]. However, the therapeutic use of invasive microwave (MW) technology for the ablative treatment of cardiac tachyarrhythmia has been suggested [4]. MW ablation has been considered a promising way of heating tissue deeper than RF currents. Since MW power deposition inside tissue decays with distance following a second-power law, as compared with the fourth-power dependence of RF ablation, deeper lesions can be obtained [5], [6]. There have been many papers on implanted microwave coagulation therapy for hepatocellular carcinoma (HCC) in recent years. Murakami et al. [7] reported that percutaneous microwave coagulation therapy could achieve complete tumor necrosis in five out of nine patients with HCC. Dong et al. [8] reported 41 cases with HCC and 10 cases with hepatic metastasis treated by percutaneous microwave coagulation that produced ablation lesion volume of 37 × 26 × 26 mm with 60 W 300 s.

Most authors believe that complete necrosis of normal hepatocytes can be achieved using a temperature of 54°C for 1 min or instantly when the temperature reaches 60°C. Liver cancer cells are more sensitive to heat than normal hepatocytes [9], [10]. To gain a satisfactory clinical therapeutic effect, it is essential to know the temperature distribution during thermal therapies. The ability to calculate the complete time-dependent temperature field in human tissue caused by ablation is necessary for planning the optimal conditions for a treatment, for monitoring and control during a treatment and for the retrospective evaluation of a treatment [11]. The calculation of the temperature field requires a detailed knowledge of the energy deposition in the tissue. A challenging aspect of these techniques is the energy coupling between the radiating system and the tissue, especially the specific absorption rate (SAR) distribution, which represents the heating ability of a heat generator of thermal ablation.

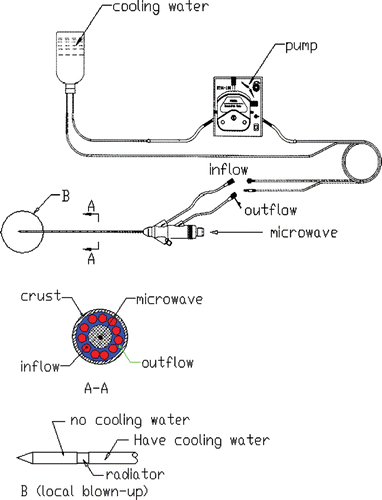
Compared with a normal microwave antenna, a water-cooled antenna can reduce the carbonization of tissue near the microwave antenna by reducing the very high ablative temperature. These carbonizations severely reduce the regional heat conductivity and reduce ablation lesion. This paper presents research on a water-cooled microwave antenna that was studied experimentally. The temperature field induced by heating from the antenna was measured with thermocouples in the phantom at different cooling water velocities. The development of the heating pattern was obtained as the 54°C contour of the temperature, and the effect of the cooling water on the temperature field and heating patterns was analyzed. Finally, to determine the SAR, the cooling water was completely blocked to dismiss any convective effects. In this situation, the temperature field was measured for the first 10 s as it was heated up, and from this the SAR distribution was derived and analytically fitted.

Materials and methods

Experimental system

Microwave generator

A model MTC-3, designed by the Institute of Microwave Electronics, Nanjing Qinghai, China, was used in the present microwave coagulation study. This microwave generator operated at 2450 ± 50 MHz with a power output of 0–100 W. The system was equipped with a low-loss cable, water-cooled microwave antenna (1.9 mm in diameter) with a surface coating to prevent tissue adhesion and a peristaltic pump to adjust the flow rate of the cooling water within the antenna. The structure of the antenna and the water circulation can be seen in Figure 1.

Figure 1. Structure of the antenna and water circulation.

The phantom and its properties

To facilitate temperature measurement with thermocouples, a muscle-equivalent microwave phantom was used instead of liver tissue, as the electric properties of both muscle and liver tissue are similar. We used the same phantom described in the literature [12]. Table I gives the phantom properties.

Table I.  Properties of phantom.

ε	σ (s/m)	ρ (kg/m^3)	c (J/kg°C)	K (W/m°C)
45	2.2	1070	3700	0.535

ε: Dielectric constant. σ: Electrical conductivity. ρ: Density of the phantom. c: Specific heat. K: Thermal conductivity

Temperature measuring system

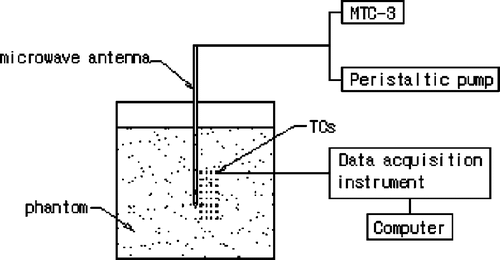
Iron-constantan thermocouples (TCs) were used to measure the temperature in the phantom because they have low microwave pickup, fast time rise, and good temperature sensitivity and reliability [13]. The TC is 0.075 mm in diameter from Omega Engineering, Inc., Stamford, CT, USA. For data acquisition the model HP34970A (Agilent Company) with 32-measurement channels was used (Figure 2).

Figure 2. Phantom experimental system.

Experimental methods

The data acquisition module was connected to a computer through an RS-232 interface to monitor the temperature variation dynamically. Thirty-two thermocouples were used to measure the transient temperature field from which the SAR distribution was determined.

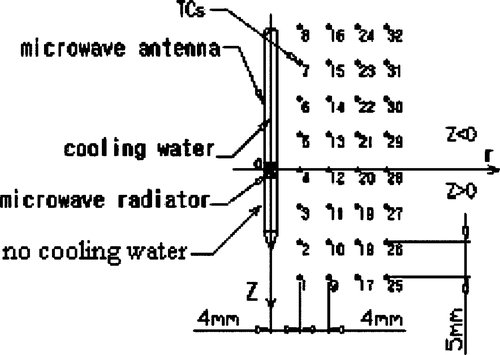
Because of the expected axis-symmetrical distribution of the temperature induced by the microwave antenna, the antenna was inserted and the TCs were placed in the same plane before the phantom was set in the container (Figure 3). The transient temperatures of the TCs were measured from the instant that microwave power was turned on. A power level of 60 W was set for 120 s of continuous heating. Flow velocities of the cooling water in the antenna were adjusted respectively to 0.22 m/s, 0.44 m/s and 0.66m/s. The temperature of each TC was recorded every second. After 120 s, the power was turned off and the phantom was allowed to cool until the temperature measured at each TC did not change by more than 0.01°C over 1 min. The same heating and cooling procedures were repeated three times. These measurements were performed at 32 TC sites each time for each flow rate of the cooling water at the same power output level. The final temperature of each TC was the average of the three-time measured values.

Experimental results

The temperature during microwave radiation at 32 sites was dynamically acquired in the phantom. The temperatures of the TCs near the radiator are depicted in Figure 4. It was seen that the temperature rose following different laws along the Z axial direction (TCs 3, 4, 5) and radial direction (TCs 4, 12). The temperature near the antenna increased very quickly, the temperature of TC 3 rose more rapid than that of TC 4 and TC 5. This was because only the microwave energy deposition in the tissue would affect the temperature distribution during 0–10 s [14], and the microwave energy deposition in the tissue was not uniform (see Figure 8 indicating SAR distribution). TC 5 was more likely to reach a steady heat transfer state after 30 s. This was due to the strong water-cooling effect in the region with Z < 0. At the same time, we could see that the time taken to reach 100°C at TC 5 was similar to the time for TC 4 in Figure 4 because the effect of water-cooling on the temperature field was very small in 20 s.

From Figure 4, the effect of water-cooling on the whole temperature field also can be seen. At TC 3, which was located in the region with Z > 0 without water cooling, the temperature reached a maximum. But the highest cooling water velocity (0.66 m/s) severely reduced the maximum temperature by about 40°C compared with the lowest cooling water velocity (0.22 m/s).

Figure 5 shows the development of a heating pattern that is defined as the region of temperature above 54°C during the heating. First, it can be seen that the heating pattern has a pear-like shape, which enlarges with heating time. However, the rate of development of the heating pattern enlargement slows down gradually. Second, in the region of Z < 0 around the antenna (the region with r < 4 mm), the heating pattern hardly develops because of the water-cooling effect. Third, because there was no cooling water, the heating pattern in the region with Z > 0 was larger in diameter than that in the region with Z < 0.

Figure 3. Antenna and TCs placed in the phantom.

Figure 4. Temperature curves of TCs near MW radiator at 60 W with different cooling water velocities. (a) TCs 3, (b) TCs 4, (c) TCs 5, (d) TCs 12.

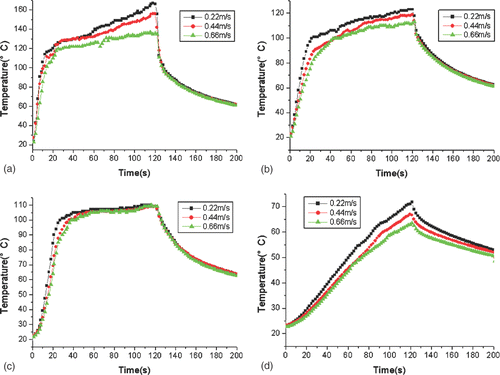
Figure 5. Heating pattern (54°C contours) at 60 W with a cooling water velocity of 0.44 m/s at different times.

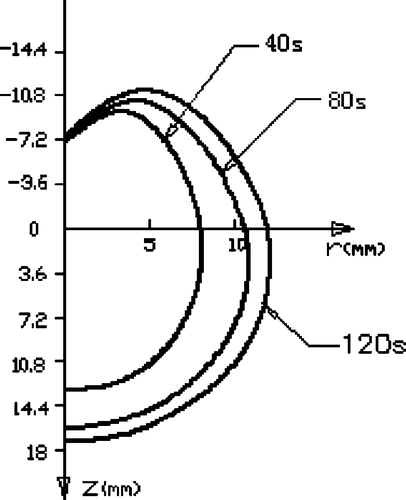
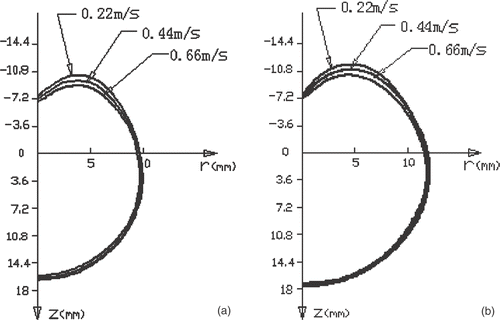
Figure 6 shows the cross-sectional temperature distribution and the extent of the heating pattern after 60 s and 120 s with different cooling water velocities. For the three given cooling water velocities, it seems that the water cooling had very little effect on the heating pattern in the region with Z > 0 where the antenna was not cooled, but the heating pattern was slightly reduced with a larger cooling water velocity in the region with Z < 0. With the two given times of temperature measurement, the heating pattern developed very slowly in the axial direction of the antenna, while in the radial direction the heating pattern developed more rapidly in the region with Z > 0.

Figure 6. Temperature distribution (54°C contours) at 60 W after (a) 60 s and (b) 120 s.

SAR distributions

Bioheat equation

The mechanism by which MW induce tissue destruction is the conversion of microwave energy into heat. The Pennes’ bioheat equation [15] governs heat transfer during thermal ablation.where ρ is the density (kg/m³), c is the specific heat (J/kg·°C), and K is the thermal conductivity (W/m ·°C), T is the temperature of tissue (°C) and Q_r is the heat generated by microwave (W/m³) and Q_m is the heat generated by metabolism. W_b is the blood perfusion (kg/m³ ·s), C_b is the specific heat (J/kg ·°C) of blood, T_b is the temperature of arterial blood (°C).

SAR distributions

In the static phantom, there was no metabolism or blood perfusion, so Q_m and W_b were assumed to be zero in equation 1. In order to obtain the distribution of the SAR of MW in the phantom, it was assumed that in the initial phase of heating up, the conductive heat transfer in the phantom is negligible (∇ · K∇ T ≈0). However, in the present study, from Figure 4 we can see that the temperature curves of TCs were affected by the cooling water even during the initial phase of heating up. Therefore, we had to separate the advection effect of the cooling water. So another experiment for SAR determination was conducted without cooling water in the MW antenna. Under this condition, Equation 1 can be simplified in the beginning of heating up as follows:Thus, the SAR is the partial derivative of temperature with respect to heating time.

Sherar et al. [14] suggest that in the determination of the SAR, the thermal diffusion artifacts can be minimized if the duration of the applied power pulse is restricted to 10 s or less. Only the microwave energy of deposition in the tissue would affect the temperature distribution during 0–10s, while conduction or convection would only affect the temperature distribution after 10 s.

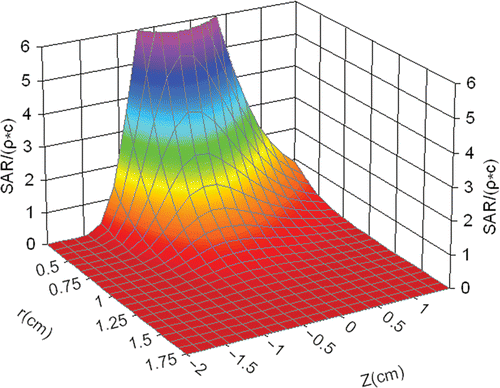
Figure 7 showed that the transient temperature rise was proportional to the heating time within the first 10 s. Therefore, SAR data were determined from the transient temperature in the initial heating phase at each TC. It is convenient to fit the SAR data to an analytical expression of equation 3. Table II gives the fitted coefficients and the fitted three-dimension SAR distribution is shown in Figure 8.

Figure 7. The evaluation of SAR for third, fourth, fifth, twelfth TCs at 60 W and cooling water velocity for 0 m/s.

Figure 8. SAR distribution at 60 W power.

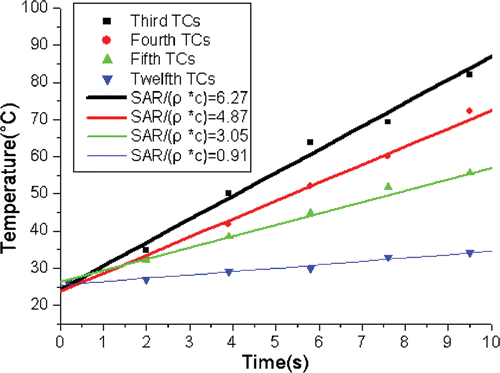
Table II.  Fitted coefficients of Equation 3.

a	b	c	d	e
14.23	0.05	0.19	−0.28	0.53

Conclusion and discussion

In this paper, the temperature field induced by a water-cooled MW antenna in a phantom was studied experimentally. A further SAR distribution was also obtained by completely blocking the cooling water within the antenna. We have illustrated the developing characteristics of the heating patterns during heating up and the effects of cooling water on the temperature distribution. The corresponding heating patterns were also analyzed.

It can be concluded that the water-cooling effect made the heating pattern with Z < 0 smaller in diameter than that with Z > 0, and a higher cooling water velocity could slightly reduce the heating pattern with Z < 0, but the highest temperature that occurred with Z > 0 could be greatly decreased, which would be good for minimizing the carbonization of tissue near the microwave antenna. These experimental results can be used to direct clinical ablation therapy, and the derived SAR distribution can also be applicable to multiple applicators for surgical planning.

There were some limitations of this study. First, in depicting of the temperature contour in Figures 5 and 6, because of the lack of temperature measuring TCs, the contour near the antenna was obtained by numerical insertion and may not be accurate. Second, because of the structure of the antenna, it was impossible to maintain a long heating time with the cooling water blocked, otherwise the antenna would burn out. Thus we could not obtain the temperature without cooling water (the SAR was obtained within a short period of heating) and could not compare it with the results collected. Third, the heating duration was selected to be 120 s, so we could not obtain the final steady temperature distribution and heating pattern, which may require a much longer heating time.

Acknowledgement

This research is supported by the National Science Foundation of China under grant no. 30470450.