SAR characteristics of the Sigma-60-Ellipse applicator

Abstract

Purpose: To characterize the basic performance of the Sigma-60-Ellipse applicator.

Materials and methods: The E-field distributions were measured using Schottky diode sheets in a cylindrical phantom (diameter 26 cm, length 50 cm), filled with saline-water (2 g NaCl/L). The phantom was positioned symmetrically in the Sigma-60-Ellipse applicator. The stability of the SAR distribution was assessed as a function of power and frequency. Furthermore, the accuracy of target steering was evaluated at various frequencies. Finally, the SAR characteristics were compared with those of the Sigma-60 and the Sigma-Eye applicators.

Results: The average 50% iso-SAR area increased from 241 to 296 cm²when the RF power increased from 100 to 1600 W. The SAR maximum was located in the centre of the applicator for the frequencies of 75–80 MHz and it moves towards the feet for higher frequencies (up to 3.5 cm at 120 MHz). The average 50% iso-SAR area decreased from 268 to 161 cm²with increasing frequency from 75 to 120 MHz. The 50% iso-SAR longitudinal length was almost stable (mean 21.3 cm) at 75–120 MHz for both power outputs of 400 and 800 W. As expected the 50% iso-SAR radial length decreased with frequency from 14.9 cm at 75 MHz to 8.4 cm at 120 MHz. There was a fair agreement between requested and measured target settings. At the lower frequencies of 75–90 MHz and at 100 MHz the SAR characteristics were almost identical to those of the Sigma-60 and Sigma-Eye applicators, respectively.

Conclusion: At the frequency range of 75–90 MHz the Sigma-60 and at 100 MHz the Sigma-Eye can safely replaced by the Sigma-60-Ellipse applicator.

• SAR
• Sigma-60-Ellipse applicator
• Schottky diode sheet
• phantom
• quality assurance
• hyperthermia

Introduction

The BSD-2000-3D system and the Sigma phased array applicators provide a new generation of equipment for planning, delivery, and control of loco-regional deep hyperthermia. The logical step in the development of the Sigma applicators’ family is having a group of applicators able to perform loco-regional deep hyperthermia in all patients’ sizes, i.e. from small to large, with tumours in the pelvic region. One of the frequently used applicators connected to the BSD-2000-3D is the Sigma-60 (∑-60). A consequence of the 60 cm diameter of the ∑-60 applicator is that it has a large water bolus. In Rotterdam the average AP-PA dimension of the patient is 22 cm, hence, the thickness of the water column resting on the stomach of the patient is on average 19 cm. For a substantial number of patients this amount of water results in the development of an uncomfortable pressure during the 90-min hyperthermia treatment. In reaction, the BSD Corporation has designed an upgraded and improved version of the ∑-60 applicator called the Sigma-60-Ellipse (∑-60-E), which is elliptical in shape. Due to the shorter height of the applicator the thickness of the water column above the stomach is reduced by 11.5 cm. The latter is expected to reduce discomfort while still offering the possibility to treat a satisfactorily large variety of different sized patients. Overall, the intention is that the ∑-60-E combines the reliability and sophisticated capability of the ∑-60 with improved provisions for patient comfort.

The ∑-60 applicator has an extensive track record with regard to quality assurance and its value has been proven in phase III trial investigations in which the benefit of adding hyperthermia to radiotherapy or chemotherapy has been demonstrated [1–9]. The United States Food and Drug Administration (FDA) accepted the ∑-60-E as a developmental packaging change in the ∑-60 applicator [10]. Replacement of the ∑-60 applicator by the ∑-60-E is in our opinion only acceptable after an extensive comparison of the basic characteristics of the both applicators.

Earlier, van Rhoon et al. found that the specific absorption rate (SAR) characteristics of the ∑-60 applicator are in good agreement with theoretically expected values [11]. In the current study we evaluated the SAR distributions of the ∑-60-E as a function of frequency and power; and the accuracy of target steering was assessed with the objective to characterize the basic performance of the applicator.

Materials and methods

Equipment

Applicator

The applicator used was the ∑-60-E phased array (BSD Medical Corporation, Salt Lake City, Utah, USA) (Figure 1A) [12]. The ∑-60-E is an array of 8 dipoles surrounding an octagonal-elliptical Lucite tube. Each dipole is orientated so that the radiated electric field is dominantly aligned with the central axis of the body positioned in the centre of the array. Each of these dipoles is individually dielectrically loaded by the water bolus. Internal power splitters allow power to be driven into four separate coaxial feed ports. Each of these input ports activate two adjacent dipole ports which are located at top, bottom, left, and right forming a dipole ring. The ∑-60-E basic frame is a cylinder made of Lucite glass with a nearly elliptical cross section and a central opening of 37cm (h) × 53 cm (w) (Figure 2A). Attached to its internal side is an integrated elastomer water bolus, with a closed silicone membrane containing deionized water which enables quick and easy patient set-up. It fills the whole space between the patient and the outer cylinder, and serves both as a cooling device for the patient's outer surface and to direct the RF waves into the body by impedance matching. The four channels of the Dodek amplifier (BSD Medical Corporation, Salt Lake City, Utah, USA) drive the eight-paired antennae of the applicator [12].

Figure 1. The Sigma-60-Ellipse phased array applicator and the cylindrical PVC phantom as placed in the measurement set-up (A), schematic representation of the phantom and place of the E-field sheets on the lower-half split of the phantom (B), a photo of the Schottky diode E-field sheet (C), the top view of two Schottky diode sheets with position of the diodes (D), and schematic representation of the measurement set-up (E).

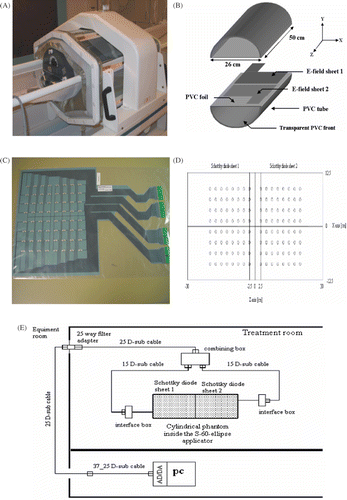
Phantom

A simple phantom configuration was used: a cylindrical PVC tube of 26 cm diameter, length 50 cm, closed at both ends, and it splits along the coronal plane into two equal parts. Each part was made watertight by gluing a PVC foil over the surface (Figure 1B). It was filled with saline water (2 g NaCl/L) to simulate average intra-pelvic tissue (σ = 0.4 Sm⁻¹at 20°C) [13]. The details of the phantom characteristics are described extensively elsewhere [11].

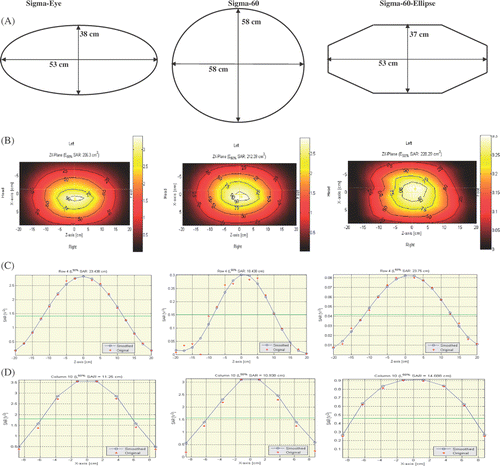
Figure 2. Schematic representation of the opening of the three applicators and their central dimensions (A), the contour plot of SAR-distribution (B), the profile of the SAR-distribution along the fourth row (C), and the tenth column of the Schottky diode sheets (D). The exposure to the phantom was applied in target position of (0, 0) cm, 800 W total power, 100% amplitude, and a frequency of 100 MHz.

Diode sheets

The flexible Schottky diode sheet (SDS) is used to measure the E-field distributions. The SDS consists of eight arrays of eight diodes mounted on a flexible 125 µm thick polyester foil, which is able to measure the E-field distribution with a resolution of 2.5 × 2.5 cm²(Figure 1C). The diodes are connected through highly resistive wires to the electronic read-out system. A detailed description of the SDS and read-out system is given elsewhere [14], [15].

SAR calculation

Electromagnetic energy is transferred to the material by polarization and rotation of dipolar molecules, and drift of electrons and ions. The amount of energy transferred by the electric field to a material can be derived from Poynting's theorem [16] where the average power (P) deposition to the material is given by:(1) where σ is electric conductivity (Sm⁻¹) and E is the complex electric field vector.

For hyperthermia the energy absorption in a material is often normalized to its mass density and is then called the specific absorption rate (SAR):(2) where ρ is mass density (kgm⁻³). Equation (2) shows that the energy absorption is directly proportional to the electric conductivity and to the square of E (complex electric field vector). The SAR_Total is defined as:(3) where E_X,Y,Z gives for the X, Y, and Z component of the E-field. The SDS measures the E-field distribution only in the main longitudinal direction (Z-component), called SAR_Z, which the formulation takes from:(4)

How well the E-field measurement with the Schottky diode sheet (SDS) represents the actual E-field depends on the size of the X- and Y-components of the field. The SAR_Z ratio, defined as:(5) can be used as a measure of the effectiveness of the E-field measurement. Calculations from the Finite Element Method in Hyperplan show that on average the SAR_Z ratio over the measurements is 94% (median 99%) for the measurement area of the SDS. Therefore, in the present study we used the term SAR-distribution, which with a very good approximation is representative for the E-field distribution.

Measurement set-up

In order to measure the SAR-distribution of the ∑-60-E applicator in the axial (Z-X) plane the following process was performed. Firstly, two SDSs were placed at the central cross-section of the lower-half split of the phantom; whereby no overlap of the SDSs occurred (Figure 1B). The upper-half split of the phantom was placed on top of the SDSs. It was made certain that good contact was applied between the SDSs and the phantom by having a small over-filling of the phantom. Then, using a level meter the phantom was positioned symmetrically in the centre of the applicator. The thickness of the water columns above and below the phantom was equal. Likewise, the water width at the left and right side of the phantom was equal with accuracy of ±0.5 cm (Figure 1A).

In this way, the SAR-distribution was measured by an array of 17 (columns) × 8 (rows)-diode sensors covering an area of 40 × 17.5 cm²(Figure 1D). To keep an equal distance between the data points a ‘virtual’ column (ninth column) is inserted. The value of the ninth column is the average of eighth and tenth columns’ values. In the next step, the SDSs were connected to the interface boxes and the interface boxes were connected to the multiplexer (combining) box. The combining box was, through the access panel, connected to a computer and the signals were transferred by an AD/DA-converter card of the computer (Figure 1E).

The water-bolus was filled and water circulation was applied during the measurement. RF power switch ON was only enabled for measuring the E-field distribution; whereby the ‘ON’ time was as short as possible to prevent significant heating of the phantom. An in-house developed MATLAB program acquired and proceeded all parameters related to the E-field and SAR-distribution for the measurements. Selected SAR-characteristics for evaluation of the applicator function were 50% iso-SAR area, longitudinal length of the 50% iso-SAR area in the Z direction (LL50), and radial length of the 50% iso-SAR area in the X direction (RL50) [see Figure 2B–D].

Experiments

The following experiments were performed 3–4 times and the results are average of the measurements.

Stability of SAR distribution as function of power

The RF power outputs used were 100, 400, 800, and 1600 W. The reason for this experiment is that the phase path of a high power amplifier is sensitive to power output. Further, the power combiners may add additional instability. The frequency applied was 77 MHz with a synchronous exposure. The synchronous exposure means an equal phase and amplitude settings, i.e. (0, 0) cm target position and 100% amplitude at top, bottom, left, and right antennae. The frequency of 77 MHz was chosen, as it is our preference to use a low frequency for the clinical application of loco-regional deep heating.

SAR distribution as function of frequency

The sensitivity of the SAR distribution, expressed as 50% iso-SAR area, LL50 and RL50, was assessed for the frequencies of 75, 77, 80, 90, 100, 110, and 120 MHz, at a total RF power output of 400 and 800 W using the synchronous exposure of the phantom.

Accuracy of target steering

This experiment was performed to evaluate the ability of the BSD-2000-3D system to perform controlled left-right SAR steering. The target steering was performed in (z-x) plane along the x-axis, i.e., left-right direction, of the phantom (see Figure 1B). The requested target positions, which were applied based on the BSD-2000 software, were from (0,−8) to (0, 8) cm by a step of 2 cm at the frequencies of 77, 100, and 120 MHz at 800 W total RF power output in the equal amplitude (100, 100, 100, 100%) settings. The measured target positions were based on the midpoint of the full width at half maximum of the SAR distributions. The difference between requested and measured target is an indication for the accuracy of target steering.

Results

Stability of SAR distribution as a function of power

SAR distributions were evaluated at the frequency of 77 MHz, (0, 0) cm target position, and 100% amplitude at the four positions (top, bottom, left, and right antennae) for different RF power outputs. The average of 50% iso-SAR area increased from 241 ± 44 cm²at 100 W (25 W per channel) to 296 ± 21 cm²at 1600 W (400 W per channel). The average LL50 (along the rows 4 and 5 of the SDSs) increased from 20.2 ± 1.7 cm at 100 W to 21.6 ± 1.2 cm at 1600 W. Furthermore, the average RL50 (along the columns 8 and 10 of the SDSs) increased slightly from 14.1 ± 0.4 cm at 100 W to 15.3 ± 0.3 cm at 1600 W.

SAR distribution as function of frequency

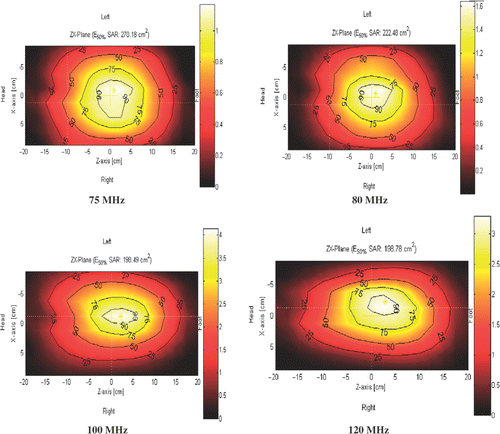
SAR distributions were evaluated in the frequency range of 75–120 MHz, (0, 0) cm target position, 100% amplitude at the four positions (top, bottom, left, and right antennae), separately at 400 and 800 W total RF power outputs to the four channels. Figure 3 shows four examples of the contour plot of the SAR distributions as a function of frequency at a power of 800 W. The SAR maximum was located in the centre of the applicator for the lower frequencies of 75, 77 and 80 MHz. At higher frequencies, the SAR maximum was slightly moved, e.g., 1 cm at 90 MHz, towards the feet, with a maximum of ∼3.5 cm at 120 MHz. This was similar for both 400 and 800 W applied powers.

Figure 3. Examples of the contour plot of SAR distributions for the Sigma-60-Ellipse applicator at different frequencies, 800 W total power, (0, 0) cm target position, and 100% amplitude.

Figure 4A shows the average of 50% iso-SAR area as function of frequency. As expected at both RF power outputs of 400 and 800 W, the average 50% iso-SAR area decreased when frequency increased. At 400 W, the average 50% iso-SAR area was 268 ± 7 cm²at 75 MHz and decreased to 161 ± 10 cm²at 120 MHz. For the power of 800 W, the average 50% iso-SAR area was 282 ± 10 cm²at 75 MHz and decreased to 163 ± 7 cm²at 120 MHz.

Figure 4. Average measurements of the Sigma-60-Ellipse applicator as function of frequency at 400 and 800 W total power, (0, 0) cm target position, and 100% amplitude: 50% iso-SAR area (A), 50% iso-SAR longitudinal length (LL50) along the rows 4 and 5 (B), and 50% iso-SAR radial length (RL50) along the columns 8 and 10 of the Schottky diode sheets (C).

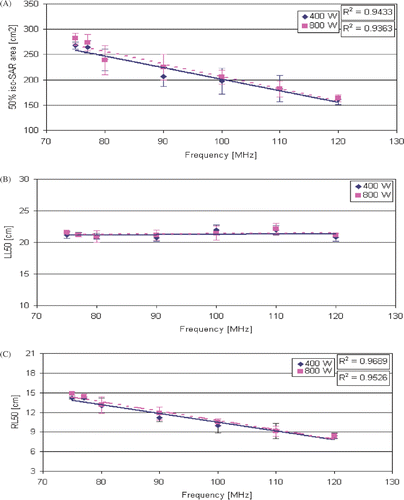
Figure 4B shows the average LL50 (along the rows 4 and 5 of the SDSs) as a function of frequency at 400 and 800 W. At 400 W, the LL50 was stable (∼21 cm) for the lower frequencies of 75–90 MHz and increased slightly to a maximum of 21.9 ± 0.7 cm at 110 MHz. Overall, the mean measured LL50 was 21.3 ± 0.5 cm. At 800 W, the minimum and maximum values for LL50 were 20.9 ± 0.9 and 22.2 ± 0.9 cm at 80 and 110 MHz, respectively (mean: 21.4 ± 0.4 cm).

Figure 4C shows the average RL50 (along the columns 8 and 10 of the SDSs) as function of frequency. At 400 W, the RL50 decreased from 14.2 ± 0.2 cm at 75 MHz to 8.4 ± 0.5 cm at 120 MHz. Similarly, for 800 W the RL50 decreased from 14.9 ± 0.3 cm at 75 MHz to 8.5 ± 0.3 cm at 120 MHz.

Accuracy of target steering

SAR distributions were evaluated at the frequencies of 77, 100, and 120 MHz, 800 W power output, and 100% amplitude at the four positions (top, bottom, left, and right antennae), for different target settings of (0, −8) to (0, 8) cm in steps of 2 cm. Movement of the target position from the left to the right side of the phantom was in a reasonable agreement with the requested target positions. Table I reports comparison between requested and measured target position at different frequencies.

Table I.  Comparison between requested and measured target position for the Sigma-60-Ellipse applicator at different frequencies, total power of 800 W, and 100% amplitude.

	Average measured (Z, X) cm at frequency of
Requested (Z, X) cm	77 MHz	100 MHz	120 MHz
0, −8.0	−1.1, −6.6	0.5, −7.7	0.9, −8.8
0, −6.0	−1.0, −6.2	0.9, −5.9	−2.2, −5.8
0, −4.0	−0.9, −5.3	1.3, −4.0	−3.0, −3.8
0, −2.0	−0.7, −1.9	1.3, −2.2	−0.9, −1.6
0, 0.0	−0.3, −0.4	−2.0, −0.4	−0.8, −0.3
0, 2.0	−0.6, 4.3	2.4, 2.3	−2.2, 2.1
0, 4.0	−0.4, 5.2	1.4, 4.1	−2.4, 4.7
0, 6.0	−0.5, 6.3	0.9, 5.3	−1.0, 6.1
0, 8.0	−1.4, 6.6	0.3, 6.9	−0.9, 7.8

Discussion

The results of the measurements performed with the ∑-60-E applicator demonstrate that the SAR distribution induced at the central cross-section of a homogeneous abdomen equivalent phantom possesses a predominantly Gaussian shape for the complete operational frequency range. The results also show that the SAR characteristics increased, up to 23%, when power output increased from 100 to 1600 W. The SAR maximum was located in the centre of the applicator for the lower frequencies of 75 to 80 MHz and it slightly moved toward the feet up to 3.5 cm at highest frequency of 120 MHz. Earlier van Rhoon et al. [11] found roughly similar results for the ∑-60 applicator. The reason for the unexpected shift is probably related to the specific electrical performance at higher frequencies of the unbalanced dipoles.

The largest 50% iso-SAR area was seen at the lowest frequency, i.e., 75 MHz, and it decreased by increasing frequency, having the smallest 50% iso-SAR area at the highest frequency, i.e., 120 MHz. The reduction of the 50% iso-SAR area and the RL50 was expected given the shorter wavelength for the higher frequencies. However, the LL50 was roughly constant over the frequency range of the 75–120 MHz. For the LL50 of the SAR distribution the length of the water bolus is decisive and therefore it is not surprising that the LL50 does not change over the frequency range of the 75–120 MHz.

The SAR distributions also show that the E-fields are quite symmetrical with respect to the left-right direction of the phantom. The target steering performance of the BSD-2000 phased array system was verified and the experiments showed that the target could be correctly moved from the left to the right side of the phantom.

Comparing our results with the reported data for the ∑-60 applicator by van Rhoon et al. [11], we considered that at different frequencies the 50% iso-SAR areas were almost equivalent for the two applicators (Table II). For the lower frequencies of 75–90 MHz the differences between calculated 50% iso-SAR areas of the ∑-60-E versus ∑-60 were 0.3 to 7%, which is within the accuracy range of the measurement system. However, for the higher frequencies of 100–120 MHz the differences were 13 to 15%. The larger 50% iso-SAR area at the higher frequencies for the ∑-60-E is caused by the longer LL50 of the ∑-60-E compared to the ∑-60 (Δ = + 10 to +16%). This difference is expected as the water bolus-patient contact length for the ∑-60-E is much longer than that of the ∑-60 (see Table III).

Table II.  Characteristic values of the Sigma-60, the Sigma-Eye, and the Sigma-60-Ellipse applicators describing the SAR distribution as a function of frequency at 800 W total power, (0, 0) cm target position, and 100% amplitude. The results for the Sigma-60-Ellipse are average of 3-4 measurements. Numbers in parentheses show 1SD.

	Applicator
Frequency	LL50* (cm)			RL50* (cm)			Calculated 50% iso-SAR area (cm^2) as an ellipse from LL50 and RL50
(MHz)	S-60^†	S-Eye^†	S-60-Ellipse	S-60	S-Eye	S-60-Ellipse	S-60	S-Eye	S-60-Ellipse
75	20.9		21.6(0.1)	15.3		14.9(0.3)	251		252
80	21.4		20.9(0.9)	13.8		13.2(1.2)	232		216
90	21.7		21.2(0.8)	12.4		11.9(1.0)	211		198
100	19.6	22.5	21.5(1.1)	9.7	10.5	10.5(0.5)	149	186	176
110	19.1		22.2(0.9)	9.2		9.1(0.8)	138		159
120	18.6		21.1(0.3)	8.2		8.5(0.3)	120		140

*The LL50 and RL50 are defined as 50% iso-SAR longitudinal and radial length, respectively. ^†The data presented for the Sigma-60 and the Sigma-Eye applicators are from van Rhoon et al. [11], [18], [19].

At the lower frequencies of 75–90 MHz the LL50s for the ∑-60-E are roughly equal to those for the ∑-60 applicator (Δ = − 2 to +3%). Furthermore, the RL50 was roughly equal for the two applicators over the whole frequency range of 75-120 MHz (Table II).

Table III.  Physical comparison of the Sigma-60, the Sigma-Eye, and the Sigma-60-Ellipse applicators as provided by the BSD Medical Corporation [12].

	Sigma-60	Sigma-Eye	Sigma-60-Ellipse
Frequency range (MHz)	60–120	100	80–110
Antenna length (cm)	45	14	45
Array/diameter max. (cm)	58	38 × 53	37 × 53
Bolus-patient contact length (cm)	∼36	∼50	∼50
Drive ports	4	12	4
Radiators	8	24	8
E-field alignment	Long axis	Long axis	Long axis
Convergent mode	2D TEM*	3D TEM	D TEM

*TEM: transverse electro magnetic.

These results show that in the frequency range of 75–90 MHz the SAR characteristics of the ∑-60-E are almost identical for the ∑-60 applicator. Taking into account that in Rotterdam our preference is to apply the lower frequencies (<90 MHz) for loco-regional deep hyperthermia, these results show that if one replaces the ∑-60 with the new ∑-60-E applicator there will be no difference in the SAR distributions. Hence, provided that other relevant treatment parameters will not change, the quality of heating is potentially equal for the ∑-60 and ∑-60-E applicators.

Table III shows the physical characteristics of the ∑-60, ∑-Eye, and ∑-60-E applicators as provided by the BSD Corporation [12]. For a more visual comparison of the three applicator Figure 2 provides in addition to the schematic design of each applicator also the SAR-distribution in the XZ-plane and the SAR profile along the main axes for the frequency of 100 MHz.

With respect to our comparison between the ∑-60 and ∑-60-E applicator there are two important design aspects in the ∑-60-E that may affect the SAR-distribution. Firstly, the bolus-patient contact length of the ∑-60-E is ∼50 cm, which is significantly larger than the ∼36 cm of the ∑-60 (Table III, row 4). Secondly, the positioning of the dipole antennae in the elliptical shell of the ∑-60-E is such that the loading of the dipole is not symmetrical. Due to the sharp angles of the Lucite shell one side of the dipole ‘sees’ more air than the other. This might result in a different behaviour of the ∑-60-E with frequency compared to the fully symmetrical loaded dipole antennae of the ∑-60.

The ∑-60-E recommended frequency range is 80–110 MHz. The reason for this is an expected lower matching, i.e., increased reflected power for frequencies below 80 MHz and a lower power output at frequencies higher than 110 MHz [17]. In our experiments the∑-60-E applicator performed equally well at 75 and 120 MHz that is outside the specific recommended frequency range.

We also compared the SAR characteristic values of the ∑-Eye applicator reported by van Rhoon et al. [18], [19] with those for the other two applicators. The results are presented in Table II, row 4 (100 MHz). The calculated 50% iso-SAR areas of the ∑-Eye and the ∑-60-E were almost equal (186 versus 176 cm², respectively, Δ = + 6%), but they were both higher than the ∑-60 (149 cm²). However, the LL50 of the ∑-Eye was slightly larger than the LL50 of the ∑-60-E (22.5 versus 19.6 cm, respectively, Δ = + 15%) and the ∑-60 (21.5 cm, Δ = + 5%). The RL50 of the ∑-Eye was similar to the RL50 of the ∑-60-E (10.5 cm) but slightly larger than the ∑-60 (9.7 cm, Δ = + 8%). These results show that the SAR characteristics of the ∑-60-E (at 100 MHz) are also almost identical for the ∑-Eye. An important advantage of the ∑-60-E over the ∑-Eye applicator is that the ∑-60-E provides more space of the lateral sides of the applicator while having the same water pressure, and thus the ∑-60-E accommodates larger patients than the ∑-Eye.

Finally, we consider that the characterization of the performance of hyperthermia applicators by phantom experiments has been demonstrated to be a useful tool to understand the specific behaviour of an applicator and to design an applicator-specific quality assurance programme [11,20].

Conclusion

Since at the lower frequencies of 75–90 MHz the SAR characteristics, i.e. the 50% iso-SAR areas, the 50% iso-SAR longitudinal and radial lengths of the SAR distributions of the ∑-60-E were roughly identical for the ∑-60 applicator, our conclusion is that the ∑-60 can safely replace the ∑-60-E applicator for loco-regional deep heating at this frequency range. Furthermore, for the same reason at 100 MHz the ∑-Eye also can safely replaced the ∑-60-E applicator.

Acknowledgement

This work was supported by the Dutch Cancer Society, grant DDHK 2003-2884. The first author was supported financially by the Shahrekord University of Medical Sciences (related to the Iranian Ministry of Health, Treatment and Medical Education). The authors would like to thank A. Ameziane and R. Canters for their technical assistance.