Quantitative analysis of 3-D conformal MRI-guided transurethral ultrasound therapy of the prostate: Theoretical simulations

Abstract

Purpose: The capability of MRI-guided transurethral ultrasound therapy to produce continuous regions of thermal coagulation that conform to human prostate geometries was evaluated using 3-D anatomical models of prostate cancer patients.

Methods: Numerical simulations incorporating acoustic and biothermal modeling and a novel temperature control feedback algorithm were used to evaluate treatment accuracy of a rotating dual-frequency multi-element transducer. Treatments were simulated on twenty anatomical models obtained from the manual segmentation of the prostate and surrounding structures on MR images of prostate cancer patients obtained prior to radical prostatectomy.

Results: Regions of thermal coagulation could be accurately shaped to predefined volumes within 1 mm across the vast majority of the prostates. Over- and under-treated volumes remained smaller than 4% of the corresponding prostate volumes which ranged from 14 to 60 cc. Treatment times were typically 30 min and remained below 60 min even for large 60 cc prostates. Heating of the rectal wall remained below 30 min_43°C in half of the patient models with only minor, superficial heating in the other cases. The simulated feedback control algorithm adjusted the ultrasound transducer parameters such that high treatment accuracy was maintained despite variable blood perfusion, changing tissue ultrasound attenuation, and practical temperature measurement noise and sampling rate.

Conclusions: Numerical simulations predict that MRI-guided transurethral ultrasound therapy is capable of producing highly accurate volumes of thermal coagulation that conform to human prostate glands.

• Ultrasound
• prostate
• thermal therapy
• MRI
• adaptive
• feedback control

Introduction

Prostate cancer is the most commonly diagnosed and the second and third leading cause of cancer related deaths among American and Canadian men, respectively 1, 2. Sensitive screening methods are increasingly detecting small volume, low grade prostate cancers in an ever younger population, where the disease usually follows an indolent course 3. A study examining the natural progression of untreated, early stage prostate cancer showed, however, that 20% of low-risk patients died from the disease within 15 years of diagnosis 4. Since there is yet no way of determining which indolent cancers will eventually become life-threatening, this study recommended early treatment of the disease. The most common prostate cancer treatments, prostatectomy and external beam radiation therapy, provide good outcomes in terms of disease control, but are associated with high complication rates affecting urinary, bowel and sexual function which can significantly reduce the patient's quality of life 5.

There is, therefore, strong motivation to develop a prostate cancer treatment that can provide good disease control while maintaining a high patient quality of life. Ultrasound therapy is becoming an attractive alternative to conventional prostate cancer therapies because it can generate precise and conformal patterns of thermal coagulation through a minimally invasive procedure. Both transrectal 6–8 and transurethral approaches are being developed. The transurethral approach is particularly attractive because it can create contiguous patterns of thermal damage, coagulate the entire prostate gland in short treatment times, and meet all of the criteria set out by an international task force on focal treatments of prostate cancer 9. Protein denaturation and thermal coagulation of cells can be induced quickly (seconds) and irreversibly by using ultrasound energy to raise tissue temperatures beyond 50°C 10. Ultrasound heating applicators have the capability to deposit energy in well-defined volumes with little dependence on passive heat conduction, thus enhancing control of the spatial pattern of thermal damage in tissue. The deposition of energy can be monitored and guided with MR temperature imaging techniques which enables treatment of the entire prostate gland (or a sub-volume) while avoiding thermal damage to surrounding important structures such as the rectum. Transurethral heating devices access the prostate gland directly, bringing the energy source as close as possible to the targeted tissue and reducing treatment times significantly. Finally, patients can be re-treated with ultrasound therapy enabling effective conservative management of the disease.

A number of ultrasound transducer designs have been developed for transurethral prostate therapy including multi-sectored cylindrical transducers 11, curvilinear transducers 12, sectored tubular transducers 13 and planar rectangular transducers 14–16. Control over the depth of heating is achieved by manipulating the ultrasound power of each transducer element and/or the transurethral applicator direction and rate of rotation. The incorporation of transducers that resonate at multiple frequencies can also improve controllability over radial depth of coagulation 17. The heating profile along the length of the transurethral applicator can be shaped by using multiple transducer elements 18, 19. This study used a virtual model of a rotating dual-frequency multi-element planar rectangular transducer that emitted directional ultrasound beams to produce regions of thermal coagulation that conformed to predefined target geometries in three dimensions (3-D).

In order to ensure that the target volume of tissue has been heated adequately and accurately, temperature measurements of sufficient spatial and temporal resolution are necessary for thermal monitoring and feedback control 20–22. Magnetic resonance (MR) imaging technology can provide such information during treatment using the proton resonance frequency shift of water in tissue 23, 24. The efficacy of using MR thermometry to guide ultrasound therapies and to control the extent of thermal damage has been demonstrated 16,25–28.

There have been several in vivo studies demonstrating the technical feasibility of producing large regions of thermal coagulation sufficient for prostate therapy 12–15,29,30. Quantitative assessment of shaping these regions to human prostate geometries in 3-D, however, has not been fully explored. In 2005, Chopra et al. introduced a method to generate heating patterns whose 2-D central axes conformed accurately to axial planar prostate boundaries using a single large rotating transducer under active temperature feedback control 31. The situation becomes more complex and the challenges more significant when using a rotating device with multiple transducer elements to shape continuous 3-D heating patterns to volumetric prostate geometries for whole-gland treatment. For example, 2-D control over the region of thermal coagulation with a single ultrasound transducer was primarily achieved by modulating the device rate of rotation 31. Because all elements of a multiple element transducer rotate at the same rate, the ultrasound power and frequency of each element must be independently controlled to shape 3-D heating patterns to complex prostate volumes. Moreover, heat conduction in the prostate from adjacent transducer heating patterns can affect the temperature dynamics, treatment control, and the final spatial heating pattern, ultimately having an impact on treatment accuracy. The goal of this work was to predict with numerical simulations the potential accuracy with which 3-D target volumes corresponding to the shapes of human prostate glands, could be thermally coagulated and to quantify the consequential heating to the immediately surrounding anatomy after MR-temperature-guided transurethral prostate ultrasound therapy. This study used anatomical models derived from high resolution MR images of prostate cancer patients and detailed numerical simulations of 3-D conformal transurethral ultrasound therapy.

Methods

This study used computer simulations, implemented in C++, to evaluate the accuracy with which volumetric regions of thermal coagulation could be shaped to target boundaries using multi-element transurethral ultrasound heating applicators and active temperature feedback. A multi-point feedback control algorithm was developed to modulate device parameters (rotation rate, ultrasound power and frequency) based on a series of temperature measurements along the surface of a target boundary. In order to evaluate the performance of the control algorithm on realistic target boundaries, 3-D models were created by segmenting MR images of prostate cancer patients. The robustness of the control algorithm was tested further in a series of simulations where tissue ultrasound attenuation, blood perfusion and temperature measurement accuracy were varied.

Patient models

Twenty 3-D models were formed by manually segmenting the pelvic anatomy on high quality MR images of men with clinically significant localized prostate cancer destined for radical prostatectomy (mean (range) age: 60.6 (50–68) years, prostate volume: 32.7 (14–60) cc, n = 20). Approval for this use of the images was obtained from the institutional research ethics board. The multi-slice axial, T2-weighted MR images were acquired using a 1.5 T MRI system (GE Signa Excite, Milwaukee, WI) with an endorectal coil (MedRad, Indianola, PA) combined with a torso phased array surface coil. The images had in-plane pixel size of 0.55 mm and a slice thickness of 3 mm with no interslice gap.

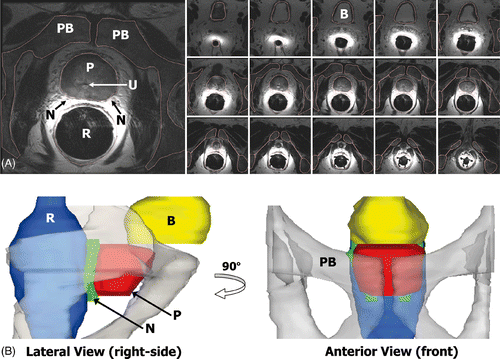
The segmentation was performed by manually contouring the boundaries of the prostate, rectum, bladder, neurovascular bundles and pelvic bone, as well as selecting the location of the urethra in each axial image of the prostate cancer patients Figure 1(A). Because the patient images were acquired without the rigid transurethral device in place, the axial images were translated to align the center of the urethra to a common axis. The prostate boundary was interpolated and sampled at every angular degree from the center of the urethra in axial planes positioned 1 mm apart along the transurethral device, producing an accurate and natural representation of pelvic anatomy such as the example shown in Figure 1(B).

Figure 1. Modeling the anatomy of a prostate cancer patient from MR images. (A) The prostate (P), rectum (R), bladder (B), pelvic bone (PB), and neurovascular bundles (N), were manually segmented to create patient-specific anatomical models. The position of the urethra (U) was also recorded to locate the virtual transurethral ultrasound therapy device. (B) The segmented structures were incorporated into numerical simulations to enable quantitative assessment of treatment strategies.

Tissue models

Thermal coagulation was calculated using a temperature threshold, Tc, of 52°C 32,33. While tissues that reached 52°C or more were considered completely coagulated (non-viable), some thermal damage can occur at lower temperatures. Tissues that accumulated a conservative thermal dose less than 30 equivalent minutes at 43°C (30 min_43°C) were considered completely spared from thermal damage 34.

The control algorithm was tuned and evaluated assuming a constant ultrasound attenuation of 0.5 dB cm⁻¹ MHz⁻¹ for all tissues. Some studies, however, have observed an increase in attenuation upon thermal coagulation of tissue 35,36. Additional simulations modeling this effect were, therefore, conducted (1) to evaluate the influence of increased attenuation on treatment time, and (2) to assess the robustness of the control algorithm under conditions of variation in tissue properties. For these calculations, ultrasound attenuation was increased linearly and irreversibly from 0.5 to 0.845 dB cm⁻¹ MHz⁻¹ as the temperature rose from 50° to 65°C, consistent with measurements performed on freshly excised canine tissues 36. All simulations assumed the ultrasound absorption was equal to the attenuation to maintain conservation of energy.

Blood perfusion was simulated as a constant value which decreased to zero in the regions of thermal coagulation. While the majority of the ultrasound therapy simulations incorporated blood perfusion at a nominal rate of 16 ml min⁻¹ 100 g⁻¹, simulations incorporating no blood perfusion as well as increased blood perfusion (32 ml min⁻¹ 100 g⁻¹) were also performed on three patient models. These values span the range of those reported in the literature for in-vivo human prostate tissue 22,37,38.

For all soft tissues, the simulations assumed a density of 1,000 kg m⁻³, specific heat capacity of 3,700 J kg⁻¹°C⁻¹, thermal conductivity of 0.5 W m⁻¹°C⁻¹, and speed of sound of 1,500 m s⁻¹ 28,32,39,40.

Device configuration

In this study, the size of the virtual individual rectangular transducer elements was set to 4 × 3 mm; a width of 4 mm is typical for transurethral devices and a length of 3 mm provided high treatment spatial resolution along the transurethral applicator while maintaining high acoustic efficiency (>50%, based on prototype devices). When these small elements are operating alone, however, the attainable depth of heating is limited and as such they are appropriate for transurethral prostate therapy only when they are a constituent of a larger multi-element transducer. The influence of individual transducer length has not been fully explored and experimental studies examining the issues of element size are underway. Up to seventeen elements were necessary to cover the length of the longest prostate in the 3-D models. The spacing between elements was set to 0 mm to model closely prototype devices which have a spacing of 100 µm.

A dual-frequency transducer was used to increase the spatial control over the deposition of energy in tissue 17. Higher frequencies are better suited to treat shallow target radii, especially those near the rectum and neurovascular bundles. Conversely, large target radii are more effectively treated with a lower ultrasound frequency. The resonant frequencies of the transducer were set to 4.7 and 9.7 MHz, consistent with prototype devices 17.

To remove thermal losses and to couple the ultrasound into tissue, water flows through the transurethral device. The temperature of the water, Tu, was set to an ambient 20°C. A rectal cooling device 13,31,41 maintained at a temperature of 15°C was modeled in all simulations to help protect the rectal wall. The rectal cooling space was defined as the region 3 mm inferior to the outer rectal wall to account for the thickness of the rectal wall and cooling device following the anatomy of Figure 1A.

Ultrasound and thermal calculations

The free-field, 3-D pressure distribution from a single rectangular transducer element was calculated using an approximation to the Rayleigh-Sommerfeld integral 42. Determining the free-field pressure distribution enabled dynamic and spatially varying tissue attenuation to be incorporated into the thermal calculations. The pressure distribution generated by the dual-frequency multi-element transducer was resolved by combining the acoustic fields from the individual elements operating at independent ultrasound powers and frequencies. The complete free-field was later scaled to account for tissue attenuation. The acoustic pressure distributions were calculated at a high spatial resolution of 0.25 mm (isotropic) to characterize the near field of the ultrasound transducers and the interactions between neighboring elements. The 3-D ultrasound power deposition in tissue was determined using the intensity of the acoustic pressure 43, and was subsequently decimated to a spatial resolution of 1 mm (isotropic) to match that of the thermal calculations.

Temperature dynamics during a transurethral multi-element ultrasound therapy were calculated using an explicit 3-D finite difference solution to Pennes’ Bioheat Transfer Equation (BHTE) 44, which approximates the thermal response in tissue due to ultrasound power deposition, heat diffusion and thermal homeostasis from blood perfusion. The spatial and temporal resolutions of the thermal calculations were 1 mm (isotropic) and 1 s, respectively. These values ensured numerical convergence of the BHTE and provided sufficient resolution to model the spatial and temporal temperature variations in tissue.

Temperature feedback

The accuracy of treatment delivery was evaluated independent of temperature measurement accuracy to understand the thermodynamics of transurethral ultrasound therapy. In these ‘ideal’ cases, temperature feedback was sampled at every second, matching the temporal resolution of the thermal calculations, with no measurement noise. In reality, however, the temperature measurements for feedback control are acquired using MR thermometry which has limited spatial and temporal resolution, and noise-limited temperature accuracy. A study by Chopra et al. 45 determined that the ability to create conformal heating patterns with a rotating transurethral device was compromised mainly by the sampling time and noise in the temperature measurements. To study the effects of temperature measurement noise on treatment accuracy, simulations incorporating measurements achievable on a 1.5 T MRI (sample at every 5 s with normally distributed noise of 1°C standard deviation), were performed on all 20 patient models. To provide a sense of system stability, one patient model was selected to investigate the effects of increasing measurement noise, from 1 to 5°C. All temperature noise simulations were repeated five times to account for the random variations in measurement noise.

Control algorithm

A revised control algorithm based on multi-plane temperature feedback was developed to produce volumes of thermal coagulation that conform to predefined 3-D prostate geometries. Feedback control algorithms have many advantages over open-loop approaches (treatment plans) because they can actively compensate for unpredictable variations in the system, such as dynamic blood perfusion 46. In this study, the control algorithm used the temperature at the prostate boundary to modulate the applicator rotation rate and the ultrasound power and frequency of each transducer element. The goal of the control algorithm was to raise the temperature of the outer surface of the prostate gland to Tc in one complete rotation of the applicator. A secondary objective of the control algorithm was to prevent tissue temperatures from exceeding an upper limit, Th = 90°C, to avoid undesirable effects such as boiling or tissue carbonization. Although the outer surface of the prostate was chosen as the target boundary in these simulations, a sub-volume within the gland could also be treated using this approach.

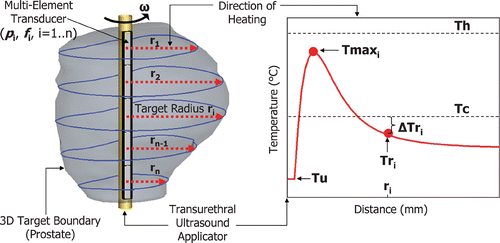
As shown in Figure 2, a 5-mm diameter transurethral applicator housing a multi-element transducer was positioned inside a continuous 3-D target boundary (the prostate). Each transducer element (i = 1 … n) emitted a directional ultrasound beam normal to the transurethral applicator creating directional, collimated heating patterns similar to the temperature profile depicted in Figure 2. Along the direction of heating, the temperature rises quickly from Tu, reaching a maximum value, Tmax_i, at about 5–10 mm from the transducer surface, then decreasing and reaching ambient body temperature within a few cm. The distance from each transducer element, i, to the 3-D target boundary along the direction of heating was defined as the target radius, r_i. The control algorithm modulated the transurethral applicator rate of rotation (ω) and the transducer elements’ ultrasound power (p_i) and frequency (f_i) based on the temperature difference (ΔTr_i) between Tc and Tr_i, as well as the value of r_i. In general, the rotation rate was dictated by the transducer element heating the largest target radius, r_i. The control parameters were updated after every temperature measurement and determined according to the following equations:where ω is the device rate of rotation (° min⁻¹), k_ω(r_i) is the rotational gain constant, p_i is the individual element acoustic power (W_acoustic), k_p(r_i) is the power gain constant, f_i is the ultrasound frequency (MHz), f_high and f_low are the high and low ultrasound frequencies of the dual-frequency elements.

Figure 2. Typical temperature profile along the direction of heating of an ultrasound transducer element. The target radius (r_i) sampled from the 3-D target boundary is used to determine the corresponding element's ultrasound frequency (f_i). The difference (ΔTr_i) between the critical temperature (Tc) and the target radius temperature (Tr_i) is used to control the element's power (p_i) and the applicator rate of rotation (ω). The maximum temperature (Tmax_i) was monitored to ensure that it did not exceed an upper limit (Th) thereby avoiding undesirable effects such as boiling or tissue carbonization.

In order to ensure a contiguous pattern of thermal damage and to minimize treatment times, the applicator rate of rotation was continuous and set to the maximum value that still permitted coagulation to the largest target radius, r_i. The rate of rotation was inversely proportional to ΔTr_i such that the applicator slowed down when target radius temperatures decreased, allowing greater local energy deposition. The rotational gain constant, k_ω(r_i), decreased with r_i and was determined through a separate series of simple tuning simulations. The maximum rate of rotation was set to 60°, 120° or 300° min⁻¹, depending on r_i, to avoid excessive speeds and to maintain a continuous pattern of thermal damage as ΔTr_i approached zero.

The ultrasound power of each transducer element was proportional to ΔTr_i such that the rate of heating decreased as Tr_i approached Tc. The element requiring the minimum ω_i was usually operating at p_max, while the power of the other elements was set to a value between p_min and p_max. The power gain constant, k_p(r_i), was set to an increasing quadratic function of r_i, determined through a separate series of simple tuning simulations. As ΔTr_i approached zero, the ultrasound power approached p_min which was set to 0.1 W_acoustic, less than 10% of p_max which was 1.2 W_acoustic (for 4 × 3 mm elements). The value of p_max was chosen to avoid the Tmax_i from attaining Th. The power of an element was turned off when either the target boundary or maximum temperature exceeded Tc or Th, respectively, allowing tissues to cool.

One exception to the relationships described above is at the beginning of a treatment when the applicator remained stationary and the ultrasound power of all elements was set to p_max. This enabled the generation of a certain amount of heat before initiating device rotation. The choice between f_high and f_low was made by comparing r_i to r_f, which was set to 13.5 mm. This threshold was determined based on keeping treatment times short, as explained previously by Chopra et al. 31.

The energy deposition per unit volume at a given location is proportional to the acoustic power and time spent heating that location. For the element, i, where ω_i = ω, the energy deposition is proportional to the ratio p_i/ω_i which is a non-linear (quadratic) function of ΔTr_i. This enables the controller to adjust the energy output more quickly in response to changes in temperature at the target boundary. Due to the bounds imposed on the ultrasound power and device rate of rotation, as well as the relatively slow rates of temperature change in tissue, the non-linear nature of the controller is not expected to cause larger oscillations in temperatures (compared to a linear model) or lead to system instability.

The control algorithm, based on temperature measurements at the target boundary, performed better than one based on thermal dose in this context of high temperature ultrasound therapy (>50°C), for reasons outlined previously by Chopra et al. 45. Thermal dose increases extremely rapidly for temperatures above 50°C and approaches a binary model for describing thermal coagulation. Such very non-linear behavior of the thermal dose model at high temperatures makes it extremely sensitive to temperature measurement noise and update rates, ultimately compromising its utility for controlling coagulation 47.

Quantitative analysis of simulation results

The simulated treatments were analyzed to determine: (1) the accuracy with which the regions of thermal coagulation conformed to the predefined 3-D target boundaries, and (2) the consequential heating of the rectal wall. The region of thermal coagulation included all tissues whose maximum temperature during treatment reached or exceeded Tc, and was defined as a 3-D boundary equal to the 52°C isosurface. Treatment difference was defined as the distance between the coagulation and target boundaries, in mm. Positive values of treatment difference represented areas where the region of thermal coagulation extended beyond the target boundary (over-treatment), and negative values represented under-treatment. Treatment accuracy was first quantified by calculating the mean and standard deviation of the treatment difference sampled across the entire target boundary. This provided a metric of how well the coagulation boundary matched the target boundary in the context of evaluating the performance of the feedback control algorithm.

The second metric of treatment accuracy was defined as the volume of the treatment difference. The over- and under-treated volumes correspond to the amount of tissue outside the prostate that was coagulated and the amount of prostate tissue that was not coagulated, respectively. These volumes were expressed as a fraction of the prostate volume for comparison across the 20 patient models. While the over-treated volume fraction is an indicator of the extent of thermal damage outside the target boundary, it is the under-treated volume fraction which determines the risk of containing viable cancerous tissue. The total treatment volume difference is the sum of the over- and under-treated volume fractions.

The analysis of the treatment results also examined heating of the rectal wall. This was performed by counting the number of 1 mm³ voxels that constituted part of the rectal wall and absorbed more than 30 min_43°C. This very conservative threshold in the rectum served as a worst-case scenario for the purposes of this study.

Results and discussion

Patient modeling

Analysis of the segmented anatomical data revealed the interesting histogram displayed in Figure 3, showing the normalized distribution of the target radius values for the prostate boundaries of the twenty patient models. The darker bars encompass the target radii sampled across the entire surface of the prostate boundary and the lighter bars represent the subpopulation that lies on the interface of the prostate and rectum. The distribution is normalized such that its total area equals 100%. For example, about 5% of the target radii across the 20-patient models lie between 7 and 8 mm and approximately 4.5% come from areas near the rectum while 0.5% come from other areas of the prostate. The shortest and deepest target radii were 4.9 and 30.4 mm respectively. For each patient, the largest prostate width and height were measured (the horizontal and vertical diameters in the axial inset of Figure 3) as well as the prostate length (along the transurethral applicator) and volume. They were (mean +/− SD, (range)): width 47.1 +/− 5.5, (38–57) mm; height 28.9 +/− 5.7, (17–38) mm; length 36.5 +/− 7.4, (27–51) mm; volume 32.7 +/− 14.2, (14–60) cc (n = 20).

Figure 3. Normalized distribution of prostate radius values sampled from the images of 20 prostate cancer patients. Prostate radius is the length from the urethra center to the prostate capsule and represents the target radius. The distribution is normalized such that its total area equals 100%. As illustrated in the top-right inset (axial), the dark bars represent samples from the entire prostate boundary while the lighter bars represent samples from the region of the prostate (P) that interfaces with the rectal wall (R).

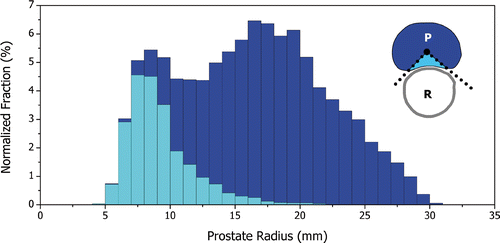
The range of target radii impacts the choice of ultrasound frequency used for therapy. From Figure 3, smaller radii are not only found at the base and apex of the prostate gland, but are, in fact, mostly located at the posterior portion of the prostate near the rectum. This means that both short and deep target radii are present in axial planes normal to the transurethral applicator. The accurate and safe coagulation of tissue at depths of 5 to 30 mm with a rotating transducer in an internally-cooled applicator was difficult to achieve with a single frequency. Dual-frequency transducers, however, showed significant improvement in the targeting of tissues over this range of radii while maintaining reasonable treatment times (<1 hour). It was verified during the tuning of the control algorithm that a 4.7/9.7 MHz dual-frequency transducer could provide the necessary flexibility for the treatment of these 20 segmented prostate boundaries.

The treatment of the posterior portion of the prostate (peripheral zone) requires careful attention because it is typically in close proximity to the rectum and is the site of the majority of cancers 48. The ultrasound frequency must be high to achieve accurate targeting of the short target radii in that region while avoiding excessive energy deposition in the rectal wall. A dual-frequency threshold, r_f, of 13.5 mm was selected based on maintaining short treatment times; however, it can be seen in Figure 3 that this threshold is also appropriate for treating radii in the direction of the rectum. The use of dual-frequency ultrasound transducers appears to play a critical role in enabling the thermal coagulation of the posterior and anterior portions of the prostate gland while also minimizing damage to the surrounding anatomy 49.

The endorectal coil used to acquire the high quality MR images of the prostate cancer patients was about 5 cm in diameter, occupying a large volume of the pelvic cavity. The coil was designed to be pressed closely against the prostate gland, thereby decreasing the distance between the rectum and prostate and increasing the area of the rectal wall in close proximity to the prostate. Consequently, any heating of the rectum was probably overestimated in this study. Similarly, the endorectal coil may also have affected the distribution of target radius values (Figure 3) by flattening the posterior portion of the prostate.

Transurethral prostate ultrasound therapy simulations

Treatment accuracy

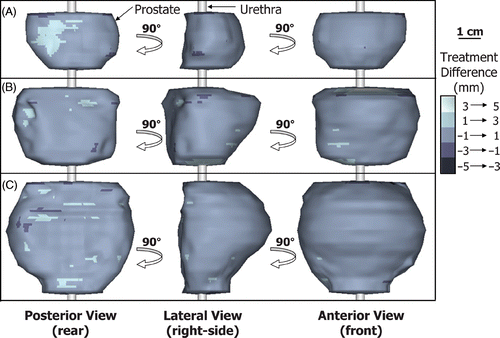
Treatment simulations performed with constant tissue ultrasound attenuation (0.5 dB cm⁻¹ MHz⁻¹), variable blood perfusion (16 ml min⁻¹ 100 g⁻¹), ‘ideal’ temperature measurements (no noise, 1 s sampling) and rectal cooling (15°C), produced regions of thermal coagulation that conformed very accurately to the predefined 3-D target boundaries of the 20 patient models. In all cases, the standard deviation of the treatment difference was less than 1 mm and the total treatment volume difference was less than 10%, relative to the corresponding prostate volume. Examples are shown in Figure 4 for small, medium and large prostate geometries (17, 37 and 60 cc), with the treatment differences encoded in grayscale on the target boundary surface. The regions of thermal coagulation conformed to within 1 mm of the target boundaries across most of the prostate gland. Similar results were obtained for all 20 patient models as summarized in Figure 5(A) which plots the mean, standard deviation and range of the treatment difference as a function of prostate volume. The mean of the treatment difference was on average 0.17 mm and ranged from −0.1 to 0.3 mm. Even though the minimum was almost always significantly greater in magnitude than the maximum, the mean of the treatment difference remained positive in 95% of cases (19 out of 20). This suggests that the treatment difference was typically small and positive which is desirable when aiming to completely coagulate the entire prostate gland. If desired, the treatment difference could be shifted towards positive or negative values by revised tuning of the control algorithm; therefore, the standard deviation of the treatment difference was used as the quantifiable measure of treatment accuracy. For the 20 patient models, the standard deviation of the treatment difference ranged from 0.4 to 0.8 mm with an average value of 0.63 mm. The tight standard deviation of the treatment difference (<1 mm for all target boundaries) is evidence of the strong capability of MRI-guided transurethral ultrasound therapy to create volumes of coagulation that conform very well to a range of different human prostate geometries. While overall treatment accuracy is high, even small positive treatment differences can cause adverse effects, for example at the neurovascular bundles. To evaluate potential complications associated with transurethral ultrasound therapy, a study examining the spatial distribution and degree of heating of the surrounding anatomy during treatment is underway.

Figure 4. Three views of typical treatment results of MRI-guided transurethral ultrasound therapy for (A) small, 17 cc; (B) medium, 37 cc; and (C) large, 60 cc prostates. The orientation is consistent with that of Figure 1. Treatment accuracy was quantified by showing the spatial location of the treatment difference on the target prostate boundary. The region of thermal coagulation was within 1 mm of the target boundary over most of these volumes.

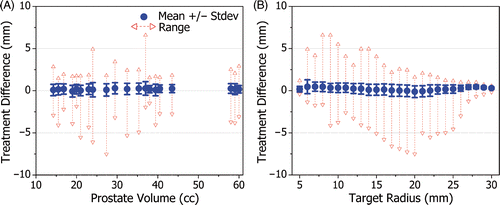
While Figure 5(A) shows that overall treatment accuracy is high for various prostate volumes, Figure 5(B) illustrates that high treatment accuracy is maintained across the entire range of target radius values. The standard deviation of the treatment difference ranged from 0.1 to 0.8 mm with an average value of 0.53 mm, demonstrating that the control algorithm performs well for all target radii.

Figure 5. The treatment difference shown as a function of: (A) target prostate volume, and (B) target radius. The standard deviation of the treatment difference remained less than 1 mm for all patient models, confirming a high degree of treatment accuracy. For all target radius values, the standard deviation of the treatment error remained less than 1 mm from 5 to 30 mm.

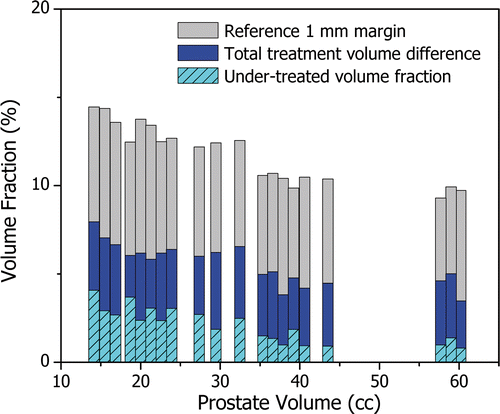
The total treatment volume difference ranged from 3% to 8% with an average value of 5.5%, expressed as a fraction of the corresponding prostate volume. The under-treated volume fraction, representing the amount of prostate tissue that might still be viable after completion of the ultrasound therapy, remained smaller than or equal to 4% and reached values below 1%. In order to put these values into perspective, Figure 6 shows the total treatment volume difference (dark bars) and the under-treated volume fraction (light hashed bars) relative to a reference margin that extents 1 mm beyond the 3-D target boundary (light solid bars) as a function of prostate volume. The over-treated volume fraction corresponds to the visible portion of the dark bars. For all prostate geometries, the total treatment volume difference was approximately half that of the 1 mm reference margin. The under-treated fraction was more significant for small prostates because in these cases the applicator rotates more quickly, on average, possibly under-sampling the target boundary. Forcing a reduction in rotational speed for these smaller prostates may further improve treatment accuracy. If the under-treated fraction were further reduced through appropriate tuning of the control algorithm, however, the total treatment difference would still remain similar causing an increase in the over-treated volume fraction. Considering that state-of-the-art conformal hypofractionated external beam radiation therapy of the prostate uses 4 mm therapeutic margins (conventional radiation therapy uses a 10 mm margin) 50, the advantages of MRI guidance during transurethral ultrasound treatment are clear.

Figure 6. The treatment difference as a fraction of the prostate volume. The total volumetric treatment difference (dark bars) remained below 8% for all 20 patient models. The under-treated volume fraction (light hashed bars) decreased with prostate volume and ranged from less than 1% to 4%. The over-treated volume fraction is represented as the visible portion of the dark bars. To put these values into perspective, the volume fraction of a reference margin extending 1 mm beyond the prostate boundary is displayed. The total volumetric treatment difference was typically half the volume of the 1 mm reference margin.

Heating of the surrounding anatomy

The thermal impact of transurethral prostate ultrasound therapy on the rectal wall was evaluated by counting the number of 1 mm³ voxels that absorbed a thermal dose of more than 30 min_43°C, a conservative threshold for partial thermal damage 34. Half of the prostate models maintained rectal heating below this threshold, 40% exceeded this threshold in 1 to 5 voxels, and 10% (2 out of 20) in 5 to 20 voxels. In all cases, the voxels that exceeded 30 min_43°C were limited to the superficial 1 mm layer of the rectal wall. This small amount of heating is probably overestimated in this study due to anatomical distortions from the endorectal MRI coil. Additional simulations performed with the rectum translated 1 mm further away from the prostate predicted that rectal wall heating remained below 30 min_43°C for all 20 patient models.

A recent study by Wootton et al. 49 showed that transurethral prostate ultrasound therapy may produce regions of excessive heating at the surface of the pelvic bone, depending on the ultrasound frequency and power as well as the dimensions of the prostate and the distance to the bone. This phenomenon was not investigated in this study because the endorectal MRI coil probably created geometrical distortions that influenced distances to the pelvic bones. Further studies examining pelvic bone heating with more appropriate patient models are warranted.

The extent of the region of thermal damage along the transurethral applicator was confined to 1–2 mm beyond the dimension of the multi-element transducer; thus, heating of the urinary sphincters and bladder was not significant.

Treatment times

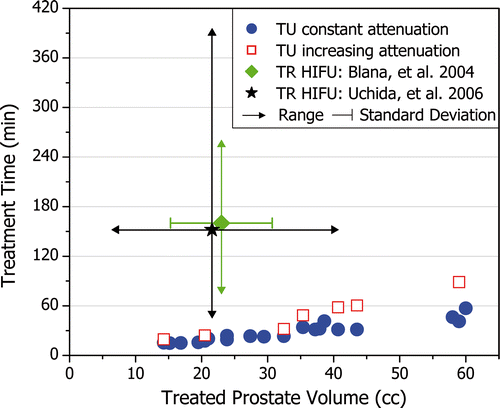
As anticipated, the total treatment time increased with prostate volume. Figure 7 shows that treatment times were typically 30 min and ranged from 15 min for a 15 cc prostate to nearly 60 min for a 60 cc prostate. Simulations which modeled increasing attenuation with temperature were also performed, leading to increased treatment times as shown in Figure 7. The increase in treatment time was greater for larger prostates because energy deposition at deep target radii was reduced, and heating from conduction became more important. Treatment times increased by 25% for small prostates (20 cc), by 50% for medium prostates (30 cc), and by 100% for large prostates (>40 cc). These treatment times for transurethral ultrasound therapy remain considerably shorter than those reported for transrectal high intensity focused ultrasound (HIFU).

Figure 7. Treatment times for transurethral (TU) ultrasound therapy increase with prostate volume. Treatment times are generally less than 30 min and remain less than 1 hour. When modeling increasing ultrasound attenuation with temperature, a large prostate (59 cc) can be treated in less than 90 min. The mean and range for treatment times reported for transrectal (TR) HIFU are shown for comparison.

Temperature feedback controller

The feedback control algorithm described in this paper is the first to adjust automatically the rate of rotation and the ultrasound power and frequency of a moving energy deposition field from multiple transducer elements in order to shape volumetric regions of thermal coagulation to predefined complex 3-D target boundaries. Other studies have used manual adjustments of these parameters 11,51 or automatic controllers that consider target boundary temperatures of a single ultrasound transducer element 31,52. Sophisticated feedback controllers for HIFU or hyperthermia procedures have been described for creating areas of uniform temperature or thermal dose, but the applications have been limited to controlling temperatures at points distributed along a line (1-D) or a plane (2-D) 25,27,28.

The control of a transducer with multiple elements is significantly more complex than that of a single element, yet necessary for shaping thermal patterns accurately in 3-D. Conformal volumes of coagulation could be produced by translating a single large transducer along the urethra; however, this approach would be highly impractical because treatment times would increase dramatically (by the number of translations) and treatment accuracy would decrease significantly (by having to use a large transducer element).

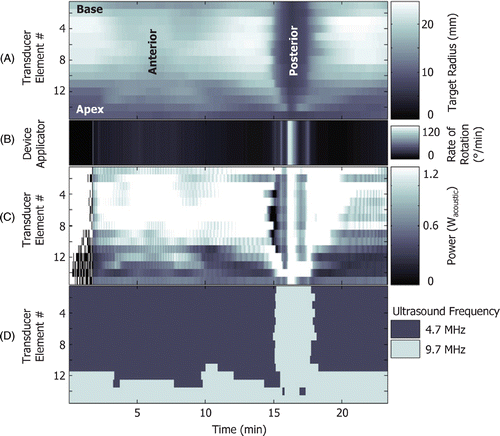
Figure 8 illustrates the variations in target radius (A) along with those which occur for the transurethral applicator rate of rotation (B) and the ultrasound power (C) and frequency (D) of a fifteen-element transducer. At the beginning of the treatment (0 to 2 min), the applicator does not rotate and the power is modulated ON/OFF allowing the generation of an adequate amount of heat. The applicator then rotates slowly while treating the anterior portion of the prostate where some target radii are large (2 to 14 min). During this period, more power is required to coagulate larger target radii. At the posterior of the prostate, when all the target radius values are small (14 to 18 min), the rate of rotation is increased and the power is adjusted accordingly. To reduce treatment times, the rate of rotation is varied such that at least one transducer element is operating at maximum power. The ultrasound frequency is modulated based on target radius values to provide increased accuracy and to decrease treatment times. The ultrasound frequency could also be adjusted in order to reduce the degree of heating to the surrounding anatomy. It is evident that this level of control made possible using active temperature feedback control could not be achieved manually.

Figure 8. Typical variation of rate of rotation and power and frequency of a fifteen-element transducer. Also shown are the current rotational angle and the boundary (target radius) seen by the transducer elements as a function of time. The treatment begins with the device in a stationary position and the power set at maximum to generate a certain amount of heat (0–2 min). Once the device starts to rotate, more power is needed to treat larger boundaries (2–14 min). When the device reaches the posterior region of the prostate where the boundary becomes more shallow, the rate of rotation increases and the power is adjusted accordingly (14–18 min).

Effect of increasing ultrasound attenuation with temperature

Treatment accuracy was evaluated on a representative subset of seven patient models where ultrasound attenuation was increased with temperature. Without adjusting the tuning of the control algorithm, treatment times increased significantly, thereby increasing the total energy deposition in the prostate and effectively counteracting the reduction in ultrasound penetration depth. In all cases, the total treatment volume difference and the standard deviation of the treatment difference increased; however, a high level of treatment accuracy was maintained. Figure 9 compares the treatment accuracy, on average, achieved under the constant and increasing ultrasound attenuation scenarios. The total treatment volume difference increased on average by 3.4%, from 6.2% to 9.6% (primarily due to an increase in under-treated fraction), yet remained smaller than the volume of the 1 mm reference margin. The standard deviation of the treatment difference increased on average by 0.4 mm, from 0.7 to 1.1 mm.

Figure 9. The effect of increasing tissue ultrasound attenuation on treatment accuracy when using a control algorithm tuned assuming constant attenuation. The average from seven treatments on representative patient models is shown for constant and increasing ultrasound attenuation. The left side of the figure shows the total treatment volume difference expressed as a percentage of the prostate volume, similarly to Figure 6. The right side of the figure shows the mean, standard deviation, maximum and minimum treatment difference, similarly to Figure 5(A). The feedback control algorithm is capable of effectively responding to unforeseen dynamic changes in ultrasound attenuation to maintain high treatment accuracy.

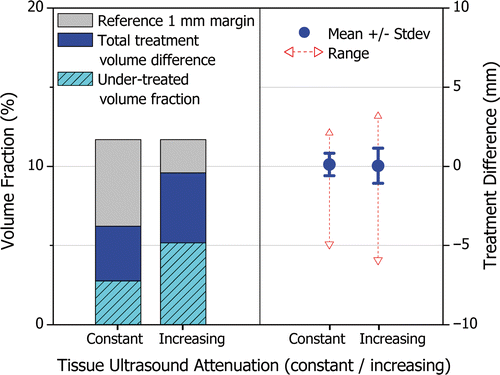
The feedback control algorithm was capable of effectively responding to unforeseen dynamic changes in ultrasound attenuation to maintain high treatment accuracy with longer treatment times. In the absence of active feedback control, the system would not be able to modulate treatment delivery in response to dynamic or unpredictable tissue changes and treatment accuracy would be severely affected.

Effect of blood perfusion

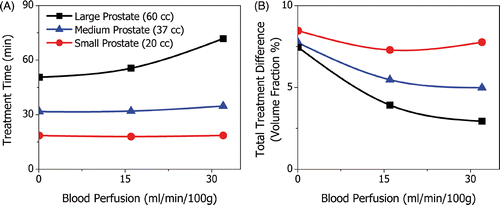
The rate of blood perfusion in the prostate and surrounding anatomy is highly variable between patients and can influence the depth of heating and temperature dynamics during ultrasound therapy 22. The effect of blood perfusion was investigated in three patient models with small, medium and large prostates (20, 37 and 60 cc). The amount of blood perfusion was varied from 0 to 32 ml min⁻¹ 100 g⁻¹, and affected treatment times and treatment accuracy. Because blood perfusion tends to maintain temperature homeostasis, it has the effect of increasing treatment times on the anterior portion of the prostate, and decreasing treatment times at the posterior where it acts against rectal cooling. For small and medium prostates, therefore, perfusion increased treatment times by less than 10% as can be seen in Figure 10(A). For the larger prostate, however, the anterior portion of the gland is more significant and treatment times increased by more than 40%. The rate of blood perfusion also affected treatment accuracy as shown in Figure 10(B). Some amount of blood perfusion is desirable because it damps the temperature response of the tissue and reduces over-treatment. For the small prostate where the applicator rotates more quickly, high levels of blood perfusion can slow the temperature response too much, thereby increasing under-treatment.

Figure 10. The effect of blood perfusion on treatment time and treatment difference shown for small, medium and large prostates. Treatment times increase with perfusion and its effect is more pronounced for larger prostates; from 0 to 32 ml min⁻¹ 100 g⁻¹, treatment times increase by <1%, 10% and 40% for the small, medium and large prostates, respectively. Blood perfusion dampens the tissue temperature response and so the total volumetric treatment difference decreases with blood perfusion. A minimum occurred for the small prostate because high levels of perfusion can lead to an increase in under-treated volume fraction.

Effect of temperature measurement resolution

Temperature measurement noise and sampling rate can affect treatment accuracy of transurethral prostate ultrasound therapy 21,45. To evaluate this effect for a multi-element transducer, treatment simulations were performed with practical 1.5 T MR thermometry temperature measurements with 1°C standard deviation noise, updated every 5 s. In general, treatment accuracy was somewhat reduced as summarized in Table I which lists the average, minimum and maximum change from the same results obtained with ‘ideal’ temperature measurements. On average, the total treatment volume difference increased by 0.40% and the standard deviation of the treatment difference, by 0.10 mm. The number of 1 mm³ voxels of the rectal wall that absorbed more than 30 min_43°C decreased or remained the same for 95% of the patient models (19 out of 20) across the five repeated simulations. In the single case where rectal wall heating increased, the number of potentially damaged voxels increased from 1 to 5 mm³.

Table I.  Change in treatment accuracy using practical vs. ‘ideal’ temperature measurements for all 20 (19) patient models.

	Average	Minimum	Maximum
Treatment time	5 min	20 s	23 min
Over-treated volume fraction	0.25%	−0.6%	2.8% (1.0%)^a
Under-treated volume fraction	0.17%	−0.3%	0.8%
Total treatment volume difference	0.40%	−0.5%	2.5% (0.8%)^a
Mean treatment difference	0.03 mm	−0.1 mm	0.3 mm
Standard deviation of treatment difference	0.10 mm	−0.1 mm	0.2 mm

^aValues in parentheses refer to the second largest difference in treatment accuracy.

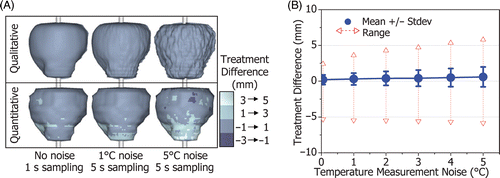
To evaluate system stability, a patient model with relatively complex prostate geometry was used in treatment simulations with increasing levels of temperature measurement noise. Figure 11(A) shows the qualitative boundary of thermal coagulation with 0°, 1° and 5°C standard deviation temperature noise, and the corresponding quantitative treatment difference plotted on the 3-D target boundary. The mean, standard deviation and range of the treatment difference are plotted in Figure 11(B). There is a gradual increase in treatment difference with temperature noise up to 5°C but the system remains stable.

Figure 11. The effect of temperature measurement noise and sampling rate on the treatment difference for a prostate with complex geometry (32 cc). (A) The qualitative shape of the region of thermal coagulation and the quantitative measure of treatment difference for a patient model with: no noise, 1 s sampling; 1°C standard deviation noise, 5 s sampling; and 5°C noise, 5 s sampling. While the treatment difference becomes noticeable for high levels of measurement noise, treatment accuracy is maintained for practical MR thermometry resolutions (1°C noise, 5 s sampling). (B) The standard deviation and range of the treatment difference increases gradually with temperature measurement noise (up to 5°C), evidence of system stability.

Conclusion

Regions of thermal coagulation shaped to human prostate geometries with MRI-guided transurethral ultrasound therapy were successfully simulated for a wide range of 3-D anatomical models obtained from images of prostate cancer patients. Numerical simulations incorporating multi-element transducer feedback control show that conformal coagulation of the entire prostate gland is possible while avoiding excessive thermal dose to the rectal wall. A high degree of treatment accuracy was achieved over a variety of prostate geometries representative of patients who would be considered for this type of therapy. Heating of the bone requires further investigations with more suitable anatomical models. Patient-specific treatments incorporating these techniques appear to be feasible.

Acknowledgements

This research was supported by the Natural Sciences and Engineering Research Council of Canada, the Terry Fox Foundation, the Canadian Institutes of Health Research and the Ontario Research and Development Challenge Fund. The MR images of prostate cancer patients were courtesy of Dr Masoom Haider, Department of Medical Imaging, Princess Margaret Hospital, University Health Network, Toronto, Ontario, Canada. The authors would also like to acknowledge Jeff Wachsmuth for his contributions to the development of the numerical simulations.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.