Solution to the bioheat equation for hyperthermia with La_1−xAg_yMnO_3-δ nanoparticles: The effect of temperature autostabilization

Abstract

This work aimed to analyze the possibility and performance of the temperature controlled hyperthermia based on AC heating of magnetic nanoparticles with low Curie temperature. Temperature dependence of dynamic magnetic susceptibility has been studied experimentally on fine powders of La_0.8Ag_0.15MnO_2.95 in the frequency range of 0.5–2.0 MHz. Critical drop of the AC magnetic losses was found in the vicinity of the Curie point, T_C = 42°C. The obtained data was used in the numerical analysis of the bioheat equations under typical conditions of the hyperthermia treatment. The mathematical model includes a spherical tumor containing magnetic particles and surrounded by concentric healthy tissue, with account made for the blood perfusion. The calculations performed for various AC power, tumor sizes and doping geometries predict effective autostabilization of the temperature at T ≅ T_C inside the tumor and steep temperature profile at the interface with the healthy tissue.

• Radiofrequency
• magnetic particles
• manganites
• Curie temperature
• temperature stabilization

Introduction

Recently, fine magnetic particles are intensively studied as agents for local heating of living tissues, especially in cancer therapy 1–6. The particles are introduced into diseased tissue and then heated by application of sufficiently strong alternating magnetic field. Typical frequencies are in the range of 0.1–1.0 MHz, with the amplitudes H ∼ 10 kA/m; this ensures predominance of magnetic losses caused by magnetization reversal and magnetic relaxation, with negligible heating by inductive currents. Local hyperthermia using magnetic microparticles has the maximum potential for selective targeting and heating diseased regions without damaging the surrounding healthy tissue 4.

Magnetic fluids containing superparamagnetic or ferrimagnetic fine particles of magnetite (Fe₃O₄) and maghemite (γ-Fe₂O₃) were explored intensively 3,6–8. These materials show sufficiently high specific absorption rate (SAR) which characterizes the AC magnetic losses per 1 g of the magnetic substance. A difficulty arises, however, when the precise temperature control is needed, which is of great importance in medical hyperthermia to protect the tissue from overheating and necrosis 2–5. Recently it was suggested overcoming this problem by the use of magnetic particles with low Curie temperature, T_C ∼ 40–50°C 9–13. At temperatures T < T_C, the material is ferro- (ferri-) magnetic with high AC losses, whereas the transition into paramagnetic phase ensures the drop of SAR and so the autostabilization of the temperature near T_C. As prospective materials, the rare-earth manganites were proposed, such as La_1-xSr_xMnO_3-δ (LSMO) 10–12 and La_1-xAg_yMnO_3-δ (LAMO) 13, the proper T_C values being provided by the choice of doping, stoichiometry and synthesis technology. For successful application, the sufficiently high value of SAR is needed, along with the narrow and steep phase transition at T_C which is crucial for temperature stabilization. Of course, the standard biomedical requirements, such as chemical stability and biocompatibility, must be ensured as well. Currently, all these problems are under investigation in a number of laboratories 8–13.

To estimate the applicability of new materials in hyperthermia treatment it is useful to perform quantitative calculation of the temperature distribution in living tissues under typical conditions of magnetic hyperthermia. Usually, such calculations are based on various versions of the Pennes’ bio-heat transfer equation 14. Many numerical simulations were carried out for a variety of hyperthermia modalities, biophysical parameters and specific tumor shapes, with account made for blood perfusion 15–33. Much work was performed using inductive currents and macroscopic magnetic implants (seeds) as heat sources 15–18,25,27,28; in some cases, the calculations were supported experimentally 16,34–36. In the present paper we deal with another branch of local hyperthermia which uses magnetic nanoparticles (magnetic fluids) 1–6. This techniques has its own specific features, just as in practical aspects (such as targeting, biocompatibility, intracell heating, etc.), so also in the heat transfer in tissues. The bioheat equation as applied to magnetic nanoparticles was analyzed recently in 31,32; for the early publications, see the review article 26 and 19–24.

The main goal of these calculations was to find an optimal set of adjustable parameters, such as the concentration, SAR, and spatial distribution of the heat sources, as well as the amplitude and frequency of the alternating magnetic field, which provide the required, strictly limited temperature rise in the tumor (as a rule, acceptable temperatures must lie in the range of 42°–44°C 15) and minimum heating of the surrounding healthy tissue. The size of the absorbed power range that gives acceptable tissue temperature distributions is calculated and suggested as a deciding factor in successful hyperthermia treatment 15,16. An inverse solution is developed to achieve constant therapeutic temperature within the tumor region 20,21. In practice, however, the absorbed power can hardly be monitored and controlled with proper accuracy during the whole hyperthermia procedure. As a result, the risk of overheating may be a problem, both in the tumor and healthy tissue.

As mentioned above, this problem can be overcome by using the low-T_C magnetic materials which provide an abrupt fall of heat generation and, hence, the autostabilization of the temperature just near T_C. Thus, the risk of overheating is eliminated automatically, without any worry about power control. This idea was firstly proposed by C.T. Cetas et al. for seed techniques 37 and revived recently for magnetic fluid modality 9–13.

From the computational point of view, the situation is as follows. In the majority of publications the heat generation was assumed to be independent of T; this approximation is well justified for the high-T_C materials, such as magnetite and maghemite, where T_C is much higher than the body temperature. In this case, the problem of the temperature autostabilization cannot be solved. Unlike that, the bioheat equation for the low-T_C materials contains a heat generation term which critically depends on temperature near T_C. The corresponding solution has not yet been analyzed for magnetic fluid modality. To investigate such solution and examine the possibility and real parameters of the temperature autostabilization is the main goal of the present communication. New experimental data on the AC magnetic losses in the recently synthesized La_1-xAg_yMnO_3-δ particles with T_C ∼ 42°C will be presented and used in the calculation. It will be shown that the temperature autostabilization near T_C can be attained with typical parameters of diseased and healthy tissues, with account made for the blood perfusion. Besides, a good space distribution of the elevated temperature is predicted, ensuring proper heating of the tumor without harmful effect on the surrounding healthy tissue.

Magnetic material

Fine powders of La_1-xAg_yMnO_3-δ were prepared and supplied by the Moscow University team 13. The proper T_C and SAR values were obtained by the chemical homogenization technique at the composition of x = 0.2; y = 0.15; δ = 0.05. The preparation technology, basic chemical-physical properties, and the problem of biocompatibility are discussed in detail in 13.

To calculate the kinetics of heating and temperature profile under hyperthermia conditions, knowledge is needed on the temperature dependence of magnetic AC losses, especially in the vicinity of T_C. To obtain these data, we have measured the imaginary part (χ″) of the dynamic magnetic susceptibility of the material under study. The χ″ value was determined from the change in the quality factor (Q) of the resonant circuit with and without the sample inside the coil. The data obtained on La_0.8Ag_0.15MnO_2.95 at ω/2π = 1 MHz are shown in Figure 1. It can be seen that the χ″ value changes only slightly in the ferromagnetic region, but drops steeply near T_C ≅ 42°C and becomes negligible in the paramagnetic phase. The results were found to be almost independent on frequency in the range of 0.5–2.0 MHz. More detailed presentation, including thorough description of the experimental techniques and the data obtained on different samples, will be published separately.

Figure 1. Temperature dependence of the imaginary part of the dynamic magnetic susceptibility measured on the La_0.8Ag_0.15MnO_2.95 powder at 1 MHz. Points are the experimental data; solid and dashed curves represent the complicated and simplified test functions, respectively.

The imaginary part of the AC susceptibility determines the absorption ability and can be related to the heat power (P) generated in 1 cm³ of the material subjected to AC magnetic field as follows 30:where μ₀ is the permeability of vacuum and H is the amplitude of the AC magnetic field. Here P is expressed in W/cm³ and the rest in SI units. Further, SAR = P/ρ, where ρ is the material density (about 6.5 g/cm³ for the manganites). Note that we express the SAR value in W/g LAMO, not per gram of metal ions as adopted sometimes in literature 2. Using the experimental value of χ″ ≅ 0.5 at room temperature (Figure 1), along with H = 10 kA/m and ω/2π = 0.8 MHz, one gets SAR = 22 W/g, in agreement with experimental data obtained recently on similar samples by AC heating of the LAMO aqueous suspensions 13. Thus our measurements of χ″ are consistent with independent experiments and can be employed in further calculations.

Mathematical model

The most important effect to be studied is the auto-stabilization of temperature caused by the critical drop of magnetic losses near T_C. To reveal this phenomenon with maximum clarity and avoid unnecessary complications, it is reasonable to restrict ourselves by spherical symmetry (that is, to use the one-dimensional bioheat equation). Thus, giving credit to detailed 3D analysis 28,31, we will follow the approach used by Bagaria and Johnson 32 which may be considered as a prototype for our calculation. Similar to 32, the diseased tissue (‘tumor’) is represented by the inner sphere with a radius r₁. The tumor (or some concentric region inside the tumor) contains uniformly distributed magnetic particles with volume concentration α ≪ 1. The mean distance between the particles is assumed to be small enough to consider the doped volume as a homogeneous effective medium with the averaged heat generation of αP W/cm³. Note that this assumption is well justified for typical parameters when working with microparticles, but cannot be applied to macroscopic seeds. Further, another sphere with the same center (r = 0) and radius r₂ > r₁ represents an ‘organ’, and the spherical layer between r₁ and r₂ is filled with healthy tissue without magnetic particles. The heat transfer in this model, with account made for blood perfusion, is described by the standard one-dimensional equations 32:where the power density P may depend on r, accounting for various space distributions of the particles. The subscripts ₁ and ₂ correspond to the inner sphere (tumor) and outer spherical layer (healthy tissue), respectively, and the subscript _b stands for blood. The following nomenclature is used: T_i, temperature; ρ_i, density; c_i, specific heat capacity; k_i, thermal conductivity; w_b, blood perfusion. The boundary conditions include the finiteness of T(0, t) < ∞ in the centre and T(r₂, t) = const. = T₀ at the outer border, where T₀ is the normal body temperature. At the interface of the tumor and the healthy tissue (r = r₁), the temperature and the heat flow are continuous:The initial conditions correspond to the normal body temperature in the whole volume, T(r, 0) = T₀.

Equations 2 and 3 seem to be analogous to those studied in 32. However, in contrast to the previous analysis, we consider the case when the generated heat power P does depend on the temperature. As a consequence, the equations become non-linear. The most important for the temperature stabilization is the specific form of χ″(T) in the critical region, see Figure 1. If the fall of χ″ were infinitely steep (rectangular, with discontinuity at T_C), the analytical solution would be available both for spheric and cylindrical symmetries. In such an ‘ideal’ case, the strict stabilization (T = T_C) is predicted inside an inner region (r_stab < r₁) which approaches the whole tumor volume at high values of the heat power. In reality, however, the drop of the AC magnetic losses is described by continuous function and so the heating temperature will depend somehow on AC power even in the critical region. Thus, the stabilization near T_C is not perfect and can be estimated quantitatively by proper analysis of Equations 2 and 3 with account made for the real temperature dependence of P. In this case, the analytical solution cannot be obtained, and the problem should be solved numerically.

To make use of the experimental data we fitted the χ″(T) dependence by the test functionwhere a = 0.0165; b = 4.17°C; T₁ = 43.35°C; T₂ = 40.88°C; Δ₁ = 1.21°C; Δ₂ = 4.56°C, shown as the solid curve in Figure 1. This function was used in all calculations presented in this paper. One should realize, however, that this complicated expression is not universal and may depend on specific sample. So we also tested the much simpler functionwhere c = 0.58; T_C = 42°C; Δ = 1.5°C (dotted line in Figure 1) which fits the most important critial region well. We found that such simplification does not lead to significant changes in the solution and thus can be recommended for express analysis. To solve the problem numerically, the method of finite differences was used. Discrete approximation was made on non-uniform grid which was refined near the interface r = r₁. Since the problem includes non-linearity (caused by the source αP), the solution can be obtained in iterative process. The implicit scheme with simple iteration process was employed, the non-linearity being included from the previous iteration. The iterations continued until the inequalitywas fulfilled, where the subscript i stands for the grid node and superscripts s, s + 1 denote the iteration numbers. The value of ε = 10⁻³ was found to be sufficient for our objectives. After the iterations converged, the next temporal step was performed and so on, until the steady state.

In the calculation, the generally adopted values of the parameters 32 were accepted, namely: ρ₁ = 1.1 g cm⁻³; ρ₂ = 1.0 g cm⁻³; c₁ = c₂ = c_b = 4.2 J g⁻¹ K⁻¹; k₁ = 5.5 10⁻³ W cm⁻¹ K⁻¹; k₂ = 5.0 10⁻³ W cm⁻¹ K⁻¹; T_b = T₀ = 37°C. The radius of the tumor r₁ was changed from 0.6 to 1 cm, with the outer radius of the organ fixed as r₂ = 4 cm. The volume concentration of the magnetic particles in the inner sphere was fixed as α = 3·10⁻³ 32,38. To study the effect of blood perfusion, the quantity w_b1 = w_b2 = w_b was varied from 0.3 to 3 mg cm⁻³ s⁻¹, the middle value of 1 mg cm⁻³ s⁻¹ being typical 32.

In what follows, the AC power is expressed through the amplitude H of AC magnetic field with the frequency ω/2π = 800 kHz, applied to the tissue containing magnetic particles with volume concentration α = 3 10⁻³. These values taken at H = 10 kA/m will be referred to as ‘standard’ ones. Note that the data presented below can be easily re-counted for other combinations of α, H, and ω for a given value of αP, see Equation 1.

Results and discussion

Some results of our calculations are shown in Figures 2–4 and listed in Tables I and II. In Figure 2A and 2B, the kinetics of heating are presented at different AC field amplitudes, both for the centre (r = 0) and the interface between the diseased and healthy tissues (r = r₁). In Figure 2, the uniform space distribution of the magnetic particles is assumed in the whole tumor area, 0 ≤ r ≤ r₁, for two different tumor radii: r₁ = 1 cm (Figure 2A) and r₁ = 0.6 cm (Figure 2B). In Figure 2C, a more complicated shape is studied, namely, the particles are uniformly distributed in the spherical layer r′ ≤ r ≤ r₁ of the tumor with the outer radius r₁ = 1 cm. Such ‘shell’ geometry may be of particular interest in the case when the magnetic particles are delivered through the blood stream, and the tumor periphery is supplied with the blood more intensively than the central area.

Figure 2. Calculated temperature kinetics in the center, r = 0 (upper set, black) and at the boundary of the tumor, r = r₁ (lower set red) for various amplitudes H of the AC magnetic field, from the bottom upwards: 7.1 kA/m (dotted); 10 kA/m (dash-dot); 14.1 kA/m (dashed); 17.3 kA/m (solid thin); 20 kA/m (solid thick). (A): r₁ = 1 cm, uniform doping; (B) r₁ = 0.6 cm, uniform doping; (C): r₁ = 1 cm, shell doping at 0.6 < r < r₁. Inset in (A) shows the kinetics at H = 10 kA/m for various values of the blood perfusion parameter, from the bottom upward: w_b = 3; 1; and 0.3 mg cm⁻³ s⁻¹.

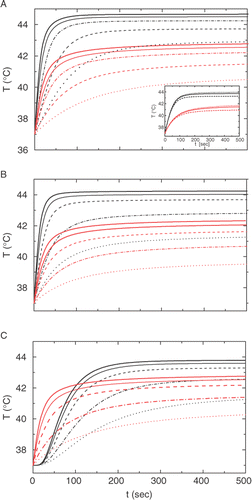
As it is seen from Figure 2A, the temperature inside the 1-cm tumor attains its steady state T_st ≅ T_C during 200–300 sec at the standard conditions and considerably faster at higher AC levels. A bit higher power is needed to attain T_C with smaller tumor radius (r₁ = 0.6 cm), Figure 2B. This rather unexpected result suggests that the heating depends on the total amount of the magnetic adsorbent stronger than on its concentration.

Figure 3. Calculated dependencies of the steady state temperature at different distances from the tumor center (shown at the curves) on the amplitude H of the AC magnetic field. The A, B, and C symbols indicate the same geometries as in Figure 2. The dashed and dash-dotted curves in (A) correspond to the blood perfusion magnitudes w_b = 3 and 0.3 mg cm⁻³s⁻¹, respectively; all solid curves are for w_b = 1.0 mg cm⁻³s⁻¹.

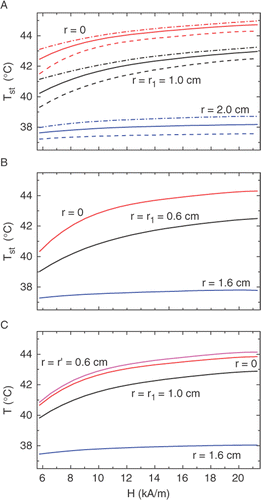
The most important feature is the temperature stabilization near T_C. To show this effect clearer, the T_st values are plotted versus H in Figure 3 for two tumor sizes and different particle distributions. Figure 3A shows also the effect of blood perfusion, with the parameter w_b changing from 0.3 to 3 mg cm⁻³ s⁻¹. Figure 3 represents the main result of this work: it can be seen that, after approaching T_C ≅ 42°C, the temperature inside the tumor depends only slightly on the AC power, thus protecting the tissue against overheating. In all cases shown, this result is achieved already at the ‘standard’ value of H = 10 kA/m. As a measure of stabilization, one can choose the temperature increment ΔT_st caused by the two-fold increase of the AC power (that is, the increase in H) above the standard value. As can be seen from Figure 3 and Table I, the value of ΔT_st does not exceed 1°C both in the centre and at the border of tumor, in the whole range of the blood-perfusion rates considered. The latter shows that a moderate change in w_b which may occur upon heating and depends on r 39 cannot affect substantially the temperature landscape.

Figure 4. Temperature profiles calculated for H = 14.1 kA/m (upper set, red) and 10 kA/m (lower set, black) at various durations of the AC heating, from the bottom upward: 50 s (dash-dot), 100 s (dashed) and steady state (solid curves). The A, B, and C symbols indicate the same geometries as in Figure 2. Thick borders show the doped region.

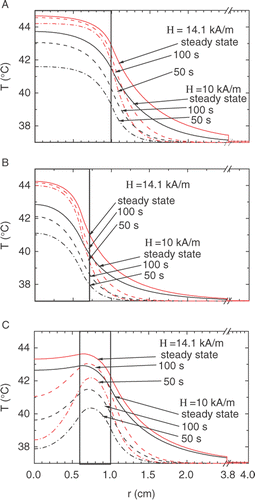
Another essential feature to be investigated is the temperature profile inside and outside the tumor. The strong temperature contrast between the diseased and healthy tissues is quite desirable since it provides minor damage of the living organ. The comparison of the temperature kinetics at r = 0 and r = r₁ is presented in Figure 2, whereas Figure 3 shows the steady-state regimes at r = 0, r′, r₁ and r₁ + 1 cm (the latter being in the healthy region). These results are also shown in Table I. In Figure 4, the calculated temperature profiles are shown at various points of time during the heating.

Table I.  Characterization of temperature stabilization under AC heating: steady state temperatures T_st at various distances r from the centre and the temperature increment ΔT_st caused by 2-fold raising of AC power above standard level (H = 10 kA/m; ω/2π = 0.8 MHz).

Volume doped with magnetic particles		0 < r < r1 r1 = 1.0 cm			0 < r < r1 r1 = 0.6 cm			r′ < r < r1 r′ = 0.6 cm r1 = 1 cm
Blood perfusion wb (mg cm^−3 s^−1)		0.3	1.0	3.0	0.3	1.0	3.0	0.3	1.0	3.0
Tst (°C) at standard conditions (10 kA/m; 0.8 MHz)	r = 0	44.00	43.76	43.27	43.07	42.86	42.41	43.23	42.65	41.57
	r = r′	–	–	–	–	–	–	43.32	42.91	42.23
	r = r1	42.07	41.67	40.96	41.18	40.84	40.25	42.15	41.55	40.86
	r = r1 + 1 cm	38.39	37.92	37.41	37.85	37.56	37.25	38.75	37.79	37.40
ΔTst (°C) at H raising from 10 to 14.1 kA/m	r = 0	0.57	0.50	0.48	0.77	0.84	1.01	0.58	0.67	0.79
	r = r′	–	–	–	–	–	–	0.58	0.71	0.89
	r = r1	0.60	0.68	0.82	0.83	0.90	1.07	0.59	0.73	0.89

To characterize the steepness of the temperature profile in the interface between the diseased and healthy tissues, we use the value of ∂T/∂r (r = r₁). The data for the three geometries and various durations of the heating are presented in Table II. It can be seen that the temperature gradient attains its maximum at t ≅ 100 sec, and then decreases a bit when approaching the steady state. To take advantage of this feature, one may suggest some sort of pulse hyperthermia, with the AC source working periodically with the pulse length of about 100 sec. This suggestion is, however, unsuitable in the shell geometry (Figure 4C), since in this case the temperature dip in the center disappears only in the steady state.

Table II.  Characterization of the temperature profile: the calculated temperatures T inside and outside of the tumor and temperature gradient ∂T/∂r at the interface at various heating durations. Assumed: H = 10 kA/m; ω/2π = 0.8 MHz; α = 0.003; w_b = 1.0 mg cm⁻³ s⁻¹.

Volume doped with magnetic particles		0 < r < r1 r1 = 1 cm			0 < r < r1 r1 = 0.6 cm			r′ < r < r1 r′ = 0.6 cm r1 = 1 cm
Heating duration (t, sec)		50	100	500	50	100	500	50	100	500
T (°C)	r = 0	41.60	43.06	43.72	41.11	42.12	42.84	37.88	39.63	42.65
	r = r′	–	–	–	–	–	–	39.92	41.26	42.91
	r = r1	39.22	40.21	41.44	38.93	39.67	40.79	39.12	40.02	41.55
	r = r1 + 1 cm	37.00	37.03	37.51	37.00	37.02	37.49	37.00	37.03	37.79
∂Tst/∂r (r = r1) (°C/cm)		−10.8	−11.6	−9.5	−10.5	−11.2	−9.9	−10.2	−10.9	−8.8

Anyway, the profile at the boundary is sufficiently steep in all geometries, providing slight enough heating outside the tumor, where the temperature does not exceed the harmless level of 37°–39°C. The steep profile is the natural consequence of the temperature constraint in the inner region (similar effect is widely used in radio engineering for forming the rectangular pulses).

Conclusion

As a conclusion, the temperature dependence of the AC magnetic losses χ″(T) has been studied experimentally on fine powder of the specially synthesized low-T_C manganite, La_0.8Ag_0.15MnO_2.95. Steep decreasing of χ″ is recorded in the vicinity of the Curie point, T_C ≅ 42°C, in the frequency range of 0.5–2 MHz. The data are fitted by the test function which was then used in the numerical analysis of the bioheat equations under typical conditions of the hyperthermia treatment. The calculations were performed for spherical tumors of different sizes, both for uniform and shell distributions of magnetic particles, and at typical values of bioheat parameters, including the effect of blood perfusion. The main result of the work is the prediction of good temperature autostabilization near T_C inside the tumor and steep temperature profile at the interface of the diseased and healthy tissues. These features are shown to be attainable at the ‘standard’ level of the AC power (H = 10 kA/m; ω/2π = 0.8 MHz) and particle concentration (α = 0.003). The effect of autostabilization becomes still stronger at higher power, but in practice the values of H, ω, and α may be restricted both by technical and biocompatibility reasons.

Thus, the fine particles of La_0.8Ag_0.15MnO_2.95 can be considered as a promising material for the temperature-controlled hyperthermia with good temperature autostabilization in the narrow range of 42°–44°C. Further advance, including still stronger stabilization at different critical temperatures within the range of interest (40°–50°C), is seemed to be quite realistic; to this end, other compositions of the same manganite family should be examined. Problems of targeting and biocompatibility are also very important for practical applications. Preliminary data obtained on the same La-Ag manganites are encouraging 13, but can be considered as the first step only. Further experimental work with living objects is necessary.

Acknowledgements

The authors are grateful to A.A. Generalov, V.V. Demidov, and B.M. Odintsov for their help and useful discussions. The work was supported by RFBR (grant numbers 08-02-00040, 07-03-01019a, 07-02-91567-NNIO-a), Russian Academy of Sciences (Programs P03-2-24 and ‘Spintronics’), and HFSP (Grant RGP-0047/2007-C).

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.