Abstract
Introduction: Contact flexible microstrip applicators (CFMA), operating at 434 MHz, are applied at the Academic Medical Center (AMC) for superficial hyperthermia (e.g. chest wall recurrences and melanoma). This paper investigates the performance of CFMA, evaluating the stability of the specific absorption rate (SAR) distribution, effective heating depth (EHD) and effective field size (EFS) under different conditions.
Methods: Simulations were performed using finite differences and were compared to existing measurement data, performed using a rectangular phantom with a superficial fat-equivalent layer of 1 cm and filled with saline solution. The electrode plates of the applicators measure ∼7 × 20, 29 × 21 and 20 × 29 cm2. Bolus thickness varied between 1 and 2 cm. The impact of the presence of possible air layers between the rubber frame and the electrodes on the SAR distribution was investigated.
Results: The EHD was ∼1.4 cm and the EFS ranged between ∼60 and ∼300 cm2, depending on the applicator type. Both measurements and simulations showed a split-up of the SAR focus with a 2 cm water bolus. The extent and location of air layers has a strong influence on the shape and size of the iso-SAR contours with a value higher than 50%, but the impact on EFS and EHD is limited.
Conclusion: Simulations, confirmed by measurements, showed that the presence of air between the rubber and the electrodes changes the iso-SAR contours, but the impact on the EFS and EHD is limited.
Introduction
Hyperthermia is the heating of tumour tissue in the range of 40–45°C and is applied in combination with radiotherapy and/or chemotherapy to improve clinical results. Superficial heating is applied for, for example chest wall recurrences and melanoma. Clinical studies have shown that additional hyperthermia can improve clinical outcome Citation[1–4], but results are strongly dependent on the achieved tumour temperatures. It is therefore important that the hyperthermia equipment provides good control over the temperature distribution.
Important properties of superficial heating devices are the effective heating depth (EHD) and the effective field size (EFS), as these determine the tumour coverage. For electromagnetic heating devices the EHD depends strongly on the applied frequency, which is usually between 434 and 2450 MHz. The EHD decreases with increasing frequency. Superficial tumours can be heated with various devices, including 434 MHz contact flexible microstrip applicators (CFMA) Citation[5], as applied at the Academic Medical Center (AMC). An advantage of these applicators is their flexibility. CFMA antennas can be bent in order to fit the curved body contour. An additional benefit is the fact that bending of the antennas increases the penetration depth Citation[5]. For larger surfaces that cannot be completely covered by a single CFMA antenna, multiple hyperthermia sessions can be applied to adequately heat the complete target region. Another option to heat larger surfaces is to use multi-element devices formed by microstrip applicators Citation[6], current sheet applicators Citation[7], dual concentric conductor (DCC) microstrip antennas Citation[8],Citation[9] or Lucite cone applicators Citation[10]. However, special care has to be taken when using such multi-element devices, to prevent under-heated regions between the elements.
During hyperthermia treatments thermometry is limited. At the AMC, temperatures are measured at the skin using several multi-sensor thermocouple probes. Another one or two thermometry catheters are inserted in the tumour tissue. Invasive temperature measurements are limited to avoid implant risks for the patient Citation[11]. This means that during treatment limited information is obtained about the temperature distribution in the heated tissue.
Several techniques to obtain accurate temperature information non-invasively are under development. Examples of these techniques are radiometry Citation[12], ultrasound Citation[13] and MRI Citation[14–16]. These methods are very promising, but not yet accurate enough to replace the customary invasive temperature measurements. Moreover, these techniques are not always suitable to be combined with the applied hyperthermia device. MRI for example, is not suitable because of the metal structures in the CFMA. Recently, a prototype thermal monitoring sheet (TMS) has been developed, which allows fast and accurate characterisation of two-dimensional temperature distributions over large surface areas Citation[17]. This technique might offer some advantages compared to clinical probes for measuring skin temperatures, but it cannot replace invasive temperature measurements, since in-depth temperature information is not provided by a TMS.
A third option to obtain more insight in the achieved temperatures in the heated tissue is hyperthermia treatment planning. This way, distributions of the specific absorption rate (SAR) and the corresponding temperature generated by a specific superficial applicator can be calculated. These simulation results can be used to adapt the treatment strategy and thus improve the achieved temperatures.
Quality assurance measurements performed to make sure that the hyperthermia equipment is functioning properly determine the EFS and EHD in tissue-equivalent phantoms Citation[18]. Furthermore, in the absence of reliable 3D temperature monitoring in the tumour, it is very important that the EFS and EHD are stable under clinical conditions. Earlier research showed that the water bolus thickness can have a strong effect on the SAR distribution Citation[19]. During SAR measurements in the past it was noticed that the reproducibility was moderate, even when the exact measurement set-up was reproduced very carefully. This paper investigates the performance of CFMA applicators, evaluating the stability of the SAR distribution, EHD and EFS under different conditions. To this end the effect of parameters which can affect the SAR distribution was examined. Evaluating the stability is important, as some parameters are difficult to control in the clinic, and insufficient thermometry data are available to verify the 3D temperature distribution. Simulated SAR distributions in a rectangular tissue-equivalent phantom, generated by CFMA applicators, were compared with existing measurement data. Three different applicator sizes were examined and EFS and EHD were compared.
Materials and methods
CFMAs
At the Academic Medical Center superficial hyperthermia is applied using contact flexible microstrip applicators. CFMAs are available with different aperture sizes and the applicator choice for a hyperthermia treatment depends on the sizes of the target area. In this study three different sizes were examined. The applicator of type 1H, with an aperture size of 7.2 × 19.7 cm, type 3H (28.7 × 20.7 cm) and 5H (19.7 × 28.5 cm) were used. These applicators were manufactured by SRPC ‘Istok’ Citation[5] and are shown in . The orientation of the principal E-field direction is perpendicular to the lines on the surface of the antenna. Bending is only possible around the axis perpendicular to these lines, which explains the need for type 3H and 5H to have approximately the same sizes but with perpendicular orientation.
The operating frequency of the applicators was 434 MHz, which is mostly applied in the clinic, but according to the manufacturer the 1H applicator can be modified to operate at 40.68 MHz, and the 3H and 5H antenna can also be used at 915 MHz Citation[5]. A detailed description of these applicators has been published Citation[5] and in this section only a short description will be presented for better understanding of the numerical model of the applicators.
A CFMA applicator consists of two coplanar active electrodes and a shield electrode. The shield electrode and the active electrodes are separated by a thin layer of fluoroplastic substrate. The electrodes are excited as a plane dipole-like microstrip antenna by means of a slot of ≈5 mm. The microstrip line is excited by the feeding pin of the coaxial cable. The direction of the field propagation in the microstrip line is fixed by a short circuit. For optimal performance of the applicator, the short circuit is positioned at approximately ¼λs from the exciting slot Citation[5], where λs is the wavelength of the field in the fluoroplastic substrate (∼44 cm).
Because of the small dimensions of the 1H applicator, a construction with a short circuit is not possible for this type. For the 1H applicator the two active electrodes with the shield electrode compose two capacitors, which are connected by a microstrip inductance. This makes up a resonant circuit tuned at the operating frequency Citation[5]. The inductance is positioned in boxes over the shield electrode, as can be seen in .
Coupling of electric fields to tissue is realised by a water bolus between the antenna and the tissue. The electrode plates are incorporated in a rubber frame, which is integrated with a thin rubber water bolus. The 2 mm thick surface of the rubber frame, which is directed inside the bolus, is covered with 5 mm high lugs to prevent collapse of the water bolus. The water bolus thickness was measured from the 1 cm high rim of the rubber frame (see). The water bolus can be considered as a dielectric resonator and the thickness is a very important parameter for the achieved SAR distribution. For clinical application, the thickness of the water bolus should be less than 2 cm to avoid a split-up of the central SAR focus caused by oscillations in the water bolus Citation[20].
Simulations
A rectangular tissue-equivalent phantom filled with saline solution (6 g/L NaCl), was modelled. The phantom was covered with a 1 cm artificial fat layer, on which the applicator was positioned.
Figure 2. Schematic representation of a CFMA. The left picture shows a longitudinal cross-section and the right picture shows the shield electrode and the active electrodes.

Simulations were performed using a voxel-based hyperthermia treatment planning system, which was initially developed for regional hyperthermia Citation[21],Citation[22]. The software is based on the finite difference time domain (FDTD) method and the implementation has been validated earlier by comparison of measured and simulated E-field distributions in tissue-equivalent phantoms, generated by a locoregional heating system Citation[21],Citation[23].
Geometrical objects were described using the generic object format (GOF) Citation[24]. The applicator definition was separated from the phantom (or patient) definition, which makes this planning system very flexible for representation of different antenna types. FDTD simulations were performed at a resolution of 2 × 2 × 1 mm3. A voxel spacing of 1 mm was applied perpendicular to the applicator in order to determine in-depth SAR profiles more accurately. The smallest wavelength is approximately 8 cm for 434 MHz in water. Thus, with the resolution applied here, there are at least ∼40 voxels per wavelength everywhere in the computational domain. The width of the exciting slot was modelled as 4 mm. The lugs to prevent collapse of the water bolus were neglected in the simulations, since they are very small and occupy little space. For the 1H applicator the inductance is meant for tuning and therefore the boxes containing this inductance were not modelled. This is justified since the obtained SAR distribution will be scaled for comparison with measurements (see Analysis section).
To avoid reflections at the boundaries of the computational domain, a nearly perfectly matched layer (NPML) boundary condition was applied Citation[25], which performs identically to the standard perfectly matched layer Citation[26]. The perfectly matched layer aims to absorb the electric field as if the domain was not truncated, and is currently the most effective absorbing boundary condition described in literature. The dielectric material between the inner and outer conductor of the coaxial feeding cable was modelled as Teflon. The source point was positioned in a ‘gap’ in the inner conductor of the coaxial feeding cable and excited by means of a triple cosine pulse. The time step applied at this resolution was 1.67 10−12 s.
The computational domain (x × y × z) was 133 ×69 × 109, 137 × 177 × 109 and 177 × 133 × 109 voxels for the applicator of type 1H, 3H and 5H, respectively. This includes 10 nearly perfectly matched layers and a perfect electric conductor (PEC) at all sides. shows a schematic representation of the modelled geometry and the computational domain. Dielectric properties applied for the simulations were obtained from literature Citation[19],Citation[27],Citation[28] and are shown in .
Figure 3. Longitudinal cross-section (yz plane) of the modelled geometry. The computational domain is surrounded by 10 nearly perfectly matched layers (PML) and a perfect electric conductor (PEC) in all directions.
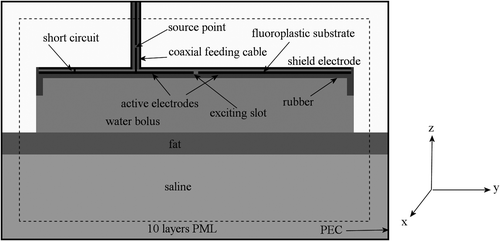
Table I. The dielectric properties used in the simulations.
Simulated water bolus thicknesses are in correspondence with the bolus thicknesses during the measurements Citation[19]. The SAR distribution in the phantom generated by the 1H and 3H applicator was simulated for a bolus thickness of 1.5 and 1.7 cm, respectively. For the 5H antenna, a water bolus of 1 and 2 cm thickness was simulated.
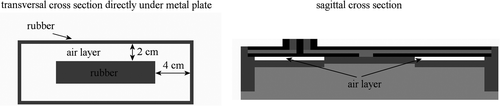
The rubber frame of the applicator is kept in place by a rubber ring along the edge, so the rubber layer is not fixed to the surface of the electrode plates. Therefore, it was assumed that the rubber layer was not in close contact over the complete area of the metal plates. For the applicator of type 1H a contact area of 11 × 2.2 cm was assumed at the centre of the aperture, which corresponds to a 2 and 4 cm air layer at the edges of the long and short sides of the applicator, respectively. This is shown schematically in . For the applicators of type 3H and 5H, variation in contact between the rubber and the metal plate was modelled to determine the impact on the SAR distribution. Close contact was modelled, as well as a full air layer between the metal plate and the rubber. Furthermore, four cases of partial, but symmetrical, contact were modelled. Two cases were similar to the case of the 1H applicator, but for the 3H and 5H applicator an air layer of 3, 5, 7 or 9 cm was modelled at the edges of both the long and short sides of the applicator. The other two modelled cases were the opposite: a contact region of 3, 5, 7 or 9 cm was assumed at the edges of both the long and short sides of the applicator, implying an air layer at the centre of the aperture. This is shown schematically in . For the 5H applicator with a 2 cm water bolus, air at the centre was modelled, with a contact region of 3 cm at the edges. One example of an asymmetric situation was simulated for the 5H applicator with a 2 cm water bolus by modelling only the right half of the above-mentioned air layer (see ). An overview of the different simulated cases is given in . The indication ‘air layer near edge’ refers to a situation as shown in , and the indication ‘central air layer’ refers to the situation depicted in . All these simulations were performed with modelled air layers of 1 mm, i.e. one voxel thick.
Figure 4. Transversal and (partial) sagittal cross-section showing the position of the air layer between the metal plate and the rubber frame for the 1H applicator.
For the 3H applicator, the impact of the air layer thickness was also investigated by comparison of the results for 1 mm and 2 mm air layer thickness.
Figure 5. Transversal and (partial) sagittal cross-section showing the position of the air layer between the metal plate and the rubber frame for the 3H and 5H applicators. The pale grey region in the transversal cross-section is rubber in the simulation with an asymmetric air layer (5H, 2 cm bolus) and air in all other cases.
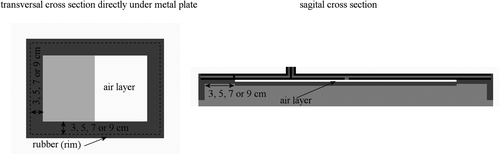
Table II. Overview of the simulated air layer configurations for the different types of CFMA applicators. The indication ‘air layer near edge’ refers to a situation as shown in , and the indication 'central air layer’ refers to the situation depicted in .
Analysis
SAR values were determined from the E-field measurements and simulations, using the relationwhere σ represents the electrical conductivity (S m−1) and ρ (kg m−3) is the density of the material. A contour plot of the SAR distribution was constructed from the values in the plane parallel to the applicator at 1 cm depth in the saline solution. The maximum SAR value in this plane was normalised to be 100%. From these contour plots the effective field size (EFS) was determined, which is defined as the area covered by the 50% iso-SAR contour Citation[29]. The simulated and measured EFS were evaluated and the variation in EFS was determined for the various different simulated areas of contact between the rubber and the electrodes.
Another important parameter, which can also be determined from these experiments, is the effective heating depth. The EHD is defined as the additional depth at which the relative power deposition has decreased to 50% of the maximum value at 1 cm depth in the saline solution. The theoretical value of the EHD for a plane wave at 434 MHz can be calculated according to Citation[30]:where f is the frequency in Hz. Measured and simulated EHD were also evaluated, as well as the variation in EHD for the various different simulated cases of contact between the rubber and the electrodes.
Results
All results from phantom measurements presented in this section were taken from Citation[19].
1H applicator
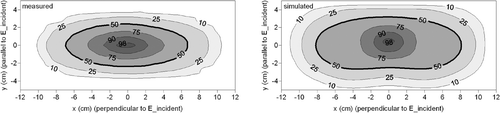
The measured and simulated contour plots of the SAR distribution at 1 cm depth in the saline solution, generated by the 1H applicator with a 1.5 cm water bolus are shown in . The measured EFS was 4.7 × 13.5 cm Citation[19]; the simulation yielded a wider EFS of 5.9 × 16.3 cm. The extent of contact assumed between the rubber layer and the metal plate is shown in . The measured and simulated EHD was 1.26 cm Citation[19] and 1.06 cm, respectively.
3H applicator
Measurements and simulations for the 3H applicator were performed with a 1.7 cm water bolus. Since the extent of contact between the rubber layer and the metal plate during measurements is uncertain, different cases of contact were modelled to determine the effect on the iso-SAR contours. The simulated air distribution between the rubber and the electrodes is depicted in , showing transversal cross-sections of the modelled geometry directly under the electrode plates. The question marks at the centre of this figure represent the measurements, of which the air distribution is unknown.
Figure 7. Transversal cross-sections of the modelled geometry directly under the metal plate, showing the air distributions in the simulations. The question marks at the centre represent the measurements, of which the air distribution is unknown.
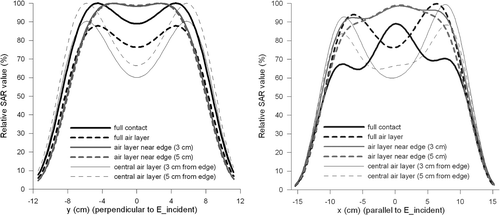
The simulated and measured iso-SAR contours are shown in . The simulated SAR distributions clearly show the alteration of the SAR pattern due to air enclosure between the rubber and the electrode plates. The simulated SAR distributions are very different, especially the sizes and shapes of the patterns inside the 50% iso-SAR contour. There is a variation in the location and size of hot spots. Depending on the extent of contact, a closed SAR maximum can be observed (e.g. upper right picture) or a split-up of the SAR maximum, either vertically (e.g. upper left) or horizontally (e.g. lower right).
Figure 8. Simulated and measured iso-SAR contours for the 3H applicator with a bolus thickness of 1.7 cm.

Two measurements were performed repeating the same measurement set-up, but with a two-day time interval. The first measurement covered the full applicator region, but the second measurement focused more to the centre region of the applicator. These two measurements show fairly different SAR patterns; one has a single SAR maximum while the other one shows a split-up of the SAR maximum. The differences in measured SAR levels were roughly 10–20%.
From the simulations in , the closest correspondence to the measurement showing a single maximum is found for the simulation with air layers of 5 cm near the edges. The measurement showed an almost square EFS of 17.7 × 17.5 cm and the simulation with air layers of 5 cm near the edges showed a more rectangular EFS of 21.9 × 16.0 cm. The measured and simulated EHD was 1.36 cm and 1.30 cm, respectively. These values for the effective heating depth are in good correspondence with the theoretical value of the EHD for a plane wave at 434 MHz. According to Equation 1 the penetration depth is 1.41 cm.
The simulation where a full air layer between the rubber layer and the metal plate was assumed showed the best qualitative correspondence to the second measurement with the discontinuous maximum. These results show that there is some variation in the measurements, which can be attributed to differences in contact between the rubber layer and the metal plate, one time or the other.
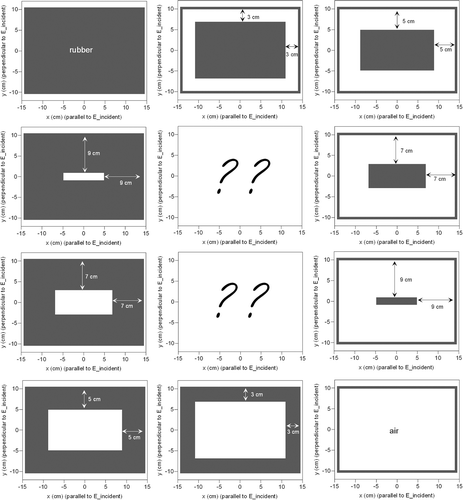
SAR profiles parallel and perpendicular to the incident E-field at the centre of the aperture (x = 0 or y = 0), are shown in , for six different cases of contact. The cases labelled ‘air layer near edge’ refer to a situation as shown in , and cases labelled ‘central air layer’ refer to the situation depicted in . The profiles in show that the extent of contact has a relatively strong influence on the shape of the iso-SAR contours with a high SAR value (>50%), where the difference in relative SAR levels can be up to 40%, but the effect on the EFS is limited. The maximum value of these profiles is not necessarily 100%, since the maximum SAR value in the transversal plane at 1 cm was normalised to 100%. lists the EHD values and the EFS sizes and areas for all the different cases. Considering ‘full contact’ as a reference case, the variation in EFS sizes is less than 2 cm, which is below 10%.
Figure 9. Simulated SAR profiles perpendicular (left) and parallel (right) to the incident E-field at the centre of the aperture of the 3H antenna. Simulations were performed with different extents of contact between the rubber and the metal plate.
The extent of contact between the rubber layer and the electrode plates also has a minor effect on the EHD. For example, the simulated EHD was 1.44 cm when a full air layer was assumed. In the case of perfect dielectric contact, a simulated EHD of 1.26 cm was found.
Table III. Simulated EHD values and the EFS sizes and area for the 3H applicator with a 1.7 cm water bolus and varying conditions of dielectric contact.
To study the impact of the thickness of the air layer between the rubber and the electrodes, the simulated results for 1 and 2 mm air, i.e. one or two voxels, were compared. The SAR distributions for the case with a central air layer and 5 cm contact at the edges (, lower left) are shown in . There is some impact of the air layer thickness on the details of the SAR distribution and the absolute differences between 1 and 2 mm air in are between 0 and 12%, but the shapes of the iso-SAR contours are more or less comparable. The EFS in with 1 and 2 mm air layer was comparable: 23.2 × 18.4 cm2 and 23.4 × 18.6 cm2, respectively. The simulated EHDs were 1.18 and 1.20 cm, respectively. For the case of 5 cm air at the edges ( top right) the EFS with 1 and 2 mm air layer thickness was 21.9 × 16.0 cm2 and 20.7 ×15.6 cm2, respectively. The EHDs for this case were 1.29 and 1.30 cm. Thus, the distribution of the air between the rubber and the electrodes is important for the SAR distribution, but the exact thickness of the air gaps is of minor importance.
5H applicator
The measured and simulated contour plots of the SAR distribution generated by the 5H applicator with a 1 cm water bolus are shown in . The air distributions assumed in the simulations are similar to those depicted in . Again, an alteration of the SAR pattern can be observed due to air between the rubber and the electrodes. Depending on the extent of contact, a single SAR maximum can be observed (e.g. upper right picture) or a split-up of the SAR maximum (e.g. lower left).
Figure 11. Simulated and measured iso-SAR contours for the 5H applicator with a bolus thickness of 1 cm.
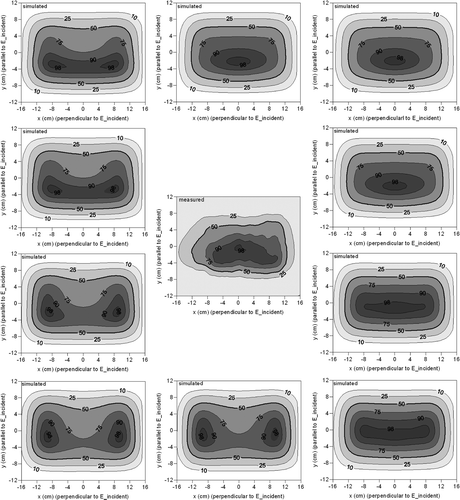
The SAR measurement in the central picture shows a single maximum and from this set of simulations, those with 3 or 5 cm air modelled at the edges of both the long and short sides of the applicator showed the closest resemblance to this measurement. The measured and simulated EHD was 1.35 cm and 1.31 cm, respectively. An EFS of 12.5 × 24 cm was derived from the measurements and the simulated SAR distribution with 5 cm air at the edges showed an EFS of 13.1 × 24.2 cm. The results of measured and simulated EHD and EFS for the 5H applicator, along with the results for the 1H and 3H applicator, are listed in .
Table IV. Measured and simulated effective field sizes and effective heating depths of the three types of CFMA applicators in the rectangular phantom.
In , SAR profiles are depicted parallel and perpendicular to the incident E-field at the centre of the aperture of the 5H antenna (x = 0 or y = 0), for six different cases of contact between the rubber layer and the metal plate. This shows again that the extent of contact has a relatively strong influence on the shape of the iso-SAR contours with a high SAR value (>50%), where the difference in relative SAR levels can be up to 30%, but the effect on the EFS is limited. lists the EHD values and the EFS sizes and areas for all the different cases. Considering ‘full contact’ as a reference case, the variation in EFS sizes is less than 2 cm, which is below 10%.
Figure 12. Simulated SAR profiles perpendicular (left) and parallel (right) to the incident E-field at the centre of the aperture of the 5H antenna. Simulations were performed with different extents of contact between the rubber and the metal plate.
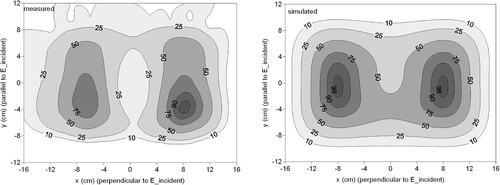
Measured and simulated contour plots of the SAR distribution generated by the 5H antenna with a bolus thickness of 2 cm are shown in . For this simulation 3 cm contact was modelled at the edges of both the long and short sides of the applicator. Both measurement and simulation showed a split-up of the central SAR focus, which is also mentioned by the manufacturer Citation[20]. Qualitatively, the simulated and measured SAR contours show a good correspondence, i.e. separate maxima at the left and at the right, but quantitatively the resemblance is not perfect. Most remarkable is the fact that the minimum SAR value at the centre is lower for the measured SAR distribution.
Figure 13. Contour plots of the measured (left) and simulated (right) SAR distribution generated by the 5H applicator with a bolus thickness of 2 cm. In the simulation, 3 cm contact was modelled at the edges.
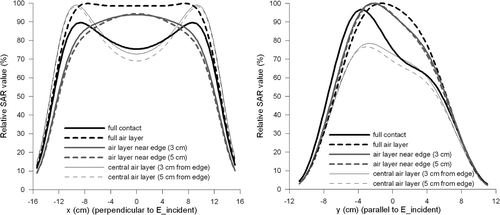
(left) shows two different measured profiles at y = 0, with a bolus thickness of 2 cm in the same measurement set-up, but from a different measurement session. One of these measured profiles (measurement 1) was reproduced from the left contour plot of . A simulated profile at y = 0 was also extracted from . For this plot the maximum SAR value along the tracks was normalised at 100%. These measured profiles again show that there is some variability in the measurements. The second measurement shows a much better correspondence with the simulated profile, which indicates that the simulation of is not incorrect, but variation in dielectric contact between the rubber and the metal plate results in variation in the SAR distributions.
Figure 14. Left: Simulated SAR profile at y = 0 reproduced from and two measured SAR profiles resulting from the 5H applicator with a 2 cm water bolus. Measurement 1 was reproduced from . Measurement 2 shows a better quantitative correspondence with the simulation than measurement 1. For all three profiles, the maximum SAR value was normalised to 100%. Right: Profile of Measurement 2 and a simulated profile with an asymmetric air layer (see ).
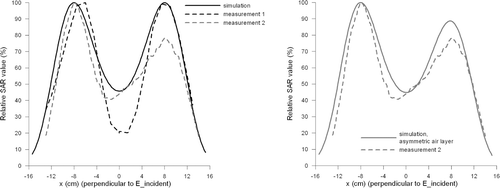
The profile of the second measurement was asymmetric, while that of the first measurement was symmetrical. This can also be explained by variation in dielectric contact between the rubber and the electrodes. Simulation with an asymmetric air layer results in an asymmetric pattern, as shown at the right hand side of .
Table V. Simulated EHD values and the EFS sizes and area for the 5H applicator with a 1 cm water bolus and varying conditions of dielectric contact.
The simulated EHD for this situation was 1.41 cm. A simulated EHD of 1.35 cm was found for a bolus thickness of 1 cm and the same sizes of the air layer between the rubber and the metal plate. This shows that the thickness of the water bolus in the clinically relevant range (<2 cm) has effectively no impact on the EHD.
Discussion
Simulations were performed for straight CFMA antennas. The stability of the performance of CFMAs was investigated, particularly the effect of parameters, which can affect the SAR distribution, effective heating depth and effective field size. Simulated SAR distributions generated by different types of CFMA antennas were compared to existing measurement data.
The surface of the rubber frame facing the electrode plates is not fixed to the plates, since this will hamper bending of the applicator and replacement of the water bolus when it has become leaky. The extent of contact between the rubber layer of the frame and the electrode plates is uncertain and the construction of the applicator does not allow any visual inspection of the contact between the rubber layer and the electrode plates.
To investigate the impact of air between the rubber and the metal plate, several different cases of partial contact were modelled. The extent of contact was found to have a relatively large influence on the simulated shape and size of the iso-SAR contours with a high SAR value (>50%), but the impact on the EFS is limited (see and , and ).
Simulations also showed that the thickness of the water bolus and the extent of dielectric contact between the rubber layer and the electrode plates have a minor impact on the EHD. Full contact yielded a slightly lower penetration depth compared to a full air layer, since air provides less effective coupling of the E-fields due to the low permittivity (εr = 1), which increases the penetration depth Citation[31]. The difference is only marginal, since rubber has a low permittivity as well (εr = 2.8). The difference in EHD between the 1H and the other two applicators can be explained by the fact that the dimensions of this applicator are smaller. The theoretical expression to determine the penetration depth (Equation 1) assumes a perfect plane wave and the electrical field emitted by the larger applicators is closer to a perfect plane wave than the electrical field of the smaller 1H applicator.
This paper explains why there is some variability in the measurement results. During measurements, very irregular and unconnected air distributions are possible. Simulations were performed with a limited set of very different simple symmetric air distributions between the rubber and the metal, but covering the fundamental cases: full air, no air, air at the borders and air at the centre. With these simulations it was possible to explain the global differences in the measured SAR patterns. For example, in a central SAR maximum or a split-up of the central SAR focus can be explained by a different extent of contact. Therefore, suboptimal contact between metal and rubber seems the only reasonable explanation for the variability in the measured SAR distributions and the limited quantitative correspondence found between measurements and simulations. For example, the measurements in and showed an asymmetric pattern while the simulations yielded a symmetric pattern, but the global patterns were comparable, i.e. closed maximum or split-up. That asymmetric pattern from the measurement was caused by some unknown irregular and asymmetric air distribution between the rubber and the electrodes, which is not covered by the limited number of symmetric situations simulated. An asymmetric air distribution will cause an asymmetric SAR pattern, as was demonstrated in . A better match between measurement and simulation would probably be possible, but will need a much larger variety of air layer configurations to be tested. The extent of contact and the exact thickness of possible air gaps is uncertain and not reproducible, which makes the SAR measurements in simple homogeneous phantoms less reproducible. Therefore, it is not very useful to invest much effort to find the best possible match. The correspondence between measurements and simulations can be quantified using a gamma method Citation[32], which combines distance-to-agreement and dose difference criteria. However, due to the variability in SAR distributions, this was not useful for this study.
showed measured and simulated SAR profiles for the 5H applicator with a 2 cm water bolus. A less pronounced minimum SAR value was found for the second measurement compared to the first measurement (difference ∼20%), and the second measurement showed a better correspondence with the simulation, where the minimum SAR value was also ∼40-50%. This again illustrates the variability in the measurements. An extra uncertainty when a large bolus thickness is applied is the measurement of the bolus thickness. Accurate measurement becomes more difficult because the water bolus is bulging when it is filled with a large amount of water. An earlier publication by Gelvich et al. Citation[20] showed that different volume oscillation modes can occur with a water bolus thickness of ∼2 cm, depending on the exact water bolus thickness.
The lugs to prevent collapse of the water bolus were neglected in the numerical model, which is justified since the impact was found to be very small (data not shown). Where the applicator is modelled on a flat surface, it is manageable to model the lugs, but in clinical practice the applicators will be bent and modelling these lugs for bent applicators becomes more cumbersome. Therefore, it was decided to neglect the lugs in the simulations.
For clinical use it is important to know the size of the area which is effectively heated by the applicator. This area is the EFS and as shown in this study the effect on the EFS is limited. Thus, in spite of the large variation in shape and size of the iso-SAR contours inside the 50% contour, the effective field size region will be heated effectively in any case. However, the variation of the SAR values inside the EFS region may have an impact in the location of hot spots. As a result, the location of possible hot spots might be difficult to predict accurately, when applying treatment planning to patient anatomies. In clinical practice less variation in size and shape of the iso-SAR contours might possibly occur in comparison to measurements with a straight applicator. Bending of the applicator compresses the rubber layer and as a result probably less variation in rubber-metal contact will occur for bent applicators. However, this hypothesis is very difficult to prove.
A next step will be simulation of SAR distributions in tissue-equivalent phantoms with a certain curvature, and later on SAR and temperature distributions in more realistic patient anatomies. The impact of variability in the SAR distribution, as mentioned in this study, has to be examined for patient anatomies. Modelling of bent applicators is the subject of current research.
Conclusion
Variation in contact between the rubber frame and the electrode plates can explain the variations that were observed in measurements with straight CFMAs. The extent of contact between the rubber and the electrode plates has a strong influence on the shape and size of the iso-SAR contours with a value higher than 50%, but the impact on the effective field size and effective heating depth is limited.
Acknowledgements
This research is supported by a grant of the Dutch Cancer Society.
Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.
References
- Perez CA, Kuske RR, Emami B, Fineberg B. Irradiation alone or combined with hyperthermia in the treatment of recurrent carcinoma of the breast in the chest wall: A nonrandomized comparison. Int J Hyperthermia 1986; 2: 179–187
- Overgaard J, Overgaard M. Hyperthermia as an adjuvant to radiotherapy in the treatment of malignant melanoma. Int J Hyperthermia 1987; 3: 483–501
- Van der Zee J, Treurniet-Donker AD, The SK, Helle PA, Seldenrath JJ, Meerwaldt JH, Wijnmaalen AJ, van den Berg AP, Van Rhoon GC, Broekmeyer-Reurink MP. Low dose reirradiation in combination with hyperthermia: A palliative treatment for patients with breast cancer recurring in previously irradiated areas. Int J Radiat Oncol Biol Phys 1988; 15: 1407–1413
- Jones EL, Oleson JR, Prosnitz LR, Samulski TV, Vujaskovic Z, Yu D, Sanders LL, Dewhirst MW. Randomized trial of hyperthermia and radiation for superficial tumors. J Clin Oncol 2005; 23: 3079–3085
- Gelvich EA, Mazokhin VN. Contact flexible microstrip applicators (CFMA) in a range from microwaves up to short waves. IEEE Trans Biomed Eng 2002; 49: 1015–1023
- Lee ER, Wilsey TR, Tarczy-Hornoch P, Kapp DS, Fessenden P, Lohrbach A, Prionas SD. Body conformable 915 MHz microstrip array applicators for large surface area hyperthermia. IEEE Trans Biomed Eng 1992; 39: 470–483
- Gopal MK, Hand JW, Lumori ML, Alkhairi S, Paulsen KD, Cetas TC. Current sheet applicator arrays for superficial hyperthermia of chestwall lesions. Int J Hyperthermia 1992; 8: 227–240
- Stauffer PR, Rossetto F, Leoncini M, Gentilli GB. Radiation patterns of dual concentric conductor microstrip antennas for superficial hyperthermia. IEEE Trans Biomed Eng 1998; 45: 605–613
- Stauffer PR. Evolving technology for thermal therapy of cancer. Int J Hyperthermia 2005; 21: 731–744
- Rietveld PJ, van Putten WL, van der ZJ, Van Rhoon GC. Comparison of the clinical effectiveness of the 433 MHz Lucite cone applicator with that of a conventional waveguide applicator in applications of superficial hyperthermia. Int J Radiat Oncol Biol Phys 1999; 43: 681–687
- Van der Zee J, Peer-Valstar JN, Rietveld PJM, Graaf-Strukowska L, Van Rhoon GC. Practical limitations of interstitial thermometry during deep hyperthermia. Int J Radiat Oncol Biol Phys 1998; 40: 1205–1212
- Jacobsen S, Stauffer P. Non-invasive temperature profile estimation in a lossy medium based on multi-band radiometric signals sensed by a microwave dual-purpose body-contacting antenna. Int J Hyperthermia 2002; 18: 86–103
- Straube WL, Arthur RM. Theoretical estimation of the temperature dependence of backscattered ultrasonic power for non-invasive thermometry. Ultrasound Med Biol 1994; 20: 915–922
- Hekmatyar SK, Poptani H, Babsky A, Leeper DB, Bansal N. Non-invasive magnetic resonance thermometry using thulium-1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetate (TmDOTA(-)). Int J Hyperthermia 2002; 18: 165–179
- Hoffmann W, Rhein KH, Wojcik F, Noeske R, Seifert F, Wlodarczyk W, Fahling H, Wust P, Rinneberg H. Performance and use of current sheet antennae for RF-hyperthermia of a phantom monitored by 3 tesla MR-thermography. Int J Hyperthermia 2002; 18: 454–471
- Clegg ST, Das SK, Zhang Y, Macfall J, Fullar E, Samulski TV. Verification of a hyperthermia model method using MR thermometry. Int J Hyperthermia 1995; 11: 409–424
- Arunachalam K, Maccarini P, Juang T, Gaeta C, Stauffer PR. Performance evaluation of a conformal thermal monitoring sheet sensor array for measurement of surface temperature distributions during superficial hyperthermia treatments. Int J Hyperthermia 2008; 24: 313–325
- Crezee J, Van Stam G, Sijbrands J, Van Haaren PMA, Zum Vörde Sive Vörding PJ, Oldenborg S, Van Wieringen N, Bel A. Quality assurance procedures for superficial hyperthermia equipment in Amsterdam. Abstracts of the 23rd Annual Meeting of the European Society for Hyperthermic Oncology. Berlin 2006; 105–106
- Lamaitre G, Van Dijk JDP, Gelvich EA, Wiersma J, Schneider CJ. SAR characteristics of three types of contact flexible microstrip applicators for superficial hyperthermia. Int J Hyperthermia 1996; 12: 255–269
- Gelvich EA, Mazokhin VN. Resonance effects in applicator water boluses and their influence on SAR distribution patterns. Int J Hyperthermia 2000; 16: 113–128
- van de Kamer JB, De Leeuw AAC, Hornsleth SN, Kroeze H, Kotte ANTJ, Lagendijk JJW. Development of a regional hyperthermia treatment planning system. Int J Hyperthermia 2001; 17: 207–220
- Kok HP, Van Haaren PMA, van de Kamer JB, Wiersma J, Van Dijk JDP, Crezee J. High-resolution temperature-based optimization for hyperthermia treatment planning. Phys Med Biol 2005; 50: 3127–3141
- Van Haaren PMA, Kok HP, Wiersma J, van de Kamer JB, Van Dijk JDP, Crezee J. Faster EM-field calculations for locoregional hyperthermia treatment planning using the FDTD method. Abstracts of the 21st Annual Meeting of the European Society for Hyperthermic Oncology. Munich 2003; 137
- de Bree J. The development of a treatment planning system for interstitial hyperthermia. PhD Thesis submitted to Utrecht University, 1998.
- Cummer SA. A simple, nearly perfectly matched layer for general electromagnetic media. IEEE Micro Wireless Comp Lett 2003; 13: 128–130
- Hu W, Cummer SA. The nearly perfectly matched layer is a perfectly matched layer. IEEE Antennas Wireless Prop Lett 2004; 3: 137–140
- Lide DR. CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data. Chemical Rubber Company Press, Boca Raton, FL 2001
- Guy AW. Analyses of electromagnetic fields induced in biological tissues by thermographic studies on equivalent phantom models. IEEE Trans Micro Theory Tech 1971; 19: 205–214
- Hand JW, Lagendijk JJ, Bach AJ, Bolomey JC. Quality assurance guidelines for ESHO protocols. Int J Hyperthermia 1989; 5: 421–428
- Hand JW. Electromagnetic applicators for non-invasive local hyperthermia. Physics and technology of hyperthermia, SB Field, C Franconi. Martinus Nijhoff Publishers, Dordrecht, Boston, Lancaster 1987; 189–210
- Kok HP, Van Haaren PM, van de Kamer JB, Crezee J. Theoretical comparison of intraluminal heating techniques. Int J Hyperthermia 2007; 23: 395–411
- de Bruijne M, Samaras T, Chavannes N, Van Rhoon GC. Quantitative validation of the 3D SAR profile of hyperthermia applicators using the gamma method. Phys Med Biol 2007; 52: 3075–3088