Subsurface thermal behaviour of tissue mimics embedded with large blood vessels during plasmonic photo-thermal therapy

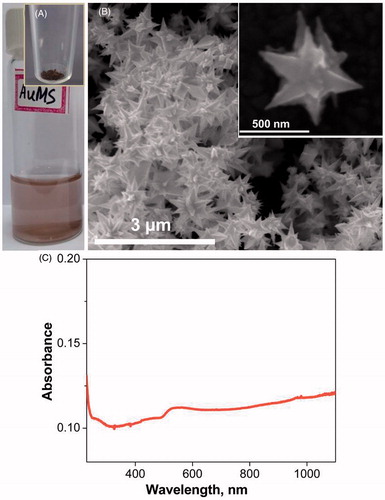
Abstract

Purpose: The purpose of this study was to understand the subsurface thermal behaviour of a tissue phantom embedded with large blood vessels (LBVs) when exposed to near-infrared (NIR) radiation. The effect of the addition of nanoparticles to irradiated tissue on the thermal sink behaviour of LBVs was also studied.

Materials and methods: Experiments were performed on a tissue phantom embedded with a simulated blood vessel of 2.2 mm outer diameter (OD)/1.6 mm inner diameter (ID) with a blood flow rate of 10 mL/min. Type I collagen from bovine tendon and agar gel were used as tissue. Two different nanoparticles, gold mesoflowers (AuMS) and graphene nanostructures, were synthesised and characterised. Energy equations incorporating a laser source term based on multiple scattering theories were solved using finite element-based commercial software.

Results: The rise in temperature upon NIR irradiation was seen to vary according to the position of the blood vessel and presence of nanoparticles. While the maximum rise in temperature was about 10 °C for bare tissue, it was 19 °C for tissue embedded with gold nanostructures and 38 °C for graphene-embedded tissues. The axial temperature distribution predicted by computational simulation matched the experimental observations.

Conclusions: A different subsurface temperature distribution has been obtained for different tissue vascular network models. The position of LBVs must be known in order to achieve optimal tissue necrosis. The simulation described here helps in predicting subsurface temperature distributions within tissues during plasmonic photo-thermal therapy so that the risks of damage and complications associated with in vivo experiments and therapy may be avoided.

Keywords:

• Computational model
• gold nanoparticles
• graphene nanostructures
• large blood vessels
• photo-thermal therapy

Introduction

Photo-thermal therapy (PTT) is a non-invasive therapeutic technique used in cancer treatment during which electromagnetic energy is converted into heat to destroy malignant/diseased tissues [1–4]. Lasers of wavelengths ranging from visible to near-infrared (NIR) are used in PTT as minimally invasive therapeutic tools in hyperthermia, where heat produced during irradiation raises the temperature of the irradiated tissue to 41–47 °C for a few tens of minutes, thereby effecting tissue necrosis [5,6]. However, a low temperature range of 41–43 °C can be used in conjunction with chemotherapy and radiotherapy. Although a wide spectral range is available and indeed used for therapeutic purposes, the NIR region of the spectrum has been traditionally considered as the ‘therapeutic window’ [7] because tissue transmissivity is highest for these wavelengths. Apart from laser-mediated hyperthermia, NIR laser irradiation is also used as an adjuvant to chemotherapy and radiotherapy [8–10]. The extent of tissue thermal damage during NIR laser PTT depends on laser specifications, optical and thermal properties of tissue, and duration of irradiation [1].

There are a few drawbacks to laser-mediated hyperthermia such as non-specific heating of tissue. This is caused by the low absorption and high scattering of light in the wavelength range of 600–1400 nm, by the tissue [11], which results in overheating of the surrounding healthy tissues. Recent studies have shown that localised heating of diseased tissue can be achieved by embedding nanoparticles in the tissue to be treated. Tuneable plasmonic nanoparticles possess high absorption in the NIR spectral region [12] due to their high surface plasmon resonance (SPR), and their presence can enhance specific heating with minimal transmission of heat to surrounding tissue. PTT in conjunction with plasmonic nanoparticles as a photo absorbing agent is known as plasmonic photo-thermal therapy (PPTT).

SPR is dependent on the type, size, and shape of the nanoparticles [12]. For the past several years, different types of nanoparticles including gold [13–18], carbon nanotubes (CNT) [19–21], and graphene [22,23] have been studied for use in PPTT. Among plasmonic nanoparticles that have been explored, gold nanoparticles have been used extensively due to their chemical stability and higher compatibility with biomaterial [24,25]. Huang et al. [14] conducted an in vitro PTT on malignant cells with anti-epidermal growth factor receptor conjugated gold nanorods (AuNRs) and normal cells. For the first time they observed specific ablation of malignant cells, with no damage to the surrounding normal cells during and after laser irradiation. Subsequently, there have been many studies on mice models and tissue phantoms to understand the effect of AuNRs on PPTT [15,17,26].

Poly(ethylene)glycol (PEG)-coated gold nanoshell (AuNS)-assisted PPTT was reported by Hirsch et al. [13], wherein mouse models carrying human breast cancer cells were subjected to NIR irradiation. In most studies NIR-PPTT used spherical gold nanoparticles (AuNP), also called gold nanospheres. AuNP can also be used during PPTT with visible lasers (∼532 nm) [27,28] due to its high SPR in the visible region. There have been a few in vivo/in vitro studies on graphene-assisted PTT [22,23,29,30]. There have also been theoretical studies on PPTT [4,17,26,31–33], some of which considered the effect of tissue blood perfusion.

During hyperthermic treatment of cancer it is essential to achieve uniform temperature distribution in the treated tissues because non-uniform heating may lead to recurrence of cancer. The presence of large blood vessels (LBVs) in the vicinity of treated tissue would result in ineffective heating of the tissue [34–37] because LBVs act as heat sinks. There have been a few fundamental studies [38–40] to correlate heat transfer with blood vessel configurations and to predict temperature distribution at the entrance of the blood vessel under a fully developed laminar flow of blood. An important work by Goldberg et al. [41] showed that tumour recurrence occurs more often when the LBVs are present near the tumour because of insufficient heating caused by the cooling effect of the blood flow. The strategies to reduce the cooling effect of LBVs have hitherto focused on reducing blood flow by either pharmacological agents [42] or by occlusion of the blood [43]. There have been a few studies on reduction of the heat sink effect of LBVs through changes in the heating protocols [44] and power deposition pattern [45] and processes such as preheating the blood in the LBVs before it enters the heated region [46]. Although preheating the surrounding and/or incoming blood before PTT appears promising, it is unrealistic in clinical situations.

Selective loading of nanoparticles to the treated site surrounding the LBVs is a practical approach to reduce the cooling effect of thermally significant blood vessels during hyperthermia treatment. There have been few studies that investigate the effects of nanoparticles during hyperthermic treatment of diseased tissues embedded with LBVs. Recently Wang et al. [47] showed the efficacy of the addition of magnetic nanoparticles to diseased tissue surrounded by LBVs during magnetic hyperthermia. This was attributed to possible vessel congestion caused by the magnetic nanoparticles.

In the present article tissue phantoms embedded with LBVs, and with and without nanomaterial, were subjected to PTT and their spatio-temporal thermal history was studied. Experiments were performed on laser heating of collagen gel embedded with simulated blood vessels carrying simulated body fluid (SBF) in the presence of two nanoparticles – AuMS and graphene. A computational model of laser light attenuation in the tissue phantom based on multiple scattering theories was also developed to validate the subsurface thermal profile obtained from the experimental observations. The results obtained show that the presence of blood vessels shifted the peak temperature towards the phantom surface and nanoparticles reduced the cooling effect of LBVs.

Materials and methods

Materials

Natural graphite flakes (95% carbon) were obtained from Active Carbon (Hyderabad, India). Ammonia (NH₃, 30%), sulphuric acid (H₂SO₄, 95–98%), hydrochloric acid (HCl, 36%) and trisodium citrate were procured from RANKEM Chemicals (Harayana, India). Phosphorus pentoxide (P₂O₅, 95%), hydrogen peroxide (H₂O_2, 98%), hydrazine monohydrate (N₂H₄·H₂O, > 99%) were purchased from SD Fine Chemicals (Mumbai), India. Merck (Mumbai) supplied potassium permanganate (KMnO_4, 98.5%). Potassium peroxydisulphate (K₂S₂O_8, 98%) was procured from Sisco Research Laboratories (Hyderabad).

Aniline was double distilled before use; AgNO₃, cetyltrimethyl ammonium bromide (CTAB), ascorbic acid, and tetrachloroauric acid trihydrate were purchased from Sigma Aldrich (St Louis, MO, USA). Purified deionised water was used throughout the experiment. Type I collagen from bovine tendon was procured from the Central Leather Research Laboratory (Chennai, India), and agar powder was also procured from Sigma Aldrich.

Sodium chloride (NaCl, >99%) was procured from Merck Specialties, Mumbai. Sodium bicarbonate (NaHCO₃, 99.9%) and Sodium sulphate (Na₂SO₄, 99.5%) were obtained from CDN Analytical Reagents (Mumbai). Potassium chlorides (KCl, 99.5%) were procured from SD fine chemicals. Magnesium chloride hexahydrate (MgCl₂.6H₂O, 99%), calcium chloride (CaCl₂, 98%) and hydrochloric acid (HCl, 36%) were procured from RANKEM Chemicals. Tris-(hydroxymethyl)-aminomethane ((CH₂OH)₃CNH₂, 99.9%) was obtained from ANGUS Chemical (Buffalo Grove,IL, USA). Dipotassium phosphate trihydrate (K₂HPO₄.3H₂O, 99%) was purchased from Thomas Baker Chemicals, (Mumbai).

Synthesis of gold mesoflowers

The oligoaniline-capped gold solution was initially prepared and used here as a seed solution for the AuMS preparation. The seed solution was synthesised by the method described in Sajanlal et al. [48]. The resultant solution containing oligoaniline-capped gold nanoparticles was used for the preparation of AuMS as seed solution. Finally, the AuMS was synthesised using the protocol available in the literature [49], and yielded AuMS with sizes of 0.5–1 μm as shown in Figure 1.

Figure 1. (A) Physical appearance of gold mesoflowers (AuMS) solution, (B) Scanning electron microscope (SEM) image of gold mesoflowers (AuMS) and (C) UV-Vis spectrum of the AuMS solution. Inset (A) shows the powder AuMS and (B) shows SEM image of a single AuMS.

Synthesis of graphene nanostructures

Graphene was prepared by a two-step process in which graphite flakes (the raw material) were first exfoliated and oxidised to graphene oxide (GO) [50], and then reduced to ‘reduced graphene oxide’ (rGO), also called graphene.

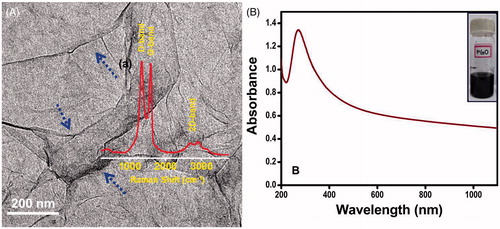
The GO was reduced to rGO as follows. First, 100 mL of GO was partially reduced using 5 g NaBH₄ and 5 g NaHCO₃ in ice-cold conditions with constant stirring for 1 h. The colour of the precipitate changed to black. This was centrifuged and washed twice with deionized water. The precipitate was then re-dispersed in water and the sulphonation step was performed using 5% HCl, 1.2 g sulphanilic acid and 2.4 g sodium nitrite in ice-cold conditions. The precipitate was centrifuged, washed and re-dispersed in DI water. Reduction was performed using 2.4 mL of hydrazine in 60 mL of (0.5%wt) pre-reduced sulphonated rGO at 80 °C for 24 h. Then 5 mL of 5% NaCO₃ solution was added to precipitate the rGO. The precipitate was centrifuged and washed with DI water. This precipitate was collected and freeze dried to get rGO powder. The rGO prepared showed an absorption peak at 270 nm as shown in Figure 2B. For simplicity, ‘Gr’ is used throughout to represent the rGO that was prepared.

Figure 2. (A) Transmission electron microscope image of graphene; the foldings are marked with blue arrows confirming the sheets are micron sized. The inset in the figure shows the Raman spectrum (a) of graphene. (B) UV-Vis spectrum of the reduced graphene oxide solution and the inset (B) shows the photograph of graphene solution.

Preparation of nanoparticle-embedded tissue phantom and simulated body fluid

One gramme of wet tissue was dissolved in 0.3 M HCl solution and the pH was set to 3.2. The pH range of 3–4 is essential for complete dissolution of tissue. The solution was then kept undisturbed for 24 h. It was then centrifuged at 4 °C at 8000 rpm to obtain a product whose viscosity was similar to animal tissue. The nanoparticles (graphene, gold mesoflowers) were separately and evenly dispersed in the liquid solution and stirred for 2 h to obtain a homogeneous mixture of tissue phantom and nanoparticles. The thermo-physical properties of collagen embedded AuMS were calculated [47]. The optical properties were assumed as α = 300 m⁻¹ and β = 530 m⁻¹ [17]. The concentration of nanoparticles in collagen gel varied between 2–3 mg/g of collagen gel.

The secondary tissue phantom (agar gel) was prepared [51] and poured into a test basin with a diameter of 10 cm and kept at room temperature for 2 h for solidification. Then, a rectangular specimen approximately 40 × 40 × 20 mm³ in size was cut from the gel using a sharp knife. The created void was then filled with the collagen gel (with or without introducing nanoparticles). The agar gel here was used as a supporting material for the collagen gel.

The SBF used to mimic the blood flow was to have ion concentration almost equal to the human blood plasma [52] and was prepared by dissolving appropriate reagents in deionised water according to the procedure described in Kokubo et al. [53]. The resultant SBF had the following ion concentrations: Na⁺ 142.0, K⁺ 5.0, Mg²⁺ 1.5, Ca²⁺ 2.5, Cl⁻ 147.8, HCO₃⁻ 4.2, HPO₄²⁻ 1.0, SO₄²⁻ 0.5 mM with an uncertainty of ±6% and pH level of 7.25. The viscosity was measured with an automated micro-capillary viscometer (Anton Paar, Graz, Austria) and found to be 8.6 × 10⁻⁴ Pa·s.

Experimental methods

In order to understand the in vitro subsurface thermal behaviour of the tissue phantoms embedded with simulated LBVs during PPTT, an experimental test section was designed and fabricated. The experimental set-up, shown in Figure 3, consisted of a test basin made of acrylic material containing tissue phantom, temperature measurement system, a dual syringe pump (TSE systems, New Delhi, India), a continuous wave diode pumped solid-state laser (MONOPOWER™-1064-500 MM, ALPHALAS, Göttingen, Germany) of 1064 nm wavelength with TEC driver (LDD1-1T-D, ALPHALAS) and an infrared (IR) camera. The acrylic basin had 10 1.5-mm holes that were drilled at 2.5-mm spacing to insert sheathed J-type thermocouples that can reach the central axis of the test basin. Silicon wafers were pasted at the inner surface of the acrylic basin to prevent the leakage of liquid agar gel. The thermocouples were calibrated and a maximum uncertainty of 0.2 °C was observed.

Figure 3. Schematic of the experimental set up. (A) Photographic view of experimental set-up. (B) Test section containing phantom and blood vessel. (1) Constant temperature bath, (2) syringe pump, (3) test section containing tissue phantom, (4) water storage, (5) power source, (6) IR camera, (7) laser head, (8) laser controller, (9) data acquisition system, (10) computer, (11) thermocouples.

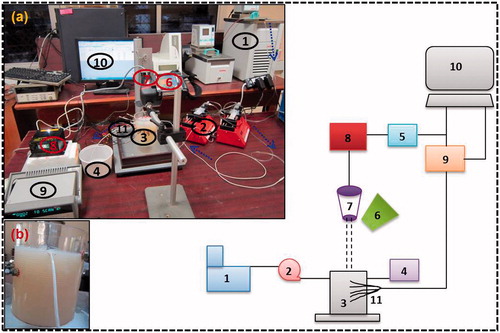
The design of the simulated blood vessel is discussed in our previous study [51]. A Teflon tube of 2.2 mm OD and 1.6 mm ID was used as a simulated blood vessel. The tube was passed through the two holes drilled on the two opposite sides of the test section, and the axis of the tube was kept at a distance of 2.5 mm from the phantom surface after solidification as shown in Figure 3 (inset b). The tissue phantom with one blood vessel is referred to as the single vessel transiting tissue (SVTT) throughout. In this study SBF was used as simulated blood and its flow was controlled using a dual syringe pump with a 60-mL syringe capacity and the flow rate maintained was 10 mL/min. The initial temperature of the tissue phantom and SBF were measured for each vascular model before switching on the laser and was found to be 21.2 °C. A container with SBF was placed in a constant temperature bath maintained at 21.5 °C. The dotted arrows show the direction of SBF flow in Figure 3 (inset a). The thermo-physical properties of the tissue phantom (Table 1) were measured with a dual needle KD2 Pro (Decagon Devices, Pullman, WA, USA) with ±2% discrepancy in measurement.

Table 1. Physical and optical properties.

Properties	Tissue (collagen)	Blood (SBF)	Blood vessel (Teflon tube)
Thermal conductivity, k (W/mK)	0.65^a	0.6	0.25
Density, ρ (kg/m^3)	1050^a	1000	2200
Specific heat, C (J/kgK)	4219^a	4200	1200
Dynamic viscosity, μ (Pa·s)	–	8.6 × 10^−4a	–
Absorption coefficient, α (m^−1)	40	200	45
Scattering coefficient, β (m^−1)	530	150	140

^a Measured.

The laser was set vertically in such a way that the aperture was placed at a distance of 10 cm from the top of the tissue phantom and the same distance was maintained for all experiments. The laser driver was used to control the laser power in the range of 300–600 mW. The diameter of the laser beam at the tissue top surface was 4–6 mm. An IR camera was used to capture the surface temperature of the tissue phantom because a thermocouple could cause error due to direct contact between the laser beam and the thermocouple. Experiments were performed at different power levels, with and without introduction of the nanoparticles, and in the presence and absence of simulated LBVs. During all experiments, the room temperature was controlled and varied between 22–24 °C. Each set of experiment was repeated at least five times (N ≥ 5) and the results are presented here as mean ± standard deviation around the mean.

Theoretical analysis

In order to predict the internal thermal history of tissue phantoms during laser-assisted PTT, two different rectangular geometries with and without nanoparticles i.e. a bare tissue phantom and a tissue phantom embedded with LBVs were developed as described below. Only AuMS were considered in the computational model. The dimensions of the geometries were taken as 40 × 40 × 80 mm³ in X, Y and Z directions respectively.

To simulate the subsurface temperature distribution on laser irradiated tissue phantom embedded with large blood vessels, a conjugate heat transfer model was solved considering the heat transfer in the phantom, blood vessels and SBF as a whole. Pennes’ model of bioheat transfer [54] includes heat conduction in bio-tissue, heat transfer due to blood flow through micro capillaries and tissue metabolic heat generation. However, in this in vitro study, the blood perfusion through micro capillaries and metabolic heat generation are absent. Hence, the modelling of energy transport in the tissue phantom and vessel wall was carried out using a heat diffusion equation and the blood flow was modelled considering convective heat transfer as follows: (1) (2) (3)

In Equations 1–3, ρ, C, k, V, T, t and Q represent density, specific heat, thermal conductivity, blood velocity, temperature, time and laser heat generation respectively. Subscripts t, bv and b indicate tissue phantom, blood vessel and blood respectively.

Laser heat generation with multiple scattering

The simplified laser models hitherto used to predict the temperature rise in tissues during the process of PTT utilises essential exponential attenuation [1] of laser light in terms of tuneable optical properties derived from single Mie scattering theory [55]. The photons that enter the tissue are absorbed and scattered by different chemical components associated with water, and the photon interaction with these chemical components are treated as light propagation through a participating medium. When photons travel deep into the tissue they experience multiple scattering [56] due to forward scattering and back scattering. Thus, light propagation in the tissue at depth z and at radius r, due to a Gaussian beam was assumed to be (4) where (5)

The first, second and third exponential term in Equation 4(4) accounts for Gaussian distribution of the laser beam with beam broadening, the attenuation of intensity due to absorption, and reinforcement of photon density due to multiple scattering, respectively. Hence, the laser heat generation [56] due to multiple scattering of photons was given by (6)

Here I is the light intensity at a given position (r, z), I₀ is the intensity at tissue surface, σ(0) is the standard deviation at the tissue surface and is taken as 2 mm, α and β are absorption coefficient and scattering coefficient respectively.

Laser heat generation using the Welch model

The laser heat generation based on a modified Beer–Lambert law [1] was modelled as (7)

Boundary conditions and numerical simulation

All boundary conditions were considered as per experimental conditions. At the inlet to the blood vessel a parabolic velocity profile with a maximum blood velocity of 0.2 m/s and blood vessel radius of 0.8 mm were considered. The convective cooling boundary conditions were considered at the top phantom surface with a slightly higher convective heat transfer coefficient of 15–30 W/m²K due to the direct effect of the room air conditioner.

The SBF temperature at the exit of the LBV was measured using a thermocouple. The transient 3D temperature distributions were now solved numerically to predict the tissue temperature distribution. The values of the optical properties and thermal properties are given in Table 1. COMSOL Multiphysics software (version 4.3, Burlington, MA) based on the finite element method was used to solve the coupled fluid flow and heat transfer with velocity tolerance and temperature tolerance of 0.0001. The energy transport in the tissue and blood vessel domain were established using the ‘conjugate heat transfer model’ on the software. A tetrahedral mesh shape was adapted for the 3D model. To ensure accuracy and computational time a finer mesh with total element size of 1648502 in the case of SVTT was selected for further calculations throughout the study. The meshed model was solved transiently by the generalised minimum residual (GMRES) iterative method with geometric multigrid preconditioner and forward difference formula for the time stepping method was used with a time step of 0.1 s and for total exposure time of 300 s.

Results

The results presented here are divided in two categories: internal variation in temperature for bare tissue, and for SVTT with blood vessels placed at two different depths.

Enhanced internal temperature response in the case of bare tissue

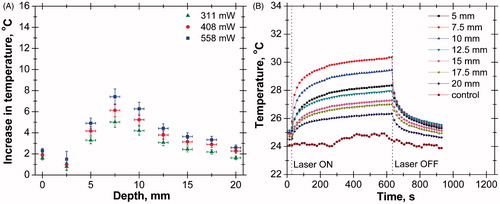
The increase in temperature at different depths and the transient temperature response at various depths of tissue phantom in the absence of nanoparticles are shown in Figure 4. The axial temperature variation in this case was measured up to a depth of 20 mm, since beyond this depth not much increase in temperature was observed (Figure 4(A)). It has been observed that the temperature increases up to a depth of 10 mm from the surface. The presence of a temperature peak at subsurface zone is caused by the interplay of thermo-optical absorbance and scattering efficacy of the phantom material [56]. The experiment was repeated for three different power levels and the peak temperature was observed at the same depth at all power levels. However, the value of peak temperature increases with increase in power level due to higher laser heat generation. Figure 4(B) shows the transient temperature distribution at various depths of tissue phantom where ‘control’ represents ambient conditions.

Figure 4. (A) Axial temperature variation for different power levels at 300 s of laser heating (in the case of bare tissue). (B) Temporal temperature distribution at different depth for power level of 408 mW (in case of bare tissue).

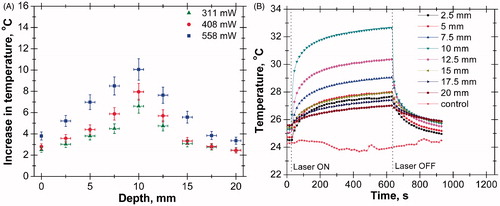
The laser was continuously irradiated for a period of 10 min and then switched off. The transient temperature responses of thermocouples were recorded for 15 min (10 min of heating and 5 min of cooling). The temperature at a depth of 10 mm from the surface was higher than that in any other axial positions. The increase in temperature at a depth of 17.5 mm was even higher than that of the surface.

The same experiments were then conducted with tissue mixed with nanoparticles, i.e. AuMS and Gr, at two different concentration levels and at the same power as shown in supplementary Figures S1 and S2. The prepared AuMS and Gr were characterised to obtain the light absorption spectra. It was found that Gr shows an absorption peak at a wavelength of 270 nm (Figure 2B). The UV-Vis spectrum analysis [49] and AuMS shows an absorption peak at 1400 nm. However, the analysis shown in Figure 1(C), was limited to a wavelength of 1100 nm. The result plotted in supplementary Figures S1 and S2 represent the rise in temperature at different depths of tissue phantom embedded with AuMS and Gr separately at concentrations of 2 mg/g and 3 mg/g respectively. It has been observed that the addition of nanoparticles not only increases the temperature rise but also that the location of the temperature shifts further towards the surface of the tissue phantom. The same trend was observed for both nanoparticles, but Gr resulted in a higher rise in temperature due to higher light absorption capacity (Figures 1(C) and 2(B)) than AuMS.

Supplementary Figures S3 and S4 represent the effect of nanoparticle concentration on subsurface thermal history of the bio material. The nanoparticles were mixed uniformly with the tissue phantom to avoid the effect of particle aggregation on temperature distribution. There might be a shift in peak temperature towards the phantom surface [56] with increase in nanoparticle concentration, but no shift towards tissue surface has been observed since thermocouples could only record temperatures at an interval of 2.5 mm. The increase in concentration results in enhancement in the rise in temperature since more volume concentration of nanoparticles would absorb more light energy and hence lead to a higher temperature rise.

Enhanced internal temperature response in case of SVTT

Figure 5 shows the temperature rise of the tissue phantom in the absence of nanoparticles at three different power levels and temporal temperature distribution at various depths. A similar trend was observed at all power levels with a maximum rise in temperature at a depth of 7.5 mm. The values plotted at 2.5 mm depth (Figure 5(A)) represent the SBF temperature at the exit of the blood vessel since the blood vessel has been placed at same depth from the phantom surface. There was an error associated with the measurement of the exit SBF temperature since it loses heat to the surrounding tissue phantom while flowing away from the heating area downstream, which results in a gradual decrease in its temperature. The corresponding outlet temperature at the exit of the blood vessel was computationally determined to be 0.8 °C with a laser power of 558 mW and an exposure of 300 s. Figure 5(B) shows the transient temperature distribution at various depths of tissue phantom in the presence of the LBV.

Figure 5. (A) Axial temperature variation for different power levels at 300 s of laser heating (in the case of single vessel transiting tissue (SVTT) at 2.5 mm depth). (B) Temporal temperature distribution at different depth for power level of 408 mW (in the case of SVTT at 2.5 mm depth).

The experiments were repeated for tissues with the AuMS and graphene nanoparticles at two different concentration levels and at same power, as shown in supplementary Figures S5 and S6 respectively. The addition of nanoparticles enhances the rise in temperature as compared to the results shown in Figure 5(A), and peak temperature also shifts towards the surface. Again, the temperature rise is higher for Gr than for AuMS due to the high light absorption capacity of Gr. Experiments were further performed to determine the effect of the depth of blood vessel on axial tissue temperature distribution and it was seen that when blood vessel is situated deeper into the tissue, the peak temperature is shifted further (supplementary Figure S7) towards the tissue surface. The axial temperature variations for the three cases – bare tissue, SVTT at blood vessel depth of 2.5 mm and SVTT at blood vessel depth of 7.5 mm – without AuMS and with AuMS are shown in Figure 6.

Figure 6. (A) Axial temperature variation in tissue without introducing gold mesoflowers (power = 408 mW, time = 300 s). (B) Axial temperature variation in tissue with introducing AuMS at concentration of 3 mg/g (power = 408 mW, time = 300 s). SVTT, single vessel transiting tissue.

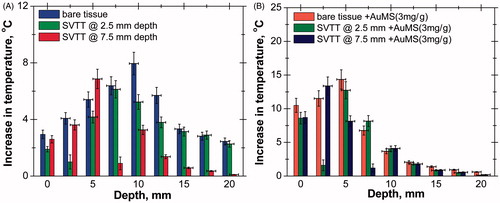
Figure 7(A) shows the maximum rise in temperature (ΔT) for various tissue–vascular networks with and without nanoparticles. In the case of bare tissue, a maximum ΔT of 38 °C was obtained for Gr due to its higher heat absorption characteristics than those of AuMS (ΔT = 19 °C) and without nanoparticles (ΔT = 10 °C). Therefore the presence of Gr results in a threefold increase in temperature rise and AuMS results in a twofold enhancement at a particular depth. However, for SVTT with blood vessels at a depth of 2.5 mm with Gr, ΔT ≈ 34 °C, with AuMS it is 16 °C, and 7.5 °C in the absence of nanoparticles. With the blood vessel situated deeper in the tissue (at a depth of 7.5 mm) ΔT is approximately 9 °C in the absence of nanoparticles and 17 °C with AuMS, for the same laser power, heating period and nanoparticle concentration.

Figure 7. (A) Maximum rise in temperature for various cases (power =558 mW, time = 300 s, 3 mg/g). (B) Position of peak temperature for various cases (power = 558 mW, time = 300 s, 3 mg/g).

As shown in Figure 7(B), the peak temperature position is at 10 mm from the phantom surface in the case of bare tissue in the absence of nanoparticles, whereas the position shifts towards the surface (at 5 mm) in the presence of AuMS. A different result was observed with an increase in the depth of the blood vessel; the peak temperature shifted from 7.5 mm for SVTT (for blood vessels at a depth of 2.5 mm) to 5 mm (in the case of SVTT with blood vessels at a depth of 7.5 mm). Moreover, the peak further shifts (for SVTT with blood vessels at a depth of 7.5 mm) towards the surface (2.5 mm) in the presence of nanoparticles.

Comparison of experimental and simulated subsurface thermal behaviour

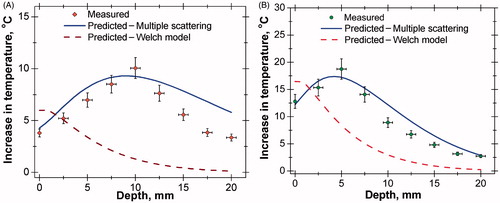
Simulations have been performed to predict the subsurface thermal behaviour of tissue phantoms for different tissue–vascular networks with and without AuMS. The simulation results predicted using the multiple scattering model (Equation 6(6) ) and the Welch model [1] (Equation 7(7) ) were compared with the measured temperature rise. Figure 8 shows the comparison of predicted and measured temperature rises in tissue phantoms for same power levels and durations of laser heating. The temperature increases up to a depth of 10 mm from the surface and then decreases, matching closely with the experimental observation as shown in Figure 8(A). The reason for obtaining peak temperature is due to re-enhancement of photon intensity at greater depth by the scattering contribution of neighbouring particles. A similar result has been found with tissue embedded with AuMS (Figure 8(B)), but the peak position is shifted towards the surface due to high light absorption characteristics of AuMS. However, the computational results obtained using the Welch model predicts the highest temperature rise at the surface and a gradual decrease along the depth due to exponential attenuation of photon intensity following a simple Lambert’s law.

Figure 8. (A) Comparison of axial temperature variation in the case of bare tissue without nanoparticles (laser power = 558 mW, time = 300 s). (B) Comparison of axial temperature variation in case of bare tissue with nanoparticles (AuMS, 3 mg/g); (laser power = 558 mW, time = 300 s). AuMS, gold mesoflowers; BT, bare tissue; Gr, graphene; SVTT, single vessel transiting tissue.

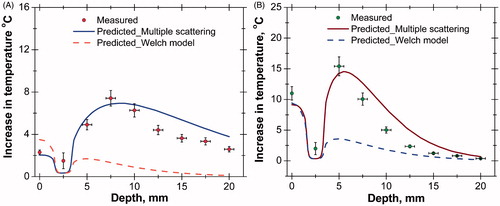
Simulations were also performed for SVTT, with the blood vessel placed at a depth of 2.5 mm from the surface, with and without nanoparticles and compared to experimental results as shown in Figure 9. The predicted temperature distribution matches measured values. The maximum rise in tissue temperature is seen to occur at a depth of 7.5 mm without nanoparticles. However, with the addition of AuMS the temperature increases and the peak shifted to a depth of 5 mm from the surface.

Figure 9. (A) Comparison of axial temperature variation in case of single vessel transiting tissue (SVTT) with blood vessel placed at depth of 2.5 mm from tissue surface without nanoparticles (laser power = 558 mW, time = 300 s, flow rate = 10 mL/min). (B) Comparison of axial temperature variation in case of SVTT with blood vessel placed at depth of 2.5 mm from tissue surface with nanoparticles (AuMS, 3 mg/g); (laser power = 558 mW, time = 300 s, flow rate = 10 mL/min).

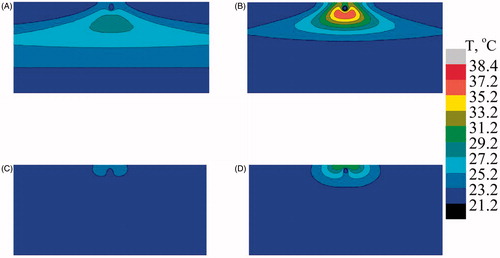
Figures 10 and 11 show the temperature profile at mid Y–Z plane for the case of bare tissue and SVTT with the blood vessel at a depth of 2.5 mm from the surface with and without AuMS. Different temperature distributions were seen for the case of bare tissue and in the case of SVTT. In the case of bare tissue, due to multiple scattering effects, the peak temperature was predicted at a particular depth from the surface (Figure 10(A)) whereas the Welch model predicted it to occur at the surface (Figure 10(C)). Furthermore, the presence of nanoparticles enhances the temperature predicted by both models (Figure 10(B, D)). However, in the case of SVTT, the Welch model predicts maximum temperature above the blood vessel (Figure 11(C, D)), while the multiple scattering model predicts it below the blood vessel (Figure 11(A, B)). Thus, the computational model helps predict the subsurface thermal profile of tissue with blood vessels situated at different position inside the bio-tissue, thereby minimising the need for in vivo experiments and the associated complications.

Figure 10. Predicted temperature distribution at mid Y–Z plane in the case of bare tissue. (A) Multiple scattering in the absence of gold mesoflowers (AuMS), (B) multiple scattering in the presence of AuMS, (C) Welch model in the absence of AuMS, (D) Welch model in the presence of AuMS (power = 558 mW, 300 s).

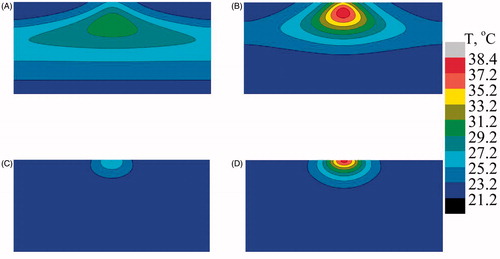
Figure 11. Predicted temperature distribution at mid Y–Z plane in the case of single vessel transiting tissue (SVTT) with the blood vessel placed at a depth of 2.5 mm from the surface. (A) Multiple scattering in the absence of gold mesoflowers (AuMS), (B) multiple scattering in presence of AuMS, (C) Welch model in the absence of AuMS, (D) Welch model in the presence of AuMS (power = 558 mW, 300 s, flow rate = 10 mL/min).

Effect of nanostructures on surface thermal profile

The surface temperature profiles of the tissue phantoms at different laser heating periods in the case of bare tissue and for the case of SVTT with the blood vessel placed at a depth of 2.5 mm from phantom surface are presented in supplementary Figures S8 and S9 respectively. These profiles represent the temperature history of collagen embedded with nanoparticles at different concentrations for the same laser power. Between the AuMS and graphene, graphene produced higher temperatures at the surface of the bare tissue than the AuMS due to the higher light absorption characteristic of graphene than AuMS. Supplementary Figures S8b–e show significant enhancement in temperature with increased nanoparticle concentrations. Similar results have also been achieved in the case of tissue embedded with LBVs; however, a lower temperature was attained at the collagen surface as compared to the collagen without LBVs. This shows that the presence of nanoparticles reduces the cooling effect of LBVs during NIR laser irradiation as already established from preceding discussions.

Discussion

The spatiotemporal temperature distribution during PTT is an important issue to ascertain complete tissue necrosis. The presence of thermally significant blood vessels in the vicinity of the targeted region does not guarantee the selective heating of the diseased tissue due to the heat sink effect of the blood vessels. However, the proper loading of nanostructures in the targeted area could improve the cooling effect of LBVs due to their high light absorption capacity. The light propagation in tissues based on Beer-Lambert’s [1] law suggests a decrease in temperature from the tissue surface due to exponential attenuation of photon intensity along its depth. In this study a collimated laser beam was used which shows an enhancement in temperature inside the phantom. The results observed are found to be consistent with reports in the literature [56]. Similar results have been obtained by Jaunich et al. [3] both numerically and experimentally, where enhanced temperature was observed at a desired subsurface location of multilayered tissue phantoms irradiated with ultra-short pulse focused laser beam. Another important study by Hirsch et al. [13] reported an enhancement in temperature both in vivo and in vitro at a particular depth of human breast carcinoma cell incubated with gold nanoshells during NIR irradiation.

In our earlier work [51] it has been already shown that the presence of LBVs in the vicinity of the heating area took away a significant amount of heat during PTT. The present experiments demonstrated, for the first time, the influence of thermally significant blood vessels in the subsurface thermal history of tissue phantoms during laser assisted thermo-therapy. The impact of these LBVs on internal temperature distribution is clearly shown in Figures 5–9. It can be concluded that without paying much attention to such subsurface thermal history of tissue embedded with LBVs, the PTT on diseased tissues embedded with or in the vicinity of LBVs may turn out to be ineffective. Although experimental investigation on the subsurface thermal effect of thermally significant blood vessels with and without introducing nanostructures has been conducted in this study, additional experiments are still necessary for more difficult cases such as considering the effect of vessel types (with different blood vessel orientation, vessel diameters and blood flow velocities) and laser specifications (lasers with different wavelengths, laser spot size, and power).

It is noteworthy that the addition of nanoparticles enhances the temperature at a depth closer to the surface but the relative enhancement is less deep in the tissue phantom for all the three cases. This is because presence of nanoparticles increases the effective absorption characteristic of tissue phantom and hence there is more light absorption near the surface. However, the accurate loading of these nanoparticles is essential to compensate the cooling effect of LBVs. The nanoparticles are either injected directly to the tumour site or through intravenous injection. To perform nanoparticle-assisted PTT successfully it is important to monitor the extent of laser heating. Because heating for a longer duration could affect the surrounding healthy tissues this can be compensated for by the addition of nanoparticles.

The cooling characteristic of the blood arises from enhanced thermal capacity of the nanoparticle-laden tissue, which in turn leads to more convective heat transfer. Enhancement in temperature was also observed in the tissue phantom embedded with LBVs, with nanoparticles. Thus nanoparticles play a significant role during PPTT in compensating for the heat sink effect of LBVs. Thus, LBVs cause anomalous subsurface thermal behaviour in the tissue phantom with and without nanoparticles. Hence it is necessary to ascertain the position of LBVs during PPTT for optimal necrosis.

The computational model developed to explain the subsurface thermal history can be immensely helpful for PPTT by predicting the cooling effect of thermally significant LBVs. The model has predicted the peak temperature deeper into the tissue due to the re-enhancement of photon intensity by the neighbouring media. The presence of nanoparticles not only increases the temperature, but the position of peak temperature has shifted towards the surface due to the higher light absorption capacity of nanoparticles. The computational model presented here is a phenomenological study established on the physical characteristics of light propagation based on the repeated scattering contribution by the neighbouring particles. Although, the in vitro experiments performed here were on non-perfused tissue phantoms, the simulation was carried out by solving Pennes’ bio-heat equation [54] to understand the significance of blood perfusion (w_b) on subsurface temperature distribution (supplementary Figure S10). Three perfusion rates were considered but surprisingly no change in position of peak temperature was noticed. However, the temperature computed on non-perfused tissue was overestimated as blood perfusion takes away heat.

Due to the complexity associated with the in vivo experiments in real clinical situations, a computational model is always helpful in predicting the thermal history of tissue during PPTT. However, several parameters need to be considered such as skin and muscle layers, and their thermo-physical properties. In this work only simple orientations of LBVs were considered but in the anatomical structure blood vessels are present with different orientations, which make the computational model more complex.

Conclusion

The subsurface thermal history of bio-tissue phantoms embedded with LBVs during laser assisted plasmonic photo-thermal heating was numerically and experimentally studied. The predicted temperature rise matches experimental observations. Two tissue–vascular networks were studied: bare tissue (without LBVs) and SVTT. In the case of tissue embedded with LBVs, experiments were performed with blood vessels placed at depths of 2.5 mm and 7.5 mm from the collagen surface. The thermo-physical properties were measured and found to be almost identical to that of real bio-tissue. Nanoparticles such as AuMS and graphene were synthesised and characterised and were mixed uniformly with pure collagen. Simulated body fluid was synthesised and used as simulated blood and was assumed to be Newtonian.

Different axial temperature distributions were observed for different tissue vascular networks and different subsurface thermal behaviours were observed for different tissue–vascular network models. It was found that the position of peak temperature changes with the position of blood vessels and with the inclusion of nanoparticles. The change in peak temperature position in both the tissue–vascular network models was defined by multiple scattering theory. The highest enhancement in thermal behaviour was observed for tissue embedded with graphene, due to the high light absorption characteristics of Gr nanostructures. The addition of nanostructures was also found to compensate the cooling effect of LBVs to a large extent and prevent excessive heat diffusion to neighbouring tissue due to highly localised capture of photons.

A computational simulation was also carried out to predict subsurface temperature distributions of tissues with or without introducing nanostructures, thereby minimising the need for in vivo experiments and the associated complications. A good match was observed between simulation and experimental results.

Acknowledgements

The authors thank S. Bakshi for providing the laser and for useful discussions. We are also thankful to T. Panda for the use of the IR camera.

Disclosure statement

A.P. received a doctoral research scholarship from the Ministry of Human Resource and Development, Government of India for this research. The authors alone are responsible for the content and writing of the paper.