Tissue shrinkage in microwave ablation of liver: an ex vivo predictive model

Abstract

Purpose: The aim of this study was to develop a predictive model of the shrinkage of liver tissues in microwave ablation.

Methods: Thirty-seven cuboid specimens of ex vivo bovine liver of size ranging from 2 cm to 8 cm were heated exploiting different techniques: 1) using a microwave oven (2.45 GHz) operated at 420 W, 500 W and 700 W for 8 to 20 min, achieving complete carbonisation of the specimens, 2) using a radiofrequency ablation apparatus (450 kHz) operated at 70 W for a time ranging from 6 to 7.5 min obtaining white coagulation of the specimens, and 3) using a microwave (2.45 GHz) ablation apparatus operated at 60 W for 10 min. Measurements of specimen dimensions, carbonised and coagulated regions were performed using a ruler with an accuracy of 1 mm. Based on the results of the first two experiments a predictive model for the contraction of liver tissue from microwave ablation was constructed and compared to the result of the third experiment.

Results: For carbonised tissue, a linear contraction of 31 ± 6% was obtained independently of the heating source, power and operation time. Radiofrequency experiments determined that the average percentage linear contraction of white coagulated tissue was 12 ± 5%. The average accuracy of our model was determined to be 3 mm (5%).

Conclusions: The proposed model allows the prediction of the shrinkage of liver tissues upon microwave ablation given the extension of the carbonised and coagulated zones. This may be useful in helping to predict whether sufficient tissue volume is ablated in clinical practice.

Keywords:

• Ablation
• contraction
• microwave
• model
• shrinkage
• tumour

Introduction

Microwave ablation (MWA) is a clinical therapeutic technique aimed at destroying pathological tissues by way of a very high and localised temperature increase. This is obtained through the absorption of an electromagnetic field at microwave frequencies (915 MHz or 2.45 GHz). Over the last decade there has been increasing diffusion of MWA devices for image-guided percutaneous insertion into the target [1–3]. Typically, MWA results in an ellipsoidal zone of dead cells, comprised of carbonised and white coagulated tissue [4] whose extension is predictable ex vivo [5] within a good degree of accuracy. Previously published clinical data demonstrated the safety and early efficacy of MWA devices applied to the treatment of solid tumours [6–10]. However, there is still need to improve the understanding of the relationship between the treatment outcome and the physical and biological variables present in clinical applications in order to achieve reproducible and predictable results [11]. To this aim, the electromagnetic, thermal, and mechanical properties of tissues need to be characterised at the temperatures achieved during MWA, which often exceed 100 °C [12–14]. In this respect, while the high temperature electromagnetic properties of tissues have been investigated [14–16], the thermal and mechanical properties of tissues still need adequate characterisation, particularly above 100 °C.

Lately, many studies have been published describing tissue shrinkage during thermal ablation [17–23]. Such a phenomenon may affect treatment safety as it can expose peripheral structures to unwanted heating, as well as efficacy because tissue shrinkage may affect the assessment of the treatment’s technical success. Specifically, given that the shrinkage associated with thermal ablation may exceed 1 cm [17], the thermally ablated area could be greatly underestimated when looking at CT and/or MR post-procedural images, for example [17–23]. The phenomenon of tissue shrinkage thus requires consideration in order to allow correct predictions and assessments of ablation outcomes.

Published studies report an average shrinkage of in vivo renal tumours treated through radiofrequency ablation (RFA) of 21% [17] and a 17.7 ± 3.4% reduction of in vivo swine lung tumor mimics during MWA [18]. Rossmann et al. measured the shrinkage of ex vivo liver kept at a constant temperature in the range between 60 °C to 95 °C for up to 15 min: the relative shrinkage increased with increasing temperature and/or time of exposure, reaching 22% at 95 °C [19]. In agreement with this result it has been demonstrated that the relative shrinkage is higher for tissues close to the applicator and for MWA with respect to RFA. Moreover, a positive correlation between shrinkage and water loss has been shown [20–22].

Recently, experiments using tissue samples with cubic geometry have been performed, which allowed for a direct and precise determination of the pre- and post-ablation specimens’ dimensions [23]. The authors report a shrinkage in agreement with the previous papers for liver tissue and larger for muscle tissue. Moreover, the authors observed that the contraction ceased when the specimen was completely carbonised and found an asymmetry of the tissue shrinkage between the parallel and orthogonal direction with respect to the microwave antenna axis [23].

Despite the relevant contributions from the cited works, to the authors’ knowledge there is as yet no model available to describe the phenomenon in the case of thermal profiles such as those obtained in MWA. Such a model would allow the control and prediction of tissue shrinkage, increasing the safety and efficacy of MWA treatments. Furthermore, it would be potentially suitable for implementation in computer-assisted simulations of clinical treatments.

Accordingly, the aim of this paper is to develop a model of tissue shrinkage for MWA, characterising the shrinkage of carbonised and of white coagulated tissues separately. To this end, several experiments were performed including heating cuboid liver specimens by means of a commercial microwave oven to study the shrinkage of totally carbonised tissues, and heating cuboid liver specimens with a RFA apparatus to study the shrinkage of white coagulated tissues (as there is minimal carbonisation using this energy source). The results of such experiments were used to build the model. Finally, an additional set of experiments was performed with a MWA apparatus to provide an initial validation.

Materials and methods

Two sets of experiments were performed in order to gain insight, respectively, into the shrinkage achieved in carbonised tissues and in white coagulated tissues under MWA. An additional set of experiments was then conducted to obtain new data to validate the model. All sets of experiments are summarised in Table 1.

Table 1. Summary of the power, time and sample size investigated in the three experimental set-ups.

Heat source	Power (W)	Time (min)	Sample size (cm)
MW oven	420, 500, 700	8, 10, 15, 20	2 × 2×2, 4 × 4×4
RFA	70	7	4 × 3×3
MWA	60	10	6.5 × 5.6 × 5.6

The experiments reported are supplemented with a further analysis of MWA data from a previous publication [23]. Specifically, results of MWA conducted at 60 W for 1, 2.5, 5, 7.5 and 10 min, on cubic specimens of ex vivo bovine liver of size ranging from 10 to 40 mm were considered there. The dimensions of the specimens were measured before and after the MWA procedure, and used to obtain a percentage linear and volumetric shrinkage of the tissue. In those experiments it was found that the 10-mm specimens were completely carbonised after about 5 min of exposure; similarly, the 20-mm specimens were completely carbonised after 10 min. As discussed there, the quantification of the shrinkage achieved in these specimens may account for the shrinkage obtainable in carbonised tissue [23]. Such quantification, not previously reported, is provided herein, at the beginning of the Results section.

Specimen preparation and characterisation

For all new experiments ex vivo bovine liver tissue was obtained from a local slaughterhouse and stored at −20 °C. The day before the experiment the liver was defrosted and allowed to reach room temperature. Then cuboid specimens were cut avoiding the inclusion of blood vessels larger than 3 mm. Their dimensions before and after the ablation procedure were determined using a ruler with an accuracy of ±1 mm.

Shrinkage of carbonised tissue: heating using a microwave oven

The aim of this set of experiments was to study the shrinkage of fully carbonised tissue. Cubic specimens were heated using a commercial microwave oven (Olimpic William, DPE s.r.l., Gussago, Italy) working at 2.45 GHz, by setting the power value and time of exposure in order to achieve a complete carbonisation of the whole sample of tissue. Different specimen sizes (20 mm and 40 mm sides) were investigated at different values of input energy (252 kJ to 504 kJ), to identify whether the shrinkage is related only to reaching complete carbonisation of the specimen or to the energy deposited into the tissue and the time duration of the process. Specifically, three 20-mm specimens were heated at a power of 420 W for 10 min, which was found to be the minimum energy required to achieve complete carbonisation of the specimen; three 20-mm specimens were heated at 420 W for 20 min, six 20-mm specimens were heated at 500 W for 15 min, three 20-mm specimens were heated at 700 W for 10 min, and finally, six 40-mm specimens were carbonised by applying 700 W for 8 min.

Shrinkage of white coagulated tissue: heating using a percutaneous RF applicator

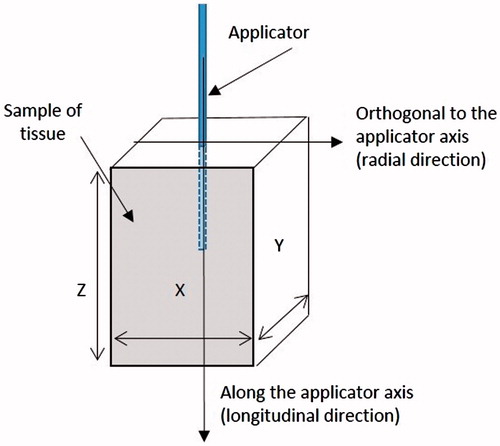
The aim of this set of experiments was to characterise the shrinkage of white coagulated tissue during MWA. Since this shrinkage depends on temperature and exposure time [19], to obtain a reliable estimation of the contraction obtained in MWA, the experimental set-up must reproduce the temperature profile and time of exposure of MWA as accurately as possible. This goal cannot be achieved by the MWA applicator used since, regardless of the power supplied to the antenna, the tissues closest to it quickly carbonise, thus precluding any ability to obtain a white coagulated zone comparable to that of MWA. To circumvent this problem a simple monopolar radiofrequency (RF) applicator was used, given the fact that its thermal profile within the tissue in the radial direction with respect to the applicator axis approximates that obtained in the white coagulated zone for MWA [2]. Thus, in this experimental set-up a straight internally cooled RF applicator with 30 mm exposed tip length, working at 450 kHz, was used (RF AMICA PROBE, HS Hospital Service SpA, Rome, Italy) to heat cuboid specimens until an impedance increase was detected. In this way the energy deposition was terminated as soon as the tissues abutting the shaft were about to carbonise [24]. Since most clinical liver MWA are performed for 5–10 min in duration [5], the target exposure time for this experiment was chosen to be about 7 min and a fixed operating power (70 W) was selected to achieve an impedance rise within the required time. In a preparatory experiment the maximum dimensions of the coagulated zone achievable with this set-up were measured, finding a length of about 40 mm along the applicator axis and a diameter of about 30 mm in the direction perpendicular to the applicator axis. Six experiments were then performed in cuboid specimens 40 mm high with a base 30 mm square, with the aim of reaching complete coagulation of the entire tissue sample. The applicator was inserted along the specimens’ longest axis, at the centre of the square base (Figure 1). The specimens were then placed in the centre of a 30-cm plastic box filled with a conductive gel to minimise the influence of the boundary conditions. Since in the experiment the ablation is stopped at the impedance rise, i.e. as soon as the tissues abutting the exposed tip begin carbonising, the ablation zone achieved in the radial direction (i.e. orthogonal to the electrode’s axis) well reproduces the white coagulated zone of the MWA apparatus; in contrast, in the longitudinal direction (i.e. parallel to the electrode’s axis), the high temperatures reached all along the electrode’s exposed tip do not allow reproduction of the longitudinal temperature profile of the white zone achieved in the MWA procedure.

Figure 1. Scheme of the set-up with cuboid specimens used to measure the shrinkage of tissue.

A single measurement of the ablated zone along the radial direction is provided due to cylindrical symmetry.

Shrinkage of ablated tissue: heating using a percutaneous microwave applicator

To validate the proposed model of the tissue shrinkage, new experimental data were obtained measuring shrinkage of ex vivo liver tissues treated with MWA using a commercial apparatus (HS AMICA) operating at 2.45 GHz [25]. Specimens were ablated at a fixed power of 60 W with an ablation duration of 10 min. Preliminary experiments show that with the chosen power and time settings the ablated zone extends about 53 mm along the applicator axis and 43 mm in the direction orthogonal to the applicator axis. Accordingly, cuboid specimens were cut to an appropriate size, with a height of 65 ± 2 mm and a base of 56 ± 4 mm square, to include the whole ablated zone. Since uncoagulated tissues do not shrink [19], the results of the validation of the model on these specimens will hold true for specimens of any geometry undergoing the same ablation protocol.

The applicator was inserted into the tissue specimen along its height until its tip reached a distance of about 5 mm from the bottom surface (Figure 1). To rule out the electromagnetic discontinuities at their surface [26] and to avoid the loss of heat by thermal convection, the specimens were surrounded by an agar phantom [23]. At the end of the heating procedure, the dimensions of the specimens as well as the longitudinal and radial extension of the carbonised and ablated regions were measured.

Notation

After MWA, tissues show marked differences on visual inspection. In particular, the tissue in the peripheral zone of ablation shows a red colour, whereas more central areas show a white colour, and the zone in close proximity of the antenna appears as black [4,12,14] (Figure 2(a)).

Figure 2. (a) Image of coagulated tissue obtained after ex vivo MWA, and (b) schematic representation of the appearance of the coagulated tissue.

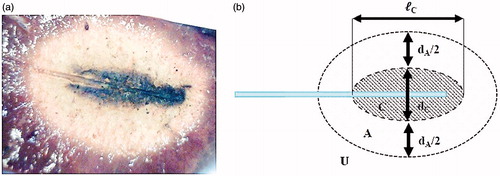
The last two zones (the ‘white zone’, and the ‘black zone’, respectively) are commonly accepted to represent the coagulated region, i.e. the area of successfully ablated tissue, which shows an elliptical shape with the long axis parallel to the applicator shaft [4]. In MWA, the white zone encompasses tissues which reached temperatures between approximately 60 °C and 100 °C, while the black region is constituted of carbonised tissues, where temperatures of 100 °C and above were reached, yielding to vaporisation of the water present in the tissues [3,12,15].

In order to establish uniform co-ordinate geometry for this study the following notations were used throughout this work to identify the many quantities of interest:

1. Since the coagulated zone shows an elliptical cross section in the longitudinal plane (i.e. along the antenna axis) and a cylindrical symmetry with respect to the applicator shaft (Figure 2(a)), the maximum dimensions of any tissue region within the coagulated zone are characterised by two parameters along two orthogonal directions: the length L (along the applicator axis, i.e. longitudinal direction) and the diameter D (along the direction orthogonal to the applicator shaft, i.e. radial direction – see Figure 1).

2. The subscripts _U (un-ablated), _A (ablated, but not carbonised), and _C (carbonised) indicate that the quantity refers respectively to the red unablated region, to the white coagulated region, and to the black carbonised region, respectively (Figure 2(b)). The subscript _N identifies quantities referring to the whole necrosis, or coagulated zone, made of the union of the white coagulated region (_A) with the carbonised one (_C).

3. The dimensions of the cuboid specimens were measured along the three Cartesian directions so that they are reported as X, Y and Z (Figure 1), with the last direction considered parallel to the applicator axis. The subscript _T refers to the whole specimen.

4. To distinguish between the dimensions of the different regions of the specimen before and after MWA, the dimensions measured before the MWA procedure are reported as capital letters, while the same dimensions after the MWA are in lowercase: e.g. D_C gives the diameter of the carbonised region before the MWA procedure, whereas d_C gives the diameter of the carbonised region after the procedure. This choice is based on the intuitive picture of a smaller piece of tissue obtained after MWA with respect to its dimensions before the procedure, according to the shrinkage phenomena.

5. The ratio between the final dimension of a tissue region after the heating and the same quantity measured before the heating procedure is named ‘contraction ratio’ and represented with the letter α. As an example, α_C,D represents the contraction ratio of the carbonised tissue along the radial direction with respect to the antenna axis (α_C,D = d_C/D_C).

The statistical analysis of the experimental data was performed using commercial software (Microsoft Excel). When the number of repetitions of a measurement was 5 or greater, the result was characterised based upon its average and standard deviation. For smaller populations the standard deviation was replaced with reporting of the maximum–minimum interval. The p-values reported in the following to assess statistical significances were calculated through two-tail heteroscedastic t-tests. The null hypothesis was rejected when the p-value was higher than 0.05.

Results

Critical analysis of previously obtained data [23]

Table 2 provides the average initial dimensions and contraction ratios α_C,D and α_C,L of the specimens for all cases where complete carbonisation of the sample of tissue was achieved in previous experiments [23] on cubic specimens of ex vivo bovine liver. In particular, according to the notation introduced, α_C,D gives the contraction ratio in the direction orthogonal to the antenna shaft (i.e. radial contraction), while α_C,L represents the contraction ratio along the antenna shaft (i.e. longitudinal contraction).

Table 2. Average contraction ratios (radial and longitudinal) of completely carbonised specimens [23].

Power (W)	Time (min)	Cube dimensions (mm)	αC,D = dC/DC	αC,L = ℓC/LC
60	5	10	0.63 ± 0.05	0.73 ± 0.05
60	7.5	10	0.70 ± 0	0.77 ± 0.06
60	10	10	0.60 ± 0.08	0.78 ± 0.10
60	10	20	0.61 ± 0.05	0.71 ± 0.05
Average			0.63	0.76
Standard deviation			0.06	0.07
Coefficient of variation			10%	9%

From Table 2 it can be seen that the contraction ratio (reported in terms of mean value and standard deviation, as well as coefficient of variation CV) does not depend on the exposure time and specimen size; moreover a slight but significant (p < 10⁻⁵) asymmetry between the radial and longitudinal shrinkage (0.63 ± 0.06 versus 0.76 ± 0.07) can be observed.

Shrinkage of carbonised tissue: heating using a microwave oven

The amount of shrinkage achieved in carbonised tissues is shown in Figure 3, depicting a cubic specimen (a) before and (b) after the heating in microwave oven.

Figure 3. (a) 40 mm cube before and (b) after the heating conducted in microwave oven supplying 700 W for 8 min. Each side of the sample decreased from 40 ± 1 mm to 27 ± 1 mm.

Table 3 reports the average linear dimensions of the samples before and after heating with the microwave oven, and the linear contraction ratio (x/X, y/Y, z/Z) evaluated for each measure. From Table 3 it is readily appreciated that the range of variation (minimum–maximum) of the calculated values are no different, either among the different directions or among the different experiments (p > 0.05). That is to say, once a tissue completely carbonises, its shrinkage is the same whatever energy is deposited into the tissue with no preferential direction. Consequently, the overall average value and the corresponding standard deviation can be evaluated, as reported in the last two rows of Table 3.

Table 3. Dimensions of the specimens before and after heating in a microwave oven.

	Heating		Before heating			After heating			Linear contraction ratio
No. of repetitions	P (W)	t (min)	X (mm)	Y (mm)	Z (mm)	x (mm)	y (mm)	z (mm)	x/X	y/Y	z/Z
3	420	10	20 ± 2	20 ± 2	16 ± 2	15 ± 2	13 ± 0	12 ± 1	0.74 ± 0.09	0.65 ± 0.07	0.79 ± 0.07
3	420	20	20 ± 2	20 ± 2	19 ± 2	14 ± 1	13 ± 1	14 ± 1	0.69 ± 0.09	0.67 ± 0.04	0.72 ± 0.04
6	500	15	20 ± 1	20 ± 1	20 ± 1	15 ± 1	14 ± 1	13 ± 1	0.72 ± 0.05	0.69 ± 0.03	0.65 ± 0.06
3	700	10	20 ± 2	20 ± 1	20 ± 1	13 ± 2	12 ± 2	13 ± 1	0.66 ± 0.05	0.63 ± 0.04	0.66 ± 0.03
6	700	8	40 ± 1	40 ± 1	40 ± 1	28 ± 1	27 ± 1	27 ± 1	0.70 ± 0.03	0.67 ± 0.03	0.67 ± 0.02
Average αC									0.69
Standard deviation									0.06
CV									9%

Comparing the results in Table 3 with those reported in Table 2, it is noted that the asymmetry of the shrinkage found in the MWA experiments is not found in the microwave oven experiments. However, the average linear contraction ratio of carbonised specimens in Table 3 (i.e. 0.69 ± 0.06) is close to the mean value of the contraction ratios of carbonised tissue from MWA experiments reported in Table 2 (i.e. 0.67 ± 0.08, evaluated as the average between the radial contraction ratio α_C,D = 0.63, and the longitudinal contraction ratio α_C,L = 0.76). Accordingly, it can be inferred that the shrinkage of carbonised tissue is independent of the heating modality.

Shrinkage of white coagulation tissue: heating using a percutaneous RF applicator

In this set of experiments, RF heating was applied (70 W at 450 kHz for 7 min) to achieve white coagulation without inducing any carbonisation. Post-experiment analysis verified that at the end of the ablation protocol the white region extended through the entire sample. A typical outcome of the RF heating procedure is shown in Figure 4, where the insertion path and absence of carbonisation of the specimen are evident.

Figure 4. Appearance of a tissue specimen after the RF heating procedure was conducted supplying 70 W at 450 kHz for 7 min.

Table 4 gives the average diameter of the white region before and after the heating, and consequent contraction ratios. The time required to achieve the impedance rise is also provided. A contraction ratio of the white coagulation zone of 0.88 ± 0.05 was obtained. The contraction ratio of white coagulated tissues α_A (Table 4) is significantly higher (p < 10⁻⁴) than the one of carbonised tissues α_C (Table 3).

Table 4. Initial (D_A) and final (d_A) dimensions of the specimens heated with RFA.

Trial	t (min)	DA (mm)	dA (mm)	αA,D = dA/DA
Average	6.9	30.8	27.2	0.88
Standard deviation	0.5	1.83	2.04	0.05
CV	7%	6%	8%	6%

Shrinkage of coagulated tissue: heating using a percutaneous microwave applicator

The average initial and final linear dimensions of the specimens ablated with the microwave applicator, and the dimensions of the carbonised and white zones are reported in Table 5. It is worth remarking that d_A refers to the white zone only, not to the overall coagulated zone, which instead also includes the carbonised zone as defined in the notation section.

Table 5. Dimensions of the specimens ablated through the percutaneous microwave applicator before and after the heating.

	Before heating		After heating
	LT (mm)	DT (mm)	ℓT (mm)	dT (mm)	ℓC (mm)	dC (mm)	ℓA (mm)	dA (mm)
Average	64.7	56.2	53.8	48.3	32.5	12.7	16.0	25.8
Standard deviation	2.42	3.66	2.48	1.86	1.22	1.03	2.37	1.72
CV	4%	7%	5%	4%	4%	8%	15%	7%

From Table 5 it can be noted that the carbonised and white regions do not extend across the whole specimens either in the radial direction (i.e. d_C + d_A < d_T) or along the antenna axis (i.e. ℓ_C + ℓ_A < ℓ_T), i.e. some tissue remained untreated.

From Table 5, an average radial contraction (D_T − d_T) of 7.9 mm is obtained, while the average radial necrosis diameter (d_C + d_A) is 38.5 mm. Adding these two data, an average radial extension of coagulated tissue before the procedure of 46.4 mm is obtained, i.e. an amount approximately 20.5% greater than that measured after the ablation. Similarly, the average longitudinal shrinkage is 10.9 mm over a necrosis length of 48.5 mm. Accordingly, the extension of coagulated tissues before the procedure was 59.4 mm, i.e. about 22.5% longer than was measured after the ablation. These data are in agreement with those previously reported in the literature [17–23].

Predictive model and its validation

To allow the prediction of tissue shrinkage it is necessary to relate the coagulated zone dimension measured after the ablation to its pre-ablation value. The predictive model proposed here considers the shrinkage of the carbonised tissues and that of white coagulated tissues separately, with the differences observed between these two regimes enabling further refinement and improved accuracy of the model (see previous sections).

From the experiments in the microwave oven, an average contraction ratio of the carbonised tissue α_C of 0.69 ± 0.06 was obtained (Table 3). However, the outcomes of previous experiments [23], summarised in Table 2, indicate that the presence of the microwave applicator influences the shrinkage distribution among the spatial directions, so that the contraction ratio of carbonised tissue in MWA is about 10% smaller in the radial direction (α_C,D = 0.63 ± 0.06) and approximately 10% larger in the longitudinal direction (α_C,L = 0.76 ± 0.07). This might be due to a mechanical constraint introduced by the applicator, which contrasts the longitudinal shrinkage along the shaft of the antenna by inducing a friction between the tissues and the applicator external surface, even if other explanations cannot be completely ruled out at this point.

From the RF experiments an average contraction ratio of the white coagulated zone α_A,D of 0.88 ± 0.05 was determined (Table 4). Unlike the carbonised zone, that is in direct contact with the applicator, the contact surface between the white region and the applicator is very limited. Accordingly, the presence of the applicator should not yield to a significant asymmetry of the contraction ratio. Consequently it was assumed that the value derived in the orthogonal direction with respect to the applicator axis is valid also in the longitudinal direction, i.e. in the direction parallel to the applicator axis. This assumption, as with those on the carbonised tissue contraction, require a validation that is partially provided below.

To summarise the assumptions in formulae: (1a) (1b) (2)

From the above reported data, the dimension of the tissue involved in the ablation procedure, i.e. which results coagulated at the end of the MWA, can be derived according to the formulae: (3) (5) for the radial (Equation 3(3) ) and longitudinal (Equation 4(5) ) direction with respect to the antenna shaft. Both in laboratory and clinical field, d_C and d_A (and ℓ_C and ℓ_A) can be measured at the end of and, although with less accuracy, during the ablation. Therefore tissue shrinkage can be known and predictable, the coefficients α_C,D, α_C,L and α_A being known.

To perform a first step of validation of the above reported equations, the data measured in the MWA experiments were used. In particular, from Table 5, the extension of the untreated tissue can be obtained as the difference between the dimension of the specimen after the heating procedure and the sum of the carbonised and white coagulated region extension. Then, Equations 3(3) and 4(5) can be used to evaluate the extension of the coagulated tissue before the procedure. The value obtained, plus the extension of the untreated tissue, can be compared finally with the dimension of the specimen before the MWA procedure. The corresponding data for the radial (i.e. orthogonal to the applicator axis) and longitudinal (i.e. parallel to the applicator axis) directions, respectively, together with the difference (error) between the analytical and the experimental data are shown in Table 6. The average of such error is 3.1 mm (5%) in the radial direction and 1.6 mm (2%) in the longitudinal direction.

Table 6. Summary of the model application to the results of the experiment with the MWA applicator.

dC (mm)	12.7 ± 1.0	ℓC	32.5 ± 1.2
dA (mm)	25.8 ± 1.7	ℓA	16.0 ± 2.4
DU (mm)	9.8 ± 1.6	LU	5.3 ± 2.5
DC (mm)	20.1 ± 1.6	LC	42.8 ± 1.6
DA (mm)	29.4 ± 2.0	LA	18.2 ± 2.7
DT model (mm)	59.3 ± 2.2	LT model (mm)	66.3 ± 3.0
DT exp (mm)	56.2 ± 3.7	LT exp (mm)	64.7 ± 2.4
Error (mm)	3.1 (5%)	Error (mm)	1.6 (2%)
DC−dC (mm)	DA−dA (mm)	LC−ℓC (mm)	LA−ℓA (mm)
7.4 ± 0.6	3.5 ± 0.2	10.3 ± 0.4	2.2 ± 0.3

Table 6 also gives the absolute shrinkage of carbonised and white coagulated tissue in the radial (D_C − d_c) and longitudinal (L_C − ℓ_c) directions as evaluated through the model. It can be inferred that over an average total longitudinal shrinkage of 12.5 mm (i.e. Avg (L_C − ℓ_C) + Avg (L_A − ℓ_A) = 10.3 mm +2.2 mm), up to 10.3 mm (i.e. about 82.5% of total longitudinal contraction) are linked to the shrinkage of carbonised tissue. Likewise, over an average total radial contraction of 10.9 mm, 7.4 mm are due to the shrinkage of carbonised tissue (i.e. about 67.9% of total radial contraction).

Discussion

In this work, experiments and analysis to characterise the shrinkage of ex vivo liver tissue during a MWA procedure were performed with the aim of developing a predictive model of the shrinkage phenomenon. Such a model is based on two constant values representing the contraction of black carbonised tissue and of the surrounding white coagulated tissue. Those constant values were determined through experiments conducted using a microwave oven and a RFA apparatus.

From the microwave oven experiments it was demonstrated that once liver tissue carbonises it no longer shrinks, even with additional increases of microwave time or power. This finding enables one to generalise the results of this experiment to liver tissues carbonised in any other way, i.e. including a MWA applicator. A constant contraction ratio α_C = 0.69 ± 0.06 was thus obtained, independent of the spatial direction. Instead, in the presence of the microwave applicator the shrinkage along the direction parallel to the applicator shaft was lower than the shrinkage in the radial direction, i.e. α_C,L > α_C,D. Friction of the tissue against the microwave percutaneous applicator was speculated to be the cause of this asymmetry, even if other causes could not be ruled out.

The shrinkage of tissues exposed to temperatures typical of the white zone increases significantly with increasing temperature and time of exposure [19]. In particular, a relative shrinkage of about 12% was obtained after 15 min of exposure of ex vivo liver at 60 °C, whereas a maximum of 22% was reported at 95 °C [19]. These data allow the determination of a minimum bound for α_A of 0.78 (i.e. α_A = 1 − 0.22), whereas the maximum bound is α_A = 1, representing negligible shrinkage. However, in percutaneous MWA only the tissues surrounding the carbonised zone are exposed to temperatures approaching 95 °C. Moreover, the exposure of the white zone tissues to such temperature is limited in time, because the carbonised region continuously expands during MWA, absorbing and converting tissues from the white zone inner boundary. It is therefore reasonable to expect that the tissue within the white zone achieved after MWA would undergo a lower shrinkage than the values above reported. In particular, assuming an average exposure time of about 200 s, the data published by Rossmann et al. [19] (e.g. Figure 6 of that paper) indicate an average shrinkage encompassing all the temperatures between 60 °C and 95 °C of roughly 10%, concordant with the average value α_A = 0.88 ± 0.05 reported here in Table 4.

It is worth noting that, while the shrinkage of carbonised tissue proved to be linked only to the change of the physical status of the tissue, enabling it to be correctly represented by a constant parameter, in the case of white coagulation this is not true, and therefore the considered value represents an average shrinkage of the white zone, modelling the temperature profile typical of MWA.

The proposed model of tissue shrinkage was tested through a set of experiments performed in MWA, showing acceptable results in terms of accuracy of prediction (Table 6). Indeed, it should be noted that the experimental accuracy in the measurements is ±1 mm (see Materials and methods above). Accordingly, the model based on the measurement of three parameters (extension of the carbonised, white coagulated, and whole sample of tissue) has a total uncertainty of ±3 mm. Looking at the errors evaluated by subtracting the model predictions from the true experimental values (Table 6), it is noted that the average values are within the experimental uncertainty.

From the average values reported in the last row of Table 6 it can be determined that, according to the proposed model, the contraction of carbonised tissue accounts for about 68% of the total contraction in the radial direction, while it contributes to 83% of the total contraction in the longitudinal direction. The contribution to the total shrinkage of the white zone contraction is therefore appreciably lower than the contribution of the carbonised zone and can possibly be neglected as a first approximation. For example, when applying the model neglecting the contraction of white coagulation tissue to the MWA experiments reported in Table 5, the average error is 0.39 mm in the radial direction (maximum error 6 mm) and 0.57 mm in the longitudinal directions (maximum error 5 mm).

In exchange for the approximations introduced, the model proposed herein allows calculating tissue shrinkage based on analytical calculus only, i.e. it does not require numerical calculus. The model proposed by Rossmann et al. [19] instead describes tissue shrinkage as a function of temperature. Therefore, to calculate it in clinical applications where temperature varies over time and space it has to be integrated over such variables, resulting in an equation not solvable analytically.

Although our model was derived and tested on ex vivo cuboidal specimens (a geometry needed to directly measure tissue contraction), it is expected to be applicable to targets of any geometry, including clinical ones, because of the negligibility of the contraction of the uncoagulated tissues [19] surrounding the ablated zone. To apply the model in clinical practice, both the coagulated and carbonised tissue extensions need to be measured after the patient treatment. Whereas the former measurement is included in standard post-treatment practice [4], the latter is not performed currently. A measurement technique of the carbonised tissue extension ought to be developed, but may be relatively straightforward given the differences in the density and other properties of the two types of tissue. Alternatively, a relation between such extension and the overall coagulated zone extension should be proved.

In order to use the model on different targets and/or different MWA apparatuses, it should be considered that the contraction ratio of the carbonised tissue along the longitudinal direction could be different depending on the microwave applicator used. Moreover, other target tissues may behave quite differently and tissues with high collagen or low water content – like many liver tumours – may present different values and behaviours for α_C and α_A. In clinical applications additional deviations from the predictions of the model could be introduced from the mechanical action of tissues surrounding the ablation zone, which were not present in the ex vivo cuboids used to derive the contraction ratio values of Equations 1(1a) and 2(2) . Moreover, it should be noted that since the proposed model focuses on the ablation zone measured at the end of the MWA it does not take into account the expansion phenomena observed in MWA during the very first minutes of the procedure [23,27]. Regardless, testing the proposed model on a wider range of target organs, experimental set-ups, MWA systems, ablation power and duration together with in vivo confirmation is required and will be the object of future experiments. Such extensive validation will test the hypotheses on which the model is based, including the accuracy with which the contraction ratio derived from the RFA experiment describes the contraction ratio of MWA white coagulated tissues. In particular, the monitoring of tissue shrinkage in real time was recently performed under CT [21,23]. This approach could be used to perform validation studies with a higher degree of accuracy.

Finally, whereas carbonised tissue contributes most to the shrinkage in many MWA apparatuses, it is substantially absent in RFA. Due to the approximation introduced in our model to describe the white zone shrinkage, its applicability to RFA shrinkage can be limited. Accordingly, a model describing the latter should be developed specifically, upon a dedicated study.

Conclusions

From experimental data, a model was proposed to account for and predict the shrinkage of liver tissue undergoing MWA, which is based upon the knowledge of the different parameters describing the shrinkage of carbonised and white coagulated tissues. Once fully validated, the proposed model may be used in clinical tumour treatments to predict whether sufficient tissue volume has been ablated.

Disclosure statement

C.A., S.C. and N.T. are employees of H.S. Hospital Service SpA, the company manufacturing the MWA apparatus used in the study. S.N.G. is a consultant of Angiodynamics and Cosman Medical Inc. for unrelated development of IRE and RF devices respectively. All other authors have no known conflicts to report. The authors alone are responsible for the content and writing of the paper.