Temperature-controlled radiofrequency ablation of different tissues using two-compartment models

Abstract

Purpose: This study aims to analyse the efficacy of temperature-controlled radiofrequency ablation (RFA) in different tissues.

Materials and methods: A three-dimensional, 12 cm cubical model representing the healthy tissue has been studied in which spherical tumour of 2.5 cm has been embedded. Different body sites considered in the study are liver, kidney, lung and breast. The thermo-electric analysis has been performed to estimate the temperature distribution and ablation volume. A programmable temperature-controlled RFA has been employed by incorporating the closed-loop feedback PID controller. The model fidelity and integrity have been evaluated by comparing the numerical results with the experimental in vitro results obtained during RFA of polyacrylamide tissue-mimicking phantom gel.

Results: The results revealed that significant variations persist among the input voltage requirements and the temperature distributions within different tissues of interest. The highest ablation volume has been produced in hypovascular lungs whereas least ablation volume has been produced in kidney being a highly perfused tissue. The variation in optimal treatment time for complete necrosis of tumour along with quantification of damage to the surrounding healthy tissue has also been reported.

Conclusions: The results show that the surrounding tissue environment significantly affects the ablation volume produced during RFA. The optimal treatment time for complete tumour ablation can play a critical role in minimising the damage to the surrounding healthy tissue and ensuring safe and risk free application of RFA. The obtained results emphasise the need for developing organ-specific clinical protocols and systems during RFA of tumour.

Keywords:

• Radiofrequency ablation
• finite element method
• Pennes bioheat equation
• PID controller

Introduction

Radiofrequency ablation (RFA) is the most extensively studied and widely applied minimally invasive thermal ablative technique in clinical practices. Earlier studies have demonstrated that, RFA is not only an effective treatment modality for primary hepatocellular carcinoma and colorectal metastases to the liver, but has also gained interest in the treatment of tumours in lung, brain, kidney, prostate and bone [1–4]. Most importantly, RFA is a faster technique that exhibits relatively fewer complications with improved cosmesis and low treatment cost as compared to the other techniques. During RFA, electrode is inserted percutaneously inside the tumorous tissue with the help of image guidance technique, through which the high-frequency alternating current (450–550 kHz) is delivered into the tissue that induces frictional heating [5]. This frictional heating leads to destruction of tumour cell by instantaneous induction of protein coagulation that irreversibly damages key cytosolic and mitochondrial enzymes and nucleic acid histone complexes at a higher temperature above 50 °C [6]. Interestingly, the higher temperatures should be strictly restricted to 100 °C to avoid tissue carbonisation and water vaporisation that increases the tissue impedance thereby limiting further electrical conduction through the remaining tissue.

Since it is very hard to predict the outcome of RFA immediately post ablation, mathematical models play a vital role in predicting the ablation zone and temperature rise within the target tissue during RFA rapidly and at a low cost. Several studies are available in the literature on mathematical modelling of RFA especially in developing and investigating new RFA protocols. In addition, improvement in existing technique, optimisation of probe geometry, placement and power level for a particular tumour size, and investigation of complex electro-biological interactions during RFA procedures have also been explored [7–13]. Although most of these studies were restricted mainly to liver investigating either employing one compartment model or two- or multi-compartment model. In one-compartment model, similar properties are being used for both tumour and healthy tissue. Whereas, in two- or multi-compartment models different properties are assigned for tumour and healthy tissues. Zorbas and Samaras [14] investigated the effect of realistic human anatomy for three different body sites, viz., liver, lung and kidney, by employing a finite difference numerical method to simulate constant voltage RFA. It was found that the results of two-compartment model are in a good approximation with those of the results obtained from realistic anatomical models. Hence, it was concluded that, tissue properties are most critical parameters as compared to the tissue geometrical details during mathematical modelling of RFA.

During RFA, different modes for controlling the electromagnetic power delivered to tissue are employed, such as power-controlled mode, temperature-controlled mode and impedance-controlled mode. In the present study, temperature-controlled mode has been used to overcome any adverse effects of charring and overheating of the biological tissue. In this mode, the generator adjusts its power output on the basis of set target temperature that is monitored via temperature sensing element embedded at the tip of electrode. Thus, the applied voltage is continuously varied to keep the tip temperature constant during RFA. Several researchers have used manual temperature control mode instead of programmed adjusted temperature control mode [8,15–17]. In the manual control mode, constant voltage is applied at the tip of electrode that is manually adjusted using trial-and-error method to maintain the tip sensor temperature below the pre-set target temperature. In the present study, programmable temperature-controlled RFA has been employed by incorporating a proportional-integral-derivative (PID) controller to monitor and maintain the tip temperature below a set temperature. Since, manual control is very time-consuming and tiresome process that involves a lot of human interaction.

In view of the above, the present work considers two-compartment model to investigate the effect of temperature-controlled RFA with monopolar multi-tine electrode in different body sites. The objective of the present work is to study the variation in predicted input voltage, temperature distribution, ablation volume and treatment time during RFA of liver, kidney, lung and breast, by incorporating clinically realistic properties for both tissue and tumour. The effect of temperature-dependent changes in electrical and thermal conductivity along with damage-dependent changes in local tissue perfusion has been accounted in this study. Furthermore, the numerical results obtained from simulation have been validated with the experimental in vitro results by conducting RFA on polyacrylamide tissue-mimicking phantom gel.

Materials and methods

Problem definition

The problem considers a simplified three-dimensional cubical model of 12 cm edge in which a spherical tumour of 2.5 cm has been embedded (Figure 1(a)). The three-dimensional multi-tine RITA Starburst XL electrode (AngioDynamics Inc., Latham, NY) has been deployed to 2 cm manufacturer’s setting with the tip of electrode placed at 1 cm proximal to the centre of tumour, as shown in Figure 1(b). The material properties used in present study [14,17–20] have been presented in Table 1. The electrical conductivity of tumours within soft tissue, viz., liver, kidney, lung and breast has been taken to be 0.5 S/m [14]. The values of density, thermal conductivity and specific heat of tumour have been assumed to be same as that of the healthy tissue [14] as presented in Table 1. It is worth to note that, the major difference between tissue and tumour properties is blood perfusion. In order to simulate the most realistic cases, the values of tumour perfusion from experimentally measured values in clinical studies [14] have been used and are presented in Table 2. Further, in the present study, the tumour blood perfusion in breast has been considered to be 5.3 × 10⁻³ s⁻¹ [17,20].

Figure 1. (a) Three-dimensional two-compartment computational domain and (b) Multi-tine monopolar electrode model used in the present study.

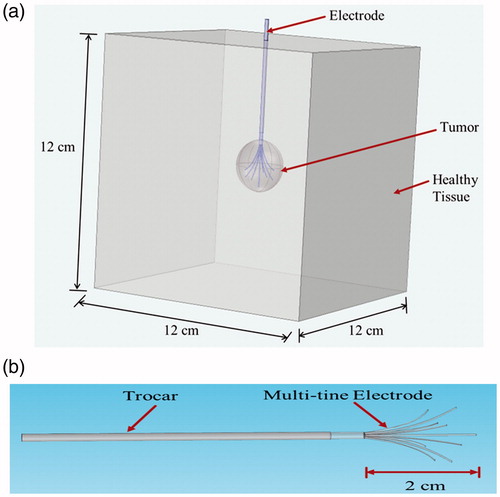
Table 1. Electrical and thermophysical properties of different tissues used in RFA modelling (460 kHz).

Material (tissue/electrode)	Electrical conductivity σ (S/m)	Specific heat capacity c (J/kg/K)	Thermal conductivity k (W/m/K)	Density ρ (kg/m^3)	Blood perfusion ωb (mL/min/kg)	Reference
Normal liver	0.143	3540	0.52	1079	902	[14]
Cirrhotic liver	0.143	3540	0.52	1079	561	[14]
Kidney	0.224	3763	0.53	1066	4161	[14]
Lung	0.122	3886	0.39	394	401	[14]
Breast gland	0.563	2960	0.33	1041	28.82	[17,19]
Breast fat	0.0254	2348	0.21	911	13.17	[17,19]
Breast muscle	0.439	3421	0.49	1090	44.04	[17,19]
Electrode	10^8	840	18	6450	–	[18]
Trocar	10^−5	1045	0.026	70	–	[18]
Blood	–	3617	–	1050	–	[19]

Table 2. Different clinical scenarios considered in the present study.

Clinical case description	Tissue perfusion (mL/min/kg)	Tumour perfusion (mL/min/kg)	Reference
Tumour in normal liver	902	111	[14]
Tumour in cirrhotic liver	561	111	[14]
Metastatic colorectal tumour  in liver	902	510	[14]
Tumour in kidney	4161	924	[14]
Adenocarcinoma in lung	401	349	[14]
Squamous carcinoma in lung	401	786	[14]
Tumour in breast gland	28.82	305.48	[17,20]
Tumour in breast fat	13.17	349.07	[17,20]
Tumour in breast muscle	44.04	291.74	[17,20]

Mathematical modelling

RFA represents a coupled electro-thermal problem wherein electromagnetic energy is applied to heat the tumorous tissue. Further, the interaction of electromagnetic waves with the biological tissues depends on the size and frequencies of the applied electromagnetic field [15]. In the lower frequency range of 450–550 kHz, as is being used during RFA, the wavelength of the electromagnetic field, i.e. 600 m at about 500 kHz, is several orders of magnitude larger than the size of the active electrode and thus, the quasi-static approximation can be used to solve the electro-magnetic problem without compromising accuracy. Therefore, a quasi-static approximation has been used in this study to calculate the “Direct-Current” (DC) voltage from the model that corresponds to the root mean squared (RMS) value of the RF voltage actually employed by solving the generalised Laplace equation: (1) where σ is the electrical conductivity (S/m) and V is the electric potential (V).

The electric field E (V/m) and the current density J (A/m²) generated within the tissue can be computed from (2) (3)

The volumetric heat generation rate Q_p (W/m³) due to radiofrequency heating is given by (4)

The temperature variation inside the biological tissues has been obtained by considering the modified version of Pennes bioheat equation [21], because of its simplicity, computational efficiency and effectiveness. (5) where ρ is density (kg/m³), c is the specific heat capacity (J/kg K), k is the thermal conductivity (W/m K), ρ_b is the density of blood (1050 kg/m³), c_b is the specific heat of blood (3617 J/kg/K), ω_b is blood perfusion rate (1/s), Q_p is the volumetric heating due to electromagnetic source (W/m³) computed using Equation (4)(4) , Q_m is the metabolic heat generation (W/m³), T_b is the core blood temperature (assumed to be 37 °C) and T is the unknown tissue temperature. During RFA, the metabolic heat generation has been neglected since the electromagnetic heat source (Q_p≈O(10⁸) is several orders of magnitude higher than the metabolic heat source (Q_m≈O(10³)) [22].

The present study assumes an increase in electrical conductivity of 2% per degree centigrade for both healthy as well as tumorous tissues and the temperature dependence of thermal conductivity has been approximated by Equation (7)(7) [12]. (6) (7) where σ₀ and k₀ are the constant electrical conductivity and the thermal conductivity, respectively, at core body temperature, T_b = 37 °C (refer Table 1).

Blood perfusion is the most critical parameter that significantly affects the accuracy of computational model [15,22–24], especially with Pennes bioheat transfer model that accounts for microvascular tissue perfusion in the absence of large blood vessels. Earlier studies have focussed on the modelling of blood perfusion by using more realistic vasculature data and modelling blood perfusion as a constant [7–9,14] or piecewise function [13,15–17,22]. Schutt and Haemmerich [24] studied the effect of variation in perfusion rates and perfusion models by considering the piecewise model, a linear decreasing model and a nonlinear decreasing model. The study reported that choice of microvascular perfusion algorithm has significant effects on final ablation zone dimensions in computational studies. Thus, in the present study, nonlinear decreasing model has been used in which blood perfusion increases initially due to vasodilation of capillaries caused by heating of perfused tissue [25] and later decreases with time/induced damage, as represented by (8)

where ω_b,0 is the constant blood perfusion of tissue (refer Table 2) and Ω(t) is the induced thermal damage.

The induced thermal damage (or damage integral) has been computed using the well-established first-order Arrhenius equation [26]. (9)

where t is the ablation time (s), A is a frequency factor (s⁻¹), E_a is the activation energy barrier (J/mol) and R is the universal gas constant (8.314 J/mol K). The kinetic parameters (A and E_a) that accounts for the morphological changes in tissue related to the thermal degradation of proteins have been taken from previous experimental studies for different tissue domains [14,27,28] and have been presented in Table 3. In the context of tissue damage, a damage integral of Ω(t) = 1 corresponds to 63% probability of cell death and damage integral of Ω(t) = 4.6 corresponds to 99% probability of cell death at a specific location. In the present study, the damage integral value of Ω(t) = 1.0 has been employed as a critical threshold to represent tissue death [26].

Table 3. Kinetic parameters for different tissues used in the present study.

Tissue	A (s^−1)	Ea (J/mol)	Reference
Liver	7.39 × 10^39	2.577 × 10^5	[14]
Kidney	6.00 × 10^34	2.385 × 10^5	[14]
Lung	7.39 × 10^39	2.577 × 10^5	[27]
Breast	1.18 × 10^44	3.020 × 10^5	[28]

Temperature-controlled RFA with a monopolar electrode is the most reliable and commonly applied technique in clinical practices for treatment of liver tumour [18]. Normally, the set target temperature at the tip of electrode is below 100 °C that eradicates any adverse effects of charring and overheating of the biological tissue such as, drastic decline in electrical and thermal conductivities and poor image resolution. In the present study, a PID controller has been incorporated in the mathematical model to limit the temperature to a set point during RFA. The PID controller gauges the input error based on closed-loop feedback and accordingly modulates the output, i.e. required input voltage for the dynamic system [22,29]. The input voltage V(t) which has been applied on the active part of electrode can be given as (10)

where V is the applied voltage (V), e is the error, i.e. the difference between set tip temperature and current tip temperature measured at a specific location which is continuously fed back to the PID controller, and K_p (0.02), K_i (0.01) and K_d (0.001) are the proportional, integral and derivative gains, respectively.

Numerical simulation set-up

The two-compartment numerical model of RFA has been solved using the FEM-based solver, COMSOL Multiphysics (COMSOL Inc., AB, Stockholm, Sweden). The discretisation of physical domain has been done using fine tetrahedral mesh elements generated by using COMSOL’s built in free mesh generator. The grid independence study has been done to determine the optimum mesh element size (=1 26 303) to reduce the computational cost, by progressively refining the mesh until the absolute error in tumour temperature nearby the tip of the electrode is negligibly small between the two consecutive sizes of mesh elements. The relative tolerance for the electric field interface and heat transfer interface has been set to 0.0001. All numerical simulations have been carried out on an Intel^® Xeon^® workstation (3.1 GHz clock speed and 64.0 GB RAM).

Initial and boundary conditions

The initial voltage of the entire tissue domain before the onset of radiofrequency energy has been considered to be zero. The boundaries of the multi-tine monopolar electrode have been set to variable voltage source (V(t)) computed by PID controller. A zero volt electric potential has been applied at the outer boundaries of the computational domain (simulating the ground pad). An electrical insulation boundary condition has been set for the portion of insulated trocar base inside and outside the computational domain. For the other inner boundaries of the numerical model, electrical and thermal continuity boundary conditions have been imposed. The initial temperature of the entire tissue has been considered to be same as that of the core body temperature, T_b (=37 °C), and the initial temperature of the RF electrode has been set to 25 °C.

Experimental set-up for RFA on phantom gel

A polyacrylamide-based tissue-mimicking phantom gel has been prepared [30] to perform in vitro RFA in order to validate the numerical model. Recipe for the tissue-mimicking gel has been provided in Table 4. A cylindrical shape plastic mould of 250 mL has been used for phantom fabrication in the present study. A RITA 1500X (AngioDynamics Inc., Latham, NY) electrosurgical RF generator has been used to deliver RF energy at a frequency of 460 kHz with output power range of 1–250 W. The RFA procedure has been performed by inserting the RITA Starburst XL electrode (AngioDynamics Inc., Latham, NY) into the phantom and nine tines of the electrodes were deployed to 2 cm manufacturer’s setting limit. Temperature-controlled RFA at a target temperature of 95 °C has been performed for 7 min. Figure 2 illustrates the experimental set-up used in this study. Utilising the similar approach of thermocouple insertion in phantom as mentioned in the study of Zhang et al. [18], two k-type thermocouples have been inserted perpendicular to the direction of electrode at a distance of 5 mm and 10 mm, respectively, just below the tip of centre tine of the electrode. National Instruments data acquisition module (NI 9214) has been used to acquire temperature data from thermocouples during RFA of phantom.

Figure 2. Photographic view of experimental set-up.

Table 4. The recipe for polyacrylamide-based tissue mimicking phantom gel (1 L with pH of 4.3).

Ingredients	Dosage
Citric acid monohydrous	24.90 g
Sodium citrate tribasic dehydrate	23.97 g
Acrylamide	95.00 g
N,N′-methylene-bis-acrylamide	5.00 g
Bovine serum albumin (BSA)	20.00 g
Glycerol	60.00 mL
Deionised water	Top up to 1.0 L
Initiator–activator pair
L-ascorbic acid	1.0 g
1% FeSO4	2.5 mL
3% H2O2	3.0 mL

Results

Experimental validation of simulation results

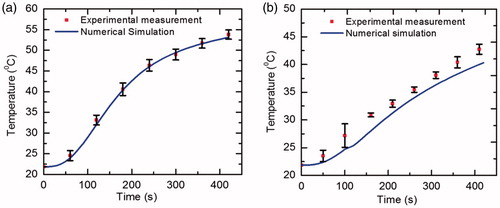
To evaluate the fidelity and integrity of numerical model, the computational results have been compared with the experimental in vitro results obtained during RFA of polyacrylamide tissue-mimicking phantom gel under same environmental conditions. The thermo-electric properties of phantom gel used in numerical simulation are σ = 0.117 S/m, ρ = 1069 kg/m³, c = 3676 J/kg/K and k = 0.59 W/m/K [30]. Since, gel phantom does not possess blood perfusion and metabolic heat generation, so their effects have been neglected during ablation procedure. Figure 3 shows the comparison of temperature distribution at two locations, viz., 5 mm and 10 mm below the electrode tip, obtained after performing temperature-controlled RFA at target temperature of 95 °C for 7 min. A good agreement has been found between the temperature distribution obtained from computational and experimental results as has been depicted in Figure 3. Additionally, the time taken to reach target temperature of 95 °C has been found to be 3.17 min and 2.95 ± 0.3 min (mean ± standard deviation) from numerical and experimental studies, respectively.

Figure 3. Comparison between the experimentally measured and numerically predicted values of temperature with time during RFA of tissue-mimicking phantom gel at different locations: (a) 5 mm below the electrode tip and (b) 10 mm below the electrode tip.

FEM RFA simulations

A numerical study has been done to perform temperature-controlled RFA on two-compartment models of four tissue sites and nine different clinical scenarios, viz., tumour in normal liver, tumour in cirrhotic liver, metastatic colorectal tumour in liver, adenocarcinoma in lung, squamous carcinoma in lung, tumour in kidney, tumour in breast gland, tumour in breast muscle and tumour in breast fat. The different clinical scenarios considered for liver and lung in the present study have been adopted from previous studies [14,27]. For breast, three different locations of tumour considered in the present study, viz., gland, fat and muscle, are based on staging guidelines given by American Joint Committee on Cancer [31]. Although half of all the breast cancers occur in the upper outer portion of the glandular tissue [31], tumour in the breast fat and muscle has also been considered to make a comparison of efficacy of RFA for different tumour locations in the breast. In the present study, a programmable temperature-controlled mode has been used by incorporating the PID controller on the tip of monopolar nine-tine electrode. Here, the tip target temperature has been judiciously set to 95 °C to avoid tissue carbonisation and charring close to the active part of the electrode. During programmable temperature-controlled mode, initially, the applied voltage increases monotonically and reaches the maximum value at a point where target temperature is reached and afterwards it declines to limit the set temperature (still it may rise if target temperature falls). In order to evaluate and compare the efficacy of RFA for different clinical scenarios, initially, the ablation time has been fixed to 10 min. The results obtained from the numerical study have been presented in Table 5.

Table 5. Computational results corresponding to each clinical scenario after 10 min of RFA.

Clinical case description	Time to reach target temperature (s)	Maximum Voltage attained (V)	Ablation volume (cm^3)				Complete ablation of tumour
			IT50	IT60	Ω = 1	Ω = 4.6
			Tumour in normal liver	154	47.22	26.56		16.19	32.45	26.32	Yes
Tumour in cirrhotic liver	148	46.85	33.69	19.53	41.64	33.09	Yes
Metastatic colorectal tumour in liver	156	48.12	26.58	16.17	32.57	26.38	Yes
Tumour in kidney	160	39.74	6.37	4.27	3.99	3.13	No
Adenocarcinoma in lung	116	41.11	101.9	45.37	133.2	92.64	Yes
Squamous carcinoma in lung	124	41.71	102.5	45.53	134.8	93.49	Yes
Tumour in breast gland	66	20.12	24.38	9.38	6.01	4.43	No
Tumour in breast fat	293	109.77	180.9	112.5	82.14	70.69	Yes
Tumour in breast muscle	78	25.08	28.71	11.73	7.32	5.32	No

IT50: Isotherm 50 °C; IT60: Isotherm 60 °C.

Variation of input voltage requirement for different tissues

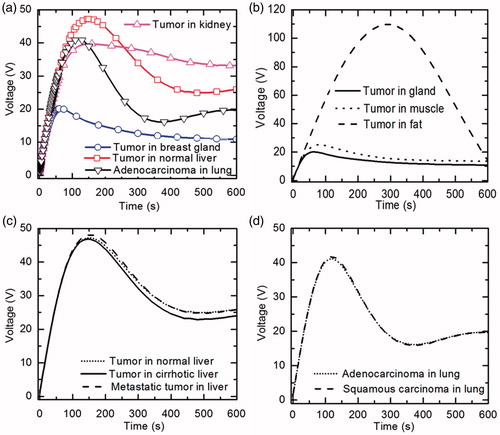
The variation of input voltage with time for four tissues, viz., tumour in normal liver, breast gland, kidney and adenocarcinoma in lung, has been shown in Figure 4(a). It can be clearly seen from Figure 4(a) that, there exists a considerable variation in the requirement of input voltage in ablating different tissues. Figure 4(b) represents the variation of input voltage with time for three different locations of tumour in breast, viz., glandular tissue, muscle and fat. The input voltage requirement is very much higher for ablating tumour located in the breast fat, with a maximum voltage of 109.77 V, as compared to the tumour located in breast gland and muscle, with a maximum voltage of 20.12 V and 25.08 V, respectively. The low electrical conductivity, low thermal conductivity and high perfusion rate of fat are the factors due to which the target temperature is reached after 293 s as compared to 66 s and 78 s in gland and muscle, respectively. The variation of input voltage with time for three different clinical scenarios of liver has been shown in Figure 4(c). It can be clearly seen from Figure 4(c) that, input voltage requirement for ablating tumour in cirrhotic liver is on slightly lower side, due to its low blood perfusion, as compared to the other two cases of liver. Further, it can be seen in Figure 4(d) that, there is a very negligible variation in the voltage requirement for tumour ablation in two clinical scenarios of lung where electrical and thermal conductivity values of both the healthy tissue and the tumour are same with an exception of having varying tumour blood perfusion rates.

Figure 4. Variation of voltage with time for different clinical scenarios: (a) tumour in different tissues; (b) tumour in breast; (c) tumour in liver; and (d) tumour in lung.

Comparison of damage volume and temperature distribution for different cases

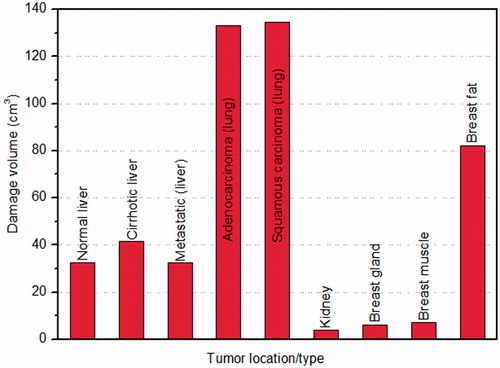
The comparison of damage volume (corresponding to Ω = 1) produced with tumour location/type after 10 min of RFA for nine different clinical scenarios has been shown in Figure 5. It is evident form Figure 5 that, low ablation volume (3.99 cm³) is produced in kidney and highest ablation volume (134.8 cm³) is produced in lung.

Figure 5. Variation of damage volume with tumour location/type for different clinical scenarios during RFA.

Different ablation volumes obtained during RFA with isothermal temperatures of 50 °C (IT50) and 60 °C (IT60) along with damage integrals of Ω = 1 and Ω = 4.6 (corresponding to 63% and 99% probability of cell death, respectively) for different clinical scenarios have been presented in Table 5. The volume of tumour before onset of ablation is 8.1472 cm³, and has been calculated by subtracting the electrode volume from the volume of 2.5 cm diameter spherical tumour. It is important to note that, complete tumour destruction (based on Ω = 1) has not been achieved in three cases, viz., tumour in kidney, tumour in breast gland and tumour in breast muscle, out of nine clinical scenarios considered in the present study after 10 min of RFA. In order to achieve the complete necrosis of the tumour located in kidney, breast gland and breast muscle, the treatment time has been extended further to 30 min.

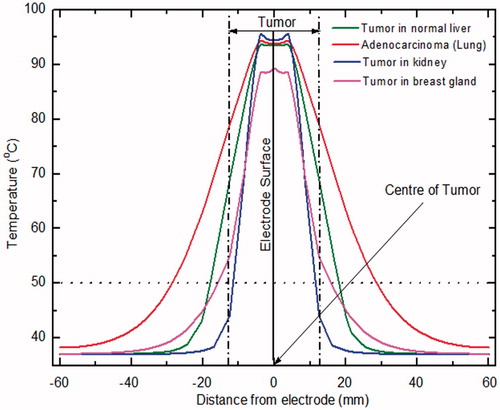
Figure 6 depicts the variation in temperature distribution with distance from the electrode (perpendicular to the electrode surface that passes through the centre of tumour) for different tissues after 10 min of RFA. It can be seen from Figure 6 that, significant variation of temperature at the tumour periphery for different tissues persists. Also, it can be observed that, the maximum temperature is achieved close to the electrode surface for all tissues, and only for the case of tumour in kidney the temperature at the tumour periphery is below 50 °C after 10 min of RFA.

Figure 6. Temperature profile obtained after 10 min of ablation procedure for different tissues as a function of distance from the electrode (measured perpendicular to electrode surface).

Estimation of optimal treatment time for complete tumour ablation during RFA

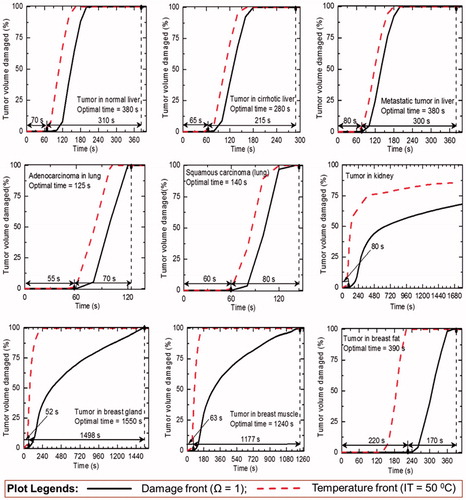
A detailed sensitivity study has been performed to determine the optimal treatment time for different clinical scenarios considered in the present study. The sensitivity study has been dictated by following criteria: (a) complete ablation of tumour volume and (b) minimal damage to the surrounding healthy tissue during application of RFA. The results of this sensitivity study for different cases have been presented in Figure 7. The optimal treatment time for complete ablation of tumour volume (along with initiation of damage) has been quantified on the basis of damage integral Ω = 1 and has been presented in Figure 7 for different clinical scenarios (except for kidney). It is worth to mention that, the tumour volume in kidney has not been completely ablated even after 30 min of ablation procedure, which has been assumed to be the maximum treatment limit for the present study. There has been a significant variation in the damage to tumour volume by two approaches, viz., IT50 and Ω = 1, as can be seen from Figure 7. Among the eight clinical scenarios (where complete damage to tumour volume has occurred in ≤30 min of treatment time), the minimum time was required for adenocarcinoma in lung (125 s) and the maximum time was required for tumour in breast gland (1550 s) to attain complete necrosis of tumour volume during RFA.

Figure 7. Damage fraction of tumour volume with time for different clinical scenarios during RFA (optimal time for kidney is not reported as tumour is not completely ablated even after 30 min of RFA procedure).

Quantification of thermal damage to the surrounding healthy tissue during different RFA protocols

A minimum damage to the surrounding healthy tissue is one of the critical requirements during RFA [12]. However, it is very important to note that, an adequate margin of at least 5 mm around the tumour is completely ablated along with the tumour to mitigate any chances of local tumour recurrence in clinical application of RFA. This is because the area within 5 mm from the tumour border is the most susceptive zone that may contain viable tumour cells, since most recurrent lesions emerge from this zone [32]. In this regard, the damage to the surrounding healthy tissue has been quantified for those six cases in which complete tumour destruction has been attained within 10 min of RFA procedure (as reported in Table 5).

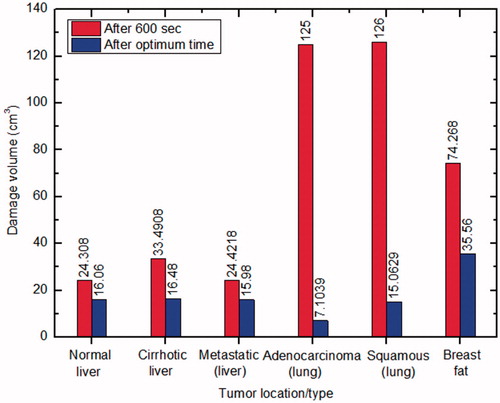
Figure 8 demonstrates the variation of thermal damage (corresponding to Ω = 1) to the surrounding healthy tissues for different cases during RFA. As depicted in Figure 8, there is a considerable variation in the damage to surrounding healthy tissue for two protocols of RFA, viz., treatment time of 10 min and optimal treatment time (presented in Figure 7).

Figure 8. Variation of thermal damage to the healthy tissue during different RFA protocols.

Assessment of temperature distribution at key locations for optimal treatment time

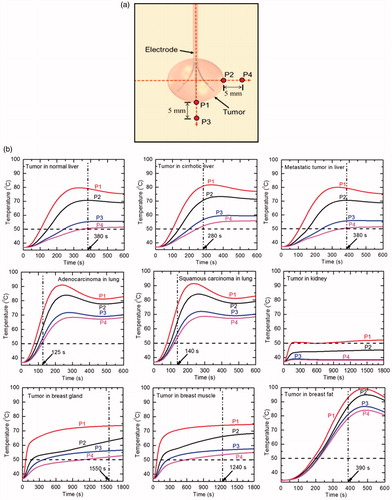
Figure 9(a) shows four temperature measuring locations that have been deliberately set on the boundaries of tumour (P1 and P2) and 5 mm away from tumour (P3 and P4). Figure 9(b) shows the temperature variation at four locations with optimal treatment time (except kidney) for different clinical scenarios used in the present study. It can be seen from Figure 9(b) that, there are considerable variations among the temperature distributions for different tissues of interest. For all the cases considered in the present numerical study, the temperature attained is maximum at point P1 which is very close to the electrode tip and minimum at point P4. The high blood perfusion rate of kidney inhibits energy deposition by taking the deposited heat out of the target volume and further convecting it away to the surrounding tissue due to which complete necrosis of tumour has not been attained even after 30 min of RFA application. Further, as can be clearly seen from Figure 9(b) that, in the case of tumour in kidney, only at point P1 the temperature is greater than 50 °C and at points P3 and P4 the temperature is even below 40 °C. Hence, for highly perfused kidney tissue, modifications like infusion of saline [27] or use of different algorithm or electrode need to be done for attaining complete tumour necrosis.

Figure 9. (a) Schematic diagram representing different temperature measurement locations used in the present study, and (b) temperature variations with time during the 10 min of RFA procedure for different clinical scenarios (RFA for kidney, breast gland and breast muscle has been performed till 30 min).

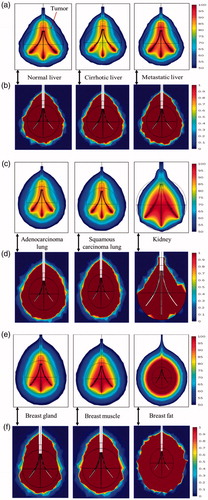
Evaluation of thermal and damage field distributions at optimal time during RFA

The thermal and damage field distributions corresponding to the optimal treatment time (except kidney) for different clinical scenarios during RFA have been presented in Figure 10. It is evident from Figure 10 that, complete tumour necrosis has taken place for all clinical scenarios, except for kidney. Further, the unnecessarily excessive damage occurred to the surrounding healthy tissue of breast fat can also be seen from Figure 10 is due to very high amount of energy deposition, as explained in the preceding section.

Figure 10. Temperature distribution (a, c and e) in degree centigrade, and damage field distributions (b, d and f) for different clinical scenarios corresponding to optimal treatment time (except kidney).

Discussion

Variation of input voltage requirement for different tissues

The numerical results obtained with a temperature-controlled RFA in two-compartment models shows that significant variation prevails in the input voltage requirement for different tissues of interest. This can be attributed due to the cumulative effect of variation in the electrical and thermal properties [15,22] of different clinical scenarios considered in the present study. As can be seen from Figure 4(a) that, input voltage requirement for the tissue with lower blood perfusion rate, like breast, is much lower as compared to highly perfused tissues, such as, liver and kidney. This is because, the target temperature will be attained much early for a tissue with lower blood perfusion rate, thereby limiting further enhancement of input voltage value. Due to this, there can be a considerable rise in the treatment time required for complete necrosis of tumour during RFA.

Comparison of damage volume for different cases

The results presented in Figure 5 show that the least ablation volume is produced in kidney after 10 min of RFA. Although kidney has higher electrical and thermal conductivity values, but prevailing higher tissue blood perfusion rates impose problems during RFA due to which there can be possible under-heating that increases the chances of tumour recurrences and reduces the treatment efficacy for large and centrally located tumours [33]. This can be attributed to the fact that, higher the blood perfusion, higher will be the heat sink effect that basically restricts the further propagation of heat into the tissue and thus decreases the size of ablation volume produced during RFA. On contrary, lung has lower electrical conductivity and thermal conductivity as compared to that of the kidney, but it has the blood perfusion rate almost 10 times lower as compared to that of the blood perfusion rate in kidney that ultimately leads to higher ablation volume. Moreover, the ablation volume produced in lung with squamous carcinoma is slightly higher as compared to the ablation volume produced in lung with adenocarcinoma despite of lower tumour perfusion rate in the latter case. This is due to the higher input voltage requirement to ablate squamous carcinoma in lung, as presented in Figure 4(d).

Further, liver has higher electrical and thermal conductivity values as compared to that of the lung, the ablation volume produced in liver is almost 4 times lower in comparison to the ablation volume produced in the lung. Among the three different clinical scenarios of liver, highest tumour ablation volume is produced in cirrhotic liver because of lower perfusion value as compared to the other two cases.

Similarly, the ablation volume produced in breast gland is only about 1.5 times higher as compared to that of the kidney even though very low perfusion rate is prevailing in the breast gland in comparison to kidney. This can be attributed to lower input voltage requirement in ablating the tumour located in breast gland as compared to that in the kidney during application of RFA, as shown in Figure 4(a). Further, from Table 5, it is evident that, the time to reach target temperature is only 66 s in breast gland in comparison to 160 s in kidney, with maximum voltage attained during ablation being 20.12 and 39.74 V, respectively. Due to this the amount of input voltage that can be applied during RFA of breast gland is limited. Moreover, among the three different locations of tumour in the breast, highest ablation volume of tumour is produced in the less electrically conductive breast fat. This is due to the requirement of highest input voltage to ablate the tumour located in breast fat as compared to the tumour located in breast gland and muscle. Thus, the surrounding tissue environment significantly affects the ablation volume produced during RFA.

Another important observation form the present study is with regard to the complete ablation of 2.5 cm diameter tumour in different cases after 10 min of RFA. For all different cases of liver and lung complete tumour ablation has been achieved within 10 min of RFA. Again, for kidney due to the presence of high perfusion rate complete ablation of tumour has not been achieved in initial 10 min of RFA application. Among the different cases of tumour in breast, complete necrosis of tumour has been attained only in the case of tumour in breast fat. This is due to the restriction of input voltage to ablate tumour in breast gland and in breast muscle as explained earlier. Thus, a significant variation in ablation volume can prevail, even for the tumour located in same body site due to change in the perfusion and/or conductivity contrast.

Further, the variations in predicted ablation volumes have been presented in Table 5 for four cases, viz., IT50, IT60, Ω = 1 and Ω = 4.6. The results demonstrate that, the ablation volume enclosed for the case of IT50 is less than the ablation volume enclosed for the case of Ω = 1, for different clinical scenarios of liver and lung. Hence, IT50 approach can be used to determine the ablation volume produced in liver and lung without much loss of accuracy. But, for the case of kidney and breast, IT50 significantly overestimates the ablation volume as compared to the case of Ω = 1. Further, the ablation volume enclosed by IT60 is on the higher side for the case of kidney and breast as compared to that enclosed by Ω = 1, which was not the case for liver and lung. This deviation can be attributed due to the significant variation of blood perfusion rate that prevails among the tumour and the healthy tissues of breast and kidney. Hence, the tissue has not got damaged although the temperature within the tissue has reached beyond 50 °C. Similar variation can be seen from Figures 7 and 10 for different clinical scenarios considered in the present study. Thus, the isothermal approach for predicting the ablation volume should not be used in breast and kidney since it may overestimate the ablation volume produced during RFA.

Significance of optimal treatment time during RFA

Based on the sensitivity study, optimal treatment time has been determined for different clinical scenarios and is presented in Figure 7. The idea is to stop RFA procedure as soon as complete tumour necrosis (along with an adequate margin of at least 5 mm) has occurred in order to minimise the damage to the surrounding healthy tissues and critical structures. The comparison of damage to the surrounding healthy tissue for two different RFA protocols has been shown in Figure 8, only for those cases in which complete tumour necrosis has been attained within 10 min of RFA procedure. For all six cases, the thermal damage to the surrounding healthy tissue is higher for 10 min of ablation procedure as compared to performing RFA up to an optimal treatment time. Moreover, this damage to the surrounding healthy tissue is more pronounced for the cases of adenocarcinoma and squamous carcinoma of lung. While comparing the damage to healthy volume for different tissues at the optimal treatment time, the maximum damage to the healthy tissue was occurred in the case of breast fat. This is due to the higher time requirement (293 s) to reach the target temperature leading to abrupt rise in the input voltage up to a maximum voltage of 109.77 V. This high voltage leads to deposit of very high amount of energy in the breast fat tissue. This excessive amount of heat is further diffused away to the surrounding healthy tissue that leads to unnecessary damage of the healthy tissue volume. Thus, the required optimal treatment time for complete tumour necrosis can play a very crucial role in safe and risk free application of RFA in clinical practice by minimising the damage to the adjacent healthy tissue. Moreover, it is also apparent from Figure 9(b) that, the considered optimal treatment time is appropriate, since for all different cases (except for kidney) the temperature at all four points is greater than 50 °C at the reported optimal time.

Thus, the present numerical study demonstrates the importance of pre-clinical modelling and simulation to evaluate the efficacy of temperature-controlled RFA in various organs. The numerical simulations can be used to provide a priori information about the possible outcomes and risk involved to the practitioners before the onset of clinical RFA. The authors believe that, results provided in the numerical study could be useful for developing new optimal organ-specific clinical protocols and systems for RFA application.

Conclusions

Several studies have proved the importance of two-compartment model over homogeneous model during RFA of tumour [12,14,16,17,27]. A constant voltage approach has been utilised along with employing mono-polar single needle type electrode in majority of these studies. However, in clinical practices, multi-tine electrodes are commonly used to attain coagulation necrosis of large size tumour by implementing programmable temperature-controlled RFA. Also, only a handful of studies dealt with the cases treated in clinical practice while majority of the studies were limited mainly to liver cancer. To date, a side-by-side comparison of ablation volume produced during RFA along with the damage to the surrounding healthy tissue for different clinical scenarios in liver, lung, kidney and breast have not been assessed. This comparison could play a vital role in enabling a risk-free and safe clinical application of RFA technique on different tissues. In the present numerical study, programmable temperature-controlled RFA with mono-polar multi-tine electrode has been performed on two-compartment models of different clinical cases of liver, lung, kidney and breast. The motive of present study is to report the variation in required input voltage, temperature distribution, ablation volume and treatment time by incorporating clinically realistic properties for both tissue and tumour in different tissues during RFA. The nonlinear piecewise model of blood perfusion has been incorporated along with the temperature dependent changes in electrical and thermal conductivity to achieve better correlation with the clinical RFA. Further, the numerical simulation results have been validated with in vitro experimental results obtained while performing RFA on phantom gel.

Based on the numerical investigations, it has been concluded that the surrounding tissue environment significantly affects the ablation volume produced during RFA. It has been found that highest ablation volume has been produced in lungs and the least ablation volume has been produced in kidney during RFA. It has also been observed that there is a significant variation in the input voltage supplied and temperature distributions among different tissues of interest. The results show that the input voltage requirement is quite high to ablate the tumour located in breast fat as compared to the tumour located in the gland and muscle. The significance of optimal treatment time for complete tumour ablation has been reported so as to minimise the damage to the surrounding healthy tissue and ensuring safe and risk free application of RFA. The maximum optimal treatment time for complete damage of 2.5 cm tumour diameter among different clinical scenarios of different tissues has been found to be 2.33 min, 6.33 min and 25.83 min for lung, liver and breast, respectively. Further, it has been found that the high blood perfusion rate of kidney is problematic for RFA, due to which complete necrosis of tumour has not been achieved even after 30 min of ablation procedure. The damage to the surrounding healthy tissue has also been quantified at the reported optimal treatment time during RFA. It has been verified during RFA that, ablation volume predicted by the damage front and conventional isotherms are not synonymous and this deviation is more pronounced for the cases of breast and kidney. The obtained numerical simulation results emphasise on the need of developing organ-specific systems and protocols to enhance the efficacy of clinical RFA.

Notes on contributors

Sundeep Singh received his Master of Technology degree in Thermal Engineering (CFD & HT) in 2012 from National Institute of Technology Hamirpur, Himachal Pradesh, India. He is currently a Ph.D. student in the Department of Mechanical Engineering at Indian Institute of Technology Ropar, Punjab, India and his research interest includes the assessment of tumour ablation with the aid of radiofrequency ablation technique.

Ramjee Repaka is an associate professor in the Department of Mechanical Engineering at Indian Institute of Technology Ropar, Punjab, India. He received his Ph.D. in Mechanical Engineering from Indian Institute of Technology Kharagpur, India. His research areas include bioheat transfer, cancer diagnosis and therapy, convective heat transfer and radiative heat transfer.

Acknowledgments

The authors would like to acknowledge Indian Institute of Technology Ropar for providing essential infrastructure to carry out the present research.

Disclosure statement

The authors alone are responsible for the content and writing of the paper and the authors report no conflicts of interest.