Gold nanorod-mediated near-infrared laser ablation: in vivo experiments on mice and theoretical analysis at different settings

Abstract

Purpose: The aim of the present study was the in vivo assessment of the effects of gold nanorod (AuNR)-mediated laser ablation (LA) of flank xenograft tumours. We investigated: the differences between intra-tumoural (T_IT) and surface tumoural temperature (T_S); the influence of AuNRs concentration and laser power (P) on both these temperatures and on tumour regression. Lastly, experimental data were used to validate a theoretical model developed to predict the effects of AuNR-mediated LA.

Materials and methods: Thirty-two nude mice were treated using near-infra-red light at two P, 3 d after injecting increasing AuNR doses. T_IT and T_S were recorded during the procedure by two thermocouples, one located within the tumour and the other one on the skin adjacent to the tumour. Tumour regression was assessed 2 d after near-infra-red exposure via Xenogen imaging. A three-dimensional temperature map was obtained by finite element modelling.

Results: T_IT and T_S difference is substantial when AuNRs are injected. Moreover, the maximum temperature reached is strongly influenced by both P and AuNR concentration. Tumours heated above 55 °C experienced regression. Good agreement between experimental and theoretical T_IT was found (maximum difference of 4 °C).

Conclusions: Data show significant influence of P and AuNR concentration on the temperatures reached during AuNR-mediated LA of solid tumours. T_S and T_IT difference increases with AuNRs concentration. Simulated temperatures agree quite well with experimental data. Together, these results represent the first step towards a rationally designed strategy to select the most promising laser settings and AuNRs concentration to improve solid tumour treatment outcomes.

Keywords:

• Gold nanorods
• gold nanorods-mediated photothermal ablation
• temperature monitoring
• in vivo trials
• finite element modelling

Introduction

Minimally invasive thermal techniques, such as Microwave Ablation, High Intensity Focussed Ultrasound, Radiofrequency Ablation and Laser Ablation (LA), hold great potential for selective treatment of cancer [1]. Among others, LA has shown promising results on different types of solid tumours, including hepatocellular carcinoma, colorectal cancer, and recently pancreatic adenocarcinoma [2–4]. The two main bottlenecks limiting widespread use of LA in clinical settings have been developing methods to (1) monitor thermal doses in real time and (2) minimise damage to off-target adjacent tissue. Addressing these challenges is essential to achieve complete ablation of the whole tumour volume while sparing sensitive surrounding healthy tissue, particularly when the tumour geometry is complex. Regarding the first aspect, temperature monitoring during the treatment has been already applied in clinics with promising results [5]. Concerning the selectivity, the use of plasmonic nanoparticles (NPs) has paved the way to new and improved strategies for LA [6–8]. If the nanoparticles are localised within the tumour, their high optical absorption coefficients allow a local conversion of the laser light into thermal energy making the treatment within the tumour more effective while reducing the morbidity caused by off-target heating.

Several studies have demonstrated and compared the efficacy of different kinds of NPs (e.g. nanospheres, nanorods and nanoshells) during near infra-red (NIR) LA [6–10]. A great effort has been devoted to improve the efficacy of AuNP-mediated LA by developing new materials, overcoming toxicity concerns associated with AuNP stabilisers, and by improving the distribution of the intra-tumoural NPs [11–14]. To assess the performances of new materials, it is crucial to investigate the efficacy of the NIR-mediated LA by monitoring the tissue temperature during the treatment. Indeed, the temperature increase mainly depends on the efficacy of the NPs to absorb the laser light, and it is the main factor that causes the tissue damage necessary for tumour regression. Temperature mapping is also pivotal to investigate the influence of the laser settings and of the amount of injected NPs within the tumour on the treatment outcomes.

Thus far, most studies investigate the effects of NP-mediated LA by assessing tumour regression [9]. Moreover, in the few studies in which temperature is monitored during in vivo LA, the measurements are performed using a thermocamera [9,15], which provides an accurate measurement of skin temperature (T_S) but it significantly underestimates the intratumoural temperature (T_IT), as demonstrated in our previous work [16]. Only rarely is T_IT monitored using internal temperature probes [17], magnetic resonance thermometry [6] or fluorescent nanothermometers [18]. Moreover, in this field, there is a multitude of factors which influences the effects of the treatment, mainly related to the NPs (e.g., the kind of NPs, their shape and size, the amount injected within the tumour and the distribution) and to the laser settings (e.g. laser power, P, and treatment time, pulse duration or continuous wave and wavelength). Therefore, it is not economical or time-efficient to experimentally optimise all these parameters in order to identify the best treatment parameters.

In order to overcome this hurdle, theoretical models can be used to test the multitude of combinations in order to predict the optimal parameters. Several authors worked on this topic by providing simulations based on the well-known bioheat equation proposed by Pennes [19]. Several models have been validated in vitro using on tissue phantoms [20,21] and prostate cancer cultures [22]. In the present work, we experimentally and theoretically investigate the influence of both the concentration of gold nanorods (AuNRs) and P on the effects of AuNR-mediated LA. Tumour regression and temperature increases are monitored during LA treatments performed on human cancer xenografts established in mice. In particular, we measure the temperature using two thermocouples, the first one placed within the tumour (to estimate T_IT), the second one on the mouse skin adjacent to the tumour (to estimate T_S). We demonstrate a quantifiable influence of both AuNR dose and P on tumour regression and T_IT. Furthermore, the results demonstrate that the difference between T_IT and T_S increases with AuNRs amount and P. Lastly, a mathematical model based on Pennes equation [19] and the Mie electrostatic approach [23] is developed to simulate the effects of AuNRs-mediated LA in this in vivo animal model. Theoretical and empirical data are compared. Future work will be focussed on applying the model to more disseminated tumours to investigate its potential to simulate the effects of AuNRs-mediated LA in different cancer settings.

Materials and methods

Experimental trials: temperature monitoring and tumour regression

Xenograft establishment and AuNR administration

Thirty-two female, athymic nude mice 6–8 weeks of age (Charles River) were maintained under pathogen-free conditions at the City of Hope Animal Resource Centre, with all procedures approved by the City of Hope Animal Care Committee. Flank xenografts required anaesthetising the mice using 2.5% isoflurane in 1.5 L/min oxygen flow. Two million Firefly luciferase expressing MDA-MB-231 human breast cancer cells were suspended in Matrigel prior to injecting 20 μL into the left flank. Seven days later, xenogen imaging was performed to confirm viable engraftment, then mice were divided into eight groups (four mice/group) before receiving 20 μL intratumoural injections of either saline or select AuNRs quantities suspended in H₂O (Table 1). The tumours were subcutaneous, at a distance of about 1 mm from the skin surface. AuNRs were supplied by Nanopartz, a division of Concurrent Analytical, and were surface coated with 11-Mercaptoundecyltrimethylammonnium bromide (MUTAB) rather than cetyltrimethylammonium bromide to avoid surfacant-related cytotoxicities. We have found MUTAB-coated AuNRs to be cytocompatible up to ∼3 mg/mL (data not shown). They had 40 nm ×10 nm dimensions and longitudinal plasmon resonances at 810 nm. A 28.5 gauge 0.5 cc insulin syringe was used for the injections. Injections were performed manually, without the aid of a controlled injection pump and took approximately 2–4 s per injection. The tumours were subcutaneous, at a distance of about 1 mm from the skin surface. Tumour volumes were measured using a calliper before treatment in order to estimate tumour volume (mm³ = L × W²/2), where L is the longest dimension and W is measured perpendicular to L.

Table 1. Laser settings and AuNR doses administered to established tumours during LA ablation.

	P(W)	PD(W·cm^−2)	Λ(nm)	Amount of AuNRs(μg)	t(min)
Group 2.1–0	2.1	1.4	810	0	5
Group 2.1–12.5	2.1	1.4	810	12.5	5
Group 2.1–25	2.1	1.4	810	25	5
Group 2.1–50	2.1	1.4	810	50	5
Group 3–0	3	2	810	0	5
Group 3–12.5	3	2	810	12.5	5
Group 3–25	3	2	810	25	5
Group 3–50	3	2	810	50	5

Laser ablation and temperature monitoring

Three days post-intratumoural treatment administration, a continuous wave, diode laser (RPMC Lasers, Inc., O'Fallon, MO) was used to expose glycerol-swabbed tumour xenografts to 810 nm light, with a spot size of 1.5 cm² (radius r_l∼7 mm). Experiments were performed at different p values and AuNRs amount (see Table 1). The AuNRs have dimensions of 41 nm ×10 nm, and result in peak absorption at 808 nm (Nanopartz^TM). During the whole treatment, both T_IT and T_S were measured by two K-type thermocouples, connected to a data acquisition system (FX100, Yokogawa, Deer Park, TX) with a sample period of 2 s. The first thermocouple was inserted into the core of the tumour to record T_IT; the second one was placed on the mouse skin adjacent to the tumour and within the laser field (a distance of 1–2 mm from the peripheral part of the tumour) to record T_S. This thermocouple was held in position by one of the experimenters in order to avoid use of tape that could interfere with the laser light.

Xenogen imaging

Tumour regression was monitored two days after laser exposure via Xenogen imaging. Mice were anaesthetised with isoflurane, then received an intraperitoneal injection of d-luciferin suspended in PBS at 4.29 mg/mouse. Light emission was measured 7 min after injection of luciferin over an integration time of 10 s using a charge-coupled device camera (Xenogen IVIS-100, Xenogen Corporation, Alameda, CA). Living Image software (PerkinElmer, Inc., Waltham, MA) was used to analyse resultant tumour flux.

Theoretical model

Thermal response of gold nanorod-mediated laser ablation

The effects of AuNRs-mediated LA in terms of tissue temperature increase were simulated by means of Pennes equation [19]: (1) where ρ is the tissue density (kg·m⁻³), c is the tissue specific heat (J·kg⁻¹·K⁻¹) and k is the tissue heat conductivity (W·m⁻¹·K⁻¹). The dependent variable – T(r,t) – is the tissue temperature, expressed as a function of spatial coordinate – x,y,z – and of time – t –. As simplifying hypotheses, tissue is assumed to be homogeneous and isotropic, and the geometry was modelled considering the cylindrical symmetry.

Other terms in Eq. (1)(1) are the following:

Q_b (W·m⁻³). The heat contribution due to blood perfusion per volume unit expressed by the following: (2) where ρ_b is the blood density (kg·m⁻³), c_b is the blood-specific heat (J·kg⁻¹·K⁻¹), w_b is the blood perfusion rate per volume unit (s⁻¹) and T_b is the blood temperature outside the treatment site.

Q_m (W·m⁻³). The metabolic heat generation due to oxidative process of lipids, proteins and carbohydrates.

Q_l (W·m⁻³). The heat source term due to photon absorption caused by laser–tissue interaction. When AuNRs are injected within the tumour, they can be modelled as miniature sources of heat, since they can achieve high absorption, while maintaining low scattering coefficients. The laser source is modelled by Lambert–Beer law [24]: (3) P (W) being the laser power, r_l (m) the radius of the laser beam and μ_f (m⁻¹) is the effective attenuation coefficient, calculated as (4) where g is the tissue anisotropy factor, and μ_a and μ_s (m⁻¹) are the absorption and scattering coefficients, respectively. Inside the tumour, μ_a= μ_at+ μ_an which takes into account the absorption coefficient of both the tissue – μ_at – and the AuNRs – μ_an –; outside the tumour is μ_a= μ_at. Similarly, inside the tumour, the scattering coefficient is μ_s= μ_st+ μ_sn, where μ_st is the tissue scattering coefficient and μ_sn is the AuNRs scattering coefficient, outside the tumour is μ_s= μ_st.

The term Q_l depends on the AuNRs optical properties, calculated according to the Mie electrostatic approach, as reported in [23] (5) where f_v is the volume fraction of the AuNRs embedded within the tissue, λ is the wavelength of the incident radiation and V_np is the volume of a single AuNR. The terms a₁, a₂ and a₃ are the polarisation of AuNR along the x, y, and z axes, respectively. They are defined as (6) where ɛ and ɛ_m are the dielectric function of the AuNRs and the surrounding medium, respectively; P_i is the geometric factor given by (7)

β=D/l, where D and l are the diameter and the length of the AuNRs, respectively.

Simulations were performed using the values listed in Table 2, assumed by the literature. The optical properties of the tissue were found in [25] and considered equal to the properties of rat tissue at 800 nm.

Table 2. Optical properties and size of AuNRs, and physical properties of the tissue used during the simulations.

Quantity	Value	Unit
ρ	1050	kg·m^−3
c	3700	J·kg^−1·K^−1
k	0.5	W·m^−1 K^−1
ρb	1060	kg·m^−3
cb	3640	J·kg^−1·K^−1
wb	0.02	s^−1
μat	5.7	cm^−1
μst	97	cm^−1
μan	40.6	cm^−1
μsn	0.0028	cm^−1
g	0.94	cm^−1
D	10	nm
L	41	nm
λ	800	nm

The tissue was modelled as a cube of healthy tissue with side length (3 cm-edge), and a central tumoural region as a sphere of 6.2 mm-diameter. The centre of the tumoural sphere was placed at 4 mm from the cube surface, with a minimum distance of 0.9 mm from the surface, in accordance with the in vivo scenario. This size has been calculated by considering the mean volume (i.e. 123 mm³) of the mice tumours measured on the 32 mice before the AuNR-mediated LA, which corresponds to a diameter of ∼6.2 mm. In our previous work, we found that when AuNRs are injected intratumoural they primarily remain in the centre of the tumour [16], with a smaller fraction distributed in the periphery. Using these prior data, we estimated that ∼75% of the AuNRs were within the central sphere defined by half of the radius of the full tumour and the remaining ∼25% were in the peripheral shell from r/2 and r. Thus, for the modelling performed here, we assumed that 75% of the AuNRs were in a central region with radius 1.55 mm and the remaining 25% in the shell from radius 1.55 mm to 3.10 mm. Simulations were carried out by finite element analysis (FEM) modelling using the software Comsol Multiphysics (COMSOL, Inc., Burlington, MA). Simulations were performed considering the treatment settings and the AuNRs reported in Table 1. A control group (no AuNRs) was also considered.

Experimental results

Tumour regression

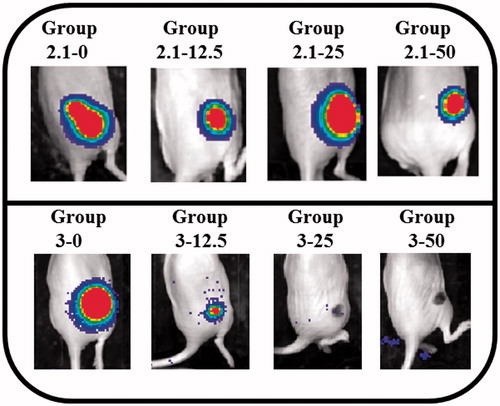
Regarding experiments at 2.1 W, in all mice there was not complete tumour regression as evidenced by robust xenogen signal 2 d after treatment (Figure 1, upper panel). At 3 W, on one hand, in all mice that received high AuNPs amount (50 μg and 25 μg), tumour regression was observed (groups 3–25 and 3–50); on the other hand, in the control group and in mice that received 12.5 μg per tumour of AuNP injections, tumour was not resorbed (groups 3–12.5 and 3–0) (Figure 1, lower panel). The dark spot seen for groups 3–25 and 3–50 is the scab resulting from thermal ablation of the tumour.

Figure 1. Representative xenogen images 2 d after AuNRs-mediated LA. All images generated using the same pseudocolour scale.

Comparison between intra-tumoural temperature and surface temperature

Since each group consists of four mice, we calculated the mean temperature value, and the standard deviation, at each instant of time, t, considering the temperature recorded in all the four mice, T_i. Then, we calculated the standard error Figures 2 and 3 show the mean temperature, both T_IT and T_S, (continuous line)± the standard error (shadowed line) calculated in the groups treated with 2.1 W and 3 W, respectively. Both T_IT and T_S increase with treatment time showing a plateau after about 2.5 min. Figures 2 and 3 show the T_IT and T_S measured at 2.1 W and 3W, respectively.

Figure 2. Temperature measured in the group treated with 2.1 W. The mean temperature trends and the standard error (shadowed lines) are reported.

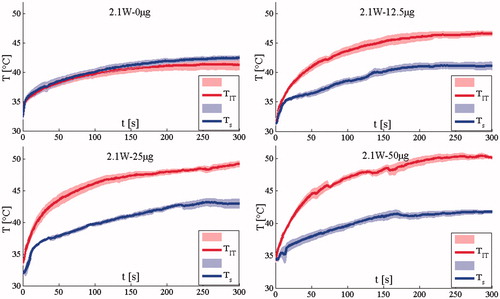
Figure 3. Temperature measured in the group treated with 3 W. The mean temperature trends and the standard error (shadowed lines) are reported.

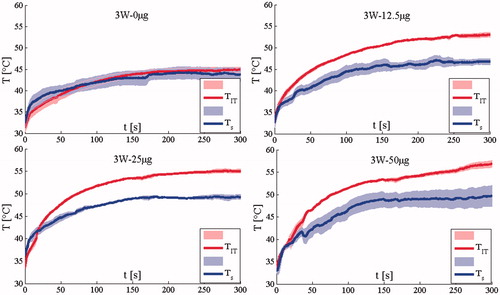
The difference between T_IT and T_s is substantial at all AuNR doses, but not for the saline control group (treated by NIR light without AuNRs). The maximum difference at the end of the treatment is almost 10 °C for the two groups treated with the highest AuNRs dose. These data demonstrate that skin surface measurements provide insufficient information regarding the T_IT increase that occurs during AuNRs-mediated LA. Lastly, we evaluated the possibility to have artefact caused by the direct absorption of laser light, but this issue did not happened. Indeed, the artefact caused by the direct absorption is shown by an abrupt increment of the temperature measured by the thermocouple as shown in several studies [26,27]. In this case, the phenomenon is negligible as shown in Figures 2 and 3.

Influence of P and AuNRs concentration on intra-tumoural temperature

Experiments show that both P and AuNRs amount influence the trends of T_IT. Figure 4 shows the mean T_IT (continuous line)± the standard error (shadowed line) calculated in the groups treated with 2.1 W and 3 W, respectively. It shows that for a given AuNR dose, the T_IT values recorded when the laser power was set at P = 3 W are higher than those recorded at P = 2.1 W. This laser-power-dependent increase in T_IT was increasingly significant as AuNR dose increased. The temperature difference was the highest (6.8 °C) in the group treated at the highest AuNR dose, and the lowest (3.6 °C) in the saline control group. The mean temperature difference was 5.6 °C. In addition to showing the mean and standard error for each group in Figure 4, the temperature measurement for each mouse is shown in Figure 5.

Figure 4. Comparison between intra-tumoural temperatures recorded using the two p values considering all the AuNRs amount. The mean temperature and the standard error (shadowed lines) are reported.

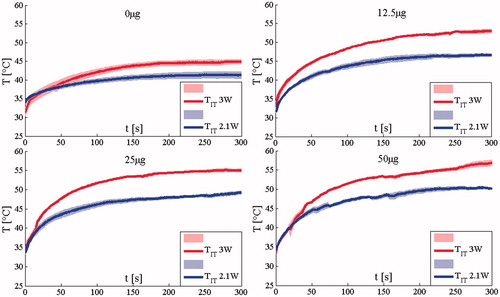
Figure 5. Intra-tumoural temperature trends recorded on all the 32 mice using the two p values considering all the AuNRs amount.

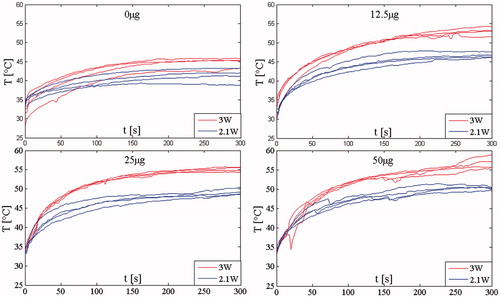
These data suggest a need to develop a theoretical model in order to efficiently and economically identify optimal parameters for LA treatments, because at least three variables need to be simultaneously adjusted: time, AuNR dose and laser power.

Simulations: results and comparison with experimental data

The theoretical model we developed was used to predict temperature increases for tumours undergoing 5 min of LA with p values of 2.1 W and 3 W for all the AuNPs amounts (Figure 6). These predictions are displayed along with the empirical temperature increases measured during our in vivo experiments.

Figure 6. Intra-tumoural temperature trends recorded during in vivo experiments (continuous lines) and by simulations (dashed lines). (A) Data at a laser power of 3 W; (B) data at a laser power of 2.1 W.

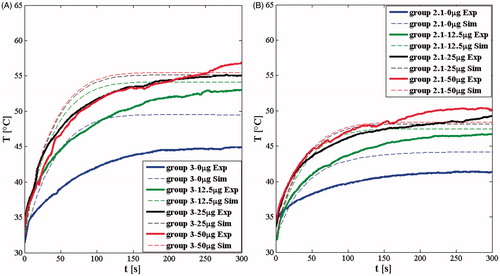
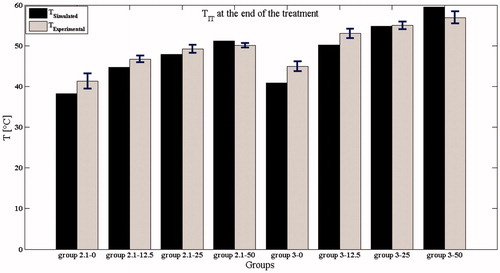
The trends of simulated temperature rise throughout the 5 min LA treatment agree well with the experimentally recorded temperature trends (Figure 6(A) and (B)). Although the initial simulated temperature rise is steeper than was measured experimentally, the final simulated temperature reached at the end of the treatment agrees quite well with experimental measurements. A detailed comparison between the experimental and the predicted temperature reached at the end of treatment is shown in Figure 7. The maximum difference between simulated and experimental final temperatures was in the saline control group treated at 3 W (5 °C), whereas the mean difference considering all eight groups is only ≈1.2 °C. The main difference between the simulations and the experiments can be explained by considering the simplifying hypotheses we used, among others, we simplified the tissue (homogeneous and isotropic), the distribution of the AuNRs (the 75% in the central part of the tumour, the 25% in the peripheral volume of the tumour), the geometry of the tumour (a sphere of 6.2 mm-diameter), the blood perfusion (considering the perfusion rate w_b as uniform in the entire tumour and equal to a reference value, 0.02 s⁻¹, reported in the literature), and we considered temperature independent in all the terms in Eq. (1)(1) .

Figure 7. Simulated (black bars) and experimental (gray bars) T_IT at the end of the 5 min-LA.

The theoretical analysis indicates that the influence of AuNR dose on temperature rise reaches a plateau: for instance, on one hand, there is a significant temperature difference among the control group, the group treated with 12.5 μg and the group treated with 25 μg, on the other hand, there is a negligible difference in temperatures achieved between the 25 μg and 50 μg groups. This phenomenon is evident at both the P levels investigated in this study. Moreover, the temperature reached and maintained within the last few minutes of treatment may be a clear sign of the presence, or absence, of tumour regression; in fact, the tumour regression was observed only in groups 3–25 and 3–50 (see Figure 1) where the T_IT was >55 °C for about the last 2 min of treatment [28].

The proposed theoretical model is accurate enough to predict the effects of AuNR-mediated LA in terms of tumour regression, and the phenomenon of saturation at high amount of AuNRs. If needed, this model could be further improved in the future by taking into account the real geometry of the tumour treated in the specific experiments, the real distribution of AuNRs and of the blood vessels within the tumour, and the temperature dependence of the single terms in Eq. (1)(1) .

Discussion and conclusion

Among minimally invasive thermal techniques, LA is gaining large popularity in the treatment of solid tumours. One of the most important challenges in the field of LA is to improve the selectivity of the treatment in particular for complex tumour geometries. The use of AuNRs has already shown promising results to accomplish this task [6–11]. The efficacy of AuNRs for LA depends on a multitude of both intrinsic (shape and size, optical absorption coefficient and material toxicity) and extrinsic (polymer coating, macrophage affinity and circulation time) material characteristics, as well as external factors, such as the use of optimised laser settings and the AuNRs concentration for effective treatment [9]. In order to figure out how laser power and AuNRs amount influence LA effects, T_S and T_IT were performed on 32 mice undergoing laser treatment. The mice were divided into eight groups using two laser power values (2.1 W and 3 W) and injecting three different amounts of AuNRs; a control group was treated at both the laser power. Although T_S is considered a good surrogate of T_IT, our results demonstrated that there is a significant difference between them; moreover, the higher is the AuNRs amount, the larger is this difference. The peak of T_IT increases with both laser power and AuNRs amount. This phenomenon strongly influences the regression of the tumour: in our study, only mice treated with the highest power (3 W) and with big amount of AuNRs experienced tumour regression (groups 3–25 and 3–50). The tumour regression in these two groups can be explained by analysing T_IT: they are the only groups in which the T_IT rise up to 55 °C, and it is higher than 55 °C for several tens of seconds (see Figure 4).

Here, we significantly expand upon our previous study [16] by investigating the effects of AuNRs-mediated LA, using different laser powers and amounts of AuNRs, and by developing a theoretical model to predict the effects of AuNRs-mediated LA during in vivo trials. The simulations agree well with experimental data (see Figure 7) showing small differences between the peak temperatures for all the eight groups. Most previous studies have not explored as large an in vivo data set. In several studies, the simulations were validated on phantoms or on cells [20–22,29]. Only a few studies present in vivo assessment of nanoparticles-mediated LA. In particular, Maksikova et al. [30] performed the simulation of T distribution in two settings of AuNRs; they injected the AuNRs in the rat in different ways (hypodermic and intramuscolar) in normal tissue – not tumour – and measured the surface temperature with thermocamera. The measurements of surface temperature can be a useful preliminary approach, but lacks from accurate information about the internal tissue temperature. Von Maltzahn et al. [9] conducted a thorough comparison of gold nanoshells and gold nanorods which included modelling of tumour heating for systemically administered polyethylene glycol (PEG)-protected AuNRs. In this work, for one laser setting, only the T_S was compared between experimental data and modelling, with good agreement observed. Here, we have extended this investigation by comparing experimental and modelling results for both T_S and T_IT for two influencing parameters on plasmonic photothermal ablation (i.e. P and amount of injected AuNRs), by using two P levels, and three AuNRs concentrations [8,17].

Besides P and the amount of injected nanoparticles, there is a multitude of factors influencing the effects of plasmonic photothermal ablation: (i) related to laser settings (i.e. treatment time, light wavelength and modality of work); (ii) to nanoparticles (i.e. kind of nanoparticles, their shape and size, their spatial distribution within the tumour); and (iii) to the target tissue (i.e. blood perfusion, optical properties, the dependency of the physical properties on temperature). All the parameters which play crucial role in the definition of heat generation and conduction inside laser-ablated tissues should be taken into account by theoretical models. In particular, the blood perfusion is specific to both the organ and the tumour: even though for simplicity in this study, the blood perfusion has been considered homogeneous within the tissue, it has a strong heterogeneous nature, depending on the kind and the size of tumour, on the presence and spatial distribution of vessels, as well as to the increase of temperature during the thermal treatment [31]. Moreover, the perfusion variability can influence the temperature rise in the tissue, thus the extent of thermal damage [32]. Increasing the value of blood perfusion leads to both a lower steady-temperature value (at the end of the treatment) and a faster temperature rise at the beginning of the treatment. Furthermore, since the AuNRs act as heat source, their distribution within the tumour is a discriminating factor on the description of the phenomenon. This distribution is mostly governed by the methods of particle delivery [33], and, usually, non-uniform spatial distributions are achieved. Soni et al. [34] theoretically investigated the effects of different spatial distributions of NPs inside the tumour (uniform, confined around the injection site, and accumulated in the peripheral tumour region) on thermal effects in the tissue. In the present study, AuNRs distribution was not formally assessed but no significant leakage to the tumour periphery was observed. We attribute the relatively even distribution to performing thermal measurements 1 week after tumour injection before the tumour grew large and dense. A recent study suggests that NP leakage can also be minimised using slow infusion rates (3 μL/min), a parameter that should be incorporated in future studies [35].

Hence, for the most accurate predictive ability, a theoretical model should take into account the patient-specific blood dynamic, the actual spatial distribution of the nanoparticles, the real shape and size of the tumour, besides all the other tissue-specific parameters, to provide an accurate prediction of the thermal effects. However, our goal in the current work was to develop a simple model that would readily allow us to quickly evaluate our basic parameters (laser power, NP dose and time of irradiation) for the design of future experiments. We thus chose to use a relatively straightforward hybrid model based on Beer–Lambert–Bouguer's law that has been used in related work to predict thermal effects of laser light on different tissues [36,37] and AuNP-mediated LA [23,32,34]. We made a number of simplifying assumptions (i.e. the spherical shape of the tumour, constant and homogeneous blood perfusion, 75% of AuNRs in the tumour centre and 25% in the periphery, and temperature independent physical constant of the tissue), and were pleased to observe that this relatively basic model is a reliable tool for the prediction of thermal effects in the scenario of AuNRs-mediated LA on mice with maximum differences between the predictions and the measured temperatures at the end of the treatment of less than 5 °C (ref to Figure 6(A) and (B)).

It clearly shows, in accordance with the experiments, that the increment of temperature values during the procedure saturates with the increase of AuNRs concentration [32]; the biggest difference between theoretical and experimental trends is observable in terms of a faster initial heating in the simulations (Figure 6(A) and (B)), and we suppose that the main responsible of this difference is due to the description of the blood perfusion contribution [31,34]; nevertheless, the temperature values predicted for the end of the treatment are close to the experimental ones (the mean difference considering the eight conditions is 1.2 °C). This study represents an experimental validation of a theoretical model at different experimental settings (P and AuNRs concentration), which could be refined by the knowledge of other experimental conditions, e.g. the measurement of temperature in several site of the tumour, the knowledge of the AuNRs spatial distribution, the blood perfusion and other patient-specific parameters. A primary prediction of this model is that AuNR dose and laser power should be chosen to ensure that the critical T_IT is reached and that the intratumoural distribution of the AuNRs will play a critical role in achieving effective heating throughout the tumour.

Disclosure statement

The authors report that they have no conflicts of interest.