Passive cooling of cutaneous and subcutaneous tissues using phase changing materials: feasibility study using a numerical model

Abstract

In many dermatological applications, lowering the temperature of skin and maintaining specific temperatures for extended periods of time are fundamental requirements for treatment; for example, in targeting adipose tissue and managing cutaneous pain. In this work, we investigate the feasibility of using phase changing materials (PCMs) as an alternative passive, open-loop, heat extraction method for cooling cutaneous and subcutaneous tissues. We used a finite difference parametric approach to model the spatial and temporal progression of the heat transferred from the skin to a PCM in contact with the skin surface. We modelled the thermal performance of different PCMs, including different thicknesses. In addition, we used our model to propose application strategies. Numerical simulations demonstrate the feasibility of using PCMs for extracting heat from the skin and upper fat layers, inducing and maintaining similar temperatures as those induced by active closed-loop cooling with a cold plate. In terms of development, the critical design parameters are the temperature range of solidification of the material, the thickness of the material, and the rate of melting. Our study suggests that PCM-based devices may offer an alternative skin and adipose tissue cooling method that is simple to implement and use.

Keywords:

• Phase change
• cooling
• skin
• fat
• passive cooling

Introduction

Cooling is commonly used in medical treatments to protect tissue, relieve pain and destroy unwanted tissue. In skin, cooling is used selectively to keep tissue from unintended and excessive heating; for example, to prevent injury to the epidermis during exposure to laser light or radiofrequency (RF) fields that target subepidermal structures like blood vessels or adipose tissue [1,2]. During irradiation of laser light or exposure to an RF field most of the energy transfer occurs at the skin surface, and the depth of deposition is a function of wavelength or frequency. If the intended target is not sufficiently close to the surface a well-established strategy is to cool the surface and increase the laser or RF power. Popular and widespread skin cooling methods in laser procedures are cryogen spray cooling, contact cooling and air-cooling. Cryogen spray cooling delivers a short spurt of a refrigerant, such as R134a, before laser irradiation. The refrigerant momentarily forms a superficial liquid pool that evaporates, extracting heat from the skin before laser irradiation. Contact cooling puts a cold and optically transparent material in contact with the skin. The material is optically transparent to the wavelength of laser irradiation, such as sapphire and functions as a window that remains in contact with the skin before, during and after laser exposure. A cold and optically transparent liquid circulating on top actively cools this window. Air-cooling blows a stream of cold air to the skin surface before, during, and after laser exposure. Other clinical procedures utilise cooling for selective tissue damage; for example, cryolipolysis, which is a well-established treatment to damage adipocytes. Cryolipolysis is based on lowering the temperature of the skin surface to approximately −1 to −7 °C for minutes, thereby inducing approximately 4 °C temperatures in the subcutaneous fatty tissue [3]. Such thermal exposure results in inflammatory accumulation of adipocyte cells that are gradually eliminated from the body, while cutaneous tissues remain viable [4,5]. The commercial device for this treatment utilises suction to bring the skin in contact with cold plates whose temperature is carefully controlled.

The cooling methods briefly described above are active cooling methods, that is, the heat extraction process relies on actuation, such as in blowing air, spurting a refrigerant and circulating a liquid or current to create a temperature difference. In terms of control, these cooling methods are either open loop if temperatures are not monitored and do not drive the cooling process, like in spray and air cooling, or closed loop if temperatures are monitored and used to drive the cooling process, like in the treatment for subcutaneous fat. In general, active closed-loop cooling methods provide higher degrees of certainty in inducing the desired temperatures at the expense of complexity in implementing such methods. In contrast, passive open-loop cooling methods can be as precise in cooling and extremely simple to implement but do not allow verification of target temperatures. As an example, consider the universal and centuries-old application of ice.

Phase changing materials (PCMs) are substances with specific phase change temperatures that are used for a wide variety of passive open-loop cooling applications [6,7]. In particular, PCMs are used as a means of maintaining a temperature close to constant during a long period of time, because during phase change the material is capable of storing a large amount of energy as latent heat, such as in ice melting. If an initially solid PCM is placed in contact with another material at a temperature higher than the PCM’s phase change temperature, then a process of cooling or heat extraction from the adjacent material takes place while the PCM melts. This process of heat extraction may last as long as it takes to melt the PCM completely. In this work, we investigate the feasibility of using PCMs as an alternative passive open-loop heat extraction method for cooling cutaneous and subcutaneous tissues.

Objective

The objectives of this work are (i) to conduct a numerical simulation of the heat transfer process that occurs when the skin is placed in contact with different PCMs, and different volumes of PCMs; and (ii) to provide guidelines for the development and design of PCM cooling applicators for skin.

Study design and methods

A finite volume parametric approach is used to model the spatial and temporal progression of the temperature of both the skin and the PCM. Contact cooling by a cold plate atop the skin is also modelled as a reference to a well-established and widely used method. Several cooling strategies are analysed with the objective of identifying what is the best way to achieve the conductive cooling of tissue using PCMs.

Geometry

The geometry of the tissue model is shown in Figure 1. It consists of skin, subcutaneous adipose tissue, and muscle. The layer thickness of skin, l_s, adipose tissue, l_f (considered herein as only fat) and muscle tissue, l_m, is 1.5, 17 and 38 mm, respectively. Below the muscle tissue, the model assumes a very well irrigated tissue that maintains a basal temperature of 37 °C. Physical and perfusion properties of skin, adipose tissue and muscle layers are listed in Table 1.

Figure 1. Model geometry of skin, adipose and muscle tissue layers. The thicknesses of the skin, l_s, subcutaneous tissue, l_f,c and muscle, l_m, layers are, respectively, 1.5, 17 and 38 mm. δ is the parametric variable that represents the PCM thickness and is calculated or set constant as described in the text.

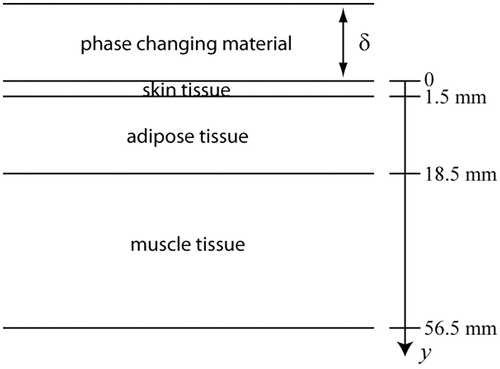
Table 1. Physical and perfusion properties of tissue layers, the density and specific heat of arterial blood are ρ_b = 927 kg/m³ and c_b = 3600 J/kg·K, respectively [4,19,20].

Tissue	Skin	Adipose	Muscle
Thickness [mm]	1.5	17	38
T1 [°C]	−22	4	4
T2 [°C]	0	17	17
cs [KJ/kg·K]	3.8	2.3	3.8
L [KJ/kg]	305	200	305
cl [KJ/kg·K]	3.8	2.3	3.8
ks [W/m·K]	0.53	0.16	0.53
kl [W/m·K]	0.53	0.16	0.53
ρ [kg/m3]	1200	850	1270
ω [1/s]	0.002	0.0006	0.0005
[W/m^3]	368.1	369.3	368.1

Passive cooling materials

Important physical properties of PCMs are the temperature range of solidification, T₁ ≤ T ≤ T₂, the latent heat of solidification, L, the thermal conductivity, k, which may be different for the solid (k_s) and liquid phase (k_l), the density ρ and the specific heat for the solid (c_s) and liquid (c_l) phases. Different PCMs were considered as candidate materials for usage in passive cooling of the skin. The physical properties of the PCMs used in this study are listed in Table 2.

Table 2. Physical properties of the phase changing materials evaluated in this study [6,7,21]; L is in [KJ/kg], ρ in [kg/m³], k_s in [W/m·K] and c in [KJ/kg·K].

PCM	Material	Supplier	T1 [°C]	T2 [°C]	L	ρ	ks	c
1	SavE HS 23 N	Pluss^®	−22	−7.6	200	1180	0.602	3.4
2	PureTemp-23	PureTemp	−23	−9	145	860	0.5	2.11
3	PureTemp-21	PureTemp	−21	−6	240	1060	0.5	1.83
4	ClimSel C-21	Climator	−21	−6	288	1300	0.6	3.6
5	ClimSel C-18	Climator	−18	−0	288	1300	0.6	3.6
6	E-19	PlusICE	−18.7	−2	282	1125	0.58	3.29
7	E-21	PlusICE	−20.6	−5	263	1240	0.51	3.13
8	E-22	PlusICE	−22	−8	234	1180	0.57	3.34
9	E-26	PlusICE	−26	−15	260	1250	0.58	3.67
10	160 g/kg NaCl		−10	−10	300	1100	0.53	3.8

Modelling of PCM and tissue heat transfer

In fine grained PCMs buoyancy effects are negligible, and the conduction mechanisms are dominant in the melting process. The governing equation for the heat transfer process in the PCM is (1) where the PCM conductivity k_c may be temperature and phase dependent. E_c is the total thermal energy of the phase changing material; T_c is the temperature; and δ the thickness of the PCM. The total thermal energy is the sum of the sensible and latent heat stored per unit volume.

For the skin, where a phase change could also occur, we use the Pennes’ equation expressed in the enthalpy form (2) where E_i is the total energy storage in each tissue layer, k_i is the thermal conductivity, the subindex i indicates the tissue layer, ρ_b and c_b are the density and specific heat of arterial blood, ω_i is the blood perfusion rate within each layer, T_b = 37 °C is the arterial blood temperature, and q_m,i is the metabolic heat generation of each layer of tissue [8]. i = 1 is for region 0 < y < y₁, i = 2 for region y₁ < y < y₂ and i = 3 for region y₂ < y < y₃, where y₁ = l_s, y₂ = l_s + l_f,c and y₃ = l_s + l_f,c + l_m.

The PCM has a thickness δ and is insulated on the top, y = −δ, where there is no contact with skin, that is (3)

At the interface between PCM and skin (4) and (5)

At the interface of consecutive layers of tissue (6) and (7)

For the bottom layer of tissue (8) where T_b is the deep tissue basal temperature. The heat equation for the PCM is solved numerically by the enthalpy method [9] as follows (9)

where  is the heat flux normal to the surface S of a volume V.

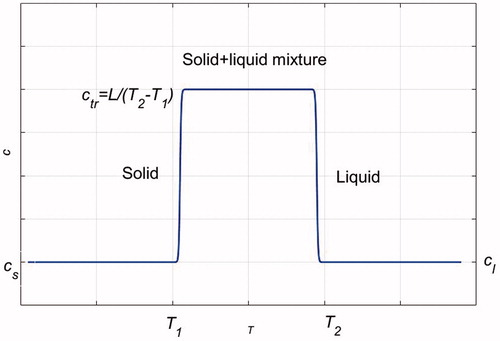
During melting, which occurs over a short temperature range, T₁ ≤ T ≤ T₂, the PCM absorbs a large amount of energy, equal to the latent heat of fusion L. This energy storage during melting is included in E in terms of an apparent specific heat c_c = c_tr = L/(T₂ − T₁), c_tr ≫ c_s, c_tr ≫ c_l. Figure 2 illustrates how the specific heat is estimated as a function of temperature. E_c is related to temperature according to (10) here the reference state of zero energy is the solid state at the temperature at which melting begins.

Figure 2. Phase-dependent specific heat of tissue and PCMs modelled as a piecewise function.

The Pennes’ equation for the different tissue layers is also solved numerically by the enthalpy method (11) where (12) is the volumetric heat generation term. For a multi-layer tissue (13) where phase change may occur. The numerical implementation of the method requires discretization of the physical domain into small subintervals called finite volumes. Each finite volume is a section of the material where conservation of energy is held. In this case, the discretization is one-dimensional and a uniform mesh was chosen. Conservation of energy at the finite volume level for a general finite volume j can be expressed as (14) where R_j − 1 is the thermal resistance between nodes j − 1 and j, while R_j + 1 is the thermal resistance between nodes j + 1 and j (15) (16)

E_j and T_j may correspond to properties of the PCM or any of the layers of tissue. In the case of the PCM, the last term of the Equation (14)(14) is zero.

The initial energy can be expressed in terms of the temperature levels as (17) (18) (19)

Once the new energies are determined from Equation (14)(14) , the new temperatures can be determined from the following relations (20) (21) (22)

This procedure is advanced in time, and in this way the time and space temperature evolution in the tissue and PCM are determined. The method was formulated using an explicit scheme and choosing an appropriate time interval Δt circumvented the related stability restrictions. The equations were solved using a uniform mesh with Δy = 0.0005 m as space interval, which resulted in 113 finite volumes for the tissue layers domain, and 20 finite volumes for a PCM domain of 1 cm. For this mesh refinement Δt = 0.05 s satisfies the stability criterion for the explicit scheme. A finer mesh Δy = 0.00025 m and smaller time interval Δt = 0.0125 s was used in a mesh refinement study for which the difference in results between fine and finer meshes was negligible.

Experimental and analytical validation of numerical model and solutions

As stated in the Objectives section, this study aims to investigate with numerical methods the feasibility of using PCMs for skin cooling. Nevertheless, we conducted a series of relatively simple preliminary experiments in order to provide a sense of the validity of the numerical approach. In these experiments, ice was used as the PCM for cooling two different substrates with thermocouples placed at the surface and within one of the substrates. The substrates were the abdominal skin of a volunteer and agar gels.

Ice cooling of abdominal skin

Cylindrical ice blocks were prepared using a 5.5 cm in diameter and 2 cm in thickness aluminium mould. One of the flat surfaces of the ice block was placed in direct contact with the abdominal skin of a volunteer, who held the ice in place using an insulated pad for preventing direct contact. The abdominal fat layer was estimated at 6 ± 0.7 mm thick from three independent calliper measurements of a skin fold. The mass of the ice block was measured at 5-min intervals during 25 min using a digital scale. As reference, ice blocks were placed atop insulated pads and their mass was also measured at the same time intervals. The temperature of the room was 18 °C. Changes in the mass of the reference were used to adjust the numerical simulations to the physical experiment. Repetitions of these experiments were carried out at 3-h intervals to allow sub-surface tissues to recover from the previous cooling experiment.

Ice cooling of agar phantoms

Gel phantoms were prepared by mixing 2% (w/w) powdered agar with dH₂O (distilled water). The agar mixture was heated in a microwave with periodic stirring until boiling. The homogenised gel was poured into a 3D printed (uPrint SE 3D printer, Stratasys, Ltd., Eden Prairie, MN) rectangular (50 × 50 × 30 mm³) mould (ABS) with embedded K-type thermocouples (OMEGA Engineering, Inc., Norwalk, CT) to ensure good thermal contact. The thermocouples were fixed along the vertical mid plane of the phantom at approximately 1 and 2 cm from the bottom surface (exact location was determined at the end of the experiment by cutting the phantom and measuring). Once the agar had visibly solidified and was allowed to chill to approximately room temperature, the gel was removed from the mould and placed onto a TE plate with a constant 37 °C surface temperature. First, the phantom was heated for 1 h. in order to reach thermal equilibrium with the environment. Next, the PCM, a block of ice, was placed on top of the gel. The block of ice was prepared by freezing dH₂O at −20 °C inside a 3.175 cm by 4.45 cm (1.25 in ×1.75 in) rectangular aluminium tube. Temperature measurements were collected with a National Instruments Temperature Input Module (NI 9211) and Hi-Speed USB Carrier (NI USB-9162) and were recorded in LabVIEW (National Instruments Corp., Austin, TX) in 10 s intervals.

Analytical solution

Finally, we used the one-dimensional analytical solution of heat transfer on a plate to validate our numerical method; that is, if the numerical method is correctly solving the governing equations then analytical and numerical solutions should be in good agreement. Governing equations and the corresponding analytical solution are summarised in the Appendix.

Results

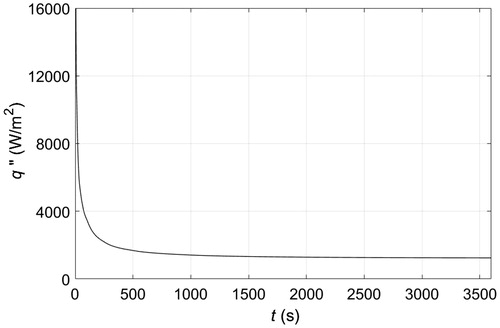
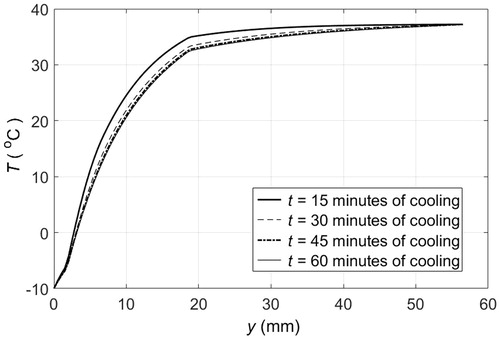
Figure 3 illustrates contact skin cooling by a cold plate that maintains the surface of the skin at −10 °C. This is the standard procedure that we use as a reference to benchmark different PCM cooling approaches. The temperature of tissue as a function of depth is shown for different cooling times. The skin surface is at y = 0, and there are three different layers of tissue that can be clearly differentiated, the second layer, 1.5 mm ≤ y ≤ 18.5 mm, is the adipose tissue, which after 15 min of cooling was partially frozen since temperatures range between −5 and 35 °C. After 30 min a steady state was almost reached with temperatures of adipose tissue between −5 and 33 °C. The upper 3 mm layer of adipose tissue was completely frozen, while the underneath layer, about 5 mm thick, was partially frozen, and the remaining adipose tissue, about 11 mm thick, remained above freezing temperatures. Figure 4 shows the heat flux extracted from the tissue through the skin surface when the skin surface temperature is maintained at −10 °C. Initially, the heat flux was high, as the temperature gradient between the skin surface and the cold plate is large, then it decreased within minutes to reach a steady state after 1000 s of cooling. The steady state reveals the constant heat flux that must be extracted to compensate for perfusion and metabolic heat generation within tissue layers, such that the temperature distribution across layers remains the same, as illustrated in Figure 3, for more than 20 min of cooling. The calculated magnitude of the heat flux extracted through the skin is in agreement with the magnitudes reported in the literature for different body parts [10].

Figure 3. Temperature distribution across different layers of tissue when the skin surface temperature remains at −10 °C: — after 15 min of cooling, — after 30 min of cooling, – · – after 45 min of cooling, ··· after 60 min of cooling.

Figure 4. Heat flux at skin surface when the skin surface temperature remains at −10 °C.

A PCM with a melting temperature of −10 °C at ambient conditions in contact with skin would initially induce similar heat transfer dynamics as the cold plate. However, the time that the skin surface remains at the target temperature would depend on the amount of PCM available for melting. Figure 5 shows the amount of PCM 10 that is required to maintain the skin surface at −10 °C as time progresses. This Figure assumes a spatially stable melting front, that is, the PCM portion in contact with skin is continuously replaced with the solid phase when it transitions to liquid. In absence of material replacement, the melting front initially at the PCM-skin interface will move up and away from the skin front as heat is transferred from the skin to the PCM. Figures 6 and 7 show the temperature distribution across tissue layers at different times when 1 and 2 cm PCM pads are applied to the skin, respectively. Figure 8 illustrates temperature distributions when a 1 cm pad is replaced every 15 min. The corresponding heat flux at the surface of the skin is shown in Figure 9. Finally, tissue temperatures using different PCMs are shown in Figure 10, which illustrates temperature as a function of time at two specific tissue depths, at the skin-fat (y =1.5 mm) and fat-muscle (y =18.5 mm) interfaces.

Figure 5. Thickness as a function of time required to maintain the surface temperature of the skin at −10 °C using PCM 10.

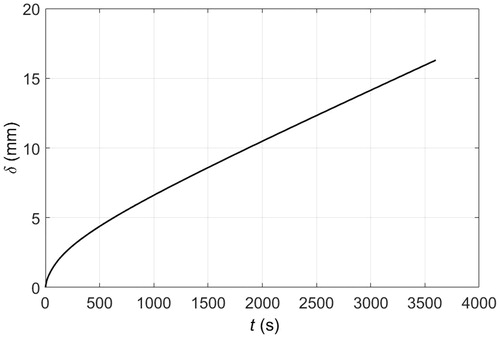
Figure 6. Temperature distribution across PCM pad and tissue layers when the skin surface is in contact with a 1 cm thick solid pad of PCM 10 initially at −10 °C: — after 15 min of cooling, – – after 30 min of cooling, – · – after 45 min of cooling, ··· after 60 min of cooling.

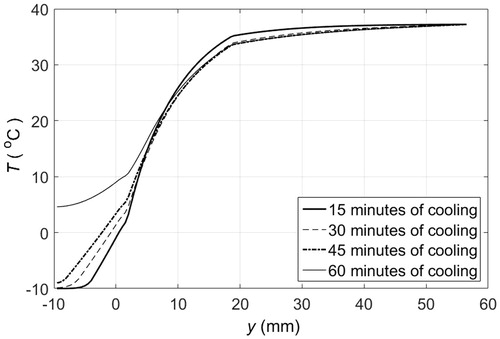
Figure 7. Temperature distribution across PCM pad and tissue layers when the skin surface is in contact with a 2 cm thick solid pad of PCM 10 initially at −10 °C: — after 15 min of cooling, – – after 30 min of cooling, – · – after 45 min of cooling, ··· after 60 min of cooling.

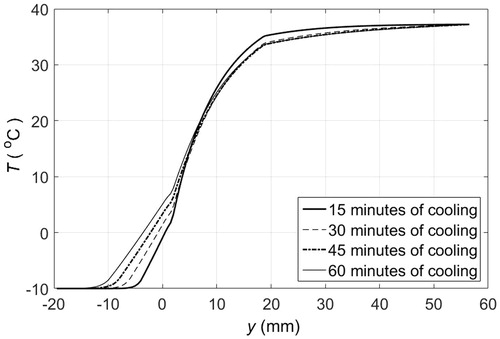
Figure 8. Temperature distribution of PCM pad and tissue layers when the skin surface is in contact with 1 cm thick solid pads of PCM 10, initially at −10 °C, that are replaced every 10 min. — after 15 min of cooling, – – after 30 min of cooling, – · – after 45 min of cooling, ··· after 60 min of cooling.

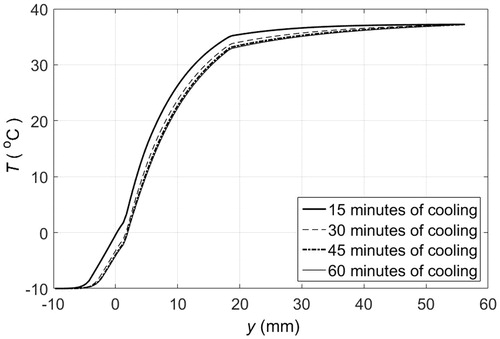
Figure 9. Heat flux at skin surface when cooled by 1 cm thick pads of PCM 10, initially at −10 °C, that are replaced every 15 min.

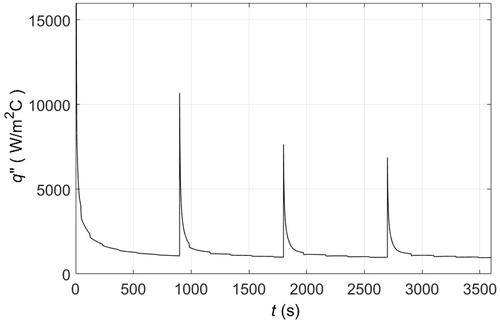
Figure 10. Temperature as a function of time at the skin-fat (—, y = 1.5 mm) and fat-muscle (– –, y = 18.5 m) interfaces: (a) skin surface is maintained at −10 °C; (b) skin cooled by 1 cm thick solid pads of PCM 1 originally at −22 °C; (c) skin cooled by 1 cm thick solid pads of PCM 5 originally at −15 °C; (d) skin cooled by 1 cm thick solid pads of PCM 8 originally at −22 °C; (e) skin cooled by 1 cm thick solid pads of PCM 9 originally at −26 °C; and (f) skin cooled by 1 cm thick solid pads of PCM 10 originally at −10 °C. PCM pads are replaced every 15 min.

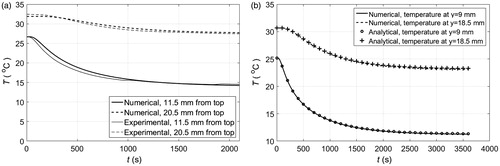
For validation purposes, we used ice as a PCM for cooling the abdomen of a volunteer and a phantom on a heating plate at 37° C. The loss of ice mass during cooling of the abdomen is shown in Figure 11(a). Each set of experiment and control measurements shown in this figure was averaged, and the resulting averaged control measurements were used to compensate the averaged experiment measurements as a DC offset. This offset accounts for losses due to the environment that are not included in our numerical model. Figure 11(b) shows the compensated average experimental measurements and the numerical calculation of ice mass loss. Experimental and numerical temperatures as a function of depth and time during ice cooling of a phantom atop a constant heat source are shown in Figure 12(a). Note that the agreement between experiments and simulations is good. However, in this case the simulation is 3D because the experimental set up was not large enough to assume a one-dimensional heat transfer process. In this simulation, we used the physical properties of water for the phantom. Finally, a comparison between solutions obtained from a one-dimensional analytical expression and our one-dimensional simulation are shown in Figure 12(b). As expected, the analytical and numerical solutions are in good agreement.

Figure 11. (a) Experimental ice mass as a function of time during cooling of the abdomen of a volunteer. Control experiment refers to ice at room temperature placed on a thermally insulated surface. (b) Experimental and numerical ice mass as a function of time during cooling of the abdomen of a volunteer. Experimental measurements were averaged and adjusted as described in the Results section.

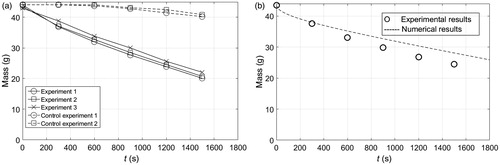
Figure 12. (a) Experimental and numerical temperature as a function of time and depth during cooling of a phantom with an ice block. Numerical results correspond to a three-dimensional simulation. (b) Analytical and numerical temperature as a function of time and depth during cooling of a phantom with an ice block. Numerical results correspond to a one-dimensional simulation.

Discussion

A phase changing material can be regarded as a device for storing energy at specific temperatures while it transitions from a solid to liquid state. If applied to the skin and the transition or phase change temperatures are lower than that of skin, then it becomes a passive and open-loop skin cooling device that is extremely simple to use and relatively inexpensive. The phase change temperatures and the amount of material available mainly dictate the performance of the PCM. The former is set by the physical properties of the PCM, a selection or fabrication aspect, and the latter by the use of the material, a design or implementation aspect. In Table 2(a), small selection of PCMs is listed from the lowest to the highest initial melting temperature. PCM 2 and 3 are organic while the rest are inorganic. Organic PCMs, derived from fatty acids and plant oils, are non-toxic, stable, fire-resistant, have high latent heat and experience minimal volume change between phases. There are three types of inorganic PCMs; these are water-based, petroleum-based and salt hydrates-based. Table 2 only shows inorganic salt hydrates PCMs. Although some manufacturers have obtained the product designation of 100% biobased for organic PCMs by the U.S. Department of Agriculture’s BioPreferred programme, further studies are warranted to establish biocompatibility when in direct contact with tissue. Table 2 lists 10 PCMs with initial melting temperatures ranging from −23 to −10 °C at the lower-boundary (T₁), and from −10 to −7.6 °C at the upper-boundary (T₂). The lower-boundary temperature would be the initial skin cooling temperature. The upper boundary temperature indicates if the skin surface would be subjected to constant or variable temperatures during the melting process, Figure 2. For example, for PCM 10 the initial skin cooling temperature would be −10 °C and remains the same during melting, while for PCM 2 the initial and final skin temperatures would be −23 and −9 °C, respectively. Selection of the appropriate PCM would be guided primarily by the clinical application.

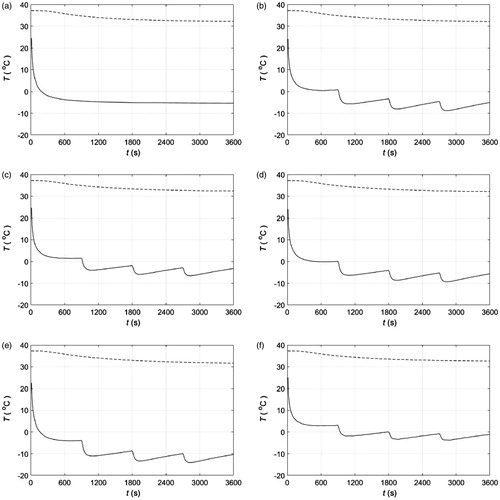
Let’s assume that the clinical application requires maintaining the skin surface at −10 °C for an extended period of time; for instance, to relieve cutaneous pain or induce damage to adipose tissue. A common approach would put a plate in contact with the skin and the plate temperature would be set to −10 °C by a thermoelectric cooler (TEC). In turn, the TEC would be regulated by a proportional integral controller that varies the current to the TEC as demanded by the plate temperature, which is reported to the controller by a thermal sensor inserted in the plate. The temperatures across the different cutaneous and subcutaneous tissue layers that would result from placing such a plate atop the skin for about 1 h are shown in Figure 3. The corresponding heat extraction from the skin by the TEC is shown in Figure 4, which also illustrates the active nature of the control method as the demand in heat flux mirrors the demand in current by the TEC to maintain the target temperature.

As long as there is sufficient material available for continuous melting, then placing PCM 10 atop the skin would induce identical cooling dynamics as those shown in Figure 3 because this material has a melting temperature of −10 °C, Table 2. Approximately, 10 cm in thickness of PCM 10 would be necessary for 30 min of skin cooling at constant melting temperature, see Figure 5, which illustrates how much PCM 10 melts when put into contact with the skin surface. In this figure, δ represents the thickness of PCM molten on the surface of the skin as a function of time. This is also the rate at which liquid PCM 10 should be removed from the skin surface to be replaced by the solid phase. A simple applicator could use a plunger to push the PCM downward along with a recovery strategy for the displaced liquid that would enable reuse of material. Most likely, the PCM would never be in direct contact with the skin because of advantages in reusing the material and in not needing to worry about safety and biocompatibility on contact. This cooling strategy of continuously maintaining the solid phase atop the skin would be appropriate for clinical applications that require constant tissue temperatures over an extensive period of time, like in targeting adipose tissue.

Clinical applications that require maintaining the temperature of tissue below certain threshold or within a range, such as in hypothermia for pain, trauma, inflammation management [11–13] or PCM-based hyperthermia treatments [14–16], could use an even more simple approach. If direct contact between PCM and skin is to be avoided, then the PCM could be packaged as a pad. The PCM pad would melt in contact with the skin but, as the PCM is a fine-grained material with small cavities in a matrix array (it is common practice to encapsulate the PCM), the molten PCM would stay in position. Thus, the PCM closer to the skin would melt first and would be superheated next. Adjacent material layers would melt in turn causing a temperature gradient within the PCM, for which the highest temperature would be at the skin surface. Figure 6 shows the temperature distribution of the different layers of tissue and the material when a 1 cm thick PCM 10 pad is placed in contact with the skin surface. The temperature of the material in contact with skin at y = 0 is above freezing after 30 min, and when the material completely melts the temperature anywhere in the material is above −10 °C, as illustrated by the temperature profiles at 30 and 60 min. A thicker PCM would result in similar cooling dynamics because the temperature gradient within the material would still be present, even though the material does not fully melt in 60 min. This is illustrated in Figure 7, where the temperature at the skin surface only increases about 1.25 °C every 15 min. Alternatively, PCM pads could be replaced at specific time intervals to keep the skin surface at a lower temperature. Figure 8 shows the temperature profiles that develop when 1 cm thick PCM pads are replaced every 15 min by fully frozen pads at the initial melting temperature. The sequential use of PCM pads helps to maintain lower tissue temperatures since 15 min is not enough time to completely melt a PCM 10. After 15 min, the temperature at the skin surface is about 5 °C above the initial melting temperature. The heat flux at the PCM-skin interface is shown in Figure 9. Replacing a partially molten PCM pad by a solid PCM pad results in an increased heat flux because of the sudden change in temperature gradient at the skin surface. If the PCM were replaced more frequently than the peaks in heat flux would be less pronounced.

The use of different PCMs would result in different tissue temperatures. Figure 10 shows the temperature at the skin-fat and fat-muscle interfaces as a function of time that result from cooling tissues with a cold plate and five different PCMs — replaced every 15 min. For the cold plate, Figure 10(a), the temperature at the skin-fat interface (y =1.5 mm) ends up at −5 °C, that is, the skin is frozen. The upper fat layer is frozen as well but the deepest layer of the fat at the muscle interface (y = 18.5 mm) remains above 30 °C. For the different PCMs, the temperature dynamics at the skin-fat interface are qualitatively identical and the magnitudes of the temperature drop are a function of the solidification or melting temperatures in Table 2. At the skin-fat interface the oscillations in temperature because of material replacement are evident; however, at the fat-muscle interface thermal oscillations are damped and negligible. Relative to the cold plate, PCM 5 maintains the temperature of the skin-fat interface closer to −5 °C than the other PCMs, Figure 10(c). For t > 1800 s the temperature oscillates ±2.5 °C around −5 °C. For the other PCMs, the average temperature is either above or below −5 °C. The initial melting temperature of PCM 5 is −15 °C.

In this work, a model is a description of a biophysical phenomenon to help visualise a phenomenon that cannot be directly observed. It is always important to know the accuracy of the description of the actual phenomenon. Ideally, the accuracy of a model would be determined by probing the phenomenon in question. Alternatively, the accuracy of a model could be indirectly assessed by comparisons to complementary models or descriptions. In order to provide a sense of the accuracy of our numerical model, we carried out two preliminary experiments using ice blocks as PCM. Figure 11(b) shows a good agreement between the calculated losses of PCM mass atop abdominal skin and the corresponding experimental measurements. Simulation and experiment include blood perfusion and metabolic heat sources. Figure 12(a) also shows good agreement between the calculated magnitudes and time evolution of the internal temperatures of a phantom and the corresponding experimental measurements. Simulation and experiment provide thermal information at different depths. Note that the simulation is 3D because the ice block was not large enough to assume a 1D heat transfer phenomenon. The one-dimensional numerical method for modelling phase change used in this study is similar to the two-dimensional method we used in [17]. As before, the method described herein is validated by comparing it to a well-established benchmark simulation [18], which corresponds to a two-dimensional slab containing initially a liquid at a constant temperature T_m, and exposed at time zero to convection with a fluid at a temperature T₁ lower than the freezing temperature of the liquid T_m. This simulation describes a freezing front moving towards the core of the slab as time progresses. The dimensionless parameters for this simulation are the following: θ_i = 9/7, where θ = (T–T₁)/(T_m–T_∞), St = 2, where St = c_s (T_m–T_∞)/L, β = (k_lc_sρ_s)/(k_sc_lρ_l) = 0.9, κ = k_l/k_s = 0.9 and Bi = hx₁/k_s = 2. Results using the numerical method described herein and those obtained in [18] are shown in Figure 13.

Figure 13. Location of the solid-liquid interface or displacement of the freezing front along the centre line of a slab filled with liquid. Time is scaled as τ = (2k_st)/(ρ_sc_sx₁). The agreement between our numerical solution and the one obtained in [18] is good.

Summary and conclusions

This work investigated PCMs as a method for open-loop, passive and conductive cooling of skin. Numerical results demonstrate the feasibility of using PCMs for extracting heat from the skin and upper fat layers, maintaining similar temperatures as those induced by cooling with a cold plate. In terms of device design, the critical parameters are the temperature range of solidification, the thickness of the material and the rate of melting. In terms of implementation, we put forward a simple replacement strategy for which the material thickness and melting rate do not limit cooling exposures. In conclusion, our study suggests that PCM-based devices may offer an alternative skin and adipose tissue cooling method that is simple to implement and use. The practicality of the proposed method lies on applying a constant temperature to the skin surface for an extended period of time by the virtue of placing a PCM atop the skin. This is controlled cooling foregoing sensors, actuators, logic hardware and power sources, including the related costs and complexity in implementing closed-loop feedback control, such as a cold plate. For rich and resourceful environments, PCMs may result cumbersome. The best use of PCMs would be where technological and human resources are limited or complexity is not necessary; for example, sustained cooling for (drug-free) pain management at home and remote locations, like a battlefield.

Acknowledgements

WF and JJM would like to thank R. Rox Anderson and the Anderson Lab at the Wellman Center for continued funding and support.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

WF and JJM would like to thank R. Rox Anderson and the Anderson Lab at the Wellman Center for continued funding and support.

Appendix

The one-dimensional heat transfer in substrate can be described by the following set of governing equation, boundary and initial conditions: (A.1) (A.2) (A.3) (A.4)

The analytical solution is the following (A.5) where and L = 0.0295 m is the phantom thickness. First, we obtained the steady state distribution of temperatures for a phantom in contact with a 37 °C surface (hot plate). Next, we used this solution as initial condition to obtain the solution for the same phantom in contact with the 37 °C surface (bottom) and a PCM at 0 °C (top). The analytical curve in Figure 12(b) was obtained from Equation A.5.