Investigation of laser pulsing parameters’ importance in Er:YAG laser skin ablation: a theoretical study conducted via newly developed thermo-mechanical ablation model

Abstract

Objective: Importance of laser pulsing parameters and tissue’s mechanical properties in the Er:YAG laser skin-tissue ablation is not adequately understood. The goal here was to develop a computational model that incorporates skin tissue’s mechanical properties to investigate the influence of Er:YAG laser pulsing parameters on tissue ablation and coagulation.

Methods: Tissue’s mechanical properties were incorporated by modeling ablation as a tissue water vaporization occurring under elevated pressures that depend on tissue’s stress–strain relationships. Tissue deformation was assumed unidirectional; therefore, a one-dimensional model was utilized. Analytical solution and experimental results were used to verify and validate the model. Then, influence of pulse duration (10 µs–2 ms) and fluence (0–30 J cm⁻²) on coagulation depth and ablation efficiency was explored.

Results: Verification and validation results suggested that the model is acceptably accurate. Minimal effect of pulse duration on coagulation depth was predicted at sub-ablative conditions. At those conditions, coagulation depth increased asymptotically to ∼90 µm with increasing pulse fluence. At ablative conditions, coagulation depth decreased asymptotically to 22–28 µm with increasing pulse irradiance. Ablation efficiency plateaued at high pulse fluences and long pulse durations. Mechanical properties were important as about 50% increase in coagulation depth and 25% decrease in ablation efficiency were predicted when considering the high strain-rate loading effect in comparison with quasi-static loading.

Conclusions: Proper tuning of Er:YAG laser pulsing parameters can substantially improve its therapeutic outcomes. The effect of these parameters varies and depends on whether the laser-tissue conditions are ablative or sub-ablative.

Keywords:

• Model
• ablation
• pulse duration
• pulse fluence
• mechanical properties
• thermo-mechanical

Introduction

Lasers are used frequently in the field of dermatology in skin tightening and remodeling [1–3], treatment of different skin and mucous disorders [4], treatment of cutaneous lesions [5,6], and recently in drug delivery where micro-craters are made in the skin to enhance transdermal drug delivery [7,8].

Laser tissue treatments are assessed through both the amount of tissue removal, which is referred to as ablation, and the amount of residual thermal damage, which is referred to as coagulation [9]. Usually maximal ablation for minimal delivered energy is sought; thus the term ‘ablation efficiency’ is utilized and defined as the mass of tissue ablated per applied laser energy. Coagulation zone thickness is important from different applicators’ perspectives, for example, Haak et al. showed that for drug uptakes in skin tissue, a thinner coagulation zone surrounding the micro-channels induced in the skin is better than a thicker zone [10]. In general, to accurately predict and improve therapeutic outcomes of a laser tissue therapy, the effect of laser-tissue parameters on ablation and coagulation is determined.

Lasers have been continuously refined and modified in order to enhance their therapeutic outcomes. Such modifications may include wavelength, power and even laser spot size. The introduction of pulsed lasers was a key element in the evolution of the field of laser therapy [11]. Pulsed lasers have opened new avenues for advancing the therapy through more precise control and selection of laser pulsing parameters, notably pulse duration and pulse fluence. Thus, laser pulse parameters have become the focus of many researchers trying to understand and quantify their effects on therapeutic outcomes [12–14].

Varying effects of pulsed laser parameters on tissue ablation and coagulation were observed by different researchers for different laser-tissue combinations. Pioneering work by Anderson and Parrish suggested the possibility of selectively targeting microstructures through employing shorter laser pulse durations than the thermal relaxation time, a concept they referred to as thermal confinement [15]. Careful tuning of laser pulse duration and fluence was shown to allow for selective blood vessel coagulation without rupture [16,17]. Depth of craters made in egg whites varied significantly with pulse duration and fluence [16–18]. Moreover, Walsh et al. observed significant increase in coagulation thickness when increasing pulse duration [19]. On the other hand, pulse duration effect on treatment efficacy of sebaceous hyperplasia was insignificant [17]. Also Ross et al. observed insignificant effect of pulse duration on thermal damage depth [20]. However, they found that ablation threshold increased with increasing pulse duration. Overall, the understanding of affecting mechanisms and importance of laser pulsing parameters in laser tissue ablation is inadequate [19–21].

Despite the importance of conducting experimental studies, they are costly, challenging to control, or inaccessible in certain research environments. In such cases, theoretical studies are viable alternatives. Many researchers have modeled laser tissue ablation with varying degrees of success. Dabby and Paek developed an earlier conventional model for laser material removal assuming the process to take place at a constant boundary temperature while neglecting phase transition [22]. This model, however, was challenged based on thermodynamic grounds by Miotello et al. [23]. McKenzie et al. developed the three zone laser tissue ablation model, which was the first of its kind to consider water latent heat of vaporization [24]. Partovi et al. developed a three dimensional steady state model assuming laser tissue ablation is a water vaporization process [25]. Next, Venugopalan et al. introduced their analytical model which linked collateral thermal damage to a new dimensionless number (Peclet number) based on the recession velocity of tissue ablation front [26]. Neither optical scattering nor transient response in the tissue was accounted for in these models. Elkhalil et al. have developed a transient numerical model that incorporates optical scattering via Monte Carlo simulation [27,28].

Nonetheless, experimental observations indicate that laser tissue ablation is an explosive process which suggests that mechanisms other than conventional water vaporization are at work [29,30]. Being explosive means that laser tissue ablation requires that the extracellular matrix be physically torn during the process. This implies that tissues’ mechanical properties are major factors in determining the ablation outcomes, as has been suggested by some researchers [31–34]. Thus far, the only attempt to incorporate tissues’ mechanical properties into a computational model was undertaken by Majaron et al. [35]. However, their model predicted weak influence of both ultimate tensile strength and Young’s modulus on ablation threshold. This is likely attributed to the assumed tissue’s microstructure that implies a fourfold increase in the tissue’s volume prior to ablation, which is unrealistic. In addition, their model is sub-ablative and only simulates laser-tissue interaction up to the point when the tissue is about to be ablated. Therefore, a mechanistic laser tissue ablation model that takes into consideration the role of tissues’ mechanical properties during an explosive phase change process is still warranted [11].

Here, we are particularly interested in the Er:YAG laser skin ablation, so we developed a computational model while taking into consideration the dependency of the skin’s mechanical properties on strain rate. The skin’s tissue water is assumed to be entrapped within cylindrical cavities. Thermodynamic properties of tissues and tissues’ water are calculated and determined at an elevated cavity pressure. The model was verified and validated based on an analytical solution and experimental results, respectively. The importance of pulse duration and pulse fluence in the Er:YAG laser skin ablation was then investigated in terms of coagulation thickness and ablation efficiency. This model should complement ongoing experimental research that continuously seeks improvements in infrared and mid-infrared laser therapies’ outcomes [9].

Materials and methods

Tissue’s microscopic structure model

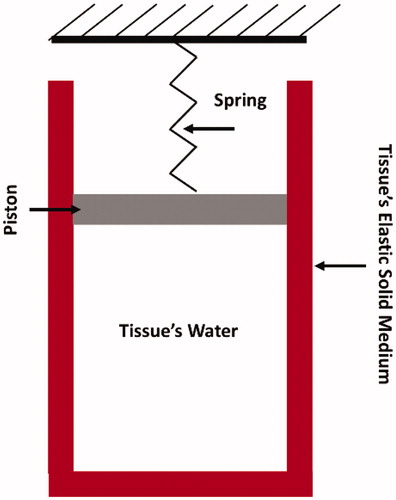
Skin tissue at the micro-level was treated as a two-component medium: tissue water, and solid elastic medium. Skin’s tissue water was assumed to be entrapped within cylindrical cavities surrounded by the solid elastic medium, as shown in Figure 1. Pressure elevation inside the cavity and tissue elastic behavior is captured through the spring-piston compound. During laser irradiation, energy is absorbed by tissue water causing its temperature, pressure, and volume to rise. Volume rising exerts tensile forces on the surrounding tissue’s solid medium, which is represented by piston rising and spring compression. Accordingly, tissue deformation was assumed to be unidirectional. The spring resists piston rising with a magnitude proportional to Young’s modulus of the tissue. This results in a pressure build-up inside the cavity, and consequently, causes an increase in the saturation temperature, that is, the temperature at which water phase transition takes place.

Figure 1. Sketch illustrating the assumed skin’s tissue microstructure. Skin’s tissue water is assumed to be entrapped within a cylindrical cavity that is attached to a spring-piston compound. The cavity’s wall represents the tissue’s elastic solid medium.

When the tissue is irradiated with laser, instant conversion of light to thermal energy and instant thermalization of tissue’s solid medium are assumed. Hence, energy density in the tissue is expressed as (1) $$e=w \Delta u_{\mathrm{w}}+\frac{\int P_{\mathrm{w}}\mathrm{d}\epsilon }{{\rho }_{\text{tissue}}}+\left(1-w\right) c_{\mathrm{s}} \left(T-37\mathrm{°C}\right)$$(1) where e is the energy density in the tissue (J kg⁻¹), w is the tissue’s water content, u_w is the specific internal energy of tissue’s water (J kg⁻¹), P_w is the absolute pressure in the cavity (Pa), ε is the tissue strain, ρ_tissue is the tissue’s density (kg m⁻³), c_s is the specific heat capacity of the tissue’s solid medium (J kg⁻¹ K⁻¹), and T is the tissue’s temperature (^oC). The right-hand side terms are the thermal energy stored in tissue’s water, and the strain and thermal energies stored in the tissue’s solid medium, respectively.

Since tissue deformation was assumed unidirectional, volume expansion of tissue’s water is approximated as (2) $$\frac{\Delta v_{\mathrm{w}}}{v_{\text{wo}}}\approx \frac{\Delta l}{l_{\mathrm{o}}}=\epsilon$$(2) where l is the tissue’s length (m), v_w is the specific volume of tissue’s water (m³ kg⁻¹), and the subscript ‘o’ denotes an initial value. Assuming tissue water’s pressure (P_w) is equivalent to the tensile stress, relationships between P_w and ε and between P_w and v_w were obtained utilizing the stress–strain curve for the skin obtained from Ref. [36].

Specific volume of tissue’s water at each stress–strain point is calculated as (3) $$v_{\mathrm{w}}=\left(1+\epsilon \right)v_{\text{wo}}$$(3)

When tissue water’s pressure and specific volume are known, thermodynamic state of the tissue’s water is determined. Consequently, temperature and specific internal energy of tissue’s water were obtained from the steam tables utilizing the Engineering Equation Solver software (EES: F-Chart Software, Madison, WI) run on a desktop PC with Intel Core i7 processor (2.66 GHz) and 4 GB DDR3 RAM. Lastly, energy density within the tissue was calculated using Equation (1)(1) $$e=w \Delta u_{\mathrm{w}}+\frac{\int P_{\mathrm{w}}\mathrm{d}\epsilon }{{\rho }_{\text{tissue}}}+\left(1-w\right) c_{\mathrm{s}} \left(T-37\mathrm{°C}\right)$$(1) . Table 1 summarizes the thermo-physical properties of the skin that were utilized in the model.

Table 1. Thermo-physical properties of skin tissue [37].

Property	Value
Water content (w)	65%
Density (ρtissue )	1100 kg m^−3
Thermal conductivity (k)	0.4 W m^−1 K^−1
Specific heat capacity of tissue’s solid medium (cs)	1670 J kg^−1 K^−1

Strain-rate dependent tissue’s mechanical properties

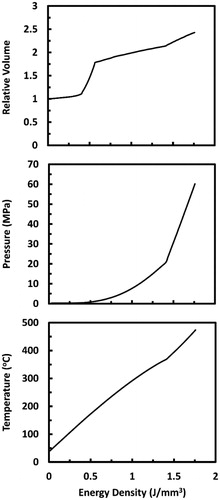
Biological tissues exhibit viscoelastic behavior; thus their deformations during laser ablation are dependent on strain rate [11]. With increased strain rate, viscous dissipation between extracellular matrix components increases causing ultimate tensile strength, modulus of elasticity, and strain energy to rise remarkably [38,39]. In skin tissues, this rise was found to be proportional to the logarithm of strain rate [40,41]. The higher the energy deposition rate, the higher the strain rate; therefore, pulsed laser irradiation can result in tissue straining at humongous rate. This means that the stress–strain curve obtained at quasi-static condition would change substantially depending on the rate of energy deposition. Exact quantification of such change is not readily available; however, a rough approximation through an iterative method was obtained, as explained next.

Laser energy deposition rate is a function of tissue’s optical properties, and laser pulse irradiance, which is the ratio of pulse fluence to pulse duration. For pure absorbing medium, where µ_a is the only relevant tissue optical property, deposited laser energy decreases exponentially with depth according to Beer–Lambert’s law. To simplify the approximation of strain rate, only energy deposited in the superficial layer, whose thickness is equal to one optical penetration depth (1/µ_a), was considered. Therefore, the first step in the iterative procedures was to approximate the average energy deposition rate as (4) $$\overline{\frac{\mathrm{d}e}{\mathrm{d}t}}\approx \frac{\Delta e}{{\tau }_{\mathrm{p}}}=\frac{{\mu }_{\mathrm{a}}{F}_{\mathrm{o}} \left(1-\hspace{0.17em}\text{exp}\hspace{0.17em}\left(-1\right)\right)}{{\rho }_{\text{tissue}}{\tau }_{\mathrm{p}}}$$(4) where µ_a is the tissue’s absorption coefficient (3000 cm⁻¹ for Er:YAG laser in skin tissue [42]), F_o is the pulse fluence (J m ^{− 2}), and τ_p is the pulse duration. The second step was to calculate the maximum energy density (e_max) defined as the energy needed to reach the strain to failure (ε_max). e_max was calculated using Equation (1)(1) $$e=w \Delta u_{\mathrm{w}}+\frac{\int P_{\mathrm{w}}\mathrm{d}\epsilon }{{\rho }_{\text{tissue}}}+\left(1-w\right) c_{\mathrm{s}} \left(T-37\mathrm{°C}\right)$$(1) . Initially, this step was performed assuming quasi-static loading. The third step was to calculate the time needed to reach ε_max, which was defined as (5) $$t_{\mathrm{f}}=\frac{e_{\text{max}}}{\Delta e}{\tau }_{\mathrm{p}}$$(5) where t_f is the time needed to reach the strain to failure (s). With strain to failure being unaffected by strain rate [40,41], the fourth step was to update the strain rate value as (6) $$\dot{\epsilon }=\frac{{\epsilon }_{\text{max}}}{t_{\mathrm{f}}}$$(6) where $\dot{\epsilon }$ is the strain rate (s ^{− 1}). The fifth step was to update the stress–strain relationship by $\text{log}\hspace{0.17em}\left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_{\text{qs}}}\right)$ following Haut et al., where ${\dot{\epsilon }}_{\text{qs}}$ is the quasi-static strain rate selected as 0.3 s⁻¹ [38]. Finally, steps 2–5 were repeated until e_max converged with error less than 1%. This approximated stress-strain relationship was then employed in the EES software to obtain the evolution of tissue’s volume, pressure, and temperature as a function of energy density, as shown in Figure 2.

Figure 2. The evolution of tissue’s relative volume (ratio of volume to initial volume), pressure, and temperature as a function of volumetric energy density in the tissue. The results are obtained using 10 J cm⁻² pulse fluence, 20 µs pulse duration, and 3000 cm⁻¹ absorption coefficient.

Numerical solution

In the current problem, complex phase change is encountered; therefore, an argument based on energy balance was adopted according to the enthalpy method [43]. Thus, the one-dimensional governing equation was expressed as (7) $$\frac{\partial e}{\partial t}=\frac{1}{{\rho }_{\text{tissue}}}\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}+\frac{\partial F_{\text{laser}}}{\partial x}\right)$$(7) where e is the energy per unit mass of tissue (J kg⁻¹), k is the tissue’s thermal conductivity (Wm⁻¹K⁻¹), and F_laser is the laser fluence (J cm⁻²). Heat losses at the tissue surfaces were neglected, so the boundary conditions were defined as (8) $${k\frac{\partial T}{\partial x}|}_{x=0}={k\frac{\partial T}{\partial x}|}_{x=\mathrm{L}}=0$$(8)

The above equations were solved numerically using control volume method, as described in Patankar’s study [44]. The physical domain was discretized into N control volumes encompassing N spatial nodes, as elaborated in Figure 3.

Figure 3. A sketch showing the discretization of the computational domain into N equal control volumes of size Δx. The dependent variables were solved at the spatial nodes placed in the center of the control volumes. Temperature profile between adjacent nodes was assumed to be linear.

Temperature profile between adjacent nodes was assumed to be linear; therefore, the equations were rewritten in the discretized form as

(9) $$e_i^{n+1}=\{\begin{array}{cc}{e}_i^n+\frac{1}{{\rho }_{\text{tissue}}}\left(\frac{k\Delta t \left(T_{i-1}^{n+1}-2T_i^{n+1}+T_{i+1}^{n+1}\right)}{{\left(\Delta x\right)}^2}+\frac{F_{\mathrm{o}}}{\Delta x}\left(\hspace{0.17em}\text{exp}\hspace{0.17em}\left[-{\mu }_{\mathrm{a}}{x}_{i-\frac{1}{2}}\right]-\hspace{0.17em}\text{exp}\hspace{0.17em}\left[-{\mu }_{\mathrm{a}}{x}_{i+\frac{1}{2}}\right]\right)\right),\hfill & 1<i<N\hfill \\ e_i^n+\frac{1}{{\rho }_{\text{tissue}}}\left(\frac{k\Delta t\left(T_{i+1}^{n+1}-T_i^{n+1}\right)}{{\left(\Delta x\right)}^2}+\frac{F_{\mathrm{o}}}{\Delta x}\left(1-\hspace{0.17em}\text{exp}\hspace{0.17em}\left[-{\mu }_{\mathrm{a}}\Delta x\right]\right)\right),\hfill & i=1\hfill \\ e_i^n+\frac{1}{{\rho }_{\text{tissue}}}\left(\frac{k\Delta t \left(T_{i-1}^{n+1}-T_i^{n+1}\right)}{{\left(\Delta x\right)}^2}+\frac{F_{\mathrm{o}}}{\Delta x}\left(\hspace{0.17em}\text{exp}\hspace{0.17em}\left[-{\mu }_{\mathrm{a}}{x}_{i-\frac{1}{2}}\right]-\hspace{0.17em}\text{exp}\hspace{0.17em}\left[-{\mu }_{\mathrm{a}}{x}_{i+\frac{1}{2}}\right]\right)\right),\hfill & i=N\hfill \end{array}$$(9) where Δt and Δx are the temporal and spatial step sizes, respectively; i is an index indicating the nodal position; and n is an index indicating the time point. These equations were solved utilizing the relationship between energy density and temperature according to Equation (1)(1) $$e=w \Delta u_{\mathrm{w}}+\frac{\int P_{\mathrm{w}}\mathrm{d}\epsilon }{{\rho }_{\text{tissue}}}+\left(1-w\right) c_{\mathrm{s}} \left(T-37\mathrm{°C}\right)$$(1) .

Ablation and coagulation

Tissue ablation criteria were based on strain to failure rather than ultimate tensile strength. Although this might seem odd, it is more reasonable since, unlike ultimate tensile strength, strain to failure is not considerably affected by strain rate [11,41]. Thus, a control volume was removed from the computational domain whenever it acquired enough energy to elongate and reach the strain to failure at the approximated strain rate.

Tissue coagulation here refers to irreversible tissue’s protein denaturation. Protein denaturation is a kinetic process, whose rate is governed by the Arrhenius equation [45]. Following the Arrhenius model, the amount of denatured protein increases exponentially according to (10a) $$S=1-\hspace{0.17em}\text{exp}\hspace{0.17em}\left(-\Omega \right)$$(10a) (10b) $$\Omega =A\underset{0}{\overset{t}{\int }}\frac{E_{\mathrm{a}}}{R_{\mathrm{u}}T}d{t}^{\prime }$$(10b) where S is the ratio of denatured protein to initial amount of native protein, Ω is the Arrhenius thermal damage parameter, R_u is the universal gas constant (8.314 J mol⁻¹ K⁻¹), T is the temperature in Kelvin, and A and E_a are the frequency factor and the activation energy, respectively, whose values for the skin tissue are 3.1 × 10⁹⁸ s⁻¹ and 6.28 × 10⁵ J mol⁻¹, respectively [35,46]. The challenge of computing Ω at each position, given that E_a and A are known, is inherent in determining the temporal temperature profile. In this study, however, Ω was calculated numerically as (11) $$A\underset{0}{\overset{t}{\int }}\frac{E_{\mathrm{a}}}{R_{\mathrm{u}}T}d{t}^{\prime }=\frac{A{E}_{\mathrm{a}}}{R_{\mathrm{u}}T}\sum _{n=1}^{N\mathrm{t}}\frac{\Delta t}{2}\left(\frac{1}{T_i^n}+\frac{1}{T_i^{n+1}}\right)$$(11) where N_t is the time point specifying the end of simulation. It is not uncommon to use Ω=1 as a thermal injury threshold [46,47]; therefore, whenever Ω reached 1 the control volume was marked as coagulated.

Model verification and validation

The model was verified based on the analytical model developed by Venugopalan et al. [26]. They modeled laser tissue ablation as a steady-state isobaric water vaporization process taking place at atmospheric pressure. In their model, they assumed that a superficial layer of saturated vapor-liquid mixture at 100 °C would form. Accordingly, the verification was performed through comparisons with the analytical model in terms of the thickness of the layer, the steady-state temperature profile outside the layer, and the movement of tissue’s ablation front with time. Because of the different ablation mechanisms in the analytical model, our computational model was modified to match the analytical model by modifying the relationship between energy density and temperature according to Ref. [28] as (12) $$T=\{\begin{array}{cc}\frac{e}{\rho c_{\mathrm{w}}}+37{}^{\mathrm{o}}\mathrm{C},\hfill & e<c_{\mathrm{w}}{T}_{\mathrm{v}}\hfill \\ T_{\mathrm{v}},\hfill & c_{\mathrm{w}}{T}_{\mathrm{v}}<e<\left(c_{\mathrm{w}}{T}_{\mathrm{v}}+L_{\mathrm{v}}\right)\hfill \end{array}$$(12) where c_w is the specific heat of water (J kg⁻¹ K⁻¹), T_v is the vaporization temperature of water at atmospheric pressure (100 °C), and L_v is the water’s latent heat of vaporization (J kg⁻¹).

Model validation was performed by comparing with experimental results obtained by Walsh et al. [48]. We have specifically selected this experimental study because it tested the effect of a wide range of laser fluences (1–15 J cm⁻²); accurately quantified tissue ablation by measuring ablated mass; utilized infrared laser, where light scattering is negligible; utilized low pulse frequency, which allows complete thermal relaxation between pulses; and utilized laser pulses that are short enough to allow neither ample heat diffusion nor tissue ablation during the pulse [11,49,50]. Absorption coefficient and specific energy of ablation were extracted from the experimental results by relating ablated mass to pulse fluence according to (13) $$m=\frac{{\rho }_{\text{tissue}}}{{\mu }_{\mathrm{a}}}\left(\hspace{0.17em}\text{ln}\hspace{0.17em}\left[F\right]-\hspace{0.17em}\text{ln}\hspace{0.17em}\left[\frac{E_{\text{ab}}}{{\mu }_{\mathrm{a}}}\right]\right)$$(13) where m is the ablated mass per unit area (mg cm⁻²), F is the pulse fluence (J cm⁻²), and E_ab is the specific energy of ablation, which is defined as the amount of deposited energy required to ablate a unit volume of a tissue: J cm⁻³. More details on this can be found in Ref. [27].

Results

The computational model is in excellent agreement with the analytical model, as shown in Figure 4. Here, a continuous wave Er:YAG laser irradiance of 150 W cm⁻² was employed. Grid refinement was conducted and a grid size (Δx) of 1 µm and a time step (Δt) of 5 µs were selected. The slight discrepancy in the vapor–liquid layer thickness between the two solutions is on the order of 0.6 µm, which is smaller than the grid size (Δx = 1 µm); and thus is attributed to an unavoidable inherent discretization error.

Figure 4. Verification of the computational model by comparing with the analytical model developed by Venugopalan et al. [26]. The comparison is made in terms of (a) temperature profile outside the vapor-liquid layer, (b) thickness of the vapor–liquid layer, and (c) tissue’s ablation front position as a function of time. Continuous wave Er:YAG laser with irradiance (I = 150 W cm⁻²) was applied. Spatial and temporal grid size of 1 µm and 5 µs, respectively, were utilized.

The computational model is also in line with the experimental results, as shown in Figure 5. However, there was a slight deviation at pulse fluences lower than 5 J cm⁻² and higher than 15 J cm⁻². At the low pulse fluences, the reported tissue mass loss is a result of tissue enhanced desiccation; and at the high pulse fluences, plasma is formed [34]. Since neither desiccation nor plasma formation were accounted for in the computational model, the model was expected to under predict and over predict the ablated tissue mass at low and high fluences, respectively. By applying Equation (13)(13) $$m=\frac{{\rho }_{\text{tissue}}}{{\mu }_{\mathrm{a}}}\left(\hspace{0.17em}\text{ln}\hspace{0.17em}\left[F\right]-\hspace{0.17em}\text{ln}\hspace{0.17em}\left[\frac{E_{\text{ab}}}{{\mu }_{\mathrm{a}}}\right]\right)$$(13) on the experimental results, an absorption coefficient (µ_a) of 400 cm⁻¹ and a specific energy of ablation (E_ab) of 1.65 J mm⁻³ were calculated. The calculated specific energy of ablation is quite close to the value predicted by the model of 1.76 J mm⁻³.

Figure 5. Validation of the computational model by comparing with experimental results extracted from Ref. [48]. The comparison is made in terms of tissue’s mass loss (ablation) as a function of pulse fluence. A pulse duration of 2 µs, a pulse frequency of 1 Hz, and an absorption coefficient of 400 cm⁻¹ are employed here.

Figure 6 presents tissue temperature as a function of time at several selected depth positions within the irradiated tissue. The simulation for tissue laser irradiation was performed by utilizing a single pulse Er:YAG with 1.21 J cm⁻² pulse fluence and 200 µs pulse duration. This pulse fluence value that is just below ablation threshold was selected to allow the delivery of the highest possible laser energy at the specified pulse duration without inducing ablation.

Figure 6. Tissue temperatures as functions of time during and after a 200 µs long Er:YAG laser pulse at several selected depths within the tissue. The time is taken from the onset of irradiation. Pulse fluence is equal to 1.21 J cm⁻². Surface tissue temperature calculated while neglecting water phase change is added for comparison.

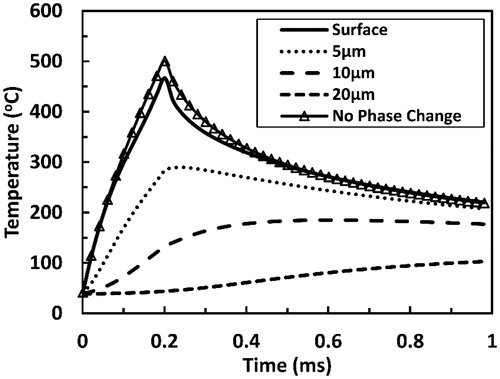
Tissue temperatures near the surface increased with time until the end of the pulse when they reached their peaks. A peak surface temperature of 470 °C was predicted. When neglecting water phase transition, a higher surface temperature peak was attained. These temperatures then decreased with time in contrast to temperatures at deeper locations, which remained constant or continued to increase beyond the pulse for a relatively long period of time. For instance, at 20 µm depth, the protein denaturation temperature of 65 °C was reached 200 µs after the end of the pulse, and the temperature there kept increasing and reached 100 °C by the end of the 1 ms long simulation.

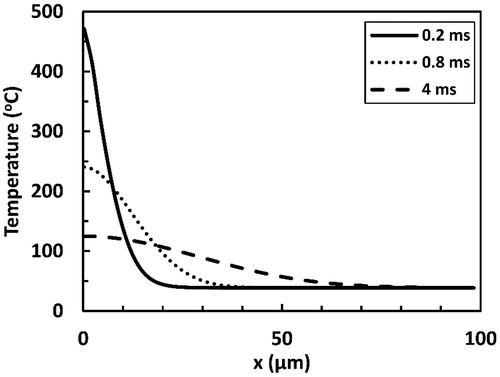
Delayed heating of deeper layers is more evident when looking at temperature profiles presented in Figure 7. For instance, at 40 µm depth, temperatures above 65 °C were attained more than 3.5 ms after the end of a 200 µs long laser pulse. Sharp temperature gradient was predicted at superficial tissue positions (x < 20 µm) by the end of the pulse. Such sharp gradient plays an important role in the delayed heating through driving considerable heat diffusive fluxes into deeper layers. This in turn caused the temperature gradient relaxation at progressing time points.

Figure 7. Temperature profiles predicted at several selected time points from the onset of laser tissue irradiation with a 200 µs long Er:YAG laser pulse. x represents the depth within the irradiated tissue with x = 0 indicating the surface. The pulse fluence is equal to 1.21 J cm⁻².

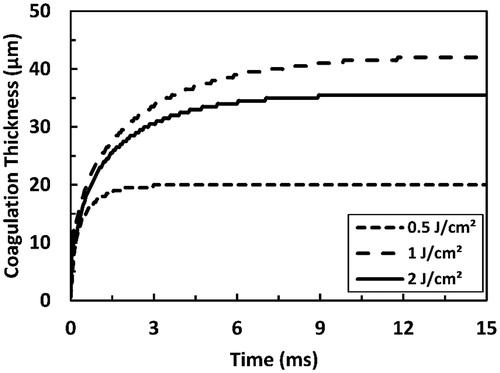
Coagulation thickness increased exponentially past a laser pulse, and tended to reach steady-state long after the pulse had ended, as depicted in Figure 8. The lower pulse fluence is, the faster coagulation thickness reaches steady-state. At sub-ablative conditions, coagulation thickness increased with increasing pulse fluence; as an example, steady-state coagulation thickness increased from 20 to 42 µm when pulse fluence increased from 0.5 to 1 J/cm². On the other hand, coagulation thickness decreased with increasing pulse fluence beyond ablation threshold; for example, steady-state coagulation thickness decreases from 42 µm at a sub-ablative fluence of 1 J/cm² to 35.5 µm at an ablative fluence of 2 J/cm².

Figure 8. Predicted coagulation thickness as a function of time as a result of irradiation with a 200 µs long Er:YAG laser pulse. Two sub-ablative fluence values (0.5 and 1 J cm⁻²) and one ablative fluence value (2 J cm⁻²) are presented. Ablation threshold here was 1.22 J cm⁻².

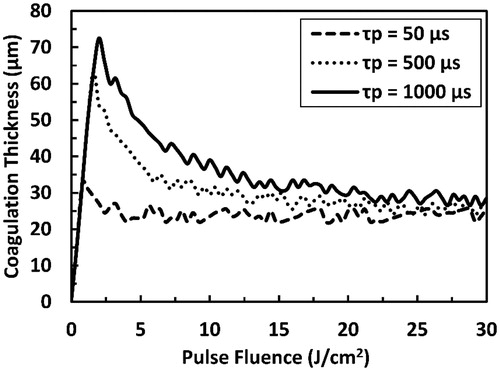
The influence of the ablation on coagulation thickness is emphasized in Figure 9. Pulse fluences corresponding to coagulation thickness peaks are equal to the ablation thresholds; therefore, with tissue ablation being at work, coagulation thickness decreased asymptotically to a plateau of 22–28 µm that is weakly affected by the pulse duration. However, at sub-ablative conditions, coagulation thickness increased monotonically with the pulse fluence and coagulation thickness peaks were higher for longer pulse durations.

Figure 9. Predicted coagulation thickness as a function of the pulse fluence as a result of irradiation with Er:YAG laser pulse at several selected pulse durations (50, 500, and 1000 µs). The total simulation time is 15 ms.

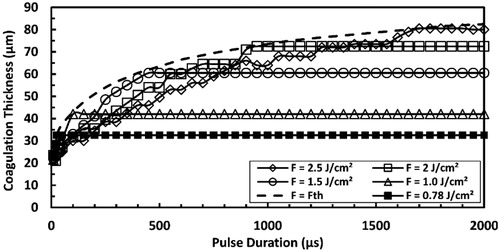
Coagulation thickness was calculated at several selected pulse fluences as a function of the pulse duration, as presented in Figure 10. Initial increase in the pulse duration resulted in increasing coagulation thickness. However, at higher pulse durations, coagulation thickness reached plateaus that were higher for higher pulse fluences. The plateau was reached when pulse duration was longer than the pulse duration corresponding to ablation threshold of an equal magnitude to the applied pulse fluence.

Figure 10. Predicted coagulation thickness as a function of pulse duration as a result of irradiation with ER:YAG laser pulse at several selected pulse fluences. F_th refers to the pulse fluence that is equal to the ablation threshold at each pulse duration and the dashed line connects the points where the transition from sub-ablative to ablative conditions occurs. The total simulation time is 15 ms.

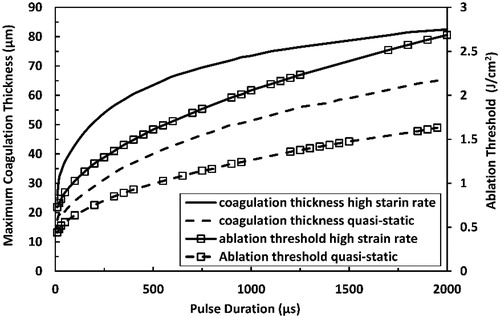
Maximal coagulation thickness and ablation threshold at each pulse duration, as presented in Figure 11, was calculated by setting the pulse fluence equal to the ablation threshold. Maximal coagulation thickness and ablation threshold increased with increased pulse duration. Maximum coagulation thickness tended to saturate with increased pulse duration before the ablation threshold. The high strain-rate loading encountered in the current study resulted in both larger coagulation thickness and higher ablation threshold than the quasi-static loading.

Figure 11. Predicted maximum coagulation thickness and ablation threshold at high strain-rate in comparison with those predicted at quasi-static loading for Er:YAG laser at pulse durations ranging from 10 µs to 2000 µs.

Influence of pulse fluence and pulse duration on ablation efficiency is illustrated in Figure 12. At short pulse durations, ablation efficiency tended to peak with increasing pulse fluence. On the other hand, at longer pulse durations, ablation efficiency increased asymptotically with increasing pulse fluence, where it reached a plateau of about 0.6 mg J⁻¹, a value that was independent of pulse duration. Similar trends at low and high pulse fluences were predicted; where, at high pulse fluences, ablation efficiency increased with increasing pulse duration and then reached the plateau, whose value was also independent of pulse fluence; and at low pulse fluences, ablation efficiency tended to peak with increasing pulse duration. Therefore, the value of the plateau was independent of both the pulse fluence and the pulse duration. Similar trends were predicted for quasi-static loading; however, with 70% higher value for the plateau of about 1 mg J⁻¹.

Figure 12. Predicted ablation efficiency as a function of both pulse duration and pulse fluence of a single Er:YAG laser pulse at (a) high strain-rate loading and at (b) quasi-static loading. Ablation efficency is the ratio between tissue-ablated mass and delivered laser energy.

Discussion

In this study, we developed a computational laser tissue ablation model based on interrelating thermo-mechanical tissue properties. The model was verified and validated in accordance with the availability of proper data. Verification and validation were performed based on a steady-state analytical solution and based on experimental data, respectively [26,48]. The model was then utilized to investigate the effect of Er:YAG laser’s pulse duration and fluence on the skin tissue ablation outcome.

The excellent agreement with the analytical solution supports the accuracy of the implemented numerical method and the written code. The good agreement with the experimental data supports the proposed thermo-mechanical ablation mechanism and the importance of strain-rate dependent tissue’s mechanical properties. Notably, a specific energy of ablation of 1.76 J mm⁻³ is predicted by the model, which is in line with the measured values between 1.5 and 1.75 J mm⁻³ [51,52]. In addition, the specific energy of ablation calculated by applying Equation (13)(13) $$m=\frac{{\rho }_{\text{tissue}}}{{\mu }_{\mathrm{a}}}\left(\hspace{0.17em}\text{ln}\hspace{0.17em}\left[F\right]-\hspace{0.17em}\text{ln}\hspace{0.17em}\left[\frac{E_{\text{ab}}}{{\mu }_{\mathrm{a}}}\right]\right)$$(13) on the experimental data is 1.65 J mm⁻³, which is less than 7% off from the model predicted value. In addition, the predicted maximum surface temperature of 470 °C compares well with measured surface temperatures in the range of 400–550 °C [53]. Although such a high surface temperature may seem odd in comparison with the atmospheric water vaporization temperature of 100 °C, it is ascribed to the mechanical integrity of the tissue causing pressure build-up and vigorous ablation [30].

Moreover, the predicted effects of pulse fluence and duration on coagulation thickness and ablation efficiency are in line with experimental observations, as summarized in Table 2. The predicted maximum coagulation depth value is within the range of values observed experimentally [9,54]. Also, the predicted minimum coagulation depth range overlaps with the experimentally obtained range [9]. Qualitatively, the predicted trend of decreasing coagulation thickness with increasing pulse fluence and decreasing pulse duration of an ablative laser is in line with experimentally observed trends [9,19]. In addition, the trend of ablation efficiency change with pulse fluence is similar to the experimentally observed trend [54]. Lastly, the overall influence of mechanical properties on ablation efficiency is captured in the model and is found to match the experimentally observed influence [34,42,49,55].

Table 2. Comparison between model predictions and experimental observations in terms of pulsed laser tissue ablation outcomes’ values and trends.

Outcome parameter’s value or trend	Model prediction	Experimental observation
Specific energy of ablation (Eab)	1.76 J mm^−3	1.5–1.75 J mm^−3 [51,52]
Surface temperature	470^oC	400–550 °C [53]
Maximum coagulation depth	90 µm	105 ± 25 µm and 75 ± 40 µm [9,54]
Coagulation versus pulse fluence and duration for the ablative modality	Asymptotically decrease with increasing pulse fluence and decreasing pulse duration	Asymptotically decrease with increased absorption coefficient, which has a similar effect as increasing pulse fluence or decreasing pulse duration when ablation is at work [9]
Minimum coagulation depth for the ablative modality	22–28 µm	16 ± 9 µm [9]
Effect of mechanical properties on ablation efficiency	Decreased in ablation efficiency with increased ultimate tensile strength and stiffness	Earlier, more rapid, and larger ablation for weaker tissues [34,49,55]
Ablation efficiency versus pulse fluence	Ablation efficiency increases and then saturates with increased pulse fluence	Saturation in ablation efficiency with increased pulse fluence [54]

Delayed coagulation of deeper tissue layers and continual growth of the coagulation zone past a laser pulse are driven by the sharp temperature gradient and the substantial residual thermal energy in tissue’s superficial layers. The high residual thermal energy approaching 1.6 kJ kg⁻¹ predicted by the end of the laser pulse is what mostly dictates the extent of the thermal damage, as inferred from the irrelevant influence of pulse duration on coagulation thickness when pulse fluence was constant and below the ablation threshold (see Figure 10). This is the case whether pulse durations were shorter or longer than the thermal relaxation time, which is defined as α/µ_a², and α is the tissue’s thermal diffusivity. In our case, the thermal relaxation time was about 100 µs.

However, the effect of residual thermal energy on coagulation thickness vanishes with increased residual thermal energy. This is deduced as the maximum coagulation thickness tends to level off with increased pulse duration faster than the ablation threshold does (see Figure 11). Such trending is attributed mostly to the cooling effect of the boundary condition imposed at the other end of the tissue and the nonlinear variation with time of the diffusive heat propagation into deeper tissue layers. The 90 µm plateau predicted for the maximum coagulation thickness at long pulse durations is in close agreement with experimental findings; where coagulation thickness of 105 ± 25 µm was obtained when employing continuous wave laser with 3000 cm⁻¹ absorption coefficient that matches the absorption coefficient of Er:YAG laser in the skin [9,42].

Increasing pulse fluence while keeping pulse duration fixed or decreasing pulse duration while keeping pulse fluence fixed are equivalent to increasing laser irradiance defined as the ratio of pulse fluence to pulse duration. Therefore, while ablation is present (i.e., pulse fluence is higher than ablation threshold), coagulation thickness decreases asymptotically with increasing laser irradiance to 22–28 µm (Figures 9 and 10). Since ablation rate is equivalently affected by both laser irradiance and absorption coefficient [26], the predicted trend is in line with the observed trend of asymptotically decreasing coagulation thickness with increasing absorption coefficient [9]. Such trend is attributed to the compression of the temperature profile and the coagulation zone by the moving tissue ablation front. The predicted 22–28 µm asymptotes are in close agreement with the coagulation thickness of 16 ± 9 µm obtained at absorption coefficient of 3000 cm⁻¹ and at very high irradiance of 4.5 GW cm⁻².

Therefore, a different thermal confinement concept is indicated that is governed by laser irradiance rather than pulse duration and is only applicable at ablative conditions. The concept implies that when laser irradiance is high enough to induce tissue ablation at a much higher rate than the rate of heat diffusion into deeper tissue layers, energy and temperature distributions are dictated by light distribution only, which renders thermal energy concentrated near the tissue surface; and consequently driving coagulation thickness to a minimum.

Tissue ablation at short pulse durations is driven by the blow-off mechanism since ablation efficiency increases with increasing pulse fluence until reaching a maximum and then decreases with the further increase in the pulse fluence, as illustrated in Figure 33(a) in Ref. [11]. At long pulse durations, tissue ablation soon reaches steady-state since ablation efficiency increases before it reaches a plateau with increasing pulse fluence, as illustrated in Figure 33(b) in Ref. [11]. The highest ablation efficiency is reached when steady-state response is well established. Therefore, the decrease in the ablation efficiency with increasing pulse duration while low pulse fluences are employed indicates that laser irradiance is not high enough to establish steady-state ablation. However, when the high irradiance is utilized, steady-state ablation is quickly established, which renders ablation efficiency unaffected by pulse duration, as noted previously [28,56].

Effect of tissue’s mechanical properties on laser tissue ablation outcome is signified through the comparison with the case of quasi-static loading. Tissues exhibit substantial increase in stiffness and ultimate tensile strength with increasing strain rate [39,41]. Therefore, at high strain rate more energy is required to ablate the same amount of tissue (i.e., specific energy of ablation becomes higher); consequently, residual energy and thermal damage will rise and ablation efficiency will decline.

All in all, to better assess and enhance the outcome of a laser tissue therapy, one needs first to classify whether the therapy or its conditions are ablative (i.e., involve physical removal of the tissue) or sub-ablative (i.e., does not involve physical removal of the tissue) because the importance of laser pulsing parameters varies among the two modalities. For the sub-ablative modality, coagulation thickness is independent of pulse duration and is minimized by decreasing pulse fluence, which implies that maximum coagulation thickness is attained when pulse fluence is equal to the ablation threshold. Ablation threshold is a function of pulse duration; thus maximum coagulation thickness is dependent on the pulse duration. For example, in cutaneous remodeling, where deep coagulation is sought, sub-ablative laser modality is often utilized, which employs long pulse durations on the order of 10 ms and low pulse fluences on the order of 1 J cm⁻² [3]. On the other hand, for ablative modality, coagulation thickness decreases asymptotically with increasing pulse duration; hence, coagulation thickness, in this case, can be minimized by increasing pulse fluence, decreasing pulse duration, or both. However, the absolute minimum coagulation thickness in the ablative modality is independent of laser pulsing parameters. Ablation efficiency is strongly influenced by pulse duration and pulse fluence when both are at their low-values side. Nevertheless, ablation efficiency plateaus when high pulse fluences and long pulse durations are utilized. In addition, at short pulse durations, ablation efficiency peaks with the pulse fluence, which suggests the existence of an optimum pulse fluence for applications requiring maximal tissue removal while utilizing short laser pulses. For instance, with an application as the laser-enhanced transdermal drug delivery, where deep microchannels and thin coagulation zone are pursued, ablative laser modality with short pulse durations on the order of 10 µs and high pulse fluences on the order of 10 J cm⁻² is employed [8].

Future improvements of the computational model may be made by accounting for water surface evaporation. In that case, evaporative cooling at the tissue’s surface should be applied and a surface water evaporation model may be utilized. Surface water evaporation may be incorporated following previous modeling works as in Ref. [57]. Water evaporation may alter tissue’s optical properties; particularly when infrared and mid-infrared lasers are used. In addition, tissue’s water content may influence tissue’s thermo-mechanical properties remarkably, and hence, altering laser tissue ablation/coagulation processes and their metrics such as the specific energy of ablation. Moreover, the effect of multi-directional cavity expansion and mechanical interactions between adjacent cavities on the ablation/coagulation processes may be captured by a dedicated three-dimensional soft-tissue mechanics model. Therefore, accounting for dynamic tissue’s thermo-physical and optical properties could be possible in future studies. Finally, complementary experimental research is also warranted in the future.

Conclusions

We have developed a computational model for laser tissue ablation that incorporates strain-rate dependent tissue’s mechanical properties. The ablation process was simulated as an explosive water vaporization process taking place under elevated pressures that were proportional to tissue’s mechanical properties. The enthalpy method was utilized in which heat diffusion and phase transition were treated on an energy argument ground. The model was verified and validated by comparing with analytical model and experimental results. The good agreement with the analytical and experimental results supported the accuracy of the model. The model was then employed to investigate the influence of Er:YAG laser pulse duration and fluence on skin tissue ablation outcome.

The effect of pulse duration and fluence varies depending on whether the laser-tissue interaction process is ablative or sub-ablative. Pulse duration effect on coagulation thickness is predicted to be irrelevant for sub-ablative processes, while for ablative processes, coagulation thickness is predicted to decrease asymptotically with increasing pulse duration. In contrast, increasing pulse fluence is predicted to cause asymptotic increase in coagulation thickness for sub-ablative processes, while for ablative ones, it is predicted to cause asymptotic decrease in coagulation thickness. On the other hand, ablation efficiency is predicted to attain an absolute maximum when applied laser pulses are operated at high fluences and long durations.

Therefore, it is important to classify whether laser tissue interaction is ablative or sub-ablative before investigating the importance of the laser pulsing parameters in future studies. Finally, attention should be paid to the pulse duration when seeking to maximize the ablation efficiency through increasing pulse fluence, since at short pulse durations there are pulse fluence values predicted to maximize the ablation efficiency.

Acknowledgments

The authors would like to thank Mrs. Grace Betts and Dr. Mohd Alsharo, who are professional native English speakers, for their help in editing for the English.

Disclosure statement

There is no potential conflict of interest to report by the authors.