Strong correlation between specific heat capacity and water content in human tissues suggests preferred heat deposition in malignant tumors upon electromagnetic irradiation

Abstract

Purpose

Tumor perfusion is considered to be the principal factor determining the build-up of therapeutically effective thermal fields. This assumes that malignancies have lower perfusions than their homologous tissues. This assumption, however, ignores the fact that several tumor types have higher perfusions than their healthy counterparts. Additionally, flow changes upon hyperthermia (39–43 °C) are non-predictable and extremely heterogeneous. Therefore, modeling temperature distribution further requires a more robust parameter, different in malignancies and healthy tissues, i.e., water content (C_w), which highly determines thermal properties upon electromagnetic irradiation.

Method

Systematic literature reviews of C_w and specific heat capacities (c_p) were conducted up to 28 February 2022, providing an updated, comprehensive data overview based on original manuscripts, reviews and databases.

Results

C_w- and c_p-values of cancers and their corresponding healthy tissues are presented. Strong correlations between these two parameters are described. In general, malignant tumors have distinctly higher C_w values than their homologous tissues. With increasing C_w in low-water-content normal tissues (<70 wt.%), c_p rises exponentially from 1.5 to 3.3 J·g^–1·K^–1. In high-water-content normal tissues (≥70 wt.%), c_p increases linearly from 3.5 to 3.8 J·g^–1·K^–1. In malignant tumors (>80 wt.%), c_p rises linearly from 3.6 to 3.9 J·g^–1·K^–1. Cancers contain up to 27% more water than their tissues of origin and must be considered as ‘high-capacitance-tissues’.

Conclusions

Hyperhydration of cancers result in higher c_p-values, causing cancers to be better heat reservoirs than corresponding normal tissues upon electromagnetic irradiation. Reliable, tissue-/cancer-specific c_p values must be considered when modeling temperature distributions in hyperthermic treatment.

Keywords:

• Tumor water content
• tumor hyperhydration
• tumor thermal properties
• tumor-specific heat capacity
• hyperthermic treatment
• tumor heat deposition

1. Introduction

Adjuvant mild hyperthermia (HT), i.e., heat treatment of malignant tumors in the range 39–43 °C which is applied within a close timeframe with radiation (RT) and/or chemotherapy (CT), has unequivocally shown distinct beneficial effects in numerous clinical studies [1–5]. HT is a proven radio- and chemo-sensitizer and can facilitate a series of anti-tumor immune responses. As a common mediating factor, HT-induced temporary increases in tumor blood flow (BF) have been considered to improve the delivery of oxygen (O₂), of anti-cancer drugs, and of components of the anti-tumor immune system to tumors. For the latter two mechanisms, a further increase in the vascular permeability of the immature, chaotic microvasculature upon HT has additionally been taken into consideration.

Since the late 1970s, quasi-selective heating of targeted tumors has been discussed because blood perfusion of cancers relative to the surrounding healthy tissues has been reported to be lower, thereby providing an effective ‘heat-trap’ [6–9]. This generalizing statement is often based on an uncritical translation of data obtained in preclinical animal experiments using fast-growing, ‘bulky’ rodent tumors [10]. In the clinical setting, BF in human tumors (e.g., breast cancers, cancers of the head and neck region, prostate and cervix cancers) can be slightly [11] or even markedly higher than in the surrounding tissues or tissues of origin.

Considering relevant clinical data, BF values in squamous cell carcinomas of the head and neck (SCCHN) are 0.30–2.40 mL g^–1 min^–1 vs. BF≈0.05 mL g^–1 min^–1 in the surrounding normal tissues [12,13]. In a clinical case study, preheat BF in a SCCHN was 1.7 mL·g^–1·min^–1 and approx. 2.3 mL·g^–1·min^–1 post heating [14]. Average BF values in breast cancers are ≈0.45 mL g^–1 min^–1 vs. ≈0.05 mL g^–1 min^–1 in the postmenopausal breast [15], and mean perfusion rates in T3 prostate cancers are often elevated up to 0.7 mL g^–1 min^–1 vs. 0.2 mL g^–1min^–1 in normal prostate [16,17]. Flow rates in these cancers and in cervix cancers [18] are, at least, 3-times higher than in their normal counterparts (‘homologous normal tissues’). These latter tumor BF (TBF) data substantially deviate from those presented by Wust [19]. For reasons of simplification, Wust presented the following ‘generalized’ TBF data for basal, hyperthermic and maximum flow: 0.05 vs. 0.10 vs. 0.15 mL g^–1min^–1 for ‘tumor’ (without any tumor type specification). In addition to these latter ‘estimated’ data, inappropriate blood flow and c_p- data presented by Lang et al. [20] (e.g., identical c_p-values for all soft tissues, inappropriate model of temperature-dependent blood perfusion for tumor) are a main source in perfusion modeling and confusion in selective heating of tumors.

For the concept that ‘the treatment of malignancy by HT, the main determinant of selectivity is tumor changes upon heating blood flow’ [21], tumor BF is believed to play the principal role in hyperthermic oncology since it critically determines convective heat dissipation and thus the ability to heat the tissue. However, tumor BF before and upon clinically relevant mild HT exhibits pronounced intratumor (spatial and temporal) and tumor-to-tumor variability which are not predictable, especially during a longer treatment period. In individual tumors even divergent BF changes during treatment sessions have been observed (for further details see [10]).

TBF changes in patients with cancer treated with adjuvant mild HT may be quite different from those seen in fast-growing, low-flow rodent tumors upon heat treatment [10]. TBF changes in patient tumors will depend on the tumor size, tumor type, location, the basal flow rate compared to the flow rate in the surrounding tissue(s), the heating-up rate and steady-state HT level achieved, the duration and number of HT sessions, and whether primaries, metastatic tumors or recurrent lesions are treated. When clinically relevant HT is applied as an adjuvant to established treatment modalities, TBF may change in non-predictable directions, and to different extents and durations. Due to these imponderables, restrictions in tumor BF cannot be the (and only) decisive parameter for a quasi-selective heating of cancerous tissues.

In this review article, we suggest another basic, possibly more robust parameter which is distinctly different in normal tissues and cancers, and which substantially impacts heat deposition: free water content. In general, water content (‘hydration state’) of normal tissues is typically ≤80 wt.% (except for cerebral gray matter, testes, fast-growing placental and fetal tissues [22]), whereas water contents in malignancies are distinctly above 80 wt.%. High water contents in neoplastic tissues were first recognized in the late 1940s [23], and confirmed by gravimetric methods, NMR, Raman and terahertz (THz) spectroscopy (for a recent review see [24]). This biophysical or physicochemical ‘hallmark’ of cancer (mostly coinciding with an increase in the volume of the extracellular space; see Chapter 3.1), has been widely under-rated or even neglected. Due to intensified microvascular leakages during therapeutic HT, the accumulation of free water further increases [10,25,26]. As a consequence of a higher water content (mainly extracellular), the specific heat capacity (c_p), a key parameter for thermal therapies, is significantly higher than in normal tissues. It is defined as the quantity of energy (heat) to be supplied to (or taken off) per unit mass of a substance (or a biological medium or tissue) in order to increase (or decrease) its temperature by 1 K (or 1 °C) in a thermodynamic process. The SI unit of c_p is [J·g^–1·K^–1]. Water has the highest c_p value of all biological media. Therefore, hyperhydrated cancers are distinctly better heat reservoirs than their corresponding healthy tissues.

Assuming insignificant heat dissipation via superficial perfusion, specific absorption rate (SAR) should be adequately increased in cancer tissue with its higher specific heat capacity according to (1) $$\text{HR}=\text{SAR}/{\mathrm{c}}_{\mathrm{p}}$$(1) in order to achieve similar heating rate (HR) as measured in normal tissue of smaller c_p [11,19,27,28]. This emphasizes the importance to consider tissue-specific values of c_p for predicting tissue heating by absorption of RT, both in kinetics and in extent, and to solve the Pennes' bioheat equation as well [27,28].

Water is ‘omnipresent’ and has the highest specific heat capacity of any liquid and tissue. In pure water, c_p ≈ 4.18 J g^–1 K^–1 for temperatures between 33 °C and 43 °C [29–31]. c_p values decrease about linearly with an increase in salinity of sea water [32,33], reaching about c_p ≈ 4.13 J g^–1 K^–1 for isotonic NaCl solution [31].

In addition, the generally higher water content in malignancies leads to a higher thermal conductivity [34–37], a higher diffusivity [38,39] and an increase in electrical conductance [40,41].

2. Interactions of electromagnetic waves with water and aqueous solutions

2.1. Relevant properties of pure water and aqueous solutions

Each water molecule (H₂O) consists of a double-electronegative oxygen ion (O^2–) which is elastically bonded with two protons (H⁺). It forms an electric dipole of 104.5° in angle, of ≈275 pm in diameter, and of O-H bond lengths of 95.84 ± 0.06 pm. The mass balance center is located on the symmetry axis of the molecule at ≈6.5 pm distance from the center of the oxygen ion. In the liquid state of aggregation, water molecules are interlinked among each other by hydrogen bonds and by forming of clusters [42,43].

In aqueous solutions, water dipoles are electrostatically interlinked with cations and anions of dissociated substances by hydrogen bonds (hydration) forming hydration spheres of ions. Dielectric properties of aqueous solutions, therefore, depend on the concentration of dissociated substances [44].

These properties are fundamental to the key role of water for tissue heating upon absorption of electromagnetic RT of different wavelength (λ) ranges, e.g., infrared RT (IR, 0.78 µm ≤ λ ≤ 1.0 mm), microwaves (MW, 1.0 mm ≤ λ ≤ 1.0 m), and radiofrequencies (RFs) within the sub-ranges of very high frequencies (VHF, 1.0 m ≤ λ ≤ 10 m) and of high frequencies (HF, 10 m ≤ λ ≤ 100 m) up to wavelengths of about 37.5 m. These wavelengths correspond to the following frequencies (ν): 384 THz ≥ ν ≥ 300 GHz (IR), 300 GHz ≥ ν ≥ 300 MHz (MW), 300 MHz ≥ ν ≥ 30 MHz (VHF) and 30 MHz ≥ ν ≥ 3 MHz (HF) [45–50].

2.2. Heating by absorption of infrared radiation (IR)

The spectral range of IR is divided into the sub-ranges of IR-A (0.78 µm ≤ λ ≤ 1.40 µm), of IR-B (1.4 µm ≤ λ ≤ 3.0 µm) and of IR-C (3.0 µm ≤ λ ≤ 1 mm) [46,47].

As depicted in Figure 1, the absorption coefficient of water increases with wavelengths up to about five magnitudes within the sub-ranges of IR-A and IR-B, and remains at high levels within the sub-range of IR-C [51–54]. Peaks at characteristic wavelengths result from three fundamental vibrations of single water molecules induced by absorption of RT within the IR-A and IR-B sub-ranges: (a) O-H symmetric stretching (v₁, at 0.94, 1.39 and 2.73 µm), (b) O-H asymmetric stretching (v₃, at 0.91, 1.34 and 2.56 µm) and (c) H-O-H bending (v₂, at 2.14, 3.17 and 6.08 µm). Cooperative combinations of v₁, v₂ and v₃ cause superposition of peaks and overtones [43,51–53].

Figure 1. Spectral absorption coefficient of liquid water as a function of wavelengths within the spectral range of infrared radiation with sub-ranges infrared-A (IR-A), infrared-B (IR-B) and infrared-C (IR-C) [51–53]. Spectral peaks and their extents are caused by basic vibrations of water molecules (v₁: symmetric O-H stretching, v₂: H-O-H bending, v₃: asymmetric O-H stretching, L₁: minor libration, L₂: major libration) and by their superposition and overtones (IR-A and IR-B), as well as by cluster/collective vibrations due to H-O ··· O stretching/bending (IR-C) [54–57]. Extents of horizontal boxes mark wavelength ranges of respective vibration types (Dashed line supplements data of the spectral absorption coefficient within 0.5 μm and 0.78 μm of the spectral range of visible radiation (VIS) for additional information).

In the sub-range of IR-C, the absorption spectrum includes 4 prominent maxima which are due to the induction of vibrations of single water molecules by bending alone at 6.08 µm, by both, bending (v₂) and libration at 4.65 µm (L₂), and by libration alone at 15 µm (L₂) and at 25 µm (L₁) [51–53].

In addition, two types of collective vibration occur in liquid water due to hydrogen bonds (H – O ··· O) between water molecules and formed clusters. Both types of collective vibration, the hydrogen bond stretching (maximum at about 55 µm) and the hydrogen bond bending (maximum at about 200 µm), result in broad absorption bands which are responsible for high values of the spectral absorption coefficient between wavelengths of about 30 µm and 1.0 mm [51–54].

2.3. Dielectric heating by absorption of microwaves (MW)

Dielectric heating of tissues results from frictional heat generated through enforced rotations of the water-dipoles by absorption of MW-RT (frequencies: 300 MHz ≤ ν ≤ 300 GHz). These motions aim to adjust the orientation of each dipole with the polarization of the electric field altering according to the frequency of applied microwave RT. However, adjustment of dipoles is increasingly delayed (in relation to phase angle of the electric field) with rising frequency applied, and extends into the range of relaxation time of water molecules. As a consequence, complex relative permittivity (ε_r) of tissue changes with angular frequency (ω = 2πν) according to (2) $${\epsilon }_r\left(\omega \right)={\epsilon }_r\prime \left(\omega \right)-i{\epsilon }_r″\left(\omega \right)$$(2) where i² = –1, ε_r'(ω) = ε_r∞ + (ε_rs – ε_r∞)/(1 + ω²τ²), and ε_r''(ω) = (ε_rs – ε_r∞) · ωτ/(1 + ω²τ²)

(ε_rs – the static permittivity, ε_r∞ – the electronic part of relative permittivity extrapolated for ‘infinite’ high frequencies and τ – the Debye relaxation time) [45,58].

The real part ε_r'(ω) quantifies the storage of external electric field energy as a function of frequency. The imaginary part iε_r''(ω) characterizes the dielectric loss of tissues due to frequency-dependent energy absorption and generation of frictional heat. It is proportional to the electric conductivity (σ) according to (3) $$\sigma \left(\omega \right)=\omega {\epsilon }_0{\epsilon }_r″\left(\omega \right),$$(3) where ε₀ ≈ 8.86 · 10^–12 F m^–1 (permittivity of the vacuum) [45].

Here, the quantity ε_r''(ω) is used to define ‘dielectric loss’ which is in agreement with cited data [44,59–61]. {Please note that this is in contrast to definitions by other authors, such as the ratio ε_r''(ω)/ε_r'(ω) [6] and the ‘loss tangent’ tan ε_r''(ω)/ε_r'(ω) [59] which additionally consider frequency-dependence of the real part ε_r'(ω)}.

τ is determined by inertia of water molecules (due to own weights and interlinks with other molecules via hydrogen bonds), and declines with rising water temperature T (due to a related increase of thermal molecular vibrations) according to Debye [58]: (4) $$\tau =4\pi \eta r^3/\text{kT},$$(4) where k ≈ 1.380 · 10^–23 Ns m^–1 is the Boltzmann constant, r ≈ 137.5 pm is the molecular radius of water, and η is the dynamic viscosity of water [42,45].

Using η ≈ 0.7 mNs m^–1 at T = 310 K (37 °C) and η≈0.58 mNs m^–1 at T = 320 K (47 °C) [62] calculated values for water are: τ ≈ 5.4 ps at T = 310 K (37 °C), and τ ≈ 4.3 ps at T = 320 K (47 °C). More precise data have been provided by Lunkenheimer et al. on the basis of several techniques for measuring broadband dielectric spectra: τ ≈ 6.0 ps at T  =310 K (37 °C), and τ ≈ 5.3 ps at T = 320 K (47 °C) [59].

Maximum values of ε_r'' are shown at Debye peak frequency ω_p = τ^–1 (or equivalently: ν_p = (2π τ)^–1). This means that the time-delay of dipoles reaches its maximum at this frequency, and this is equivalent to the maximum of both, the dielectric loss in the water and the spectral maximum of microwave absorption. Moreover, as relaxation time declines with temperature increments (see Equation (4)(4) $$\tau =4\pi \eta r^3/\text{kT},$$(4) ), the Debye Peak frequency increases equivalently. In the same way, the extent of the maxima of dielectric loss declines with the increase in water temperature. For experimental data, see Figure 2, curves 2 and 3 [59].

Figure 2. Dielectric loss ε" of pure liquid water at temperatures of 2 °C (curve 1), 37 °C (curve 2) and 47 °C (curve 3), and of intracellular water at 1 °C (curve 4, open circles) as a function of frequency between 300 MHz and 20 THz [59,63]. Relaxation times decreased in pure water from τ ≈ 18 ps at 2 °C to τ ≈ 6 ps at 37 °C, and to τ ≈ 5.3 ps at T = 47 °C [59]. Debye Peak frequencies at ν_p ≈ 9 GHz (2 °C), at ν_p ≈ 26 GHz (37 °C) and at ν_p ≈ 30 GHz (47 °C), and extents of peak maxima of dielectric loss at ε'' ≈ 40% (2 °C), at ε'' ≈ 36% (37 °C) and at ε'' ≈ 34 (47 °C) [59]. Respective data for intracellular water at 1 °C: τ  ≈  20 ps, ν_p ≈ 8 GHz, and ε'' ≈ 27 (at maximum) [63].

For frequencies above that of the Debye Peak frequency, inertia of water molecules becomes more and more noticeable, and thus dielectric loss decreases with increasing frequency to insignificant values within the sub-range of IR-C (Figure 2). Therefore, heating due to enforced rotations of water dipoles becomes more and more ineffective, whereas cluster vibrations effectively contribute to water heating, as described above.

Dielectric loss of intracellular water shows a similar spectral distribution as measured in pure liquid water of comparable temperature. However, its maximum is significantly smaller. For experimental data, see Figure 2, curves 1 and 4 [59,63].

2.4. Dielectric heating by absorption of radiofrequencies (RF): very high frequencies (VHF) and high frequencies (HF)

Mechanisms of dielectric heating of aqueous solutions, biological media and of tissues using VHF and HF are the same as described above for microwaves. Heating results from oscillations of ions interlinked with water dipoles and of free electrons caused by applied RFs [6,48]. Due to inertia of the hydration spheres, the phase difference between the alternating electric field and oscillations increases with frequency. This results in a dielectric loss and in the generation of frictional heat. As depicted in Figure 3, dielectric loss in different tissues and in NaCl solutions (salinity between 0.5% and 0.9% w/v) increases to a similar extent with decreasing frequency [60,64]. In addition, data in Figure 4 show that dielectric loss caused by microwaves and by RFs also increases with (increasing) water content of tissues [61,65].

Figure 3. Dielectric loss ε" in splenic hematoma (curve 1, squares), intestinal leiomyosarcoma (curve 2, dots), hemangiopericytoma (curve 3, stars)) and in NaCl solution of different salinity: 0.9% w/v (curve 4, open triangles), 0.5% w/v (curve 5, solid triangles) as a function of frequency between 10 MHz and 20 GHz. Data for NaCl solutions were measured by Gadani DH et al. [60]. Data for splenic hematoma and for both tumor tissues were calculated using data of conductivity measurements performed by Schepps and Foster [64] according to Equation (3)(3) $$\sigma \left(\omega \right)=\omega {\epsilon }_0{\epsilon }_r″\left(\omega \right),$$(3) .

Figure 4. Dielectric loss ε" in normal tissues (blue symbols: fat (triangles, upward), bone (triangles (downward), lung (dots), muscle (stars)) and in NaCl solution (salinity = 0.4% w/v, black hexagon) at frequencies of 13.56 MHz (curve 1, solid symbols) and of 434 MHz (curve 2, open symbols) as a function of water content of tissues. Data for dielectric loss were calculated using data of conductivity measurements by Kok and Crezee [65] according to Eq. 3(3) $$\sigma \left(\omega \right)=\omega {\epsilon }_0{\epsilon }_r″\left(\omega \right),$$(3) . Data for water content according to Pethig and Kell [61].

3. Water content and specific heat capacities of malignant tumors vs. corresponding normal tissues

3.1. Methodology of data collection

For this updated review, systematic literature reviews of tissue water contents and specific heat capacities were conducted (published before 28 February 2022) to provide a comprehensive data overview based on original manuscripts, reviews and databases. We searched PubMed, Medline, Web of Science, Embase databases, Scopus, ScienceDirect and ResearchGate. The search terms included: water content, human tissues and body fluids, specific heat capacity, HT treatment modeling, tumor/cancer hyperhydration and thermophysical properties.

3.2. Differential water content of normal and cancerous tissues

As already indicated in the Introduction section, cancer tissues generally have a distinctly higher water content compared to their corresponding/homologous tissues (mean water content of body fluids, selected normal tissues and biological media are listed in Tables 1 and 2; for data collections of water contents of healthy tissues see [35,99,100,112,113]). Increased water content of malignant tumors has been proposed as a ‘marker’ for noninvasive tumor detection, providing precise localization of the lesion and information on the adequacy of surgical margins [114]. In addition, tissue water percentage has been suggested to be a prognostic biomarker of early cancer recurrence [101].

Table 1. Mean water content (C_w) and specific heat capacity (c_p) of liquid water, body fluids, normal human tissues (selection) and biological media*.

Tissues etc.	Cw [wt.%]	cp [J·g^–1·K^–1]
Water (33–43 °C)	100	4.18
Agar (2.5% w/v)	97	4.13
Blood, plasma	91	3.9
Whole	80	3.6
Placenta	87	3.8
Egg white	85	3.8
Testis	85	3.8
Brain, gray matter	83	3.7
Whole brain	78	3.65
White matter	70	3.6
Kidney	79	3.7
Prostate	79	3.65
Lung, parenchymal	79	3.9
Spleen	78	3.6
Uterus	79	3.65
Eye, cornea	77	3.6
Lens	66	3.2
Cartilage	75	3.6
Myocard	75	3.7
Liver	74	3.6
Skeletal muscle	73	3.6
Pancreas	73	3.55
Mammary, gland	60	3.0
Adipose	50	2.3
Skin**	63	3.4
Stratum corneum	20	2.0
Epidermis	75	3.6
Hypodermis	30	2.7
Body, whole	61	3.3
Connective tissues	60	3.4
Tense	33	2.4
Lysozyme solution	28	2.3
Adipose tissue	22	2.35
Breast (postmen.)	21	2.2
Bone, cortical	13	1.65
Yellow marrow	15	2.0
Red marrow	40	2.65
Tooth, dentin	10	1.5
Enamel	1–2	0.7

*References describing the water content of individual tissues and biological media are listed in Section 3.2, references for specific heat capacities are listed in Section 3.3.

For standard deviations and ranges of water contents see [35] (number of studies: 1–6). For standard deviations and ranges of c_p-values see [35,66,67] (number of studies: 1–6).

**Water content rises in the epithelium from the stratum cornea to the basal layer (15–70 wt.% [68]).

Table 2. Mean water content (C_w) and specific heat capacity (c_p) of normal human tissues vs. corresponding tumor tissues (selection).

Tissues [References]		Cw [wt.%]	cp [J·g^–1·K^–1]
Breast	Normal (whole breast)	53	3.0
[69–83]	Cancers	≈ 80	3.85
Brain	Normal (whole brain)	78	3.65
[84–89]	Primary malignancies, metastases	88	3.95
Skin	Normal	61	3.4
[68,90–98]	Cancers	82	3.75
Lung	Normal	79	3.5
[66,82,99]	Cancers (primary, metastatic)	85	3.8
Liver	Normal	74	3.6
[100–104]	Hepatomas	≈ 80	3.8
Pancreas	Normal	73	3.55
[103,105,106]	Cancers	84	3.8
Prostate	Normal	79	3.65
[107–111]	Cancers (Gleason 1)	80	3.65
	Cancers (Gleason 2–5)	76	3.5
[103]	Cancers (all)	84	3.8
Kidney	Normal	79	3.7
[103]	Cancers	84	3.8

Values are averaged means.

The generally higher water content in cancer tissues is mostly due to plasma leakage from the immature, hyperpermeable tumor microvessels arising during tumor angiogenesis and the absence of an adequate lymphatic drainage, both of which result in an expansion of the interstitial space [115,116]. Another pathogenetic factor leading to hyper-hydration of malignant tumors is passive hyperemia (vasocongestion, i.e., an increase in microvascular blood volume) such as is seen in inflammatory breast cancer, high-grade gliomas [117], non-small cell lung cancer, and various types of non-melanoma cutaneous malignancies.

Increased water content of experimental cancers has consistently been reported (usually in the context of detection methods initially involving tissue desiccation and gravimetry, then magnetic resonance techniques, and more recently Raman and terahertz spectroscopy and imaging. The generally higher water content of primary and metastatic cancers, highly proliferative embryonic and fetal tissues is mostly due to an expansion of the extracellular space and passive hyperemia [22,101,117–119]. In highly proliferative placental, embryonic, fetal and testicle tissues, intracellular hyperhydration greatly contributes to increased water contents.

Differential water contents have been extensively described for normal tissues (Table 1) and malignancies (Table 2):

1. normal breast (whole pre- and post-menopausal breast, fibro-glandular and breast adipose tissues) and breast cancers [69–81];

2. healthy brain (with specific data for gray and white matter structures), and primary and metastatic brain tumors [84–89];

3. normal skin and malignant skin tumors [68,90–98];

4. normal tissues and cancers of the alimentary tract, liver and pancreas (e.g., oral cancer vs. normal mucosa [120], gastric cancer [121], colorectal cancer [122], normal liver and liver metastases [102], hepatocellular carcinomas (HCCs, hepatomas) [101,105], pancreatic cancer [106]. Note: In HCCs, percentual water content increases with histological grades and thus can be used as a potential biomarker for the diagnosis and prognosis of HCCs [101];

5. adipose tissue [98,123,124];

6. musculo-skeletal system (e.g., skeletal muscle [98,125,126], tendon [127], cartilage [128], bone [98]);

7. in prostate cancers, the interstitial volume is enlarged compared to the peripheral zone of normal prostate [107,108]. Controversially, the water content (derived from T1 and T2 measurements in prostate cancers of Gleason grades 2–5) is reported to be less than in peripheral and transition zones of normal prostate tissues [109–111]. In a recent article, Agafonkina et al. [103] have communicated a mean water (moisture) content for healthy prostate of 82% (range: 79.2%–85.5%) and for prostate cancer 84% (range: 79.4–86.3%).

3.3. Differential specific heat capacity of malignant tumors and corresponding normal tissues

As a consequence of generally higher water contents, malignant tumors have a higher specific heat capacity (see Tables 1 and 2; for comprehensive databases and literature surveys see [34,35,66,67,82,99,104,129–131]).

Note: (a) During HT treatment of breast cancers, one is often confronted with an increased BF in the tumor compared to normal, surrounding tissue [15,83]. Furthermore, in the treatment field, different tissue types and tissue layers are exposed, to varying degrees, to electromagnetic heating (see Table 3). This complex situation must be considered when quantifying temperature distributions using computational modeling due to different specific heat capacities, water contents, BF rates (and microregional changes thereof during treatment), and thermal conductivities of the tissue layers exposed. (b) The average specific heat capacity for prostate cancers listed in Table 2 does not consider the generally lower water contents in high-grade prostate cancers, as discussed above. In addition, specific heat capacities have been reported to vary considerably with the extent of cancerous involvement [132].

Table 3. Water contents (C_w) and specific heat capacities (c_p) of the multilayer tissue structures exposed in hyperthermia treatment of breast cancers.

Tissue layer	Cw [wt.%]	cp [J· g^–1· K^–1]
Skin
Stratum corneum	20	2.0
Epidermis	75	3.6
Dermis	60	3.3
Subcutis	30	2.7
Breast, gland	60	3.0
Adipose tissue	50	2.3
Muscle	73	3.6
Breast cancer	80	3.85

Values are averaged means, see data in Table 2 [68,83].

3.4. Correlation between specific heat capacity and water content in normal tissues and corresponding malignancies

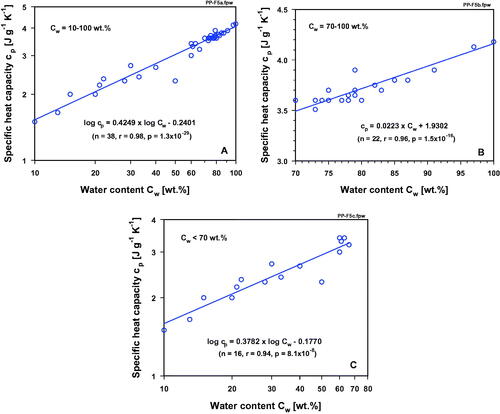
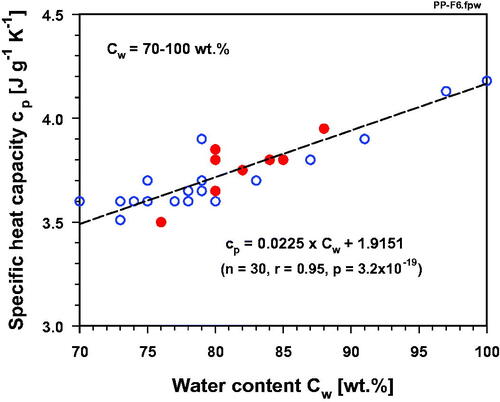
In order to demonstrate the stringent correlation between water content and specific heat capacity (c_p) in normal tissues (see Figure 5(A)), c_p -values are plotted over a large range of water contents (C_w = 10–100 wt.%, values taken from Table 1). In a log-log graph, the correlation can best be described by a linear function. When this correlation is separately presented for high-water-content tissues (C_w ≥ 70 wt.%) and low-water-content tissues (C_w < 70 wt.%), a clear linear relationship is evident only for the higher water contents (Figure 5(B)), whereas an exponential drop of c_p with decreasing water content can be demonstrated in the tissues having lower-range water contents (Figure 5(C)). For normal tissues an approximately linear correlation between c_p and water content (71–84%) was also described by Cooper and Trezek [133]. A close linear relationship was also discussed by Duck [134] for tissues with a water content higher than that of fat. A linear relationship was also suggested by Takata et al. [135] for calculation of the specific heat capacity of pig skin with known water contents. All malignant tissues listed in Table 1 have water contents > 75 wt.%. These data (red dots in Figure 6) fit into the range of the high-water-content normal tissues, i.e., c_p-values also exponentially rise with increasing water content of malignant tumors. Breast cancers, skin cancers and malignant brain tumors usually contain 10–27% more water than their surrounding tissues, and thus must be considered as ‘high-heat capacitance tissues’ [83]. Neglecting these clinically relevant differences and using simplified assumptions is, therefore, not justified if, for example, SAR values have to be assessed or temperature distributions have to be modeled for optimizing HT treatment sessions. In this context, we have to remember a quotation of Albert Einstein: ‘Everything should be made as simple as possible, but not one bit simpler’, especially in times of precision medicine.

Figure 5. Specific heat capacity c_p of liquid pure water, body fluids, normal human tissues (selection), and biological media as a function of mean water content within the ranges C_w = 10–100 wt.% (5A), C_w = 70–100 wt.% (5 B), and C_w < 70 wt.% (5C) according to data listed in Table 1.

Figure 6. Specific heat capacity c_p of liquid pure water, body fluids, normal human tissues (selection), biological media (blue circles), and of tumor tissues (selection, red dots) as a function of mean water content within the range C_w = 70–100 wt.% according to data listed in Tables 1 and 2.

4. Conclusion

In general, malignant tumors are ‘high-heat capacitance tissues’ compared to their normal surroundings or corresponding, homologous tissues. This pathophysiological characteristic is due to their higher water content and should be considered as another principal factor in modeling temperature distributions, as higher specific heat capacities preferentially facilitate heat deposition in cancerous tissues. One should therefore not primarily, or even exclusively, focus on unknown, non-predictable and/or heterogeneous BF conditions before, during and changes upon fractionated heating sessions [136,137], as BF cannot be the only predictive and overall dominating factor. High water content, which leads to distinctly higher specific heat capacities, may be a more robust pathophysiological factor, particularly due to the additional hydration of tumor tissues which results from intensified microvascular leakages induced by clinically relevant HT. These considerations are of great practical relevance in the clinical setting.

Acknowledgments

The authors thank Professor A. Graham Pockley, Nottingham Trent University (UK), for linguistic support.

Disclosure statement

The authors declare that this review was conducted in the absence of any commercial of financial relationship that could be constructed as a potential conflict of interest.