3D motion strategy for online volumetric thermometry using simultaneous multi-slice EPI at 1.5T: an evaluation study

Abstract

Purpose

In presence of respiratory motion, temperature mapping is altered by in-plane and through-plane displacements between successive acquisitions together with periodic phase variations. Fast 2D Echo Planar Imaging (EPI) sequence can accommodate intra-scan motion, but limited volume coverage and inter-scan motion remain a challenge during free-breathing acquisition since position offsets can arise between the different slices.

Method

To address this limitation, we evaluated a 2D simultaneous multi-slice EPI sequence with multiband (MB) acceleration during radiofrequency ablation on a mobile gel and in the liver of a volunteer (no heating). The sequence was evaluated in terms of resulting inter-scan motion, temperature uncertainty and elevation, potential false-positive heating and repeatability. Lastly, to account for potential through-plane motion, a 3D motion compensation pipeline was implemented and evaluated.

Results

In-plane motion was compensated whatever the MB factor and temperature distribution was found in agreement during both the heating and cooling periods. No obvious false-positive temperature was observed under the conditions being investigated. Repeatability of measurements results in a 95% uncertainty below 2 °C for MB1 and MB2. Uncertainty up to 4.5 °C was reported with MB3 together with the presence of aliasing artifacts. Lastly, fast simultaneous multi-slice EPI combined with 3D motion compensation reduce residual out-of-plane motion.

Conclusion

Volumetric temperature imaging (12 slices/700 ms) could be performed with 2 °C accuracy or less, and offer tradeoffs in acquisition time or volume coverage. Such a strategy is expected to increase procedure safety by monitoring large volumes more rapidly for MR-guided thermotherapy on mobile organs.

Keywords:

• Thermometry
• registration
• echo planar imaging
• simultaneous multi-slice
• respiratory motion
• thermo-ablation

Introduction

The respiration-induced motion of abdominal organs causes significant challenges to measure accurate MR temperature maps using the proton resonance frequency shift technique [1,2]. This includes motion-related artifacts that induce periodic phase variations, displacement during the acquisition of a given slice, together with in-plane and through-plane displacements between successive acquisitions of the same slice. The timescale of the acquisition is therefore a determinant factor for accurate monitoring of the treatment. Proof of concept of MR thermometry on abdominal organs has been demonstrated with high-intensity focus ultrasound (HIFU) [3,4] or microwave [5] ablation using standard gradient echo imaging at the cost of limited temporal resolution (∼6 s). The use of rapid imaging techniques such as echo planar imaging (EPI) and parallel imaging, combined with real-time image processing techniques was found robust against the intra-scan motion, respiratory-related susceptibility artifacts during free breathing thermal-ablation in the heart [6–8] or liver [9–11]. Segmented-EPI sequence combined with MR pencil-beam navigator [12] for motion tracking or respiratory gating [13] improved the frame update but remain limited in volume coverage (∼1 s, 1–3 slices). Single-shot trajectories drastically reduce the acquisition time (∼100 ms per slices) [9,14] while providing volumetric coverage of the ablation. Recent techniques in MR thermometry in moving organs have also been reported in the literature using either alternative sequence acquisitions or hybrid susceptibility compensation method: direct correction from the k-space measurements of B0 field variation due to respiration has been demonstrated using segmented-EPI [15] and a gated spiral-out trajectory acquisition was combined with multi-baseline approaches [16]. Lastly, the combination of multi-baseline and referenceless techniques (using projection onto dipole fields) has been demonstrated using segmented EPI [17]. However, two pitfalls are not addressed by such techniques. First, even with such fast MR acquisition, the presence of intrascan motion (such as through-plane motion) between adjacent slices may prevent the spatial and temporal continuity of the information contained in a voxel and will ultimately impact the temperature estimate. The latter resulting in temperature oscillating patterns. Secondly, increasing again volume coverage is of major interest to monitor both the targeted region and surrounding healthy tissues during the therapeutic procedure and thus increase patient safety. The size of hepatocellular carcinoma (HCC) varies a lot (from <1 to >10 cm) but standard treatment performed with a single probe under MRI guidance assume a maximum size of 3 cm [18]. During the ablation, thermal conduction in the probe can create temperature elevation in an unwanted area. The use of HIFU energy also requires the monitoring of skin temperature and tissue close to the ribs due to potential reflections and associate unwanted temperature elevation all along the course of the ultrasound waves. Such concerns can be translated in large fov coverage (more than 30 mm) in all directions. Simultaneous multi-slice (SMS) may thus be exploited for MR-thermometry to increase volume coverage at constant time or to reduce acquisition duration for a given volume of interest surrounding the targeted region [19–21] and could reduce such imperfections. Nevertheless, the use of ultra-fast SMS echo-planar imaging (EPI) imaging raises additional concerns. First, combined with in-plane parallel image reconstruction, the reconstructed images may be subject to a reduction of image signal-to-noise ratio (SNR) [19]. Secondly, the reconstructed images may be subject to slice leakage [22], due to imperfect separation of the signal of aliased slices. Considering an acquisition with two slices, one located on the heating, the other distant, this problem would lead to the mixing of the measurement and would imply both a reduction and an overestimation of the temperature estimate, on the respective slices. Although SMS was found robust in recent studies on static phantoms using laser interstitial thermal therapy (LITT) and HIFU [19,21], the presence of motion could increase slice leakage on reconstructed images since the estimation of GRAPPA and SMS operators for image un-aliasing might not occur as the same respiratory phase. It is therefore essential to investigate whether temperature measurement is valid in such a context and up to what value of a multiband acceleration.

The present study performed at 1.5 T investigated i) the impact of multiband (MB) acceleration for monitoring temperature evolution ii) the impact of a 3D registration workflow to reduce potential artifacts in temperature imaging related to out-of-plane motion. The performance of the sequence was evaluated in terms of the temporal standard deviation of temperature (or temperature uncertainty), potential false-positive heating and repeatability with multiband acceleration factors of 1, 2 and 3.

Methods

All experiments were performed on a 1.5 T clinical MRI (MAGNETOM Aera, Siemens Healthineers, Erlangen, Germany).

Acquisition sequence on phantom

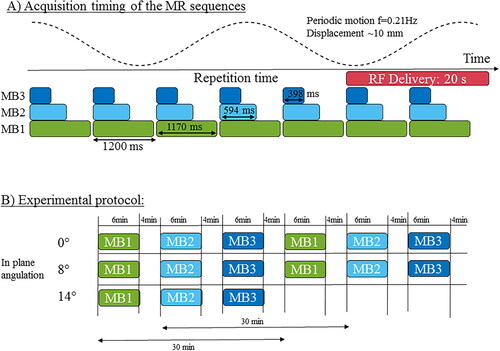
12 slices of a prototype 2D single-shot SMS-EPI were acquired every 1.2 s over a total duration of 6 min (Figure 1(A)). Three different MB factors (1, 2, and 3) were combined with in-plane parallel imaging (GRAPPA acceleration), a factor of 2 with 50% oversampling in the phase encoding direction was set. Therefore, the slice acceleration factor being the product of in-plane acceleration and multiband acceleration range from 2 to 6. Sequence parameters were: TE = 19/27/28 ms and TR = 955/671/445 ms for MB 1, 2 and 3 respectively, FOV = 180 × 180 mm², spatial resolution 1.6 × 1.6 × 3mm³ voxel size, FA = 60°, 6/8 partial Fourier and pixel bandwidth = 1565 Hz/pixel, slice gap 10% (0.3 mm). The phase encoding direction was set in the right-left direction. The frame update between successive dynamic acquisitions (1.2 s) was kept identical regardless of the multiband acceleration factor. Two body matrix (2 × 18 channels in reception) surrounding the gel were set both parallel to the motion direction in a sagittal orientation, allowing the activation of 24 receiver channels for image reconstruction. To simulate a respiratory motion, a cylinder shape gel phantom composed of 3% agar was positioned on a motor-driven platform to generate a horizontal oscillating translation of the sample with an amplitude of 10 mm at a frequency of 0.21 Hz to mimic the typical respiratory rate of patients at rest. The plane perpendicular to the main axis of the cylinder corresponds to the coronal plane in the conventional orientation of the human body (z being the axis of the tunnel, (x,y), (x,z), (y,z) are the transverse, coronal and sagittal planes, respectively). The motor-driven platform was moving in the coronal plane in the head-foot direction to mimic the respiratory motion. The RF needle was inserted parallel to the main axis of the gel phantom. To simulate the out-of-plane motion, the acquisition plane was tilted by 0°, 8° and 14°. The rotation axis was the (x) axis perpendicular to the sagittal plane (y,z). Figure 1(B) shows the acquisition protocol: each acceleration factor was successively performed, for a slice plan tilted at 0° (N = 2), 8° (N = 2) and 14° (N = 1). A delay of at least 4 min was observed between consecutive thermometry sequences to ensure total cooling of the gel to room temperature resulting in a 30 min delay between measurements with the same multiband acceleration factor.

Figure 1. Acquisition timing and experimental protocol. (A) Multi-slice temperature images were dynamically acquired every 1.2 s for 6 min. Three different multiband accelerations were tested, with a minimum acquisition time of 398 ms. To simulate a respiratory motion, a periodic displacement of the phantom (f = 0.2 Hz) was generated with an amplitude of 10 mm. (B) The slice position was rotated from 0° (in-plane motion), 8°, 14° to investigate the influence of an out-of-plane motion on the thermometry results. Each acquisition set was repeated twice (except for 14° rotation) with a minimum delay of 4 min between consecutive acquisitions, to investigate the repeatability of the measurement.

Acquisition sequence on a volunteer

This study promoted by the Center Hospitalier Universitaire De Bordeaux (CHUBDX2017/21) was approved by the regional Protection of Persons Committee under the reference ID-RDB: 2017-A03313-50. The subject gave written informed consent and was conducted in accordance with the principles embodied in the Declaration of Helsinki. Twelve temperature slices in coronal orientation were acquired sequentially using the same sequence as the phantom study. The two body matrix were set in a coronal plane in the spine and front location as in a conventional abdominal scan, allowing the activation of 36 receiver channels for image reconstruction. To avoid the aliasing of the patient’s arms, two saturation bands were positioned on each side of the volunteer. The phase encoding direction was set in the right-left direction. Other sequence parameters were kept identical: TE = 27/27/28 ms and TR = 1430/726/726 for MB1, 2 and 3 respectively, FOV = 200 × 200 mm², spatial resolution 1.6 × 1.6 × 3mm³ voxel size, FA = 60°, 6/8 partial Fourier and pixel bandwidth = 1565 Hz/pixel, slice gap 10% (0.3 mm). The time between successive dynamic acquisitions (1.43 s) was kept identical regardless of the multiband acceleration factor. To characterize the respiratory motion of the volunteer, motion amplitude was estimated using two intensity profiles located on the liver dome and the gall bladder. The respiratory rate was estimated using the Fourier transform of the first motion descriptor (see Thermometry calculation).

RF-ablation device

Two MR-compatible RF electrodes were inserted vertically into the gel and connected to a programmable RF generator (Image Guided Therapy, Pessac, France) located outside the Faraday cage. RF energy was delivered at 20 W during 30 s, after acquiring 40 dynamic acquisitions (or repetition) of the thermometry sequence to create an atlas of reference images for correcting phase oscillations related to respiratory-induced susceptibility changes.

Image reconstruction

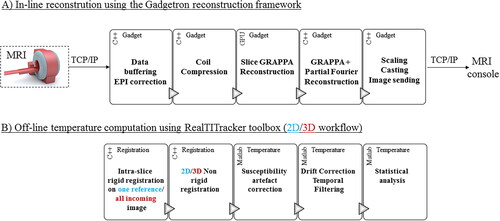
The raw data files were transferred on-line and converted into ISMRM Raw Data format [23]. The conversion and reconstruction support both the prototype version of Siemens and the CMRR C2P version [24]. The SMS factor, blipped caipi factor, and the interleaved acquisition pattern was integrated into the ISMRMRD format. SMS-EPI reconstruction could thus be performed in-line in the Gadgetron framework [6]. A schematic block diagram of the implementation is shown in Figure 2(A). EPI ghost-Nyquist correction and coil compression were implemented to compute phase navigator and coil reduction per stack of slices instead of independently for each slice. Slice-aliased images were separated using a standard slice-GRAPPA algorithm [25] (5 × 5 kernel, neither leak block [22] nor dual kernel [26,27] was used). Then, the Gadgetron implementation of GRAPPA and partial Fourier (PF) reconstruction were applied to correct for phase-encoding undersampling in image reconstruction. The grappa kernel was estimated based on a reference scan including 24 lines per slices played once at the beginning of the acquisition. The navigator for ghost-Nyquist correction are 3-lines navigator with an inverted readout (RO) gradient. They were played before the GRAPPA and before the MB reference scans (both acquired once) and then played for every incoming dynamic acquisition. The use of the specific phase navigator per slice being mandatory for optimal image reconstruction, the navigator of reference scans (GRAPPA and MB scans) were thus used for every incoming dynamic acquisition whatever the motion state.

Figure 2. In-line reconstruction and temperature calculation. (A) In-line reconstruction was performed using the Gadgetron framework. A schematic block diagram of the implementation is presented (a Gadget being a reconstruction module in which data passes through). EPI ghost-Nyquist correction and coil compression were implemented to compute phase navigator and coil reduction by a stack of slices instead of independently for each slice. Average and specific phase navigators were up-streamed to the reconstruction Gadget. Slice-aliased images were separated using a slice-GRAPPA algorithm already available. Both CPU and GPU versions of the pipeline were implemented. (B) Temperature calculation was reprocessed offline: two different workflows were investigated: while the 2D workflow corrects the intra-slice motion only for the first reference image, the 3D workflow corrects the intra-slice motion for each incoming volume. Then correction of residual in-plane respiratory motion and associated susceptibility variations and compensation of spatial-temporal drift were used to compute temperature maps.

Registration

The large volumetric coverage (12 adjacent slices, covering 36 mm in the slice direction) at each dynamic acquisition allowed us to consider each stack of 2D images as a pseudo-3D volume. In order to do that, two motions in the slice direction (Figure 3) must be considered:

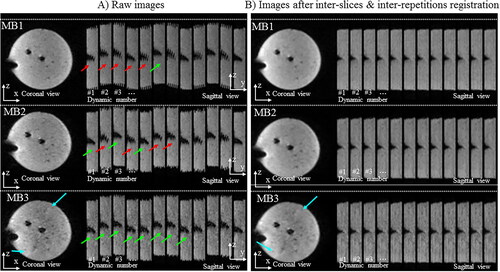
Figure 3. Influence of the multiband acceleration in presence of translation motion. Experimental data obtained on a moving agar gel phantom with three different MR-acquisitions. A periodic motion along y (vertical direction on images) was applied on the gel. One repetition in the (x,y) plane and twelve successive repetitions in the (x,z) plane are displayed for multiband (MB) acceleration factors of 1, 2, and 3 (TR= 955/671/445 ms) without (A, left panel) and with (B, right panel) 2D motion correction workflow.

• The inter-repetition motion between successive pseudo-3D volumes that depict a global oscillatory pattern.

• The intra-repetition motion within each pseudo-volume corresponding to the displacement between individual slices acquired in successive shots during the same dynamic acquisition. This displacement is either continuous or in a zigzag pattern depending on the MB acceleration factor.

To account for the effect of out-of-plane motion, two algorithms were implemented and tested. First, a 2D approach that does not correct for out-of-plane motion and a second approach utilizing a 3D motion correction algorithm to take into account for out-of-plane motion.

2D workflow (no out-of-plane motion correction):

1. The intra-repetition motions of the image of reference were compensated using a rigid algorithm that minimizes the displacement between adjacent slices. This process was only performed once.

2. Non-linear 2D motion compensation was performed independently on each slice for all incoming dynamic acquisitions to compensate for the inter-repetition motion. Horn and Schunck (H&S) with a principal component analysis (PCA) based optical-flow algorithm [28] from the RealTITracker free toolbox [29,30] previously evaluated for rapid thermometry [31] was used.

3D workflow:

1. The intra-repetition motions of all images were compensated using a rigid algorithm that minimizes the displacement between adjacent slices. This process was performed at each dynamic acquisition and resulted in a pseudo-3D volume.

2. Non-linear 3D motion compensation was performed on the pseudo-3D volume for all incoming dynamic acquisitions to compensate for the inter-repetition motion. In this case, the presence of out-of-plane motion between the up and down phase of the respiratory motion could be measured and compensated. A 3D H & S optical flow from the RealTITracker free toolbox was used.

The registration is used for different purposes in the study. The 2D approach was applied on different multiband acquisition to freeze the motion to ease the comparison of multiband acceleration. Secondly, the 2D and 3D approach were applied in multiband acquisition with a tilted acquisition plane to measure the impact of out-of-plane motion. For each case, the motion correction approaches were evaluated qualitatively by visual inspection and quantitatively by computing the RMSE between the registered images and the reference image over 60 dynamic acquisitions.

Thermometry calculation:

Correction of respiratory-induced susceptibility artifacts was then performed using a parameterization of the phase using a PCA on a pixel-by-pixel basis [32,33]. The approach is divided in two steps: a learning phase that estimate the influence of displacement on phase susceptibility using a model parametrization and an interventional step in which, based on the actual motion state, the phase correction (noted P_correction) is estimated and subtracted from the current temperature image to remove the motion-induced susceptibility artifacts. In the learning phase, a PCA was applied on a collection of motion fields to get motion descriptors (noted as D_i). Then, a first-order variation of local phase changes due to motion is considered and can be written as a linear combination of motion descriptors and a set parameterized magnetic field model (noted as B_i). During the intervention, the largest PCA-based motion descriptors were estimated from the current motion field. In the presence of non-linear 3D motion compensation, this parameterization was extended in the slice direction to model the phase in 3D. The dimension of the PCA basis decomposition (i.e., number of eigenvectors and associated eigenvalues) was set to 15. $$P_{\mathit{correction}}\left(x,y,z\right)=\sum _{i=0}^{i=N-1}{D}_i{\mathrm{B}}_i\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)+{\mathrm{B}}_N\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)$$

Spatial-temporal drift correction and temporal filtering was also extended in 3D, based on the initial implementation [6]. The correction assumes a spatiotemporal first-order polynomial function. At each time step, 3 binary labels are computed and combined using their intersection in a final binary label. The first label masked the low SNR voxels using the averaged magnitude images. The second label masked the low uncertainty voxels with the temporal standard deviation of temperature (<3 °C). The third label masked the high-temperature values using the current temperature image (<4 °C). Then, using a temporal sliding window of 20 dynamic acquisitions, the coefficients (a, b, c, d, e) of the first-order polynomial function are estimated at each time step to compute the temperature drift map and subtract to the current temperature map. $$\mathit{Drif}\mathrm{t}\left(x,y,z,t\right)=a.x+b.y+c.z+d.t+e$$

Analysis of temperature data:

The temporal standard deviation of temperature σ(T) was computed in each pixel from all slices over the first 40 dynamic acquisitions acquired before RF energy delivery. A mask was automatically created on each slice to exclude voxels displaying σ(T) higher than 3 °C. Please note that this methodology includes a bias in the analysis but help to mask the region of interest where the temperature measurement is not acceptable (on the electrode for example). This mask was created once for a given slice orientation and applied to each following acquisition to provide quantitative analysis of temperature data on the same voxels. The distribution of σ(T) values were analyzed on a 15 × 15 ROI located near one RF electrode.

To measure the bias between the two measurements, the root mean square temperature error (RMSE) was computed over 60 dynamic acquisitions during the heating period. Such a metric was used to compare: (i) temperature elevation between static and moving gel conditions for a given multiband acceleration factor, (ii) temperature elevation between different multiband acceleration factors when the gel was moving.

To investigate the impact of a multiband acceleration on temperature elevation, the repeatability of measurements with the 3 multiband acceleration factor was also evaluated using Bland Altman plots. A sequence of six acquisitions on a moving gel with RFA was thus performed in controlled conditions (see protocol in Figure 1(B)). Since the acquisition was not synchronized with the motion, all temperature maps from different acquisitions were not initially registered at the same location. Thus, additional rigid displacement correction was applied on each measurement to register them in a unique position. Then, a common region of interest (ROI) was defined to compare the same location. The final number of voxels in the common ROI was 61 and the analysis was conducted over 60 consecutive measurements during RF delivery, resulting in 3660 points per scatter plot, the number of scatter plot being 9.

Results

Figure 3(A) shows the influence of the multiband acceleration in the presence of translation motion. Raw images on the left panel show both the intra-repetition motion (motion during the same dynamic acquisition) and inter-repetition motion (motion between successive dynamic acquisitions). Translational motion between adjacent slices in the (y, z) plane during the same dynamic acquisition are more pronounced for MB1 than for MB2 and MB3, resulting in visible shifts between adjacent slices (red arrows). Increasing the multiband acceleration factor reduces through-plane misalignment inherent to conventional slice-by-slice acquisition on a moving target (green arrows), but also increases residual aliasing artifacts (blue arrows). The result of the 2D motion compensation algorithms is presented in Supplementary Figure 1 and in Figure 3(B) where all stacks of slices (or pseudo-3D volumes) are registered at the same location regardless of the multiband acceleration factor.

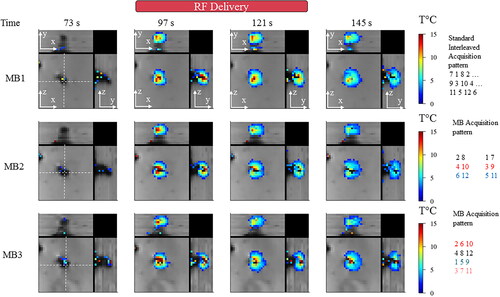
Figure 4 displays representative magnitude images and overlaid temperature maps on a moving agar gel in a zoom-in view close to the electrode, using an orthogonal representation at four different times (before, during, after radiofrequency delivery). The acquisition time for acquiring the 12 slices was 955 ms, 671 ms, and 445 ms for MB1, 2 and 3, respectively. A temperature rise close to 15 °C was reached for each acquisition with a resulting heated region of 10 × 8 voxels at the end of energy delivery. The temperature distribution in the (x, z) and (y, z) planes show similar shapes whatever the MB factor during both the heating and cooling periods. A potential signal leakage between simultaneously excited slices could result in the presence of false-positive temperature spots. To investigate such a typical scenario, the MB acquisition pattern is shown in Figure 4. As an example in the MB2 case, the third stack of slices requires the unfolding of slice #6 located in the vicinity of the electrode and #12 located far from the electrode. The presence of temperature elevation in slice #12 would indicate false-positive temperature spots. Such an artifact was not observed under the conditions being investigated.

Figure 4. Influence of multiband acceleration factor during temperature monitoring. Experimental data obtained on a moving agar gel phantom using three different MR acquisitions with an MB factor of 1, 2, 3 respectively. 3 orthogonal views are reported, the motion is aligned with the z-axis. For each acquisition, two temperature maps during heating and two maps temperature maps before/after heating are shown. RF delivery was sent at dynamic acquisition #70 for 30 s. The (x,y) and (y,z) planes indicate that spatial homogeneity of the heating is preserved into each pseudo-volume. Similar behavior during temperature rise and cooling is noticeable. Slices far from the electrode do not show interslice leakage artifacts. A minimum threshold of 2 °C was used for displaying temperature maps.

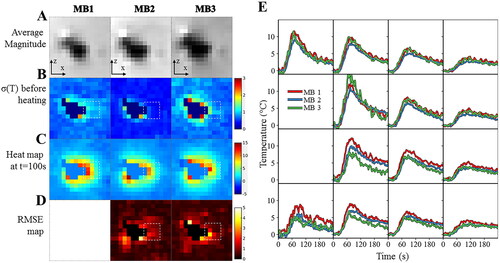
Figure 5 displays the image and temperature maps of slice #8 using a second representation of the previous acquisitions. The temporal standard deviation of the temperature before heating was assessed in an ROI surrounding an electrode and resulted in mean ± std values of 0.7 ± 0.2, 0.5 ± 0.2, 0.8 ± 0.3 °C for MB 1, 2 and 3, respectively. The RMSE per voxel was computed over 60 dynamic acquisitions during the heating period and the associated temperature rises were plotted as a function of time in the right panel (Figure 5(E)). We note a good agreement between temperature curves acquired with different acceleration factors, except for 2 or 3 voxels in the immediate vicinity of the electrode. The maximum temperature change was 13.5, 15.4, 13.0 °C for MB1, 2, 3 respectively while the mean and maximum RMSE in the ROI was 0.66 and 4.40 for MB2 and 0.66 and 4.37 for MB3 respectively.

Figure 5. Influence of multiband acceleration factor. Experimental data obtained on a moving agar gel phantom using three different MR acquisitions with an MB factor of 1, 2, 3 respectively. (A). Average registered magnitude image close to the electrode (B), temporal standard deviation temperature maps (or temperature uncertainty) before heating (C) temperature maps during heating (D), RMSE maps over 60 consecutive temperature images acquired during RF delivery. Results for each acquisition are plotted: 1 (left), 2 (middle) and 3 (right). (E) Temperature evolution in a 4 × 4 kernel (see dashed square line) of voxels located close to the electrode with a multiband acceleration of 1 (in red), 2 (in blue) and 3 (in green). The slice number is 8.

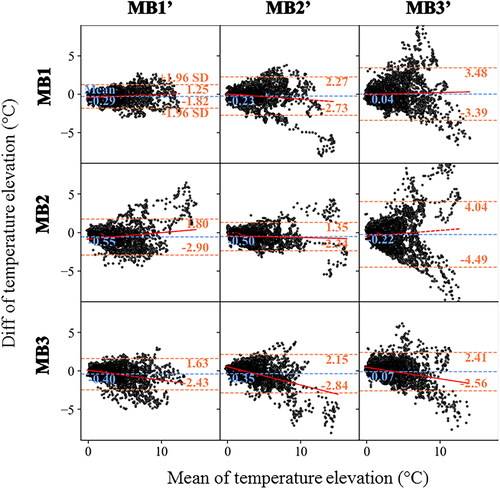
Figure 6 compares the repeatability of two temperature measurements with either the same (diagonal boxes) or a different multiband acceleration factor (off-diagonal boxes). As an example, the top left corner box shows the comparison between two measurements (MB1 vs MB1′) spaced by a 30 min delay. The difference between the two measurements is small, with a 95% uncertainty below 2 °C (1.2 °C/−1.8 °C), regardless of the temperature rise. The fit indicates no bias with a mean value of −0.3 °C. The center box (MB2 vs MB2') shows similar results with no bias (mean = 0.5 °C) but with a greater dispersion. The scatter plot of the bottom right box (MB3 vs MB3') has a larger dispersion (2.4 °C/−2.6 °C) with a proportional bias. The comparison between multiband acceleration factors differ between acquisitions: while the lower triangular boxes (MB1' vs MB2, MB1' vs MB3, MB2' vs MB3) report 95% uncertainty below 3 °C, the upper triangular boxes (MB1 vs MB2', MB1 vs MB3', MB2 vs MB3') report 95% uncertainty up to 4.5 °C and with a larger dispersion.

Figure 6. Evaluation of the repeatability of two measurements in the selected ROI around the electrode with the same or different MB. Experimental data obtained on a moving agar gel phantom using a sequence of six MR acquisitions (2 times for each multiband acceleration of 1, 2, 3) performed in controlled condition. The experimental protocol is presented in Figure 1(B). The resulting temperature rises around the electrode (60 consecutive temperature images acquired during RF delivery) is compared using Bland Altman plots either with the same multiband acceleration (diagonal boxes) or with a different multiband acceleration (off-diagonal boxes). For each plot, the bias (blue dotted lines) and limits of agreement (orange dotted lines) are indicated. The fit of the dots (red lines) indicates either no bias, a fixed bias or a proportional bias.

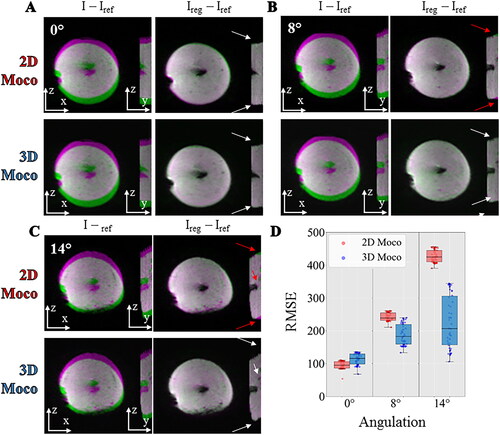
Figure 7 compares the registration workflow (2D vs. 3D) in the presence of out-of-plane motion with different angulations between the motion direction of the gel and the slice orientation. The differences between the reference image and the current image before and after registration were overlaid on the magnitude image using a color code for a given dynamic acquisition. In the absence of out-of-plane motion (0° angulation of the stack of slices, Figure 7(A)), no registration mismatch could be observed for both 2D and 3D workflows. In presence of out-of-plane motion (Figure 7(B,C)), residual misalignments are visible near the electrode and close to the border of the gel using the 2D workflow but disappear using the proposed 3D workflow. The differences are relatively small due to the limited contrast into the gel. The RMSE between the registered images and the reference image over 60 dynamic acquisitions are shown in the box-and-whisker plots displayed in Figure 7(D). The registration accuracy of the 2D workflow was found slightly superior to the 3D workflow for 0° angulation (mean value ± std RMSE 2D: 95.4 ± 11.3, 3D: 113.5 ± 17.1). At 8° angulation, the 2D workflow succeeded in maintaining similar accuracy (mean value ± std RMSE 2D: 241.9 ± 12.3, 3D: 187.9 ± 31.5) while at 14°, the accuracy in RMSE decrease by a factor of 2 while the 3D workflow produced better results (mean value ± std RMSE 2D: 427.2 ± 18.7, 3D: 225.7 ± 79.0).

Figure 7. Influence of motion correction in presence of out of plane motion. Experimental data with a multiband acceleration of 2 obtained on a moving agar gel phantom with the angulation of 0° (A), 8°(B), 14°(C) between the imaging plane and the main direction of the motion. For each, two different registration workflows 2D (top) versus 3D (bottom) are compared by showing the difference between the current image and the reference image before (I–I_ref) and after registration (I_reg–I_ref). The difference is overlaid on the magnitude image using a color code (green-pink). The white and red arrows indicate the absence or the existence of residual misalignments, respectively, close to the electrode or at the border of the gel. RMSE computed over 60 repetitions between the registered images and a reference image are shown (panel D) in a box and whisker plot for 3 different acquisitions on a moving agar gel phantom with an angulation of 0°, 8°, 14°. For each, the 2 different registration workflow 2D (red) versus 3D (blue) are compared.

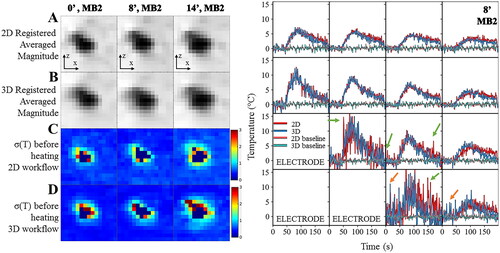
In Figure 8, the temperature uncertainty for the two calculation workflows (2D vs. 3D) in the presence of different angulation were found similar although slightly lower in the 3D case due to the presence of additional interpolation in the slice direction. The temperature curves for the out-of-plane motion of the 8° case, acquired with MB2, were plotted as a function of time in the immediate vicinity of the electrode. Similar temperature evolution of the two workflows was observed during both the heating and cooling period. Nevertheless, the 2D workflow produces typical patterns of temperature artifacts due to residual out-of-plane motion either with small oscillations of the temperature, or larger oscillations close to the RF electrode (green arrows). The 3D workflow provided better compensation by reducing the presence of temperature spikes and oscillations but reduced temperature estimation in other voxels (orange arrows).

Figure 8. Influence of the registration workflow in presence of out-of-plane motion (8°). Experimental data obtained on a moving agar gel phantom using a multiband acceleration of 2. (Right) Registered averaged images (A,B) and temperature uncertainty (C,D) with 2D (A,C) or 3D (B,D) registration for the tilted acquisitions. (Left) Temperature evolution in time close to the electrode with 2D (in red) and 3D (in blue) registration workflow. The acquisition was performed with MB = 2. Green and orange arrows indicate typical patterns of temperature artifacts due to residual out-of-plane motion either with small oscillations or larger oscillations close to the RF electrode.

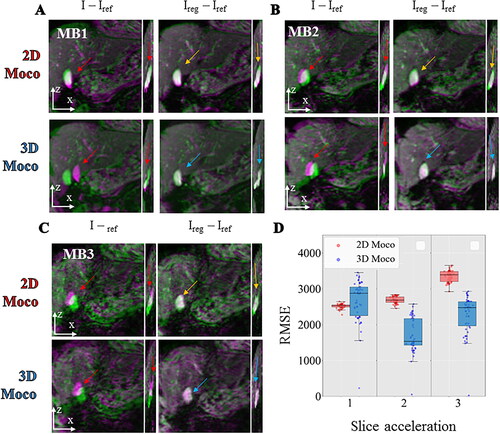
Acquisitions were then performed in the liver on a volunteer under free breathing with MB factors of 1, 2, and 3. The respiratory rate of the volunteer was estimated to 0.33 Hz and 0.34 Hz on MB1 and MB2 acquisition, respectively. The corresponding intensity profiles and histogram distribution of estimated displacements are shown on Supplementary Figure 2. The maximum motion amplitude located on the liver dome and the gall bladder were 20.8 mm and 11.2 mm (MB1) and 8 mm and 12 mm (MB2) respectively. The corresponding movies are available as Supplementary files 3a and 3b. Supplementary Figure 4 shows the impact of MB acceleration on two slices with or without 2D motion registration and points image quality improvement with better sharpness due to MB2 acceleration and to motion registration in the liver vascularization system, in the stomach and even on the ventricle wall. Figure 9 compares qualitatively and quantitatively the registration workflow (2D vs. 3D) for all acquisitions. After visual inspection of the image, a net decrease of image quality is visible at MB3 while MB2 achieves a similar performance than MB1. The red arrows indicate the misregistrations that will happen in both planes in the absence of motion correction. A color code (green-pink) overlaid on the magnitude image highlights the misregistration between the current and reference image. No major difference between both workflows is visible in the imaging plane, but an improvement is noticeable in the perpendicular plane for instance near the gallbladder. The RMSE between the registered images and the reference image over 50 dynamic acquisitions are shown in the box and whisker plot displayed in Figure 9(D). The registration accuracy of the 2D workflow was found to be like the 3D workflow for 0° angulation (mean value ± std RMSE 2D: 2515 ± 64, 3D: 2669 ± 590). At 8° and 14° angulation, the 2D workflow succeeded has a decreased accuracy (8°: mean value ± std RMSE 2D: 2687 ± 96, 3D: 1704 ± 493) and (14°: mean value ± std RMSE 2D: 3350 ± 161, 3D: 2275 ± 529). To investigate the potential impact on temperature estimate, Supplementary Figure 5 shows the temporal standard deviation in slices 9–12 for MB1 and MB2 with 2D or 3D processing workflow. The presence of large phase variations (red arrows) resulted in all cases in increased temperature uncertainty (purple arrows) at the interface of the lung, liver and heart. Mean and standard deviation located in a favorable ROI (white square, 21*21*12 = 5292 voxels) were 2.6 ± 1.3, 1.8 ± 0.6, 2.3 ± 3.1 for the 2D workflow, 3.3 ± 1.9, 2.1 ± 1.0, 2.3 ± 2.6 for the 3D workflow for MB1, MB2, and MB3 respectively.

Figure 9. Comparison between 2D vs 3D motion correction in in vivo acquisition of the liver with different multiband acceleration factors. For each, 2 different registration workflows (top: 2D, bottom: 3D) are compared by showing the difference between the current image and the reference image before (I–I_ref) and after registration (I_reg–I_ref). The differences are overlaid on the magnitude image using a color code (green-pink) for each multiband acceleration 1 (panel A), 2 (panel B), 3 (panel C). RMSE computed over 50 repetitions between the registered images and a reference image are shown (panel D) in a box and whisker plot for 3 different acquisitions on a moving agar gel phantom with a multiband acceleration of 1, 2, 3. For each, the 2 different registration workflow 2D (red) vs. 3D (blue) are compared.

Discussion

The simultaneous multi-slice (SMS) echo planar imaging (EPI) technique has been widely used in fMRI and diffusion MRI [34] but its application in interventional MRI remains limited. Similarly to fMRI, the monitoring of thermal ablation relies on dynamic acquisitions where the challenges are both spatial resolution, volumetric coverage of the area being treated and the frame update rate. Nevertheless, the potential presence of false positives during an interventional procedure may hinder the adoption of this method in clinical routine.

Temperature mapping available in clinical routine mainly relies on conventional gradient-echo imaging (FLASH or segmented-EPI) with an update time varying between 1s and 8s, assuming similar MR parameters (12 slices, …). While such a solution offers acceptable results on static organs [35], it has been demonstrated that the use of EPI sequence drastically reduces the acquisition time and offers the flexibility to map temperature in mobile organs [6,8,9,36] by reducing intra-scan motion. To reduce interscan motion (since apnea cannot be an option for a typical treatment duration of several minutes), synchronizing the acquisition with the physiological motion can be used [2,5,37], resulting in an update time equal to the typical duration of the physiological motion (typically 0.2 Hz for breathing). Alternatively, images can be acquired continuously, provided that appropriate motion compensation algorithms are used in real-time to compensate for the effect of displacement on the magnitude and phase images to correctly compute temperature images and accumulated thermal dose maps over the complete treatment. In the conventional slice-by-slice approach, a tradeoff must be made between high temporal update and large spatial coverage of the temperature monitoring. The simultaneous multi-slice (SMS) echo planar imaging (EPI) technique offers enhanced volume coverage at constant acquisition time or an increase in update time for a given stack of slices. It is also compatible with continuous acquisition and triggering/gating on the physiology of the patient.

The present study performed at 1.5 T using multi-slice EPI thermometry investigated (i) the impact of the multiband acceleration of temperature evolution and (ii) the impact of a 3D registration workflow to reduce potential artifacts in temperature imaging related to out-of-plane motion.

The proposed acquisition pattern includes 12 slices acquired in an interleaved pattern covering 36 mm in the slice direction. We first demonstrated that the increase of the multiband acceleration reduces, as expected, the intra-repetition motion (the displacement between each slice of the same dynamic acquisition). As a drawback, the increase of the multiband acceleration (up to 3) combined with GRAPPA parallel imaging (slice acceleration of 6) induces the presence of aliasing artifacts at moderate levels on the agar gel and at a higher level on the volunteer. In fMRI, the combination of multiband acceleration (MB > = 3) combined with parallel imaging (GRAPPA 2) must be considered with caution. Such acceleration implies an amplification of g-factor noise [25] and the possibility of false positives due to slice leakage [38]. Additionally, as underlined by Borman et al. [19], a limited coil coverage is available in interventional MRI which will impact the reconstruction and the applicability of SMS.

The transition of SMS acquisition from neuroimaging to abdomen imaging increases the complexity of the acquisition and the reconstruction process (the aliasing slice separation). Indeed, a conventional field of view in neuroimaging is more suited to the reconstruction process as the typical ratio of the number of voxels between the ROI (the brain) and background (the noise) is lower than in abdominal imaging. Liver imaging is mostly performed in transversal orientation, which maintains a similar ratio in the image. In such configuration, SMS acquisition has been used in various protocols ranging from DWI [39,40] images to elastography [41]. In the present work, the acquisition is done in free breathing and is set in the coronal plane to encode the main direction of the respiratory motion in the imaging plane. Therefore, in comparison to transversal plane orientation and at fixed resolution and field of view, the field of view in coronal imaging contains few voxels in the background which complicates the aliasing separation of the signal. Additionally, this orientation plane is also more prone to folding artifacts (due to the arms). A 50% oversampling was therefore set in the phase encoding direction to ease the reconstruction process and maintain sufficient image quality.

The combination of SMS with 2D motion registration successfully applies and freezes both the intra-repetition motion and inter-repetition motion. It allows the monitoring of temperature evolution in every voxel during 6 min and also a direct comparison of temperature uncertainty and estimates across datasets. To investigate the presence of false-positive temperature spots, the spatial distribution and temperature evolution of temperature maps for each acquisition were compared (Figures 4 and 5). Temperature evolution in the vicinity of the electrode was found in agreement for the different multiband acceleration. However, higher σ(T) (spatial mean ± standard deviation over the ROIs) values were observed for MB3 but remain close to 1 °C uncertainty. No signal leakage between simultaneously excited slices was reported.

In this work, we also investigate the use of statistical tests for MRI thermometry by evaluating the repeatability of two measurements of the three different parameters (multiband acceleration factor of 1, 2, and 3). Indeed, MRI temperature mapping sequences are difficult to evaluate due to the inherent nature of these experiments. Fiber-optic measurement is often used as a gold standard, but the comparison with MRI temperature estimation remains challenging due to both the partial volume effect and the absence of volumetric measurement for such devices. Evaluation of MR thermometry protocol involves heating and returning to the initial state is not guaranteed. Depending on the nature of the phantom (gel, muscle), its partial destruction is not avoidable. To minimize such a phenomenon, small heating by radiofrequency energy <20 °C in gel agar was performed. A sequence of six acquisitions was performed under controlled conditions.

Bland-Altman plots (Figure 6) were used to compare the resulting temperature maps and to identify the reproducibility of the measurements. The 95% uncertainty was found below 2 °C for the measurements without multiband acceleration and with MB2. The two acquisitions were spaced 30 min apart and two other acquisitions were inserted during this period. Uncertainty up to 4.5 °C and a larger dispersion was found when comparing the measurement with and without multiband acceleration. It is noticeable that the increased difference is higher for higher temperature values. It could be due to residual aliasing or increased local g-factor but a scenario involving imperfect registration and/or partial volume effect is possible as these outliers correspond to the same voxel location and are mostly located close to the artifact of the RF needle. Indeed, to estimate the reproducibility of temperature evolution in presence of motion, dedicated processing was needed to minimize all potential bias. Typically, as the acquisition triggers were not synchronized on the periodic motion, the reference image of each acquisition was different. Therefore, all acquisitions were co-registered using a simple translation transformation to guarantee a fair comparison. The existence of the partial volume effect is a second issue and remains a limiting factor that registration cannot compensate for, as a significant gradient of temperature could exist within a voxel (the acquisition resolution being 1.6 × 1.6 × 3 mm³). Lastly, the use of radiofrequency energy implies a non-uniform energy distribution (in comparison with LITT energy deposition) which makes the acquisition comparison more difficult and sensitive to artifacts. Thus, the methodology presented in the article should be considered as a work in progress to improve the reproducibility and evaluation of MR temperature mapping under control conditions.

A second aim of this work was to investigate how the benefit of multiband acceleration in acquisition time (TR= 671 ms at MB2, TR = 445 ms at MB3 instead of TR = 955 ms at MB1) could help to reduce the presence of out-of-plane motion. The presence of out-of-plane motion decreases the uncertainty of temperature monitoring. In practice, a residual motion, orthogonal to the imaging plane, is often visible and results in the oscillation of the temperature. The voxels in the imaging plane are alternately located on the (n) and (n + 1) slice depending on the respiratory cycle. By performing a 3D registration, the proposed workflow aims to minimize the out-of-plane motion between dynamic acquisitions. The sequence acquisition being independent of the respiratory cycle, the acquired pseudo-volume will differ between the ascending and descending phase of respiration. Therefore, the inter-repetition motion was frozen using the combination of multiband acceleration and with rigid motion correction between slices as shown in Figure 1. Then, the 2D registration workflow was extended in the slice direction to obtain 3D motion correction and 3D susceptibility correction. A comparison of the two workflows (2D vs. 3D) was performed on the magnitude (Figure 7) and temperature (Figure 8) images with different levels of out-of-plane motion. The 3D workflow was found suitable to register an out-of-plane motion at the border of the gel or in the vicinity of the electrode. Altogether, these plots in Figure 7 show that the 3D workflow achieves either similar or better performance whatever the angulation under the conditions being investigated but a broader dispersion of the RMSE is visible.

The acquisition was tested on a single volunteer, his respiratory pattern was regular but somewhat rapid (0.33 Hz). Significant motions up to (20 mm) were compensated by the motion algorithm. Knowing that the liver ablation may be done under respiratory assistance, the current case can be considered as more complicated than under artificial respiration. Due to the presence of a significant phase, the temporal standard deviation was strongly affected at the liver-lung-heart interface, such an effect could have been compensated by better shimming. Nevertheless, acceptable temperature uncertainty (∼2 °C) were found for all acquisition in an ROI located at the center of the liver. The 3D workflow increases the temperature uncertainty in MB as the temporal resolution (1.43 s) was half of the respiratory rate. For the MB2 acceleration, the application of the 3D workflow was found both favorable and unfavorable depending on the location.

Limitations

The benefit of the 3D workflow on temperature was more difficult to assess. While some improvements were noticeable with a decrease of the temperature spike close to the electrode, some variability is reported in Figure 8. The result of the proposed correction method is hampered by the current characteristics of the image reconstruction. Indeed, to perform GRAPPA reconstruction, a reference scan (24 lines) is acquired for each slice to reconstruct a low image resolution and compute the coil map sensitivity at the beginning of the acquisition. The coil map sensitivity is then applied to estimate the GRAPPA kernel being used for the in-plane un-aliasing step. The coil map sensitivity being computed only once and kept for dynamic acquisitions, it fixes the phase reference per slice. This reference scan being acquired without any triggering, the coil map sensitivity of each slice may differ depending on the respiratory cycle. Consequently, when performing 3D motion correction, the displacement of voxels (and associated phase value) between adjacent slices can be interpreted as a small temperature if the reference phase of the adjacent slice image is different. Further modification of the sequence could be envisioned to improve the accuracy of the method by fixing the reference scan at the same respiratory phase. Additionally, the proposed workflow could be combined with a respiratory belt to trigger the sequence on the respiratory phase at the cost of temporal resolution. In such a case, it could offer great flexibility in image orientation while maintaining a high-volume coverage. The motion registration workflows will remain compatible to compensate for residual motion.

The proposed framework is designed to be robust to irregular motion patterns but had some limitations. The presence of spontaneous motions such as a larger amplitude of respiration will be compensated by both the motion correction and the susceptibility artifact correction. The latter can extrapolate the phase variation of a ‘non-seen’ displacement. Additionally, the acquisition pattern of 12 slices limit the risk that the target being out of the field of view. Nevertheless, other spontaneous motions like a strong contraction of the liver might happen during the heating and will strongly impact both the registration and the motion-induced susceptibility correction. In such a situation, the presence of a new magnetic environment will invalidate the previous susceptibility estimation and cause erroneous temperature maps. A reference-less method could be envisioned [42] in this scenario. Lastly, slow physiological drifts may also occur during the such procedure [29]. The typical ablation duration being 10 min, such drifts are unlikely to impact the proposed method but it is not been evaluated in this study.

To facilitate sub-second reconstruction, the current implementation includes a dedicated coil compression algorithm for SMS acquisition (on the CPU), slice-GRAPPA reconstruction (on the GPU) and 2D/3D motion correction (on the GPU). The real-time compatibility (processing time and minimal latency) was quantified for the 2D workflow for all MB acceleration using the gel and volunteers acquisitions (Supplementary Figure 6). For the MB reconstruction, the current version supports real-time reconstruction up to TR = 0.6 s and 0.84 s for the gel and volunteer acquisitions respectively using MR parameters of the study. The addition of registration and thermometry processing increased the minimal TR to 1.9 s and 2.3 s while a TR of 1.2 s and 1.43 s were used in the study for the gel and volunteer acquisitions respectively, preventing from real-time usage. Nevertheless, other code optimizations could be envisioned: (i) Coil compression to 8 coils with similar image features and noise improve the image reconstruction time by a factor of 2. The timing decrease from 84 s to 51 s and 255 s to 107 s for the gel and volunteer acquisitions respectively. (ii) Masking, all the thermometry processing (notably the PCA estimation and susceptibility correction) were computed on all voxels of the images although a large number of voxels with low signal intensity could be excluded from this processing to save computation time. (iii) Parallel branching, motion correction could be parallelized on multiple GPUs as the Gadgetron support such a feature. Although untested, the proposed implementation, combined with the use of current hardware supporting multi-GPU and the addition of the suggested code optimizations, would most certainly result in a real-time application whatever the TR.

On-line scanner SMS implementations have reached a high level of maturity and are being used in major studies such as the Human Connectome Project [43] or the UK Biobank [44]. Such sequences could easily be used to quickly expand volumetric temperature mapping for therapeutic applications. To ease the use of the SMS-EPI in such a context, support our findings and promote the reproducibility of the results, an open-source reconstruction code was developed, additional information are available in the OPEN-SOURCE section. Additionally, the use of split-slice GRAPPA [22] was not investigated in this work (not implemented). This may reduce the slice leakage but may in turn increase the noise amplification [45]. Other acquisition schemes [20,46] or reconstruction could be envisioned but were out-of-scope [47] of this work.

Finally, the sequence and reconstruction were tested with a home-made RF device. Future investigations with clinical devices also need to be evaluated in terms of accuracy and safety. RF or microwave energy may generate a high level of noise [37] that might impact both the proposed SMS reconstruction and the registration framework. The use of multi-band RF pulses increases the risk of RF power deposition. The proposed protocol (single-shot gradient echo acquisition pattern, MB accelerations <3 and long TR) is much less intensive than any standard fMRI or diffusion protocols and limit the risk of unwanted SAR elevation. However, its use with medical devices must be done with care, even for MR-compatible devices. It will result in a higher SAR value than a normal RF pulse. No unexpected temperature elevation (in the range of the uncertainty of the method) was reported at the vicinity of the RF electrodes during the experiment.

Conclusion

This study presents the first evaluation of MR-thermometry using SMS-EPI acquisition in presence of motion. While increasing the SMS factor to 3 induced some aliasing artifacts, it reduced the displacement between adjacent slices and thus allowed for reconstructing a 3D volume (180 × 180 × 36 mm³) more precisely, with acceptable temperature uncertainty (<2 °C). Pseudo-volumetric temperature imaging could thus be performed without compromises on acquisition time and resulting temperature images showed similar patterns independent of the SMS acceleration factor (up to 2). Such a strategy is expected to increase procedure safety by monitoring wider volumes more rapidly for MR-guided thermotherapy on mobile organs.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

The data that support the findings of this study are available at this link (https://doi.org/10.5281/zenodo.7643565). To ease use of the SMS-EPI in such a context, support our findings and promote the reproducibility of the results, an open-source reconstruction code (https://github.com/LIRYC-IHU/gadgetron-sms) was developed to ensure an optimal phase reconstruction for temperature reconstruction. Compatibility with the two widely available SMS sequences on Siemens scanners (the commercial product and the CMRR C2P) were set up. In-line reconstruction presented in the study is therefore accessible to all major fMRI sites where CMRR sequences are usually available. After a minor modification on the scanner, the proposed reconstruction can be used with a limited latency (the code being not yet optimized for real-time reconstruction). Compatibility with in-plane parallel imaging and partial Fourier has only been tested for multiband acceleration of 2 and 3 which currently limits the use of the reconstruction for other applications.

Additional information

Funding

This work received financial support from the French National Investments for the Future Programs: ANR-10-IAHU-04 (IHU Liryc) and Laboratory of Excellence ANR-10-LABX-57 (TRAIL), and the research programs ANR-17-CE19-0007 (CARTLOVE), ANR-19-CE19-0008-01 (CARCOI) and Equipex ANR-11-EQPX-0030 (MUSIC). This study received financial support from the French government in the framework of the University of Bordeaux's France 2030 program/RRI "IMPACT.