Application of a new self-regulating temperature magnetic material Fe₈₃Zr₁₀B₇ in magnetic induction hyperthermia

Abstract

Introduction

The temperature control of magnetic hyperthermia therapy mainly relies on circulating water cooling and regulating magnetic field intensity, which increases complexity in clinical applications. Using magnetic materials with appropriate Curie temperature has become an effective means to solve temperature monitoring and potentially achieve self-regulating temperature.

Methods

A self-temperature-regulating Fe₈₃Zr₁₀B₇ magnetic material was prepared. Based on this material, a simplified model of magnetic hyperthermia for arm tumors was established and verified using the finite- element method. The influence of magnetic field intensity and frequency on the heating power and temperature rise rate of different-sized and shaped magnetic media was studied. Additionally, factors such as the size, quantity, and spatial arrangement of the magnetic media were analyzed for their impact on the damage to tumors with different volumes and shapes.

Results

Spherical shape is the most suitable for magnetic hyperthermia media, and the radius of the spherical magnetic media can be chosen according to the size of the tumor. For tumors with a radius below 10 mm, using magnetic media with a particle size of 3.5 mm is recommended. The optimal magnetic field conditions are H0 (10–12 kA/m) and f (110–120 kHz).

Conclusion

Based on the good magnetic properties and heating performance of the Fe₈₃Zr₁₀B₇ magnetic material, it is feasible to use it as a magnetic medium for magnetic hyperthermia. The results of this study provide references for the selection of thermal seed size and magnetic field parameters in magnetic hyperthermia.

Keywords:

• Self-regulating temperature
• magnetic induction hyperthermia
• numerical simulation

1. Introduction

Magnetic induction hyperthermia (MIH) will generate a higher temperature in a tumor by implanting a magnetic medium into the tumor with an applied magnetic field [1–6]. Many works have revealed the biological effects of hyperthermia on macroscopic and microscopic levels [7–10], suggesting that the magnetic medium absorbs energy and the surrounding temperature increases, leading to apoptosis and necrosis of tumor cells in the range of 41 °C and 46 °C [11–14].

In clinical aspects, many researchers verified the excellent efficacy of MIH [15–17]. Stea et al. [18,19] conducted MIH on glioma patients with thermoseeds, and the treatment temperature reached over 42 °C, proving the feasibility of thermoseeds implantation for interstitial hyperthermia in brain tumors. Deger et al. [20,21] conducted a phase II clinical trial of thermoseeds MIH in 57 prostate cancer patients. Subsequently, after two years of clinical observation, the content of the average PSA (prostate-specific antigen) of 12 patients decreased to normal levels. Johannsen et al. [22] used the experimental results to prove the feasibility of magnetic fluid in the treatment of the prostate. Maier-Hauff et al. [23] injected magnetic fluid into the intracranial of 14 patients with glioma of the brain, and the tumor volume of the patients decreased by 75% after AMF hyperthermia, indicating that MFH had a better inhibition on the growth of tumor cells and a stronger killing effect on them.

As a vital part of MIH, the character of the magnetic medium is an influential factor affecting the treatment results, which needs in-depth research [24–26].Over the past decades, research on the magnetic media of MIH has focused on magnetic thermoseeds, ferromagnetic glass ceramics, and magnetic fluids. Masakazu et al. [27] synthesized ferromagnetic hematite microspherical particles with SiO₂ as the core and coated withγ-Fe2O3 magnetic particles, which met the requirements of hyperthermia temperature. Ji et al. [28] studied the PFCS glass-ceramics magnetic properties, and induction heating capacity, the results showed that PFCS could induce apparent cell death of LoVo cancer. The theoretical formula for power absorption was derived by Wu et al. [29] using the electromagnetic field constraint equation and compared the power absorbed per unit volume of several millimeter-level ferromagnetic thermoseedss. With using the thermal fluid model of Comsol Multiphysics, Astefanoaei, et al. [30] studied the temperature field of tumor tissue with Fe_67.7Cr₁₃Nb_0.3B₂₀ magnetic nanoparticles used in hyperthermia, the results show that the nanoparticles can maintain a stable temperature range under suitable conditions.

​Previous studies have discussed the role of materials with good magnetothermal properties in MIH, but there has been no in-depth study on how to achieve accurate temperature control during MIH implementation, which is what this paper wishes to discuss.

This paper uses Fe₈₃Zr₁₀B₇ as the magnetic media, which is Fe-based bulk metallic glass with great properties such as high permeability, low coercivity, small anisotropy, and lower Curie temperature [31]. This low Curie temperature point performance ensures that it does not warm up after reaching the Curie temperature point and thus has absolute temperature control performance for MIH. However, it has yet to be studied the application in MIH, thus enabling self-regulating temperature mechanism. In this paper, we provide some references for the application of self-regulating temperature nanomaterials in MIH by comparing the experimental results of self-regulating temperature magnetic materials with the results of finite element analysis.

2. Numerical method

2.1. Establishment of the MIH model

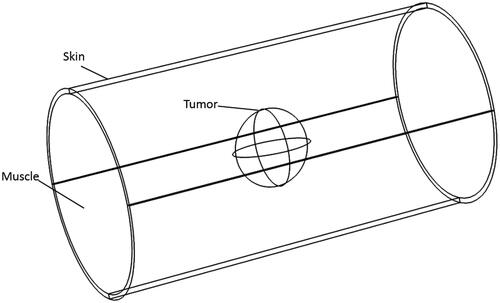
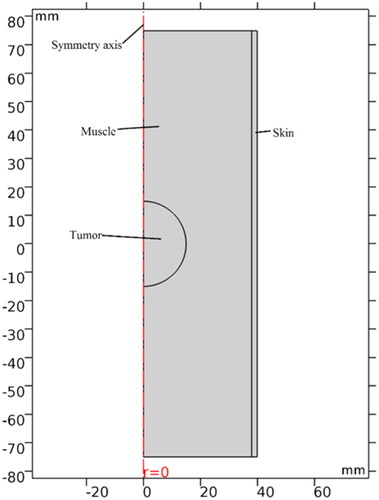
This paper adopts the human upper arm as the study subject and assumes the vascular tissues and skeletal tissues surrounding the tumor regions are muscle tissue; Figure 1 shows the simplified upper arm three-dimensional MIH model, the cylinder with a radius of 4 cm and height of 15 cm, the skin thickness is 2 mm. Additionally, set the tumor diameter to 1–4cm, which determines the size and position of the magnetic medium.

Figure 1. A wireframe rendering of the MIH model.

2.2. Physical parameters

Table 1 shows the physical parameters of biological tissues [32,33]. Table 2 shows the parameters of Fe₈₃Zr₁₀B₇. As shown in Figure 2(a), the diffuse peak state near an angle of 45° indicates that the sample strip phase structure is essentially amorphous, while diffuse peaks at 15–30° are peaks of amorphous glass substrate. The narrow magnetic hysteresis loop (Figure 2(b)) means the heat generation of Fe83Zr10B7 is mainly caused by eddy current loss [34]. The Curie temperature of the material was tested by TGA [35,36]and PPMS, as shown in Figure 2(c,d), and the calculated Curie temperature was 75.13 °C and 75.98 °C respectively. In order to facilitate calculation, the Curie temperature set in this paper is 75 °C.

Figure 2. (a) The XRD pattern of Fe83Zr10B7. (b) The magnetic hysteresis loop of Fe83Zr10B7. (c) The thermogravimetric curve obtained by thermogravimetric analyzer under a static magnetic field, the inset is the first derivative of the thermogravimetric curve. (d) The M-T curve obtained by PPMS, the inset is the first derivative of the M-T curve.

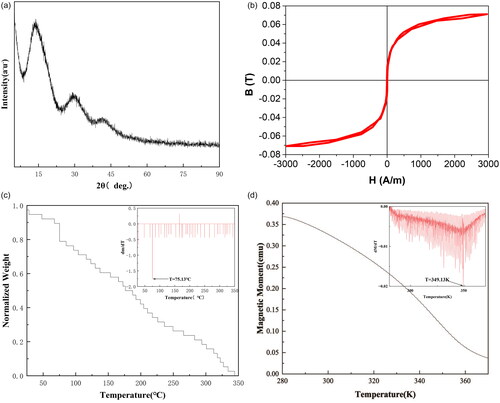
Table 1. Physical parameters.

	Density ρ[kg/m^3]	Specific heat Cp[J/kg/^oC]	Thermal Conductivity λ[W/m/^oC]	Conductivity σ[S/m]	Relative permittivity εr[1]	Blood perfusion Rate wb[s^-1]	Basal metabolic heat rate Qmet[W/m^3]
Muscle	1090	3421	0.49	0.356–0.407	5.23E3–9.02E3	6.72E4	992
Skin	1109	3391	0.37	3.3E4–1.9E3	1.09E3–1.12E3	1.96E3	1830
Blood	1050	3617	0.52	0.702–0.721	4.69E3–5.17E3	－	－
Tumor	1050	3500	0.50	0.356–0.407	5.23E3–9.02E3	8.33E4	5790
Air	1.2	1004	0.03	0	1	－	－
Water	994	4178	0.6	5.7E10–3.3E7	84.64	－	－

Table 2. Fe₈₃Zr₁₀B₇ parameters.

Density ρ[kg/m^3]	Specific heat Cp[J/(kg·^oC)]	Thermal Conductivity λ[W/m/^oC]	Conductivity σ[S/m]
7230	456	90.7	4.15E5
Relative permittivity εr[1]	Saturation magnetization Bs[mT]	Maximum relative permeability μm[1]	Coercivity Hc[A/m]
1	71	366.8	5.639

The detailed derivations are in equations (1)-(6).

2.3. Equations and boundary conditions

Considering the metabolic heat production and blood perfusion of biological tissues, we use Pennes bio-heat transfer equation [37] to calculate the temperature distribution of the tumor and surrounding tissues: (1) $$\rho {\mathrm{C}}_P\frac{\partial T}{\partial t}=\nabla (k\nabla T)+{\rho }_b{C}_b{w}_b(T_b-T)+Q_{\mathit{met}}+Q_{ml}$$(1) where ρ is the tissue density [kg/m³], C_p is the tissue heat capacity [J/kg/°C], t is the treatment time [s], T is the tissue temperature [°C], k is the tissue thermal conductivity [W/m/°C], ρ_b is the blood density [kg/m³], w_b is the tissue blood perfusion rate [1/s], C_b is the specific heat of the blood [J/kg/°C], T_b is the blood temperature [°C], Q_met is the tissue metabolic heat production rate [W/m³]. Q_ml is the magnetic loss [W/m³], which can be considered as eddy current loss power in this paper [34].

Deduce the eddy current loss as follows: set the cylinder with conductivity σ, radius R, and height h in an alternating magnetic field in which magnetic induction intensity B varies with time. Divide the cylinder into thin-walled cylinders with width dr, circumference 2πr and thickness h, and the induced electromotive force of any thin-walled cylinder is: (2) $$\epsilon =-\frac{d\Phi }{dt}=-\frac{d\left(\stackrel{\rightharpoonup }{B}\cdot S\right)}{dt}=-\pi r^2\frac{d\stackrel{\rightharpoonup }{B}}{dt}$$(2)

The instantaneous power of the wall is: (3) $$dP=\frac{{\epsilon }^2}{R}=\frac{{\pi }^2{r}^4}{\frac{2\pi r}{\sigma \mathit{hdr}}}{\left(\frac{d\stackrel{\rightharpoonup }{B}}{dt}\right)}^2=\frac{\pi \sigma h{r}^{3}dr}{2}{\left(\frac{d\stackrel{\rightharpoonup }{B}}{dt}\right)}^2$$(3) integrate the equation (3)(3) $$dP=\frac{{\epsilon }^2}{R}=\frac{{\pi }^2{r}^4}{\frac{2\pi r}{\sigma \mathit{hdr}}}{\left(\frac{d\stackrel{\rightharpoonup }{B}}{dt}\right)}^2=\frac{\pi \sigma h{r}^{3}dr}{2}{\left(\frac{d\stackrel{\rightharpoonup }{B}}{dt}\right)}^2$$(3) over 0∼R: (4) $$P_{-}{}_{\mathit{cylinder}}=\frac{\pi \sigma h{R}^4}{8}{\left(\frac{d\stackrel{\rightharpoonup }{B}}{dt}\right)}^2$$(4) take the direction of the magnetic field parallel to the Z axis, and set the conditions outside the boundaries as magnetic insulation: (5) $$\{\begin{array}{c}{H}_{\mathrm{x}}=0\\ H_{\mathrm{y}}=0\\ H_{\mathrm{z}}=H_0\end{array}$$(5) (6) $$\stackrel{\rightharpoonup }{n}\times \stackrel{\rightharpoonup }{A}=0$$(6) Where H₀ is the magnetic field intensity [A/m], and the product of H₀ [A/m] and frequency f[Hz] cannot exceed 4.85 × 10⁸[Am⁻¹s¹] [38]. In particular, the range of the product can be expanded to 5 × 10⁹[Am⁻¹S¹] [39,40].

​This paper applies the biological heat transfer module in all domains. Set the initial temperature of the tumor and normal tissue at 37 °C, the initial temperature of the skin at 33.5 °C, and the initial temperature of magnetic media at 25 °C. The heat -transfer caused by the convection on the surface of the skin is considered in boundary condition: (7) $$-k\left(\frac{\partial T}{\partial n}\right)=h\left(T-T_{\mathit{air}}\right)$$(7) where h is the convective heat transfer coefficient, valued as 6 W/m²/°C [41], and T_air is the air temperature, taken as 25 °C. The other boundaries are assumed to maintain a constant temperature of 37 °C.

2.4. Selection of damage threshold

In order to express the damage degree of tissue in the treatment process more intuitively, the equivalent thermal dose theory of Sapareto and Dewey [42] is adopted in this paper, which converts the heating time at arbitrary temperature to the equivalent heating time at 43 °C: (8) $$\mathrm{CEM} 43(\mathrm{t})={\int }_{{\mathrm{t}}_0}^{{\mathrm{t}}_{\text{ultimate}}}\beta {\left(\mathrm{T}\right)}^{\left(316-\mathrm{T}\left(\mathrm{t},\mathrm{x},\mathrm{y},\mathrm{z}\right)\right)}dt$$(8) (9) $$\beta \left(\mathrm{T}\right)=\{\begin{array}{l}0\\ 0.25\\ 0.5\end{array}\begin{array}{c}\\ \\ \end{array}\begin{array}{c}\mathrm{T}<312\mathrm{K}\\ 312\mathrm{K}\le \mathrm{T}<316\mathrm{K}\\ 316\mathrm{K}\le \mathrm{T}\end{array}$$(9) where t₀ and t_ultimate represent the time the heating starts and ends, respectively. T (t,x,y,z) is the function of temperature over time at a certain point of tissue, and β is the constant function related to temperature. Rhoon and Yarmolenko [43,44] stated that the thermal dose threshold of reversible and irreversible damage to muscle tissue is 40 min and 80 min, respectively. Therefore, the equivalent thermal dose of 40 min and 80 min is adopted as the tissue reversible and irreversible damage threshold, respectively. It can be judged that the tumor is completely damaged if the integrated value of the lowest temperature of the tumor is greater than 80 min.

3. Results and discussion

3.1. Multi-physical field coupling method verification

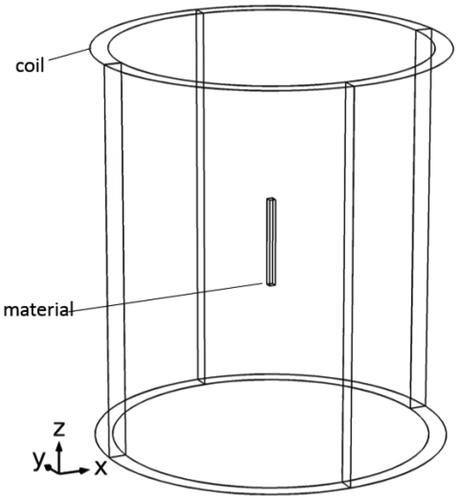
Use Fe₈₃Zr₁₀B₇ to prepare a rectangular magnetic media with a thickness of 1.44 mm and a length of 20 mm. Put the magnetic media in an alternating magnetic field generated by LH-15 induction heating equipment provided by Dongguan Lihua mechanical equipment Co., Ltd. the temperature probe is fixed on the surface of the magnetic media, and the coil used in this paper with a radius of 78 mm and height 95 mm has nine turns. As shown in Figure 3(a), the energizing solenoid coil with a height of 95 mm and radius of 78 mm is a 9-turn hollow copper tube. In order to avoid the experimental error caused by the joule heat of the copper pipe, circulating cooling water at 20 °C is used in the copper tube.

Figure 3. (a) The experimental scheme for measuring heating curves of Fe83Zr10B7 rectangular. (b) Cylindrical fresh pork tissue and Air-core copper coil used in MIH experiment. (c) Diagram of in vitro tissue experiment.

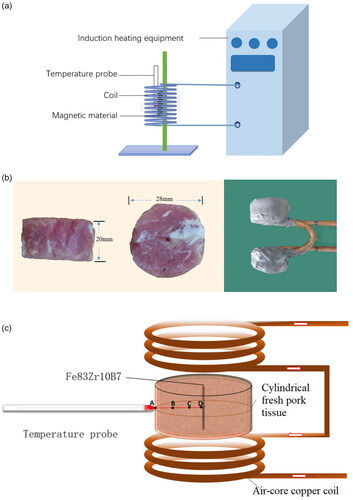
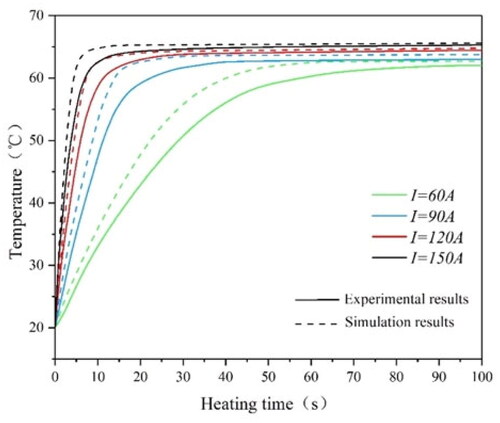
In order to verify the reliability of the experiment, a three-dimensional calculation model is designed by using Comsol Multiphysics in this paper. As shown in Figure 4, the solenoid and the magnetic media are parallel. Moreover, the geometrical centers of both frames should coincide. The size of the coil and material is consistent with the experiment. As shown in Figure 5, the experimental and simulated values of the surface temperature of Fe₈₃Zr₁₀B₇ rectangular under different current conditions at 60 kHz are recorded. We also embed the magnetic media into a fresh pork tissue to measure the temperature rise; the experimental and simulated values are shown in Figure 6, which is similar to Figure 5. The simulated value is always slightly higher than the experimental value, and the reason may come from the deviations of environment between experiment and the simulation, but the final stable Curie temperature is basically unchanged; and the relative error is less than 2% which is within the allowable range.

Figure 4. The three-dimensional heating model.

Figure 5. The comparison of the surface temperature of Fe₈₃Zr₁₀B₇ rectangular between simulation and experimental results under different heating conditions at f = 60kHz.

Figure 6. Simulation and experimental temperature rise curves of four temperature measuring points in fresh pork tissue.

3.2. Selection of material’s shape

However, the uneven distribution of induced current generated by magnetic media in the magnetic field will lead to uneven heating power. Therefore, this paper studied the initial average heating power density of spherical, rectangular, and cylindrical media at different angles (0–90°) between the central axis and the magnetic field direction by taking the volume average of power density, as shown in Figure 7. The curves of the initial average heating power density of three shapes with various angles under the conditions of T_materials=37 °C, f = 90kHz, and H₀= 5 kA/m are demonstrated in Figure 8. The sizes of these shapes are shown in brackets.

Figure 7. The angle between the direction of the applied magnetic field and the central axis of the cylindrical and the rectangular varies from 0° to 90°.

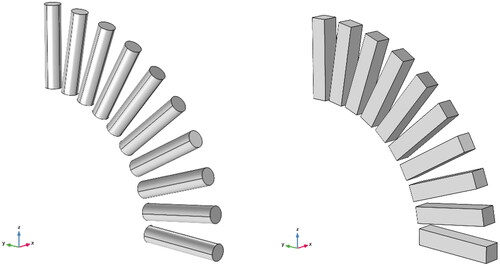
Figure 8. The initial average heating power density of three shapes of Fe₈₃Zr₁₀B₇ material with various angles at f = 90kHz, H₀=5kA/m and T = 37 °C.

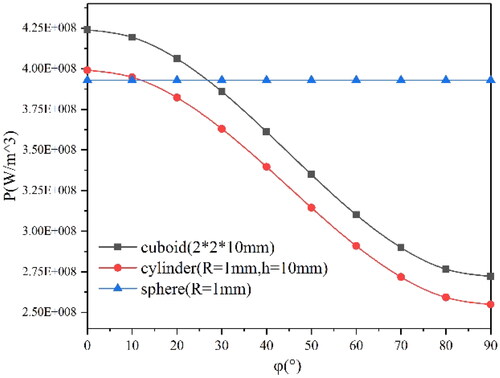
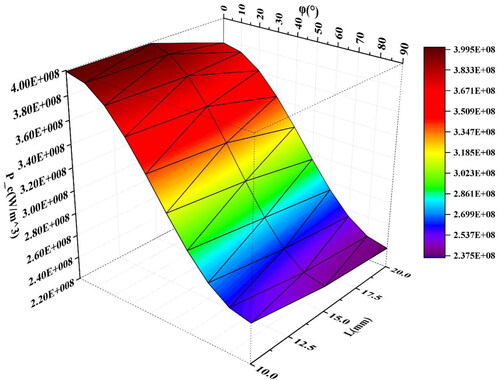
As shown in Figure 8, for rectangular and cylindrical materials, the average heating power density decreases with the angle increase, due to the change of the distribution and magnitude of the induced current caused by the change of the angle. Take the simulation results of cuboid material as an example, as shown in Figure 9; with the increased angle, the induced current moves to the two bottom surfaces from the side surface, which is larger than the bottom surfaces, and causes a reduction of overall heating power. However, for the spherical media, the average heating power is independent of the direction of the applied magnetic field because of the symmetry. This paper also explores the influence of rectangular length on the average heating power density under the magnetic field condition of f = 90kHz and H₀= 5 kA/m. As shown in Figures 9 and 10, the average heating power density tends to decrease slightly with the increase of L while R is constant.

Figure 9. The induced current density distribution of a Fe₈₃Zr₁₀B₇ cuboid at f = 90kHz, H₀=5kA/m.

Figure 10. The initial heating power density of a Fe₈₃Zr₁₀B₇ cylinder with a radius of 1 mm.

​In the actual course of hyperthermia, the shape of the tumor tissue may change after heating, which will cause a change in the position of the implanted medium and thus affect the heating power. Moreover, tumors of different sizes also require different lengths of material, which are difficult to monitor and control in treatment. Therefore, spherical material is preferred for multi-physical coupling analysis.

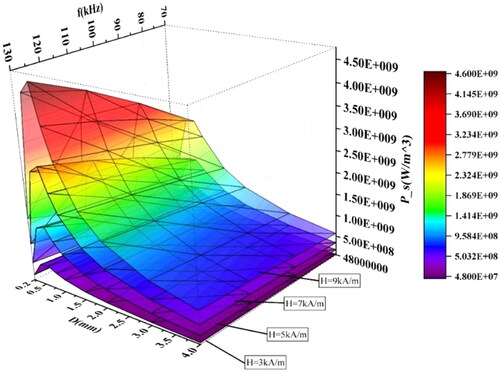
The conditions of Figure 11 are as follows; particle size D ranges from 0.2 mm to 4 mm, the f ranges from 70 to 130 kHz, and the H_0and are 3 kA/m, 5 kA/m, 7 kA/m, and 9 kA/m respectively. It can be seen from the figure that under the condition of constant particle size, the average heating power increases with the increase of f and intensity, and the higher the H₀, the greater the average heating power increases with frequency. Under the condition of constant H₀ and f, the average heating power density of the material reaches the largest value when the size is 0.7mmr. The influence of f on average heating power gradually decreases as the size decreases or increases from 0.7 mm when the size is below 0.7 mm.

Figure 11. The heating power density of Fe₈₃Zr₁₀B₇ spherical.

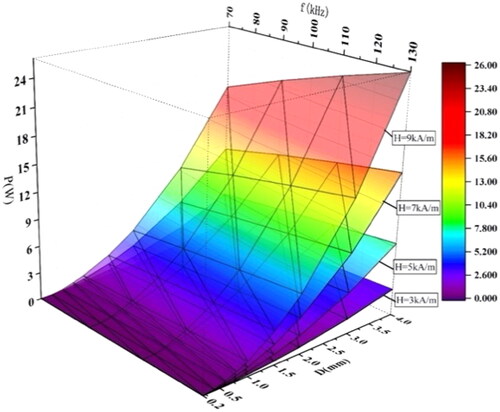
Although the magnetic media with a diameter of 0.7 mm has the largest heating power density, the overall heating power may be less than the larger magnetic media with a small heating power density. The product of the power density and the volume of the heating medium is the overall heating power. Figure 12 depicts the influence of particle size and f on heating power under different magnetic field strengths. As expected above, the overall heating power maybe not be maximum when the heating power density is maximum, and the heating power of spherical materials is positively correlated with particle size, f, and H₀. The larger the H₀ is, the more obvious the increase in heating power is.

Figure 12. The heating power of Fe₈₃Zr₁₀B₇ spherical.

Assuming radius R, heat capacity at constant pressure Cp, density ρ of the tumor are constant, the initial temperature is T₀, the blood temperature is T_b=37 °C, and only blood perfusion can take away the heat, the average heat power loss caused by blood perfusion can be described as： (10) $$P_b=\frac{4\pi R^3}{3}\cdot \frac{{\int }_0^{t_{\mathrm{u}}}{\rho }_b{C}_b{w}_b[T(t)-T_b]}{t_{\mathrm{u}}}$$(10) When t = 0, T(0)= T₀; When t = t_u, T(t_u)= T.

In order to simplify the calculation, assume the temperature curve of the tumor is a quadratic function: (11) $$T(t)=\frac{T_0-T}{t_u^2}{t}^2+\frac{2(T-T_0)}{t_u}t+T_0$$(11)

Then equation (10)(10) $$P_b=\frac{4\pi R^3}{3}\cdot \frac{{\int }_0^{t_{\mathrm{u}}}{\rho }_b{C}_b{w}_b[T(t)-T_b]}{t_{\mathrm{u}}}$$(10) can be described as: (12) $$P_b=\frac{4\pi R^3}{3}\cdot {\rho }_b{C}_b{w}_b\cdot \frac{2T+T_0-3T_b}{3}$$(12)

Therefore, the average heating power of a tumor arising from temperature T₀ to T in time t required is: (13) $$P=\frac{4\pi R^3}{3}\left[\frac{\rho C_p\left(T-T_0\right)}{t_{\mathrm{u}}}+\frac{{\rho }_b{C}_b{w}_b(2T+T_0-3T_b)}{3}\right]$$(13)

Take a tumor with R = 10mm as an example. If the temperature rises from 37 °C to 43 °C within 1 min, get p = 1.5 W through equation (13)(13) $$P=\frac{4\pi R^3}{3}\left[\frac{\rho C_p\left(T-T_0\right)}{t_{\mathrm{u}}}+\frac{{\rho }_b{C}_b{w}_b(2T+T_0-3T_b)}{3}\right]$$(13) . Considering the heating power will decrease with the increase in temperature, take P = 3W as the heating power. According to the results shown in Figure 12, the heating power can reach 3 W when the diameter D is larger than 1.5 mm. Considering that magnetic media with a large size will increase the wound area and aggravate the patient’s pain, we use the spherical magnetic media with a diameter of 1.5 ∼ 4.0 mm as the magnetic media in the MIH simulation study.

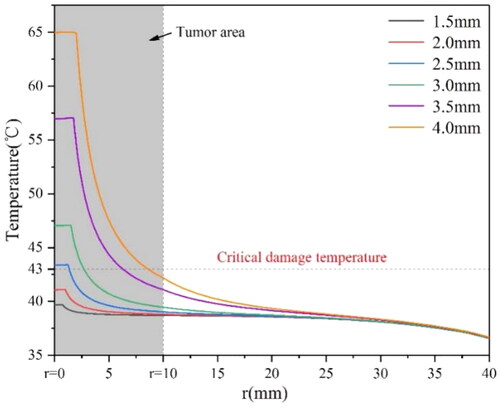
Figure 13 shows that when r reaches 3 mm, the temperature of some tumor tissues reaches the thermal damage temperature of 43 °C; when the r is 3.5 mm, the distance range at 43 °C is about 6 mm. When r reaches 4 mm, the tumor with a radius less than 7.5 mm can rise to over 43 °C. Therefore, for the tumor with a radius of 5 mm, the magnetic media with a diameter of 3.5 mm should be considered for treatment. F [34] or the tumor with a radius of 10 mm, the magnetic media with a diameter of 4 mm should be considered. For larger tumors, multiple implantations would be suggested.

Figure 13. Temperature distribution along the radius from the tumor center under the conditions of f = 90kHz and H₀=9kA/m of magnetic media with various diameters.

3.3. Analysis of thermal damage

The model shown in Figure 14 has been established to investigate the effect of an alternating magnetic field on tissue damage. The blank area is air, and the magnetic field direction is parallel to the axis. Figure 15 shows the temperature distribution in the tissue under the condition of f = 240kHz, H₀=15kA/m, t = 60 min. It can be seen that the highest temperature of the tissue reaches to 39.96°Cwithout the magnetic media, lower than the critical tissue damage temperature of 43 °C. The temperature gradually decreases along the symmetrical center due to the heat exchange between the skin and the surrounding air. ​In order to better study the effect of magnetic field conditions on tissue temperature, in this paper we calculate the average body temperature, excluding the skin, and use the equivalent heating time obtained by integrating it in time as the equivalent thermal dose.

Figure 14. The arm model of the human body.

Figure 15. The temperature distribution in normal tissue and tumor under the condition of f = 240kHz and H₀=15kA/m for 60 min.

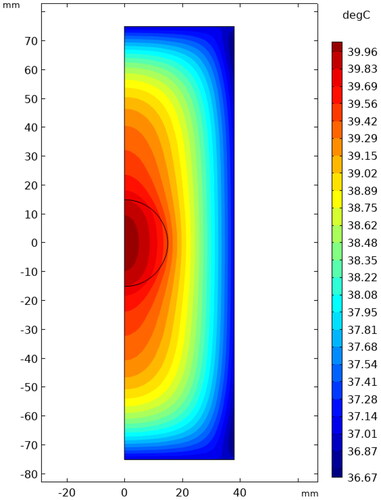
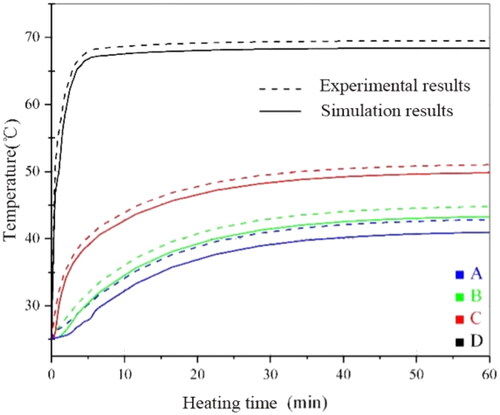
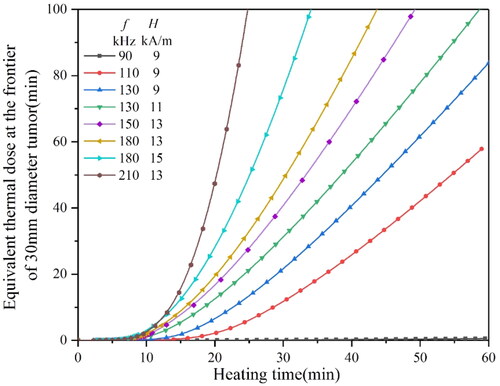
It can be seen from Figure 16 that under the condition of f = 240kHz and H₀=15kA/m, the equivalent thermal dose of normal tissue at 60 min is less than 5 min, far less than the reversible tissue damage threshold of 40 min. Therefore, MIH under this magnetic field condition is feasible.

Figure 16. The equivalent thermal dose curves of tissue under different magnetic field conditions.

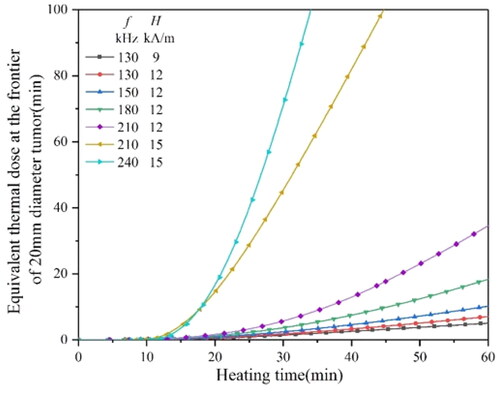
It can be seen from Figure 17 that when the H₀ is 9 kA/m, the f should be more than 120 kHz to achieve an equivalent thermal dose of 80 min in a short time, while when the H₀ is more than 10 kA/m, the f only needs 110 kHz or 120 kHz. Figure 18 indicates that, with the increase in tumor size, it needs higher H₀ and f to reach the equivalent thermal dose of 80 min. When the H₀ reaches 15 kA/m and H₀ reaches above 200 kHz, the equivalent thermal dose of 80 min can be reached quickly.

Figure 17. The equivalent thermal dose curves of a 10 mm diameter tumor heated by a 3.5 mm diameter material under different magnetic conditions.

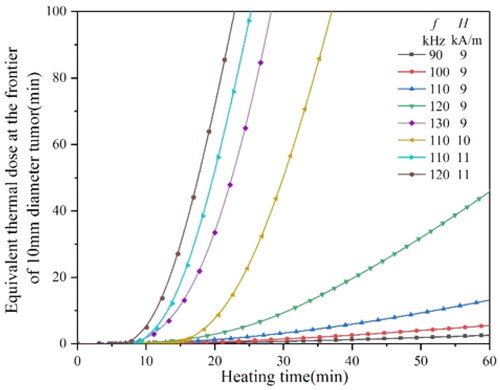
Figure 18. The equivalent thermal dose curves of a 20 mm diameter tumor heated by a 4 mm diameter material under different magnetic field conditions.

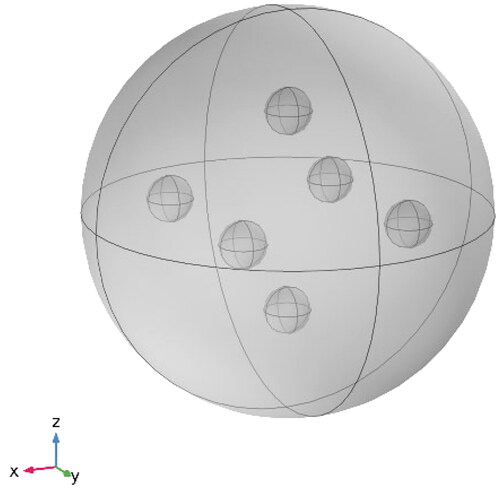
​In this paper, we use a multi-point placement method to distribute the heat generated by the magnetic media more uniformly for tumors with a diameter larger than 30 mm. The heating model is shown in Figure 19, 2 spherical magnetic mediums are implanted along the x-axis, Y-axis, and z-axis, respectively, and each two coaxial magnetic mediums are symmetrically distributed around the center of the tumor.

Figure 19. The heating model arranged by six spherical magnetic mediums.

Figure 20 shows that when the H₀ is above 9 kA/m, and the magnetic f is above 130 kHz, the equivalent thermal dose of 80 min could be reached within 60 min. Only if the H₀ is above 13 kA/m and the f is above, 180 kHz can the equivalent thermal dose reach 80 min in a short time.

Figure 20. The equivalent thermal dose curves of a 30 mm diameter tumor heated by six spherical magnetic mediums under different magnetic conditions.

4. Conclusion

In this paper, the multiphysics coupling model of MIH is established by using Comsol Multiphysics. The spherical magnetic media is selected as the optimal research object after analyzing the influence of shapes in the magnetic field. The optimal treatment conditions are obtained by studying the thermal damage caused by different sizes and positions of magnetic media under different magnetic field conditions. For tumors with a radius of 10 mm, the optimal magnetic field conditions are H₀ = (10–12kA/m) and f = (110–120kHz) when using the magnetic media with a diameter of 3.5 mm for treatment. For tumors with a radius of 20 mm, the optimal magnetic field conditions are H₀ = (15–16kA/m) and f = (210–240kHz) when using the magnetic media with a diameter of 4 mm for treatment. For tumors with a radius of 20 mm, the optimal magnetic field conditions are H₀ = (13–15kA/m) and f = (180–210kHz) when using six spherical magnetic mediums with a diameter of 3.5 mm for treatment. This paper can be used as a reference for applying Fe83Zr10B7 in MIH.

The simulation models in this study ignore the blood vessels, bones, and complex tissues surrounding tumors, which may affect the accuracy of the simulation results. In addition, the Fe₈₃Zr₁₀B₇ is a strip material; the laboratory has not yet been able to make it into a spherical or cylindrical shape; it may affect the accuracy of simulation results due to the human error exist in the machining process, which is a problem to be considered in future research. In conclusion, considering the suitable Curie temperature and the magnetic properties of Fe₈₃Zr₁₀B₇, it is feasible to be used as self-regulating temperature magnetic media in the future MIH.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The study of this paper is supported by the Zhuhai Industry-University-Research Cooperation and Basic & Applied Basic Research Project [ZH22017003210078PWC].