A comparison of models using removal effort to estimate animal abundance

Abstract

This paper compares methods for modeling the probability of removal when variable amounts of removal effort are present. A hierarchical modeling framework can produce estimates of animal abundance and detection from replicated removal counts taken at different locations in a region of interest. A common method of specifying variation in detection probabilities across locations or replicates is with a logistic model that incorporates relevant detection covariates. As an alternative to this logistic model, we propose using a catch–effort (CE) model to account for heterogeneity in detection when a measure of removal effort is available for each removal count. This method models the probability of detection as a nonlinear function of removal effort and a removal probability parameter that can vary spatially. Simulation results demonstrate that the CE model can effectively estimate abundance and removal probabilities when average removal rates are large but both the CE and logistic models tend to produce biased estimates as average removal rates decrease. We also found that the CE model fits better than logistic models when estimating wild turkey abundance using harvest and hunter counts collected by the Minnesota Department of Natural Resources during the spring turkey hunting season.

Keywords:

• catch–effort
• abundance estimation
• removal sampling
• Bayesian analysis
• hierarchical models
• validation set
• goodness of fit

1. Introduction

The abundance of an animal population can often be estimated from counts that are modeled by a binomial or multinomial model with the exact model form dependent on the sampling method used to collect the counts. Royle and Dorazio 16 developed a hierarchical framework to model animal abundance and occurrence in a closed population from spatially replicated counts collected using a variety of sampling methods. One such sampling method, removal sampling, involves capturing and removing animals from a population over successive periods in time and possibly distinct spatial locations. Information about the population size just prior to the start of removal sampling is provided by the size and rate of decrease in successive removal counts.

Estimates of abundance based on a removal count model, or a similar replicated count model, are sensitive to the modeling assumptions made about the probability of removal, or detection, of animals in the population. Studies by Dorazio and Royle 3 4 and Pledger 14, among others, showed that estimates of abundance can behave very poorly if the distribution used to model the probability of removal is not properly specified. Therefore, careful thought must be given about how to model the probability of removal and whether this probability is constant across sampling periods and sampling locations. Dorazio et al. 1 compared hierarchical models of abundance for analyzing removal counts obtained at spatially distinct locations and found that the best fitting models allowed site-specific removal probabilities. Such site-specific removal, or detection, probabilities can also be modeled with covariates that vary across sites or sampling periods. For example, Kéry et al. 11 and Forsyth et al. 6 used a logistic model for probability of detection that depended on sampling effort and habitat covariates.

This paper focuses on comparing removal probability models that incorporate a covariate that measures removal effort. We consider both a logistic regression specification for the removal probability and a catch–effort (CE) specification that assumes a Poisson process for removal effort [Chapter 7]18. Both models will allow for heterogeneity in the removal probability by modeling it as a function of a measure of removal effort (e.g. number of hunters, number of lobster traps) for each sampling period and location. Logistic models of this type have been studied before but little research has been done on exploring the usefulness of a CE model for the removal probability in the hierarchical framework developed in 16. We applied both models to wild turkey harvest data collected by the Minnesota Department of Natural Resources (MN DNR) with the goal of determining which removal probability specification results in the best estimates of abundance and which is the most useful for predicting harvest rates for a given level of effort. We used Bayesian validation and goodness-of-fit (GOF) techniques to compare the fit of these models on the wild turkey harvest data and also conducted a simulation study to evaluate the behavior of each model for various population and removal scenarios.

Section 2 describes the logistic and CE models that will be compared and Section 3 outlines our Bayesian analysis and GOF tests. Section 4 describes the wild turkey and simulation results and Section 5 contains a discussion.

2. The model

2.1. Sampling method

Mark–recapture, point count, and removal surveys are common sampling methods used to estimate animal abundance or indices of abundance. In this paper, we will focus on the latter method of data collection and assume that removal counts were measured for at least two periods in time at spatially distinct locations. We will also include harvest counts collected during a hunting season in our definition of removal counts. This method of removing animals will induce a multinomial likelihood on the sequence of counts observed for each time period if we assume the population of animals in that region is closed, except for removals, during the removal (hunting) time periods. The regional data model is parameterized by N, the number of animals in the region, and p, the removal (harvest) probability for each time period. If more than one region is sampled, the full data likelihood will be the product of regional multinomial likelihoods which can model regional homogeneity (e.g. all regions might share the same p) or heterogeneity. We will consider models that allow for regional heterogeneity in both abundance and removal parameters.

Suppose m successive removal counts are observed in each of n distinct sample units surveyed. While these units could be points or line transects, we will assume that the sample units are non-overlapping areal regions since we are particularly interested in modeling harvest counts collected on this scale. Each region i contains a local population of N _i animals prior to the start of the first removal period and during period j the removal probability p _ij is the same for each animal in region i. Let y _ij be the number of animals removed from region i during period j with giving the total number of animals removed in region i. The vector of removal counts observed within a given region i has the following multinomial model:

The probabilities in this multinomial model are functions of the removal probabilities p _ij with

representing the probability that an animal is removed during, but not before, period j. We also assume that the ’s are independent vectors given the local abundance parameter N _i and the removal parameter . Our goal is to estimate both the local abundance N _i and local removal p _ij parameters.

2.2. Using removal effort to model the probability of removal

Let g _ij measure the removal or hunting effort expended in region i during period j. We will consider two methods of modeling the removal probability p _ij as a function of effort g _ij .

2.2.1. A CE model

The first model for p _ij that we will consider has a CE specification. Let θ _i be the probability that an animal is removed with one unit of effort in region i. If we assume that effort is additive (i.e. each unit of effort acts independently and has the same probability of removing an animal) and θ _i is constant across all n periods, then the probability of survival (non-removal) for an animal in region i during period j is . Our removal probability for an animal in this region and period is then

While we will use the per-unit removal probability expression of p _ij , it is often parameterized in terms of a catchability coefficient so that 18 19.

The per-unit removal probability θ _i could be modeled in a variety of ways depending on the data available and assumptions made regarding the population and removal sampling. We will consider a simple fixed-effects model specification

for i=1, …, n, where a _i and b _i are constants used to model the known heterogeneity in removal probability across regions. If we lack this prior knowledge about regional heterogeneity, we will use the same N(a, b) prior for all logit-scaled probabilities θ _i . Alternatively, we could use a hierarchical specification to model regional variation in removal probability

for i=1, …, n, where μ_η and are unknown hyperparameters that are given priors p(μ_η) and . The hierarchical model assumes that all logit-scaled probabilities θ _i are realizations from a common meta-level model with the meta-level parameter μ_η controlling the mean logit-scaled per-unit removal probability across all n regions and controlling the heterogeneity.

Of course alternative models for θ _i are possible. If no per-unit removal heterogeneity is present, we could use a uniform prior to model the constant removal probability . If the probability of removal could vary across regions and removal periods and relevant covariates are available, then we can model η _ij as a function of time- and region-specific covariates x _ij and parameters which could also be region or time dependent.

2.2.2. A logistic regression model

The second type of specification for p _ij that we will consider is a logistic regression model. We will then model the removal probability p _ij as

We will allow the parameters in this logistic model to vary across regions since the CE model in Section 2.2.1 allowed similar regional variation in the per-unit removal probability θ _i . Also as done in Section 2.2.1, we will compare a fixed-effects and random-effects parameterization of this model. The fixed-effects version will place a two-dimensional multivariate normal prior on the logistic model parameters

for i=1, …, n, where is a known prior mean vector, is a known prior variance vector, and I a two-dimensional identity matrix. The hierarchical random-effects version will be

for i=1, …, n, where and are, respectively, the unknown meta-level population mean and variance vectors. Both meta-level parameter vectors will be given priors and . Additional covariates could also be added to either the fixed- or random-effects models.

2.2.3. Comparing models

Figure 1 displays removal probability p _ij as a function of effort g _ij for the CE and logistic specifications for four values of θ _i and α_{1, i} . The intercept α_{0, i} was chosen so that p _ij was equal to approximately 0.01 when effort was equal to 0 (). Under the CE specification, p _ij will always be equal to 0 when effort is 0. The logistic model yields a sigmoidal function of effort for various values of α_{1, i} , while the CE model displays steep ascents to 1 for the larger values of θ _i (0.10, 0.05) and an almost linear function of effort for small values of θ _i (0.001). A more general comparison of the two model forms can be derived if we consider 1−p _ij the probability that an animal survives (not removed during) a removal period. The logit model (6) assumes that each additional unit of effort will change the odds of survival by the factor , while the CE model (3) assumes that each additional unit of effort will change the probability of survival by the factor 1−θ _i (or ).

Figure 1. Probability of removal during one removal period for (a) the CE specification for θ _i of 0.1, 0.05, 0.01, and 0.001 and (b) the logistic specification p _ij =1/[1+exp(−α_{0, i} −α_{1, i} g _ij )] with α_{0, i} =−4.6 and α_{1, i} of 0.1, 0.05, 0.01, and 0.001.

2.3. Modeling abundance

We will use a Poisson distribution to model local abundance N _i

where λ _i is the mean animal abundance in region i. This approach allows us to model the variation in abundance that often occurs in animal populations that reside across different geographic regions. Of course with areal sample units differences in local abundance could simply be due to differences in the sizes of the sampled regions. Therefore, we will let the mean regional abundance be equal to area A _i times density, or where γ _i is the average density of animals per unit area in region i. We will use a hierarchical specification to model the log-density φ _i which will allow us to quantify both a regional mean density level and the regional heterogeneity in density. This model will have the form

for i=1, …, n. The mean parameter μ_φ describes the average log-density across all regions and the variation in these regional log-density levels is captured by . Both parameters are given prior distributions p(μ_φ) and .

3. Bayesian analysis

The joint posterior for any of our proposed models will have the form

with Ψ _i representing each model's removal probability parameters (θ _i or ) and, if needed, ψ representing the model's meta-level parameters. The multinomial probabilities given in Equation (2) are simply functions of these Ψ _i . Vectors with no subscripts denote the collection of all i=1, …, n regional vectors (e.g. ). For the hierarchical models in Equations (5), (8), and (9), we chose a conjugate normal prior for all mean meta-level parameters μ_η, , and μ_φ, while uniform priors were used to model the meta-level standard deviations σ_η, and σ_φ.

We used WinBUGS 12 and R 15 to fit and analyze the models described in Section 2 using Markov chain Monte Carlo (MCMC) simulations, but we preferred specifying a marginalized version of Equation (10) since it had better MCMC convergence properties than did the full joint posterior described by Equation (10). The marginalized model removed the local abundance parameters N _i by summing the joint distribution of the data and N _i , , over the values N _i =y _i. to ∞ which induces a Poisson distribution with mean on the individual removal counts y _ij . After fitting this marginalized model, the posterior can be approximated by using the data augmentation algorithm of Tanner and Wong 21 (see [pp. 286–290]17 for more details on this marginalization and data augmentation process).

3.1. Model comparison

We considered several criteria when comparing our models. The deviance information criterion (DIC) suggested by Spiegelhalter et al. 20 measures both the fit and complexity of a model, with lower values given to good fitting, parsimonious models. DIC is the sum of p _D , the effective number of parameters in the model, and , the posterior expectation of the deviance . For the models described in Section 2, WinBUGS measures p _D as where is the deviance measured at the posterior expectations of φ _i and Ψ _i .

We also computed the posterior predictive loss criterion suggested by Gelfand and Ghosh 7 as an alternative to DIC since work by Millar 13 suggests that DIC may not be a trustworthy comparison measure when fitting hierarchical models to count data. The posterior predictive criterion that minimizes the posterior predictive expectation under squared error loss is a linear combination of a GOF measure and a predictive variance measure for an unknown replicate set of responses . The predictive criterion is for k>0 with smaller k resulting in larger penalties for models with larger predictive variance. Smaller values of D _k indicate better fitting models. While there is no closed form of D _k for our models, Monte Carlo estimates of G and P are easily obtained from the WinBUGS simulation results for each model.

3.2. Model validation

Models were also assessed using residuals and GOF measures computed for a validation sample that consisted of the removal counts that were observed during the last m−[mtilde] removal periods (1<[mtilde]<m) available in the data set. Let denote the set of responses that were used to fit a model and denote the validation sample. The model under review was fit using for all i=1, …, n regions and the validation set was compared with the responses expected from the predictive posterior . The joint distribution of and , given N _i and Ψ _i , is multinomial, which means that the posterior of given , N _i and Ψ _i is also a multinomial distribution with parameters adjusted appropriately. If we revert back to the original parameterization of the multinomial sampling model shown in Equation (1), then this posterior is equal to

where is the number of animals remaining in region i after the first [mtilde] periods and

are the removal probabilities for periods conditioned on surviving periods 1 through [mtilde].

3.2.1. Residuals

The fit of the predictive posterior was analyzed by checking the Bayesian residuals of the validation sample. The Bayesian residuals were defined as

with denoting the standardized Bayesian residuals. The predictive expectation and variance of the validation sample are estimated by generating multinomial realizations from Equation (11) using the posterior draws of N _i and π _ij given by the WinBUGS simulation.

3.2.2. Goodness of fit

We also used the validation set to assess each model with a GOF test that used the χ² discrepancy measure suggested by Gelman et al. [p. 175]8. Three types of tests were considered, the first being an omnibus check of a model's ability to predict the number of removals made during the periods [mtilde]+1 through m. Since the validation sample is multinomial, the cumulative number of animals removed over the last m−[mtilde] removal periods, denoted as , will have a binomial distribution with parameters Ñ _i and . The mean and variance for this binomial distribution will be used to form the first GOF test statistic:

As with any GOF test, we will compare the value of T ₁ computed with the observed validation sample, denoted here as , to the values of T ₁ that one would expected from totals [ttilde] _i drawn from the binomial distribution specified above. A Bayesian p-value will be formed by weighting these binomial probabilities by the posterior distribution of the local abundance Ñ _i and removal probabilities used to compute the test statistic (12). If , then the Bayesian p-value for this GOF test is

We can estimate this p-value as follows

	(1) Generate a draw of from the posterior .
	(2) Generate a realization of from a Binomial distribution.
	(3) Compute the observed test statistic value and the theoretical value .
	(4) Repeat steps 1 through 3 H times and [pcirc] 1 will be equal to the proportion of times that is greater than or equal to the observed statistic .

Estimates of p ₁ that are small indicate that cumulative removal counts produced by the model's predictive posterior do not adequately match the actual cumulative removal counts observed in the validation sample.

The remaining two GOF tests are constructed in a similar manner. The second GOF test will assess how well a model can predict the number of removals made for each of the m−[mtilde] removal periods in the validation set. Recall that these individual removal counts are multinomial given , Ñ _i and , so the GOF test statistic will be

The third test is designed simply to check the GOF of individual regions

The Bayesian p-values for the test statistics T ₂ and T _{3, i} , denoted as p ₂ and p _{3, i} , are constructed in a similar manner as was p ₁ in Equation (13).

4. Examples

4.1. The wild turkey harvest

The wild turkey (Meleagris gallopavo) was successfully reintroduced in Minnesota during the 1960s and 1970s after its extirpation from the state in the late 1800s. In 1978, a spring turkey hunting season was started in southern Minnesota and by 2010 wild turkeys could be hunted legally throughout half of the state each spring during eight 5- to 7-day hunting periods. The wild turkey hunt is regulated by allocating a fixed number of hunting permits per season (hunting periods) for each turkey permit area (TPA) in the state.

An accurate assessment of the abundance of wild turkey populations in the state is needed for wildlife managers to determine permit allocations for each season. Demand for these permits is typically greater than the number of permits available, so deciding how many permits to allocate each year is important both for the viability of turkey populations and the satisfaction and safety of hunters. The MN DNR regulates the number of permits issued each year and requires hunters to register each harvested bird (only one bird per permit is allowed). Each recorded harvest indicates the location (TPA) and time period that the harvest occurred. We are interested in using hunter and harvest counts from the spring season to estimate the abundance of wild turkeys prior to the start of the season.

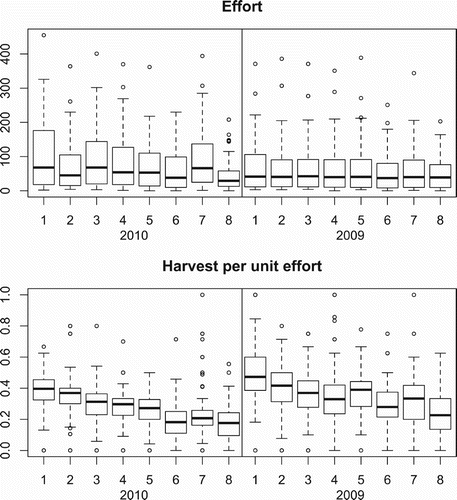
Our sample units are the TPAs open for hunting during the m=8 spring time periods. In 2010, there were n ₁₀=77 TPAs and in 2009, there were n ₀₉=76. The size A _i of each TPA is measured in square miles. Removal effort g _ij is measured by the number of permits issued for each TPA and time period combination. Harvest (removal) counts y _ij are also measured for each TPA and time period combination, and since the vast majority of harvested birds during the spring season are male (e.g. 99.5% in 2010), we will use these harvest counts to assess the abundance of the male portion of the wild turkey population. Figure 2 shows removal effort and harvest per unit effort for 2010 and 2009. The effort in 2010 is higher and more variable than 2009. The total number of permits issued was 46,451 (603.3 per TPA) in 2010 and 36,187 (476.1 per TPA) in 2009. Even after accounting for the additional TPA opened in 2010, the total number of permits issued increased by over 10,000 from 2009 to 2010. The decrease in uniformity of effort across the eight time periods from 2009 to 2010 was primarily due to changes in spring turkey hunting regulations. The MN DNR increased the number of permits made available to hunters for time periods 7 and 8 by 110% from 10,582 in 2009 to 22,250 in 2010 and of these permits available for the 2010 season, approximately 46% were issued to hunters 5. Both years show a decreasing trend in harvest per unit effort over the 8 time periods, which somewhat levels out during the final weeks of the season. This trend is not surprising since the removal of birds in early time periods will leave fewer available for harvest in later time periods.

Figure 2. Effort, measured by number of hunting permits issued, and harvest per unit effort for the eight hunting periods (1 through 8) in 2009 and 2010.

The models that we considered assumed that p _ij was the probability of removal for each wild turkey and each of the g _ij permit holders used the same amount of effort to attempt to harvest one bird during hunting period j in region i. We fit each model separately for 2009 and 2010 since our main goal in this paper is to assess the fit of an abundance models for a given year rather than tracking abundance trends over multiple years (which is future work). Section 2.2.1 describes the two CE models that we considered: the ‘CE’ model refers to the fixed-effects specification (4) of the per-unit removal probability θ _i and the ‘hierarchical catch–effort’ (HCE) model refers to the hierarchical specification of θ _i given in Equation (5). Estimates from these CE models were compared to estimates obtained from the two logistic models described in Section 2.2.2: the ‘Logit’ model refers to the fixed-effects specification of the removal probability p _ij given in Equation (7), while ‘HLogit’ refers to the hierarchical modeling of this parameter shown in Equation (8).

Vague prior distributions were given to most model parameters. For the abundance model described in Section 2.3, we placed a normal prior with mean 0 and variance 100 on the meta-level mean μ_φ and a uniform prior from 0 to 5 on the meta-level standard deviation σ_φ. Identical priors were used for the meta-level mean μ_η and standard deviation σ_η parameters for the HCE model in Equation (5). In the HLogit model (8), N(0, 100) priors were chosen for and uniform(0, 10) priors where used for the standard deviations (k=0, 1). Priors for the fixed-effect CE and Logit models in Equations (4) and (7) were also normal distributions centered at a _i =d _{k, i} =0 with a variance of for k=0, 1 and i=1, …, n.

WinBUGS was used to fit each model using three chains of length 100, 000 with a burn-in of size 50, 000 and a thinning frequency of 30, resulting in a final simulation size of 5000. Convergence was assessed by the scale reduction factor 9 and a visual inspection of the mixing of the chains created for each parameter. Most parameters had scale reduction factors within 0.01 of 1 and all factors were with 0.09 of 1, which, along with the visual inspection, indicated adequate convergence for all models.

Table 1 compares the CE and logistic models using DIC and the posterior predictive loss criterion discussed in Section 3.1. The values of k=1 and k=9 put a downscaling factor of 0.50 and 0.90, respectively, on the GOF measure G when estimating D _k . Interestingly, the DIC measure favors the CE models in both years while the posterior predictive loss criterion D _k only favors these models in 2010. In 2009, both CE models have smaller posterior variance (P) but higher GOF measures (G) when compared with the logistic models. Thus, when k=1 the CE looks like the best model choice but when k=9 the HLogit does slightly better. The non-hierarchical parameterizations of both the CE and logistic models decreased the average deviance of the model when compared with the hierarchical version (similar results were shown in 1) but the complexity and predictive variances of the hierarchical models were smaller since they allowed regional removal probability parameters (either η _i or β _{k, i} ) to be shrunk toward a common mean (either μ_η or ).

Table 1. Model comparison using DIC (with average deviance ¯Dev and the effective number of parameters p _d ) and using the estimated posterior predictive loss criterion with k=1 and k=9.

Year	Model	p D	¯Dev	DIC	Ĝ	[Pcirc]	[Dcirc] 1	[Dcirc] 9
2009	CE	96.5	3171.6	3268.2	13,716.1	13,476.2	20,334.2	25,820.6
	HCE	86.5	3192.9	3279.3	14,450.0	13,273.6	20,498.6	26,278.6
	Logit	158.2	3179.9	3338.2	12,144.9	14,713.1	20,785.6	25,643.5
	HLogit	100.8	3230.1	3330.9	13,060.7	13,882.1	20,412.5	25,636.8
2010	CE	110.2	3167.4	3277.6	9507.1	15,064.1	19,817.6	23,620.4
	HCE	98.8	3198.6	3297.4	10,081.9	14,689.4	19,730.4	23,763.1
	Logit	178.3	3184.0	3363.2	8205.9	16,569.3	20,672.3	23,954.7
	HLogit	132.0	3304.6	3436.6	9631.7	15,353.5	20,169.4	24,022.1

Model validation was done using the first [mtilde]=4 time periods to fit each model and harvest counts from the last four time periods (periods 5–8) were used as the validation sample. Analysis of the Bayesian residuals (Section 3.2.1) for the validation sample shows that the 2010 standardized residuals were fairly similar for both CE and logistic models but there was slightly less variation (extreme values) for the CE models for the 2009 validation sample. In general, both models seem slightly more prone to overestimation of the harvest counts during the validation sample time periods. This overestimation suggests that there may be some TPA where the removal probability decreases at some point during the hunting season.

The first GOF test indicates no significant lack-of-fit in each model's ability to predict the total harvest for time periods 5–8 (CE: [pcirc] ₁ equals 0.44 and 0.42 for 2009 and 2010, respectively; HCE: 0.61 and 0.49; Logit: 0.42 and 0.22; HLogit: 0.56 and 0.25). All models do show a significant lack-of-fit in at least one TPA when predicting the time-period-specific harvest counts (all ). With 76 and 77 individual GOF tests (test 3) for each year, we would expect about 4 of the TPA-level tests to be significant at the 5% level if no lack-of-fit was present. The CE models for both years have between 16 and 18 regions with [pcirc] ₃ less than 5%, while the logistics models for both years have between 15 and 33 significant TPA-level tests at the 5% level. Figure 3 displays which TPAs have significant lack-of-fit at the 5% and 1% levels, with regions in the southeastern portion of Minnesota standing out for all models in both 2009 and 2010 and regions in the northern range of the hunting region standing out in 2010. The lack-of-fit in these clusters of TPAs is likely due to violations in the assumptions of equal and independent per-hunter effort and constant per-hunter removal probability that all models share. The results of GOF tests suggest that there are some issues with GOF for some TPAs, but the tests also indicate that the CE models have better overall fit for both 2009 and 2010 when compared to the logistic models. Similar results were indicated by the model comparison criteria given in Table 1.

Figure 3. p-Values for individual TPA-level GOF tests (T ₃) for 2009 (a) and 2010 (b). TPAs with GOF p-values [pcirc] ₃ between 1% and 5% are shaded medium gray, while TPAs with p-values below 1% are shaded in dark gray. Regions with no significant lack-of-fit at the 5% level are shaded light gray.

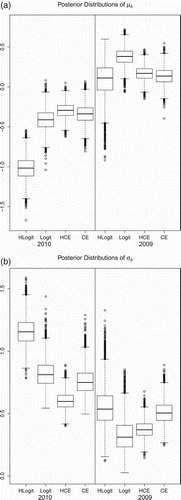
Figure 4 displays the posterior distributions for the meta-population level log-density parameters μ_φ and σ_φ. As indicated by the predictive posterior criteria [Pcirc] given in Table 1, the posterior distributions under the HCE model have less variation than the other models under consideration. Both CE models have similar posterior expectations for μ_φ but the posterior under the HLogit model supports smaller values of μ_φ than does the Logit model and both CE models. All models, expect the 2009 Logit model, support heterogeneity in log-density with posteriors for σ_φ that are not concentrated near 0.

Figure 4. Posterior distributions for (a) μ_φ and (b) σ_φ.

Table 2 gives estimates of the meta-population density parameters γ for the HCE and HLogit models. The mean and variance for the log-normal distribution of γ were computed as functions of the mean and standard deviation of where and . Monte Carlo standard errors were computed for each posterior mean estimate using the consistent batch means standard error estimator described in 10. Both models estimate mean regional density to be approximately 1.3 turkeys per square mile in 2009, while in 2010 the HCE model estimate drops to 0.90 and the HLogit model estimate drops to 0.72. The HCE model produces smaller credible interval for these parameters than the HLogit model. The HCE model also produces smaller estimates of than the HLogit model for both years, most notably in 2010. This 2010 HLogit heterogeneity in the γ _i is possibly due to the influence of the removal probability intercept parameter α₀ which gives the logit-scaled removal probability at 0 effort. In 2010, the mean removal probability of HLogit with 0 effort is for one period which results in unrealistically large harvest probabilities for TPAs that have small amounts of effort for each removal period. The overall harvest rate in these regions is larger for the HLogit model than all other models which results in density estimates that are much smaller than other models. In 2009, the mean removal probability with 0 effort for the HLogit model is much smaller with . Note that we did explore logistic models with no intercept term but their fit was much poorer than the models that did include α₀.

Table 2. Estimates of the metapopulation parameters for abundance and removal probability in the HCE and logit (HLogit) models.

Parameter	Model	Mean (MCSE)	Median	95% CI
2009
μγ	HCE	1.275 (0.002)	1.272	1.084, 1.495
	HLogit	1.297 (0.003)	1.299	0.915, 1.672
	HCE	0.495 (0.001)	0.483	0.324, 0.729
	HLogit	0.781 (0.003)	0.735	0.439, 1.364
μη	HCE	−7.367 (0.002)	−7.367	−7.572, −7.160
ση	HCE	0.550 (0.001)	0.549	0.414, 0.700
	HLogit	−4.647 (0.005)	−4.681	−5.180, −3.928
	HLogit	0.882 (0.002)	0.889	0.577, 1.147
	HLogit	0.0158 (0.00004)	0.0158	0.011, 0.020
	HLogit	0.006 (0.00002)	0.006	0.003, 0.009
2010
μγ	HCE	0.899 (0.001)	0.893	0.749, 1.076
	HLogit	0.723 (0.002)	0.706	0.511, 1.040
	HCE	0.598 (0.001)	0.582	0.427, 0.855
	HLogit	1.264 (0.006)	1.176	0.692, 2.345
μη	HCE	−7.036 (0.001)	−7.035	−7.228, −6.838
ση	HCE	0.555 (0.001)	0.549	0.416, 0.726
	HLogit	−3.027 (0.002)	−3.023	−3.240, −2.834
	HLogit	0.415 (0.002)	0.413	0.203, 0.642
	HLogit	0.010 (0.00002)	0.010	0.008, 0.013
	HLogit	0.005 (0.00002)	0.005	0.003, 0.008
Note: Monte Carlo standard errors (MCSE) are given for each estimated posterior mean.

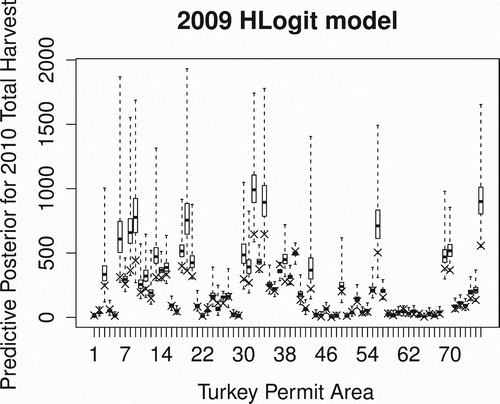
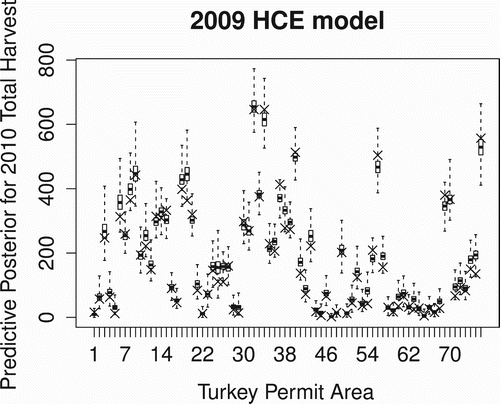
We also considered the management task of allocating hunting permits for an upcoming hunting season by assuming no change in abundance and removal probability so that we could use the 2009 models to estimate 2010 harvest totals for a given amount of effort. Using the actual number of hunters in 2010, we used the 2009 model to compute the predictive posterior distributions for the (unseen) 2010 harvest total for each of the 76 TPAs where hunting was permitted in 2009. Figures 5 and 6 show these predictive posteriors for the HLogit and HCE models, respectively, along with an × marking the actual harvest total from 2010. While both models tend to overestimate the harvest total, likely due to the larger 2009 abundance estimates (Table 2), the HCE model would be the preferred model for prediction purposes since it produces predictive posteriors with smaller variation than the HLogit model.

Figure 5. Each boxplot displays the TPA-level predictive posterior distribution for the total harvest predicted from the 2009 HLogit model using the hunter counts from 2010. Each×denotes the actual 2010 total harvest.

Figure 6. Each boxplot displays the TPA-level predictive posterior distribution for the total harvest predicted from the 2009 HCE model using the hunter counts from 2010. Each×denotes the actual 2010 total harvest.

4.2. Simulation results

We also conducted a simulation to study properties of the HCE model proposed in this paper using removal counts generated from the catch-per-unit-effort process described in Section 2.2.1. For comparison purposes, we also fit the hierarchical logistic regression model (HLogit) in Equation (8) to these simulated removal counts. The number of regions (n=30) and log-density parameters were held fixed for the simulation, but the logit-scaled removal probability parameters and number of removal periods (m) were allowed to vary. We also assumed that each region had equal area of A _i =1 so that the mean density of about also measures the mean abundance in each region. Removal effort varied throughout the regions and was designed to decrease from removal period 1 to m. For each unique data generating process, we obtained 100 realized removal counts and used WinBUGS to fit the HCE and HLogit models. The prior distributions and chain lengths described in Section 4.1 were also used in this simulation study. Parameter estimates (posterior means) and 95% credible intervals were obtained for each model and we computed the root mean square error (RMSE) and relative bias () for each estimator and the average credible interval length and coverage rate.

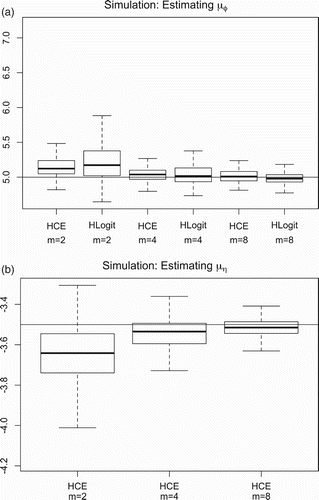
Table 3 compares log-density parameter estimates and provides HCE removal probability estimates for data generated using m=8 removal periods and varying levels of hunter effort and catchability. The average total removal effort per region () was either 48.8 or 488 units of effort and the mean logit-scaled per-unit removal probability ranged from to μ_η=−7. For each level of effort and mean removal probability, the average probability of harvest across all regions for the data generating process was calculated as

where . Table 3 shows that when harvest probabilities are at their highest (above 50%) both the HCE and HLogit models perform well when estimating mean meta-level parameters (small relative bias and RMSE, coverage rates near 95%). As the harvest rate decreases, we see an increase in both the bias, RMSE, and interval length in the mean abundance estimates from both the models with the HLogit model performing worse than the HCE model. At this lower harvest level, both the models also underestimate the regional density variability σ_φ, though the coverage rate of each model's interval estimates are still near the nominal 95% rate. The HCE model also tends to underestimate the logit-scaled removal probability mean parameter μ_η and overestimate the regional removal probability variation σ_η, and this bias gets worse as the harvest rate decreases.

Table 3. Simulation results based on 100 sets of removal counts generated from the catch-per-unit-effort process described in Section 2.2.1.

DGP				Estimator properties
Harv		Parameter	Model	Average	RMSE	Relative bias	Coverage	Length
76.4%	48.8	μφ=5	HCE	5.013	0.098	0.262	95	0.401
			HLogit	4.977	0.097	−0.464	94	0.420
			HCE	0.517	0.126	3.480	96	0.331
			HLogit	0.517	0.065	3.391	97	0.298
			HCE	−3.515	0.045	−0.433	99	0.202
			HCE	0.103	0.063	106.9	99	0.219
58.6%	48.8	μφ=5	HCE	5.043	0.122	0.866	91	0.440
			HLogit	5.046	0.198	0.927	90	0.667
			HCE	0.504	0.077	0.862	93	0.309
			HLogit	0.488	0.075	−2.327	98	0.336
		μη=−4	HCE	−4.041	0.100	−1.031	93	0.366
			HCE	0.152	0.113	203.67	98	0.359
27.9%	48.8	μφ=5	HCE	5.536	0.866	10.717	89	2.169
			HLogit	6.132	1.649	22.644	82	4.004
			HCE	0.372	0.157	−25.579	89	0.574
			HLogit	0.396	0.133	−20.815	97	0.605
		μη=−5	HCE	−5.576	0.938	−57.613	87	2.312
			HCE	0.338	0.299	576.7	85	0.637
70.0%	488	μφ=5	HCE	5.003	0.096	0.057	96	0.402
			HLogit	4.979	0.113	−0.416	97	0.463
			HCE	0.518	0.071	3.547	95	0.300
			HLogit	0.519	0.079	3.753	96	0.307
		μη=−6	HCE	−6.010	0.062	−1.025	94	0.235
			HCE	0.105	0.067	110.24	98	0.251
35.9%	488	μφ=5	HCE	5.169	0.327	3.372	92	0.993
			HLogit	5.675	1.174	13.506	82	2.695
			HCE	0.428	0.126	−14.449	91	0.470
			HLogit	0.415	0.123	−16.960	94	0.545
		μη=−7	HCE	−7.200	0.370	−2.827	92	1.099
			HCE	0.271	0.240	442.04	90	0.566
Note: For each scenario, we fixed n=30, m=8, μφ=5 and but let the removal probability parameters and effort vary.

Figure 7 shows simulation results for varying the number of hunting periods (m=2, 4, 8). The HCE and HLogit models show a tendency to overestimate the mean abundance μ_φ as the number of removal periods m decrease and the HCE model tends to underestimate μ_η as m decreases. We also considered a scenario with m=8 time periods and μ_φ=5 with μ_η equal to −3.5 during periods 1–4 and then dropped μ_η down to −3.7 during periods 5–8. We found that both the HLogit and HCE models underestimated abundance (relative bias of −3.1% and −1.7%, respectively) and have less than optimal 95% confidence interval coverage rates (68% and 84%, respectively). We were surprised to find that the HCE model produced an average estimate of that was greater than both of the values of μ_η used in the data generating process (−3.5 and −3.7). We think that this may have occurred because the HCE model overcompensated for the larger than expected drop in removal counts during periods 5–8 by overestimating the overall probability of removal (i.e. if more animals were harvested in the initial periods then there will be fewer to harvest in the later periods). This positive bias in estimating the removal probability is the reason for the negative bias in abundance estimates.

Figure 7. Each boxplot shows the distribution of estimates of (a) μ_φ and (b) μ_η obtained from 100 removal samples with m=2, 4, or 8 removal periods with μ_η=−3.5 and μ_φ=5.

5. Discussion

The CE models for the wild turkey harvest data generally fit as good or better than the logistic removal probability models that we considered (Table 1). The validation sample GOF results indicate that all models can estimate total harvest for the last four periods given results from the first four periods (test 1), but all models show some lack-of-fit when broken down into an assessment of the per-period harvest count predictive capabilities. Again though, the CE models show less lack-of-fit than the logistic model (Figure 3).

These results suggest that the catch-per-unit-effort specification for the per-period removal probability is preferred over the logistic model for our wild turkey harvest data. While the assumption of additivity in the CE model is strong, it is actually not any stronger than the assumptions inherent in the logistic model when using removal effort as a covariate. In the logit model, each additional unit of effort will change the odds of survival by the factor while with the CE model, each additional unit of effort will change the probability of survival by the factor 1−θ _i . Regardless of the model, each additional unit of effort has the same effect on either the odds or probability of survival and violations of the additivity assumption will result in biased estimates from either model. Both models also currently assume that the effect of each unit of effort on the probability of removal (e.g. the parameter θ _i or α_{1, i} ) is the same across all eight hunting periods and the removal probability p _ij is constant during hunting period j. As described by Seber 18, these assumptions are often not completely satisfied when using removal effort to estimate abundance. Weather conditions and variation in individual hunter ability are likely sources of day-to-day variation in the removal probability for each unit of effort. We could also see a small decrease in p _ij during hunting period j due to the catch limit of one bird per permit which may result in a small decrease in effort during the 5–7-day-long hunting period. Our simulation results suggest that both models are prone to underestimating abundance when the removal probability drops halfway through an eight-period-long hunting season.

While the CE model we considered in this paper looks promising, we believe it could be improved by pursuing two avenues. First, we could relax the i.i.d. assumptions made for the TPA-level density γ _i and per-unit removal probabilities θ _i and allow some form of dependence to exist between TPAs at this level. One option would be to model densities using a conditionally autoregressive (CAR) model for one (or both) of these parameters as was done with point-count data by Webster et al. 22. Alternatively, Dorazio et al. 2 propose using a Dirichlet process prior to model φ _i when we lack the covariates needed to explain variation in abundance across the region of study. While the CAR model will place a spatial dependence on the parameters, the Dirichlet process prior will allow a weaker dependence to exist between regions that may, for example, have similar densities due to similar habitat but which may not be located next to one another. The second avenue to pursue will be to add a temporal scale to the model so that we can estimate changes in abundance across multiple years. While the current (non-dynamic) version of the HCE model shows promise when predicting future harvest totals (Figure 6), such predictions will likely be improved by allowing future abundance level to change over time with a dynamic population model. A temporal HCE model will be valuable from a management perspective since it will monitor abundance over multiple years and predict next years harvest rates based on any number of permit allocation (effort) scenarios.

Acknowledgements

This work was supported in part by a Hewlett Mellon Fellowship from Carleton College. The authors thank Dr John Fieberg, MN DNR, and Dr Robert Dorazio, US Geological Survey, for their suggestions on this paper.

Additional information

Notes on contributors

Eric Dunton

Present address: Shiawassee National Wildlife Refuge, US Fish, Wildlife Service, Saginaw, MI 48601, USA.