What makes a liquid crystal? The effect of free volume on soft matter

Abstract

In this article, we probe the formation of liquid crystal and soft crystal phases as a consequence of minimising the free volume of the system either through design engineering of molecular shape or through deformation of molecular architecture. Following this concept, a number of realisations were made, for example, smectic A phases with variable layer spacing, smectic C phases without layer shrinkage, lattices of free space and fibres in N_TB phases.

Keywords:

• free volume
• smectic
• soft matter
• liquid crystal
• soft crystal
• NTB

Prologue: At the start of my thesis research in 1974, the knowledge of the structures of smectic liquid crystals was somewhat limited. Even though his thought predated the discovery of ferreoelectric behaviour in liquid crystals, George Gray had the idea that smectic C (SmC) liquid crystals might underpin potential new display applications. As I launched into synthesising new SmC variants, I started to think about why molecules should tilt over in their layers, and then onwards to question why do certain materials exhibit different forms of smectic B (SmB) phases, which was before their classification as hexatic and crystal B phases, etc. In those days I became very much interested in how the molecules pack together in condensed phases. With protractors, compasses and graph paper, the Cartesian coordinates of the atoms of a variety of molecular structures in their all trans forms were located, and their mass axes were determined for their structures by computer methods using ticker-tape which used to shoot out of the machine in volumes to yield just one result – the minimum moment of inertia. Flipping the structures about their inertia axes by 180° yielded the surface contours and the rotational volumes of the molecules. Packing them together in ways to minimise the free volume gave snapshot pictures of the local structures of various mesophases.[1] Over the passing years, I discarded this methodology for the following reasons: (1) the molecules in liquid crystal phases are rotationally disordered and are in dynamic fluctuation as demonstrated by neutron scattering studies [2,3]; (2) X-ray data showed that the molecules pack close enough together that they interpenetrate each other’s independent rotational volumes, meaning they share each other’s space [4,5]; (3) there were no ways to simulate the interpenetration of space, and what was free space and what was not; (4) there were only a few families of materials that could provide full data sets on structure versus phase formation; to this day there are still relatively few full homologous series of materials being reported; and lastly (5) there was no discussion of how to determine the energy cost of not fully packing space with molecules in order to minimise the remaining free volume. However, with the advent of research exploring liquid crystal materials of unconventional structure and new modelling methods such as density functional theory (DFT) simulations becoming available, our work again began to explore the steric packing arrangements of the molecules in condensed phases.[6–10]

Then recently, one of my students wrote an article calling some molecular architectures (in terms of materials) pro-mesogens. This surprised and confused me. I gathered that it really meant a substructure of a material that was itself a good mesogen. In the case presented, it was the cyanobiphenyl unit selected for this accolade, but as George Gray said of his targeting of cyanobiphenyls for display applications, ‘I knew what I was doing by using the cyano group to compensate for loss of molecular length [aspect ratio], while at the same time providing the strongly polar molecular structure’. Even George knew that the relatively short biphenyl structural motif was not the best for supporting mesophase formation. In fact, it is poor, so why then call it a pro-mesogen?

So now I will jump forward to our more recent studies about mesophase formation and stability.

1. Introduction

One might think that good ‘nematic motifs’, so-called ‘pro-mesogens’, might be based on systems that have large aspect ratios such as sexiphenyl (see structure 1 in Figure 1). This material has a clearing point above 500°C [11] as opposed to 34°C for 4-pentyl-4′-cyanobiphenyl, that is, it has good nematic thermal stability. The interesting feature of sexiphenyl is that it does not have a dichotomous or polychotomous structure, where the molecular architecture is divided into two or more chemically dissimilar sections, for example, non-polar-polar, aromatic–aliphatic, etc., and therefore the dominant interactions of sexiphenyl are principally through π–π stacking. Dichotomy and polychotomy are perfectly good descriptors of molecular architecture, and predate the use of nano- or microphase segregation as adjectives (discussed later). For sexiphenyl, therefore, the only structural feature it has, which is relevant to the formation of liquid crystals, is its aspect ratio (molecular length to breadth). Thus, when the material melts, the solid collapses because of the increasing molecular rotations and fluctuations, and the nematic phase gains from the lattice energy evolved at the phase transition, and the retention of orientational ordering.

Figure 1. The transition temperatures and melting points (°C) for sexiphenyl, 1, quinquephenyl, 2, and 2′, 3″′′-dimethylsexiphenyl 3.

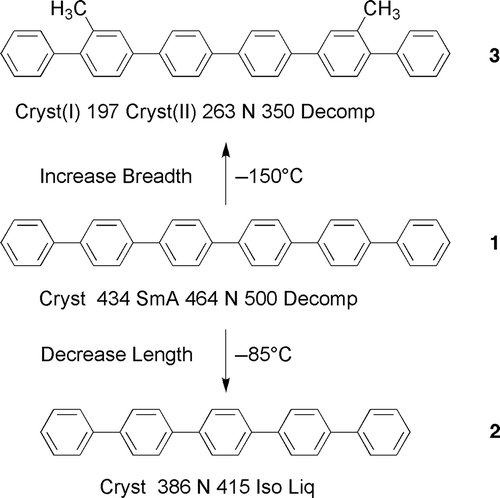
The importance of the aspect ratio is reflected in the comparison of the clearing point of sexiphenyl with those of quinquephenyl, 2, and 2′, 3″″-dimethylsexiphenyl, 3, shown in Figure 1. For quinquephenyl, with one less phenyl ring than sexiphenyl and a smaller aspect ratio, there is a drop in the clearing point of 85°C, whereas broadening the molecular architecture as in the case of dimethylsexiphenyl there is a comparative drop in the clearing point of 150°C.

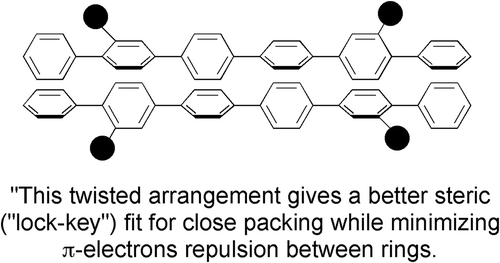
The relative differences in the aspect ratios, 1 to 2 relative to 1 to 3, suggest that the lower clearing point would be expected for quinquephenyl instead of dimethylsexiphenyl, particularly as the methyl groups may affect less the aspect ratio for dimethylsexiphenyl, 3, in comparison to sexiphenyl, because they could be buried in the overall structure due to interannular twisting and molecular motion. Thus, the degree of the relative comparisons cannot be due to the aspect ratio alone. Subramaniam and Gilpin [12] took this concept further by classically assuming such behaviour for dimethylsexiphenyl was due to a twisted arrangement of the phenyl groups allowing a better steric fit of the molecules packing together in a lock and key arrangement (see Figure 2). This might be the case in the solid state, but it cannot be true at temperatures of over 300°C in the nematic phase where the molecules are in thermal motion, fluctuating and gyrating wildly, where opportunities for electrostatic and steric interactions are limited. This is the essence of liquid in the ‘liquid crystal’, and to think of the molecules being organised into well-ordered arrays where electrostatic interactions are dominant is very unlikely. Rather it is more likely that methyl groups affect the closeness of intermolecular approach, thereby increasing the free volume, meaning that the formation of the liquid state is easier, that is, the reverse of Subramaniam and Gilpin, and hence the clearing point is lower. Thus, the nematic phase is entropically favoured by being orientationally ordered.

Figure 2. The twisted structure of dimethylsexiphenyl producing a better steric fit of the molecules together in a lock and key arrangement as predicted by Subramaniam and Gilpin. The black discs represent the methyl groups.

Having pondered how the minimisation of the free volume might work in determination of mesophase formation and mesogen design for complex materials, we returned to consider the situation of flexible rods, that is, for molecules normally encountered in everyday research in liquid crystals. One way we might imagine what happens to the molecules in a nematic phase is to examine the motions of live eels or worms laid out on a tray with only one constraining wall below them. They bulk together, and in continuous motion they minimise the free volume to arrive at an orientationally ordered state. Similar observations can be made via the examination of how granular particles become organised in mechanical fields by flow or vibration.

We appreciate that discussing mesophase formation in terms of the minimisation of the free volume, over a wide range of length scales and temperature stability, might seem to be naive, as we have been anonymously told. However, previous studies showing that, even as the molecules in liquid crystal phases are undergoing rapid movement, generalised or optimised shapes of molecules summed over a large number of molecular conformers appear to give a reasonable approach for examining potential molecular packing arrangements.

Examining percentage volume changes or packing fractions at various phase transitions can provide information on the space available for molecules to pack in a mesophase, and hence on their organisation and freedom to move. For example, volume changes at nematic to liquid phase transitions are usually small, which are reflected in the small enthalpies for the transitions that are observed. Leadbetter et al. [13] reported that the volume change at the SmA to N transition for 4-octyl-4′-cyanobiphenyl (8CB) is only about 0.05%, whereas for the N to I transition it amounts to 0.35%. These results indicate that the change in the local ordering of the molecules is also comparatively small, indicating that the smectic A (SmA) phase has similar ordering/disordering of the molecules as found in the nematic phase, that is, the SmA phase is similar in its local structure to that of the nematic phase, which in turn is also similar to that of a liquid. Thus, molecular clustering in such phases is a possibility, but it will be dynamic with clusters forming and breaking. Similarly, Das et al. [14], showed that the packing fractions for the smectogenic undecyloxy and dodecyloxy cyanobiphenyls (nOCBs) were close in value for the SmA phase and the liquid, but substantially different between the SmA and the solid, as shown in Table 1. Thus, even for the SmA phase, the organisation of the molecules in the mesomorphic state is much closer to that of the liquid than to the solid.

Table 1. The packing fractions (Pf) for the undecyloxy and dodecyloxy cyanobiphenyls (nOCBs) for the SmA phase to the liquid and the SmA to the solid.

nOCB	Solid	Change in Pf	SmA	Change in Pf	Liquid
11OCB	0.717	0.071	0.646	0.015	0.631
12OCB	0.681	0.046	0.635	0.005	0.630

The differences between the packing fractions for various phases have been described in detail for a number of materials by Wolfgang Wedler in the Handbooks of Liquid Crystals [15] and theories of molecular packing by Mikhail Osipov in the following edition of the same set of books.[16] More complex molecular architectures, for example, where the molecules have zigzag shapes, have been reported by Osipov and Gorkunov.[17] However, such theories do not delve deeply into the complexities of molecular shape, its ability to morph from one form into another, and the time scales on which this can be achieved (the bigger the molecule the longer the time), and hence the relationship between thermodynamic and kinetic stability.

In the following, the stability of mesophase type, and hence the enhancement of mesophase formation, will be discussed in terms of molecular design, particularly the ‘under’ and ‘over’ filling of molecular volumes. Thus, the models presented could be considered as steric formulations; however, this is not the point when the possibility of mesophase formation is evaluated. The focus should also include consideration of the space remaining in the overall structure. Excessive space is entropically disfavourable, and as such it should be minimised, with the consequence that space may have periodic lattice-like ordering. (In the following discussion, mesomorphic behaviour and the stability of mesophase type will be compared with respect to upper transition temperatures because the melting point in this context is not important as it is dependent on paramorphosis, reheating from a melt, or the solvent used in crystallisation to give the pure material.)

2. Filling and overfilling space for calamitic systems

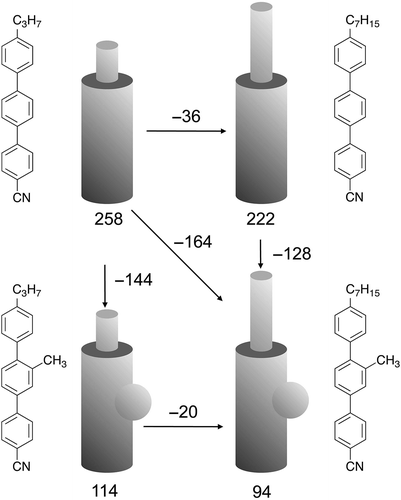
It is clear for ‘calamitic systems’ that cylindrical molecules pack together to maximise utilisation of the space available, and therefore minimise the free volume. Having discussed already rigid rod-like molecules, such as sexiphenyl, it is clear that if a lateral group is attached to the rod the relative N–I clearing point drops considerably. If a flexible chain is attached to the terminus of a rigid rod-like unit, and again a lateral moiety attached to the side of the rod, the fall in the clearing points is similarly very large. For example, for the 4-alkyl-4″-cyano-p-terphenyls, increasing the terminal chain from C3 to C7 the clearing points fall by 36°C, whereas the attachment of a lateral methyl group results in a fall in the clearing point for 4-alkyl-2′-methyl-4″-cyano-p-terphenyls of 144°C for the propyl terminal chain and 128°C for the heptyl analogue (see Figure 3). These falls are similar to those experienced for dimethyl sexiphenyl versus sexiphenyl itself. Thus, it is established, irrespective of the terminal chain, that lateral substitution has a greater effect on clearing points than terminal substitution. Again, given the molecular motions, interannular twisting and steric repulsion, it is likely that there is a larger free volume associated with lateral substitution versus terminal substitution, and neither can fill space as efficiently as the non-substituted parents.

Figure 3. Comparisons between the clearing point N to I transition temperatures (°C) for the 4-alkyl-4″-cyano-p-terphenyls (propyl and heptyl, top), and the 4-alkyl-2′-methyl-4″-cyano-p-terphenyls (propyl and heptyl, bottom).

Taking the chain-aromatic joined unit, or the unit with a rigid centre and two flexible chains, as the basic architectures for forming so-called calamitic mesophases, we can now fill space by adding substituents at the termini of the chains or in lateral positions as shown in Figure 4.

Figure 4. Possibilities for rod-like design in calamitic systems (left), and positions for filling in space with substituents; terminal (top), lateral (bottom).

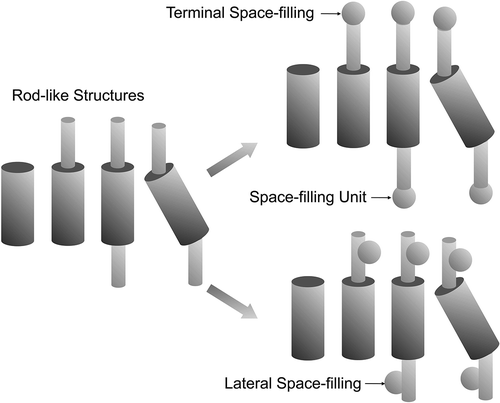
Taking first the addition of units at the termini, as shown in the top of the Figure 4, by using as an example terminally co-joined systems based on the 4-alkoxy-4′-cyanobiphenyls. For aliphatic chains up to the heptyl chain length, the parent materials (without terminal groups) exhibit nematic phases, for the undecyl homologue onwards only SmA phases are seen, whereas in-between both nematic and SmA phases are present.

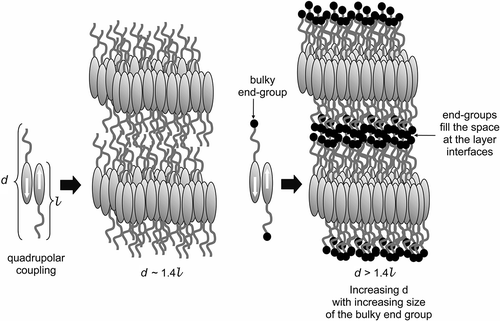
The stabilisation by quadrupolar interactions usually results in the formation of a bilayer structure for the SmA phase where the layer spacing is approximately 1.4× the molecular length and invariant with respect to temperature.[18] This typical outcome has resulted in the bilayer smectic phase being given a separate identity and code letter, SmA_d (it should be noted however that 11CB has a d/l ratio of 1.36 and for 12OCB it is 1.48).

Incorporating a bulky group at the terminus of the aliphatic chain results in the clearing point falling as the size of the group is increased. The accompanying fall in the melting point has resulted in materials being created that melt at or around room temperature and remain in their smectic phases up to 70°C, thereby providing potentially useful materials for displays. In particular, terminal siloxane groups have been claimed to have extremely beneficial properties for the stabilisation of the SmA phase with accompanying lowering of the melting point. A model was presented where the siloxanyl units stabilised the mesophase structure by microphase segregation of the silyloxy units.[19]

However, if the phase behaviours of cyanobiphenyls possessing terminal tert-butyl or trimethylsilyl units are compared, it is clear that there is little difference between the two, as shown in Table 2 for their relative transition temperatures. The melting points are within a degree of one another, and the clearing points are of 1.6°C difference. Although the layer spacing for 11OCB is 1.48 times the molecular length and is invariant with respect to temperature, both the tert-butyl and trimethylsilyl terminated systems exhibit layer spacings that vary from 1.55 to 1.58 times the molecular length from the liquid to SmA transition to a reduced temperature of 20°C.

Table 2. Transition temperatures (°C) for terminally substituted cyanobiphenyls with tert-butyl or trimethylsilyl units, with those of 4-undecyloxy-4′-cyanobiphenyl (11OCB) for comparison.[20]

X	Cr		SmA		Iso
H	●	71.5	●	87.5	●
–C(CH3)3	●	54.9	●	83.3	●
–Si(CH3)3	●	55.1	●	81.7	●

Another important point to note is that there is very little evidence to suggest that the terminal units have little freedom to move; on the contrary, the evidence (simulations and experimental studies) shows that the ends of the terminal chains are rotating rapidly such that the end groups might as well be considered to be spherically disposed. Thus, as the temperature falls, the layer spacing increases because the central parts of the molecules pack tighter together forcing the terminal groups into the interface between the layers, thereby increasing the layer spacing.

Effectively, the results are the same for both terminal systems irrespective of carbon or silicon being at the central region of the terminal group. Hence, the silyl system is not special in terms of nano- or microphase segregation; simply the terminal groups get squeezed into the interfaces between the layers (see Figure 5) in order to occupy the diminishing free space as the material is cooled. Similarly, there is nothing special about the layer structure being a bilayer; the spacing varies appropriately with the size of the terminal group and the temperature, and is formed in order to reduce the free volume and stabilise the quadrupole. Thus, there is no need to classify smectic systems as A_d.

Figure 5. The structure of the bilayer SmA phase stabilised by quadrupolar interactions (left), and the structure of the SmA phase with the molecules possessing terminal substituents that are squeezed into the layer interface to give so-called ‘microphase segregation’ (right).

An outcome of this structuring is that the layering becomes better defined, as shown by sharpening of the X-ray diffraction pattern and the appearance of second- and third-order diffraction peaks. Similarly, the appearance of multiple diffraction peaks is often seen for the layered phases of bent core liquid crystals and hydrogen-bonded systems as in materials that have terminal sugar units.

So far only bulky and/or non-polar end groups have been discussed; however, at this molecular length scale, it is also worthwhile investigating electrostatic/polar effects. Recently, we, and others,[6,21,22] have reported on the inclusion of halogens at the terminal position in aliphatic chains of various materials, particularly with reference to the formation of SmA and SmC phases. However, when incorporated into the terminal positions of the alkoxy cyanobiphenyls, layered mesophase formation becomes suppressed, and the nematic phase predominates.

If the schematic in Figure 5 is considered, the terminal groups, which are shown as black discs, could be interpreted as a sea of halogens located at the interfaces of potential layers. However, their electrostatic repulsions are strong enough to prevent layers from forming. The quadrupolar interactions between the molecules, however, increase the effective aspect ratio (length to breadth ratio) by dimerisation, thereby stabilising nematic formation.

Table 3 shows the transition temperatures and mesophase classification for the ω-halogeno-methyleneoxy materials in comparison with the unsubstituted parent 4-alkoxy-4′-cyanobiphenyls. Unlike the parents, the ω-chloro- and ω-bromo-analogues exhibit nematic phases but not smectic phases, even under substantial supercooling. The clearing points are lower, but the melting points are higher than those of the parents. This phase/structure correlation extends further to include terminal hydroxy units as well, as shown in Table 3. For the monohydroxy-analogues, the N–I clearing points are higher than those of the terminal-halogeno compounds and the parents, even though the methylene spacers are shorter in length. A similar situation is found for terminal diols based on solketal. Although there is a greater propensity for H-bonding, the phases formed are still nematic. It is only when the terminal groups have a greater potential for templating and more H-bonding sites that layered phases reappear. Consequently, the terminal glucose derivatives, as shown in Table 4, do not exhibit nematic phases, but are instead smectogenic. In this case, the sugar units are squeezed into the interfaces between the layers where they form dynamic H-bonding networks and template for one another. With the increased H-bonding and molecular mass, the smectic to liquid clearing points are higher than any of the other materials discussed here.

Table 3. Transition temperatures (°C) for terminally substituted cyanobiphenyls with halogens or hydroxyl units, with those of 4-alkoxy-4′-cyanobiphenyl (nOCBs) for comparison [22,23].

X	m	Transition temperatures (°C)
		Cr		SmA		N		Iso
H	8	●	54.5	●	67.2	●	81.0	●
H	9	●	61.3	●	77.9	●	80.0	●
H	10	●	59.5	●	83.9	–	–	●
Cl	8	●	71.7	–	–	(●	63.9)	●
Cl	9	●	72.7	–	–	(●	64.9)	●
Cl	10	●	73.0	–	–	(●	66.0)	●
Br	8	●	79.8	–	–	(●	63.7)	●
Br	9	●	78.4	–	–	(●	58.6)	●
Br	10	●	72.6	–	–	(●	66.2)	●
HO	3	●	84.8	–	–	●	113.9	●
HO	5	●	59.9	–	–	●	106.3	●
HO	7	●	67.4	–	–	●	99.9	●
HOCH2CH(OH)–	1	●	114.5	–	–	●	127.6	●
HOCH2CH(OH)–	4	●	94.5	–	–	●	123.6	●

Table 4. Transition temperatures (°C) for terminally substituted cyanobiphenyls with glucopyranoside units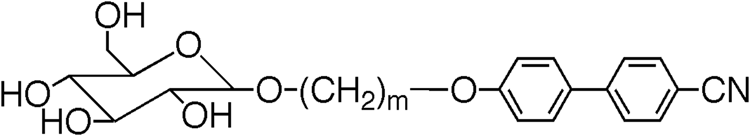 [22].

	Transition temperatures (°C)
m	Cr		SmA		Iso
9	●	105.4	●	132.5	●
10	●	111.3	●	137.9	●
11	●	110.6	●	138.2	●
12	●	125.5	●	140.0	●

3. Molecular tilt and space filling

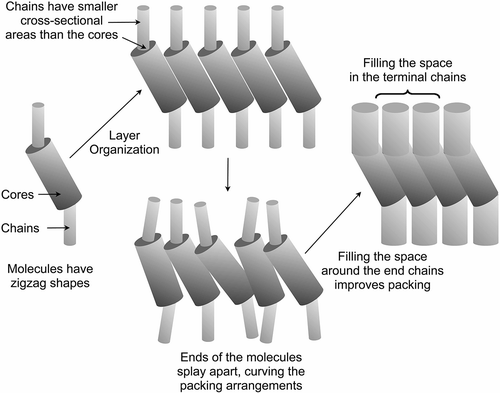
Over a number of years, one topic of particular importance has been the investigation of the microscopic origins of the molecular tilt that drives the formation of certain lamellar phases, that is, SmC, hexatic I and F, etc. Typically tilted phases are formed by rod-shaped molecules that have a central rigid unit with two flexible units joined to either end of the core. As the temperature is lowered, the rod-shape molecular architecture conformationally changes to give a zigzag structure, as shown in Figure 6. This occurs because the packing requirements of the molecules become improved and the free volume is reduced.

Figure 6. Schematic representation of the packing of molecules with a gross zigzag shape into a phase type in which the molecules are tilted with respect to the layer normal.

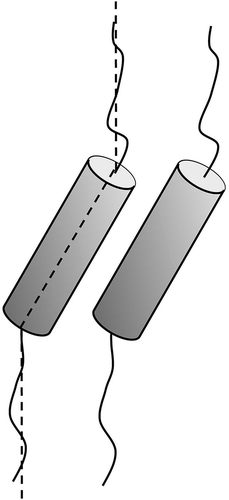
From a theoretical standpoint, two distinct models for the tilting of the molecules can be identified; those based upon electronic factors, for example, the McMillan model,[24] and those based on steric considerations, such as the model of Wulf.[25] McMillan’s model of the SmC phase was developed based primarily on the fact that, at the time, the majority of molecular architectures known to support the formation of the SmC phase all possessed polar functionalities, that is, esters, ethers, Schiff’s bases, etc., which were positioned towards the ends of the rigid aromatic core system.[24,26,27] Thus, it was assumed that these ‘terminal outboard dipolar units’ were responsible for driving the formation of a tilted molecular arrangement. In McMillan’s model of the SmC phase formation, the molecular rotations are assumed to freeze at the SmA–SmC transition, and the tilt is driven by the intermolecular dipolar torque formed by the interactions of the ‘terminal outboard dipolar units’. Conversely, Wulf developed a steric model, which was in opposition to the dipolar model of McMillan, where the packing of zigzag-shaped molecules was proposed to be similar to that of the stacking of chairs. The molecules in these arrangements are effectively tilted with respect to their layer planes, thereby supporting the formation of tilted phases. In the SmC phase, the out-of-plane organisation of the molecules is likely to be more well-defined than in the SmA phase. However, it should be noted that when the cross-sectional areas of the central core and the terminal chains do not match then curvature in the packing of the molecules will arise and layer distortion will occur in a similar way to the way in which amphiphiles form curved packing structures [28–30] (see Figure 7). Such distortions can be localised into defects, which can affect the organisation of tilted phases in devices in the form of chevrons.

Figure 7. Space filling and reduction in free space in the Wulf model of the SmC phase.

However, experimental results suggest that neither electronic nor steric models alone provide a complete rationale for the origins of molecular tilting. This point is well illustrated by the series of materials reported by Goodby et al. [31] presented in Table 5.

Table 5. The molecular structures and transition temperatures (°C) of the series of esters reported by Goodby et al.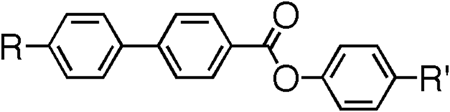 [31].

R	R′	Transition temperatures (°C)
–OC8H17	–OC8H17	Cr 110 SmB 116 SmC 165 SmA 200 Iso. Liq.
–OC8H17	–C8H17	Cr 110 SmB 110.5 SmC 132.5 SmA 184 Iso. Liq.
–C8H17	–OC8H17	Cr 98 SmB 112 SmC 125 SmA 171 Iso. Liq.
–C8H17	–C8H17	Cr 102 (G 67 SmB 96) SmA 153 Iso. Liq.
CH2H5CH(CH3)(CH2)3–	–CH2CH(CH3)C2H5	Cr 86 (SmC 78.1) SmA 96.1 Iso. Liq.

In the development of ferroelectric chiral SmC* phases for electrooptic devices, it was found, as for SmA phases, that the incorporation of bulky terminal groups into the mesogens could lower melting points, thereby improving upon operational temperature ranges.[32–36] In addition, we have also found that the incorporation of bulky groups can improve upon misalignment and self-rectification from shock damage. By introducing bulky end groups, they sterically hinder the coming together of the ends of the molecules, and as a consequence prevent the opposing splay of the ends of the molecules. Thus, the cross-sectional areas of the cores and the chains are effectively similar in size, as shown in Figure 7 (right).

The question then arises, should only one end of the molecules be substituted with a bulky group or should both ends be? In comparison to materials that exhibited SmA phases as described earlier, we examined the mesophase properties of numerous materials including the 4-(4′-alkoxy-2′,3′-difluorobiphenyl)benzoates, which were systematically substituted at the terminal ends of the alkoxy chains with trimethyl silyl groups. The results in Table 6 show that the clearing points fall sharply for the nematic to liquid phase transitions from the unsubstituted parent to the mono-substituted analogues. However, the nematic to SmC phase transitions, albeit monotropic, were higher in value in comparison to the parent. Remarkably, the incorporation of two terminal bulky groups results in all mesomorphic behaviour being lost.

Table 6. Transition temperatures (°C) for substituted 4-(4′-alkoxy-2′,3′-difluorobiphenyl) benzoates.[37]

		Transition temperatures (°C)
R	R′	Cr		SmC		N		Iso
C5H9–	C5H9–	●	99.8	(●	98.9)	●	182.5	●
(CH3)3Si(CH2)3–	C5H9–	●	127.3	(●	121.0	●	125.9)	●
C5H9–	(CH3)3Si(CH2)3–	●	131.2	(●	124.0)	●	135.3	●
(CH3)3Si(CH2)3–	(CH3)3Si(CH2)3–	●	114.91	–	–	–	–	●

Thus, this is a case where the parent has underfilled space, the disubstituted material is overfilled, but the mono-substituted system was just right.

Typically one would focus on molecular shape and steric structure, rather than the free space. However, if we examine the implications for free space, assuming one bulky group and head to tail arrangements of the molecules as being the ground state, the highest SmC to N transition temperatures are obtained, whereas having no bulky end groups causes splaying between the molecules which increases the free volume and as a result a lower SmC to N transition temperature; conversely, two bulky end groups force the molecules apart and increase the free volume between the molecules to a larger extent which is entropically costly to the system, and so no phases are formed (see Figure 8). Although only three examples are given, the results obtained are typical for other materials we have prepared, indicating that the electrostatic interactions are probably not as important to tilted phase formation as predicted by McMillan.

Figure 8. Structure (b) supports the higher SmC to N transition temperature, structure (c) is less likely to support tilted phase formation and structure (a) is the parent system.

Thus far it is clear that in the nematic phase the molecules randomly pack into a linear arrangement, whereas for the SmA phase there is a density modulation in the direction of packing of the long axes, but for the SmC phase the density modulation is at an angle to the packing direction. However, in all cases the molecules try to organise in a one-dimensional (1D) linear array. If we now move to a two-dimensional (2D) system, the rod-like molecules must take on a three-dimensional (3D) shape, as discussed in the following section.

4. Helicity, synclinicity, anticlinicity and space filling

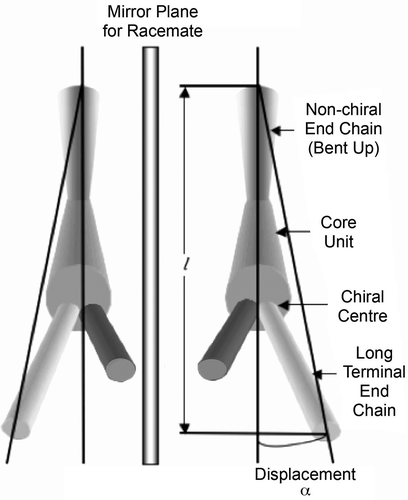
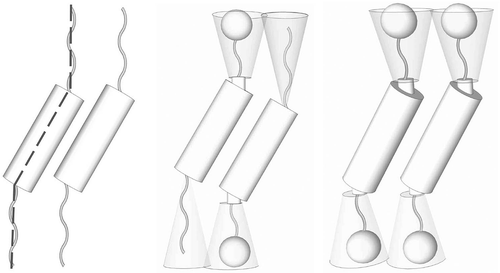
As described above, synclinic systems can be composed of molecules that have zigzag-shaped molecular architectures. Such structures however have mirror planes associated with them. However, if one of the terminal units is bent out of the plane of the molecular architecture, at an angle α, to give a ‘bend-twist’ molecular shape, then the overall structure will be handed, as shown in Figure 9.[38] Such bent and twisted molecules can exhibit mirror images and both left- and right-handed bulk-packing arrangements. If these arrangements separate into two domains, then the phase is a conglomerate and a soft crystal. However, in order to minimise the free volume, the molecules can form helical arrangements. Again, for molecules that possess no stereogenic centres left- and right-handed helical macrostructures can be obtained. However, if a stereogenic centre is present, then the molecules will form a helical macrostructure of one hand only.

Figure 9. The bent and twisted molecular architectures of zigzag-shaped molecules.

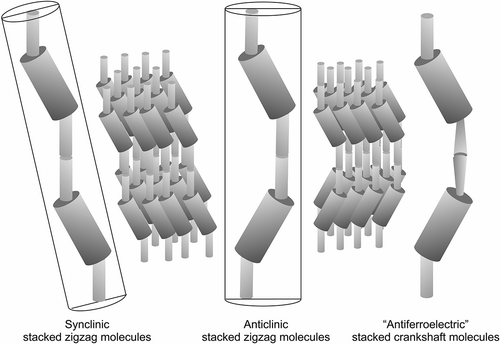
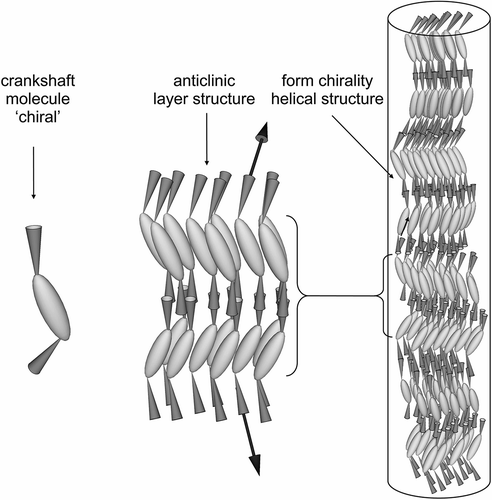
The question then arises; will the helix be based on a synclinic or anticlinic arrangement of the molecules? The two possibilities are shown in Figure 10. The packing volume for zigzag synclinic organisation is less in comparison with the anticlinic arrangement, and therefore might be expected to be favoured, which is indeed the case. However, for a bent-twisted molecular shape the anticlinic packing becomes competitive, particularly when the molecules have a relatively fixed conformational structure. This is usually the case for materials that possess 2-methyloctyl terminal chains where the branching point is near to the aromatic core, as shown in Figure 9. The anticlinic arrangement is preferred over the synclinic structuring because the transmission of molecular information between layers causes the layers to rotate relative to the layer planes in the synclinic ordering as shown in Figure 11. This organisation is less efficient and requires defect formation compared with the anticlinic ordering, which is shown in Figure 12.

Figure 10. The synclinic and anticlinic packing arrangements in tilted mesophases.

Figure 11. Layer rotation in the synclinic phase of molecules with bent and twisted molecular architectures.

Figure 12. The anticlinic helical organisation of molecules with bent-twisted shapes.

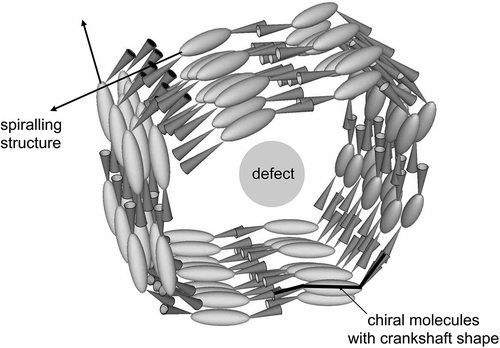
In these figures, it can be seen that the stronger intermolecular electrostatic interactions are similar to one another, but the better packing for the helical anticlinic structure has a lower free volume and therefore the density of the molecules may be greater, hence the attractive electrostatic interactions are more numerous.

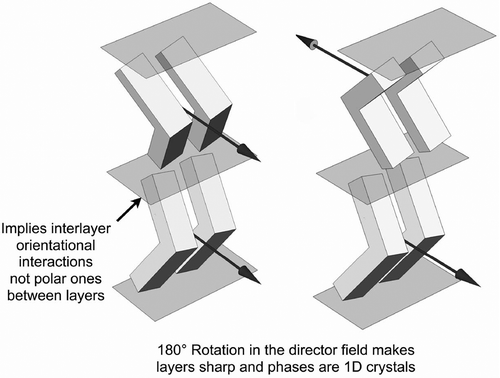
Molecules with so-called bent core architectures also exhibit synclinic and anticlinic phases, as shown in Figure 13. However, their architectures are probably zigzag shaped with respect to the terminal chains, which might be expected to be perpendicular to the layers. Nevertheless, for the anticlinic phase the 180° rotation in the director field from layer to layer indicates that the layers are well-defined, as shown by the number of out-of-plane diffraction peaks seen by X-ray. This is in keeping with a staggered π–π overlap between adjacent aromatic cores of the molecules, which is often found in the solid state, and where rotation is restricted and as a consequence the material may be polar. In terms of multiple diffraction peaks from the layers, the B2, B4 and B5 phases have been shown to exhibit a minimum of three reflections, with some as many as five or six, indicating that such systems are in fact 1D soft crystals.[39] This will have potential ramifications for mixture development and eutectic design employed in applications of materials for device development.

Figure 13. The synclinic and anticlinic structures for the phases of bent core materials.

5. Bent dimers and twist-bend phases

We now turn to larger molecular systems, from bimesogens, to dendrons, dendrimers and to supermolecules. Here we see less emphasis on electrostatic interactions and more on molecular shape.

Bimesogens that have methylene spacer units sandwiched between aromatic moieties, which carry polar terminal groups, as shown in Figure 14, for the 1,ω-di-(1″-cyanobiphenyl-4-yl)alkanes (CBnCBs),[40] exhibit relatively normal behaviour when the methylene chain is of an even parity. However, when the number is odd a transition from a classical nematic phase to a twist-bend nematic phase (N_TB) can occur.[41]

Figure 14. (colour online) The molecular structures of 1,ω-di-(1″-cyanobiphenyl-4-yl)alkanes (CBnCBs) (top) and a minimised structure of CB11CB showing its bent molecular architecture (bottom).

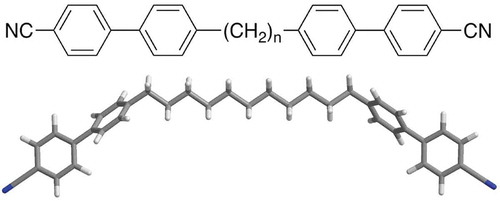
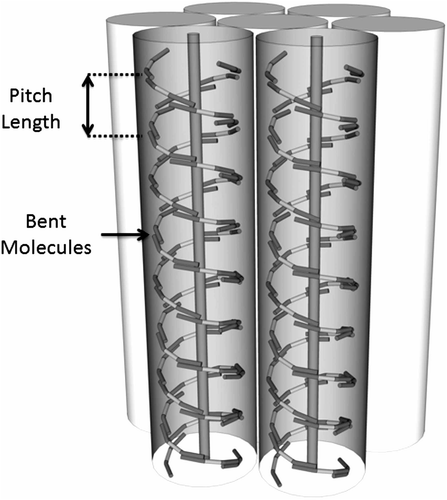
Many studies on the structural features of the twist-bend modification of the nematic phase have been performed in recent years. The results obtained indicate that the twist-bend nematic N_TB mesophase has a structure in which the molecules intercalate to give a spiralling organisation which is spatially homogeneous, that is, the molecular arrangement in the N_TB phase is nematic-like rather than lamellar.[41–43] Despite the spatially homogeneous nature of the N_TB phase, its associated defect textures are strikingly similar to those observed for smectic mesophases because they exhibit both focal-conic and parabolic defects.[44] The repeat of the helical pitch (~80 Å) acts as the equivalent length of three molecules, and supports the formation of lamellar-like phases even though the molecules can be anywhere along the helical axis, that is, the lamellar structuring does not depend on layer ordering of the individual molecules. Nevertheless, something of a consensus has now emerged in that the heliconical model of Dosov is a good descriptor of the phase. In particular, measurements of the electroclinic effect in 1,ω-di-(1″-cyanobiphenyl-4-yl)heptane (CB7CB) appear to support the idea of the N_TB phase having a pitch length of a few nanometres.[45]

The question now to be addressed is why the molecules form a helicoidal structure. The strong quadrupolar interactions between the cyanobiphenyl will cause intercalation between the molecules. For materials with even parity spacers, this will form an extended zigzag ordering of the molecules. However, for the materials with odd parity, alternation and intercalation of the bent molecular structures leads to a relatively well-packed structure as shown in Figure 15. These two arrangements for even and odd parity spacer systems are thus similar to the synclinic and anticlinic systems described in Section 4. However, for the anticlinic system twisting reduces the likelihood of defect formation and minimises the free volume. In the case of the odd parity system, there is a void volume created by the quadrupolar interactions. The free volume can only be reduced in this case by again forming a helical structure. This creates a fibre-like structuring of the bent core molecules to give a twist-bend phase.

Figure 15. The alternating intercalating packing arrangement of a dimesogen 1,ω-di-(1′-cyanobiphenyl-4-yl)undecane (CB11CB) with odd parity. Reproduced with permission of the Royal Society of Chemistry from Mandle et al.[46]

These ideas are predicated on the aromatic parts of the molecules being able to form quadrupoles with neighbouring molecules, but if we now turn to the structure–property correlations we have developed for a variety of dimers (shown in Figure 16), it can be seen that the molecules do not have to be strongly polar, they do not have to have a specific bend angle or specific linking groups – esters or ethers it does not matter. The only structure that appears to be important is rigid terminal groups (aromatic or alicyclic) and a flexible joining group, which will allow for molecular twisting. Furthermore, mixed polar/non-polar bimesogens also are capable of exhibiting N_TB phases, and lateral substitution of the rigid mesogenic units affects transition temperatures, but it does not prevent formation of the N_TB phase.

Figure 16. Some material types found to exhibit the N_TB phase. Polar systems, apolar systems (this work) and mixed ether/ester-linked systems [46–48]. Reproduced with permission of the Royal Society of Chemistry from Mandle et al. [47]

Electrostatic models of the N_TB phase are, therefore, unlikely to generate satisfactory explanations about phase establishment and stability, and therefore an alternative approach is required. Firstly, it should be noted that the N_TB phase has a high viscosity,[49] and for numerous materials does not exhibit an electrooptic response.[12,28] Therefore, a heliconical arrangement where the molecules are able to move relatively freely is unlikely. Secondly, it has been shown that the order of the N to N_TB phase transition was dependent on the rate of temperature change, and that there was a contribution from kinetic as well as thermodynamic properties, and indeed there was an indication that at some rates the transition was similar to that for polymer formation.[47,48] These observations indicate there is ‘supramolecular’ fibre formation. A simple explanation lies in the minimisation of the free space created by the packing of the molecules together. The best and tightest packing of the molecules together is through a spiral arrangement to give a rope-like structure. Packing fibres together then results in the formation of a hexagonal structure. Here one has to be careful in assuming this is a hexagonal/columnar liquid crystal phase, when this might not be the case. Nevertheless, Bruce et al. [50] proposed that the ‘N_X’ phase exhibited by bent dimers was a columnar nematic phase long before the current research on N_TB phases became topical.

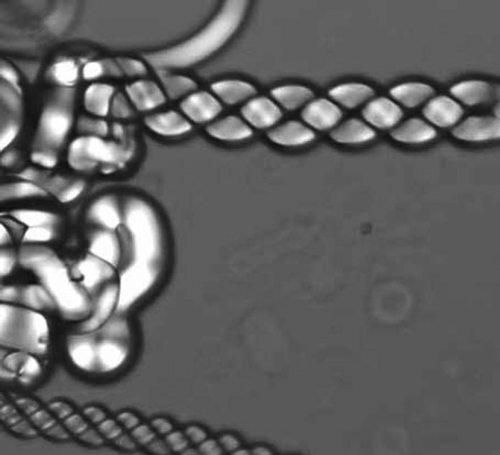
In terms of the formation of helical fibres, there are numerous examples in the literature concerning the structures of biopolymers. For example, collagen, poly-L-glutamine [51] poly-benzyl L-glutamate (PBLG),[52] etc., all exhibit chiral fibres of one type or another. Of particular interest are the liquid crystal properties of PBLG, which show microscope textures that are almost identical to those of the N_TB phase (note that the textures in reference [52] are much better reproduced than in reference [53]). Livolant and Bouligand indicated that each fibre is composed of looped polymer strands forming two backbones twisted together, which then form hexagonal packing arrays.[53] Similar structural constructs have been found with small molecule systems such as phospholipids. For example, 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) shown in Figure 17 forms both lyotropic and thermotropic liquid crystal phases. It exhibits filamentary textures composed of jelly-roll layers, and in addition it can strengthen the filaments and minimise their volumes by forming helical arrangements, as shown in Figure 18.

Figure 17. 1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC).

Figure 18. The texture of the helical structure of 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) (×100).

In a similar way, we have suggested a construction where the molecules in the N_TB phase associate to give helical ‘supramolecular’ fibres, and we suggested that depending on the cooling rates at the N to N_TB transition either lamellar or hexagonal phases could be formed. This was evident from the formation of free-standing films of the N_TB phase (see film under supplementary information from reference [47]).

In terms of the establishment of the hexagonal phase, the ‘supramolecular’ fibres minimise the free volume, and packing them together in a hexagonal array will further minimise the free volume (see Figure 19). The formation of this phase will be kinetically driven and will probably not be observed by experiments that employ rapid cooling to establish formation of the N_TB phase, such as freeze fracturing. However, the molecules in the ‘supramolecular’ fibre will not have periodic long-range ordering and therefore this modification will exhibit similar structural properties as proposed for the columnar nematic phase proposed by Bruce et al. [50].

Figure 19. Proposed hexagonal packing arrangement of the N_TB ‘supramolecular’ fibres.

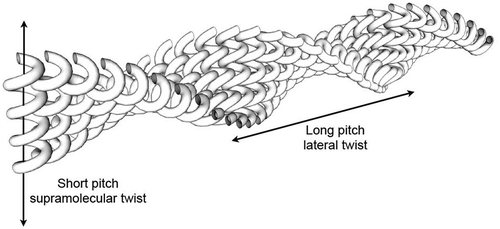
For phases that exhibit twisted ribbon structures, there is also the possibility that when they pack together a lateral twist will be induced to form.[54] By analogy, if one takes two bolts and pushes the thread together so that they interleave, the long axes of the bolts will twist relative to one another. The tighter the pitch of the helical thread of the bolt the longer is the pitch of the induced helix. If this is the case in the N_TB phase, a very long pitch helix could be formed perpendicular to the molecular twist of 8 nm measured from freeze fracture.[55] Figure 20 shows a schematic for the formation of one set of helical supramolecular structures that pack together to give a long pitch helix that is perpendicular to the axes of the smaller supramolecular helices.

Figure 20. Helical fibres packing together to give a superstructure with long pitch.

This is a possibility for phases that do not possess other forms of ordering such as layers, but in the case of the twist grain boundary (TGB) phase where the twist occurs in the planes of the layers, the competition between twist and layers’ stability results in frustration. The frustration is ameliorated by the inclusion of screw dislocations as shown in Figure 21.[56] The inclusion of screw dislocations leads to the formation of grain boundaries that are periodic, and hence the phase is effectively a 1D crystal. Remarkably some materials exhibit inversions of twist sense in the TGB phase as a function of temperature, indicating that the grain boundaries are mobile and can melt and reform.[57]

Figure 21. Structure of the TGB phase. [58] Copyright Wiley-VCH Verlag GmbH & Co. KGaA reproduced with permission.

6. Supermolecules: minimisation of the free volume and the distortion of molecular shape

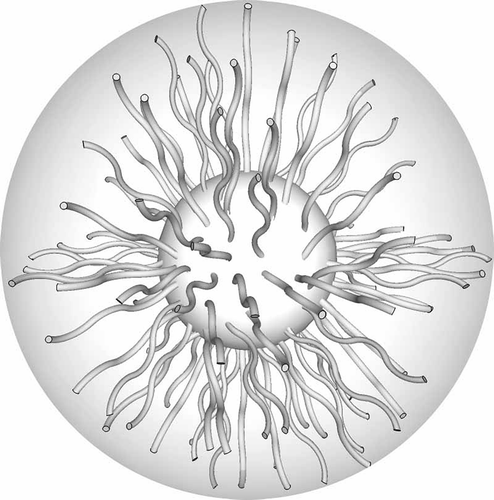
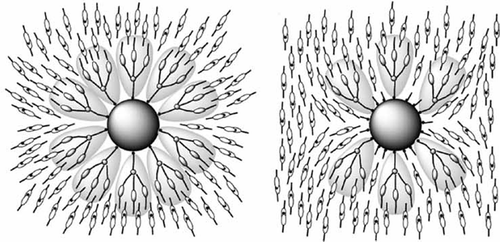
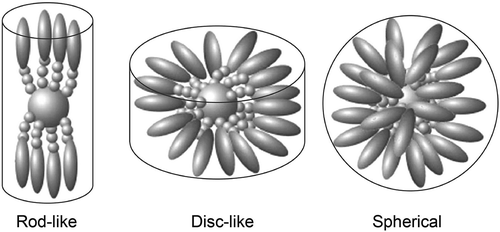
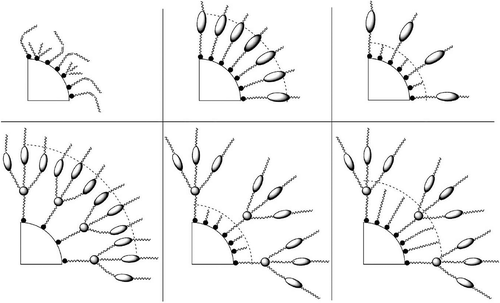
The discussion of dimesogens leads on to the next topic of large-scale molecular systems. These might be supermolecular covalently bonded systems, or supramolecular materials that are formed by associations of various kinds, for example, ionic, H-bonding, etc. For these materials, the centre of the molecular architecture harbours either a scaffold or a nanoparticle, and attached are various substituents from aliphatic chains to liquid crystal moieties. In the gas phase, the substituents will spread out as much as possible in order to maximise the space occupied as shown in Figure 22 for a scaffold that is substituted with aliphatic chains.

Figure 22. A nanoparticle substituted by aliphatic chains in the gas phase.

Assume now that the aliphatic chains can be substituted at their ends with rod-like mesogens. These can be either terminally or laterally attached. For the terminally attached mesogens, there are three possible mesophase forms that can be obtained depending on the density of the mesogens on the surface of the scaffold. For a low density of mesogens, if they are radially oriented on the surface at the exterior, there will be a large amount of free space. This is minimised by the mesogens packing tightly together, thereby forming a rod-like structure, which will then support the formation of lamellar phases. For a high density of mesogens, they are radially distributed and hence the molecular architecture is ball-like, which supports the formation of cubic or micellar phases. Between these two extremes, the architecture is disc-like and the phases formed are columnar (see Figure 23). The formation of these three types of phase is predicated on minimising the free space. Thus, it hardly matters what the chemical structures and interactions of the mesogens are when the density is low; invariably nematic or lamellar phases ensue, with the variation being transition temperature.

Figure 23. Dendritic materials with increasing mesogenic units from left to right, and the phases that they support.

When the mesogens are laterally attached to the aliphatic chains, the formation of nematic phases is supported. Other novel phases with tubular structures can be formed where the scaffolds strongly interact. Again minimisation of the free volume is important to the formation of such phases. An important observation made on these materials is that the transition temperatures across a series of compounds remain relatively stable as a function of the number of mesogenic groups. Take, for example, the family of compounds shown in Figure 24. The clearing points for the trimer, hexamer and dodecamer vary by less than 5°C, even though the scaffold is changed and the molecular mass quadruples. Furthermore, for the nematic to SmC transition, the variation is less than 1.5°C.[59–61]

Figure 24. Effect of numbers of mesogens on transition temperatures (°C) for a series of laterally appended supermolecules [59–61]. Reproduced with kind permission from Springer Science and Business Media.

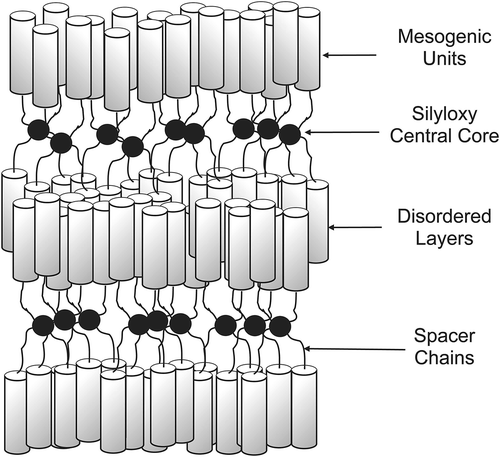
When the spacer chain between the mesogenic groups and the scaffold is varied, then the transition temperatures also vary. This is because as the spacer chain is increased in length the internal flexibility of the molecular architecture increases. The longer the spacer, the easier it is for the mesogenic groups to interact and the overall shape of the molecule becomes nearer to being rod-like. As a consequence, the free volume is minimised. For example, consider the alkyloxy-cyanobiphenyls substituted tetrakis-(dimethylsiloxy)silanes shown in Figure 25. Although shown as a spherical structure in the figure, to minimise the free volume these materials form rod-like structures, with either pairs of arms coming together as shown in Figure 26, or four or three arms coming together.[62] The pairs of arms ‘together’, as shown in Figure 26, demonstrate how close they are and the overall rod-like molecular architecture. The obvious mesophase that is generated by such a structure is lamellar, as shown in Figure 27. In general, the lamellar phase has a structure where rod-like supermolecules pack such that there is no positional ordering of the molecules in the plane and out of the plane of the layers.[63,64] The only way in which the tetramers can form such a phase is by molecular distortion away from a spherical shape to give a rod-like conformational structuring.

Figure 25. Transition temperatures (°C) for the tetramers of alkyloxy-cyanobiphenyls substituted tetrakis-(dimethylsiloxy)silanes.

Figure 26. The molecular shape of tetramer with a C₁₁ spacer unit shows the minimised structure in the gas phase at absolute zero using a Silicon Graphics system operating with Quanta and CHARMm software.

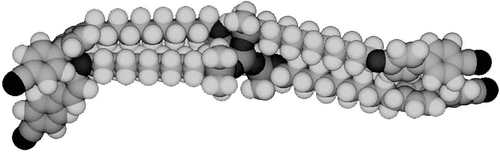
Figure 27. The structure of the lamellar phase of the alkyloxy-cyanobiphenyls substituted tetrakis-(dimethylsiloxy)silanes.

The materials with C₄ and C₆ spacers exhibited only lamellar phases, whereas the tetramer with a C₁₁ spacer showed an additional unidentified phase at 38.7°C. The phase behaviours and transition temperatures (°C) are shown together in Table 7. When the number of methylene units is increased, the isotropisation temperatures increase accordingly. This is because the longer the methylene chain the more flexible is the structure and the conformational freedoms allow for the architecture to become more rod-like. For the shorter analogues, the structure is more rigid and conformationally less rod-like. This means that for the shorter analogues the free volume is larger and the aspect ratio is lower than for the higher homologues.

Table 7. Transition temperatures (°C) for the tetramers of alkyloxy-cyanobiphenyl substituted tetrakis-(dimethylsiloxy)silanes.

Spacer (n)	Tg (°C)	SmX–SmA (°C)	SmA–Iso Liq (°C)
4	−9.6	–	88.7
6	−14.7	–	118.7
11	−6.3	38.7	129.7

Thus, the need to form molecular architectures that occupy the least volume, unless they share space, determines mesophase formation for supermolecules, dendrimers and dendrons, and coated nanoparticles. This includes bimesogens, Janus supermolecules.[67] The phases that these materials form have been listed as lamellar, columnar and cubic, and all have various levels of crystallinity, which will be discussed later. However, it should also be noted that polymorphism in the liquid crystalline state, for example, smectic polymorphs, is often limited in the behaviour of super- and supramolecular systems, as too is the formation of bicontinuous cubic phases.

7. Coated nanoparticles with hierarchical structures

The concept of the minimisation of the free volume can be applied in more complex systems such as those based on coatings of 3D nanoparticles [68–73] and 2D surfaces as in self-assembled monolayers. [74,75] Typically the surfaces of such systems are coated with surfactant materials that are not necessarily covalently bonded to the surface, and so the surfactant molecules can move on the surface depending on the coating density. For example, consider gold nanoparticles of ~3 nm in diameter coated with ω-n-(4-cyanobiphenyl-4′-yloxy)alkylthiol ligands, as shown in Figure 28 for the octyl material. In this figure, the ligands are of an anatomically correct size relative to the diameter of the gold particles. As with many nanoparticles coated with liquid crystal surfactants, the resulting supramolecular system is not liquid crystalline. However, coated supramolecular nanoparticles can be suspended in liquid crystal hosts to give colloidal systems. Figure 28(a) thus shows a sketch of the chemical structures of the ligands symmetrically bound to the surface, whereas in Figure 28(b) the space-filling structures are shown. Although tighter packing could be achieved with more surfactant molecules bound to the surface than is shown, the picture depicts the experimentally determined density. Equally, spreading out the ligands on the surface shows that there is substantial space between the ligands on the exterior surface, thus Figure 28(c) shows how they might associate to give better packing at the poles of the particle scaffold. This arrangement with few ligands at the equator was supported by dielectric and X-ray diffraction studies.[71]

Figure 28. Gold nanoparticles of ~3 nm in diameter coated with ω-n-(4-cyanobiphenyl-4′-yloxy)octylthiol ligands: (a) a sketch of the bonds, (b) a space-filling model for ligands in the gas phase at 0 K, (c) bunching of the ligands at the poles of the nanoparticle. Reproduced with permission from Draper et al. [71]. Copyright Wiley-VCH Verlag GmbH & Co. KGaA.

In this model, if the footprints for the attachment points of the ligands at the surface are smaller than the cross-sectional areas of the ligands, then parts of the surface will be left unsubtituted. This will likely allow interactions to occur between the nanoparticles resulting in coagulation, which is often seen in such systems. Filling space at the surface can alleviate this problem through using mixtures of surfactants as described for coated quantum dots composed of cadmium selenide or zinc sulphide as shown in Figure 29. The surfactants tested included a rod-like mesogen A, a dendron composed of mesogens B, a short-chain-length surfactant C, a long-chain surfactant D and a branched-chain surfactant E. The mixing of the various surfactants together, as shown in Figure 29, determined how much of the space above the nanoparticle surface was filled. Filling the surface reduced the interactions between the particles to a minimum and thereby stabilised the colloid–liquid crystal host system (in this case the host tested was 5CB). It was found that this was best achieved with mixtures of mesogenic dendrons and surfactants with linear aliphatic chains, as shown by the bottom right-hand two mixtures shown in Figure 30.

Figure 29. Surfactants used as ligands for quantum dots. Reproduced with permission from Prodanov et al. [76]. Copyright 2013 American Chemical Society.

Figure 30. Schematic of mixed surfactants in their proportions used as ligands attached to quantum dots (quarter circle).

In this approach, the nanoparticles disturb the local ordering of the host liquid crystal molecules around them. In turn, the interactions of the liquid crystal molecules with the surfactant molecules impose their orientational ordering in the surfactant shell, such that the spherical architecture of the coated nanoparticles essentially becomes tactoidal. In this way, mutual ordering of the molecules of the host liquid crystal and those of the surfactant minimises the orientational energy of the system and decreases the distortion of the liquid crystal ordering around the nanoparticles. This is especially effective when the surfactant shell is composed of molecules that are ‘pro-mesogens’ with those that are aliphatic. In this case, the structure of the surfactant shell allows penetration of the molecules of the host between the molecules of the surfactant (see Figure 31) where a dendritic shell is compared with a mixed system. The smaller distortion of the liquid crystal host around the particles gives rise to lowering of their tendency to aggregate and enhances the stability of the colloid.[76]

Figure 31. A liquid crystal host and coated nanoparticle colloidal system. (Left) The surfactant shell is composed of mesogen dendrons; (right) the surfactant shell is a mixture of mesogenic dendrons and aliphatic chains.

8. Disc-like systems and interfacial space

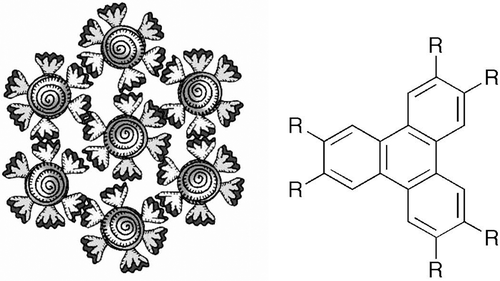
Often material systems possessing disc-like molecules are treated as extensions based on the structures and properties of rod-like molecules. However, this is not necessarily an appropriate approach to understanding such materials. For example, simple rod-like molecules, such as sexiphenyl, can exhibit nematic phases; however, disc-like equivalents such as triphenylene, corenene, etc., are not mesogenic. Conversely, when aromatic disc-like materials, such as triphenylene, are substituted with a number of aliphatic chains, then columnar phases appear. The number of aliphatic chains is required to be relatively high, for example, greater than four, for a hexagonal-shaped molecular disc. In these materials, the aliphatic chains fill the space between the aromatic cores as shown by the schematic in Figure 32. However, the space is extensively filled at the edges of the discs, whereas at the junctions between three discs there is greater space available for the packing of the chains together, as shown in Figure 33 for hexagonal columnar phases.

Figure 32. Hexagonal arrangement of aliphatic substituted aromatic disc that forms the basis of the structure of columnar liquid crystals.

Figure 33. The columnar structure of disordered and ordered hexagonal phases.

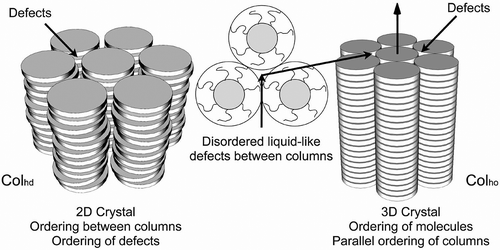
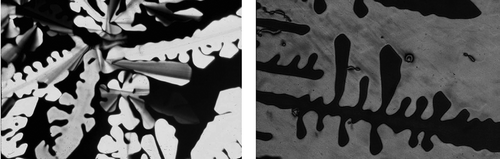
Unlike rod-like systems, it is very difficult for disc-like molecules to pack together in columns without forming defects between them and subsequently between the columns. Rod-like materials are usually capable of distorting their structures in order to minimise defect formation; however, for disc-like materials in columns, defects form in hexagonal arrays. Thus, not only do the columns pack together in a 2D crystalline array so too do the defects, thereby creating a lattice. For the disordered columnar phase, the lattice is 2D, but when there is the additional ordering of the molecules along the column axis the gross structure is crystalline with a 3D lattice; these phases are soft crystals rather than liquid crystals. The photomicrograph of the dendritic texture of the hexagonal disordered columnar phase, depicted in Figure 34, shows that the phase possesses crystal properties, and for comparison the dendritic texture of the crystal B phase is included. These observations are similar to the situation with the soft crystal phases formed by rod-like molecules where the Bcryst, E, G, H, J and K phases have 3D positional ordering of the molecules.

Figure 34. (Left) The dendritic texture of the disordered hexagonal columnar phase growing on cooling from the isotropic liquid (×100); (right) the dendritic texture of the crystal B phase (×100).

The relationships to crystals imply that columnar phases should not exhibit conventional binary phase diagrams as found for smectics. Instead, they should exhibit depression of the melting points (transition to the liquid) giving eutectic points with respect to the concentrations of the two components, and continuous miscibility across the phase diagram is unlikely, as shown in the phase diagram in Figure 35 for two related benzoate derivatives of triphenylene.

Figure 35. The binary phase diagram as a function of temperature (°C) and concentration (mol%) for two benzoate esters of hexahydroxytriphenylene.

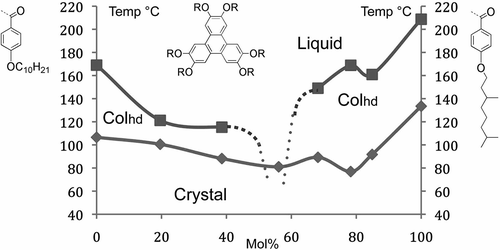
In the following, an interesting extension to this argument can be made. Consider a disordered hexagonal columnar phase composed of disc-like molecules of different diameters. Structurally the columns will act as tubes of diameter equal to the diameter of the largest discs. In a mixed system, this will be the case because the closest approach to one another of the tubes will be the same as the largest discs. As the columns are disordered, there is no need for the centres of the discs to be aligned along the central axes of the tubes, and in fact some of the smaller discs may be off centre with respect to the axes. Thus, the centres of mass need not be along the column axes and therefore the hexagonal packing array of the columns need not be exactly periodic (see Figure 36). Conversely, the defects between the columns will be in a hexagonal periodic array as determined by the largest molecules in the columns, and therefore the defects (or free space) will possess a lattice-like organisation, implying that there will also be a related lattice energy.

Figure 36. A disordered hexagonal columnar phase made up of molecules of different diameters, which are laterally and vertically disorganised along the column axes. The defects between the columns, shown by the heavy lines, will possess long-range periodic ordering.

In the columnar phases described, the peripheries of the molecular discs are composed of flexible chains. Thus, many such systems have multiple substituents in order to fully fill the space around the central aromatic cores of the molecules, hence hexa-substitution is quite common for these materials. Reactions chemistry does however allow for a variety of substitution patterns to be achieved, including 1,3,5-trisubstitution. However, for these types of material there is a great deal of free space between the arms, and therefore the likelihood of mesophase formation is low. However, this is not always the case as demonstrated by the work of Lehmann et al. [77]. Trisubstituted benzenes were shown to exhibit columnar phases, and in an attempt to rationalise this behaviour, a model where the three arms of the molecules were allowed to ‘flop’ parallel to the column axes was developed to give a pyramidal-like structuring. Thus, the arms fill space by coming together as shown in Figure 37. This is similar to the way in which dendrimers form rod-like structures, the way that phasmids form columnar phases, and the way in which bolaphiles form hexagonal phases.[78]

Figure 37. Star-like molecules conformationally change to form columns where the arms of the molecules become almost parallel to the axes of the columns.

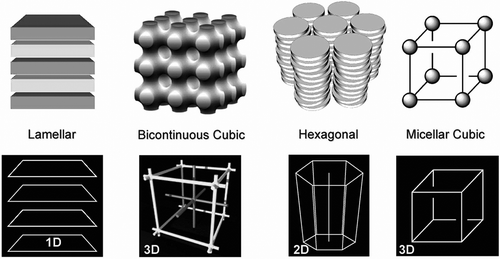
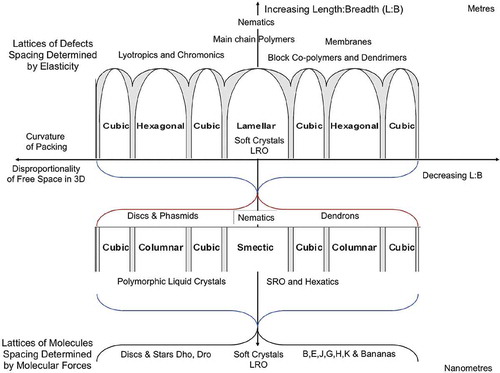
Returning to the general concept of the introduction of curvature into the packing of molecules in condensed phases. The degree of curvature starts with little or no curvature in a lamellar phase and ends with the formation of spheres in cubic phases, as shown in Figure 38. This concept applies to low molar mass materials to amphiphiles, and to block copolymers. At the low molar mass level, polymorphism can occur as for smectics (SmA, SmC, and Hexatics B, I and F, and soft crystal smectics B_cryst, E, G, H, J and K), discotics (D_ho, D_hd, D_rd, P2₁/a,P2/a, C2/m and D_obd) and cubics (Ia3d, Pn3m, Im3m), but at longer length scales polymorphism becomes rarer. For short length scales, periodicity can be of a modulated form as in the density modulations of the layers in smectics or the geometric decay of order in hexatics. However, for longer length scales, positional order is no longer modulated because larger molecular systems tend to have less disordering across interfaces, as for lamellar phases. Thus, to quote Leadbetter,[64] ‘The distinguishing feature of these (smectic) phases is the presence of a single density wave, with a wave vector QA and QC parallel to the director for the SmA phase and at an angle to it for the SmC phase. Usually this density wave is almost purely sinusoidal in contrast to the rather sharp gaussian function characteristic of an ordered crystal. Thus although the wavefronts may properly be called layers, the usual representation of these as well-defined sharp layers is very misleading’. Consequently, lamellar phases might be considered as 1D crystals, as previously described. For longer length scales, similar arguments apply to the hexagonal phase, which has a 2D lattice, and to cubic phases, which have 3D lattices. In these phases, the lattices are determined by the defects associated with interfacial disordering. However, they will exhibit melting and crystallisation of crystals, that is, they should exhibit supercooling rather than reversible phase transitions. Take, for example, the phase behaviour of the 3′-nitro-4′-alkoxybiphenyl-4-carboxylic acids where the chain lengths are C₁₆ or longer.[63] The C₁₆ homologue exhibits SmA and SmC phases and the so-called D and S₄ phases. It was shown that the D phase was cubic and later the S₄ was a columnar phase. The phase sequences for this material are shown in Figure 39. The transition from the SmA phase to the isotropic liquid is reversible; however, the transitions from the SmC phase to the D phase and from the SmA phase to the D phase show considerable hysteresis. Conversely, the degree of hysteresis with transitions to the columnar phase is less pronounced; however, it is possible for the D and columnar phases to coexist. Moreover, the rate of cooling and heating can affect which phase is formed. These results indicate that the smectic phases are liquid-like, but that D and columnar phases are quasi-crystalline, and that the smectic phases cannot coexist whereas the columnar and D phases can. Another consequence is that the crystallinic phases may not be necessarily co-miscible and phase segregate.

Figure 38. The relationship between condensed phase structures and crystallinic ordering.

Figure 39. The phase behaviour of 3′-nitro-4′-hexadecyloxybiphenyl-4-carboxylic acid [63].

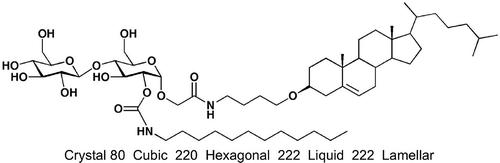
Hysteresis with respect to phase transitions particularly in relation to soft crystals versus liquid crystals can be affected by kinetic as well as thermodynamic properties. For example, the transition from the nematic to nematic twist bend phase appears to be affected by kinetic properties as shown by varying the temperature of the scanning rates and observing the thermal fluctuations seen in a free-standing film of the N_TB phase.[47] Additionally, phase transitions affected by kinetic properties can have varying transition temperatures depending on the scan rate and the reversal of the scan and hence its history. For the glycosteroid shown in Figure 40, on heating it melts from a crystal to a cubic phase, which persists up to nearly the clearing point, whereupon a transient hexagonal phase is formed. However, on cooling, a lamellar phase is observed, which persists to temperatures below the melting point, whereupon a glass is formed.[79] Clearly, the phase behaviour is not purely thermodynamic because the same phases should be seen on cooling as well as heating. It was proposed that once in the isotropic liquid the large molecules had time to reorganise, and on cooling a different organisation was obtained than that seen on the first heating. Such behaviour is problematic for studies where fine control over temperature and the ability to observe bulk properties without wall effects from the sample preparation are not available. Other materials, which usually have large molecular structures such as dendrimers and super- and supramolecules, can also suffer from slow reorientation at phase transitions in comparison to the rate of change of temperature. For instance, certain supermolecules based on octasilsesquioxane scaffolds exhibit nematic phases where for the first heating cycle reorientation of the supermolecules is slow, but on subsequent cooling and heating, nematic and columnar phases were observed once the lower viscosity of the liquid state had been experienced.[80]

Figure 40. Phase behaviour and transition temperatures (°C) for a glycosteroid.

9. Soft crystals, hexatic phases and quasi-liquids

Periodic order in soft materials can be defined as long range, with geometric decay, or short range, and the periodicity can be related to ordering of the molecules, elastic deformations or to the defects in the system. For example, consider the nematic phase, the conventional nematic phase has no periodic ordering, the chiral nematic has long-range periodic order associated with a helical supramolecular structure, the blue phase has long-range periodic order associated with defects and the nematic twist-bend phase has long-range order associated with molecular helical ordering. There are three other forms of nematic phase: the biaxial nematic phase, but the discovery of this phase has not been convincingly proven yet; the polar nematic phase, but its presence depends on external fields so strictly it is not a bulk nematic phase; and the cubatic nematic phase,[81] which remains a theoretical possibility. There are also many ‘cluster-type’ nematic phases, but these are usually found under applied external fields and where molecular reorientation is slow.

The bulk textures of the ‘nematic’ phases are shown in Figure 41. The top-left photomicrograph (×100) shows a conventional nematic, which does not exhibit any periodic structure, whereas the other three textures reflect their relative long-range ordering. The chiral nematic phase shows a continuous change in order associated with its helical pitch; the other two phases however are crystallinic. Locally the molecules in all of the phases are translationally disordered, and if this is how the nematic phase is classified, then all are nematics. However, this misses the point that the molecules need not express the periodic ordering or the classification of phase type. Nematic phases are considered to be elastic continuum fluids, and as such long-range order could be expressed through the elastic properties, as in the helix of the chiral nematic phase, whereas the defects created by the double twist cylinders in blue phases, and the packing of the quasi-fibres of the N_TB phase, produce lattices. Consequently, the repeating ‘unit’ of defined size need not be molecular. Thus, the chiral nematic phase is nematic, whereas the other phases are soft crystals and presumably will have properties associated with crystals, that is, lattice energies, supercooling, etc. This also raises another question, ‘will the fundamental understanding of the phase behaviour of condensed phases at the molecular level still apply to complex fluids where the repeat distances are not of molecular dimensions?’

Figure 41. (a) The schlieren texture of the nematic phase; (b) the formation of droplets of the chiral nematic phase as it forms from the isotropic liquid; (c) the growth of cubic structures in the liquid for the formation of the blue phase; and (d) the stepped texture of the twist bend phase, where the steps are associated with the correlation length (all ×100).

If we now consider the general structures of condensed phases formed by rod-like molecules, then apart from the nematic phase the structures of the smectic and soft crystal phases can be evaluated in terms of the extent of the positional order, as shown in Figure 42. For example, the soft crystal phases have periodic order in the planes of the layers, and also between the layers; in the case of the crystal B phase, it has hexagonal order in the plane, but between the layers it can have three types of layer correlation, AAA, ABAB, ABCABC, where A, B and C correspond to the positions of the layers as they stack one upon another.[82,83]

Figure 42. Molecular ordering in the smectic state of matter showing the stepwise breakdown in order progressing from the solid to the liquid.

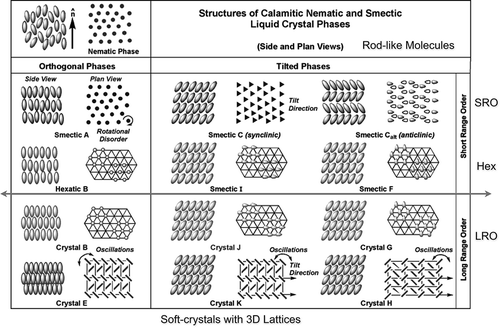
So the soft crystal phases can be considered to have 3D long-range order. For the hexatic phases, there is in-plane geometric decay in the positional ordering within the layers, but apparently there are no correlations between the layers. Thus, the hexatic phases can be considered to have 2D quasi long-range order and 1D short-range order; sometimes, the B, I and F phases have been called stacked hexatic phases. For smectic phases A and C, there is no long-range in-plane or out-of-plane ordering of the molecules; therefore, it has 3D short-range order.

However, it is possible that there could be other combinations of ordering, that is, three variations of in-plane and three variations of out of plane in total, for example, a stacked crystal could have 2D in-plane crystal ordering and 1D out-of-plane short-range order. Due to the possibility of having positional order that is in between short range and long range, condensed phases composed of nanoscale objects, that is, molecules, can have a richer polymorphism than for systems composed of larger entities such as dendrimers, polymers, coated nanoparticles, etc. For example, the ordering between layers in smectic phases is associated with density modulations where the layers are actually virtually non-existent; in comparison for dendrimers, the positions of the layer interfaces in the lamellar phase are fairly well-defined and the phase has a higher degree of crystallinity. Thus, for larger systems where the ordering is dependent on defects, etc., there is less likelihood that hexatic order will be found. Consequently, it appears that the crossover from nanoscale to mesoscale ordering is in the 80–100 Å regime. A phase diagram for materials over all length scales, length to breadth ratios and curvature of packing, based on the observations made, might take the form shown in Figure 43, where the vertical axis is associated with entities with rod-like shapes (molecules to logs in a river), whereas the horizontal axis is associated with entities with disc-like or spherical shapes.

Figure 43. (colour online) Relationships between mesophase types, length scales and anisotropy when the free volume is minimised.

10. Summary

Much of this article is based on research that was published before the discovery of mesophases formed by disc-like molecules, side chain substituted polymers, dendrimers, bent core materials or polyphilic substances, and on computer simulations using Monte Carlo or DFT simulations. Therefore, the use of minimising the free volume and examining the steric interactions between molecules might appear old fashioned, but in many cases such concepts have not been applied to large and complex systems, and as recently as 2010 we were being asked what was the evidence for coated gold nanoparticles being of tactoidal shape. So while we concede that the methodology we use may be tried and tested, it has not been applied to novel materials, new mesophases and old but not fully explained data. Moreover, it appears that the concepts may be applied from the nanoscale upwards to the macroscale. The results drawn from synthetic chemistry, X-ray diffraction, optical and thermal studies, and modelling indicate the following:

• The stability of the nematic phase is primarily dependent on aspect ratio.

• The structure of the interdigitated smectic Ad as originally conceived as being invariant with respect to temperature with a layer spacing of 1.4 times the molecular length [64] is incorrect, and interdigitation occurs to suit molecular packing and varies as a function of temperature as the packing volume varies. This has implications for devices based on the SmA phase and employing cyanobiphenyls as main host materials.[84,85]

• For the SmC phase, molecular engineering is required to fill the free space as much as it is to produce materials that will form tilted arrangements of the molecules. Filling space has to be just right without underfilling or overfilling if materials are to be produced which form bookshelf alignment in devices. The McMillan and Wulf models are partially correct but do not give the whole picture for tilted phase formation.

• In anticlinic phases of rod-like and bent core systems, if the tilt alternates from one layer to the next, then the phases are soft crystals with long-range ordering of the tilt perpendicular to the layers. This allows for enantiomorphic phase formation, which is not possible for liquid-like phases. Where the systems are chiral as in antiferroelectric phases, and there is a transition from the anticlinic phase to the synclinic ferroelectric phase, the transition is often mediated by the formation of ferrielectric phases. For the Ising and clock models, these phases will, like anticlinic phases, be quasi-crystals. Not surprisingly, therefore, there is usually hysteresis of the phase transitions to and from the synclinic phase.

• The evidence that the blue phase and the twist bend phase are nematic phases based on X-ray diffraction showing that there is ordering of the molecules relative to a director field, but there is no positional order, then the classification is acceptable. However, both phases exhibit long-range order. The blue phase could be considered to be a 3D crystal based on its lattice of defects. Again transitions to and from blue phases show hysteresis. Similarly, long-range order in N_TB phases is reflected in the possibility of forming a columnar structure, and not surprisingly the phase exhibits little or no electrooptical response, which is contradictory to normal nematic behaviour.

• The D and S4 phases associated with 3′-nitro-4′-alkoxybiphenyl-4-carboxylic acids show hysteresis of the transition temperatures, indicating that they are probably crystal phases. This means that these phases need not appear in the standard sequencing of liquid crystal phases. It may be that a cubic phase could appear at a temperature below a SmC phase on cooling[86] (see Figure 44) or above, which is probably due to competition between kinetic and thermodynamic processes.

• Columnar phases based on disc-like molecules, where there is disordering of the molecules along the column axes, are potentially 2D crystals, whereas columnar phases that have ordered arrangements of the molecules along the column axes are 3D crystals. For these situations, one might expect binary phase diagrams to have similarities with those of conventional crystals, and there is some evidence for this. From these studies, we raise the issue of the potential for having lattices composed of defects and effectively free space.

• For larger molecular systems such as dendrimers, deformation of the molecular architecture can take place to give tactoidal, discoidal or spherulitic topologies; materials of this type typically pack to give lamellar, columnar and cubic phases, which are soft crystal phases. These studies and those of the D and S4 phases indicate that phases can coexist. They may have relevance in biological systems, which because of their sizes may experience coexistence of different phases in membranes for example.

• Finally, we note that worms, snakes, eels, fish, etc., and sweets, jelly beans, jelly worms, granular matter, etc., when in motion will all try to minimise their free volumes, as shown in Figure 45.

Epilogue: Many parts of this article were presented at the 2012 and 2014 Annual British Liquid Crystal Society Conference and were discussed with George Gray shortly before he passed away.

Figure 44. A cubic phase occurring below a SmC phase on cooling.

Figure 45. Shaken jelly worm sweets.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the Engineering and Physical Sciences Research Council [grant number EP/L012375/1], [grant number EP/J007714/1], [grant number EP/E064299/1]; the Leverhulme Trust, the European Science Foundation; Kingston Chemicals; DERA/QinetiQ; and the Wild Trust.