Free volume, molecular grains, self-organisation, and anisotropic entropy: machining materials

ABSTRACT

In this article, the relationship between molecular architecture and the formation of twist-bend phases is reviewed under the context of shape dependency. We conclude that the twist-bend phase is a universal phenomenon, which occurs in a wide variety of materials, for dimers through to main chain polymers. In the process, the chemical information on molecular design is effectively lost or irrelevant, and molecular topology takes precedence over electrostatic interactions in mesophase formation. As a consequence of this macro-scale material, engineering by shape alone becomes a possibility, potentially more phases may be realised, and entropy is anisotropic.

Graphical Abstract

KEYWORDS:

• Anisotropic entropy
• molecular grains
• dense packing
• nano/macro crossover

Time is not a scalar, but a variable in both reality and perception. It seems but a few minutes ago that George Gray suggested that I look at the reasons why molecules tilt over in layers in the smectic C phase, and if there was any potential for their uses in displays. His simple questions led to work on simulations of the molecules of materials that were found at the time to exhibit tilted smectic C, I and F phases, and ultimately to the unravelling of the structures of the smectic state of matter. With graph paper, compasses, protractor and access to a card reader and rudimentary computer, the mass inertia axes for a number of molecules were determined while in their all-trans conformations [1,2], and the rotational volumes of the molecules were depicted using reflection symmetry. Then the battle began; was the driving force for tilting electrostatic [3] or steric [4] or both? Although simplistic, the models and ensuing property–structure correlations were subsequently used as a basis for material design. By the early 1990s, there became a need at research centres such as DERA (Malvern, Worcestershire, UK) to estimate ‘material properties’ of targeted materials before costly synthesis was considered, and so began bridging the gap between the nano-molecular structures and those of the complex macroworld. Indeed, it is only recently that chemists have started to use modelling as a tool in the rational design of lead compounds (with optimum properties) in their synthetic programmes [5,6]. For want of a better expression, electrostatics appeared to lead the way not only in material design but also in determining mesophase formation and stability. Steric factors at a molecular level still proved useful, but integrated rotational shape lost favour. Therefore, it is quite surprising that the simulation of local dense packing, invoking shape entropy, without recourse to electrostatics has recently provided insights into the self-assembly of particles, including those of liquid crystals [7–9]. Are there any experimental examples of such real systems or materials? The answer is probably no, partly because of the complexity and dynamic behaviours of liquid crystals. However, we have found one family of mesogens for which we think this could be true. These materials are ‘liminal’. They sit at the transformation of many structures and properties, for example, nano to macro, low molar mass to polymer, thermodynamic to kinetic, nematic to smectic, etc., and have the potential to give a new understanding of mesophase formation and properties. The materials exhibit the so-called ‘twist-bend’ phase.

At York we have been intrigued by the recent reports that liquid crystal dimers and dimesogens with relatively flexible but bent architectures exhibit twist-bend nematic (N_TB) mesophases [10]. This ‘so-called’ nematic phase was shown by scanning electron microscopy (SEM) and freeze fracture to possess a local helical organisation of bent-shaped molecules, which twist around a heli-axis to give heliconical arrangement of pitch in the range of 7–9 nm. Although there is no positional ordering of the molecules, the periodicity resulting from the helix can be seen via polarised light microscopy [11] and in the defects formed by the liquid crystal phase on the macro-scale. Surprisingly, the bulk properties of this new phase are not commensurate with those observed for nematic or chiral nematics phases. For instance, from the syntheses of approximately 100 examples of materials [12] that exhibit the twist-bend phase, we find that there is no observable Brownian motion; the mesophase is highly viscous; the phase exhibits a mixed kinetic–thermodynamic transition from the nematic phase as studied by calorimetry, which is more in keeping with polymeric systems than those of low-molar-mass materials; related oligomers [13] and polymers [14] also exhibit the twist-bend phase; and most revealing of all, there is little or no response to applied electric fields in comparison to nematic or chiral nematic phases, which readily exhibit low-voltage dielectric responses [11]. Moreover, early reports suggesting that the twist-bend phase is unique and limited to only a few materials does not hold true because the variety of materials, with differing molecular structures, that exhibit the twist-bend phase is large [12]. Thus, it is doubtful that the twist-bend phase is truly nematic, but is associated with a new and general form of soft matter [11].

In order to develop property–structure correlations for the twist-bend phase, we examined in detail such phases formed by the materials given by the general structure in Figure 1. These ranged from dimesogens to polymesogens, where we define the repeat as being a mesogenic unit, which is similar to the notation used for peptides where the amino acids may be identical (polymeric, as in polyaniline) or different [15,16].

Figure 1. General structures of materials that exhibit the twist-bend phase.

In developing property–structure correlations, we investigated the relationship between mesophase stability and bend angle. We found that an angle of between 110° and 130° is required to support the formation of the twist-bend phase, irrespective of specific bond angles (e.g. between methylene or methyleneoxy units, etc.) or the dipole moments or polarisabilities of the various functional groups in a molecular architecture [17]. A bend angle of near to 120° gives the most temperature stable twist-bend phase; see Table 1 for a small sample of five related materials. The local circular packing corresponds to approximately six overlapping molecules per twist of the local helical structure of the phase, which is similar in number to the estimation of five to six molecules per twist of 360° observed by SEM (see Figure 2).

Packing six molecules in two dimensions produces either an intercalated structure or a circular arrangement with a packing void at its centre (Figure 2(a)). This second arrangement allows for an expulsion of the bend into the third dimension (Figure 2(b)), thereby minimising the free volume, increasing the packing density, and randomising the positions of the molecules about a heli-axis (Figure 2(c)), which consequently increases the entropy and reduces the free energy. In comparison to an intercalated structuring, this arrangement has more advantages in terms of the energetics. It is also important to note that the organisation is only dependent on the bent architectures of the molecules and not to their conformational structures. Moreover, with any twisted organisation there is the possibility of two twists at right angles to one another, and in the case of the pitch length for the principal helical structure, for the materials investigated the results are all very similar, and in the 8–9 nm range, no matter what the details of the molecular aspect ratios are or the electrostatic properties [10,18–21]. Overall, the results indicate that molecular topology determines the twist-bend phase stability and the pitch length.

Taking the concept further of shape being the primary determinant in the formation of the twist-bend phase, we compared the transition temperatures for the nematic phase to the isotropic liquid, and the nematic phase to the twist-bend phase. A linear dependency was found across a range of nearly 100 di-, tri-, tetra-, hexa-, oligo- and polymeric-mesogens (see Figure 3), composed of various functional groups and motifs, as shown in Figure 3. It should be noted that there is a little scattering of the data for some oligomers at high temperatures, which is due to decomposition [22,34]. The linear behaviour indicates that the chemical information for these materials is of little importance in affecting the condensation of the system in the formation of the twist-bend phase. In conventional materials, there is always a variation in the relationships between the clearing points to the isotropic liquid and subsequent phase transitions obtained on cooling because the transitions are dependent on the intermolecular interactions coupled with the degree of amphiphilicity. Therefore, if we compare the results for homologous materials with odd methylene parity (bent shape shown in Figure 3) with examples of some similar materials of even parity (rod-like), we find that the relationship between the liquid to nematic phase and the nematic to smectic A phase or nematic to smectic C phase transitions for the even parity materials is not linear but randomly scattered, as shown in Figure 4(a,b) [35,36].

The results so far suggest that twist-bend materials exhibit some properties similar to those of polymers; thus, calorimetric studies were used to elucidate further the thermodynamic aspects of the N to N_TB phase transition [11]. Figure 5 shows the nematic to twist-bend phase transition with respect to the fall in temperature (°C min⁻¹). Normally, as a scan rate is increased, the peak shape sharpens as the resolution improves. However, for 1,11-di-(1″-cyanobiphenyl-4-yl)undecane (CB11CB) the transition becomes second order and then that of a glass, i.e. similar to that of a polymer. Thus, the slower the scan rate, the more time the twist-bend phase has to form an organised (quasi-crystallinic) structure, i.e. a helix, and the free volume decreases, whereas the faster the scan, the less time is available, and the more disorganised is the structure (mosaic) of the phase and the free volume increases. This indicates that there is a reasonable degree of kinetic behaviour at the phase transition in addition to thermodynamic. Consequently, for faster cooling rates, this results in an easier response to an applied electric field near to the phase transition. In addition, the extent of the diffuse molecular motions associated with the phase transition is clearly seen on cooling in the microscopy studies of free-standing films [11].

Figure 2. Illustration of the effect of the bend angle on the thermal stability of the twist bend phase in relation to molecular shape. The space filling molecular shapes were generated via density functional theory simulations(DFT) using the B3LYP function and the 6-31G(d) basis set for the dimesogens. (Note the greyscale is inverted for the terminal groups to demonstrate molecular orientation.)

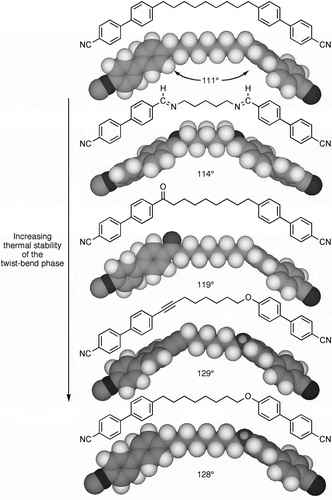
Figure 3. Two-dimensional packing of six bent dimers with bend angles of 120° (a); expulsion of the packing into the third dimension to give a twisted structure (b); and the formations of a helical structure with minimisation of the free volume (c).

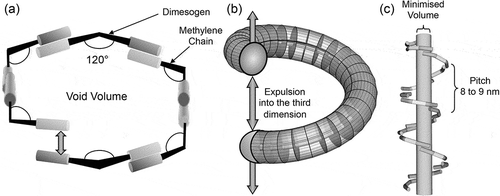
Figure 4. Plots of the T_{N-Iso liq} versus the T_NTB–N temperatures (°C) for dimers, dimesogens and oligomers with odd parity numbers of spacer chains. The data was taken from refs. [10,11,20,22–28], and recent publications also support this analysis [29–33].

Figure 5. Plot of the nematic to isotropic liquid and the nematic to smectic A (a) and smectic C (b) phase transition temperatures (°C) [35,36].

Flory and Fox [37,38] demonstrated for polymer systems that the glass transition is linked to the melting point and directly to the free volume, at which point the free space available for molecular motions is at a minimum. The differential scanning calorimetry (DSC) results therefore support the hypothesis that the nature of the N to N_TB phase transition is associated with the condensation of the structure determined by the free volume and dense packing of the molecules, which are dependent on molecular shape. This treatment, coupled with the previous study, indicates that the molecules can be considered as molecular grains, where topology under the constraint of the minimisation of volume is the determinant for phase condensation and phase transition. Consequently, these studies demonstrate that the phase transition to the twist-bend phase will be universal, and will be observed for many families of molecular and macromolecular materials with differing structures polymorphisms, degree of polymerisation and dispersities.

Thus, apart from the reports of the twist-bend phase being exhibited by dimer and oligomers, as might be expected, the phase can be linked to macromolecular materials such as main chain polymers, lyotropic polypeptides and flagella. For example, Ungar et al. [14] reported nematic to nematic phase transitions for thermotropic random copolymers (included in the results in Figure 3) that possess odd-parity numbers of methylene units in the linking chains between the aromatic units. Although it is not clear that the lower temperature nematic phase is a twist-bend phase the possibility was speculated upon recently [39]. Further, the liquid crystal phase of poly(γbenzyl L-glutamate) exhibits microscopic textures that are almost identical to those of the twist-bend phase. Livolant and Bouligand indicated that the phase was composed of polymer fibres that are looped thereby forming two backbones twisted together, which then form hexagonal packing arrays [40]. Additionally, Barry et al. reported a first-order phase transition driven by entropy in suspensions of helical flagella from an isotropic liquid into a liquid–crystalline state that possessed novel chiral symmetry [41]. Optical textures of this phase consist of striped patterns with alternating light and dark regions, which correspond to differing director orientations. Fluorescent labelling reveals that the flagella are in phase with one another, and despite the lack of positional order there is long-range ‘phase’ ordering. It was proposed that the formation of a conical phase is driven by simple packing constraints, with the excluded volume between two helices being significantly larger when they are out-of-phase with respect to one another than when they are in phase and so minimisation of the excluded volume dictates a preference for in-phase packing leading to the emergence of a conical mesophase.

Consequently, in forming a helical structure, there is also the possibility of forming fibres, with multiple strands, as shown in Figure 6, and examples of a dimesogen and a tetramesogen are shown in Figure 7. The physical evidence for the formation of fibres is demonstrated by thermal polarised light microscopy as shown in Figure 8(a). In this photomicrograph, the presence of a linear defect is seen across the bottom third of the picture. The defect line has upper and lower domains with short lines at an angle of 30° to the normal to the horizontal line. These two domains are left- and right-handed helices, which are on average 5 μm in width, with the short lines corresponding to the change in the director field relative to the polarisers. Figure 8(b) shows CB11CB in a 5 μm cell coated with antiparallel buffed polyimide, with the domains showing a folded arrangement typical of the folding often seen by polymers, but on a much larger scale.

Figure 6. DSC thermograms for the nematic to twist-bend phase transition of CB11CB at varying cooling rates.

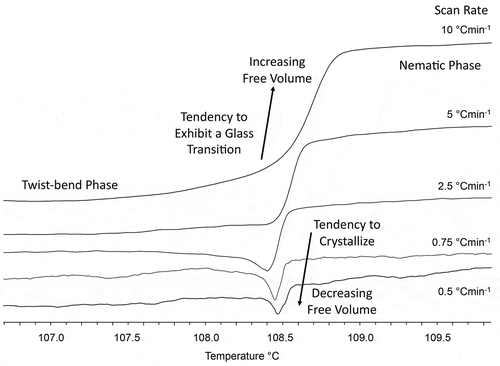
Figure 7. Individual molecules form a helix, which when packed together form a ribbon. In the ribbon, the helices can move easily in a spiralling rotation along the heli-axis. Across the helical axes, there is little flow.

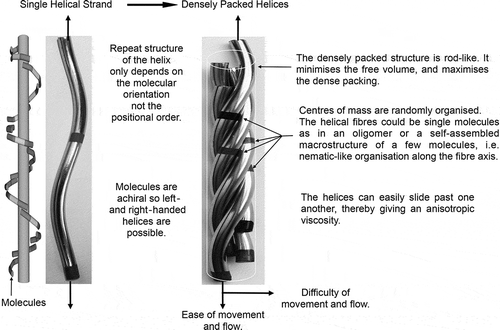
Figure 8. Examples of a dimesogen and a tetramesogen as strands. It should be noted that it is possible to form doubled-up or looped molecular architectures.

Figure 9. Photomicrograph of the defect texture of the twist-bend phase showing focal-conic and helical domains (compound 7 in ref. [39], ×100) (a), and the folded texture of CB11CB in an antiparallel aligned polyimide coated cell (×200, 5-m spacing) (b).

This structuring is simply the twisting of one helical strand about another (or several others). However, the centres of mass of the molecules along the strands need not be commensurate, and therefore the only periodic order associated with the pitch length is determined by molecular topology, hence the result that the measured pitch values are similar. Furthermore, in the fibrous structure, the molecules are densely close-packed, thereby minimising the free volume. Along the heli-axes of the strands, the molecules will move more freely in a spiralling way than they can across the fibre axes. This means that the viscosity is also anisotropic. Experimentally, this has been reported for the viscosities of molecular (dimesogens) and macromolecular (flagella) materials [41]. Moreover, helical flagella were observed to diffuse along the helical axis in a manner akin to a ‘nut on a bolt’ with diffusion being significantly faster parallel to this axis with respect to perpendicular diffusion. Recent NMR diffusion experiments similarly have demonstrated anisotropic diffusion in the twist-bend phase of CB7CB [42]. Thus, the ease of diffusion of the molecules in a spiralling manner along the heli-axis means that the entropy will also increase in the same direction because of the lack or positional ordering, thereby potentially reducing the free energy.

From these studies, we conclude that the twist-bend phase is a universal phenomenon, which occurs in a wide variety of materials, and over length scales greater than nano for dimers through to main chain polymers. In the process, the chemical information is effectively lost or irrelevant, and molecular topology takes precedence in mesophase formation. Following are some possibilities that arise from this hypothesis:

1. Given that dimers have the smallest molecules that support the formation of the twist-bend phase, there appears to be a crossover from nanoscience to macroscience at around 50–100 nm. Furthermore, the changeover could be associated with the relationship between surface area versus volume of the molecules, with the surface area being dominant at the nanoscale, and the volume dominant at larger length scales. At nano-length scales, the electrostatic interactions will be important, whereas for the macro-regime the spatial shape is important.

2. In the nanoworld, molecular materials form structures based on allowable electrostatic interactions permitted by steric structure, whereas shape and minimisation of the free volume determines the formation of condensed phases via the density of packing. This applies to molecular shape, conformational structure and distortion of shape (as exemplified by dendritic and colloidal liquid crystals). Indeed, shape in terms of a quasi-solid entity is effectively a distortion of space itself.

3. Molecules appear as molecular grains in the macroworld, and have properties similar to those of granular matter.

4. Periodic ordering in macrosystems does not need to have periodicity based on molecular entities, but periodicity based on translational order such as pitch length as for the twist-bend and twist-grain phases, or arrangements of defects as for columnar and blue phases. At these length scales, the structures effectively will be crystalline (soft), and as such they will exhibit phase diagrams similar to those of crystal systems rather than comiscibility as found for liquid crystals. For example, discotic nematics should be comiscible, whereas columnar discotics may not.

5. Phase transitions are dependent on kinetic changes as well as thermodynamic, and glass transitions could occur as a function of scan rate.

6. Entropy may be directional, and therefore so too the free energy.

7. Anisotropic properties can be determined by spatial confinement as opposed to electrostatic interactions.

8. These possibilities could have consequences for other non-liquid-crystal systems such as colloids, metamaterials, dendrimers, biomaterials, bioparticles, etc., and will thereby allow mesoscopic engineering of matter at the interface between the nano- and macro-regimes.

In summary, over 25 years ago I looked at some dimesogens for Luckhurst, and thought they might exhibit an edge dislocation phase, but my reason for writing this article is that there now appears to be some new basic scientific concepts involved with the formation of the twist-bend phase, which do not conform to the conventional views of liquid crystal structures and properties, and possibly to our understanding of mesoscale systems. May be Luckhurst was correct when he wrote the following:

Liquid Crystal dimers and trimers exhibit a range of unusual properties, which are fascinating in their own right, and which also parallel those found for semi-flexible main-chain liquid crystal polymers. This close similarity suggests that dimers and oligomers should form good model systems for their polymeric counterparts. [43]

And indeed may be we are seeing the possibility of a new field of ‘the engineering of granular, molecular matter’ developing.

Acknowledgements

I would like to give my gratitude to Drs Cowling, Saez, Moore, Mandle, Davis and Sims for their continual support, their inputs into our developing ideas, and their numerous discussions. I am also indebted to the EPSRC for its continued support of my research through the following grants, EP/J007714/1, EP/K039660/1 and EP/M020584/1. I am also grateful to Prof CT Imrie and Dr SJ Cowling for arranging the publication of this compilation of articles.

Disclosure statement

No potential conflict of interest was reported by the author.

Additional information

Funding

The author is indebted to the EPSRC for its continued support of my research through the following grants: EP/J007714/1, EP/K039660/1 and EP/M020584/1.