Developmental relations between mathematics anxiety, symbolic numerical magnitude processing and arithmetic skills from first to second grade

ABSTRACT

We investigated the levels of and changes in mathematics anxiety (MA), symbolic numerical magnitude processing (SNMP) and arithmetic skills, and how those changes are linked to each other. Children’s (n = 264) MA, SNMP and arithmetic skills were measured in Grade 1, and again in Grade 2, also including a mathematics performance test. All three constructs correlated significantly within each time point, and the rank-order stability over time was high, particularly in SNMP and arithmetic skills. By means of latent change score modelling, we found overall increases in SNMP and arithmetic skills over time, but not in MA. Most interestingly, changes in arithmetic skills and MA were correlated (i.e. steeper increase in arithmetic skills was linked with less steep increase in MA), as were changes in SNMP and arithmetic skills (i.e. improvement in SNMP was associated with improvement in arithmetic skills). Only the initial level of arithmetic skills and change in it predicted mathematics performance. The only gender difference, in favour of boys, was found in SNMP skills. The differential effects associated with MA (developmentally only linked with arithmetic skills) and gender (predicting only changes in SNMP) call for further longitudinal research on the different domains of mathematical skills.

KEYWORDS:

• arithmetic
• gender differences
• latent change score modelling
• mathematics anxiety
• symbolic numerical magnitude processing

Introduction

Numerous people experience mathematics anxiety (MA), “the feelings of tension and anxiety that interfere with the manipulation of numbers and the solving of mathematical problems” (Richardson & Suinn, 1972, p. 551), which may have a negative impact on various areas in life, including academic situations (Ashcraft, 2002; Dowker et al., 2016). An often-reported finding is a negative connection between MA and mathematics performance (Barroso et al., 2021). One view on the underlying mechanisms contributing to this connection suggests MA to be associated with deficits in low level numerical magnitude processing (i.e. intuition about quantity and mental manipulation of non-symbolic or symbolic magnitudes, supported by approximate number system [Dehaene, 2011; Vanbinst et al., 2016]) that subsequently compromise the development of higher-level mathematical skills, such as arithmetic (Maloney et al., 2011). This question is still unresolved, as some studies have found support for this assumption (e.g. Lindskog et al., 2017), and some others not (e.g. Colomé, 2019).

Among younger children, the findings on the negative connection between MA and mathematics performance are less clear, and the role of numerical magnitude processing in this context is virtually unexplored. Some studies, mainly cross-sectional, demonstrate the presence of MA already in early grades (although see Szczygieł & Pieronkiewicz, 2021) and its coupling with inferior mathematics performance (e.g. Cargnelutti et al., 2017; Gunderson et al., 2018; Primi et al., 2020), while other studies have failed to detect this negative connection (Haase et al., 2012; Krinzinger et al., 2009). This also applies to the linkage between MA and numerical magnitude processing. Some evidence shows MA to be negatively connected with numerical magnitude processing (Pantoja et al., 2020), while some have found this to be limited only to symbolic, not non-symbolic numerical magnitude processing (Gómez-Velázquez et al., 2015; Hart et al., 2016).

As the above associations have not been explored from a developmental perspective, we will in this study expand on previous research by investigating the longitudinal relations between MA, symbolic numerical magnitude processing (SNMP) and arithmetic skills from first to second grade. Thus, this is, to our knowledge, the first study to examine the developmental relations between these three constructs among school beginners. Moreover, as findings on gender differences in young children’s MA have been mixed (Dowker et al., 2016; Zhang et al., 2019) or entirely disregarded, in previous studies, we will also look at the role of gender in these developments.

The relation between mathematics anxiety and mathematics performance

MA is considered as a multidimensional construct, which is best represented by two distinct dimensions, affective and cognitive (Ho et al., 2000). Both dimensions become apparent in anticipation of solving problems as well as during actual problem solving. The affective dimension of MA (MA-A) refers to feelings of nervousness, tension, fear and unpleasant physiological reactions, when having to solve mathematical problems in everyday and academic situations or when anticipating the need to do so (Namkung et al., 2019). For example, a student may experience fear and increased heart rate when thinking of a forthcoming math class or a math exam at school. The cognitive dimension of MA (MA-C), in turn, refers to negative thoughts, expectations and worries in connection to one’s anticipated performance in mathematics-related situations (Namkung et al., 2019). For example, a student may feel extremely worried about not succeeding to solve math problems correctly.

Despite decades of research on the connections between MA and mathematics performance (Carey et al., 2015; Dowker et al., 2016), only recently has more attention been paid to younger children. Of studies investigating these relations among children aged six to eight, the majority of research has focused on the MA-A, followed by studies combining both affective and cognitive dimensions (MA-Com), and, finally, by a few studies exploring only the MA-C (for an overview of all these studies, see Appendix).

While cross-sectional studies have consistently found a negative relation between MA-A and children’s mathematics performance (e.g. Caviola et al., 2017; Primi et al., 2020; Van Mier et al., 2019), even after controlling for other types of anxiety (e.g. trait anxiety) and cognitive factors (i.e. IQ, working memory) (Lauer et al., 2018; Wu et al., 2012, 2014), this is not the case for studies focusing on the MA-C only (e.g. Dowker et al., 2012, 2019; Haase et al., 2012; Wood et al., 2012). Then again, studies with measures of MA-Com also report a negative relation between MA and mathematics performance (Harari et al., 2013; Jameson, 2013; Kucian et al., 2018). These results thus suggest that at this age, it is children’s negative emotionality in mathematics situations rather than worry about one’s performance that is linked to inferior mathematics performance.

This is partly in contrast to findings from a recent meta-analysis on school-aged children, which showed both dimensions of MA to be linked with mathematics performance equally strongly (affective, r = −.31; cognitive, r = −.32) (Namkung et al., 2019). Some possible explanations for this might be that in later grades, schools are setting more formal curriculum-guided performance expectations for students’ mathematics learning, students’ skills are formally assessed more frequently (e.g. math tests) and students start to become more aware of their emotions, as well as realistic of their own level of performance compared to their peers’ performance (Denham, 2006). Experiencing learning of mathematics as difficult and receiving negative feedback from formal assessments may, in turn, increase student’s feelings of negative thoughts, expectations and worry for mathematics performance (Sorvo et al., 2017).

Cross-sectional findings do not, however, reveal how MA and mathematics performance are related to each other over time. Only a handful of longitudinal studies have been conducted on young children (see Appendix), and the results are mixed. Findings have shown arithmetic skills to predict later MA-C, but neither MA-A nor MA-C to predict arithmetic performance (Sorvo et al., 2019), thus lending support for the deficit theory (e.g. Ma & Xu, 2004; Wang, 2020); both MA-A (Cargnelutti et al., 2017) and MA-Com (Ching, 2017) to predict later arithmetic and mathematics performance, thus following the debilitating anxiety model (Carey et al., 2015); no longitudinal relations between MC-C and arithmetic performance (Krinzinger et al., 2009) and, finally; reciprocal predictions between MA-A and mathematics performance (Gunderson et al., 2018), although with the effect of mathematics performance on MA-A being considerably stronger than vice versa.

The few studies available investigating developmental changes simultaneously in MA and mathematics performance in children show MA to be relatively stable over time (β = .33–.63) and performance in mathematics even more so (β = .63–.91) (Cargnelutti et al., 2017; Gunderson et al., 2018; Krinzinger et al., 2009; Sorvo et al., 2019). Instead, findings concerning mean-level change during the early grades are also mixed, suggesting both increase (Krinzinger et al., 2009) and decrease from grade to grade (Gunderson et al., 2018; Pantoja et al., 2020; Sorvo et al., 2019). Note, however, that the average level of MA in the beginning of the first grade is usually extremely low (Szczygieł & Pieronkiewicz, 2021), thus defining the onset of the change.

The role of numerical magnitude processing

There has been an increasing interest in identifying cognitive factors that may affect the relation between MA and mathematics performance (e.g. Beilock & Carr, 2016; Passolunghi et al., 2016; Schneider et al., 2017; Skagerlund et al., 2019). Numerical magnitude processing (NMP) is considered as one possible underlying factor in the development of mathematics but also when it comes to the aetiology of MA. The association between NMP and mathematics performance seems to partly depend on the number format used in the NMP tasks. Studies using a symbolic format (i.e. Arabic digits) have demonstrated more consistent findings and stronger associations on mathematics performance than studies using non-symbolic format (i.e. dots) (De Smedt, Noël, Gilmore, & Ansari, 2013; Schneider et al., 2017). SNMP has been found to be linked with mathematics achievement within and across different grades in elementary school (Brankaer et al., 2017; Holloway & Ansari, 2009). Of subdomains of mathematics, SNMP has especially been found to be a strong predictor of arithmetic fluency, and students performing well in SNMP to exhibit more effective arithmetic strategy use (i.e. being faster in retrieving facts and using procedural strategies) (e.g. Bartelet et al., 2014; Vanbinst et al., 2016). Interestingly, Lyon et al. (2014) found this relation to change dynamically across the primary school years, and suggested that when getting older, the children are relying more on accessing the ordinal information in numerical symbols than the relative magnitude of them. Therefore, we might see a diminishing strength in the relation between SNMP and arithmetic skills over early school years.

In relation to MA, one suggested view is that poor functioning of NMP negatively affects learning of symbolic numbers, and further creates negative feelings in mathematics, which then leads to avoidance of mathematics and inferior mathematics performance (Lindskog et al., 2017; Maloney et al., 2011). In line with this, some studies have reported a negative association between MA and either symbolic (Maloney et al., 2011; Núñez-Peña & Suárez-Pellicioni, 2014) or non-symbolic NMP (Lindskog et al., 2017; Maldonado Moscoso et al., 2020) among older students. Further, Skagerlund et al. (2019) found SNMP to mediate the effect of MA on arithmetic performance, thus implying that MA might interfere with the processing of numerical stimuli, which then negatively affects arithmetic performance. In contrast to these findings, Colomé (2019) did not find evidence for less precise NMP in students with high MA, while Braham and Libertus (2018) showed MA to moderate the relation between NMP and mathematics performance, but only on applied math problems.

While the role of NMP in the relation between MA and mathematics performance is not yet clear in older students, it is even less clear in younger ones. Interestingly, the few available studies addressing the relation between MA and NMP, either directly or indirectly, suggest that MA might be negatively associated with SNMP, but not with non-symbolic NMP (Gómez-Velázquez et al., 2015; Hart et al., 2016; Wang et al., 2015). We clearly lack studies on school beginners that would investigate not only concurrent but also the developmental relations between NMP (and particularly SNMP, given the previous findings), MA and mathematics performance.

Gender differences

The role of gender in mathematics development and MA has received considerable attention (Barroso et al., 2021; Lindberg et al., 2010). This is partly because girls tend to be underrepresented in science, technology, engineering and mathematics (STEM)-related study and career fields later on (National Science Foundation & National Center for Science and Engineering Statistics, 2019), which has raised the question of what factors might explain this discrepancy and at which points in development we may start to see gender differences. Generally, boys and girls tend to show similar levels of early mathematical skills (Kersey et al., 2018) and later mathematics performance at school, although some gender differences (in favour of either girls or boys) have been reported on a national level in several countries (Reilly et al., 2019).

Findings concerning gender differences in MA have been more inconsistent. Although research has shown no gender differences in the connections between MA and mathematics performance (Barroso et al., 2021; Zhang et al., 2019), females tend to report higher MA compared to males, but mostly among older students and adults (Hart & Ganley, 2019; Hembree, 1990). Findings on young children are somewhat mixed. A majority of studies have not shown any gender differences (Ching, 2017; Dowker et al., 2012; Harari et al., 2013; Hartwright et al., 2018; Kucian et al., 2018; Primi et al., 2020; Ramirez et al., 2013; Wu et al., 2014), while in some studies, girls have reported experiencing more MA than boys (Gunderson et al., 2018; Lauer et al., 2018; Sorvo et al., 2017), and sometimes also boys have been found to display higher MA than girls (Dowker et al., 2019). One possible explanation for these progressively more systematic gender differences in MA draws on students’ increasing awareness of gender stereotypes about academic abilities (McKown & Weinstein, 2003). Indeed, some evidence suggests that the endorsement of gender stereotypes in mathematics (e.g. “mathematics is a male domain”, “boys are good at maths”) by females, tends to lead to an overestimation of one’s level of MA (Bieg et al., 2015; Steffens et al., 2010).

Present study

Research on young children’s MA and its connection with mathematical skills and performance is currently lacking longitudinal studies, which would help us to understand the early developmental relations. Further, the role of gender in MA is still unclear. In this longitudinal study, we extend prior research by investigating the levels of and changes in MA, SNMP and arithmetic skills from first to second grade, and how those levels and changes are linked with each other and to second grade mathematics performance. Our five research questions (RQ) with accompanying hypotheses (H) are outlined below.

RQ1. How are MA, SNMP and arithmetic skills connected with each other at grades one and two?

We expect to find negative concurrent relations between MA and arithmetic skills in both grades (H1.1) (e.g. Jameson, 2013; Kucian et al., 2018). Although prior research is still very limited as to the relation of SNMP and MA, we anticipate them to be negatively associated (H1.2) (Gómez-Velázquez et al., 2015). Further, positive relations between SNMP and arithmetic skills are expected (H1.3) (Schneider et al., 2017).

RQ2. How stable are MA, SNMP and arithmetic skills over time, in terms of both rank-order stability and mean-level change?

We anticipate significant stability in MA and even more so in mathematical skills (H2.1) (e.g. Sorvo et al., 2019). We would also expect to detect significant development in terms of mean-level increase in children’s arithmetic and SNMP skills from first to second grade (H2.2) (Gunderson et al., 2018). As we start to follow the children from the first grade, we presume the initial level of MA to be quite low (Szczygieł & Pieronkiewicz, 2021), and therefore expect to see either no change or a slight increase in it on average (H2.3).

RQ3. How are changes in MA, SNMP and arithmetic skills linked with each other?

Since there is no direct previous evidence available, we make the following assumptions based on the findings on concurrent relations or longitudinal predictions. We expect the changes in SNMP and arithmetic skills to be positively associated so that improvement in one skill is related to improvement in the other (H3.1) (Schneider et al., 2017). As previous longitudinal studies have typically found a negative link between MA and arithmetic skills (e.g. Sorvo et al., 2019) and in cross-sectional studies between MA and SNMP (Gómez-Velázquez et al., 2015), we assume an increase in arithmetic or SNMP skills to be linked to a decrease in or less steep increase of MA or vice versa (H3.2).

RQ4. Are there gender differences in the levels of and changes in MA, SNMP and arithmetic skills?

We expect to find no gender differences in the levels of and changes in either SNMP or arithmetic skills (H4) (Kersey et al., 2018), but we refrain from specific hypotheses regarding MA due to the mixed findings in previous studies (Dowker et al., 2019; Gunderson et al., 2018; Primi et al., 2020).

RQ5. How do the levels and changes in MA, SNMP and arithmetic skills predict curriculum-based mathematics performance?

We expect the levels of and changes in SNMP and arithmetic skills to positively predict mathematics performance (H5.1) (Jordan et al., 2003; Schneider et al., 2017). Based on recent meta-analyses (Namkung et al., 2019; Zhang et al., 2019), we also expect MA to predict mathematics performance negatively (H5.2).

Methods

Participants

This study is part of a longitudinal project investigating the development of children’s numeracy skills. A total of 264 Norwegian children participated in the study (45.3% girls, M_age= 6 y. 9 m, SD = 3.33 m), and were followed up from first to second grade. Children came from five public schools (n = 12 classrooms) in the capital area of Norway. As reported by their parents, 10.6% (n = 230) of the children spoke Norwegian as their second language, and most of the children were from families with parents having at least a Bachelor’s level degree (fathers: 85.2%, mothers: 89.1%). An ethical approval was applied for and given by the Norwegian Centre for Research Data before the data collection, and children’s parents and teachers gave their consent for the study accordingly.

The children in Norway start schooling in August, the year they turn six, and teaching follows the guidelines of the national core curriculum (The Norwegian Directorate for Education and Training, 2013). By the end of the second grade, the children are supposed to have achieved certain competence goals in mathematics. For example, in Numbers to operate with numbers up to 100, count and compare numbers and use varied strategies in addition and subtraction; in Geometry to recognise and describe 2- and 3-dimensional figures, to use mirror symmetry and to explore geometric pattern; in Measurement to measure and compare length and area with non-standard and standard units, tell time, and to recognise Norwegian coins and use those for buying and selling; and in Statistics to collect, note and illustrate data using for example tally marks and bar graphs (see more in detail: The Norwegian Directorate for Education and Training, 2013)

Measures

Mathematics anxiety

Seven items measuring MA in the context of mathematics lessons and doing homework were used from the Achievement Emotions Questionnaire – Elementary School (AEQ-ES) (Pekrun et al., 2007). The items related to MA in exam situations were not used from AEQ-ES, as children in Norway do not yet have formal mathematics exams at school at this age. The AEQ is intended to measure MA as a unidimensional construct (Lichtenfeld et al., 2012), although the items seem to reflect both cognitive (e.g. “When I do math homework, I worry if I will ever understand it.”) and affective (e.g. “When I think about math class, I get nervous”) aspects of MA. Each question was read aloud to the children due to developing reading skills in this age group. Then the child answered the question on a 5-point Likert scale (1 = not at all – 5 = very much), with anchored displays of faces showing increasing emotional intensity, which should help children in understanding the meaning of the Likert scale better than using only numbers (for details, see the AEQ-ES test description in Lichtenfeld et al., 2012).

To test the unidimensionality of our measurement of MA, we ran a series of confirmatory factor analyses on time 1 and time 2 data comparing one- and two-factor solutions (i.e. MA-Com vs. separate MA-A and MA-C as implied by item wording). At time 1, the fit of both one- and two-factor models were good and similar, χ²(14) = 37.59, p = .0006; CFI = .96; RMSEA = .081; SRMR = .052, and χ²(13) = 37.11, p = .0004; CFI = .96; RMSEA = .085; SRMR = .052, respectively, but the correlation between the factors in the two-factor model was .98. The time two results were virtually identical. Both one- and two-factors fit the data well, χ²(14) = 33.38, p = .0025; CFI = .97; RMSEA = .076; SRMR = .053, and χ²(13) = 29.22, p = .0072; CFI = .98; RMSEA = .072; SRMR = .046, respectively, but the correlation between the factors in the two-factor model was .90. We also ran additional analyses to compare the patterns of correlations between the one- and two-factor solutions and other variables at both time points. As shown in Table S1 in the Supplementary material, the correlations were very similar across both solutions. Given the above, the two-factor model was rejected due to being less parsimonious with no significant added value, and we chose to proceed with the one-factor model.

Table 1. Descriptive statistics of measures at t1 and t2 by gender.

Measure	Time point	α	All			Girls			Boys
			N	M	(SD)	n	M	(SD)	N	M	(SD)
SNMP-A	t1	.858	259	17.29	(4.19)	119	17.16	(4.05)	140	17.41	(4.32)
	t2	.882	245	19.53	(4.40)	112	18.86	(4.51)	133	20.09	(4.25)
SNMP-B	t1	.841	259	7.97	(3.91)	119	6.82	(3.06)	140	8.94	(4.29)
	t2	.880	244	11.06	(4.65)	112	9.37	(3.99)	132	12.49	(4.70)
Addition	t1	.881	258	5.76	(4.38)	119	5.46	(4.02)	139	6.01	(4.66)
	t2	.917	245	11.00	(6.31)	112	10.65	(5.90)	133	11.30	(6.65)
Subtraction	t1	.900	256	4.50	(3.82)	117	4.10	(3.38)	139	4.83	(4.13)
	t2	.892	243	7.72	(5.13)	111	7.51	(5.13)	132	7.89	(5.14)
Word problems	t1	.775	258	11.24	(3.38)	119	11.28	(2.99)	139	11.20	(3.70)
	t2	.786	242	14.14	(3.54)	111	14.37	(3.04)	131	13.95	(3.91)
Math scale	t2	.933	240	48.02	(12.42)	110	48.43	(11.87)	130	47.67	(12.90)
Math anxiety	t1	.788	256	1.25	(0.49)	118	1.26	(0.44)	139	1.24	(0.53)
	t2	.836	242	1.20	(0.43)	112	1.18	(0.43)	132	1.21	(0.44)

Note: SNMP-A = symbolic numerical magnitude processing with 1-digit numbers (max. 60 p.), SNMP-B = symbolic numerical magnitude processing with 2-digit numbers (max. 60 p.), Addition = addition fluency (max. 45 p.), Subtraction = Subtraction fluency (max. 45 p.), Word problems (max. 34 p.), Math scale = curriculum-based mathematics performance (max. 75 p.) and Math anxiety = larger value indicates more anxiety (Likert scale 1–5).

Symbolic numerical magnitude processing

The SYmbolic Magnitude Processing (SYMP) Test (Brankaer et al., 2017) was used to measure children’s symbolic numerical magnitude processing. There are two subtests, one with one-digit and another with two-digit numbers. Each sub test has 60 digit pairs, presented in four columns of 15 pairs. The child needs to cross out the larger of the two digits in a pair, in a given time of 30 s per subtest (see test and item description more in detail: Brankaer et al., 2017). One point is given for a correct answer and zero for an incorrect answer, the sum score for each subtest, thus being the number of the items correctly solved in 30 s.

Arithmetic skills

A standardised test Regnefaktaprøven [Test of arithmetic facts] (Klausen & Reikerås, 2016) was used to measure children’s addition and subtraction fluency, and WISC-V: Regning [Arithmetic] (Wechsler, 2017) for arithmetic word problem solving. In Regnefaktaprøven there are 45 items (either addition or subtraction) per page and the child has 2 min to solve as many items as possible for each subtest. One point is given for a correct answer and zero for an incorrect answer, the sum score for each subtest thus being the number of items correctly solved in 2 mins. In WISC-V Arithmetic, a word problem is read aloud for a child one at a time. For the first five items, pictures are presented to support solving the problem, and the rest of the problems are given only verbally. The child has 30 s to solve each problem and to give the answer verbally. The test will be stopped after three consecutive errors. One point was given for a correct answer and zero for an incorrect answer or if the time limit is exceeded.

Mathematics performance

To measure the learning of mathematics content the children are taught in the second grade, a curriculum-based mathematics performance test was developed (Mononen, 2019), as such test was not available in Norway at the time of the study. The test includes tasks, which reflect the expected competence aims in mathematics after Grade 2 in the National Curriculum (The Norwegian Directorate for Education and Training, 2013)¹, as well as tasks, which are often included in the mathematics textbooks and typically used in the second grade: Numbers (1–100; e.g. number sequences, numbers on the number line, addition and subtraction), Geometry (e.g. recognition of figures, symmetry), Measurement (e.g. length [cm, m], telling time, money) and Statistics (reading bar graphs), with a total of 75 items. One point is given for a correct answer and zero for an incorrect answer. Children proceeded from task to task with the guidance of a research assistant, who read the task instructions aloud for the children.

Procedure

When needed, the test instructions were translated first into English and then into Norwegian, and the item level questions were also back translated to ensure the correspondence and quality of the translations, either by the research team members fluent in both languages or using authorised translators. Children were tested as part of the larger data collection in the project. The first data collection in the first grade (t1) took place within two months, between March and the beginning of May 2019, and the second data collection (t2) seven months later in the second grade, between October and November. The schools participated in the data collection in the same order in spring and autumn, in order to keep the distance between the two measurement points as equal as possible for all the participants. At both time points, the children participated one half a day (3–4 h) session at the data collection site, during which they were tested individually (WISC-V Arithmetic) and in small-groups of 2–3 (mathematics performance test) or of 4–5 children (AEQ-ES, SYMP, Regnefaktaprøven) by trained research assistants studying (special) education. Small breaks and a lunch break were given between the assessment sessions. About 14% of the data (i.e. the data of three randomly chosen participants from each classroom for each test) were double coded. The correlations of sum scores between the coders ranged between r = .885–1.00, with coding errors connected to some children having few items in a test with non-matching scores. When needed, the original data (papers) were checked regarding the non-matching sum scores, and the final data matrices corrected accordingly.

Data analysis

Latent change score modelling (LCS) within the structural equation modelling (SEM) framework is a powerful and flexible technique to investigate, for example, how parallel developmental processes unfold over time (McArdle, 2009). Within this approach, observed measures are used to estimate latent factors that represent both latent states and latent changes. This is particularly suitable in the present context, as we are interested in looking at how MA, SNMP and arithmetic skills change across the school year, and how those changes are linked with each other. Different approaches have been introduced to examine interindividual differences in intraindividual change through latent change scores (McArdle & Hamagami, 2001; Steyer et al., 1997). Here we will follow a parametrisation where the latent difference variables are directly connected to observed indicators (Steyer et al., 2000).

The first step is to specify a latent state model describing latent states for each measurement occasion (see model A in Figure 1). This is practically equivalent to a longitudinal confirmatory factor model (Widaman et al., 2010). A prerequisite for a meaningful interpretation of latent scores is strong factorial invariance, as we need to ensure that the constructs at each measurement occasion are measured in the same metric and have the same origin of measurement (Vandenberg & Lance, 2000). Therefore, all models will be specified with time-invariant item intercepts and factor loadings. To take into account indicator-specific effects that potentially bias the estimates (i.e. when items correlate with themselves across the measurement points due to identical wording or other method effects), the models may be extended to either include residual correlations between identical items across the measurement occasions or to specify indicator-specific method factors (see Reuter et al., 2010). Here we will use the former approach and specify correlated errors across the measurement points.

Figure 1. An illustration of a latent state model (longitudinal confirmatory factor model) for construct X with three indicators and two measurement points (A), a latent change model for construct X (B), and a bivariate latent change model for constructs X and Y with a predictor and an outcome (C). Factor loadings (λ) and intercepts are set to be invariant within constructs and over time in all models. Dashed lines represent latent correlations. Correlated residuals between respective items across the measurement points omitted for the sake of clarity.

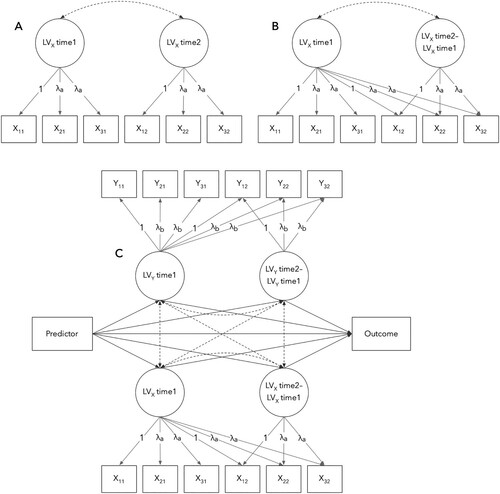
The next step is to extend the latent state model into a latent change model (see model B in Figure 1), for which additional loadings from the latent factor representing the latent state at t1 to the items measured at t2 are specified. By doing this, the latter latent factor now represents latent change scores between t2 and t1. Such a latent difference variable can now be treated like any other latent variable within the SEM, meaning that it can, for example, correlate with other latent variables or serve as a predictor or an outcome. This is illustrated in model C in Figure 1. In a bivariate latent change model, latent difference scores are estimated for two different constructs, thus allowing the examination of correlations between latent changes. Further, these changes can be predicted by additional variables or set to predict later outcomes.

In the present study, to address our research questions stepwise, we (1) estimated a multivariate latent state model on MA, SNMP and arithmetic skills with time-invariant item intercepts and factor loadings, (2) extended this to a multivariate latent change model, (3) added gender as a predictor on latent states and changes and (4) included math performance as an outcome to be predicted by the initial states and latent changes, while taking into account possible gender differences.

All analyses were conducted using the Mplus -modelling software version 8.5 (Muthén & Muthén, 2019), apart from descriptive and correlation analyses for each measure, which were done in IBM SPSS Statistics (version 27). In the analyses, MA items were treated as ordered categorical variables, due to which all models were estimated using a robust weighted least squares estimator (WLSMV) and the associated pairwise deletion approach to handling missing data (Asparouhov & Muthén, 2010). Following Finney and DiStefano (2013), we used the comparative fit index (CFI) in conjunction with root mean square error of approximation (RMSEA) to evaluate model fit along with the chi-square statistic.

Results

Descriptive statistics of each measure at t1 and t2 for all children and by gender, with reliability values, are presented in Table 1 and correlations between the variables in Table 2.

Table 2. Correlation matrix of variables at t1 and t2.

Measure	Time point	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.
1. SNMP-A	t1	–
2. SNMP-A	t2	0.59***	–
3. SNMP-B	t1	0.54***	0.41***	–
4. SNMP-B	t2	0.53***	0.57***	0.69***	–
5. Addition	t1	0.50***	0.45***	0.54***	0.47***	–
6. Addition	t2	0.53***	0.49***	0.54***	0.55***	0.72***	–
7. Subtraction	t1	0.49***	0.43***	0.49***	0.46***	0.79***	0.68***	–
8. Subtraction	t2	0.46***	0.40***	0.39***	0.49***	0.62***	0.73***	0.65***	–
9. Word problems	t1	0.41***	0.33***	0.31***	0.24***	0.51***	0.49***	0.51***	0.39***	–
10. Word problems	t2	0.39***	0.33***	0.34***	0.35***	0.55***	0.61***	0.52***	0.47***	0.52***	–
11. Maths scale	t2	0.48***	0.33***	0.35***	0.42***	0.55***	0.57***	0.57***	0.52***	0.41***	0.55***	–
12. Maths anxiety	t1	−0.18**	−0.09	−0.09	−0.06	−0.22***	−0.18**	−0.16**	−0.10	−0.24***	−0.25***	−0.25***	–
13. Maths anxiety	t2	−0.10	−0.05	−0.09	−0.03	−0.21**	−0.19**	−0.15*	−0.11	−0.24***	−0.30***	−0.24**	0.77***

Note: SNMP-A = symbolic numerical magnitude processing with 1-digit numbers, SNMP-B = symbolic numerical magnitude processing with 2-digit numbers, Addition = addition fluency, Subtraction = Subtraction fluency and Maths scale = curriculum-based mathematics performance.

***p < .001.

**p < .01.

*p < .05.

The multivariate latent state model with factor loadings for each construct and intercepts for respective items across the measurement points fixed equal fit the data adequately, χ²(247) = 410.41, p < .001; CFI = .92; RMSEA = .050 (CI90% = .041, .058), thus demonstrating sufficient measurement equivalence over time (see Table 3 for model estimates and latent correlations). Latent correlations across the measurement points, ranging from .62 for MA to .86 for arithmetic skills, showed considerable rank-order stability in all constructs. SNMP and arithmetic skills were strongly connected with each other at both measurement points (r = .78 at t1, and r = .75 at t2), and they also correlated negatively with MA. However, these associations were moderate at best, and appeared slightly stronger at t1. The correlation between SNMP and MA in the second grade (r = –.13) was no longer statistically significant. The latent means indicated some increase across the measurement points in both SNMP and arithmetic skills, but less so in MA.

Table 3. Descriptive statistics and latent correlations from the latent state model.

	M	SD	Latent correlations
			SNMP t1	Arithmetic skills t1	Math anxiety t1	SNMP t2	Arithmetic skills t2	Math anxiety t2
SNMP t1	17.11	9.10	1.00
Arithmetic skills t1	11.36	4.50	0.78**	1.00
Math anxiety t1	−1.52	0.74	−0.34**	−0.46**	1.00
SNMP t2	19.75	12.10	0.85**	0.65**	−0.19*	1.00
Arithmetic skills t2	14.00	6.48	0.78**	0.86**	−0.32**	0.75**	1.00
Maths anxiety t2	−1.60	0.80	−0.14	−0.28**	0.62**	−0.13	−0.34**	1.00

Note: t1 = First measurement occasion at Grade 1, t2 = Second measurement occasion at Grade 2, SNMP = symbolic numerical magnitude processing. Note, that the latent means for math anxiety are estimates based on categorical indicators.

*p < .05,

**p < .01.

The multivariate latent change model (with an identical model fit) verifies this observation showing significant overall latent change in SNMP (ΔM = 2.64, p < .001) and arithmetic skills (ΔM = 2.64, p < .001). Variances were also significant, pointing out to individual differences in those changes (Table 4). This was also the case for MA, despite the non-significant overall change in it. Latent correlations showed changes in SNMP and arithmetic skills to be positively associated with each other (r = .36, p = .010), meaning that improvement in SNMP was associated with improvement in arithmetic skills and negatively with MA (r = –.25, p = .093 for SNMP, and r = –.38, p = .009 for arithmetic skills). That is, improvement in SNMP, and particularly in arithmetic skills, was linked with the less steep increase or steeper decrease in MA. Moreover, the change in MA also correlated positively with the initial levels of SNMP (r = .22, p = .016) and arithmetic skills (r = .19, p = .054), indicating that higher SNMP and arithmetic skills at the first measurement point were somewhat connected with the steeper increase or less steep decrease in MA. Note, however, that the onset of change in MA was already lower among those higher in initial SNMP and arithmetic skills. Interestingly, also, initial SNMP was linked with change in arithmetic skills (r = .25, p = .018), suggesting that improvement in arithmetic skills was stronger when previous SNMP was higher.

Table 4. Descriptive statistics and latent correlations from the latent change model.

	M	SD	Latent correlations
			SNMP t1	Arithmetic skills t1	Math anxiety t1	SNMP t2	Arithmetic skills t2	Math anxiety t2
SNMP t1	17.11	9.10	1.00
Arithmetic skills t1	11.36	4.50	0.78**	1.00
Maths anxiety t1	−1.52	0.74	−0.34**	−0.46**	1.00
SNMP t2–t1	2.64*	3.38*	−0.04	−0.06	0.20	1.00
Arithmetic skills t2–t1	2.64*	1.68*	0.25*	0.05	0.13	0.36**	1.00
Maths anxiety t2–t1	−0.08	0.59*	0.22*	0.19*	−0.40**	−0.25	−0.38**	1.00

Note: t1 = First measurement occasion at Grade 1, t2 = Second measurement occasion at Grade 2, t2–t1 = Latent difference score from t1 to t2, SNMP = symbolic numerical magnitude processing.

*p < .05.

**p < .01.

Next, we included gender as a predictor to examine whether the levels and changes in each construct were similar for girls and boys. Again, the model fit was acceptable, χ²(265) = 447.13, p < .001; CFI = .92; RMSEA = .051 (CI90% = .043, .059), and the results showed no gender differences in the initial levels and changes of MA and arithmetic or the second grade mathematics performance. However, against our expectations, gender did have an effect on both the initial level of SNMP (β = .40, p = .006) and the change in it (β = .52, p = .018), thus suggesting boys to have slightly higher scores in initial SNMP and somewhat steeper increase in it over time.

Finally, we estimated a model with mathematics performance as an outcome, with adequate fit, χ²(283) = 474.30, p < .001; CFI = .92; RMSEA = .051 (CI90% = .043, .058). Mathematics performance was positively predicted by both the initial level of arithmetic skills (β = .64, p < .001) and the change in it (β = .29, p = .017), indicating that better mathematics performance at second grade was connected with both better initial arithmetic skills and improvement in it. Contrary to our assumptions, neither the levels of SNMP and MA in the first grade, nor the changes in them, predicted second grade mathematics performance. Main findings are shown in Table 5 and illustrated in Figure 2.

Figure 2. Summary of main results from the multivariate latent change model with gender as a predictor and math performance as an outcome. For clarity, only effects and correlations at p < .05 (solid lines) and p < .10 (dashed lines) are displayed (along with unstandardised factor loadings).

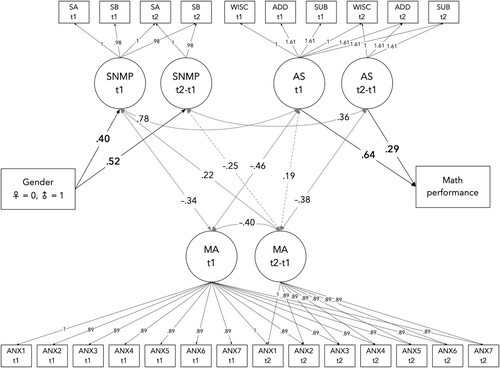
Table 5. Predictive effects from the bivariate latent change model with gender as predictor and maths performance as an outcome.

	SNMP t1			Arithmetic skills t1			Maths anxiety t1			SNMP t2–t1			Arithmetic skills t2–t1			Maths anxiety t2–t1			Maths performance t2
	β	z	p	β	z	p	β	z	p	β	z	p	β	z	p	β	z	p	β	z	p
Gender	.40	2.72	.007	.14	1.00	.318	−.14	–0.84	.402	.52	2.37	.018	−.18	–0.83	.405	.18	0.76	.448	−.05	−0.79	.434
SNMP t1																			−.03	−0.19	.848
Arithmetic skills t1																			.64	5.28	.000
Maths anxiety t1																			−.05	−0.68	.496
SNMP t2–t1																			.01	0.09	.928
Arithmetic skills t2–t1																			.29	2.39	.017
Maths anxiety t2–t1																			.04	0.44	.657

Note: t1 = First measurement occasion at Grade 1, t2 = Second measurement occasion at Grade 2, t2–t1 = Latent difference score from t1 to t2 and SNMP = symbolic numerical magnitude processing.

Discussion

Using latent change score modelling, this study investigated the levels of, changes in and mutual connections between MA, SNMP and arithmetic skills from first to second grade. The participating children had received formal mathematics instruction for just over half a year when their MA, SNMP and arithmetic skills were measured for the first time. The second measurement took place seven months later, in second grade. Thus, we had an unprecedented opportunity to investigate the emerging developmental relations between these three constructs, their relation to curriculum-based mathematics performance, and the role of gender in their development.

One encouraging finding in our study was that children reported rather little MA in the beginning of their schooling. Yet, our study gives further support for the concurrent negative relation between arithmetic skills and MA (H1.1) (Harari et al., 2013; Jameson, 2013; Kucian et al., 2018). Arithmetic skills were negatively, although only moderately, connected with MA at both grades. In line with previous studies, then, low arithmetic skills seem to be associated with MA already at the beginning of school (e.g. Harari et al., 2013; Sorvo et al., 2017). As there are rather significant individual differences in children’s developing arithmetic skills (see also Reeve et al., 2018), they become increasingly more aware of their own skills compared to the other children in their classroom. This, coupled with the emphasis on the importance of learning and performing basic arithmetic already in the early grades, may induce experiences of MA in children, especially if their basic skills are inferior. The negative association between MA and arithmetic found in our study might, then, reflect the increasing social comparison among children and the centrality of arithmetic in early instruction. However, our evidence on parallel changes do not permit inferences about the causal ordering of MA and arithmetic skills.

We also found a moderate negative relation between MA and SNMP in first grade in line with previous research (Gómez-Velázquez et al., 2015), and in support of our hypothesis (H1.2). However, this connection diminished to non-significant when children were in second grade. A possible explanation for this change could relate to the nature of the tasks and how they represent students’ exposure to similar tasks in school. The SYMP test requires an understanding of the meaning of 1- and 2-digit numbers, and quick, intuitive response by choosing the bigger one of the number pair, whereas the arithmetic test requires an active manipulation of numbers and providing an answer orally or in writing. As the children are already in their early years of schooling constantly exposed to number symbols and 1- and 2-digit numbers, following their mathematics curriculum (The Norwegian Directorate for Education and Training, 2013), the tasks in the SYMP test might have been more familiar to the children, and, also, less cognitively demanding than the tasks in the arithmetic test. Perhaps, then, the SYMP test did not provoke anxiety in children anymore in the same way as the more challenging arithmetic test. This concurs with the findings of Colomé (2019), who also found no relation between SNMP and MA in older students.

When looking at the concurrent relations between mathematical skills, we found children’s SNMP and arithmetic skills to be strongly linked with each other in both first and second grade (r = .78 vs. r = .75, respectively). These results are in line with our hypothesis (H1.3) and concur with prior findings (Schneider et al., 2017). Some theories suggest that the relation between SNMP and arithmetic may diminish over primary school years, as arithmetic becomes more complex and performing arithmetic tasks demand more use of ordinal than cardinal meaning of numbers (Lyon et al., 2014). Our findings, however, did not support this.

Latent correlations across the measurement points showed high (rank-order) stability for MA (r = .62), and even higher for arithmetic skills (r = .86) and SNMP (r = .85), thus confirming our hypothesis (H2.1) and agreeing with previous studies (Cargnelutti et al., 2017; Gunderson et al., 2018; Sorvo et al., 2019). Also, as expected, children’s SNMP and arithmetic skills improved from first to second grade (H2.2), while the average level of MA remained at the same low level (H2.3). Note, that as the average MA was already rather low in the first grade, following some previous findings (Szczygieł & Pieronkiewicz, 2021), a further decrease was quite implausible.

The culture of mathematics education in Norway may partly explain the low level of MA students experienced in the beginning of schooling. Mathematics instruction in the first and second grade emphasises playful numerical activities, use of technology (e.g. math learning games), and use of concrete manipulatives while working with abstract mathematical concepts. Children are not graded or assessed with any regular high-stake mathematics tests. Therefore, in the early grades, many children find maths learning at school enjoyable and interesting (Tuominen, Niemivirta, Korhonen, Tapola, & Mononen, 2021), as opposed to something to be anxious about.

Note, however, that the variance of the slope of MA was significant, thus indicating individual differences in the development, despite the non-significant overall change. This also applied to the changes in SNMP and arithmetic skills. Thus, the teachers should be aware that the children begin to follow different developmental paths already from early on and might therefore be in need of different types of targeted educational support.

When further looking at how changes in MA, SNMP and arithmetic skills were related to each other, we found children’s improvement in SNMP to be linked with improvement in arithmetic skills, as hypothesised (H3.1). The change in arithmetic skills was also associated with the change in MA, thus indicating the improvement in arithmetic to be linked with the less steep increase or steeper decrease in MA. However, since this connection was not found between the changes in MA and SNMP, our hypothesis (H3.2) was only partially supported. Note that these findings do not permit causal inferences, meaning that the detected developmental connections as such could be a result of reciprocal relations (Gunderson et al., 2018) or directional effects – that is, arithmetic skills influencing MA as per the deficit theory (Wang, 2020) or MA influencing arithmetic skills as per the debilitating anxiety model (Cargnelutti et al., 2017). However, to our knowledge, this is the first study to show arithmetic skills and MA to be developmentally linked in terms of correlated changes over time.

In sum, the role of SNMP in relation to MA diminished when children got older, while the negative association between arithmetic skills and MA was stronger both concurrently and over time. Yet, SNMP and arithmetic skills were also developmentally strongly related.

Gender differences were detected only in SNMP skills so that boys performed slightly better than girls in the first grade, and interestingly, also showed a somewhat steeper improvement over time. However, since no gender differences were found in arithmetic skills or in curriculum-based mathematics performance, concurring with previous research on early mathematical skills (Kersey et al., 2018), our hypothesis (H4) was partially supported. As to the level of MA, we found no gender differences, which is in line with the majority of previous research on young children (e.g. Ching, 2017; Hartwright et al., 2018; Wu et al., 2014), nor did we detect gender effects on the changes in MA. Given the assumption of gender stereotypes explaining gender differences in MA (Bieg et al., 2015; Steffens et al., 2010; Watt, 2004), this would suggest either that such stereotypes are not (yet) present in this particular context or that the children are not (yet) aware of those (McKown & Weinstein, 2003).

As the final goal in our study, we investigated whether the levels of and changes in MA, SNMP and arithmetic skills predict curriculum-based mathematics performance in the second grade. Our findings showed that mathematics performance was predicted only by both the initial level of and change in arithmetic skills, thus providing limited support for our hypotheses (H5.1; H5.2). Although we cannot entirely rule out a possible collinearity effect due to the high correlation between SNMP and arithmetic skills, thus possibly undermining the predictions of SNMP, it would seem that particularly higher arithmetic skills as well as more notable improvement in those skills contribute to more advantageous learning of curriculum-based mathematics (Jordan et al., 2003).

Limitations and future directions

This study is one of a few investigating young children’s MA and mathematics performance longitudinally, and, to our knowledge, one of the first to address developmental changes. The timeframe from the first to the second assessment time point was only seven months, although including a transition from first to second grade. To get an even better developmental view on the relations under investigation, a more comprehensive follow-up period would be needed in future studies. A longer time lag with additional measurement points would also permit more options to examine both developmental trajectories and directional relations between changes over time, thus providing a better insight into the mutual longitudinal connections between MA and mathematics performance, and the long-term consequences of such developmental dynamics (Aldrup et al., 2020). A longer follow-up might also reveal us, if and at what age the different dimensions of MA start to separate clearer from each other. In our study, based on factor analyses, the AEQ turned out to work best as a combined measure (Ma-Com), although it included statements directed to catch both dimensions of MA. Further, our study included only SNMP and arithmetic as measures of mathematical skills, although children’s mathematics performance was measured with tasks covering different curriculum-based mathematics topics. In future studies, it might be of interest to investigate how other domains of basic mathematical skills, such as counting skills (Maloney et al., 2011), known to be linked with mathematical learning difficulties, are developmentally connected with MA.

As the focus in most studies has been on numerical tasks (e.g. arithmetic), the inclusion of non-numerical tasks (e.g. geometry) might help to understand the characteristics of mathematics that are most likely to induce anxiety. Added value could also be gained by taking into account differences in trait anxiety and domain-general skills such as working memory, both known to be related to MA (e.g. Hembree, 1990; Passolunghi et al., 2016). Controlling for trait anxiety would help to remove the effect of general anxiety (Wu et al., 2012), while adding a measure of working memory might help to understand the possible mediating factors between MA and math performance (Justicia-Galiano et al., 2017).

Finally, the fact that our sample of children was somewhat selective due to the conditions of data collection must be taken into consideration. For practical reasons, the participating children came from schools close to our test site, and mainly from families of middle or higher educational level. For better generalisability of the findings, more representative samples would be essential.

Conclusions

Our longitudinal study provided new knowledge about the developmental relations between MA, SNMP and arithmetic skills during the first years of schooling. On average, children improved in their arithmetic and SNMP skills from first to second grade, whereas the level of experienced MA remained stable and rather low. Most interestingly, improvement in SNMP was linked with improvement in arithmetic skills, while the change in MA was more connected with change in arithmetic skills than with change in SNMP. The findings suggest that over time, MA may become more directly linked with arithmetic skills than with more intuitive numerical magnitude processing skills, and that difficulties in learning basic arithmetic may expose children to increases in mathematics-related negative emotions. Not only is this theoretically and empirically intriguing but also it has important practical implications. The teachers should be aware that despite the children are generally displaying little MA, significant individual differences exist in both these experiences and how they change over time, with some children experiencing MA already in early grades. This calls for a particular sensitivity to such experiences and constructive means to support children when a school subject becomes intimidating.

Acknowledgements

The authors thank all the participating children, their teachers and parents, as well as the research assistants involved in the data collection.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

The data are available upon request from the correspondent author.

Additional information

Funding

This work was supported by the Norwegian Research Council [grant number 283396] for the first author.

Notes

1 The Norwegian national curriculum in mathematics was revised in autumn 2020 after the data collection.

Appendix

Table A1. Overview of the studies (n = 27) of the relations between children’s (6–8 y.o.) mathematics anxiety and mathematics performance.

Author(s)	Design^a	Grade (age in years for the lowest grade)	N	Name of scale (dimensions of math anxiety)^b	Mathematical domain	Anxiety-performance relation	Gender differences
Cargnelutti et al. (2017)	L	2–3 (7.6)	198 (of which 80 in G3)	SEMA (MA-A)	Arithmetic (computations and word problems), Maths achievement test	Yes: in G3. Indirect effect of G2 mathematics anxiety on G3 performance	Not reported
Caviola et al. (2017)	C	3–5 (8.7)	1013	AMAS (MA-A)	Mathematics achievement test, Arithmetic (computations)	Yes: weak negative relation	The scale was reported to be invariant across gender, but no gender differences per se were investigated
Ching (2017)	L	2–3 (7.2)	264	Mathematics Anxiety Scale for Young Children (MA-Com)	Arithmetic (computations and word problems)	Yes: Mathematics anxiety G2 contributed on G3 performance, even after controlling for prior working memory, IQ, number skills and general and test anxiety; children with high working memory and MA showed poorer performance especially in more difficult tasks	No gender differences either in the level of anxiety or performance
Dowker et al. (2012)	C	3 and 5 (7.5)	89	MAQ (MA-C)	Arithmetic (computations)	No	No differences either in the level of anxiety or performance
Dowker et al. (2019)	C	1 (6.3 and 6.8)	116^c	MAQ (MA-C)	Arithmetic (computations)	No	Boys (English sample) showed more anxiety
Gunderson et al. (2018)	L	1 and 2^d (7.2, incl. both grades)	634	CMAQ-R (MA-A)	Applied word problems (arithmetic and measurement)	Yes: reciprocal relation	Girls reported more anxiety in the end of each grade; no gender differences in relation
Haase et al. (2012)	C	1–6 (7)	207^e	MAQ (MA-C)	Arithmetic (computations)	No	Not reported
Harari et al. (2013)	C	1 (6.8)	101	Mathematics Anxiety Scale for Young Children (MA-Com)	Arithmetics (computations), Counting, Maths concepts	Yes: Negative reactions and numerical confidence, but not worry, related to performance	No gender differences
Hartwright et al. (2017)	C	2–6 (7)	79	EAM (MA-Com)	Maths achievement test, Number line	Yes: negatively related to mathematics achievement, working memory mediated the relation	No gender differences in the level of mathematics anxiety
Jameson (2013)	C	1–5 (not reported)	438	CAMS (MA-Com)	Maths achievement test (inc. counting, arithmetic, word problems)	Yes: negative relation (r = −.19)	Not reported
Justicia-Galiano et al. (2017)	C	3 and 5 (8)	167	AMAS (MA-A)	Arithmetic (computations and word problems), Teacher-rated mathematics achievement	Yes: Working memory and self-concept mediated the relation	Not reported
Krinzinger et al. (2009)	L	1–3 (7.5)	149	MAQ (MA-C)	Arithmetic (computations)	No	Not reported
Kucian et al. (2018)	C	Grade not reported, age range 7–13 (8.6 incl. whole sample)	172^f	MAI (MA-Com)	Mathematics achievement test, Arithmetic (calculations), Number line	Yes: negative relation, those with developmental dyscalculia experienced higher level of mathematics anxiety	No gender differences in the level of anxiety or maths performance
Lauer et al. (2018)	C	1–5 (7)	394	CMAQ (MA-A)	Curriculum-based maths test (incl. arithmetic, measurement, geometry, and algebraic thinking)	Yes: even after controlling for verbal and spatial anxiety and reading ability; working memory did not moderate the relation, mathematics anxiety more pronounced with older children	Gender did not moderate the relation, however, girls reported experiencing more mathematics anxiety (d = 0.33)
Lu et al. (2019)	C	K (not reported)	355	YCMAX (MA-Com)	Applied problems (computations), Quantitative concepts (number patterns, symbols)	Yes	Not reported
Pantoja et al. (2020)	L	1–3 (not reported)	162	CMAQ-R (MA-A)	Number line estimation (0–100 and 0–1000), Applied word problems	Yes: 1st grade MA predicted later performance in applied problems up to 3rd grade, while controlled for number line estimation. MA was predicting number line performance depending on the number range and grade.	Not reported
Primi et al. (2020) Study 1	C	1–2 (6.6)	150	EES-AMAS (MA-A)	Arithmetic (computations)	Yes: negative relation (r = −.21)	No differences in the level of anxiety
Primi et al. (2020) Study 2	C	1–3^g (6.4 and 7.1)	223	EES-AMAS and CMAQ-R (MA-A)	Arithmetic (computations, word problems), Teacher-rated mathematics achievement	Yes: negative relations (for Italy; UK in brackets); EES-AMAS: r = −.38 (−.32) for Arithmetic and r = −.30 (−.34) for Teacher rated. CMAQ-R: r = −.39 (−.43) for Arithmetic and r = −.32 (−.29) for Teacher rated.	No differences in the level of anxiety or maths performance in either country
Ramirez et al. (2016)	C	1–2 (6.6)	256	CMAQ (MA-A)	Applied word problems (e.g., arithmetic and measurement), Maths problem solving strategies (addition)	Yes: negative relation (r = −.28), children with higher working memory and high mathematics anxiety show lower performance; use of advanced problem solving strategies partially mediates the relation between maths anxiety and performance in these children	Not reported
Ramirez et al. (2013)	C	1–2 (6.7)	154	CMAQ (MA-A)	Applied word problems (e.g., arithmetic and measurement)	Yes: but only for those having relatively high working memory	No differences in the level of anxiety
Sorvo et al. (2017)	C	2–5 (8.4)	1327	Researcher-developed scale (incl. two items from MAQ) (MA-Com)	Arithmetic (computations)	Yes: especially anxiety in math-related situations; decrease in anxiety across grades	No differences related to relation; Girls reported higher anxiety but only related to answering teacher’s questions in maths class
Sorvo et al. (2019)	L	2, 3, 4 and 5^d (8.4)	1321	Researcher-developed scale (incl. two items from MAQ) (MA-Com)	Arithmetic (computations)	Yes: performance predicted later anxiety about fear of failure, but neither anxiety dimensions predicted performance; the mean level of anxiety decreased in each grade	Not reported
Van Mier et al. (2019)	C	2 and 4 (8.1)	124	CMAQ-R (MA-A)	Arithmetic (computations)	Yes: but only on girls	Even though the overall levels of anxiety and performance were quite similar, higher levels of anxiety negatively predicted performance only on girls
Vukovic et al. (2013)	L	2–3 (7.8)	113	Mathematics Anxiety Scale for Young Children (MA-Com)	Arithmetic (computations), Mathematical applications (incl. word problems, algebra, and data analysis/probability), Geometry	Yes: higher level of anxiety in G2 predicted lower gains in performance (Maths applications), but only for those having higher working memory	Not reported
Wood et al. (2012)	C	1–3^h 1–6^i (7)	621^h,i	MAQ (MA-C)	Arithmetic (computations) and country specific maths achievement tests	No	Not reported
Wu et al. (2012)	C	2–3 (7.6)	162	SEMA (MA-A)	Maths achievement test (incl. numerical operations and maths reasoning/problem solving)	Yes: especially problem solving, even after controlling for trait anxiety and IQ	Not reported
Wu et al. (2014)	C	2–3 (8.3 incl. both grades)	366	SEMA (MA-A)	Maths achievement test (incl. numerical operations and maths reasoning/problem solving)	Yes: even after controlling for IQ; children with mathematical difficulties experienced more maths anxiety than typically achieving children	No gender differences

^a C = cross-sectional, L = longitudinal.

^b Maths anxiety dimension: cognitive (MA-C) = self-deprecatory thoughts and worries related to one’s mathematics performance; affective (MA-A) = feelings of tension, fear and physiological reactions, when one is faced with mathematical problem solving; MA-Com = measure including both dimensions – SEMA = Scale for Assessing Early Mathematics Anxiety (Wu et al., 2012) – AMAS = Abbreviated Maths Anxiety Scale (Hopko, Mahadevan, Bare, & Hunt, 2003) – Mathematics Anxiety Scale for Young Children (Harari et al., 2013) – MAQ = Mathematics Attitudes and Anxiety Questionnaire (Thomas & Dowker, 2000) – CMAQ-R = Child Maths Anxiety Questionnaire-Revised (Gunderson et al., 2018) – EAM = Mathematics Anxiety Scale [Escala de Ansiedade a Matemática] (Carmo, 2008) – CAMS = Children’s Anxiety in Maths Scale (Jameson, 2013) – MAI = Math-Anxiety-Interview (Kohn et al., 2013) – CMAQ = Child Maths Anxiety Questionnaire (Ramirez et al., 2013) – YCMAX = Young Children’s Maths Anxiety Scale (Lu et al., 2019) – EES-AMAS = Early Elementary School Abbreviated Maths Anxiety Scale (Primi et al., 2020; adapted version of AMAS by Hopko et al., 2003).

^c British n = 67, Chinese (Hong Kong) n = 49.

^d Each grade was followed up for one year.

^e Typically performing n = 171, low-performing in mathematics n = 36.

^f Developmental dyscalculia n = 76, typically performing n = 96.

^g Italian n = 102, British n = 121.

^h German n = 450.

ⁱ Brazilian n = 171.