Registration Probabilities and Pulse-Height Distributions of Coincidences in Optical Particle Counters

Abstract

In conventional optical particle counters chains of particles' coincidences may occur as a result of continuous view volume illumination and sampling. Because of these coincidences, probability of the presence of several particles in a view volume given by the well-known Poisson distribution cannot be interpreted as a coincidence registration probability. Particle registration probability distribution accounting for chain coincidences is calculated for optical counters with the first maximum of the counter pulse chosen for counting. Registration probability of the doublets is obtained numerically also for counters with the choice of the global maximum of the counter pulse for counting. Pulse-height probability density functions (pdf) are calculated for square, triangular, and Gaussian pulses. It is shown that pdfs of apparent multiplets are resolved in counters with rectangular response pulses and sufficiently high resolution. However, in counters with any nonrectangular response pulses the coincidences have overlapping pulse height distributions. It is shown that counters with the Gaussian pulses allow measuring 30% higher aerosol concentrations compared with the square pulse counters. Aerosol size distribution distortions invoked by coincidences are estimated.

A method of counter view volume determination using coincidences is suggested.

INTRODUCTION

Optical particle counters are widely used in science and practice for the determination of aerosol number concentration and size distribution. One of the principal errors of these counters is caused by particles' coincidences, which is the simultaneous presence of several particles in the counter's view volume. As a result, the measured aerosol number concentration may be lower than the true concentration. The size distribution as measured may apparently be shifted towards larger particles, because two or more particles in the view volume may be conceived as one larger particle. On the other hand, there may be coincidences of particles, which singly are too small to be registered (“subcountable” particles), that may increase the measured concentration of the countable particles. Presence of subcountable particles may significantly distort the measurement data. Whitby and Willeke (1979) discussed this error and pointed out that it may be diminished by reducing the view volume or by diluting the aerosol in the inlet to the counter. Below we consider only countable particles.

Probability of coincidences depends on average number of particles μ in the view volume. If an aerosol with the number concentration N_t is measured by a photoelectric counter having a view volume v, the average number of particles in the view volume will be (Whitby and Willeke 1979):

[1]

It is well known (Whitby and Willeke 1979) that probability P_k of occurrence of exactly k particles at the same time in the view volume (apparent k-multiplet) is given by the Poisson distribution:

[2]

If particle counting is conceived as a discrete process consisting of separate operations of filling, counting, and emptying the view volume, then the relationship in Equation (2) may be considered also as a probability R_k to register a k-multiplet (k≥ 1). In this case the formula in Equation (2) may be used to express the measured aerosol number concentration (or more exactly, its mean value) N_m (Whitby and Willeke 1979):

[3]

This is the product of the probability P_c =1−e ^−μ of occurrence of any number of particles within the view volume, interpreted as a probability of a count, and of the number of view volumes in the unit aerosol volume 1/v. Equation (3) implies that with increasing μ the measured concentration tends to 1/v. However, the experimental data indicate that the number of counts diminishes at high counter loading (Pisani and Thomson 1971). This contradiction arises because measurements by the conventional counters with continuous sampling and continuous view volume illumination cannot be treated as a process consisting of aforementioned discrete operations. ¹ Presence of particles in the counter's view volume does not necessarily involve their registration. A particle can enter a view volume when it is still occupied by one or more particles. Thus particle occurring within the view volume can be coupled to previous particles and thus only extend already existing pulse width. Pisani and Thomson (1971) pointed out that probability of a count is not P_c but e ^−μ, which is the probability that a particle enters the empty view volume (formula in Equation (2), k=0). It means that the mean value of measured concentration is related to the true aerosol concentration by (Pisani and Thomson 1971):

[4]

One can obtain, using (Equations (1)) and (4), that

[5]

(Equations (3)) and ((5)) are compared in Figure 1 (curves a and b, accordingly). The formula in Equation (5) shows that the measured concentration reaches a maximum at μ=1 and then decreases for the increasing μ (Figure 1, curve b). It means (cf. Equation (1)) that aerosol concentration N_t is a double-valued function of measured quantity N_m . Thus, for aerosol concentration determination an additional information is required, besides the count rate. In particular, a low pulse count rate recorded by the particle counter does not indicate low aerosol concentration (μ≪1) because it may occur also at high concentrations (μ > 1) (Figure 1, curve b). Dead time of counting, accumulated during measurements registered with help of a high-speed clock (TSI Inc. 1994), allows distinguishing between these two cases.

FIG. 1 Measured concentration dependency on loading: a—in accordance with Equation (3); b—in accordance with Pisani and Thomson's Equation (5).

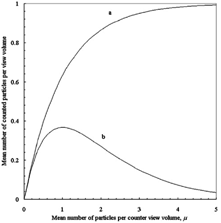
Particle counters are normally used for measurement of relatively low number concentrations when coincidence errors do not exceed 5% (μ<0.05, cf. Equation (4)). However, the intervals separating the response pulses may be statistically analyzed to expand the counters' measurement range (Julanov et al. 1984).

Equations (4) and ((5)) hold if the counting voltage threshold is zero, or, alternatively if a photodetector's pulse immediately achieves its maximum (square pulses). In the last case the duration τ of particle motion within the view volume (τ=v/Q, where Q is the aerosol flow rate) coincides with the time τ _T during which the counter is disabled by a single particle. Generally, constants τ and τ _T may differ markedly (see below). For the TSI CPC counter τ∼5 μs and τ _T ∼4 μs (TSI Inc. 1994). Thus, the condition of 5% coincidence error for the CPC counter is

Other time constants characterizing the process of particle counting are the photodetector's response time and the stretching time τ _s . The response time of modern photodetectors is several orders of magnitude less than τ (Vendier et al. 1996) and may be neglected. Time τ _s characterizes pulse stretching when it is used to read the signal amplitude (Whitby and Willeke 1979). Probability P_s that the stretching device is ready to work is (Whitby and Willeke 1979):

Thus, if pulse stretching technique is used, all the counting probabilities must be multiplied by the above quantity.

As was mentioned before, the Poisson distribution in Equation (2) (as well as Equation (4) of Pisani and Thomson 1971) does not allow us to determine the registration probabilities of k-multiplets. The goal of this article is to derive the distribution of these probabilities for different k≥1. Additionally, we analyze the pulse-height probability distributions of the particle coincidences. The data obtained is used to propose a method of the counter view volume determination using coincidences.

REGISTRATION PROBABILITIES OF k-MULTIPLETS

It was already indicated that presence of a k-multiplet in the counter view volume does not involve necessarily its registration because of possible coupling with previous particles. Coupling with the following particles also may preclude k-multiplet registration. Probability of such chain coincidences evidently increases with increasing particle concentration. Long chains of such events may occur, significantly increasing the counter pulse width. At sufficiently high concentrations the pulse width extends indefinitely, thus paralyzing the counter (TSI Inc. 1994). This phenomenon is well known in nuclear radiation detection (dead-time correction; see Price 1958).

Consider the registration probabilities of single particles and apparent multiplets accounting for the chain coincidences. As the movement of particles into and through the view volume is essentially a stochastic process, particles enter the view volume at the time moments that are randomly distributed along the time axis. This time moment distribution depicts a queue of particles to be counted. It follows from the queuing theory (Feller 1968) that time intervals between particles are exponentially distributed:

[6]

In the above P(t) is the probability that the time interval between arrivals of two successive particles is greater than t and λ is the average number of arrivals per time unit. The formula in Equation (6) follows from the Poisson distribution in Equation (2) (Feller 1968). In passing we mention that in contrast with Equation (6) Julanov et al. (1984) assumed a uniform distribution of the particles' arriving times, implying similar distribution of the interparticle time intervals. Probability that the time interval between arrivals of two successive particles is less than t will be:

[7]

Probability density of the distribution in Equation (7) is

[8]

Following Princen and Kwolek (1965) assume that two consecutive particles are registered separately if the time interval t between their entrances is greater than τ, i.e., we suppose that the time τ _T during which the counter is disabled is equal to the time of single particle presence in the view volume. Otherwise μ, appearing in all the following equations, must be multiplied approximately by τ _T /τ (see below). A particle may be registered as a single one if and only if its preceding and following interparticle time intervals are greater than τ. It means that the registration probability R ₁ of a single particle, in view of statistical independence of the interparticle time intervals, is (cf. Equation (6))

[9]

since λ=μ/τ. Unlike probability P ₁ of one particle occurrence in the view volume, given by Equation (2) for k=1, the probability to register a single particle monotonically decreases with μ.

The case of doublets is more complicated because they may be separate and chained. Two successive particles form a separate doublet, if the time interval t between them is less than τ and the preceding and the following interparticle time intervals are larger than τ. Probability C _2s of such an event is (cf. Equation (7)):

Three consecutive particles form a chain doublet if (1) the time intervals, t ₁ and t ₂, between them are less than τ (chain of two doublets); (2) the sum of these intervals is larger than τ (to exclude triplet); and (3) the preceding and the following time intervals are larger than τ. During the time t ₁+t ₂ the counter's view volume will be continuously occupied by one or more particles and the photodetector's pulse may achieve some maximum, then decrease being still higher than a threshold and increase again. It is known (Whitby and Willeke 1979) that in many designs, when the counter photodetector's signal reaches its maximum, a pulse shaper begins to work and a multichannel analyzer reads the signal amplitude. Therefore, we will assume here that the first peak of the photodetector signal is to be chosen for counting. The case of a counter with the choice of the global maximum for counting (Kudryavtsev et al. 1997) will be shortly considered later. Probability C _2c of a chain doublet is given by the double integration (cf. Equation (8)):

[10]

accounting for the inequalities t ₁<τ, t ₂<τ, and t ₁+t ₂ > τ.

A chain doublet may be followed by a string of i particles wherein each interparticle time interval is less than τ. There may also be particles in such a chain that form a k-multiplet with the k > 2, generating a maximum higher than that of the chain doublet. It does not affect counting because it is not the first maximum. Using the formula in Equation (6), one can obtain that probability C_i of such a chain is

Thus, the overall probability R ₂ to register a doublet is

[11]

provided that the number of sampled particles N≫1.

Three successive particles form a separate triplet if the time interval t ₁+t ₂ is less than τ and both preceding and following interparticle time intervals are greater than τ. Probability C _3s of such an event is

Suppose that three consecutive particles are followed by a forth particle separated from the third one by a time interval t ₃. These four particles form a chain triplet if t ₁ + t ₂ < τ, t ₃ < τ but t ₁ + t ₂ + t ₃ > τ (to exclude quadruplet). Probability C _3c of the chain triplet, with preceding and following time intervals being larger than τ, will be (cf. formula in Equation (10))

Calculating the innermost integral one obtains

Thus, probability R ₃ to register a triplet will be (cf. formula in Equation (11))

Similarly, probability R_k to register a k-multiplet will be:

[12]

Thus, we obtained the registration probability distribution for the apparent k-multiplets. It is analogous to the Poisson distribution in Equation (2) but accounts for the chain coincidences. Summing up the registration probabilities given by Equation (12) over all k(1⩽k<∞) gives the probability of any count that is equal to e ^−μ in accordance with Pisani and Thomson (1971).

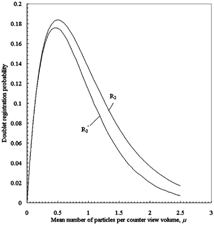
Consider shortly a particle counter in which the global maximum of the photodetector's signal is chosen for counting. This case is more complicated. We consider only single monodisperse particles and doublets. Probabilities to register a single particle and a separate doublet will be the same as above. However, calculating the registration probability of a chain doublet, one must take into account that a chain cannot include k-multiplets with k > 2. (Strictly speaking, a pulse height of multiplet with k > 2 may be less than that induced by a doublet. However, this possibility may be ignored for counters with square pulses and sufficiently high resolution (see below).) Consider, for example, a chain including 5 particles with each of the interparticle time intervals t ₀, t ₁, t ₂ and t ₃ being less than τ. One should impose t ₀+t ₁ > τ, t ₁+t ₂ > τ, and t ₂+t ₃ > τ to exclude occurrence of the k-multiplets with k > 2. Probability C′_2,5 of such a chain will be (cf. formula in Equation (10))

The overall probability R′₂ to register a doublet will be

We calculated this value for m up to 10 for the different μ, using Mathematica software package. It may be shown that the truncation error is an increasing function of μ, not exceeding 5% for μ=1.5. The calculated data are given in Figure 2 (curve b), showing also curve a obtained from the formula in Equation (11). Probability R ₂ is always greater than R′₂ because the former spreads over wider set of events.

FIG. 2 Doublet registration probability for two types of particle counters: R ₂—for counter with the choice of the first maximum of a photodetector's signal for counting (Equation (11)); R′₂—for counter with the choice of the global maximum of a photodetector's signal for counting (numerical calculation).

In the next section we calculate the pulse-height probability distributions of signals resulting from particle coincidences.

PULSE-HEIGHT PROBABILITY DISTRIBUTIONS OF COINCIDENCES

Calculation of pulse-height distributions of particle coincidences is based on the fact that intensity of light scattered by two or more particles in a counter view volume is the sum of the light intensities scattered by separate particles. However, it does not mean that the amplitude of the resulting signal would necessarily be the sum of the component amplitudes. The resulting amplitude depends on the shape of the component pulses and the interparticle time interval. We consider here square, triangular, and Gaussian single-particle pulses. The resulting signals, calculated below, allow drawing conclusions about several features of pulse-height distributions for other shapes of single particle pulses.

Square Pulses

Suppose that a single particle pulse has a square shape. Such is likely to occur when the signal shape is influenced mostly by the light intensity distribution in the view volume (Gebhart 1993) and this distribution is uniform, as may be expected for aerosol spectrometers (Knollenberg and Veal 1992). Julanov et al. (1984) also use the square pulse model. Of course, nonuniformities of photodetector, amplifier, etc. and optoelectronic noises may distort the signal shape and, besides, invoke some pulse-height distribution for identical particles (counter instrumental function f _in). We assume here that such a distortion is small, but take into account the influence of the instrumental function. This approach simplifies analysis of the pulse-height distributions of coincidences, because only in the case of the square pulses a k-multiplet signal amplitude would be exactly the sum of the component amplitudes independently of interparticle time intervals. In particular, the square pulse model allows straightforward analysis of the influence of the counter resolution on the pulse-height distributions of coincidences. Size resolution or resolving power of a counter is its capability to distinguish two monodisperse aerosols of different particle sizes (Gebhart 1993). Generally this capability depends not only on the inherent counter properties (width and profile of its instrumental function), but also on the data processing technique, the fineness of the counter calibration and the experimental errors. It is difficult to define a general unambiguous resolution criterion (Jones et al. 1995). To be specific we characterize the counter resolution by a relative standard deviation of its instrumental function, although the reciprocal quantity is also adopted (Price 1958).

In the square pulse model a k-multiplet pulse height is the sum of random component pulse heights and the pulse-height probability density function (pdf) of such a sum may be found as a convolution integral (Freund 1972). In case of two particle coincidences the pdf of apparent doublets is

[13]

where f _in(x) is the pulse-height distribution of particles of size x, u is the photodetector voltage and u_m is the maximum voltage invoked by single particles. Since the resulting pulse height is independent of the primary pulses separation, the above equation does not account for the relationship in Equation (8).

However, the counter instrumental function f _in may be quite close to the normal distribution (Whitby and Willeke 1979). In this case the multiplet probabilities will also be approximately normally distributed with the mean value and the variance equal to the corresponding sums of the means and the variances of primary singlet pdfs (Freund 1972). Besides, we have to account for the registration probabilities of the multiplets (Equation (12)). Consider, for example, pulse-height distributions of counters with resolutions 10% and 20%. Assume that the mean value of normal distribution of singlets is 100 mV. Then its standard deviation (SD) will be 10 and 20 mV, accordingly. Apparent doublets will have normal pdfs with the mean value 200 mV and SDs 10 √2 and 20 √2 mV, accordingly. Suppose that instead of apparent doublets we have singlets with the same light scattering equivalent size. Then the mean value of their normal pdf will be also 200 mV, but their SD will be 20 and 40 mV, accordingly. Thus, the apparent doublets (and generally any apparent multiplets) have a narrower pdf.

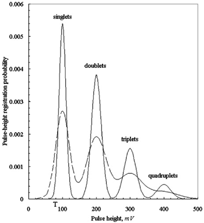
Pdf of the triplets, quadruplets etc. may be determined similarly. For the mean number of particles in a view volume μ=1, i.e., for quite pronounced coincidence effect, one can receive the resulting pdfs depicted in Figure 3 for counters with resolutions of 10% and 20%. One can see in Figure 3 that the multiplets' peaks are separated for counters with resolutions better than ∼10%, which is comparable to resolution of modern optical counters (Whitby and Willeke 1979; Hering and McMurry 1991).

FIG. 3 Pulse-height probability density functions for counter with square response pulses; mean number of particles in the view volume μ=1; bold line—counter resolution 10%; dotted line—counter resolution 20%.

Triangular Pulses

Many counters do not have uniform view volume illumination. Such counters cannot generate square response pulses. In particular, TSI CPC counter (TSI Inc. 1994) has a pulse of the form given in Figure 4a. Although this instrument measures only aerosol number concentration, its optical system design is similar to that of other optical counters (TSI Inc. 1994), which may have analogous response pulses.

FIG. 4 Isosceles triangular pulse approximation: (a) CPC counter photodetector pulse, (b) superposition of two isosceles triangular pulses for z < τ/2, (c) superposition of two isosceles triangular pulses for z > τ/2 (see the text).

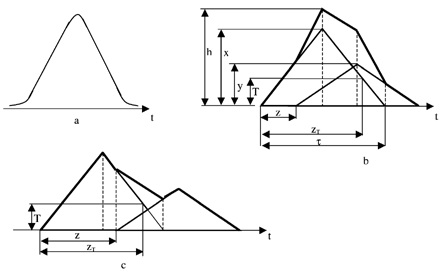
We assume that the first maximum of the photodetector signal is used for counting and find the pdf of apparent doublets F(h), where h is the height of the first maximum of the signal caused by a doublet. The pulse, given in Figure 4a is approximated by an isosceles triangle. Two pulses overlapped are shown in Figures 4b and c. The pulses have width τ at the base; the right pulse (of the particle that enters the view volume later) is shifted by z time units. Figures 4b (z<τ/2) and c (z > τ/2) show two kinds of possible resulting pulses. Therefore, we consider below two cases, accordingly: (1) τ2 > z > 0 and (2) z_T > z > τ/2. They both contribute to the pdf of apparent doublets F(h). However, as shown below, their contributions are essentially different. There is also an additional case, (3) τ > z > z_T , not contributing to F(h); here z_T is the time-shift corresponding to the counting threshold T (see Figure 4).

Consider case (1) τ/2 > z > 0 (Figure 4b). Let the left and the right pulses have heights x and y, respectively. One can see that situations x > y and x<y are symmetrical. Therefore, it is sufficient to find pdf for x > y and double it. The height h of the resulting pulse is:

[14]

Thus, both pulses influence the height of the resulting pulse. However, the heights of the component pulses are added only if z=0, i.e., in the case (having zero probability) where the particles enter the view volume simultaneously. More exactly, the probability of such an event is negligible for particles much smaller than the view volume. Inequalities ∞ > x > y > 0, 0<z<τ/2, and Equation (14) together yield the following upper boundary for y:

where h must exceed the threshold t. Assume, as in case of the square pulses, that the counter instrumental function in Equation (13) is a normal distribution. Accounting for Equations (8) and (13), one can obtain the following relationship for one part F ₁ of the doublets' pdf:

[15]

where G is the Gaussian function.

Consider the case (2) z_T > z > τ/2 (Figure 4c), giving additional constituent F ₂(h) of the doublet pdf. In this situation the second particle's pulse does not exert any influence on the first maximum of the resulting pulse that is equal to the height of the leading particle's pulse, i.e., h=x > T. There may be events when the second pulse gives rise to a separate count. It happens when the resulting pulse first drops below the threshold t and then exceeds it (cf. Figure 4c). One can see that it happens when a trail pulse has a height y satisfying the conditions T<y<τT/(τ−z)/2. Such coincidences do not cause count loss, albeit the number of these events is small in case of counters with sufficiently high resolution. We do not include them into the doublets'pdf. A relationship for F ₂ may be found as above, using Equation (8):

[16]

where z_T =τ−τT/(2x) and y _min=τT/2/(τ−z). Equation (16) gives for F ₂(h) a normal distribution multiplied by a constant, if T=0.

The mean value of z_T is τ _T —mean time during which the counter is disabled for a single particle. Thus, for counters with sufficiently high resolution,

[17]

In case (3) τ > z > z_T , when the interparticle time interval z exceeds z_T , all of the trail particles are registered separately. Such instances are also excluded from the doublet pdf. Thus, with knowledge of the doublet registration probability (Equation (11)) we can calculate the doublet pulse-height pdf F(h):

Integration of F(h) over all h for T=0 gives the following normalizing constant N_n :

[18]

to be used below.

The integrals in Equations (15) and (16) were calculated numerically. The results of the calculations for counters with resolutions 5–30% for μ=1 and μ=3 are given in Figures 5 and 6 for the mean value of the singlet pdf of 100 mV. It was assumed also that the threshold voltage is close to zero.

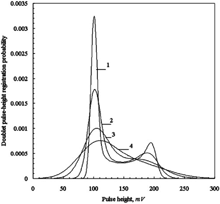
FIG. 5 Doublet pulse-height probability density functions of counter with isosceles triangular pulses; mean number of particles in the view volume μ=1: 1—counter resolution 5%, 2—counter resolution 10%, 3—counter resolution 20%, 4—counter resolution 30%.

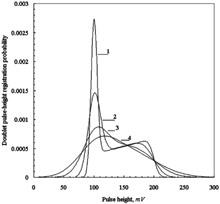
FIG. 6 Doublet pulse-height probability density functions of counter with isosceles triangular pulses; mean number of particles in the view volume μ=3: 1—counter resolution 5%, 2—counter resolution 10%, 3—counter resolution 20%, 4—counter resolution 30%.

As one can see from Figure 5 and Figure 6, the doublet pdf may have a bimodal structure. The left mode of the probability distribution falls approximately within the limits of the singlet pdf. For high counter resolutions it is invoked mostly by the pulses considered in case (2) when z_T > z > τ/2. The right mode of the doublet pdf is invoked mainly by the pulses considered in the case (1) when τ/2 > z > 0. A fraction of this mode increases with increasing μ. The bimodal structure of the doublet pdf is well defined for the resolutions better than about 20%.

The bimodal shape of the doublet pdf points out that generally the pdf of k-multiplets for any k may have up to k modes with the most left mode falling approximately within the limits of the singlet pdf. Indeed, similarly to the doublets for any k-multiplets we have to deal with the same two intervals for z: (1) τ/2 > z > 0 and (2) z_T > z > τ/2. Events, when only one pulse begins within the interval (1) and other pulses within the interval (2), give rise to the formation of the pdf left mode similar to the singlet pdf, although fraction of this mode diminishes with increasing μ. Events, when two pulses begin within the interval (1) and other pulses within the interval (2), give rise to the formation of the pdf second mode similar to the doublet pdf right mode and so on. Thus, k-multiplet pdfs are overlapping for any k.

Gaussian Pulses

Most typical for the optical particle counters is probably a bell (quasi-Gaussian) shape of the photodetector signal (Gebhart 1993). However, overlapping of Gaussian pulses is a more complicated problem than considered in the previous section. There is no simple relationship, like in Equation (14), between the height of the resulting pulse and the heights of the primary pulses. Thus, numerical calculations were attempted from the very beginning.

The primary pulse was approximated by the Gaussian function with a standard deviation σ in the interval from −3σ to 3σ, i.e., τ=6σ, and overlapping of two such pulses was analyzed. For Gaussian pulses the following relationship for time, during which a counter is disabled for a single particle, may be received:

[19]

giving slightly different values compared with Equation (17).

It was assumed as before that the heights of pulses are normally distributed with the mean value 100 mV and the relative standard deviations ranging between 5% and 30%.

We have to determine only the height of the first maximum of a resulting pulse rather than its location. For known corresponding heights x and y of the first and the second pulses and the time shift z between them the required height may be easily found numerically. Preliminarily we divide the voltage axis into a sufficient number of channels (1 mV channel width provides sufficient calculation accuracy) and can determine a channel wherein the calculated height falls. Further, we calculate the probability P_h of the calculated height h as a product of probabilities of x, y, and z (cf. Equation (8)):

which is added to the mentioned channel. Determining the heights of the first maximum for any possible x, y, and z, we accumulate these probabilities over all channels and receive as a result the required probability distribution.

The above-described procedure was successfully tested and verified against the square and triangular pulse models. The accuracy of calculations was checked using the constant in Equation (18). Deviation from this constant never exceeded 1%.

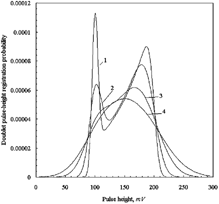
The results of calculations for μ=0.05 and μ=1 are given in Figures 7 and 8. In order to estimate a nonrectangular pulse shape influence we may compare data of Figures 5 and 8 obtained for the triangular and Gaussian pulses for the same μ=1. Both distribution families have well-defined bimodal structures and locations of modes are close for high counter resolutions. Shapes of the left peaks are almost identical because for the high counter resolutions they are invoked mainly by the single particles. Bimodal structure of distributions becomes unresolved for degrading resolutions. Influence of the pulse shape is pronounced for the right peaks whose forms differ markedly.

FIG. 7 Doublet pulse-height probability density functions of counter with Gaussian pulses; mean number of particles in the view volume μ=0.05: 1—counter resolution 5%, 2—counter resolution 10%, 3—counter resolution 20%, 4—counter resolution 30%.

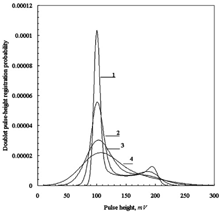
FIG. 8 Doublet pulse-height probability density functions of counter with Gaussian pulses; mean number of particles in the view volume μ=1: 1—counter resolution 5%, 2—counter resolution 10%, 3—counter resolution 20%, 4—counter resolution 30%.

Probability density functions, given in Figures 3 and 5–8, were received for zero counting thresholds. The threshold's influence depends on its value and the shape of the counter response pulses. In case of square pulses this influence is trivial: pulses with heights below the threshold are discriminated and all the corresponding probabilities must be zero. However the decline of counting efficiency is negligible for counters with sufficiently high resolution (Figure 3). For nonrectangular pulses the counting threshold may influence the pdfs shape (cf. Equation (16)). In order to estimate this effect we calculated the doublet pdfs of the considered above triangular pulses for T=50 mV. The results obtained showed that this effect is small.

Overlapping of the k-multiplet pulse-height distributions found for triangular and Gaussian pulses takes place for pulses of any shape except square pulses. Indeed, with any nonrectangular pulse shape there exists an interval of the time separations of pulses that the trail pulses does not influence the first maximum of the resulting pulse. It means that the pdf of any k-multiplet has a peak invoked by the single particle pulses leading to the overlapping of k-multiplet pdfs, albeit a fraction of this peak diminishes with increasing μ. Thus, separability of the multiplet pulse-height distributions is a unique feature of the square pulses. On the other hand, the count loss invoked by coincidences is the largest for the square pulses, because in this case the counter is disabled during all time τ that a particle stays in the counter view volume. Nonrectangular pulses are more advantageous in this respect. If we assume that the threshold equals to the half of the mean pulse height, then Equation (16) gives for the Gaussian pulses: τ _T =0.7 τ. Thus, 30% higher aerosol concentrations may be measured under the same count loss. Due to coincidences the total particles' count will be diminished by factor 1–0.7 μ (cf. Equation (4)) for small μ.

For small μ total count is caused mostly by the singlets and doublets (cf. Equations (4), (9), and (11)). Therefore, it is sufficient to consider the doublet pulse-height distribution (Figure 7) for estimation of measured aerosol size spectrum distortions invoked by coincidences. Calculations show that for high resolutions the left mode contains a larger portion of this distribution, i.e., about 0.4 μ (cf. Equation (11)). Thus, accounting for Equation (9) concentration of particles with the pulse height 100 mV will be diminished by the factor about 1−μ. At the same time it will be increased by the factor of about 0.3 μ as a result of coincidences of particles with pulse heights exceeding 50 mV. This mixing of different particle concentrations leads to an increasing homogeneity of the measured aerosol size distribution.

DETERMINATION OF THE COUNTER VIEW VOLUME

View volume is one of the main parameters of the particle optical counters. It is a volume in which aerosol particles may be observed by the counter photodetector. The view volume may depend on the particle size (Nikiforova 1979; Gebhart 1993), although in some studies such a dependency was not detected (Baumgardner et al. 1992).

Knollenberg (1979) described optical methods of the view volume determination with uncertainty of about 20% (Baumgardner et al. 1992). Bader et al. (1972) suggested the dilution method requiring a highly stabilized aerosol concentration. The view volume may be determined also by fitting the experimental dependency of the indicated aerosol number concentration versus its true concentration (Pisani and Thomson 1971). This implies that the true aerosol concentration must be known. The view volume may also be estimated if a width τ of the counter pulses is known, since τ=ν/Q.

Here we suggest method of the view volume determination based on analysis of the monodisperse aerosol pulse-height distribution distortions caused by the particle coincidences. This method allows increasing accuracy of the view volume determination and does not utilize data about the true aerosol concentration.

Consider the counters with square pulses in which coincidences invoke the pulse-height distributions with the resolved peaks of the apparent multiplets (Figure 3). It allows deriving equations for the view volume determination. Denote, in the example of Figure 3, the number of pulses with heights greater than 50 mV as n ₁ and the number of pulses with heights greater than 150 mV as n ₂. If n ₁ and n ₂ are known, then (cf. Equations (1), ((4)), and ((9))

Error analysis shows that the best conditions for the view volume determination will be achieved when μ≅1. In this case N_m reaches its maximum value (Figure 1). The derivative of the function (n ₁−n ₂)/n ₁ Log(n ₁/(n ₁−n ₂)) is close to zero and an uncertainty of v will come only from the error of a total count. This last may be easily made less than 20%.

Equation (20) holds provided that the counting efficiency of particles occurring in the view volume is close to 100%. Suppose however, that the counter's threshold is located at some t in the limits of the peak of singlets, i.e., 150 mV > t > 50 mV (Figure 3). In this case the doublets' peak may be used for the view volume determination. Let us suppose that in example of Figure 3 the numbers of pulses with heights greater than 150 and 250 mV are determined, n ₂ and n ₃, accordingly. Then one can obtain, using Equations (4), ((9)), and ((12)), that

This equation allows determination of μ. Since n ₁−n ₂=N_te ^−2μ (cf. the formula in Equation (9)), one can obtain, using Equation (4), that

Then one can find the particle concentration N_t and the view volume v, using Equation (1):

The best conditions for the view volume determination in this case will be achieved when μ≅1.5, because n ₂ has maximum value and the derivative of function μ(e ^−μ−e ^−2μ) is close to zero for μ≅1.5.

The view volume dependence on the particle size is linked with its illumination nonuniformity. In this case the counter response pulses cannot have a rectangular shape. Thus, contributions of the apparent multiplets into the counter pulse-height distribution will not be separable (Figures 5–8). In this case, in order to determine the counter's view volume, the inverse problem of restoration of the apparent aerosol size distribution may be considered. It is an example of the inverse problem, wherein it is known a priori that “aerosol” consists of singlets and apparent multiplets. Methods of solution of the inverse problem are suggested elsewhere (Lekhtmakher and Shapiro 1993). Using monodisperse aerosols with different sizes for the view volume determination one can investigate this volume dependence on the size of aerosol particles.

CONCLUSIONS

Poisson distribution of the probability of occurrence of k particles simultaneously in the counter's view volume cannot be considered as the probability to register the coincidences, because this distribution does not account for the chains of coincidences.

Probability to register an apparent k-multiplet depends on the design of a particle counter. This probability is shown to be μ ^k−1 e ^−2μ/(k−1)! (μ, mean number of particles per view volume) for the counters with choice of the first peak of a photodetector's signal for counting.

Pulse-height distributions of coincidences are resolved in counters with rectangular particle pulses and sufficiently high resolution.

Apparent k-multiplet's pdfs for counters with triangular and Gaussian pulses may have up to k modes with the left mode falling within the limits of the singlet pdf.

Analogously any apparent k-multiplet's pdf for any nonrectangular counter response pulses have a mode falling within the limits of the singlet pdf, albeit a fraction of this mode diminishes with increasing μ. Thus, coincidences in counters with nonrectangular pulses have overlapping pulse-height distributions.

Counters with the Gaussian pulses allow measuring the 30% higher aerosol concentrations comparing with the square pulse counters with the same coincidence error.

Coincidences of particles may be used for the determination of view volume of the particle counters.

Notes

¹However, such an approach turns out to be valid for counters operating in a pulsed mode (Zhulanov et al. 1985).