Energy-Balanced Oscillatory Model for Description of Particles Deposition and Re-Entrainment on Fiber Collector

Abstract

The pattern of filling of the internal space in fibrous filters strongly influences the behavior of the filter at the stage of nonsteady-state deep bed filtration. The model of single-fiber loading with deposited particles, including the resuspension effect, is presented. Structures of deposited charged particles from the range of diameters 0.01–10 μm deposited on the electret fiber of diameter 30 μm were calculated. Results of calculations indicate that the distribution of deposits around the fiber depend on particle size. Fractal dimension and local porosity of deposits depend on the predominant mechanism of deposition. The incorporation of the resuspension effect into the deposition models shows significant differences of the geometry of dendrites in comparison with the case of model in which resuspension was neglected.

INTRODUCTION

The rational design of filtration process should be based on reliable predictions of the dependence on the effluent concentration and on the pressure drop variations with time for a given set of the operating conditions, i.e., particle concentration and size, filter packing density, size of filter element, gas velocity, etc. The pattern of filling of the internal space with the porous structure of fibrous filters strongly influences the behavior of the filter at the stage of nonsteady-state filtration. The initial deposition of particles on the clean collector (nucleation) and dendrite deposition in the next step of the process determine the properties of filters.

The knowledge of a dynamics of dendrite growth can provide important information about the structure of clustering particles collected on a single fiber of the filter. It is especially important for filtration of submicron particles for which the convective diffusion is a predominant mechanism of deposition. Péclet number, which is a measure of the contribution of convective to diffusional effects on particle deposition, is a controlling process parameter.

The comprehensive theoretical model of dendritic deposition of submicron particles on a single fiber was proposed by Payatakes and Gradoń (1980) and Gradoń (1980). The authors calculated the efficiency of deposition, dynamics of dendrite growth, and pressure drop during the fiber loading for a wide range of particle and fiber Knudsen numbers. According to the assumption adopted in this model, the structure of dendrite was idealized. The dendrites were defined by a set of integers M_k, which represent the number of particles in the kth layer of the dendrite. This model reduced the local porosity of deposits to the value of porosity of sets of spheres packed in hexagonal cells. More realistic structures of dendrites were obtained from the Monte Carlo simulations of the growing process of particle dendrites on a fiber, as proposed by Kanaoka et al. (1980). Baumgartner and Löffler (1987) demonstrated the three-dimensional structures of deposited polydisperse aerosol particles obtained from the numerical simulations. These papers present only qualitative pictures of deposits. Recently, Moskal and Konopka (2000) and Oh et al. (2002) derived the models for particle deposition on charged fiber collector.

Process of clustering is still far from understanding of the real picture occurring in the filter structure. This is especially true for a loaded filter, where already deposited particles can be resuspended into the gas and then deposited at another part of the filter. Recently Przekop et al. (2003) proposed the cellular automata probabilistic model extended to the lattice–Boltzmann approach for description of the local structures of deposited matte particles and their clusters on the filter fiber. They found as a conclusion at the moment of intermesh of neighboring dendrites the effect of particle–particle interaction, adhesion–cohesion effects, and the influence of the re-entrainment of deposited particles. The aim of this study is a new approach for a description of that process.

DEPOSITION OF AEROSOL PARTICLES ON A SINGLE FILTER FIBER

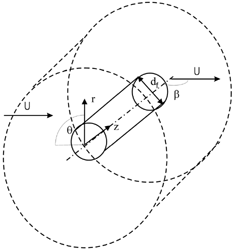
The single fiber-in-cell model will be used for analyzing particle motion and deposition during the nonsteady-state process. In this model one fiber of diameter d _f is placed centrally (Figure 1), in a finite volume of a fluid, called the unit cell. Motion and deposition of aerosol particles in such a system is achieved by applying Newton's second law to obtain the particle equation of motion. This equation includes the forces balance in defined gas flow structure.

FIG. 1 Single-fiber in cell geometry.

Gas Flow Model

A generalized Kuwabara-Happel model was used for calculation the gas flow structure around a fiber for assumed angle β between axis of the collector and the general direction of gas flow. Dimension of Kuwabara cell is defined by vanishing the shear stresses at its edges and is a function of packing density of fibers in the filter structure. Components of the gas velocity for cylindrical coordinate system (u _r , u _θ, u _z ) have a form

[1]

[2]

[3]

where U is mean interstitial velocity and Ku is Kuwabara constant; Ku = α−0.5ln α−0.75+0.25α².

Particle Motion

Determination of structures of deposited particles on the filter fiber requires the knowledge of a history of the individual particle and its position and velocity vectors. The Lagrangian method of analysis should be used for description of the process. Particle trajectory is calculated for the generalized Besset-Boussinesqu-Ossen equation, which in simplified form is reduced to the expression

[4]

where m is a particle mass and v is the particle velocity vector.

The drag forces for small, spherical particles satisfying Stokes law can be expressed by

[5]

where C _s is Cunnigham factor,

[6]

and l is the mean free path of the gas molecules.

The external forces considered in this article are represented by electric forces: Coulomb forces between particle and fiber

[7]

and between charged particles,

[8]

polarization forces,

[9]

and image forces,

[10]

where e is the unit vector in direction connecting centres of particles or centre of particle and axis of fiber, Q _f is the electrical charge of fiber, Q _p is the charge of the particle, ϵ is the permittivity of free space, ϵ _p is the relative dielectric constant of a fiber, d _f is the fiber diameter, and r is the position of the center of particle.

Brownian Displacement of Aerosol Particles

Foundations of the Brownian Dynamics (BD) were established by Chandrasekhar (1943) for a Stokesian particle in stationary fluid and for a force-free field. In this work extension of BD for the case of moving fluid at presence of the external forces derived by Podgórski (2001a, b) was used. Integration of Equation (4) for the time interval Δ t, small enough that the host fluid velocity u _i and external force F _i ^(ext) may be assumed constant over (t,t+ Δ t), gives the following bivariate normal density probability distribution functions ϕ _i (Δ v _i ,Δ L _i ). During time interval Δ t the particle will change its ith component of velocity by Δ v _i and it will be displaced by the distance Δ L _i in ith direction:

11

This distribution may be rearranged to a more convenient form of the product of two Gaussian distributions:

[12]

The expected values of particle velocity change ⟨Δ v _i ⟩ and the linear displacement ⟨ Δ L _i ⟩ are expressed as

[13]

[14]

where τ is particle relaxation time given by

[15]

The standard deviations σ _vi , σ _Li are as follows:

[16]

[17]

where k _B is the Boltzmann constant and T is the absolute temperature.

The coefficient of correlation is given by

[18]

We can therefore formulate the following generalized algorithm for the Brownian dynamics. For a given initial particle position and its initial velocity components v _i at a moment t, we calculate the local fluid velocity u _i and the external forces F _i ^(ext). Then one calculates the expected values ⟨ Δ v _i ⟩ and ⟨ Δ L _i ⟩ from Equations (4) and (5) and the correction coefficient ρ from the Equation (6). Next, we generate two independent random values G _Li , G _vi , which have Gaussian distribution with zero mean and unit variance. Finally we calculate the change of particle velocity Δ v _i and the particle linear displacement Δ L _i during time stem Δ t from the expressions accounting for deterministic and stochastic motion:

[19]

[20]

All the steps are repeated for each coordinate i = 1,2,3. Having determined the increments Δ v _i and Δ L _i , the new particle velocity at the moment t + Δ t is obtained as v _i (t + Δ t) = v _i +Δ v _i , and in the same manner the new particle position is calculated. After completing one time step of simulations, the next step is performed in the same way.

RESUSPENSION OF DEPOSITED PARTICLES

When a particle is deposited on the collector or on the already deposited particle, the short range forces acting between particles in a built-up cluster play a crucial role and strongly influence the final structure of deposits.

Short Range Interactions Between Particles: Adhesion

There are two dominating models of particles adhesion proposed by Johnson et al. (1971), known as JKR theory, and Derjaguin et al. (1975), named DMT theory. The JKR model assumes that adhesion-inducted deformations are entirely elastic. The deformations could be calculated from three terms: the elastically stored energy from creating the contact zone, the mechanical potential energy, and the surface energy. The JKR theory assumes that interaction forces exist at the contact area only. When the applied load is negative, contact area decreases. This means that the force of adhesion may be defined as the opposite to the force required to separate two bodies:

[21]

where γ is work of adhesion. The contact area corresponding to this force is not zero. However, it jumps to zero as the surfaces spontaneously separate.

The DMT theory did not approach the problem of particle adhesion from a contact mechanism perspective. It takes into account the molecular attraction in the noncontact zone. The analysis consists of two steps: determination of the shape of the particle near the contact surface and calculation of the sticking force. The applied load causes a pressure distribution over the contact area. The DMT model assumes that this distribution is given by Hertz equations. The theory considers the generalized force of particle attraction, F _s , the elastic reaction force, F _e , and the adhesion force, F _a = F _s −F _e . When the sphere just touches the plane (“point contact”) there is no deformation and the adhesion force has the maximum value:

[22]

Muller et al. (1980) proposed a model, later called MYD, in which the surface forces were calculated by doing a pairwise summation of interaction potentials between atoms while assuming that atoms in the particle interacted with those in the substrate via a Lennard-Jones potential and the motion of one atom did not effect the position of neighboring atoms. According to MYD theory, both the JKR and DMT models are its subsets and have their ranges of validity. The JKR model is proper for compliant materials, large particles, and high works of adhesion, whereas the DMT model is valid for small particles, more rigid materials, and lower surface energies.

Mechanism of Resuspension

The resuspension model is based on works by Reeks et al. (1988) and Ziskind et al. (2000). These authors assumed that the adhesion force and elastic reaction force considered in the JKR theory could be described by an equation of harmonic movement with dumping effect. Extending this approach, one can assume that the interaction between particles also have an oscillatory character. The displacement of a particle at the cluster attached to the neighboring particles can be expressed as follows:

[23]

where x is the displacement from equilibrium position, b is the coefficient of oscillations dumping, k is the coefficient of “spring” stiffnes, and m is the mass of the particle. Equation (23) describes the energy-balanced oscillatory model. Coefficient of stiffness can be calculated from

[24]

The elastic constant κ is given by

[25]

where ν _i and E _i are Poisson's ratio and Young's modulus of particle and substrate, respectively. The coefficient of dumping b = b _f + b _m , where b _f is fluid dumping and b _m is mechanical dumping:

[26]

[27]

The process of resuspension is caused by external forces, but the transmission of stress by interactions between particles is also important. Interaction between particles (or particle and collector) vanishes when the distance between them is larger then y _b . For contact surface particle–surface,

[28]

and for a particle–particle case,

[29]

MODEL CALCULATION AND DISCUSSION OF RESULTS

Model of particle deposition including effects of resuspension was used for simulation of the process of particle clustering on the single fiber.

Cylindrical fiber of diameter d _f = 30 μm was exposed for the stream of monodispersed aerosol particles with diameters from the range 0.01–10 μ m. It was assumed that the fiber was unipolar positively charged with a charge density 0.9 nAs/m and aerosol particles were equilibrium negatively charged. It was assumed that charges were concentrated in the center of the fiber. The attenuation of electrostatic forces due to particle accumulation was neglected. The following values of particle and fiber material were used for calculation of k, b, and y _b ; E ₁ = 8.01*10¹⁰ Pa, E ₂ = 2.15*10¹¹ Pa, ν₁ = 0.27, ν₂ = 0.28, and γ = 0.15 J/m².

Simulations were performed for the fiber skewness from the range 0–90°. Face velocity of the aerosol was equal to 0.1 m/s. Pressure was assumed to be 1 atm and temperature 25°C.

When the distance between particles (or particle and collector) was shorter than y _b , the adhesion effect was included in the model. So, the phenomena that combine aggregation of particles and resuspension of previously deposited particles were incorporated into the model. Equation (23) includes both the attractive and repulsive parts, so the bouncing-off effect was also taken into account. It was assumed that the initial velocity of a particle at the edge of a Kuwabara cell was the same as the fluid velocity and the gas flow structure was not disturbed by the presence of deposited particles.

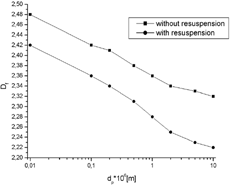
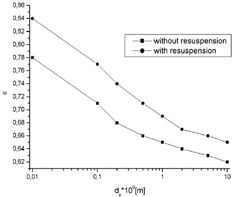
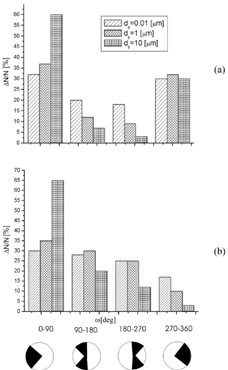
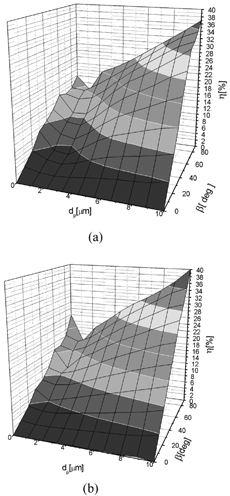
Figure 2 shows the distribution of deposits on the part of the fiber exposed to the stream of aerosol particles. When the resuspension effect was incorporated in the model, the number of deposited particles, their distribution, and their structures are different from these, which were obtained for the case when the distribution was neglected. The analyses of the geometry of dendrites obtained for both cases also confirms it. The fractal dimension of deposits and local porosity of dendrites as functions of aerosol particle diameter are shown in Figures 3 and 4, respectively. When the resuspension of deposited particles is incorporated into the model, calculated dendrites have more slender structures and, as a consequence of this, their fractal dimension is lower than for the case when resuspension is neglected. The reason of this effect is that during initial deposition single particles are resuspended to the airflow rather then clusters. Porosity of deposits with resuspension is obviously higher than for compact structures obtained in cases where resuspension is neglected. The local porosity of deposited matter, ϵ _d , influences the behavior of the nonsteady-state filtration. The method of calculation of ϵ _d was shown elsewhere (Przekop et al. 2003). As it is shown in Figure 4, the ϵ _d decreases with increasing of particle diameter. The fractal dimensions of dendrites were calculated as slopes of the curves ln(R _g ) versus ln(N). R _g is defined as distance from the center of the fiber to the top of the particle cluster, and N is number of deposited particles in the cluster. It is interesting to note that for smaller particles, when the diffusional deposition of particles has stronger influence on deposition rate over convective and electrostatic effects, the cluster of deposited particles is more distributed in a space and its structure is more compact (has a higher fractal dimension) than that obtained at the higher values of Peclet number. Decreasing both the fractal dimension and porosity and increasing the particle diameter, which may seem confusing, is produced by the definition of these parameters. The porosity is computed locally, while the fractal dimension is computed taking into account all the space around fiber. In addition, for higher values of the particle diffusion coefficient more deposited particles are observed around the fiber. When the Peclet number increases, due to increasing of convective and/or electrostatic drifts of particles, the clusters of deposited particles become more slender, regular in shape, and are located in the front of the collector. This effect is enhanced when the particle diameter increases significantly and inertial effects become the predominant mechanism of deposition. Such particles are distributed mostly at the front of the fiber, as shown in Figure 5. This picture also shows how the deposits are redistributed when the resuspension effect is incorporated in the model of fiber loading. Resuspended particles move close to the fiber surface are deposited at the rear part of the fiber. The picture of distribution of deposits around the fiber is different at the presence of resuspension. The effect of the fiber orientation, β, on the efficiency of deposition for different particle diameter is shown in Figure 6. Generally, when the resuspension is neglected the calculated deposition efficiency is 10–20% higher than for that which incorporates the particle re-entrainment. The fiber orientation strongly influences the deposition effect, especially for large particles for which deterministic effects are predominant for particle deposition.

FIG. 2 Picture of dendrite structures; results in simulations, d _f = 30 [μm], d _p = 1 [μ m], Q _f = −9 * 10^{− 9} [C/m] (airflow from the upside), (a) with resuspension and (b) without resuspension.

FIG. 3 Fractal dimension of deposits as function of particle diameter; β = 90°.

FIG. 4 Local porosity of dendrites as a function of particle diameter; β = 90°.

FIG. 5 Angular distribution of deposited particles (a) with resuspension and (b) without resuspension.

FIG. 6 Relation between single-fiber efficiency, particle diameter, and angle between axis of the fiber and direction of main gas flow β; (a) with resuspension and (b) without resuspension.

CONCLUSIONS

The model of a single-fiber loading with particles including the resuspension effect can explain some important phenomena which occur in the fibrous filter media. Rationalization filter structure requires knowledge of the temporary and spatial behavior of the nonsteady-state deposition process, including information on the configuration of dendrites, their fractal dimension, and their local porosity, as well as the restructurization of deposits due to re-entrainment and redeposition. The model proposed above provides some information on these items. The simplification, assumed in the model, related to the dynamical changes of the boundary conditions for the carrier gas flow caused by continuous deposition of particles can be eliminated through incorporation of the lattice-Boltzmann approach for description of the particle deposition process, as it was proposed in our previous study (Przekop et al. 2003).