Conversion of Multicomponent Aerosol Size Distributions from Sectional to Modal Representations

Abstract

A new method for converting a multicomponent aerosol size distribution from sectional to modal form is presented. The sectional distribution is fit with multiple lognormal modes using a nonlinear least-square regression that considers both the overall mass distribution and individual component distributions. The new method is compared to other conversion methods that assign sections to modes arbitrarily or that fit only the total mass distribution. Results of conversion tests using example distributions show that the multicomponent fit method is able to define a modal distribution that more accurately represents the original sectional distribution than do other methods. Total and component mass are conserved, the size, shape, and location of peaks match the original distribution, and modal compositions allocate components to the same size range as in the sectional representation. It is also able to convert distributions with relatively few size sections or where the size sections do not span the entire distribution, and it does not propagate errors when distributions are converted repeatedly between sections and modes.

INTRODUCTION

Aerosol dynamic processes (i.e., coagulation, nucleation, condensation, and deposition) that govern aerosol formation, growth, and evolution depend on the number, size, and composition of particles. In the atmosphere, these aerosol characteristics determine the influence of particles on health, climate, cloud formation, and visibility (Seinfeld and Pandis 1998; Hinds 1999; Pope 2000). To accurately predict these impacts, the size and composition distribution of the aerosol must be known. The true aerosol distribution encompasses a population of individual particles, each with its own distinct mass, shape, and composition. Since in most cases an exact accounting for each individual particle is impossible, alternate representations of the size distribution are required.

Two of the most common approaches for describing aerosol size distributions are sectional and modal methods. Both have been widely used in atmospheric models (Warren and Seinfeld 1985; Yong and Seinfeld 1992; Jacobson 1997a, 1997; Lurmann et al. 1997; Whitby and McMurry 1997; Wilck and Stratmann 1997; Fitzgerald et al. 1998; Harrington and Kreidenweis 1998). Sectional methods were originally developed by Gelbard and Seinfeld (1980) with a variety of subsequent improvements and adaptations (Gelbard 1990; Yong and Seinfeld 1992; Jacobson 1997a, 1997; Trautmann and Wanner 1999). In a sectional representation the particle size range is divided into a finite number of sections, and all particles within a given size section are represented with the same composition. Modal methods were first introduced by Whitby (1978) and have continued to be refined (e.g., Binkowski and Shankar 1995; Whitby and McMurry 1997; Whitby et al. 2002). A modal representation treats the aerosol size distribution as a set of individual, typically lognormal, distributions or modes. All particles within a given mode are represented with the same composition.

One of the difficulties in aerosol modeling is adequately describing the compositional heterogeneity of an aerosol population. Sectional methods are able to represent differences in composition as a function of particle size. Modal methods can represent compositional differences among particles of the same size. Since modal and sectional methods each take a different approach to representing the aerosol distribution, each contains unique size and compositional information, which may be lost when converting from one form to the other.

Methods for accurately converting sectional distributions to modal form have several potential applications. To be used within modal air quality models, size-segregated field measurements must be converted from sections to modes. Hybrid sectional–modal models such as UAM-VPM, where certain aerosol processes use a sectional representation and others use a modal representation, also require conversion between sections and modes. A reliable conversion technique would also provide an additional approach for directly comparing sectional and modal distributions.

We present here a new method for converting a multicomponent aerosol size distribution from sectional to modal form. In this method, the overall sectional size distribution is fit with multiple lognormal modes. Additionally, components within a section are distributed between modes such that all particles corresponding to a given mode have similar compositions. The method is evaluated with example size distributions, and the results are compared to those from other conversion methods.

SIZE DISTRIBUTION REPRESENTATIONS

In a sectional size distribution, the exact distribution of aerosol particles is approximated by a discrete number of sections. The mass size distribution of a multicomponent aerosol with NC individual components can be written in a sectional representation with NS sections as (Warren and Seinfeld 1985)

[1]

where M _ij is the mass of component i in size section j; q _i (d _p ) is the mass size distribution function of component i; and d _{pj − 1} and d _pj are, respectively, the smallest and largest particle diameters in section j. The sectional distribution is thus defined by the variables M _ij and d _pj .

In a modal distribution, the aerosol distribution is represented as the sum of several individual distributions or modes (Whitby and McMurry 1997),

[2]

where q(d _p ) is the approximated total mass size distribution, q _k (d _p ) is the mass size distribution of mode k, and NM is the total number of individual modes. Modes are often described with a lognormal equation (Seigneur et al. 1986; Seinfeld and Pandis 1998),

[3]

where Q _k is the total mass in mode k, and σ _k and d _pk are the standard deviation and median diameter of mode k. For multicomponent aerosols the mass of component i in mode k, Q _ik , can be defined as

[4]

where x _ik is the mass fraction of component i in mode k. Therefore, the variables, Q _k , σ _k , d _pk , and x _ik define a lognormal modal distribution.

CONVERSION METHODS

In this article we are interested in converting a multicomponent aerosol from one size distribution representation to the other. Recall that a sectional distribution is defined by the parameters M _ij and d _pj , and a modal distribution is defined by Q _k , σ _k , d _pk , and x _ik . It is important to note a key difference in how sectional and modal distributions are constructed. A modal distribution spans the entire size range, but a sectional distribution includes only the size range of its sections. For an aerosol distribution that extends beyond the upper or lower section boundaries, a portion of the particle mass will not be included in a sectional distribution, while it will be accounted for in a modal distribution. As a result, the total mass in a sectional representation may be less than that in a modal representation of the same distribution:

[5]

The lefthand term in Equation (5) is the sum of all components in all sections, and the righthand term is the sum of all components in all modes. To compare sectional and modal quantities directly we can define a modified modal component mass, Q _ik ′, which is the mass of component i from mode k that lies within the size boundaries, d _p0 and d _{p NS} , of a given sectional distribution:

[6]

Whereas Q _ik is the integrated mass over all sizes, Q _ik ′ includes only the mass within the size range defined by the sectional distribution. When the sectional size range is large enough to capture the entire distribution, Q _ik and Q _ik ′ will be essentially the same.

The goal, therefore, in converting between sections and modes is to calculate the parameters for one type of distribution given the parameters of the other type. First we present the relatively straightforward process of converting a modal to a sectional distribution, and then we consider in detail the more difficult sectional to modal conversion.

Modal-to-Sectional Conversion

When converting a modal distribution (Q _k , σ _k , d _pk , and x _ik ) to a sectional distribution (M _ij , d _pj ), the section size boundaries, d _pj , must first be specified. Then the multicomponent modal distributions are mapped into the size sections to determine the mass of each component in each section, M _ij :

[7]

The integral term in Equation (7) represents the mass of component i from mode k that will be placed in section j, which we will define as T _ijk :

[8]

The variable T _ijk combines both sectional and modal information. Using T _ijk as the basis for what we consider the true aerosol distribution, a correct sectional distribution will have sectional masses, M _ij , that are a subset of T _ijk :

[9]

Similarly, a correct modal distribution requires that Q _ik ′ values comprise a different subset:

[10]

Converting modes to sections using Equation (7) is a two-step procedure wherein Q _ik is first converted to T _ijk by integrating over sections j, followed by the summation over modes to reduce T _ijk to M _ij . Unfortunately, a similar simple procedure is unavailable for the reverse process of converting sections to modes.

Sectional-to-Modal Conversion

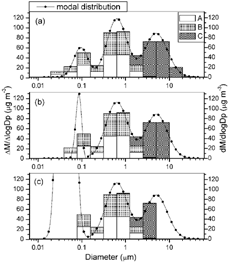
Unlike modal-to-sectional conversion, where the continuous modal functions are integrated to determine precisely the mass in discrete sections, the reverse process of converting sections to modes is not exact. The challenges in doing this can be illustrated with the following example. A sectional distribution with 8 sections and equal amounts of A and B is shown in Figure 1. Component A is concentrated in the smaller size sections, and component B is found primarily in the larger sections. In converting this, or any, distribution from a sectional to a modal representation, there are at least three criteria for what we may consider a proper fit.

FIG. 1 Sample aerosol distribution with two overlapping populations.

First, to be physically meaningful, mass must be conserved. Both the total aerosol mass and the mass of individual components must be the same in modal and sectional representations. Second, the overall modal size distribution should be a good fit to the sectional distribution. As seen with the mode curves in Figure 1, the number of modes and their height, width, and position should be such that the shape of the modal distribution is as close as possible to that of the sectional distribution.

TABLE 1 Regression equations for total mass fit and multicomponent fit conversion methods

Third, for a multicomponent distribution, components should be allocated to the correct mode. The goal is to create compositionally distinct modes, which if converted back to sections would result in a similar composition distribution. In Figure 1, for example, there appear to be two distinct types of particles, one that is pure A and another that is pure B. In this case, component A should be assigned exclusively to the smaller mode, and component B to the larger mode. Difficulties arise when considering sections where modes overlap. A sectional representation assumes particles have the same composition, which has the effect of mixing particles of different compositions. When converted to modes, sections need to be unmixed so that particles of similar composition are placed in the same mode. In Figure 1, the middle sections contain significant amounts of both A and B. They should be unmixed, so that particles assigned to the smaller mode are made of pure A, instead of a mixture of A and B. The best way to unmix sections while meeting the first two criteria is not obvious and will be explored in the following sections.

There are various possible approaches for converting sections to modes. We will consider three different methods: (1) an arbitrary fit, where each section is assigned to a specific mode; (2) a total mass fit, where modes are fit to sections based on total aerosol mass without unmixing sections; and (3) a multicomponent fit, which attempts to meet all three criteria for a proper fit by fitting modes based on total aerosol mass and component mass fractions.

Arbitrary Fit.

Perhaps the simplest approach for fitting modes to sections is to assign sections in a given size range to a specific mode. For this work, section boundaries at 0.078 μ m and 2.5 μ m are used as the dividing line between nuclei, accumulation, and coarse modes. All sections larger than 2.5 μ m are assigned to the coarse mode, those between 2.5 μ m and 0.078 μ m are assigned to the accumulation mode, and those sections less than 0.078 μ m are assigned to the nuclei mode. The median diameters of the three modes, d _p1, d _p2, and d _p3, are set as 0.03, 0.3, and 6 μ m, and the standard deviations, σ ₁ , σ ₂, and σ₃, are 1.7, 2.0, and 2.2, respectively, based on values suggested for atmospheric aerosol emissions (Binkowski 1999).

The arbitrary fit method is used in some form to prepare emissions data for most modal air quality models (Binkowski and Shankar 1995; Ackermann et al. 1998; Binkowski and Roselle 2003; Mebust et al. 2003). Particulate emissions inventories typically report PM_2.5 and PM₁₀ mass emissions, in what is essentially a two-section distribution. Because no additional size distribution information is available, PM_2.5 emissions are assigned to the accumulation mode, and particles larger than 2.5 um are placed in the coarse mode. Modes created by this method may or may not be a good fit to the original sectional distribution, since most of the modal parameters are arbitrarily specified. Referring back to the three criteria for a proper fit, only the first criterion, conservation of mass, is met in all cases.

Total Mass Fit.

To create modes that are a better fit to sections, a numerical curve-fitting routine can be used to minimize the difference between modal and sectional distributions. In the total mass fit method, the modal parameters which describe the total mass distribution, Q _k , σ _k , and d _pk , are determined using a nonlinear least-square regression (More et al. 1980). Equations (11) to (14) in Table 1 comprise the set of equations to be minimized by regression for the total mass fit.

Equation (11) fits total mass in individual sections, where the first term is mass within a section as defined by the sectional distribution, and the second term is total mass within that size range from all modes in the modal distribution. The T _jk term is an integral over the size range of section j,

[19]

and is the mass from mode k that lies within the size boundaries of section j. By minimizing the error in Equation (11) for each section, a modal distribution is produced that resembles the sectional distribution from which it was derived. Equation (12) specifies conservation of total mass, where the first term is total aerosol mass in all sections and the second is total aerosol mass in all modes that fall within the sectional size range. Equations (13) and (14) specify nonnegative values for Q _k and σ _k . To account for the different magnitudes of terms in these equations, Equations (11) to (13) are normalized by total mass, Σ _i Σ _j M _ij , so that terms in all four equations are approximately of order 1. Additionally, to ensure nonnegative values, Equations (13) and (14) are further weighted by a factor of 10.

A modal distribution with NM modes will have 3 * NM unknown parameters. Regression Equations (11) and (12) provide NS + 1 equations for a sectional distribution containing NS sections. As a result, the total mass fit method requires at least 3 * NM − 1 sections to fit a modal distribution with NM modes. To create a distribution with 2 modes, for example, a sectional distribution with at least 5 sections is needed, and 3 modes requires 8 or more sections. If the number of sections is less than the minimum required, standard deviations and/or median diameters of the modes can be specified as in the arbitrary fit.

Composition is not considered in the total mass fit regression but is accounted for in a second step that calculates modal composition, x _ik , as an average of the sectional mass fractions, x _ij , weighted by the mass in a section going to that mode, T _jk ,

[20]

Equation (20) has the effect of dividing the mass in a section between each of the NM modes, while assuming the mass sent to each mode has the same composition as that of the entire section. The total mass fit makes no attempt to unmix components in a section when allocating them to modes.

This step of allocating components to modes introduces some error, especially for modes with large areas of overlap. In Figure 1, for example, section 5 contains both A and B. The total mass fit method will divide this section between the two modes, and both portions will have the same composition of A and B, causing some A to be assigned to the larger mode and some B to the smaller mode. As a result, while the total mass fit method produces a modal distribution that meets the mass conservation and overall mass fit criteria, it may not correctly distribute components among modes.

Multicomponent Fit.

The new multicomponent fit method we have developed considers component mass and mass fractions in addition to total mass when performing the nonlinear least square regression. By fitting to total mass and composition simultaneously, it is able to unmix the section compositions and create a modal distribution that correctly mirrors the original sectional distribution. Unlike the arbitrary and total mass approaches, the multicomponent fit can satisfy all three criteria for a successful conversion from sections to modes.

The multicomponent fit regression includes Equations (11) to (14) from the total mass fit method plus composition Equations (15) to (18) as shown in Table 1. Using known values of sectional parameters M _ij and d _pj , the nonlinear least-squares routine determines values of modal parameters Q _k , σ _k , d _pk , and x _ik that minimize the error in these equations.

The primary additional equation included in the regression is Equation (15), which fits the modal component distribution, to the sectional component masses. The first term is the mass of component i in section j from the sectional distribution, and the second term is the same quantity derived from the modal distribution. Equation (16) specifies conservation of mass for each component, where the first term is total mass of component i in the sectional distribution and the second term is total mass of component i in the modal distribution. Equations (17) and (18) require that modal mass fractions be nonnegative and sum to 1.

As with the total mass fit, Equations (11) to (13) are normalized by total mass, Σ _i Σ _j M _ij . The new component mass Equations (15) and (16) are normalized by total component mass, Σ _j M _ij . Equations (13), (14), and (17) are also weighted by a factor of 10 to provide a reasonable balance between the regression constraints when finding a solution. This set of weighting values was found to work well for several distributions examined in this study, but has not been widely tested on other distributions.

For a modal distribution with NM modes and NC components, there will be 3 * NM + NC * NM unknown parameters. Equations (11), (12), (15), (16), and (18) provide NS + NC + NC * NS + 2 equations. In general, as long as there are more sections than modes (NM < NS) the regression can find a realistic solution. As a result, for the same number of modes and components a multicomponent fit requires fewer sections than does a total mass fit.

The multicomponent fit method satisfies all three fitting criteria for converting sections to modes. Total and component masses are conserved, and both component and total mass distributions are fit to the original sectional distribution. An important feature is that particles of similar composition are gathered into the same mode, essentially unmixing populations that have been combined in a sectional distribution.

METHOD EVALUATION

Figure 2 shows one of several hypothetical sectional distributions used to test our conversion method. This distribution has 12 sections, logarithmically spaced between 0.01 μ m and 40 μ m, and 3 components, A, B, and C. Component A is concentrated in the smaller sections, while components B and C are present in the larger sections with varying ratios. The individual component masses, M _ij , and section boundaries, d _pj , for this distribution are listed in Table 2.

FIG. 2 Original sectional distribution and converted modal distributions created using arbitrary fit, total mass fit, and multicomponent fit methods.

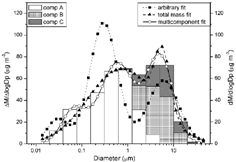
TABLE 2 Parameters for sectional distribution shown in Figure 2

		Component mass in section (μ g m^− 3)
Section	Aerosol diameter range (μ m)	A	B	C
1	0.010–0.020	0.035	0.000	0.000
2	0.020–0.039	3.575	0.000	0.000
3	0.039–0.078	9.528	0.000	0.000
4	0.078–0.156	9.940	0.000	0.000
5	0.156–0.312	14.173	0.000	0.000
6	0.312–0.625	20.109	0.000	0.000
7	0.625–1.25	20.391	0.286	0.123
8	1.25–2.5	9.407	6.781	2.906
9	2.5–5	2.522	13.431	5.756
10	5–10	0.009	13.024	8.682
11	10–20	0.000	3.059	3.059
12	20–40	0.000	0.139	0.324

TABLE 3 Converted modal distribution parameters

	Converted distributions
	Arbitrary			Total mass			Multicomponent
Mode	1	2	3	1	2	3	1	2	3
Q k (μ g m^− 3)	13.1	84.1	50.0	—	125	23.7	21.0	69.0	57.6
σ k	1.70	2.00	2.20	—	5.34	1.47	1.84	2.34	1.94
d pk (μ m)	0.03	0.30	6.00	10^−9	0.74	5.68	0.07	0.59	5.04
x A (%)	100	88.0	5.1	—	71.5	4.5	99.9	99.8	0.0
x B (%)	0.0	8.4	59.3	—	18.4	59.9	0.00	0.2	63.8
x C (%)	0.0	3.6	35.6	—	10.1	35.6	0.1	0.00	36.2

Since there are not well-defined peaks in this sectional distribution, the overall size distribution could be represented reasonably well with three, two, or even one mode. The compositional distribution, however, suggests that there are at least two distinct populations of particles, a smaller diameter mode containing primarily component A and a larger diameter mode composed of mainly B and C. In the results presented here, a modal distribution with 3 modes was assumed when fitting the sectional distribution.

This sectional distribution was not derived from an exact lognormal distribution and therefore does not have a modal distribution that fits it exactly. The three fitting criteria will be used to assess whether a calculated modal distribution provides a good fit to the sectional distribution. Another way to help judge the fitted modal distribution is to convert it back to sections, using Equation (1). For the recreated sectional distribution, the overall size distribution and the distribution of components in sections should be similar to that in the original sectional distribution.

The sectional distribution, shown in Figure 2 and with parameters listed in Table 2, was converted to a modal distribution using the arbitrary, total mass, and multicomponent fit methods. Values of the modal parameters Q _k , d _pk , σ _k , and x _ik calculated by each of the three conversion methods are listed in Table 3. In Figure 2, conversion results for the arbitrary fit (marked with squares), total mass fit (triangles), and multicomponent fit (circles) are compared to the original sectional distribution. Figure 3 compares the recreated sectional distributions.

FIG. 3 Original sectional distribution and sectional distributions created from converted modal distributions: (a) original sectional distribution, (b) arbitrary fit, (c) total mass fit, and (d) multicomponent fit.

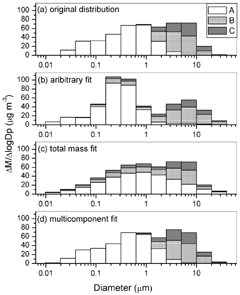
In the arbitrary fit method, sections are preassigned to modes and standard deviations are fixed, so mode 2 is forced to have a large peak height in order to maintain the same total mass as the broader sectional distribution. At the same time, mass in the larger diameter mode 3 is underestimated. As a result, the overall modal size distribution from the arbitrary fit method differs greatly from the original sectional distribution. When determining modal composition, there is no component B or C in the original sections smaller than 0.078 μ m, so mode 1 is pure component A. Mode 2 is mostly component A, but also contains sizeable fractions of B (8.4%) and C (3.6%). Mode 3 is a mixture of B and C with a smaller amount of A (5%). These components are distributed evenly throughout the individual modes, so that when the modes are converted back to sections (Figure 3b), B and C now appear in 0.01 μ m particles; originally they were only significantly present above 1.25 μ m.

For the total mass fit method, one of the defined modes has a median diameter very close to zero (10^{− 8}μ m) and can be disregarded, leaving a distribution with 2 modes. Compared with results of the arbitrary fit method, mode 2 has a larger total mass and a much larger standard deviation, while mode 3 has much less mass and is narrower. The overall modal distribution from these two modes, shown in Figure 2, fits the sectional distribution quite well, considering the arbitrary shape of the sections.

Since mode 2 contains most of the aerosol mass and more than the total mass of component A, components B and C make up almost 30% of mode 2. Mode 2 also has a large standard deviation that extends it over all sizes. Together, these factors have the effect of mixing most of the aerosol mass and spreading out the same composition of A, B, and C over the entire size range, as seen in Figure 3c. The distribution of components is very different from the original one, showing even more diffusional error than the arbitrary fit method.

The multicomponent fit method produces modes that are different from those obtained with the total mass fit method because it fits the overall distribution and the component distributions at the same time. Modes 1 and 2 are composed almost exclusively of component A, and together contain less mass than mode 2 from the total mass fit. Mode 3 is much larger than it was with the total mass fit and contains essentially all of components B and C. The multicomponent fit method is able to separate component A from components B and C into distinct modes by adjusting the modal parameters that define the overall mass size distribution. The total mass fit method, which ignores composition when fitting the size distribution, gives the best fit of the overall size distribution but misrepresents the allocation of components. The size distribution from the multicomponent fit method is not quite as accurate, but the component distribution is much more consistent with the original sections.

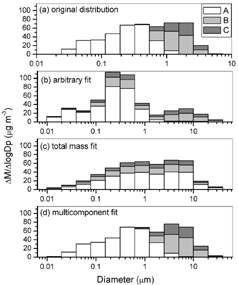
Another advantage of the multicomponent fit method is that composition errors do not propagate when a distribution is converted repeatedly between sections and modes. To demonstrate this, the sectional distribution in Figure 2 was converted to modes and back to sections 5 times using each of the conversion methods. The resulting sectional distributions are shown in Figure 4 along with the original distribution. When using the multicomponent fit, after the first conversion cycle, which transforms the irregular distribution into lognormal modes, the distribution stays the same. With the total mass fit, the overall size distribution remains constant after the first cycle, but components continue to mix, and after 5 iterations all sections have a nearly identical composition. For the arbitrary fit, both the overall and individual component distributions continue to change for each iteration, but components do not mix as rapidly as with the total mass fit.

FIG. 4 Original sectional distribution and sectional distributions created after 5 conversion cycles between sections and modes: (a) original sectional distribution, (b) arbitrary fit, (c) total mass fit, and (d) multicomponent fit.

Comparing the overall results for this example distribution, the arbitrary fit method conserves mass but has difficulty fitting the size and component distributions; the total mass fit method is able to conserve mass and fit the size distribution but distorts the component distribution; the multicomponent fit method can satisfy all three criteria for a good fit, correctly allocating components in addition to fitting the size distribution and conserving mass. Similar results were obtained in tests with other sectional distributions.

The multicomponent fit also works well at converting distributions with fewer size sections and where the size sections do not span the entire distribution. If a sectional distribution is derived from a perfectly lognormal distribution, it can typically be reproduced exactly. Even for more realistic sectional distributions that are not exactly lognormal and that contain most but not all of the full particle size range, the multicomponent fit can provide a reasonable modal distribution. An example of sectional distribution with 3 distinct peaks and 3 components is shown in Figure 5. When all 12 sections (0.01–40 μ m) are used, the converted modal distribution is an accurate fit of the sectional distribution, as seen in Figure 5a. When only 8 sections (0.04–10 μ m) are used (Figure 5b), a modal distribution with 3 modes is also created. The second and third modes are very similar to results with all 12 sections, but the first mode is much narrower when only 8 sections are used. If only 6 sections (0.078–5 μ m) are provided (Figure 5c), much more sectional information is lost, and the converted modal distribution is much less reliable. With only the smallest section indicating the presence of a first mode and no difference in composition distinguishing it from the second mode, a huge nuclei mode is created. Extrapolating beyond the sectional size range in this manner is not recommended. The portion of the distribution within the sectional size range may remain accurate, but trying to create an entire mode outside of the known size range is bound to result in errors.

FIG. 5 Modal distributions created using multicomponent fit method to convert original sectional distribution with (a) 12 sections, (b) 8 sections, and (c) 6 sections.

CONCLUSIONS

In this work a new method is presented for converting a multicomponent size distribution from sectional to modal form. A sectional distribution is fit with multiple lognormal modes using a nonlinear least-square regression that considers both the overall mass distribution and individual component distributions. Results of conversion tests show that the multicomponent fit method is able to define a modal distribution that accurately represents the original sectional distribution. This new method offers much more accurate fits than other approaches that assign sections to modes arbitrarily or that fit only the total mass distribution. These other methods tend to misrepresent the overall size distribution and are subject to compositional diffusion within the distribution. With the multicomponent fit method total and component mass are conserved, the size, shape, and location of peaks match the original distribution, and modal compositions allocate components to the same size range as in the sectional representation. It is also able to convert distributions with relatively few size sections or where the size sections do not span the entire distribution.

NOMENCLATURE

d p	=	particle diameter (μ m)
d pk	=	median diameter of mode k (μ m)
d p(j − 1)	=	lower size boundary of section j (μ m)
d pj	=	upper size boundary of section j (μ m)
M ij	=	mass of component i in section j (μ g m− 3)
NC	=	total number of components
NM	=	total number of modes in modal distribution
NS	=	total number of sections in sectional distribution
q(d p )	=	aerosol mass size distribution function (μ g m− 3)
q i (d p )	=	mass size distribution of component i (μ g m− 3)
q k (d p )	=	mass size distribution of mode k (μ g m− 3)
Q ik	=	mass of component i in mode k (μ g m− 3)
Q ik ′	=	mass of component i from mode k within sectional size boundaries (μ g m− 3)
Q k	=	total mass in mode k (μ g m− 3)
T ijk	=	mass of component i in section j from mode k (μg m− 3)
T jk	=	mass in section j from mode k (μ g m− 3)
x ij	=	mass fraction of component i in section j
x ik	=	mass fraction of component i in mode k
σ k	=	standard deviation of mode k

Subscripts

i	=	component number, 1 to NC
j	=	section number, 1 to NS
k	=	mode number, 1 to NM