A Generalized Approximation for the Thermophoretic Force on a Free-Molecular Particle

Abstract

A general, approximate expression is described that can be used to predict the thermophoretic force on a free-molecular, motionless, spherical particle suspended in a quiescent gas with a temperature gradient. The thermophoretic force is equal to the product of an order-unity coefficient, the gas-phase translational heat flux, the particle cross-sectional area, and the inverse of the mean molecular speed. Numerical simulations are used to test the accuracy of this expression for monatomic gases, polyatomic gases, and mixtures thereof. Both continuum and noncontinuum conditions are examined; in particular, the effects of low pressure, wall proximity, and high heat flux are investigated. The direct simulation Monte Carlo (DSMC) method is used to calculate the local molecular velocity distribution, and the force-Green's-function method is used to calculate the thermophoretic force. The approximate expression is found to predict the calculated thermophoretic force to within 10% for all cases examined.

The source file mentioned in this article is available online at http://taylorandfrancis.metapress.com/openurl.asp?genre=article&id=doi:10.1080/02786820490490001. To access this file, click on the issue link for 38(7), then select this article. In order to access the full article online, you must either have an institutional subscription or a member subscription accessed through www.aaar.org.

INTRODUCTION

A small, motionless particle suspended in a quiescent gas with a temperature gradient experiences a thermophoretic force; momentum is transferred to the particle by the mean thermal motion of the surrounding gas molecules. The thermophoretic force induces particle motion even in the absence of gas flow, causing the particle to move from warmer towards cooler gas regions. A manifestation of thermophoresis was first reported by Tyndall (1870), who observed a dust-free zone surrounding a hot body immersed in a dusty gas. Thermophoresis is of practical interest in a wide range of applications, including aerosol thermal precipitators, aerosol manufacture of fiber optics, gas cleaning, nuclear reactor safety, semiconductor processing, and the protection of valuable surfaces from particle contaminant deposition. Due to the broad range of applications as well as its fundamental scientific interest, thermophoresis has been widely studied over the past century (for comprehensive reviews, see Waldmann and Schmitt 1966; Derjaguin and Yalamov 1972; Talbot et al. 1980; Zheng 2002).

This work considers the thermophoretic force for freemolecular particles, where the particle radius, R _p , is assumed to be much smaller than the gas mean free path, λ. In terms of the particle Knudsen number, Kn _R = λ/R _p , the particle free-molecular limit is achieved for Kn _R → ∞. In this limit, the velocity distribution function of the surrounding gas molecules is not appreciably altered by the presence of the particle, and the net force acting on the particle can be found directly by calculating the net rate of momentum transferred to the particle by the incident and reflected molecules (momentum-transfer method). In the earliest applications of the momentum-transfer method, analytic forms of the incident velocity distribution were used. In the first application of this approach, Epstein (1924) assumed a Maxwellian velocity distribution for an equilibrium gas and calculated the drag force acting on a translating free-molecular sphere. Later authors used Chapman-Enskog (CE) distributions to calculate the thermophoretic and diffusiophoretic forces acting on a spherical, free-molecular particle suspended motionless in a nonuniform continuum gas (Derjaguin and Bakanov 1959; Bakanov and Derjaguin 1959; Waldmann 1959). Phillips (1972) approximated the free-molecular flow between two parallel walls of unequal temperature as the sum of two half-range Maxwellians and used the resulting velocity distribution to calculate the thermophoretic force in this highly noncontinuum limit. A gas–surface interaction model is needed to determine the momentum contribution of the molecules reflected at the particle's surface. Typically, the assumption is made that a fraction α of molecules undergo diffuse isothermal reflection (i.e., with perfect accommodation at the particle temperature) and the remaining fraction (1-α) is reflected specularly (i.e., with identical tangential velocity components but with opposite normal velocity component). Additional reflection models have been proposed in the literature for thermophoresis (e.g., Talbot et al. 1980; Phillips 1972; Gallis et al. 2001).

Recently, Gallis et al. (2001) demonstrated that the thermophoretic force on a spherical, free-molecular particle can be predicted using the momentum transfer method (applied via a force Green's function) coupled with molecular velocity distribution functions calculated by the direct simulation Monte Carlo (DSMC) method of Bird (1994). A particularly valuable aspect of this work is that it allows the determination of the thermophoretic force in complex continuum and noncontinuum flows. Thus far, Gallis and coworkers have applied the DSMC–force-Green's-function method to studies of pure-gas thermophoresis in rarefied (low-pressure) heat conduction (Gallis et al. 2001, 2002a), in the Knudsen layer near walls (Gallis et al. 2002b, 2003a), and in polyatomic gases (Gallis et al. 2002a, 2003b).

In all of these studies, Gallis and coworkers found the thermophoretic force vector, F _th , to be related to the translational gas heat flux, q ^tr = −K ^tr ▿ T, the mean molecular speed, and the particle cross-sectional area in a particularly simple fashion first suggested by Vestner (1974):

[1]

where the constant of proportionality, ξ, is termed here the thermophoresis parameter and K ^tr is the translational part of the coefficient of thermal conductivity. The thermophoresis parameter depends on the local molecular velocity distribution, but in a surprisingly weak way. For example, both theoretical (Waldmann 1959; Phillips 1972) and numerical studies (Gallis et al. 2001; 2002a, b, 2003a, b) have shown variations in ξ of less than 10% over a wide range of velocity distributions. Thus, for engineering applications, Equation (1) offers a reasonably accurate, simple expression for predicting the thermophoretic force on a particle based on local, macroscopic gas properties. Implementation of Equation (1) requires a proper choice for the thermophoresis parameter and a careful interpretation of the local gas properties.

The purpose of this article is to provide clear guidelines for the application of Equation (1) to a wide range of problems, from thermophoretic protection of critical surfaces to soot transport in flames. Recommendations are presented for how to prescribe ξ and how best to interpret the local gas properties. Conditions for which Equation (1) becomes less accurate are identified. Calculations of the thermophoretic force are performed using the DSMC–force-Green's-function method for a stationary, spherical particle much smaller than the gas mean free path. All calculations are performed for a quiescent gas, i.e., mass transfer by convection or diffusion is neglected and the net particle force arises solely from thermophoresis. Results are presented for monatomic gases (helium and argon) and polyatomic gases (nitrogen and carbon dioxide). Both continuum and noncontinuum system conditions are considered (the gas flow around the particle is always taken to be free molecular). In the continuum limit, results are presented for single-species gases and gas mixtures. In the noncontinuum limit, calculations explore the effect on thermophoresis of particle proximity to walls, gas rarefaction, and high heat flux.

THEORY

For a free-molecular particle, the calculation of the thermophoretic force can be decoupled into two parts: (1) the calculation of the local molecular velocity distribution function, f(u), and (2) the calculation of the resulting force using the momentum transfer method. The molecular velocity distribution function gives the fraction of molecules at a position in space that have a velocity vector u, which has x,y, and z components lying in the ranges u to u + du, v to v + dv, and w to w + dw, respectively. The calculation of the velocity distribution of a dilute, monatomic gas requires the solution of the Boltzmann equation (Chapman and Cowling 1970):

[2]

where n is the number density at position x, G is an external force per unit mass, and the integral on the right-hand side accounts for changes to the velocity distribution resulting from binary molecular collisions. In this collision integral, the subscript “1” denotes the collision partner, the superscript “*” denotes postcollision conditions, σ is the collision cross section, u _r is the relative speed of the colliding molecules, and Ω is the solid angle. In a gas mixture, a separate distribution function must be defined for each species, and a population balance similar to Equation (2) is derived for each species, although additional terms appear, allowing for interspecies collisions. For a polyatomic gas, the presence of internal energy modes complicates the derivation, although Chapman and Cowling (1970) provide a formulation called the generalized Boltzmann equation.

Analytic solutions of the Boltzmann equation are difficult to obtain because of the mathematical complexity inherent in solving a multidimensional, transient, integro-differential equation. Solutions are available in certain geometries for free-molecular gas flows, where collisions can be neglected (e.g., Bird 1976). For highly collisional flows, Chapman and Enskog have presented an approximate theory for describing continuum gas flow that has found widespread application (see Chapman and Cowling 1970). CE theory requires that the local gas Knudsen number be small.

More recently, molecular gas dynamics methods have been used to investigate the Boltzmann equation outside the ranges that have been treated analytically. In particular, these numerical methods are attractive, as they make no a priori assumptions regarding the magnitude of the local gas Knudsen number. One implementation of molecular gas dynamics that has been widely employed is the DSMC method of Bird (1976, 1994). In DSMC, large numbers of computational molecules are used to represent the gas. During a time step, these computational molecules move ballistically, reflect from boundaries, and collide with other molecules in the same computational cell according to prescribed rules. Predictions for the velocity distribution function are made by accumulating the velocity states of molecules passing through each computational cell. Similarly, macroscopic gas properties (e.g., density and temperature) are determined by sampling various moments of the distribution function over long times. Gallis and coworkers (2001; 2002a, b, 2003a, b) have recently applied Bird's DSMC method to study gas-phase heat conduction between parallel walls under a wide range of conditions.

Once the molecular velocity distribution is known, the resulting force on a suspended particle can be calculated by the momentum-transfer method. Gallis et al. (2001) showed that application of the momentum transfer method is greatly facilitated by using the force Green's function, which represents the force on a spherical particle from a delta-function incident molecular velocity distribution function. A spherical particle of velocity u _p is placed in an incident stream of gas molecules with mass m and velocity u (or velocity c = u – u _p with respect to the particle reference frame). The particle is taken to have a uniform temperature T _p , a consequence of assuming that the particle is small and that its thermal conductivity is large compared to the gas thermal conductivity. Although Gallis et al. (2001) considered an extended version of the Maxwell gas–surface interaction model, in this work the molecules are assumed to experience only “isothermal” diffuse reflections from the particle surface (the reflected molecules having a half-range Maxwellian molecular velocity distribution function at the particle temperature). The force Green's function is determined from the rates of delivery and removal of momentum by the incident molecules and the isothermally reflected molecules, respectively. These rates are integrated over the hemispherical surface of the particle that is exposed to the incident gas molecules (Gallis et al. 2001). For isothermal diffuse reflection, the force Green's function reduces to:

[3]

where _p is the mean molecular speed corresponding to the particle temperature. The force on a spherical particle from an arbitrary molecular velocity distribution function f[u] is determined by integration:

[4]

where ∫ f[u]d u = 1. For the present case of a motionless particle in a quiescent gas, the particle-temperature–dependent term in Equation (3) vanishes when performing the integration in Equation (4). Although the force Green's function was originally derived for a monatomic gas, Gallis et al. (2002a) have shown that the same result applies for a polyatomic gas. The heat-transfer Green's function (Gallis et al. 2001) is neglected here for motionless particles.

The force Green's function is equally convenient for use with analytic or simulated velocity distribution functions. Gallis et al. (2001) showed that Equations (3) and (4) can be applied with an analytic Maxwellian velocity distribution to reproduce Epstein's (1924) drag or with two half-range Maxwellians to reproduce Phillips' (1972) result for free-molecular gas flow. Gallis et al. (2001) also describe how to apply the force Green's function with DSMC-calculated velocity distribution functions.

NUMERICAL APPROACH

The numerical simulations presented in this work use the DSMC method to calculate the local molecular velocity distribution function and the force Green's function to calculate the thermophoretic force on a suspended particle. Gallis et al. (2002a, b, 2003a, b) provide the foundation for the present discussion. Many of these earlier studies, however, assumed idealized gases (e.g., hard-sphere argon) for comparison with theoretical predictions. The calculations presented here are intended to provide more realistic simulations by using collision parameters that are based on real gas properties. For more complete details of the DSMC method, see Gallis et al. (2002a, b, 2003a, b), and for a discussion of the force Green's function see Gallis et al. (2001).

The Variable Soft Sphere (VSS) molecular-interaction model as implemented by Bird (1994) is used for the following DSMC simulations. The collision process is specified in terms of a reference molecular diameter (Bird 1994):

[5]

where μ _ref is the gas viscosity at a reference temperature, taken here to be T _ref = 273.15 K For single-species calculations, the parameter Ω is obtained from a best fit of experimental viscosity data to the theoretical viscosity temperature dependence expected for the VSS model (Bird 1994, Table A1):

[6]

Bird (1994, Table A3) provides values for the angularscattering parameter, α determined from the gas self-diffusion coefficient at the reference temperature. For gas mixtures, intra-species collisions are treated with the appropriate single-species Ω and α, while interspecies collisions are treated with Ω₁₂ and α₁₂ based on diffusion-coefficient data (Bird 1994, Table A4).

For polyatomic gases, the reference diameter is calculated with Equation (5), but additional parameters are needed to describe collisions in which translational and internal energy can be exchanged. Although the DSMC method can accommodate rather complicated models for internal energy modes, the fully excited rotational modes and partially excited vibrational modes encountered under typical gas conditions are grouped together into a single number of internal energy modes, ζ _int (Bird 1994). Following Bird's (1994) formulation, the partition of internal energy in a collision is treated with the Borgnakke-Larsen model using ζ _int and the rotational relaxation collision number, Z _int . In this model, Z _int represents the number of collisions required for translational and internal energy to be exchanged. The DSMC calculations presented in this work use the molecular properties and collision parameters tabulated in Appendix A of Bird (1994) that are based on experimental data (see Table 1). Bird's Table A1 gives 2 internal energy modes for nitrogen, which is a linear diatomic molecule with 2 fully excited rotational modes and 0 fully excited vibrational modes at T _ref . Table A1 gives ζ _int = 3.7 for carbon dioxide, which is a linear triatomic molecule that has 2 rotational modes and an additional 1.7 effective internal energy modes to approximate the partially excited vibrational modes. The rotational and vibrational modes are grouped together for carbon dioxide and rounded to the nearest integer ζ _int = 4, as required by the present implementation of the Borgnakke-Larsen model. The calculations for both nitrogen and carbon dioxide assume Z _int = 5; this is a good estimate for nitrogen near standard conditions (see Bird 1994, Figure A2) but of unknown merit for carbon dioxide. Molecular collisions with walls are treated with perfect accommodation, i.e., thermal, tangential, and normal accommodation coefficients are unity.

TABLE 1 Molecular model properties under standard conditions (P _ref = 101,325 Pa and T _ref = 273.15 K)

Gas	ζ int	Z int	Ω	α	Viscosity coefficient μ ref × 10^5 Nsm^−2	Molecular mass m× 10^27 kg	Diameter d× 10^10 m
He	0	—	0.66	1.26	1.865	6.65	2.30
N2	2	5	0.74	1.36	1.656	46.5	4.11
Ar	0	—	0.81	1.40	2.117	66.3	4.11
CO2	3.7	5	0.94	1.61	1.380	73.1	5.54
He/Ar	—	—	0.725	1.64	—	—	—
From Appendix A in Bird 1994.

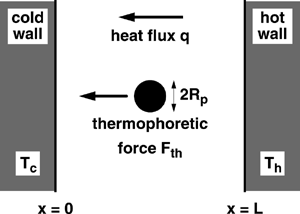
The DSMC method described above has been incorporated into the massively parallel (MP) code Icarus (Bartel et al. 2001). Icarus was developed for MP simulations of general twodimensional and axisymmetric rarefied gas flows. The present calculations are performed on the ASCI Red MP computer at Sandia National Laboratories. Typical simulations employ 500 dual-processor nodes and run for 24 h. The present simulations are performed for a simple geometry: a motionless spherical particle suspended between two infinite, parallel walls of unequal temperature separated by a 1 mm (0.001 m) gap. A schematic diagram of this situation is shown in Figure 1. The temperatures of the left and right walls are T _c = 173.15 K and T _h = 373.15 K, respectively. The present conditions give a temperature gradient of 200 K/mm, which is ten times larger than used in previous DSMC–force-Green's-function studies. The gas is assumed to be quiescent (no mass flow); consequently, heat transfer between the walls is determined by conduction (radiation is not relevant). This mathematically one-dimensional problem is actually solved using a two-dimensional computational geometry with Icarus: the rectangular domain is enclosed by the cold and hot walls and two specularly reflecting surfaces. Results are averaged in the direction parallel to the walls to improve statistical accuracy.

FIG. 1 Schematic diagram of a particle (with size greatly exaggerated) suspended between parallel walls at unequal temperatures.

Four gases (helium, argon, nitrogen, and carbon dioxide) are simulated individually or in combinations. For the single-species calculations, the system pressure is made as small as possible (to minimize computational expense) while still achieving the continuum limit in the interior; for the same wall separation, the continuum result applies up to much higher pressures (e.g., ambient). In practice, the pressure is selected so that the 1 mm domain is approximately 42 mean free paths across, where the mean free path is defined as:

[7]

where μ and ρ are the gas viscosity and density. The base pressures for single-species helium, argon, nitrogen, and carbon dioxide calculations are 5.56, 2.00, 1.87, and 1.24 Torr, respectively. At the base pressures, all four gases share the system Knudsen number, Kn _L = λ/L = 0.0237. Pressures for gas mixtures (see Table 2) are selected to give similar Kn _L . The standard computational mesh is composed of 200 × 100 square cells; cell widths in both directions are ∼0.2λ, satisfying the constraint indicated by Bird (1994) that cell sizes should be less than one-third the molecular mean free path. Time steps are chosen to be small enough to ensure that molecules travel, on average, no more than one-third of the cell size in a time step, satisfying another constraint indicated by Bird (1994). Calculation time steps are summarized in Table 2. Calculations using different meshes and/or time steps, and with 30 or 60 computational molecules per cell, are almost identical to the base-case calculations. Simulations are initialized using a constant temperature profile at the arithmetic mean of the two wall temperatures. To obtain steady results, averaging is initiated after transients have decayed.

TABLE 2 Calculation parameters

Gas	Pressure (Torr)	Time step (ns)
100% He	5.56	3
75% He, 25% Ar	5.00	3
50% He, 50% Ar	4.00	3
25% He, 75% Ar	3.00	3
100% Ar	2.00	8
100% N2	1.87	8
100% N2	0.187	8
100% N2	0.0187	8
100% CO2	1.24	8

The thermophoresis parameter in each cell is calculated according to Equation (1) using the cell-based, time-averaged moments for the heat flux, the thermophoretic force, and the temperature calculated during the DSMC simulation, where the thermophoretic force is calculated using moments specified by the force-Green's-function method, as described by Gallis et al. (2001, 2002a, b).

CONTINUUM GAS

Single-Species Monatomic Gas

Working independently, Waldmann (1959) and Derjaguin and Bakanov (1959) used CE theory and the momentum transfer method to calculate the thermophoretic force acting on a free-molecular particle suspended in a motionless, monatomic gas supporting a temperature gradient. CE theory assumes that the local molecular velocity distribution for a nonuniform gas differs from an equilibrium Maxwellian, f ⁽⁰⁾, by a small perturbation, Φ⁽¹⁾, which is proportional to the local Knudsen number, Kn (Bird 1994, Section 3.5):

[8]

[9]

Higher-order terms Φ^(k)∝ Kn ^k have been truncated from the full CE expansion to give Equation (8), which is valid only for Kn « 1. For a stationary, pure gas, Φ⁽¹⁾ has the form

[10]

where A is a function only of T and u, and x is position (Bird 1994, p. 66). The coefficient A is usually obtained as a series of Sonine polynomials. In the first approximation for A (i.e., using only the first term in the Sonine polynomial series), CE theory gives a velocity-distribution perturbation that is independent of the molecular collision model (e.g., Bird 1994, p. 173):

[11]

where K ₁ is the first approximation of the gas thermal conductivity (Chapman and Cowling 1970) and β² = m/(2k _B T) It is for this first approximation that Waldmann (1959) derived the well-known result given by Equation (1), with the thermophoresis parameter obtaining the following value:

[12]

Derjaguin and Bakanov (1959) used a similar approach to determine the particle thermophoretic drift velocity, but these authors did not explicitly report an expression for the force. Mason and Chapman (1962) suggested an alternative to the momentum transfer method based on the CE mixture theory in which the particles are treated as “heavy” molecules; Monchick et al. (1963) later showed that the CE mixture theory gives the same result as Waldmann if the proper interaction model is used. Experimental studies (Waldmann and Schmitt 1966; Li and Davis 1995a, b) and subsequent theoretical studies (e.g., Yamamoto and Ishihara 1988; Loyalka 1992; Beresnev and Chernyak 1995) support the Waldmann result (see also the recent review by Zheng 2002).

More accurate approximations to the CE velocity distribution can be found by constructing high-approximation Sonine polynomial expansions for A. Unlike the first approximation, higher approximations depend on the choice of molecular collision model. For molecular collision models with a repulsive force that obeys an inverse power law (IPL), Chapman and Cowling (1970) give an analytic second approximation for Φ⁽¹⁾ (see also Bird 1994, Equation 3.88). Using the corresponding second approximation for the velocity distribution with the force Green's function gives a second approximation for the thermophoresis parameter:

[13]

where the strength of the repulsive force enters through the viscosity temperature exponent, Ω. Values of ξ₂ for selected gases are given in Table 3. The Maxwell collision model is a special case of the IPL for which Ω= 1; in this case Equation (13) equals the first-approximation result given by Equation (12). This result is expected; Chapman and Cowling (1970) have shown the first-approximation CE solution provides an exact solution for a Maxwell collision model.

TABLE 3 Thermophoresis parameters for pure gases from CE analysis of equivalent IPL molecules

Gas	Ω	ξ1	ξ2	ξinfin;
Hard sphere	0.5	0.679 061	0.694 151	0.697 618
—	0.6	0.679 061	0.691 341	0.693 698
—	0.7	0.679 061	0.688 415	0.689 896
—	0.8	0.679 061	0.685 384	0.686 196
—	0.9	0.679 061	0.682 261	0.682 588
Maxwell	1.0	0.679 061	0.679 061	0.679 061
He	0.66	0.679 061	0.689 598	0.691 404
N2	0.74	0.679 061	0.687 214	0.688 404
Ar	0.81	0.679 061	0.685 075	0.685 832
CO2	0.94	0.679 061	0.680 990	0.681 168

Chapman and Cowling (1970) show how arbitrarily high approximations can be obtained for the IPL collision model. Following their prescription, Gallis et al. (2002b) combined CE theory for the IPL collision model with the force-Green's-function method to derive higher approximations for the thermophoretic force. Gallis et al. (2002b) found that ξ _k depends on the viscosity temperature exponent, Ω, and the degree of the approximation. Infinite-approximation limits for the thermophoresis parameter for selected gases are given in Table 3. As expected, the infinite approximation for a Maxwell gas equals the first-approximation result of Equation (12). The hard-sphere (HS) collision model represents a second special case of the IPL with Ω= 0.5; in this case, the infinite-order thermophoresis parameter is

[14]

where the numerical coefficient is accurate to the indicated precision. Gallis et al. (2002b) compared simulations based on the DSMC–force-Green's-function method with the theoretical values predicted with IPL–CE theory. To best approximate an inverse power law molecular model, Gallis et al. (2002b) selected the VSS collision parameter Ω to match that for the desired IPL gas and found α by matching the VSS and IPL Schmidt numbers. The DSMC-calculated values of ξ for Maxwell and HS molecules are in excellent agreement with Equations (12) and (14), verifying both the theoretical analysis and the numerical implementation.

Real gases do not share the (Ω, α) pairings used in previous DSMC simulations that approximate IPL molecules. Thus, DSMC–force-Green's-function calculations are performed for the parallel-wall geometry using the (Ω, α) pairings that Bird (1994, Appendix A) recommends for simulating real gases. Calculated temperature profiles for helium and argon are shown in Figure 2a. Both curves exhibit small temperature jumps at the walls; the argon curve shows more curvature because the thermal conductivity of argon has a stronger temperature dependence than that of helium (i.e., Ω is larger for argon than helium). Calculated profiles of the thermophoresis parameter for helium (open symbols) and argon (filled symbols) are shown in Figure 2b. The calculations clearly show the behavior first reported in Gallis et al. (2002b); ξ is constant across the interior but increases slightly in the Knudsen layers adjacent to the walls. Also shown in Figure 2b are the IPL–CE theoretical results for the first-approximation value ξ₁ (solid line) and the infinite-approximation value ξ_∞ for each gas (dotted line for helium, dashed line for argon). It is in the uniform central region of each profile that the continuum limit is obtained. In this region, the calculated values and the ξ₁ value agree to within 2%, whereas the calculated values and the corresponding ξ_∞ values agree to within 0.1%.

FIG. 2 Profiles of (a) temperature and (b) thermophoresis parameter for monatomic gases: helium and argon.

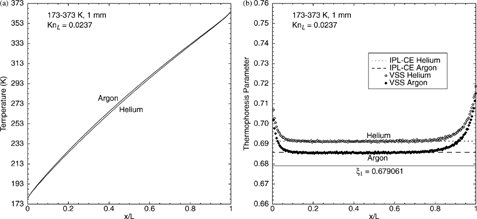
As a validation exercise, the DSMC-calculated temperature and heat-flux profiles are used to determine an effective thermal conductivity for each gas. The calculated temperature profiles in the interior 40% of the domain (away from the near-wall Knudsen layers) are fit to an analytic solution for the parallel-wall heat conduction problem assuming K ∝ T ^Ω (see Gallis et al. 2002a, Equation (8)). The fitting process provides a best-fit value for the ratio of the heat flux to the thermal conductivity; the DSMC-calculated heat flux is then used to determine K. Predicted values for the thermal conductivity of helium and argon at 0°C are 0.146 and 0.0165 W/(m²·K), respectively; these values agree to within 0.5% with the tabulated values given by Kestin et al. (1984). This agreement is well within the estimated accuracy cited by Kestin (0.7%) and the numerical uncertainties estimated for the calculated thermal conductivities (1%). Convergence studies (e.g., refinements in cell size and time step) suggest that numerical errors in the DSMC predictions for the thermal conductivity and the thermophoretic force are similar, while uncertainties in the thermophoresis parameter are significantly less (0.1%).

According to CE theory for IPL molecules, the Maxwell and HS collision models give rise to thermophoresis parameters that differ by less than 3%. Viscosity temperature exponents for all of the monatomic gases tabulated in Bird (1994, Appendix A) fall within a range 0.66 ≤ Ω ≤ 0.85, which is bounded by the Maxwell and hard-sphere values. Consequently, for real monatomic gases, the thermophoresis parameter is expected to fall within the narrow range bounded by Equations (12) and (14). This result was anticipated by Waldmann (1959), whose original derivation included high-approximation terms, although he correctly argued that the resulting corrections to the thermophoretic force would be small. As an example, Waldmann considered the second approximation for a Lennard-Jones 6–12 molecular model and showed that the thermophoresis coefficient is increased by 1% for realistic temperatures. Although the high-approximation CE analysis for the IPL collision model shows larger variations in ξ than for the Lennard-Jones model, in both cases the variations are still only a few percent.

For a single-species monatomic gas, the thermophoretic force can be approximated to within 3% using Equation (1) with the first-approximation thermophoresis coefficient ξ₁, the local heat flux, and the local mean thermal velocity. For greater accuracy, the theoretical IPL–CE infinite-approximation value ξ_∞(Ω) appropriate to the gas can be used. Errors resulting from uncertainties in local gas properties (temperature, heat flux) and particle–gas accommodation coefficients are typically larger than any errors introduced by using the first approximation for the thermophoresis parameter.

Single-Species Polyatomic Gas

A complete, rigorous solution of the CE theory for a polyatomic gas is not available. Waldmann (1959) was the first to recognize that, because only momentum transfer is involved, the thermophoretic force should be estimated using the translational part of the coefficient of thermal conductivity (i.e., the translational part of the heat flux) in Equation (1). Vestner (1974) considered thermophoresis for nonspherical particles in a polyatomic gas and arrived at the same conclusion. Waldmann (1959) suggested approximating the translational thermal conductivity for a polyatomic gas according to Eucken's theory:

[15]

Although CE theory shows that the Eucken expression is accurate to first approximation for monatomic gases, Waldmann noted that this expression could be in error by 10–20% for polyatomic gases (see also Waldmann and Schmitt, 1966). If more accuracy is needed, one of a variety of sophisticated transport-property estimation methods must be pursued (e.g., Reid et al. 1987; Dixon-Lewis 1984; Kee et al. 1986). Fortunately, these estimation methods typically separate the thermal conductivity into its translational and internal energy components and approximate the translational part by

[16]

where f ^tr depends on the gas Schmidt number and other gas properties (see Reid et al. 1987, Equation 10–3.7; Kee et al. 1986, Equation (17)). For a monatomic gas, all of the estimation methods reduce to f ^tr = 5/2 and agree with Eucken's result. The application of Reid's estimation method for nitrogen and carbon dioxide gives f ^tr = 2.32 and 2.00, respectively (where gas Schmidt numbers and total number of internal energy modes are taken from Bird 1994, Tables A1 and A3). Thus, the translational part of the thermal conductivities of nitrogen and carbon dioxide are 8 and 20% less, respectively, than the Eucken prediction. Application of the estimation method suggested by Kee et al. (1986) gives a similar value for nitrogen, f ^tr = 2.29, but its prediction for carbon dioxide, f ^tr = 2.20, is significantly larger than Reid et al. (1987). Thus, estimation of the translational part of the thermal conductivity can introduce uncertainties of as much as 10% in the calculation of the thermophoretic force.

Gallis et al. (2002b, 2003b) used the DSMC–force-Green's-function method to study the thermophoretic force in nitrogen using Bird's recommended values for the collision parameters: ξ _int = 2 and Z _int = 5. Gallis et al. (2003b) also performed simulations in which parameters associated with the internal energy modes were varied over a wide range, i.e., with 20 internal energy modes and for relaxation collision numbers of Z _int = 1 and ∞ A value of ξ _int = 2 corresponds to diatomic molecules like nitrogen, whereas ξ _int = 20 corresponds to large polyatomic molecules (many internal energy modes). The value Z _int = 1 produces the maximum possible rate of exchange between translational and internal energy: this occurs at every collision. On the other hand, the value Z _int = ∞ produces a zero rate of exchange: the molecules are dynamically monatomic, although they carry internal energy passively. Gallis et al. (2003b) calculated the local thermophoresis parameter from Equation (1), using the translational heat flux, which is readily available from a DSMC simulation. They found that the thermophoresis parameter is insensitive to the choices for the internal energy collision parameters and is in excellent agreement with Equation (1) using the IPL–CE theoretical prediction for a molecule with the same value of the viscosity temperature exponent as nitrogen: ξ_∞(Ω = 0.74) ≈ 0.688404. Thus, these authors suggest that the thermophoresis parameter for a polyatomic gas can be estimated with the appropriate IPL–CE value.

DSMC calculations are performed for a diatomic gas (nitrogen) and a polyatomic gas (carbon dioxide) for a 200 K/mm temperature gradient. Calculated temperature profiles for nitrogen and carbon dioxide are shown in Figure 3a. Both curves exhibit small temperature jumps at the walls; the carbon dioxide curve shows more curvature in the interior because its thermal conductivity has a stronger temperature dependence than nitrogen. Calculated thermophoresis-parameter profiles are shown in Figure 3b, along with the IPL–CE theoretical values, ξ₁ and ξ_∞. The calculated results for nitrogen and carbon dioxide are within 2% of the first approximation, ξ₁, and show excellent agreement (0.1%) with their respective IPL–CE theoretical values: ξ_∞(Ω= 0.74) ≈ 0.688404 and ξ_∞(Ω = 0.94) ≈ 0.681168. The present calculations extend the previous conclusions of Gallis et al. (2003b) for nitrogen to much higher heat flux. An additional DSMC calculation wherein carbon dioxide is modeled as a diatomic gas (ξ _int = 2) produces statistically indistinguishable results for the thermophoresis parameter, showing the insensitivity of the results to the approximation ξ _int = 4 (instead of 3.7). Thus, the present results support the use of Equation (1) for a polyatomic gas with the appropriate IPL–CE value of the thermophoresis parameter.

FIG. 3 Profiles of (a) temperature and (b) thermophoresis parameter for polyatomic gases: nitrogen and carbon dioxide.

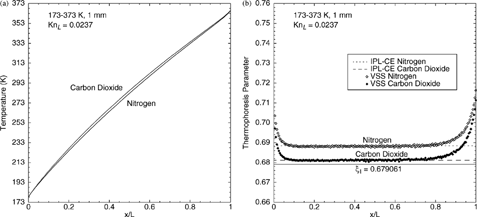
As a validation exercise, the DSMC-calculated temperature and heat-flux profiles are used to determine the total and translational thermal conductivities for each gas. For nitrogen, the calculated total thermal conductivity at 0°C is 0.0244 W/(m²·K), which is within 1% of the value interpolated to 0°C from a table reported by Stephan et al. (1987). The same DSMC calculations give K ^tr = 0.0174 W/(m²·K), which corresponds to f ^tr = 2.36 and which is in good agreement with the value estimated using either Reid's or Kee's method. For carbon dioxide, the calculated total thermal conductivity at 0°C is 0.0162 W/(m²·K), which is 7% higher than the value interpolated to 0°C from a table reported by Eckert and Drake (1972). The fact that the calculated values are slightly higher than reported values is due in part to the fact that the calculation uses a slightly larger number of internal energy modes than recommended (4 versus 3.7). The same DSMC calculations give K ^tr = 0.00888 W/(m²·K), which corresponds to f ^tr = 2.27 and which is in good agreement with the estimated value using Kee's method but is about 13% higher than the value from Reid's method. Because the translational part of the thermal conductivity cannot be measured, it is difficult to determine which value is more reliable. For diatomic gases (e.g., nitrogen), the uncertainty in the translational thermal conductivity is typically 1%, while for polyatomic gases (e.g., carbon dioxide) the uncertainty could be as large as 10%.

For a single-species polyatomic gas, the thermophoretic force can be approximated to within 3% using Equation (1) with the first-approximation thermophoresis coefficient ξ₁, the local translational heat flux, and the local mean thermal velocity. If greater accuracy is desired, the thermophoresis parameter for a polyatomic gas can be estimated with the IPL–CE theoretical prediction for a monatomic gas with the same value of the viscosity temperature exponent, ξ_∞(Ω). Errors resulting from uncertainties in estimating the translational heat flux are typically much larger than any errors introduced by using the first approximation for the thermophoresis parameter.

Gas Mixtures

For a free-molecular particle suspended in a gas mixture, the total thermophoretic force acting on a particle is found by summing over the individual contributions from each species:

[17]

[18]

where for species i, q _i ^tr and K _i ^tr are the translational heat flux and the translational thermal conductivity, respectively; c _i is the mean molecular speed: and ξ _i is the thermophoresis parameter. The complexity inherent in Equation (17) is that K _i ^tr and ξ _i do not equal their single-species values but are complicated functions that depend on the temperature and the mole fractions of all species. While the CE procedure has been extended to multicomponent systems (e.g., Hirschfelder et al. 1954), the solution is complicated, particularly when the mixture includes polyatomic gases. Instead of providing a rigorous the oretical solution, the present approach is to perform a set of DSMC simulations for a gas mixture and to identify reasonable approximations.

Heat conduction between two parallel walls of unequal temperature is considered for a mixture of two monatomic gases of widely disparate mass: helium and argon. Three DSMC simulations are performed for mole-based mixtures containing 25, 50, and 75% helium. 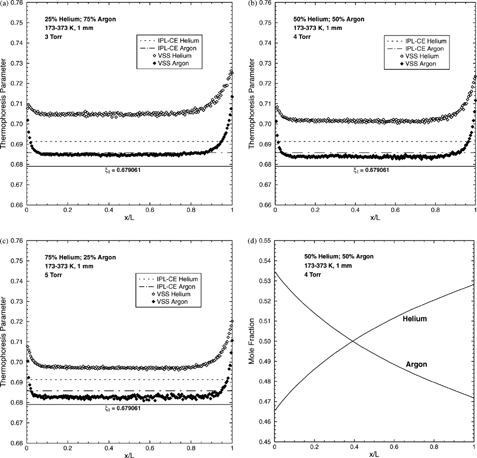The DSMC method allows independent tracking of the heat flux and thermophoretic force for each species; thus, the thermophoresis parameter ξ _i for each species is calculated from local values for F _th,i , q ^tr _i , and _i The resulting thermophoresis-parameter profiles are shown in Figure 4a–4c. In these figures, the helium and argon results are indicated by open and filled diamonds, respectively. All of the thermophoresis parameter profiles show the same general shape observed for the single-species cases (Figure 2b): a uniform central (continuum) region surrounded by Knudsen layers wherein the thermophoresis parameter increases slightly toward the walls. Although the thermophoresis parameter in the central region does change with composition, this change is small. Also shown in Figures 4a–4c are the IPL–CE single-species theoretical values for helium and argon, ξ_∞(Ω= 0.66) = 0.691404 and ξ_∞(Ω= 0.81) = 0.685832, respectively, and the first-approximation value, ξ₁. For argon, the single-species value is seen to be a good approximation for all three cases. For helium, the thermophoresis parameter is noticeably higher than its single- species value, and this difference increases with decreasing helium fraction. Even for helium, however, the thermophoresis parameter in the interior region never differs by more than 2% from the single-species value. Notably, the interior-region thermophoresis parameter for either gas in all three simulations differ by no more than 4% from the first-approximation result. Thus, the use of ξ₁ in Equation (17) introduces errors in the thermophoretic force of no more than 4%. These results suggest that, lacking better data or calculations, the thermophoretic force for a general gas mixture can be calculated with Equation (17) using ξ _l for each gas.

FIG. 4 DSMC results for helium–argon mixtures. Thermophoresis-parameter profiles for (a) 25% helium, 75% argon; (b) 50% helium, 50% argon; and (c) 75% helium, 25% argon. (d) Mole-fraction profiles for a nominally 50%–50% mixture.

The greater error in applying Equation (17) is typically the determination of the amount of translational heat carried by each gas component, particularly for mixtures including polyatomic constituents. For mixtures of monatomic gases, a CE-based theory exists (Kestin et al. 1984), and the total heat flux can be measured experimentally as a check of the theory. For mixtures including polyatomic gases, the transport-estimation references given earlier (Reid et al. 1987; Dixon-Lewis 1984; Kee et al. 1986) provide methods for calculating the mixture thermal conductivity. Although these methods can provide reasonable estimates of the total thermal conductivity, estimations of the translational contribution are probably less accurate.

If greater accuracy is needed, one option is to perform DSMC simulations of the desired gas mixture. As an example of the accuracy that can be obtained for monatomic-gas mixtures, the thermal conductivities predicted by the present DSMC simulations of helium-argon mixtures are compared to the accurate tabulation of Kestin et al. (1984). The calculated temperature and heat-flux profiles for each species are used to determine an effective thermal conductivity for each species; the mixture thermal conductivity is obtained by adding these contributions. Predicted values for the mixture thermal conductivity at 0°C are 0.03054, 0.0513, and 0.0847 W/(m²·K) for the cases with 25, 50, and 75% helium, respectively; these values agree within 1.4% with the tabulated values given by Kestin et al. (1984). This uncertainty is slightly larger than the uncertainty cited by Kestin (0.7%) and the numerical uncertainty for DSMC herein (1%). One explanation is suggested by Figure 4d, which shows the mole-fraction profiles for a calculation initially having a 50%–50% mixture of helium and argon. Although there are exactly the same number of molecules of each species in the domain, the steady-state DSMC result shows clear spatial variations in gas composition. These concentration gradients arise from the well-known thermal diffusion effect (Chapman and Cowling 1970), in which heavier molecules migrate toward colder gas regions (analogous to thermophoresis if a heavy molecule is thought of as a light particle). Consequently, helium accumulates preferentially at the hot wall (x/L = 1), while argon accumulates at the cold wall. Since the heat flux depends on the local concentration and concentration gradient, some differences between the present calculations (with concentration gradients) and the Kestin et al. (1984) values (tabulated for a fixed concentration in the absence of gradients) are expected.

For gas mixtures, the thermophoretic force can be calculated from Equation (17) using the first-approximation thermophoresis coefficient ξ₁, the local translational heat flux, and the local mean thermal velocity for each species. Calculations for helium-argon mixtures show that the error in this approximation can be up to 4%. Some improvement is obtained if the thermophoresis parameter for each gas constituent is estimated with the IPL–CE theoretical prediction for a monatomic gas with the same value of the viscosity temperature exponent, ξ_∞(Ω). Errors resulting from uncertainties in estimating the translational heat flux for gas mixtures (especially including polyatomic gases) are typically much larger than any errors introduced by using the first approximation for the thermophoresis parameter.

NONCONTINUUM GAS

In the previous sections, the domain length scale and pressure are suitably chosen for each gas or mixture to ensure continuum gas behavior in the interior of the domain. Continuum behavior is indicated by the constant value of the thermophoresis parameter obtained across the interior and by the good agreement of this value with the theoretical IPL–CE value obtained with the Ω appropriate to the gas. Recently, Gallis et al. (2004) used independent means to confirm that continuum (CE) behavior is closely approached in the region wherein ξ is constant. Near a wall, however, the continuum description breaks down as the gas adjusts to the Maxwellian velocity distribution of molecules reflected by the walls. This phenomenon leads to the development of Knudsen layers (noncontinuum gas regions that extend several mean free paths away from the wall). It is within these noncontinuum Knudsen layers that the thermophoresis parameter increases from its constant (continuum) value in the interior to a maximum at the wall; this behavior is observed in all of the previous continuum simulations and is discussed in more detail below.

Noncontinuum gas behavior in the interior region of the parallel-wall geometry can be obtained by one of three approaches: (1) lowering the gas pressure, (2) reducing the wall separation, or (3) increasing the temperature gradient. The first two approaches achieve noncontinuum behavior by increasing the system Knudsen number, Kn _L = λ/L, by increasing the gas mean free path or by reducing the characteristic system length, whereas the last approach achieves noncontinuum behavior by increasing the local Knudsen number, here (λ/T)|▿T |. In the first two approaches, a molecule travels proportionally farther away from the walls before colliding with another molecule, to the point that, for large values of Kn _L , the wall influence extends throughout the domain. Calculations presented below for nitrogen at reduced pressures explore the effect of noncontinuum (rarefied) conditions on the thermophoresis parameter. Calculations illustrating the effect of high-temperature gradients on the thermophoresis parameter are also included below.

Near-Wall Effects

All of the thermophoresis-parameter profiles presented in the previous section share the same general shape: ξ is constant across the interior but increases slightly near the walls. This general pattern is observed for single-species monatomic and polyatomic gases, as well as for monatomic gas mixtures. The observed near-wall noncontinuum behavior occurs as the gas adjusts to the Maxwellian velocity distribution of molecules reflected by the walls. It is within this noncontinuum region, or Knudsen layer, that the thermophoresis parameter increases from its constant (continuum) value in the interior to attain a maximum at the wall. Gallis et al. (2002b, 2003a) studied this problem and found that the near-wall effect leads to modest increases, 5%, in the thermophoresis parameter for isothermal, diffuse molecular reflection at the walls. The wall effect increases with increasing wall specularity but is still only a 10% correction for a completely specular reflection. Gallis et al. (2002b) presented a simple analytic model that describes the near-wall effect and verified the model against DSMC–force-Green's-function simulations for argon-like Maxwell and HS gases. The present work using realistic collision models supports the previous work, showing near-wall increases of less than 5% for helium, argon, nitrogen, carbon dioxide, and for mixtures of helium and argon. The present results differ from previous analyses, which predicted that the thermophoretic force would be strongly effected near walls (Havnes et al. 1994; Chen and Xu 2002).

In a continuum gas bounded by a wall, it is recommended that the near-wall effect be neglected and that the thermophoretic force be calculated everywhere in the domain as for a continuum gas, i.e., using Equation (1) for a single-species gas or Equation (17) for a gas mixture. The first-approximation thermophoresis coefficient ξ₁ is usually accurate enough for most applications, although some improvement is obtained if the appropriate thermophoresis parameter ξ_∞(Ω) is used. Neglecting the wall effect generally introduces errors of 5%, which are probably less than the uncertainties in estimating the translational heat flux (particularly for polyatomic gases or for gas mixtures). If greater accuracy is needed, the approximate near-wall correction of Gallis et al. (2002b) can be applied to the best-available interior estimate for ξ. Finally, it is noteworthy that the thermophoretic force is increased (relative to the continuum result) near both cold and hot walls, i.e., particles are more strongly repelled by a hot wall and are more strongly attracted by a cold wall than would be expected based on Equations (1) or (17).

Rarefied Gases

This section explores changes in the thermophoresis parameter that result from noncontinuum effects due to increasing rarefaction (decreasing gas pressure) in the parallel-wall geometry. Analytic limits for the thermophoretic force in this geometry are available in both the continuum and free-molecular limits. The continuum limit, obtained for vanishing Kn _L , has already been discussed. In the free-molecular limit, Kn _L → ∞, molecules travel back and forth between the cold and hot walls without colliding with each other. For isothermal diffuse reflections, the region between the walls is characterized by two streams of half-range Maxwellian molecules, with higher energy molecules streaming downward from the hot wall and lower-energy molecules streaming upward from the cold wall. Expressions for the thermophoretic force and the heat flux between two walls when both the system and the particle are free molecular (Kn _L → ∞ and Kn _R → ∞) are given by Gallis et al. (2002a). The thermophoresis parameter can be shown to be

[19]

In this limit, the thermophoresis parameter is independent of gas properties, is constant across the domain (as is molecular velocity distribution), and equals a maximum of 3/4 in the limit of vanishingly small temperature differences. Interestingly, even for this highly noncontinuum case, the thermophoresis parameter differs by no more than 10% from the IPL–CE first approximation for a continuum gas.

For intermediate Knudsen numbers, the thermophoresis parameter can be obtained only by numerical simulation. Calculations are performed for nitrogen using the DSMC–force-Green's-function method for temperature gradients of 20 and 200 K/mm. Figures 5a and 5b show simulated thermophoresis-parameter profiles for nitrogen at four pressures corresponding to Kn _L = 0.0237, 0.237, 2.37, and ∞ (free-molecular flow). At Kn _L = 0.0237, both the low-gradient and high-gradient cases show the behavior observed in the previous near-continuum cases: a constant thermophoresis parameter across the interior surrounded by increasing regions near the walls. Both cases show excellent agreement with the theoretical IPL–CE result ξ_∞(Ω= 0.74)≈ 0.688404 for nitrogen (dotted lines), confirming that the continuum-limit thermophoresis parameter is not dependent on the temperature gradient for |▿T| < 200 K/mm. The 20 K/mm case shows noticeably more statistical scatter than the 200 K/mm case because the departure from equilibrium is proportionally smaller. In the free-molecular limit (Kn _L → ∞) for the 20 K/mm case, the thermophoresis parameter is uniform across the domain and equal to the theoretical value of 0.75. At the higher gradient, the profile remains uniform but the value decreases slightly to 0.7366, in excellent agreement with Equation (19).

FIG. 5 Thermophoresis-parameter profiles for nitrogen for varying degrees of rarefaction at two temperature gradients, (a) 20 K/mm and (b) 200 K/mm. Dotted line is IPL–CE value for nitrogen.

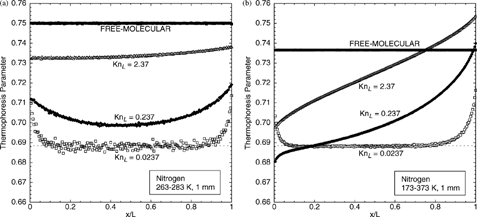
At intermediate Kn _L , the profiles for the two different temperature gradients differ markedly. At 20 K/mm, the thermophoresis parameter profiles for Kn _L = 0.237 and 2.37 are nearly constant (2%) across the domain and are completely bounded by the continuum and free-molecular limits; this trend also is seen in earlier work by Gallis et al. (2002b) with argon. Thus, for low-temperature gradients (heat flux), the thermophoresis-parameter profiles for rarefied flow differ by no more than 10% for any Kn _L . At 200 K/mm, however, the ξ profiles for intermediate Kn _L show noticeable variations (8%) across the domain and are not bounded by the continuum and free-molecular limits. Nevertheless, even for the highly noncontinuum case of a high heat flux in a low-pressure gas, variations in ξ are typically less than 10%, so the use of the first-approximation value ξ₁ in Equations (1) or (17) provides a comparable accuracy for estimating the thermophoretic force. If greater accuracy is required, calculations of the thermophoretic force in general-geometry, rarefied flows can be made using the DSMC–force-Green's-function method.

In a noncontinuum (rarefied) gas, it is recommended that the thermophoretic force be calculated as for a continuum gas, i.e., using Equation (1) for a single-species gas or Equation (17) for a gas mixture. The first-approximation thermophoresis coefficient ξ₁ is usually accurate enough for most applications, although errors can be on the order of 10%. If greater accuracy is needed, an accurate flow solution for the geometry under consideration is required. Analytical solutions for special situations (e.g., free-molecular flow in the parallel-wall geometry) or numerical solutions for more general situations (e.g., from DSMC) can provide this information.

Heat-Flux Effects

The simulations presented in this work are all performed with a rather large temperature gradient, 200 K/mm. Such large gradients are not easily sustained and are encountered only in highly energetic systems such as shocks or flames. Despite these large temperature gradients, simulations with continuum conditions predict thermophoresis parameters that are in excellent agreement with theoretical predictions based on CE (continuum) theory and with previous DSMC simulations (Gallis et al. 2002b, 2003b) for a much smaller temperature gradient, 20 K/mm. Recent work has shown that the CE approximation does begin to break down when the local Knudsen number is not small, e.g., for temperature gradients of 400 K/mm (Gallis et al. 2004). The previous section indicates that the effect of the temperature gradient on the thermophoresis parameter becomes more pronounced at lower pressures (higher Kn _L ). Nevertheless, the thermophoresis parameter usually remains within 10% of ξ₁.

The above recommendations can be applied with confidence for temperature gradients up to at least 200 K/mm, provided that the gas pressure is sufficiently high to ensure that the continuum limit is achieved away from walls.

CONCLUSIONS

A general, approximate expression is described that can be used to correlate the thermophoretic force acting on a free-molecular, motionless, spherical particle suspended in a quiescent gas supporting a temperature gradient. The thermophoretic force is equal to the product of the thermophoresis parameter, the gas-phase translational heat flux, the particle cross-sectional area, and the inverse of the mean molecular speed. Waldmann (1959) used CE theory to obtain the first-approximation value for the thermophoresis parameter, ξ₁ = 0.679061; the present numerical simulations suggest that this value can be used with acceptable accuracy to calculate the thermophoretic force on particles in monatomic and polyatomic gases and their mixtures. For particles suspended in continuum gases, the first-approximation value is accurate to within 4%. For single-species continuum gases, the use of the infinite-approximation value ξ_∞(Ω) can reduce this error to below 0.1%. Calculations of the thermophoresis parameter at low (20 K/mm) and high (200 K/mm) temperature gradients are indistinguishable in the continuum limit, suggesting that the present conclusions apply over a very wide range of heat flux. Although the above conclusions are based on a one-dimensional situation, they apply equally well in any continuum flow if the thermophoretic force and the translational heat flux are interpreted in the vector sense.

For continuum polyatomic gases and gas mixtures, the largest source of error in computing the thermophoretic force is probably the determination of the gas-phase translational heat flux. In some cases, the uncertainty in partitioning the heat flux may introduce errors of 10–20%, even when sophisticated property-estimation techniques are used. This error source remains large because the translational heat flux cannot be measured experimentally for polyatomic gases and mixtures thereof.

Somewhat larger deviations in the thermophoresis parameter are observed in the noncontinuum gas limit. In the Knudsen layer connecting a continuum CE gas with an adjoining wall, the thermophoresis parameter increases by 5% for fully accommodating walls and 10% for fully specular walls. For rarefied (low-pressure) conditions in the parallel-wall geometry, the thermophoresis parameter can be 10% larger than the first-approximation estimate; variations across the domain of 10% are also observed. Even for these highly nonequilibrium cases, however, the functional form of the thermophoretic force remains unchanged from the continuum form—only a relatively small adjustment (10%) in the thermophoresis parameter is needed. Unlike the analysis of the continuum limit, the calculations performed for rarefied conditions apply only for the onedimensional parallel-wall geometry.

All of the previous conclusions apply to the case of a motionless, spherical, free-molecular particle suspended in a quiescent gas. Prediction of the thermophoretic force becomes increasingly complicated for nonspherical particles or when the particle diameter becomes comparable to the gas-molecule mean free path. Particle drag arises if the particle or the gas are in relative motion, and diffusiophoretic forces must be considered when concentration gradients lead to net gas transport (see Waldmann and Schmidt 1964). However, these effects are independent of one another, and their contributions can be summed for low-speed flows with small fluxes.

NOMENCLATURE

	=	mean molecular speed, = (8k B T/πm)1/2(m/s)
p	=	mean molecular speed at the particle temperature, p = (8k B T p /πm)1/2(m/s)
c	=	gas molecule velocity relative to the particle, c = u – u p (m/s)
f[u]	=	molecular velocity distribution function (s3/m3)
f (0)	=	Maxwellian molecular velocity distribution function (s3/m3)
f tr	=	translational energy factor in thermal conductivity expression (—)
F th	=	thermophoretic force (N)
F δ	=	force Green's function (N)
K	=	gas thermal conductivity (W/(m·K))
k B	=	Boltzmann constant (1.380658 × 10−23 J/K)
Kn L	=	system Knudsen number, λ/L(—)
Kn R	=	particle Knudsen number, λ/R p (—)
L	=	distance between left and right walls (m)
m	=	gas molecule mass (kg)
n	=	gas number density (1/m3)
P	=	gas pressure (Pa)
q	=	gas heat flux vector (W/m2)
R p	=	particle radius (m)
T	=	gas temperature (K)
T c	=	cold-wall temperature (K)
T h	=	hot-wall temperature (K)
T p	=	particle temperature (K)
u	=	gas molecule velocity (m/s)
u	=	gas molecule speed (m/s)
u p	=	particle velocity (m/s)
x	=	distance from the left (cold) wall (m)
Z int	=	number of collisions required to exchange rotational and translational energy (—)

Greek Symbols

α	=	angular scattering parameter (—)
β	=	inverse of the most probable molecular speed (s/m)
Φ(1)	=	nonequilibrium part of Chapman-Enskog distribution (—)
λ	=	gas molecule mean free path (m)
μ	=	gas viscosity (kg/(m·s))
ρ	=	gas density (kg/m3)
Ω	=	viscosity temperature exponent (—)
ξ	=	thermophoresis parameter (—)
ζ int	=	number of molecular internal energy modes (—)

Superscripts

int	=	part of a quantity arising from the internal energy modes of a gas
tr	=	part of a quantity arising from the translational energy modes of a gas
(k)	=	order of term in Knudsen number

Subscripts

CE	=	value from Chapman-Enskog theory
FM	=	value for free-molecular flow
i	=	species number (—)
ref	=	value at reference conditions T ref = 273.15 K and P ref = 101,325 Pa
1	=	first-approximation value
∞	=	infinite-approximation value

Abbreviations

CE	=	Chapman-Enskog
DSMC	=	Direct Simulation Monte Carlo
MP	=	massively parallel
VSS	=	Variable Soft Sphere

Acknowledgments

This work was performed at Sandia National Laboratories. Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the United States Department of Energy under Contract DE-AC04-94AL85000.