A Moment Method for Evaporation Using a Logarithmic Size Distribution with the Smallest Size

A moment method of the log-normal distribution with the smallest size is applied to evaporation by newly introducing correction factors obtained from the error function. In this article, the improved moment method is tested for the evaporation, and is compared with the exact solutions calculated by the CIP semi-Lagrangian (CIP-SL) method. In small particle regime, the size distributions and the time histories of the total number and volume per unit volume are reproduced by the moment method for the evaporation near the smallest size. In large particle regime, however, the differences between the moment and exact solutions are larger with time, after the exact distribution spreads to the smallest size. This new moment solver can reproduce the evaporation near the smallest size even when large time step size is given, and thus is expected to be used for the parameterization of the evaporation of small particles in aerosol-transport model.

INTRODUCTION

Moment methods of the log-normal size distribution are used for simulations of aerosol dynamics. In these methods, the size distribution parameters (geometric mean size and standard deviation) can be directly obtained from the three moments of the size distribution in an entire size region from 0 to ∞ . Since the moment method is simple and efficient (e.g., Lee et al. 1984; Pratsinis 1988; Park et al. 1999), this method has been incorporated into aerosol-transport models as the parameterization of microphysical processes (e.g., Binkowski and Shankar 1995; Yamamoto and Tanaka 1998).

The moment method for evaporation has been developed by several researchers (e.g., Brock and Oates 1987; Seo and Brock 1990). Under the condition that the smallest volume v _S is sufficiently small, Brock and Oates (1987) applied the moment method to the semi-infinite domain from v _S to ∞ . The moments integrated from 0 to ∞ cannot be applied to the evaporation near v _S . Although the correct moment value should be calculated by using the error function in the case of v _S ≠ 0 (as will be discussed in this article), the error function has not been considered in previous studies of moment methods. At the present stage, under the condition that the peak volume of the log-normal size distribution is close to the smallest volume v _S , the moment method for the evaporation with the smallest size has not been in detail studied as yet. In this article, I propose a new moment method for the evaporation near v _S , in which the error function is utilized in order to accurately calculate the moments (the total number and volume of particles).

The qth order logarithmic distribution of Espensheid et al. (1964) is defined by

where N _T is the total particle number per unit volume over the entire size region from 0 to ∞, r is the particle radius, r _M is the modal mean radius, and σ _M is the standard deviation (e.g., Takahashi 2003). For any q, the integral of f _q (r) over the entire size region equals the total number N _T . The size distribution and its geometric mean radius depend on the order q. The generalized logarithmic function [1] can be rewritten as

where v is the particle volume and v _M is the modal mean volume. The log-normal distribution (LND), which has been widely used in aerosol sciences, is expressed as the function of q = −1. When zero is set as q, f _q (r) becomes the zeroth order logarithmic distribution (ZOLD). ZOLD has been sometimes assumed as the distribution function of particles in calculating radiative transfer and scattering (e.g., Toon and Pollack 1976; Quirantes and Delgado 1997; Quirantes et al. 1997), and has been also used as the fitting function of stratospheric aerosols (Gras and Laby 1981), cirrus clouds (Sassen et al. 1998), and particles in flame (Rumminger and Linteris 2002).

Instead of LND, the volume log-normal distribution (VLND) is also used in aerosol simulations (e.g., Seigneur et al. 1986; Zhang et al. 1999). The volume-weighted distribution is expressed as

in the qth order logarithmic distribution of Espensheid et al. (1964). When −4 is set as q, v× v ^{(q + 1)/3} becomes unity in [3]. Thus, VLND can be expressed by the −4th order logarithmic distribution f ₋₄(v);

where V _T is the total volume over the entire size region written as

In the same way as VLND, the mass-weighted log-normal distribution (MLND) is also easily described by

where ρ _P is the particle density, and [mtilde] _T is the total mass over the entire size region written as

In [4], [5], [6], [7], v _M and σ _M are the size parameters of the −4th order logarithmic distribution f ₋₄(v). As discussed in the previous section, since VLND and MLND can be easily obtained from [4], [5], [6], [7] using the −4th order logarithmic size parameters, f ₋₄(v) is available for the moment methods of VLND and MLND.

The modal mean volume obtained from the moments is different among LND, ZOLD, and VLND (MLND). In the moment method, the governing equations described by the size parameters (v _M and σ _M ) depend on the assumed distribution function. If the qth order logarithmic function of Espensheid et al. (1964) is introduced into the moment method, the moment equations of LND, ZOLD, VLND, and MLND can be unified to a same equation of the qth order logarithmic distribution. Thus, LND (q = −1), ZOLD (q = 0), VLND (q = −4), and MLND (q = −4) can be easily incorporated by appropriately choosing q in a same moment solver. Although Yamamoto (2004a) applied the qth order logarithmic function to the Brownian coagulation, other processes have not been considered as yet. In this study, the qth order logarithmic distribution of Espensheid et al. (1964) is utilized for evaporation process, in order to easily incorporate various logarithmic functions into the moment method.

The moment method in the semi-infinite domain from v _S to ∞ should be developed to simulate the evaporation near v _S . In this article, the moment equation with the smallest size is derived on the basis of the qth order logarithmic function. The improved moment method for the evaporation is tested, and is compared with the exact solutions obtained from the semi-Lagrangian solver (Yamamoto 2004b).

MOMENTS OF THE LOGARITHMIC FUNCTION WITH THE SMALLEST SIZE

The moments of the qth order logarithmic function [2] in the semi-infinite size region from v _S to ∞ are discussed in this section. The kth order moment is written as

where

The above relation is obtained from Appendix A. As v _S is approached to zero, the correction factor α _k becomes unity. Instead of the M _k integrated over the semi-infinite region from v _S to ∞, we introduce the moment m _k satisfying the following relation;

From [8] and [12], m _k is written as

where m ₀ = N _T . In this case, v _M and σ _M can be defined as follows (Yamamoto 2004a);

[14] and [15] are derived in Appendix B. Since the correction factor α _k is newly introduced into the moment method with the smallest size, the size parameters (v _M and σ _M ) can be easily obtained from the moments divided by α _k (m _k = M _k /α _k ) in the same way as previous moment method assuming the entire size region from 0 to ∞.

In previous moment methods, the moment integrals from 0 to v _S are remained as the errors of the total number (M ₀) and the total volume (M ₁). When v _M ∼ v _S , the errors cannot be neglected in the moment calculation. On the other hand, the new method can accurately calculate the moment integrated from v _S to ∞ on the assumption of the logarithmic size distribution ([8], [9], [10], [11]), since the moment errors due to the integrals from 0 to v _S are removed by introducing the correction factor α _k .

BASIC EQUATIONS

The governing equation is described by

where f(v, t) is the particle size distribution function and I(v) is defined as the evaporation rate of particle volume as follows:

(e.g., Seinfeld and Pandis 1998). The moment equation of [16] is written as,

The growth rate in small particle limit is proportional to v ^2/3, while the growth rate in small particle limit is proportional to v ^1/3 (e.g., Pratsinis 1988). Accordingly, the evaporation rates for the small and large particle regimes are

respectively. Here Kn is the Knudsen number obtained from the mean free path of the condensing vapor and the particle radius. In this method, the Kelvin effect (the correction of the evaporation rate by particle curvature) is not considered. The dependence of the evaporation rate on temperature is included in A _FM and A _CO . Instead of setting several parameters (such as temperature, saturation ratio, and so on), A _FM and A _CO are set as constant in the evaporation rate. From [18], [19], [20], the moment equations are rewritten as

in the small particle regime, and

in the large particle regime.

From the relation [12], since

[21] and [22] are

For the small particle regime, the evaporation moment equation is

where

Here the time differentiation operators are

For the large particle regime, the evaporation moment equation is

where

TESTS

To examine the validity of the above method, the numerical solutions are compared with the exact solutions calculated by the CIP semi-Lagrangian (CIP-SL) solver using cumulative number distribution (Yamamoto 2004b) on the basis of the cubic interpolated propagation (CIP) method (e.g., Yabe and Aoki 1991; Yabe et al. 2001). The initial and experimental conditions are listed in Tables 1 and 2. For Tests I–IV, the initial conditions are written as

and the numerical experiments are conducted using the moment method of f ₋₁(v). Here, N ₀ is the particle number (cm⁻³), D is the particle diameter (cm), D ₀ is the initial geometric mean diameter (cm), v ₀ is the initial geometric mean volume (cm³), and σ ₀ is the initial geometric standard deviation (−). For Tests V−VII, the initial conditions are written as

where

In these cases, the numerical experiments are conducted using the moment method of f _{− 4}(v). The initial standard deviation ranging from 1.2 to 1.8 has been given for nuclei mode in the simulations under the atmospheric condition (e.g., Seigneur et al. 1986; Zhang et al. 1999). Thus, the initial standard deviation is set at 1.2 and 1.8.

TABLE 1 Initial conditions

	q	D 0	σ0
	−	μm	−
Test I	−1	0.02	1.20	N 0 = 1.00 × 10^7 cm^− 3	LND
Test II	−1	0.02	1.80	N 0 = 1.00 × 10^7 cm^− 3	LND
Test III	−1	0.6	1.20	N 0 = 1.00 × 10^7 cm^− 3	LND
Test IV	−1	0.6	1.80	N 0 = 1.00 × 10^7 cm^− 3	LND
Test V	−4	0.02	1.20	V 0 = 1.00 μm^− 3 cm^− 3	VLND
Test VI	−4	0.02	1.80	V 0 = 1.00 μm^− 3 cm^− 3	VLND
Test VII	−4	0.04	2.10	V 0 = 1.00 μm^− 3 cm^− 3	VLND

TABLE 2 Experimental conditions

		dt	JMAX
	A	s	−
Test I	A FM = −1.00 × 10^− 8 in [19]	0.4	92
Test II	A FM = −1.00 × 10^− 8 in [19]	0.4	92
Test III	A CO = −1.00 × 10^− 13 in [20]	4.	112
Test IV	A CO = −1.00 × 10^− 13 in [20]	4.	112
Test V	A FM = −1.00 × 10^− 8 in [19]	0.4	92
Test VI	A FM = −1.00 × 10^− 8 in [19]	0.4	92
Test VII	A FM = −1.00 × 10^− 8 in [19]	0.4	92

The smallest diameter is set at 0.01 μ m for all calculations. In the moment method, the governing moment equations are solved by the fourth order Runge-Kutta method. In the CIP semi-Lagrangian method, the J-space grid system of a = 1.2, b = 1.0, r ₁ = 0.005 μ m (r ₁ is the radius of the particle of J = 1 in the J space) is utilized (Yamamoto 2004b).

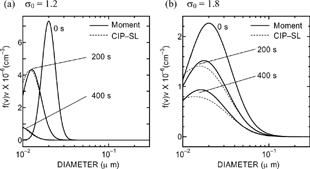
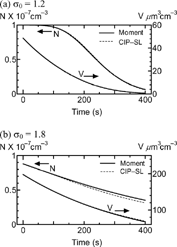
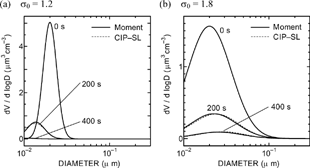
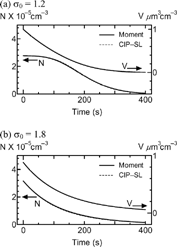
Figure 1 shows the size distributions in the small particle regime (Tests I and II). Equations [26], [27], [28], [29], [30], [31], [32] are solved in the moment method. As the initial geometric standard deviation σ ₀is wider, the difference of the size distribution from the exact solution (dashed curve) is larger. For small σ₀(= 1.2), the total volume per unit volume V rapidly decreases with time. When the particles spread to the smallest size (t ≈ 75 s), the total number per unit volume N begins to decrease with time in Figure 2a. Even when aerosols are almost evaporated at 400 s (Test I), the relative errors of N and V are 7.2% and 5.6%, respectively. For large σ₀(= 1.8), N and V are slowly decreased, since many particles remain in large size region. Although the relative error of N is large (12% at 400 s), the error of V is small (2.9%) in Figure 2b (Test II).

FIG. 1 Size distributions for (a) Test I and (b) Test II.

FIG. 2 Time histories of N and V for (a) Test I and (b) Test II.

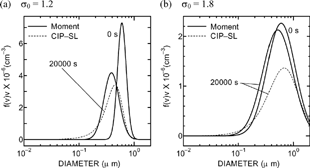
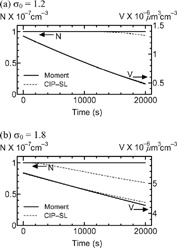
Figure 3 shows the size distributions in the large particle regime (Tests III and IV). Equations [34], [35], [36], [37], [38], [39], [40] are solved in the moment method. The distribution for the exact solution is deviated from the log-normal function. The asymmetry across the peak diameter (dashed curves in Figure 3) increases with time. After small particles reach to the smallest size, N decreases with time in the CIP-SL method. On the other hand, N is constant in the moment method, since the distribution does not spread to the smallest size. The differences between the moment and CIP-SL methods cannot be ignored in Figure 3. Since the removal of particles at the smallest size v _S is not simulated in the moment method for the large particle regime, the difference between the two methods is larger with time for N (Figure 4). Although the error of N is large (6.6% in Test III and 46% in Test IV at 20000 s) in the moment method, V has relatively small error (2.1% in Test III and 2.3% in Test IV at 20000 s) in comparison with N. The error of V is cancelled because of relatively high number concentration in smaller size region.

FIG. 3 Size distributions for (a) Test III and (b) Test IV.

FIG. 4 Time histories of N and V for (a) Test III and (b) Test IV.

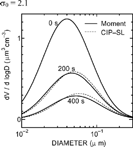
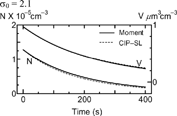
Figure 5 shows the volume distributions in the small particle regime (Tests V–VII). Equations [26], [27], [28], [29], [30], [31], [32] are solved in the moment method. In the cases of σ ₀ = 1.2 and 1.8, although the slight differences between the two methods appear in Figures 5a and 5b, the distributions are well reproduced. The time histories of N and V for the moment method are almost the same as those for the CIP-SL method in Figures 6a and 6b. The relative errors of N are 3.5% in Test V and 6.5% in Test VI at 400 s, and the errors of V are 3.2% in Test V and 3.9% in Test VI. Even when large σ ₀ (= 2.1) is initially set in Test VII, the differences between the two methods are not extraordinarily large in Figures 7 and 8 (14% for N and 4.9% for V at 400 s).

FIG. 5 Size distributions for (a) Test V and (b) Test VI.

FIG. 6 Time histories of N and V for (a) Test V and (b) Test VI.

FIG. 7 Size distributions for Test VII.

FIG. 8 Time histories of N and V for Test VII.

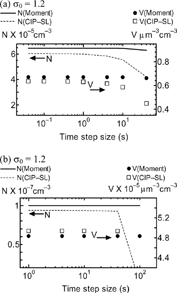
Figure 9 shows the sensitivities of N and V to time step size dt. For the CIP-SL method, the time step size smaller than 1 s is required to accurately calculate N and V in Test I, and the value smaller than 10 s is required in Test III. In the cases of large time step size, N and V become smaller, as dt is larger. On the other hand, N and V for the moment method are not dependent on dtin Figure 9. We can choose large time step size in the moment method.

FIG. 9 Sensitivities of N and V to time step size in (a) Test I and (b) Test III.

The computational cost was measured on our computer system (Intel Xeon processor of 1.7 GHz), in which Compaq Visual Fortran ver. 6.5. was installed on the Windows 2000 OS. In the moment calculation, the error function DERFC is called from the numerical library IMSL. The evaporation coefficients (β ^FM , β ^CO , γ ^FM , and γ ^CO ) are recalculated at each stage of the fourth order Runge-Kutta scheme with four stage time integration. In the CIP-SL calculation (Yamamoto 2004b), the integrals over the size region (such as the total volume, mass, and surface area per unit volume) are not calculated at each time step in this measurement. Thus the CIP-SL solver is simple and efficient. For a time-step size of 0.04 s in Test I, the CPU time of the Runge-Kutta moment method (5.16 × 10⁻¹ s) is longer than that of the CIP-SL (1.56 × 10⁻¹ s). The inefficiency of the moment method is caused by the inefficient time-integration scheme. Since the accuracy of the new moment method is mainly examined, the efficiency of time integration scheme is ignored in the present study and the program is not optimized. Instead of the fourth order Runge-Kutta scheme, other efficient schemes utilized for solving chemical reaction equation (e.g., Jacobson 1999) should be chosen in the moment parameterization of microphysical processes.

CONCLUSIONS

A moment method of the log-normal distribution with the smallest size v _S is developed by newly introducing correction factor α _k on the basis of mathematical relationships of [12], [13], [14], [15]. In this study, the qth order logarithmic function of Espensheid et al. (1964) and the error function are applied to the moment method for the evaporation in the semi-infinite domain from v _S to ∞ . Since LND, VLND, and ZOLD can be expressed by the qth order logarithmic distributions (f _{− 1}, vf _{− 4}, and f ₀, respectively), these distribution functions can be easily utilized by appropriately choosing q in a moment solver using f _q (v). In the same way as previous moment method in the entire domain from 0 to ∞, the simple moment equations derived in this study can be utilized for the evaporation under the condition of v _S ≠ 0.

The improved moment method is tested for the evaporation, and is compared with the exact solutions calculated by the CIP semi-Lagrangian (CIP-SL) method. In small particle regime, the size distributions for the evaporation are well reproduced, unless the initial standard deviation is large. In addition, we can reproduce the time histories of the total number and volume per unit volume, even when the size distribution is located near v _S . In large particle regime, however, the size distribution is different from the exact one. After the exact distribution reaches to the smallest size, the differences between the two methods increase with time.

The results for the moment method are not dependent on the time step size dt. For the evaporation near the smallest size v _S , although sufficiently small time step size is required in the CIP-SL simulation, large time step size can be set in the moment method.

As mentioned in the previous section, LND and VLND (also ZOLD) are easily utilized in a moment method of the qth order logarithmic distribution in the semi-infinite domain from v _S to ∞ . This new moment solver can reproduce the evaporation near the smallest size v _S even when large time step is given, and thus is expected to be used for the parameterization of the evaporation of small particles in aerosol-transport model.

APPENDIX A

The integrand of [8] is described as

From the following relations

[A1] is rewritten as

Thus the kth moment is

[A5] is rewritten as [8] through the following transformation;

APPENDIX B

v _M and σ _M can be derived from [13]. The first and second order moments are written as

The above equations are rewritten as

The distribution parameters (v _M and σ _M ) expressed by [14] and [15] can be obtained from [B3].