Piecewise Polynomial Solutions of Aerosol Dynamic Equation

This paper presents a discretization technique for particle dynamics equation based on piecewise continuous approximations of the solution. The growth terms are re-solved using a Discontinuous Galerkin approach, and the coagulation by a collocation approach. The method fits in the general framework recently proposed by the author. The discontinuous approximation allows better representations of distributions with sharp peaks. Numerical tests reveal that accurate solutions can be obtained with a very small number of size bins. An efficient software package AeroSolve which implements the proposed algorithms was developed.

1. INTRODUCTION

Particulate matter (aerosol) processes are “emerging as a new frontier” in environmental studies (Ramanathan et al. 1998). Aerosols negatively affect human health, reduce visibility, and modify warming through scattering and absorption of solar radiation.

To study accurately the effects of aerosols it is necessary to resolve aerosol number and mass distributions as a function of chemical composition and size. Treatment of aerosol processes leads to (at least) an order of magnitude increase in the overall computational time of an air quality model; this is mainly due to repeatedly solving the aerosol chemistry (or chemical equilibria) for different particle sizes. Therefore there is a clear need for rigorous, reliable and efficient computational techniques for aerosol simulations. In particular, there is a need for methods that accurately solve aerosol dynamics using a small number of size bins (discretization points), such that the time for aerosol chemistry calculations (which is proportional to the number of bins) is manageable.

Three major approaches are used to represent the size distribution of aerosols: continuous, discrete, and parameterized. In this paper we focus on continuous models (i.e., continuous size distributions and the general dynamic equations in continuous form). A survey of several popular numerical methods for particle dynamic equations is given in Zhang and Wexler (2002).

Several algorithms were proposed for solving coagulation. Jacobson (1999, Section 16) developed the semi-implicit discretization scheme which conserves volume and is unconditionally positive and stable. sandu (2002) we proposed a Newton-Cotes quadrature approach for solving the aerosol coagulation equation. Gelbard and Seinfeld (1978a), b, (1980) used a cubic spline approximation of the solution and orthogonal collocation. Cubic splines with collocation are also used by Tsang and Hippe (1988). Pilinis (1990) uses a Galerkin approach with linear basis functions. Sandu and Borden (2003) developed a general framework for the numerical treatment of aerosol dynamics that encompasses both Galerkin and collocation type methods.

The growth (condensation/evaporation) equation is discretized with numerical methods that solve the advection equation. CIT, UAM-AIM uses the Bott (1989) scheme. Kim and Seinfeld (1990) use a version of moving sectional method. In UAM-AERO and SAQM-AERO (Lurmann et al. 1997) a Godunov-type scheme is employed, with moving bin boundaries. Jacobson (1997b) allows the mean particle sizes to grow. Dhaniyala and Wexler (1996) proposed numerical schemes for condensation and evaporation of aerosols (Dhaniyala and Wexler 1996). Tsang and Hippe (1988) treat growth with a moving finite element technique. A Galerkin method with linear basis is employed by Pilinis (1990). Nguyen and Dabdub (2001) proposed a quintic spline approach and a semi-Lagrangian flux approach (2002). Different solutions of the growth equations were proposed in Binkowski and Shankar (1995), Kim and Seinfeld (1990), and Lurmann et al. (1997).

Comprehensive models were developed to treat aerosol dynamics in conjunction with other processes like chemistry, transport and radiation. Examples include the models of Jacobson (GATOR 1997b), Pandis, Wexler, and Seinfeld (1993), Meng, Dabdub, and Seinfeld (1998), Wexler, and co-workers (1994); and Zhang and Wexler (2002). Seinfeld and Turco (1995) use the stiff solver SMVGEAR to resolve growth and coagulation simultaneously. Coupled aerosol dynamics and chemistry models have been developed by Jacobson (1997b), (2002), who proposed a variety of numerical techniques to solve them.

In this paper we develop a family of methods for solving the aerosol dynamic equations following the general framework proposed by Sandu and Borden (2003) for the numerical treatment of aerosol dynamics. The new approach is based on piecewise polynomial approximations of the solution, and is motivated by the Discontinuous Galerkin method of Cockburn and colleagues (Cockburn, Lin, and Shu 1989; Cockburn 2003). What distinguishes this approach from the methods previously proposed is the fact that the particle size distribution is approximated by a discontinuous function. This allows a more accurate, less diffusive representation of particle distributions with sharp peaks when a small number of size bins is employed.

The discretization procedure is presented in the context of single component particle populations described by number densities; but it can be directly extended to mass or volume densities and multiple component particles.

The paper is organized as follows. Section 2 presents the particle dynamic equations. Section 3 develops the piecewise polynomial approach to the discretization of aerosol dynamic equation. Section 4 focuses on software aspects. Numerical results are presented in Section 5, and conclusions in Section 6.

2. THE GENERAL PARTICLE DYNAMIC EQUATION

In this paper the continuous particle size distributions are considered functions of particle volume (v) and time (t). For simplicity we consider single component particles, but the discretization techniques can be directly generalized to multiple components. The size distribution function (number density) of a family of particles will be denoted by n(v,t); the number of particles per unit volume of air with the volume between v and v + dv is n(v,t)dv (dv is an infinitesimal increment). This describes completely a population of single-component particles. Similar formulations can be given in terms of volume, surface, or mass densities (Pilinis 1990). The volume density is (v,t) = vn(v,t).

The aerosol population undergoes a series of physical and chemical transformations which lead to changes in number density according to Gelbard and Seinfeld(1978a)

The different terms in Equation (1) describe, in order, the modification in the number of particles due to growth, creation of particles of volume v by coagulation, loss of volume v particles due to coagulation, increase in particle number due to sources (nucleation, emissions) and decrease due to depositions. Here I(v,t) = dv/dt is the particle growth rate (due to condensation/evaporation) and β _v,w = β _w,v is the coagulation kernel function. This integro-differential equation is subject to a specified initial condition n ⁰(v), and to the boundary condition of no zero-volume particles.

In practice one assumes that the particle population has a nonzero minimal volume and a finite maximal volume, i.e. the dynamic equation is solved on a finite volume interval [V _min, V _max]. Note that this equation is no longer self-consistent; for V _min ≤ v < 2 V _min the upper integration limit is smaller than the lower integration limit in the positive coagulation term; we therefore introduce the convention that the positive coagulation term is zero whenever the upper limit is smaller than the lower integration limit.

Particle sizes span orders of magnitude, and to reveal the particle distribution logarithmic coordinates are popular. If we denote

the dynamic equation in number density formulation becomes

Complex models treat particles composed of multiple chemical constituents. Let v _q (v,t), q = 1,…;,m be the volume of the q-th chemical component in particles of volume v = ∑ _{q = 1} ^m v _q . The multi-component aerosol population is described by the individual volume densities of each constituent ^q (v,t) = v _q (v,t) n(v,t); the total volume of component q (per unit volume of air) contained in all particles having individual volumes between v and v+dv is ^q (v,t)dv. The total particle volume density is

The condensation/evaporation rate of species q is I ^q (v,t) = dv _q /dt, and the total particle growth rate is I = ∑ _{q = 1} ^m I ^q . It is customary to use the scaled growth rates

Under these transformations the volume densities of each constituent ^q (v,t), q = 1,…,m change according to Gelbard and Seinfeld (1978a) and Pilinis (1990)

These m integro-differential equations are coupled through the total volume density (v,t) and the chemical and thermodynamical transformation term K( ₁,…, _m ,t). The system (4) is subject to the initial and boundary conditions

In this paper we do not consider the chemical terms. In logarithmic coordinates (2) the dynamic Equations (4)–(5) becomes

with the initial and boundary conditions

Note that due to the finite size range an additional boundary condition for ^q (x = X _max,t) is necessary when simulating evaporation (growth with negative H).

3. PIECEWISE POLYNOMIAL DISCRETIZATIONS

Following the general approach we developed by Sandu and Borden (2003), the dynamic equation is solved by a semi-discretization in particle size followed by a time integration of the resulting system of ordinary differential equations. In this section we briefly outline the application of this discretization framework for piecewise polynomial basis.

For simplicity of the presentation in this section we discuss the discretization of the dynamic Equation (3) in the volume density, logarithmic formulation. We emphasize however that the discretization method is very general and can be easily applied to volume and mass densities as well as multiple components.

The finite log volume interval is divided into s bins I _j = [X _j ^B ,X _{j + 1} ^B ]. The point X _j ^B is the boundary point between the bins I _{j − 1} and I _j , with the endpoints X ₁ ^B = X _min and X _{s + 1} ^B = X _min. The center of bin I _j is denoted by X _j . The solution is represented by a k-th order polynomial inside each bin I _j . The polynomials in different bins do not need to satisfy any continuity conditions across bin boundaries, therefore this representation of the solution is only piecewise continuous.

The polynomial representation inside each bin is written in terms of the orthogonal Lagrange basis polynomials. The set of Lagrange polynomials up to order 3 defined on [−1,1] reads

Inside bin I _j the solution is represented as

If we use s bins and polynomials of order k then the total number of degrees of freedom used to represent the solution is ndof = s × (k+1). These degrees of freedom are the solution coefficients u _j ^ℓ(t) in each bin.

At the initial moment the continuous (in size) distribution (x,t ⁰) is available. The discrete solution coefficients are obtained by projecting the solution onto the discrete space,

In what follows for simplicity we will use the single index notation; the vector u of discrete coefficients and the family {φ _i } _i of basis functions have ndof components. The bin component u _j ^ℓ becomes u _{(j − 1) × s + ℓ + 1} in the single index notation, and similarly for the basis functions.

For multiple chemical components the volume density distribution of component q, and the total volume density distribution are represented in discrete form as

3.1. Coagulation

To obtain a discrete form of the coagulation equation we consider the set of k + 1 Gauss points inside each bin as collocation points. This results in a set of ndof collocation points {Z _j }_{1 ≤ j ≤ ndof}. The piecewise polynomial solution (Equation 8) is inserted into Equation (6). The resulting relation is evaluated at the collocation points {Z _j }_{1 ≤ j ≤ ndof}. This gives a set of ndof ordinary differential equations to solve for the time evolution of the ndof parameters.

As shown by Sandu and Borden (2003) the collocation approach leads to the following discrete form of the coagulation equation

with the mass matrix

and the coagulation tensor

In the Equation (11)

Volume Conservation

The method (Equation 11) is an approximation of the continuous equation, which is not volume conservative. The continuous coagulation equation is volume conservative for an infinite volume interval. If coagulation produces particles of volume greater than the largest bin size, this volume is lost. If we assign this volume to bin s (i.e., the last bin contains all particles of volume larger than X _ndof ^B ) the method becomes globally volume conservative. The total volume of the discrete distribution is

To preserve this quantity its time derivative must equal zero. Summing for all q components in Equation (11) and left-multiplying by m ^T leads to

In the above we denote c ^T = m ^T A ⁻¹. A sufficient condition for total volume conservation can be obtained, for example, by redefining the coagulation tensor sections B ^{(s − 1)(k + 1) + i} (which correspond to the i-th polynomial coefficient of the density in the last bin) as

This condition can be interpreted as having all particles of volumes larger than X _ndof ^B mapped onto the last bin.

3.2. Growth

The growth part of Equation (6) has the form of a conservation law with flux function f and source terms

This equation is to be solved subject to an initial distribution and the boundary condition of no zero-sized particles (Seinfeld and Pandis 1997, Section 12). The equations for different components q are coupled through the first source term, and possibly through the growth rates H ^q if they depend on volume densities.

The discretization of the source terms will be discussed in Section 3.3. The discretization of the (homogeneous) conservation law is based on the Discontinuous Galerkin formulation of Cockburn et al. (Cockburn, Lin, and Shu 1989; Cockburn 2003). For bin I _j and component of order ℓ

Since the solution is discontinuous across the bin boundaries, the flux f across the bin boundary is not defined, and is replaced by a numerical flux h which depends on the values in the left and right bins.

For the Godunov formulation used in this paper the numerical flux is given by the flux function evaluated at two sides of the boundary:

Equation (13) can be written in a compact form as

where the first term represents the flux function integral over each bin, and the second the nonlinear numerical flux terms.

Note that in order to obtain total variation diminishing solutions limiting of the slopes must be applied. The reader should consult Cockburn (2003) for more details. In the numerical experiments presented in this paper we do not use slope limiting.

3.3. Sources and Sinks

The sources and sinks equation

can be discretized (in the Galerkin approach) as

Here S ^q is the ndof-vector with components S ^q _i and R(t) is the ndof-dimensional matrix given by

The discrete sources and sinks equation using the collocation approach reads

3.4. Chemistry

The chemical reaction terms in Equation (4)

are evaluated on the discretized volume density distributions (10) leading to

The chemical Equation (16) can be discretized using the collocation approach to obtain

Note that the right hand side vector requires ndof evaluations of the chemical rates K ^q .

Similarly, Equation (16) can be discretized in the Galerkin framework to obtain

Here ℓ is the index of the bin where the basis function φ _j is nonzero. The number of evaluations of chemical rates K ^q depends on the number of quadrature points used to compute the integrals in Equation (17). A particularly attractive approach is a discretization of the volume densities with piecewise linear polynomials, and an evaluation of the integrals in Equation (17) by applying the midpoint rule in each of the size bins. This approach provides a second order accurate discretization in particle size with only (s = ndof/2) evaluations of the chemical rates (i.e., one evaluation of rates per size bin).

3.5. Simultaneous Discretization of the Dynamic Equations

A coupled solution of coagulation, growth, nucleation, emissions and deposition is of interest; it will, for example, better capture the competition between nucleation of new particles and condensation on existing particles for gas-to-particle conversion (Zhang et al. 1999). Combining Equations (11), (14), (15), and (17) leads to the coupled system of ordinary differential equations

Note that the same A,B,G are used for all components q.

3.6. Time Stepping

The system in Equation (18) can be solved by any appropriate time-stepping method. The system has a particular form: the growth term is linear, while the coagulation term is bilinear. In Sandu and Borden (2003) we combined the linearized backward Euler scheme for coagulation with Crank-Nicholson for growth and sources/sinks to achieve second order time accuracy, and unconditional stability of the coagulation term. In this paper we consider the explicit, strongly stable second order Runge–Kutta method

This method is appropriate for the integration of the hyperbolic growth Equation (8). Strongly stable third and higher order Runge–Kutta methods are also available.

4. SOFTWARE AVAILABILITY AND IMPLEMENTATION ASPECTS

To make the code efficient a careful implementation of the method is important. The integrals are obtained numerically using a 4-point Gauss quadrature inside each bin. The sparsity in the tensor B is exploited in two ways. First, the finite support of all basis functions make a large number of entries of B equal to zero. We predict the zero terms based on the analysis of the function support and only compute the integrals for those terms that are nonzero. Second, the tensor is stored in a sparse format and all tensor multiplication operations are done efficiently in this format. In addition to the sparsity of B, the mass matrix A is block diagonal (with each block corresponding to each bin; the dimension of the blocks is k + 1, with k the polynomial order in the discretization). The sparse implementation leads to an order of magnitude decrease in the total cpu time when compared to the non-sparse implementation.

The numerical algorithms described in this paper have been implemented in a software library AeroSolve (Sandu 2003). The software is freely available and can be obtained from the web address http://people.cs.vt.edu/~asandu/Software/AeroSolve.

5. NUMERICAL RESULTS

Problem A

In this test problem we solve the growth equation for multiple components in the mass density formulation

where p ^q (μ,t) is the mass density, H ^q (μ,t) the growth rate of component q, and

The test problem considered here has m = 2 chemical components. The initial distributions are shown in Figure 1 (upper panels) and are obtained from the superposition of 3 lognormal distributions (modeling the nucleation, accumulation, and correlation modes). The first species condenses on the particle and the second species evaporates at the rates

This test problem admits the analytical solution

We solve the test problem on the interval t ⁰ = 0, t ^F = 6 hours.

FIG. 1 The solutions of the growth equation with Discontinuous Galerkin and Bott methods for the first component (left) and second component (right). Initial concentrations (upper plots), linear discretizations (middle plots), and cubic discretizations (lower plots). For all simulations the Discontinuous Galerkin solution is faster and more accurate.

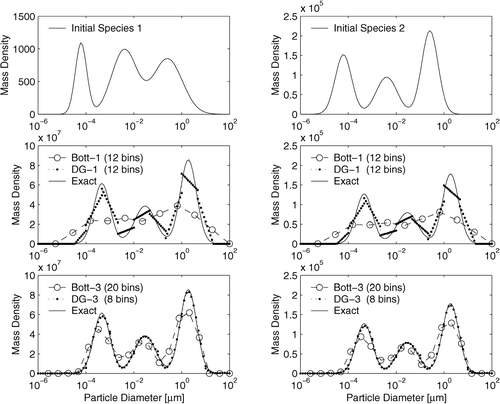
The growth equation is solved with Discontinuous Galerkin (DG) and with the widely used Bott (1989) method, and the results are shown in Figure 1 (bottom panels). Time stepping is performed using the second order Runge–Kutta method (19) with the very small time step 3.6 seconds. This step is two orders of magnitude smaller than necessary for the equation but allows us to measure more accurately the relative cpu times of the two discretizations.

The middle Figure 1 plots show the low accuracy numerical solutions obtained with piecewise linear DG with 12 bins and first order Bott algorithm with 12 bins. The DG solution takes about two thirds of the CPU time required by the Bott solution (on a Pentium M processor, 1.7 MHz with the Intel Fortran90 compiler), while the Bott solution takes 0.44 seconds. The DG solution is not only more accurate but is faster as well.

The lower Figure 1 plots show the higher accuracy numerical solutions obtained with piecewise cubic DG with 8 bins and third order Bott with 20 bins. The cpu time of the DG solution is about half the CPU time of the Bott solution. Again the DG solution is less expensive and more accurate.

Problem B

For the numerical experiments we first consider the test problem from Gelbard and Seinfeld (1978b), which admits an analytical solution. Let N _t be the total initial number of particles and V _m the mean initial volume. The initial number distribution is exponential, the coagulation rate is constant, and the growth rate is linear with the volume:

The analytical solution (see Gelbard and Seinfeld 1978b) is

We solve the dynamic equation for β _o = 2.166 × 10⁻⁶ cm³h⁻¹ particles⁻¹, σ _o = 0.02 h⁻¹, N _t = 10⁴ particles, V _m = 0.03 μm³. The values are chosen such that coagulation and growth have effects of comparable magnitude.

The equation was solved on the time interval [t _initial = 0, t _final = 48 h] with a small time step Δ t = 6 min; the timestep was chosen such that the time discretization errors are small compared to the size discretization errors. The volume interval is V _min = 10⁻³ to V _max = 1 μm³. The use of a finite volume interval introduces errors in the coagulation right-hand-side. The numerical solutions will be expected to recover the analytical solution (only) within this error margin.

The accuracy of the numerical solutions at the final time is measured against the analytical (or reference) solution by the root-mean-square (RMS) error norm

The threshold th = 500 particles cm⁻³ μm⁻³ makes the error indicator to ignore the smallest part of the number distribution.

To compare the relative merits of different discretization orders we first show the solutions obtained with ndof = 12 degrees of freedom. There are 12 bins for piecewise constant polynomials, 6 bins for piecewise linear polynomials, 4 bins for piecewise quadratic, and only 3 bins for the piecewise cubic discretization.

Figure 2 shows the computed solution for the growth equation, Figure 3 the solution for the coagulation equation, and Figure 4 the solution for the coupled coagulation and growth equation. For plotting purposes the values of the piecewise polynomial computed solution is shown at 10 different point inside each bin (and plotted with squares). The piecewise character of the solution is clearly visible for the zeroth order discretization, but for higher order polynomials the solutions are relatively smooth.

FIG. 2 The solutions for the growth equation obtained with ndof = 12 degrees of freedom, different discretization orders. The number of bins is 12 (order 0), 6 (order 1), 4 (order 2), and 3 (order 3). The numerical solution is plotted at 10 points (squares) in each bin. Higher order discretizations are very accurate despite using a small number of bins.

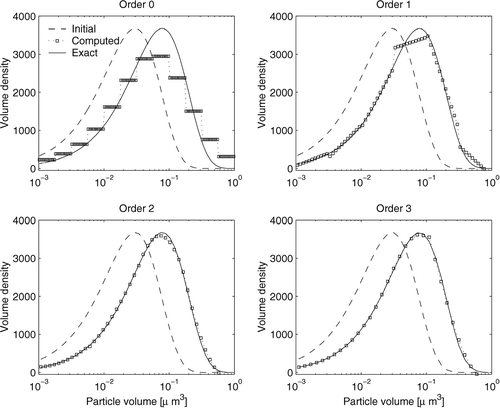
FIG. 3 The solutions for the coagulation equation obtained with ndof = 12 degrees of freedom, different discretizations. The number of bins is 12 (order 0), 6 (order 1), 4 (order 2), and 3 (order 3). The numerical solution is plotted at 10 points (squares) in each bin. Higher order discretizations are very accurate despite using a small number of bins.

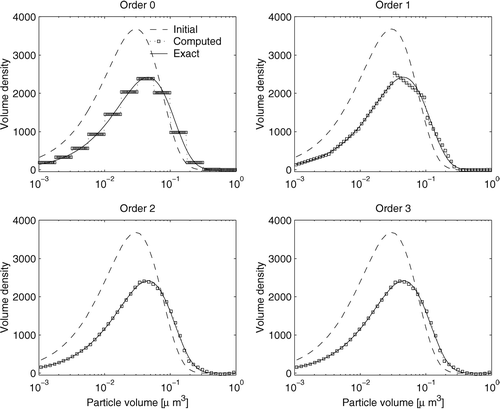
FIG. 4 The solutions for the full (coagulation and growth) equation obtained with ndof = 12 degrees of freedom, different discretizations. The number of bins is 12 (order 0), 6 (order 1), 4 (order 2), and 3 (order 3). The numerical solution is plotted at 10 points (squares) in each bin. Higher order discretizations are very accurate despite using a small number of bins.

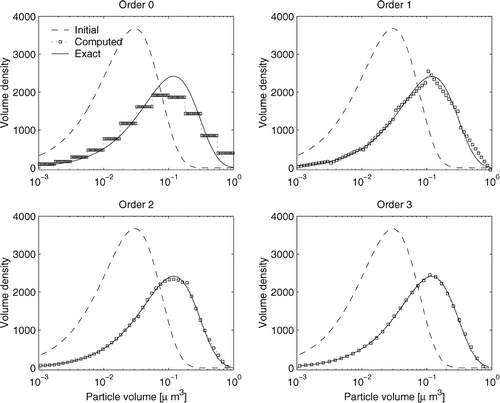
All discretizations compute accurately the final solution for all cases (growth only, coagulation only, and coagulation plus growth). The second and third order numerical solutions are hardly distinguishable from the exact solution, even if they only use 4, and respectively 3 bins.

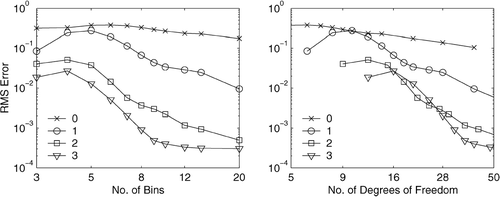
The decrease in numerical error with increased number of bins for the full coagulation and growth solution is shown in Figure 5 left. The slopes at which the errors decrease indicate different discretization orders. To compare the relative performance of different polynomial orders the errors are plotted against the number of degrees of freedom in Figure 5 right. We see that for equal computational work the higher order discretizations produce more accurate solutions; in particular the piecewise quadratic discretization seems to be well suited for solving aerosol dynamics.

FIG. 5 Errors in the numerical solutions of the full (coagulation and growth) equation. The errors are plotted against the number of bins (left) and against the number of degrees of freedom (right).

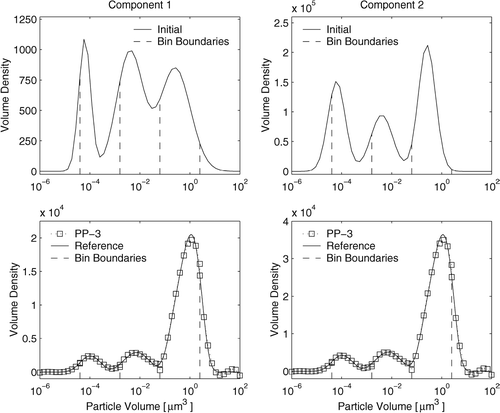
Problem C

This test problem solves the coagulation and growth of two-component aerosol in the volume density formulation (Equation 6). The initial density is the sum of three log-normal distributions and is similar to the one used in test problem A (but with a different interpretation of the profile). The coagulation kernel is constant, β _o = 2.166 × 10⁻⁶ cm³h⁻¹particles⁻¹, and the normalized growth rates for the two species are H ¹ = 0.1 h⁻¹ and H ² = − 0.04 h⁻¹. The simulation time interval is 4 hours. The initial and the final distributions are shown in Figure 6. The three-peak profile is a numerically challenging test, nevertheless the third order piecewise polynomial discretization gives a very accurate solution with only 5 size bins. The rms error (20) for a threshold th = 100 particles cm⁻³ μm⁻³ is 7.2 × 10⁻⁴ for the first component and 6.5 × 10⁻⁴ for the second component.

FIG. 6 The evolution of the 2-species aerosol (test problem C). Top panels: the initial distribution. Bottom panels: the final distribution computed with the third order piecewise polynomial discretization and only 5 bins is very accurate (error ∼10⁻⁴).

6. CONCLUSIONS

Simulation of aerosols plays a significant role in air pollution modeling. For a correct representation of particles in the atmosphere one needs to accurately solve for the size distribution of particle populations.

In this paper we proposed a family of discretization methods for the aerosol dynamic equation based on piecewise polynomial discretizations of the particle size distribution. The distinguishing characteristic of this approach is the approximation of the solution by a discontinuous function, which allows an accurate representation of distributions with sharp peaks with only a small number of size bins.

The growth term is discretized using the Discontinuous Galerkin approach, while the coagulation term is discretized using a collocation approach. The performance of the methods is illustrated on two test problems which admit analytical solutions. Problem A has a smooth, exponential volume density which undergoes coagulation and growth. Problem B is a growth problem with two chemical components having lognormal mass densities.

The piecewise polynomial discretization has a number of attractive features, which make it a good candidate for use in air quality simulations:

•	The method allows a consistent and simultaneous treatment of coagulation, growth, sources, and sinks;
•	Accurate solutions are obtained with a very small number of bins. Increased accuracy is possible for a fixed number of bins by increasing the order of polynomial approximations, i.e., by increasing the number of degrees of freedom inside each bin;
•	For the single component coagulation test the piecewise polynomial discretization of coagulation has a comparable performance with the semi-implicit method for low accuracy solutions, and is more efficient for high accuracy. For the multiple component growth test problem the piecewise polynomial—discontinuous Galerkin discretization (without limiting) is more efficient than the Bott method.

While the piecewise quadratic approximation seems to offer the best accuracy work compromise, the piecewise linear discretization is especially attractive for three dimensional models where particle dynamics is coupled with chemistry and thermodynamics; in this case a midpoint evaluation of the integral terms can be used to couple aerosol dynamics and chemistry terms, therefore requiring only one evaluation of the chemical terms per bin.

Several numerical methods (like Bott for growth and semi-implicit for coagulation processes) have been extensively tested in three-dimensional simulations and have been proved to be stable, accurate, and efficient. While the proposed family of methods is promising, a complete assessment of its performance can only be done within a three-dimensional model context. Future work is needed to assess the usefulness of the piecewise polynomial discretization for practical air quality modeling.

Acknowledgments

This work was supported by NSF through CAREER award ACI-0413872 and NSF ITR award AP&IM 0205198. Part of the implementation originates from the M.S. thesis work of C. Borden at Michigan Technological University. The author thanks M. Z. Jacobson for providing the original implementation of the semi-implicit method.