Evaluation of the Exact Coagulation Kernel under Simultaneous Brownian Motion and Gravitational Settling

Abstract

The analytic representation of the exact coagulation kernel for combined Brownian motion and gravitational settling entails an infinite sum of ratios of modified Bessel functions. Heretofore, the evaluation of this sum has been limited to relatively small arguments due to computational difficulties, hindering the numerical solution of the general dynamic equation in computational aerosol transport simulations. An approximation and an asymptotic extension have been available, but their accuracy for large arguments has not been established, and they have been shown to lead to numerical diffusion and oscillation. Using multiple-precision arithmetic, exact values for the kernel are presented in this paper for large arguments, and it is shown that both the asymptotic and approximating formulae provide a poor fit in the range of practical interest. Based on the results, the asymptotic formula is rectified and it is shown that the approximation is no longer needed. Practical formulae are given to facilitate rapid numerical evaluation of the exact kernel for all arguments.

1. Introduction

In the case of a multimodal particle size distribution where an appreciable quantity of particles appears across both ends of the spectrum, coagulation by both gravitational settling and Brownian motion may be important. The usual handling of simultaneous Brownian and gravitational coagulation is the addition of the individual collision rates, a.k.a. coagulation kernels, as shown in Equation (1), referred to as sum kernel. For binary collisions of particles with radii a and b, the first term, K _B , represents the kernel due to Brownian motion, while the second term, K _G , is the kernel of gravitational settling:

T, k, and μ are the absolute temperature, Boltzmann's constant, and the dynamic viscosity of the fluid, respectively. Despite that inter-particle and fluid forces are neglected here, Equation (1) often appears in this form in the numerical solutions of the dynamic aerosol transport equation, particularly in cases when such forces have second-order importance. The sum kernel does not account for the enhanced collision rate due to diffusive processes in the wake of falling particles and due to the relative motion of particles. Hence, the exact kernel, K _BG , is greater than the sum kernel, K _B + K _G . In considering these effects, Simons and coworkers (1986) rigorously derived the rate of deposition of particles having a radius b onto a particle of radius a as a result of simultaneous Brownian diffusion and relative velocity due to gravitational settling. A correction factor for the sum kernel was introduced, γ, equivalent to the ratio of the true kernel and the sum kernel, K _BG = γ (K _B + K _G ), in terms of an infinite sum of ratios of modified Bessel functions I and K of half integer order, as follows:

Here, β is a dimensionless quantity which shows the relative importance of diffusion versus gravitational settling:

where V is the relative velocity, derived elsewhere (Batchelor 1982), and D _B is the mutual diffusion coefficient in the classical sense (D _B = D _a + D _b ), which when substituted, yield the right hand side of the above equation. Other parameters have their usual meaning. The Cunningham slip correction factor, which is applied to the collision kernels to extend their validity from the continuum regime to the free molecular flow regime, can be readily incorporated in Equations (1) and (3). Further, the formalism used throughout this article is capable of including terms accounting for interparticle forces.

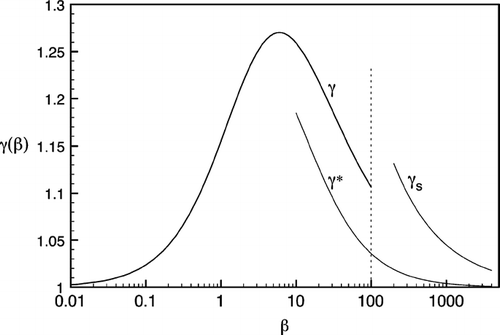
A graphical representation of Equation (2) is shown in Figure 1 up to β = 100. For arguments β > 100, γ (β) is a slowly varying function that gradually smoothes into unity. But just how gradually?, and with what function values?, have been unresolved questions since the derivation of this formula twenty years ago, due to heretofore insurmountable numerical difficulties in evaluating the function above β = 100. An asymptotic extension and an analytical approximation were obtained by Simons et al. (1986) and Williams (1988), bracketing the values of the function (shown in Figure 1), but their error rate has not been established because the function values have been unknown beyond β = 100. This has been a long-standing problem in computational aerosol transport modeling, particularly in situations when the combined Brownian and gravitational settling dominates the coagulation regime. If during the course of numerically solving the dynamic aerosol distribution equation the true γ (β) function values are used up to β = 100, switching to one of the approximations beyond this argument gives rise to a discontinuity in the iterative solution, which leads to numerical instabilities, e.g., oscillations. Such discontinuity exists at all arguments of the function up to impractically high values.

FIG. 1 The γ (β) function and its approximations. Solid line is the exact function, Equation (2), as evaluated by Simons et al. for β ≤ 100; the two thin lines are the approximations: γ *, Equation (4) (Williams 1988), and the asymptotic formula γ _s , Equation (5), with C = 4.496 (Simons et al. 1986).

Therefore, in order to assure unconditional convergence, at least in this regard, correct and accurate evaluation of Equation (2) is essential. Using a 64-bit computer platform and multiple precision arithmetic, the γ (β) function has been evaluated up to an argument of β = 20,000 and reported here. It was found that Simons' asymptotic expression overpredicts the function, which is rectified here using the presented results by proposing an amended expression. In addition, practical formulae are given in order to facilitate rapid numerical evaluation of the kernel for all arguments without the need for approximations.

2. Background and significance

For diffusion-dominated regimes β is small, whereas in cases when gravitational settling has higher importance (as measured by the relative particle velocity), it is large. For example, in the case when ρ /T = 3.3, particle sizes of a = 0.5 μ m and b = 1.0 μ m give β = 5.6, while a = 1.0 μ m and b = 5.0 μ m give β = 1190.5. Note that a large β does not necessarily indicate a large absolute size for one of the coagulating particles. Because of the absolute value in Equation (3), it is the relative discrepancy in particle sizes that has importance, and therefore β is indicative of the relative dominance of Brownian versus gravitational coagulation. Although this includes the asymptotic case when one of the particles is so large as the ultra-Stokes drag is non-negligible, this paper does not examine that condition. Thus it is assumed that the flow regime is such that Equations (1) and (2) provide a reasonable description of coagulation, subject to the limitations set forth above.

When Brownian coagulation dominates (K _B ≫ K _G ), there is a diffusive influx of smaller particles into the region around the larger particles undergoing sedimentation. Using an expansion in small values of β, Simons et al. (1986) showed that this effect can be considered as a source term for diffusive flow, and the contribution of the gravitational settling to the total coagulation kernel is twice compared to what the sum kernel predicts (K _B + 2 K _G ). As the relative dominance of Brownian coagulation decreases, β increases, and at β = 6 γ has a local maximum of ∼ 1.27. The value of γ gradually decreases thereafter as β further increases. The graphical form of γ (β) is reminiscent to a lognormal function, albeit it is asymmetrical, having a terminus at β = 0, and a tail asymptotically approaching γ = 1 as β → ∞, shown in Figure 1. The largest discrepancy between the exact and the sum kernels occurs at particle diameters for which β ≈ 6. Figure 2 shows the bounds of β, as function of particle radii, at which γ is greater than 1.25 and 1.1: The area bound by the β = 0.55 and β = 100 lines represent (a, b) pairs for which γ exceeds 1.1, while in the area between β = 3.5 and β = 12 γ > 1.25. Because the falling large particle creates a depleted region in its immediate vicinity, the maximum in the function γ (β) occurs at relative particle sizes where the additional flux of small particles into the region of the falling large particle is the highest.

FIG. 2 Parametric plot of β (a,b). For 3.5 ≤ β ≤ 12, γ > 1.25. For 0.55 ≤ β ≤ 100, γ > 1.10. Because of the absolute value in the function [3], the plot is symmetric to the a = b line.

In gravitational settling dominated regimes, the values of the function γ (β) are not known with sufficient accuracy for βs where the discrepancy between the sum kernel and the true kernel is still non-negligible. This occurs at values of β ≥ 100 where the numerical solution of the dynamic equation of aerosol transport can develop oscillations if γ is allowed to drop to 1.0, i.e., if the discrepancy between the sum kernel and the true kernel is ignored. Because coagulation is described by a non-linear integro-differential equation, its solution can lead to numerical instability for discontinuous γ. Simons et al. (1986) successfully computed the γ values up to β = 100. However, beyond that value an asymptotic estimate has been needed thus far (Simons et al. 1986; Williams and Loyalka 1991), as practical evaluation of Equation (2) becomes increasingly difficult when relying on computations with a finite number of digits. The sum shown in Equation (2) has a gradually slowing convergence for large orders, n. For each successive ratio of the Bessel functions, the difference | ∑ I _{ν + 1}/K _{ν + 1} – ∑ I _ν/K _ν|, where ν =1/2 ⃛−n + 1/2, becomes progressively smaller, while I _ν/K _ν precipitously decreases for large arguments (Figure 3). For example, for n = 4000, I _{n + 1/2}(1000) = O (E-2284) and K _{n + 1/2}(1000) = O (E+2281). Simons' asymptotic estimate, however, suffers from the fact that it does not provide a smooth interface with the exact γ, thus it, too, gives rise to a discontinuity.

FIG. 3 The logarithm of the ratio of the modified Bessel functions I _{n + 1/2}/K _{n + 1/2} for selected fixed arguments as function of the order n. Note that the logarithmic scale is in addition to the function evaluation ln (I _{n + 1/2}/K _{n + 1/2}).

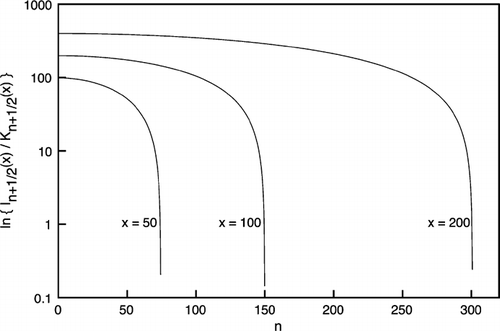
This presents a predicament because for large arguments (β > 100) the number of terms needed for convergence in Equation (2) progressively increases. Thus, the larger the argument, the higher order functions must be evaluated. Simultaneously, the values of the modified Bessel functions I and K rapidly increase and decrease, respectively, for increasing arguments. Owing to the finite size of the computer's internal number representation, at large arguments and large orders a disastrous loss of digits occurs leading to cancellations, and this sum becomes very difficult to evaluate by conventional means. For example, quadruple precision computations on a 64-bit platform can yield reliable results only up to β = 100 without employing asymptotic approximations. Accurate evaluation of the infinite sum of Equation (2) for β > 100 poses considerable difficulties even on today's high-performance computing platforms.

Williams and Loyalka (1991, p. 198) give an approximate formula, γ *(β), for γ in terms of the second-order exponential integral, which does not entail the evaluation of an infinite sum:

This approximation is obtained from the solution of the diffusion equation using statistical arguments for homogeneous turbulence (Williams 1988) following the method of Saffman and Turner (1956). The latter provides expressions for turbulent coagulations based on fluctuation theory via a probability density function written for the relative particle velocities. Although according to Williams (1988), Equation (4) is “less satisfactory,” it gives a lower bounding estimate of γ for all arguments above β = 10 and could be used as a quick analytical approximation (albeit poor) when the exact function values are unknown. However, using the results presented in this paper this formula is no longer necessary to estimate γ .

Simons et al. (1986) performed an asymptotic analysis of the expression (2) for very large arguments, as mentioned above, and found that

For the trial function employed in the asymptotic analysis, C = 4.496 was used. Although the latter formula gives a smaller absolute discrepancy than the approximate Equation (4), it still gives rise to a discontinuity when one switches from the exact formula (Equation [2]) or its approximation (Equation [4]) to the asymptotic representation for all arguments of practical significance (β ≤ 20 000). For example, γ (300) = 1.05737, γ*(300) = 1.01302, γ _s (300) = 1.10033, which represents a 77% and 74% discrepancy between the exact value of γ −1 and the results using the approximate and asymptotic formulas, respectively. For β = 20 000, the discrepancy between γ −1 and γ _s −1 is still about 50%. Note that γ −1 is used here, because it is the deviation from the sum kernel, which is used as a metric in evaluating weather the sum kernel gives a sufficiently accurate representation of the coagulation for the purpose of solving the general dynamic equation. Figure 1 shows the approximation Equation (4) and the asymptotic formula (5) together with the exact value of γ. This paper will show that the coefficient C = 4.496 in Equation (5) is incorrect in the range ∼ 1000 ≤ β ≤ 20,000, and that C = 2.843 gives a significantly better approximation.

The analytical representation of the sum kernel is possible only when inter-particle forces, such as electrostatic and van der Waals, are neglected. Further, the particle collision efficiency, which is the ratio of the coagulation kernel with fluid effects to that without, is not included in the above development, although the formalism is capable of accepting it. Williams (1988) derived a formula for γ in which a correction for collision efficiency is included. Surprisingly, due to an asymptotic form of the radial particle velocities which entails easily integrable rational polynomials, numerical evaluation of γ with modification for fluid effects is simpler than without. However, the results thus obtained are not accurate due to the asymptotic approximation mentioned. Williams' unified theory of aerosol coagulation (1988) gives reliable ways to compute the simultaneous coagulation kernels for various flow regimes, except it does not provide satisfactory accuracy for the combined Brownian and gravitational coagulation kernel for β ≥ 100, which hinders the efficient numerical solution of the general dynamic aerosol equation in computational aerosol transport problems. This limitation is resolved in this article.

3. Methods and results

Because of the large precision required for the evaluation of the sum in Equation (2), the computational method must utilize multiple-precision arithmetic, which extends the computer's machine precision beyond what its 32-or 64-bit (or higher) platform would permit. There are numerous computer programs available for the evaluation of the modified spherical Bessel functions I and K, which can be adapted to multiple or extended precision arithmetic. Most notably, Cody's algorithm to compute sequences of modified Bessel functions (Cody 1983, with modifications in 1989, and Cody 1993) implements Miller's recursion method. This algorithm uses forward recurrence for computing K, and backward recurrence for I via Olver's (1954) uniform asymptotic expansion in the index n. Computation of K is completely stable as both K _1/2 and K _3/2 are elementary functions. Although the application of backward recurrence for I is numerically stable, it requires a very high initial precision in the first trial value at the seed order of N, at which the recurrence begins. Although Miller's backward recurrence algorithm gives a precision not less than the number of digits in the integer part of the trial value (Olver 1964), if the chosen N is too small, the accuracy of the result will be insufficient. Because the seed order required for a precision of M decimal places depends on the function argument and on multiples of M, as N ∼ 3M + β (Heald 1990), and because M is not known beforehand but must be chosen sufficiently large to avoid cancellations due to loss of leading digits in Equation (2), a computationally expensive iterative algorithm must be used.

An alternate and more efficient method for the present purpose is to use the Wronskian representation, which permits the recursive evaluation of the ratios I/K directly, without the necessity of generating values for I. The Wronskian (Luke 1972), may be written in the form of ratios as follows:

Here, the order ν is arbitrary, with the exception that it cannot be a negative integer. The advantage of this method is that it avoids using Olver's uniform expansion, which for large arguments introduces truncation errors whose order approaches the value of the (n + 1)st term, and no trial value is needed for the recursion.

A computer program utilizing multiple-precision arithmetic based on methods described by Smith (1996, 2003) was written to evaluate the exact formula, Equation (2), employing the Wronskian in forward recursion, which provides completely stable computations. This way, function values of γ (β) were obtained up to an argument of β = 20,000. Beyond this value γ is within 0.4% of unity, and the asymptotic formula (5) with a modification in its coefficient, as outlined later, has a smooth transition and it provides an acceptable means of evaluation. Table 1 summarizes the results, showing γ −1 values at selected β arguments, and Figure 4 shows the functions γ, γ*, and γ _s in the domain of 100 ≤ β ≤ 20 000. Values of γ up to β = 60 are identical to their counterparts to four significant figures as published by Simons et al. (1986). The number of terms needed for convergence was found to be in the order of O (qβ), where q = 0.8 for small β and it is a weakly decreasing function of β, as it may be inferred from Figure 3 by observing the position of the saltus for each I _{n +1/2} /K _{n +1/2} ratio. The required numerical precision was O (β/2) digits.

FIG. 4 The γ (β) function at large arguments. Solid line is the exact function, Equation (2), as evaluated by this work. Thin lines are γ _s , Equation (5), with C = 4.496 (Simons 1986), and γ*, Equation (4) (Williams 1988), as indicated. Dashed line is the adjusted γ_s with C = 2.843 (this work).

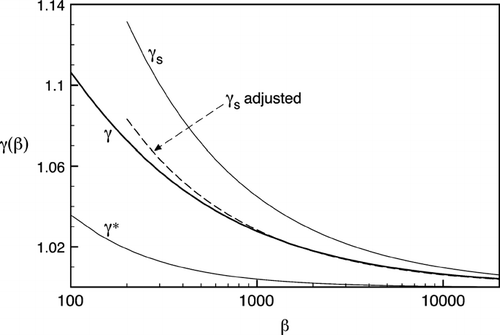
TABLE 1 Fractional deviation from the sum kernel, γ −1, at selected arguments, β, as computed in this work. Values of γ −1 up to β = 60 are identical to their counterparts to four significant figures as published by Simons et al. (1986)

β	γ −1	β	γ −1	β	γ −1	β	γ −1
0.0	0.0	6.0	2.70221E−1	150.0	8.53388E−2	1000.0	2.76964E−2
0.05	1.21450E−2	8.0	2.66557E−1	200.0	7.25623E−2	1500.0	2.15169E−2
0.10	2.36158E−2	10.0	2.59134E−1	250.0	6.38151E−2	2000.0	1.79594E−2
0.50	9.62476E−2	20.0	2.18224E−1	300.0	5.73708E−2	3000.0	1.38945E−2
1.00	1.55083E−1	40.0	1.66761E−1	400.0	4.83840E−2	4000.0	1.15681E−2
2.00	2.18931E−1	60.0	1.38095E−1	500.0	4.23197E−2	5000.0	1.00294E−2
3.00	2.48712E−1	80.0	1.19561E−1	600.0	3.78952E−2	10000.	6.41966E−3
4.00	2.62777E−1	100.0	1.06404E−1	800.0	3.17835E−2	20000.	4.09497E−3

In order to facilitate rapid evaluation of γ for all arguments, a least-squares fit was performed on the resultant data. A total of 90 values of β were used for the analysis. No simple fit was found that could encompass the entire range of β, from 0.0 to 20,000, with an acceptable χ ² value and residual error. Therefore, the range of β was split to two parts, 0 < β ≤ 5.5 and 5.5 ≤ β ≤ 20 000. In all cases an effort was made to limit the approximation to the lowest order while minimizing χ² and the relative piecewise error. The fits were sought in the following forms:

Statistical analysis showed that the χ² values of all of the fits presented here are in the order of 10⁻⁸ or lower. The relative discrepancies of the fit at the true function values are always in the order of 10^{− 4} or lower. Table 2 summarizes the fit parameters for Equations (7) and (8) in their respective ranges.

TABLE 2 Least squares fit parameters for γ (β). Equations (7) and (8) give the trial formulas

Coefficients	Index, i	Fit 1, Equation (7) (0.0 < β ≤ 5.5)	Fit 2, Equation (8) (5.5 < β ≤ 1110)
a i	1	−1.7812145E−1	+2.0431602E−1
	2	−2.0380564E−2	−1.4966887E−2
b i	1	+2.7554519E−2	—
	2	–2.6500765E−3	+1.1512218E+1
	3	—	−2.9804985E+1
	4	—	+3.2890094E+1
	5	—	−1.4543126E+1
c i	1	—	+1.1212502E−1
E	−	+1.1986361E00	+1.3038558E−1
χ^2		2.238E−8	7.650E−8

Numerical analysis of the results at large arguments indicates that for 1110 ≤ β ≤ 20 000 the asymptotic formula (5) gives a good fit to the computed values of γ, provided the coefficient C is set to 2.843 instead of 4.496. As Figure 4 shows, Equation (5) with C = 4.496 overestimates the accurate value of γ −1 in this range by more than 50%. Using C = 2.843 provides a fit which is within ∼ 5% or less throughout this range, with χ² = O (1.0E-8). The accuracy of Equation (5) was not investigated for β > 20,000.

4. SUMMARY

The exact coagulation kernel for combined Brownian and gravitational settling, based on the rigorous solution of the governing equation for diffusion and relative velocity, entails an infinite sum of the ratio of modified Bessel functions, as given in Equation (2). Practical evaluation of the sum for large arguments (β > 100) has not been heretofore successful due to the requirement of large computational precision. Consequently, the quality of the approximations given in Equations (4) and (5) has not been established beyond β = 100.

In this work, accurate values for the function γ (β) are given up to β = 20,000. It is found that the approximation given in Equation (4) provides a poor estimate for β > 100, however, it is no longer needed for practical computations, as accurate values of γ are possible to obtain by multiple-precision arithmetic using the exact formula Equation (2). It is further found that in the range of 1110 ≤ β ≤ 20,000, C = 2.843 in the asymptotic formula (5) gives a much better agreement with the exact values of γ than C = 4.495 suggested by Simons et al. (1986), and it avoids the discontinuity, mentioned in the foregoing.

Practical formulae are given in terms of least-squares fits to obtain the values of γ for 0.0 < β ≤ 20,000. These fits not only provide a convenient way to evaluate γ (β), but are especially useful in computational aerosol transport and coagulation problems where the evaluation of γ is needed at multiple values of β.

The recommended algorithm in using the appropriate least-squares fit (Table 2) is as follows:

For the range 0 < β ≤ 5.5, use Fit 1. For the range 5.5 ≤ β ≤ 1110, use Fit 2. For the range 1110 ≤ β ≤ 20,000, use Equation (5) with C = 2.843. Do not extrapolate any of the fits provided in Table 1. Careful extrapolation of Equation (5) with C = 2.843 may yield acceptable results, since for β > 20,000 the discrepancy between this formula and the exact function values are marginal. The properties of function C(β) have not been investigated for β ≫ 20,000.