The Permeability Distribution (PD) Method for Filter Media Characterization

Abstract

Cake filtration is frequently used for the removal of particulate solids from fluids in industrial processes. The build up of a filter cake is usually accompanied by a decrease in overall permeability of the filter leading to an increased pressure drop over the filter medium. For an incompressible filter cake that builds up on a homogeneous filter cloth (surface filtration mode), a linear pressure drop profile is expected over time. However, occasionally experiments show curved pressure drop profiles. Whereas pressure drop profiles with increasing slope are generally ascribed to cake compression and/or depth filtration, pressure drop profiles with decreasing slopes are only ascribed to inhomogeneities in the filter. Such inhomogeneities can arise due to filter cake patches and/or an inhomogeneous filter cloth itself. In this work a method is proposed that transforms the pressure drop profile of a filter into a permeability distribution (PD) of the filter medium, thus accounting for possible inhomogeneities of the medium. The determination of the PD is looked at as an inverse problem of an integral transformation. The method is applied to experimental filter pressure drop data of laboratory scale jet-pulse cleaned bag filter plants. It is found that even clean filter media can exhibit a significant permeability profile.

Abbreviations

PD

=

permeability distribution

1. INTRODUCTION

Dust removal from gases is frequently accomplished by surface filtration (Löffler et al. 1988). The gas pervades the filter medium while the dust particles are retained by the surface of the filter where they build up a filter cake. The formation of a cake is accompanied by a decrease in the overall filter permeability. In other words, the flow resistance increases as a filter cake builds up.

Baghouse filters with fabric filter bags are frequently employed in industrial dust removal applications for high dust concentrations. The filter medium is arranged as cleanable cylindrical filter bags, which are pervaded by the process gas. The dust cake is commonly removed by reverse jet pulses (Koch et al. 1996; Peukert & Wadenpohl 2001). The change of permeability during the filter cake development/cleaning cycle causes the pressure drop across the filter to vary with time, making it difficult to maintain the desired steady flow through the process plant.

The fiber material in filter media can be a polymer, e.g., polyamides or polytetrafluoroethylene or of mineral origin, such as glass wool. Occasionally metal fibers are used. The choice of the fibers depends on the filtration conditions including temperature and possible chemical attack. The filter medium consists of separate fibers that are processed into either a woven cloth or a needlefelt. The latter frequently has a supporting woven scrim, on which the needlefelt is produced. Such a needlefelt combines the mechanical strength and air permeability of a woven material with the good dust separation characteristics of a felt (Löffler et al. 1988). Generally, both the internal structure and surface properties of fabric filter media are inhomogeneous.

The permeability of filter media carrying cake is usually described in terms of the separate contributions of the filter cloth resistance and the filter cake resistance. The contribution of the filter cloth is usually reported as a single permeability value for a specific type of filter medium; the permeability is determined in a standardized test EN ISO 9237, or from base pressure drop measurements on thoroughly cleaned industrial filters that are subjected to a gas flow.

The contribution of the filter cake to the pressure drop is frequently captured by a constant value based on the cake mass loading per unit area, i.e., a proportionality of cake resistance and cake mass per unit of filter area. The assumption of a constant dust mass flow to the filter thus implies a linear increase in pressure drop (Löffler et al. 1988). However, experimental findings show that this linear assumption is not always justified. Strangert (1978), Leubner and Riebel (2001), and Hoff et al. (2005) find that the pressure drop increases rapidly immediately after initiating filtration starts; however, the rate of increase slows as the filter cake develops. Leubner and Riebel (2001) ascribe their experimental findings to inhomogeneities in the filter cloth, but provide little detail. The time variation of the pressure drop across a filter is decisive for the operating pressure drop level of a filter. A pressure drop curve with a decreasing slope, but the same asymptotic slope, is always above the linear curve increase. Thus, a filter actually exhibiting such a curved pressure drop profile will operate during filtration cycles at an average pressure above the ideally expected linear case.

Gradual cake compression cannot account for the observed pressure drop profiles, since it would increase the pressure drop slope. Increasing pressure drop slopes are reported to originate from depth filtration too, where particles are deposited inside the filter cloth. Both processes increase specific dust cake resistance (Schmidt 1997).

Chen et al. (2001) present a detailed experimental study of the pressure drop over three cleanable needlefelt filter media that were challenged with monodisperse dust. They report a rather fast initial pressure drop increase, that slows over the course of filtration. This effect was observed on all filter media for particle sizes 5, 10, and 20 μ m. The initial slope for 5 μ m particles was, however, slightly lower, which indicates depth filtration, possibly because the smallest particles may be able to penetrate deeper into the filter medium than larger particles. The rapid pressure drop increase at the beginning of filtration is ascribed to inhomogeneous pore filling the filter medium surface; the rate of increase slows once a homogeneous cake develops. Chen et al. (2001) hypothesize that a two-stage cake development within and on top of the pores occurs for the larger particles that they studied. They observed that the deposited particle mass at the end of stage one, i.e., pore filtration, did not depend on the particle size. Stage two is homogeneous filter cake build up over the entire area of the filter medium. The flow resistance increased linearly with decreasing particle size in contrast to previous reports of a quadratic dependency on size (Kozeny 1927, cited in Löffler et al. 1988). The experimental findings in Chen et al. (2001) suggest that the initial cake build up is inhomogeneous, which may result from an inhomogeneous pore structure, but no quantitative analysis is given.

Dufrêche et al. (2002) study fluid flow in Stokes regime two-dimensionally through a highly idealized porous layer. The model geometry considered is a uniform sieve with regular perforations, i.e., a flat plate with regularly arranged holes. Fluid can only pass through the actual perforation. The streamlines are correspondingly deflected upstream of the sieve and are concentrated through the perforation. Cake build up simulations with Lagranian particle tracking, neglecting any slip between the fluid and particles, yields a preferential cake development on or close to the perforation. The deposited cake is treated as continuous porous solid with fixed, isotropic flow resistance properties. Its hydrodynamics can be described by Darcy's law. Subsequently an altered flow field with filter cake present is calculated, and further cake build up can be simulated. Thus, an inhomogeneous filter cake gradually develops around the perforation. The apparent permeability of the growing filter cake is calculated and for thin cakes the apparent permeability of the inhomogeneous filter cake is significantly lower than the corresponding permeability of a homogeneous cake with the same mean thickness. The apparent permeability approaches the mean value as cake growth proceeds. This again implies that at a constant flow rate and constant upstream solid concentration, i.e., time-linear mean cake growth, the pressure drop is initially increasing faster, since the pressure drop and the permeability are inversely proportional. Here the inhomogeneity of the filter cake is not exclusively attributed to the pore structure of the medium, but also to the upstream flow. The modeling of the filter medium as uniform sieve with regular holes, i.e., as the combination perforation–impermeable plate, is not directly applicable fabric filter media, and Dufrêche et al. (2002) rightfully mention their main application in membrane filtration. Although this model is not applied to the complex structure of a fabric filter medium, its findings are phenomenologically interesting for fabric filtration as well.

Modeling the filter plant operation introduces another perspective on inhomogeneity of the filter. Duo et al. (1997), Dittler and Kasper (1999), Kavouras and Krammer (2003), and Mao et al. (2006), for example, propose their respective models. In these models, the filter area is divided into different model areas, each carrying patches of filter cake. The size of each patch and cake thickness on the patch is derived from the degree of regeneration and the operational setup of the filter, i.e., whether or not the filter is divided into compartments that are cleaned separately. Since cake patches of different thicknesses impose correspondingly different flow resistances, an inhomogeneous flow situation arises. Darcy's law typically captures the fluid flow through the filter medium and filter cake. The build up of a filter cake is governed by the solid mass reaching the filter, i.e., all particles that are transported to the filter form the filter cake. Both, compressible and incompressible cakes are simulated. The models proposed in the literature simulate this situation, accounting for the contributions of various mechanisms of the filter operation such as an incomplete filter regeneration (all models), a compartmented filter setup (explicitly by Kavouras and Krammer 2003), an initial depth filtration stage (Mao et al. 2006), and a two-dimensional flow field (Dittler and Kasper 1999). However, the inhomogeneous distribution of the filter cake and, thus, of the filter permeability is exclusively attributed to the history of the filter cake, i.e., previous filtration and regeneration cycles. None of the filter operation models available in the literature consider, or even describe, an inhomogeneous filter medium itself.

This work comprises the deduction of a one-dimensional filter model based on flow governed by Darcy's law that allows for inhomogeneous filter medium permeability. The filter medium permeability is taken as a distribution, rather than geometrically resolved. This distribution can account for pores in the filter medium that lead to inhomogeneous flow and consequent inhomogeneous cake build up. Based on that model a method is derived for the identification of the filter medium permeability distribution from the pressure drop increase curve during filtration. Such a filter medium permeability distribution yields structural information about the filter medium that is relevant for filtration. Filter pressure drop data sets from two different experimental setups are used as input for the proposed method. Thus the available experimental series presented elsewhere are used and additional experimental work is not performed. The permeability distribution is a time-free representation of filter medium features, which have a direct effect on the transient pressure drop behavior in the course of filtration. It is shown that inhomogeneous filter media can only operate at a higher pressure drop level than homogeneous media given the same integral filter media permeability and the same operational parameters such as dust load and cycle times.

2. CAKE FILTRATION MODEL

A cake filter model for filter media with distributed permeability is developed. Starting from an illustration of the cake filtration on an inhomogeneous filter medium, the required mathematical framework is derived. Hereafter homogeneous refers to a property that is independent on the location on the filter, whereas inhomogeneous can vary with filter location.

In Figure 1a, the plain filter medium is displayed schematically. The filter medium is illustrated by vertical lines depicting pores penetrating the filter medium vertically. The pore size varies thereby symbolizing the local permeability of the filter medium, i.e., small pores (dense lines) have a higher flow resistance, than the wider pores. The filter model assumes Darcy flow through the filter medium and thus the relation of flow velocity and pressure drop is linear:

FIG. 1 Schema of a cross-section of a filter medium with inhomogeneous permeability and the corresponding flow field at a certain pressure drop level. (a) clean filter medium and (b) filter medium carrying a filter cake layer.

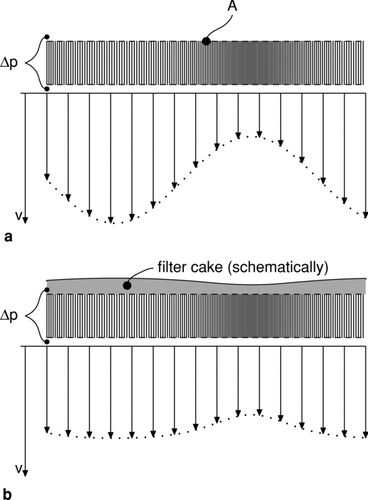
Equation (1) is the proportional relation between the pressure drop Δ p and the flow velocity v across the filter medium. It is given at time t = 0, which henceforth refers to the beginning of filtration. The proportionality factor is the ratio of the permeability k₀ of the filter medium and the dynamic gas viscosity η_g. The velocity profile in Figure 1a illustrates the effect of the inhomogeneous permeability of the filter medium: At locations with a lower permeability the flow velocity is also lower, and according to Equation (1) this is a directly proportional relation. The depicted flow velocity is taken directly after or even in the filter cloth. Downstream of the filter viscosity effects will equalize the velocity profile rapidly. The superficial flow, i.e., the flow velocities in or through the filter medium, encountered in filtration is mainly perpendicular to the filter medium.

It should be noted that, although one-dimensional cake build up is assumed, flow is not restricted to be perfectly perpendicular to the filter medium; rather the cake build up is sufficiently well described one-dimensionally along the streamlines.

Filtration takes place when the fluid upstream contains particles. The particles are retained by the filter medium. During cake filtration the particles deposit onto the filter medium and subsequently onto already deposited particles, thereby forming a filter cake. Figure 1b depicts the idealized cake formation where a filter cake is formed on the filter medium. Since the flow field for the filter medium is inhomogeneous due to a distributed permeability, cake formation is also affected. Cake is forming faster in areas with an initially high flow velocity, since more particles are deposited in these areas. This is reflected by the filter cake thickness in Figure 1b, which is higher in areas with a higher permeability of the filter medium and thus a higher initial flow velocity. However, the filter cake itself represents a flow resistance too. Under the assumption of an internally homogeneous cake, i.e., a cake that has a constant specific flow resistance on a Darcy scale (cf. Dufrêche et al. 2002), the flow resistance is proportional to the filter cake thickness. Mathematically this fact can be captured by Equation (2). Here the left-hand side is the reciprocal value of the filter cake permeability, i.e., the filter cake resistance. The right-hand side is the cake mass loading per unit area z that, under the assumption of an internally homogeneous cake, corresponds to a certain cake thickness. The proportionality factor is the specific cake resistance α _m .

When a filter cake is present, the fluid flow is determined by the combined flow resistances of filter medium and filter cake. The flow resistances of filter medium k ₀ ^{− 1}(A) and filter cake k _c ^{− 1}(t,A) are in series and thus add linearly:

The fluid flow when cake is present is determined by a linear relation similar to Equation (1) but with the combined permeability k instead of just k ₀:

The permeability depends on both the location on the filter A and the filtration time t. The latter dependency describes the evolution of the permeability as cake build up proceeds. The mechanistic cake build up is described by solid continuity. In cake filters, almost all the dust that is transported to the filter is retained on the filter to form a cake. Here it is assumed that the upstream solid concentration is constant, so the filter cake mass balance reads:

Equation (5) gives the direct proportionality between cake build up and flow velocity.

The filter cake depicted in Figure 1b causes, as stated, additional flow resistance. To overcome that increased resistance and keep the total volume flow constant (constant flow filtration) the pressure drop increases. In classical filtration theory a homogeneous filter medium and a homogeneous filter cake build up give a linear pressure drop increase (Löffler et al. 1988). However, if the filter medium is inhomogeneous but an internally homogeneous cake builds up the pressure drop increases nonlinearly with a decreasing slope.

3. MATHEMATICAL MODEL DEVELOPMENT

In this section, a mathematical pressure drop model is developed for a filter that leads to a characteristic function of the permeability of the filter medium. This pressure drop model is based solely on the equations that comprise the cake filter model (Section 2) and the respective assumptions.

The time derivative of Equation (2) is

and the time derivative of Equation (3) is:

Expressing the solid area load term in Equation (6) by Equation (5) and subsequently k _c (t,A) by k(t,A) using Equation (7) gives:

Here the filtration velocity v(t,A) can be expressed by Equation (4), which reads:

In this equation, both the permeability and the pressure drop are time dependent. However, Equation (9) can be rearranged by separating variables. Thereby evaluating the derivative on the left-hand side of Equation (9) gives:

Equation(10) is a differential equation with separated variables k(t,A) and Δ p(t), respectively. Integrating from time zero to t on the right-hand side and the corresponding permeabilities on the left-hand side gives:

Hereby, the relation k(t = 0,A) = k ₀ (A) is used, reflecting that at time t = 0 the permeability relates only to the permeability of the filter medium (cf. Equation [1]). In Equation (11) the right-hand side is only time dependent, i.e., it does not show any dependency on the filter area. That implies that the evolution of the permeability with the distributed initial value k ₀ (A) is related by only one scalar value which is be abbreviated to s(t), hence termed filter state.

The physical meaning of Equation (11) is that the evolution of the permeability on any area element A of the filter is solely determined by the evolution of the pressure drop over time. This is because the build up of the filter cake is the reason for the changing permeability which, in turn, is merely determined by the filtration velocity and thus the pressure difference over the filter.

Equations (11) and (12) lead to an additive relation that describes the permeability by two contributors, the initial permeability k ₀ ⁻²(A), only depending on the filter area and the filter state s(t) only depending on time. Thus, a separation of variables is accomplished in the integrated form too.

In other words, the flow situation of the unloaded filter medium (Figure 1a) depends only upon the local domain. Based on that, the subsequent filter cake build up is only determined by the scalar filter state s(t), which is only time dependent.

So far the filter is considered on a scale resolving the inhomogeneities on the filter location A. However, to describe a filter by a pressure drop model the entire filter must be considered. By integrating over all filter locations A, i.e., the entire filter area A _tot, in Equation (4) one obtains:

The left-hand side represents the volume flow through the entire filter [Vdot], which is constant for constant flow filtration. Rearranging Equation (14) and expressing the permeability by Equation (13) yields:

Equation (15) represents a direct relation between the pressure drop and the initial permeability function k ₀ (A). For simplifying the representation of this relation slightly and with respect to further mathematical treatment, it is advisable to introduce the abbreviation:

The filter location A identifies an area of the filter with its permeability value. The permeability is not resolved locally. Thereby the relation between the location A and the permeability, i.e., k ₀ or u, can be inverted. Since no assumptions on the nature of the general area variable A were made, it can be replaced by A _dist representing the cumulative filter area. By normalizing A _dist with the total filter area A_tot this distribution function can be introduced in dimensionless form by:

Here Φ (u) is the cumulative permeability area distribution function. Since u is unambiguously linked to k ₀ (Equation [16]), Φ (u) shall be termed the permeability distribution (PD). The limits of integration of Equation (15) are changed accordingly to account for the substitution of the variable of integration by Equation (17):

The form of Equation (18) with a function as variable of integration is called Riemann-Stieltjes integral. In this equation both Δ p and s appear depending on time t. It is shown below that the filter state s is treated as a parameter and therefore the explicit time dependency can be omitted. The constant values are abbreviated by a single factor p_c:

which gives

Equation (20) contains s, which depends on the pressure drop Δ p and time t according to the definition of Equation (12). Filter data are generally available as Δ p over time t. Equation (12) is manipulated mathematically to explicitly obtain time t as a function of filter state s and the PD Φ (u). The mathematical treatment of Equation (12) is given in the Appendix. By defining the abbreviation

one obtains an explicit relation between t and s:

Thus filtration time t and pressure drop Δ p are linked via the filter state s as a parameter, for a set of constants p _c and t _c and a PD Φ (u).

Equation (22) is a unique assignment between time t and filter state s, since any increase in s on the right-hand side is directly reflected by an increase in t.

4. PERMEABILITY DISTRIBUTION (PD) METHOD

The outcome of the mathematical filter model consists of two equations, Equations (20) and (22). They are linked via the filter state s as model-inherent parameter. It can be seen that the pressure drop and the time axis are scaled by the composite parameters p _c and t _c, respectively.

Equation (22) is the relation between time t and filter state s. The main feature of this relation is that it is a bijective assignment, i.e., every value of t corresponds to exactly one value of s and vice versa. Thus the measured time can be unequivocally converted to filter state s. Consequently a measured Δ p(t) can be converted to exactly one corresponding Δ p(s).

Equation (20) has the form of the generalized Stieltjes transformation. This integral transformation is treated by Hirschmann and Widder (1955) who give an inversion formula for this problem, i.e., a way to identify the distribution function Φ (u) from the left-hand side, i.e., Δ p(s). More importantly their inversion theory is based on uniqueness and the integral kernel in Equation (20) is captured by that theory. Thus the inverse problem underlying Equation (20) is unambiguously determined. A given pressure drop curve Δ p(s) has one and only one possible underlying permeability distribution function.

The filter model outlined above is the core of the henceforth termed the PD method: A measured pressure drop vs. time profile of a filter is converted into a PD of the filter. This is accomplished via inversion of Equation (20). Since this equation contains the filter state s as a parameter, the time is converted to the filter state by using Equation (22), which is likewise uniquely invertible. Since no restrictions on the range of t and s were made, theoretically any arbitrary part of the left-hand side function, i.e., Δ p, can be chosen as input for the PD method.

Implementation

The available inversion theory for the Stieltjes transform makes use of arbitrary high derivatives of the Δ p(s) function. Thus the inversion theory does not straightforwardly lead to the computation of the distribution function. Practically numerical methods succeed in solving the problem, which are discussed in detail by Koch (2008). The hitherto continuous PD, Φ (u), is discretized. Equations (20) and (22) are rewritten in the discretized formulation, whereby the integration is approximated by the rectangle rule:

The PD Φ (u) and the variable u are discretized with index i into m intervals. In the approximation of the integral the frequency distribution Δ Φ _i is used, which will be defined as the discrete difference Δ Φ _i = Φ _i − Φ _{i − 1}. The discretization of the cumulative distribution function Φ is fixed with a constant Δ Φ _i = 1/m. The PD is obtained via optimization with the u _i 's being the optimization variables. The optimization goal is the sum of square errors of the difference of the measured and computed pressure drop curves.

The optimization goal computes the functions Δ p via Equation (23) and t via Equation (24) for a given set of optimization variables u _i . The filter state s is hereby arbitrary, which allows for the computation of a parametric pressure drop curve [t(s),Δ p(s)] for a sufficiently large number of different s-values. These s-values are chosen to compute a pressure drop curve on a time range that is covering the entire measured pressure drop curve at a resolution superior to the experimental sampling rate. This computed pressure drop curve is linearly interpolated to each experimental measurement time value. Thus, for each experimental point a computed pressure drop value is obtained and the sum of the square errors can be calculated. The optimization problem is an unconstrained nonlinear problem and is solved with a commercially available code (Matlab® Optimization Toolbox). To increase the performance of the solver the variables u _i are scaled to vary around unity. The initial guess supplied to the optimization algorithm is a vector of identical u _i -values, i.e., a homogeneous PD.

It should be noted that the PD method uses only well-established parameters expressed by p _c and t _c (defined by Equations [19] and [21], respectively). Among these parameters only the specific cake resistance α _m must be determined experimentally, because all other parameters that affect these two coefficients are the design parameters of the filter plant and are thus usually well known.

Since the measured pressure drop difference is in general affected by a measurement error, the inversion of the measured Δ p(s) function is in practice inconsistent, i.e., one cannot obtain a PD that exactly fits every measurement point. However, more importantly the accuracy of the inversion must be examined. A detailed evaluation is performed and given elsewhere Koch (2008), since it would exceed the scope of this article.

5. EXPERIMENTAL

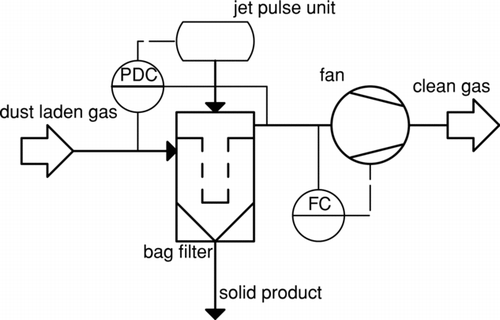
Experimental pressure drop data, on which the PD method is applied, was gathered from two different laboratory-scale bag filter plants. Both filter plants consisted of a two-screw feeder that supplied a constant mass flow of dust to a dispersion nozzle via a vibrating chute. Pressurized air dispersed the dust in the nozzle. The dispersed dust was mixed with the gas stream, which was sucked through the filter plant by an induced draft fan. The gas volume flow after the filter was recorded and controlled to a certain set value via the frequency-controlled fan. The dust-laden gas entered the filter housing near the bottom. In the filter housing three filter bags were mounted on wire cages. The bags were pervaded by the dust-laden gas from the outside to the inside. Dust particles were retained at the outer surface of the filter bags. The clean gas flowed upwards inside the filter bags and was collected in the clean gas header. Due to the dust that accumulated on the filter bags, a filter cake formed and the overall permeability of the filter decreased. As the fan kept the volumetric flow rate of the gas constant, the pressure drop through the filter increased. The filter was regenerated either after a certain pressure drop over the filter was reached or after a certain time interval for filtration had elapsed. Filter regeneration was carried out by a reverse air jet pulse. Each filter bag could be regenerated separately. In Figure 2a basic flowchart of these filter plants is given. The plants, however, differed in the actual specification and scale.

FIG. 2 Basic flow chart of the experimental facilities used.

The experimental plant #1 was also designed for optical thickness measurements of the filter cake. This plant is also presented by Saleem et al. (2005) and Saleem and Krammer (2007) and relevant operational parameters are given in Table 1. The plant operated at ambient temperature and atmospheric pressure. Commercial grade non-precipitated limestone CaCO₃ with a mass mean diameter of 5 μm and a bulk density of 1200 kg· m⁻³ was used as sample dust. The filter medium in the experiment was a polyphenylensulfide (PPS) and polyimide (PI) needlefelt on a polyimide (PI) supporting scrim which was heat treated on the dust side. Only the online measurements of pressure drop across the filter and gas volumetric flow rate are used in this work. The measurement locations are shown in the flowchart in Figure 2 indicated by PDC for pressure difference and FC for flow. The dust concentration is calculated according to:

The specific cake resistance value α _m is determined from the slope of the linear asymptote of the pressure drop curve as discussed below.

TABLE 1 Design data of laboratory scale bag filter plants

Plant	Atot	[mdot] c	η g	α m	[Vdot]
#	m^2	kg s^−1	Pa s	m kg^−1	m^3 h^−1
1	2.04	8.4 10^−4	1.8 10^−5	6.67 10^9	240
2	0.53	1.5 10^−5	2.0 10^−5	—	40

The controlled gas volume flow changed slightly due the response time of the control loop. To account for a slightly varying gas volume flow the measured pressure drop Δ p _exp is corrected to a single set volume flow [Vdot], listed in Table 1, according to Equation (26).

Another set of experiments was carried out at a different filtration plant #2. Details of this test series can be found in Koch et al. (2007). The basic features were similar to the filtration plant #1 presented already. The different plant specifications are given in Table 1. Here no specific cake resistance value is given, because several different values are determined corresponding to each filter start up. The sample dust used was commercially available quicklime CaO with a mass median diameter of 5 μ m and a bulk density of 1000 kg· m⁻³. The bag filter medium used during these experiments was a polytetrafluoroethylene (PTFE)/PI needlefelt with a PTFE supporting scrim and a Membratex® surface treatment. The aim of the experiments was to study the evolution of the conditioning of filter media in typical dry flue gas cleaning conditions, i.e., at an elevated temperature of 140°C and atmospheric pressure over time. A slipstream of the off-gas of a natural gas burner was used as flue gas in which the sample dust is dispersed. The entire plant was insulated and electrically heated to keep the operation temperature at the desired level and avoid local condensation.

6. RESULTS AND DISCUSSION

Figure 3 shows the start up of filter plant #1; this is termed the ramp test. The filter medium does not carry any filter cake and is thoroughly cleaned at the beginning of this experimental run. The vertical dashed line indicates the point in time when the dust dosing equipment was activated. Subsequently one observes an increase in pressure difference, i.e., the pressure drop ramp. Thus the overall permeability of the filter is decreasing.

FIG. 3 Pressure drop and volume flow at filter start up (in order to provide a more concise presentation the volume flow is displayed as floating mean value with 20 seconds two sided window length).

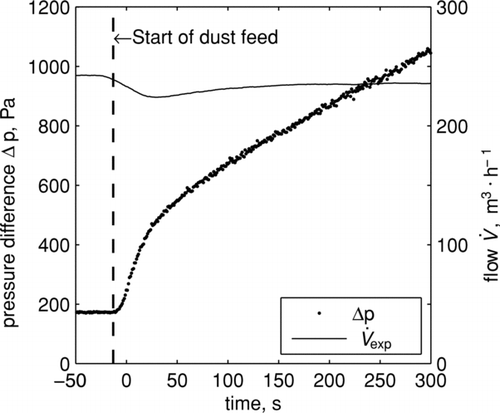
The pressure drop curve has a positive curvature for the initial short period of 15–20 seconds after dust dosing started. During this period, the dust concentration in the filter housing increases until it reaches a constant value. The filter plant is equipped with an optical measurement system, i.e., a glass window is installed in the filter housing and the increase of dust concentration can be observed qualitatively. Also the average gas residence time in the filter housing is in the observed range of time. The filter housing contains a raw gas volume of approximately 0.8 m³, which leads to an average residence time of 12 s at the operation point displayed. Assuming infinite backmixing in the filter housing, which is justified given the turbulence observed in the filter housing, 80% of the final dust concentration is reached after approximately 19 s. More interestingly, the curvature of the pressure drop curve changes when a constant dust concentration in the housing is reached. A pronounced decrease in the pressure drop slope can be observed.

Since this is the start up of the filtration plant on a clean filter cloth, inhomogeneous dust deposition cannot be attributed to residual cake patches attached to the filter cloth. Cake compression and/or depth filtration could only account for an increasing pressure drop slope.

Finally, the transient pressure drop increases linearly, which can be explained by a practically equalized permeability profile over the filter. This entails homogenous flow and the cake builds up homogeneously. The slope of the transient pressure drop asymptote can be directly used to obtain the specific cake resistance α _m by combining Equations (4) and (8) for equalized permeability, i.e., no dependency on A has to be considered:

For practical use one cannot employ the limit but should consider long times at which the pressure drop increase is linear.

Figure 4 shows the pressure drop profile during semi-continuous operation. After filter start up, which is similar to the experiment presented in Figure 3, the filter is regenerated when reaching a pre-set maximum pressure drop level of 1200 Pa. The entire filter is not directly exposed to a jet-pulse at every regeneration step. Only one out of three filter bags is cleaned at a time. Filtration then continues until the maximum pressure drop level is reached again and the next bag is cleaned in sequence.

FIG. 4 Pressure drop profile during semi-continuous filter operation. The pressured drop increases until 1200 Pa is reached. During regeneration one of three filter bags is directly exposed to a jet pulse.

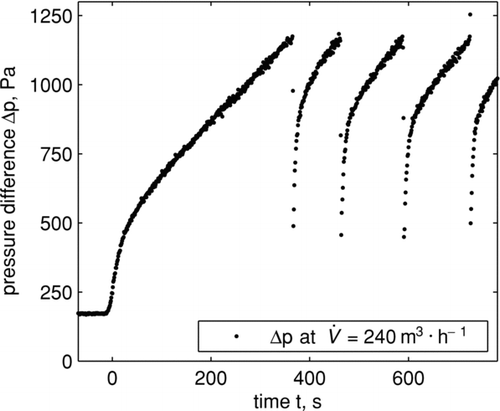
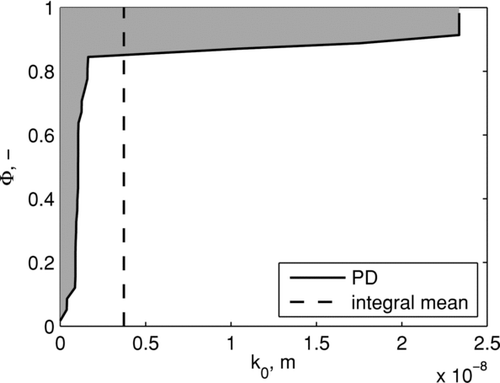
The PD method is applied to experimental data displayed in Figure 3. The initial progressive pressure drop increase is omitted and the remaining pressure drop data are used as input for the PD method. The resulting PD Φ (k ₀) is displayed in Figure 5 alongside its integral mean value, i.e., the apparent permeability of the clean filter cloth. Note that the PD Φ (k ₀) depending on the permeability is directly obtained from Φ (u), since k ₀ and u are unambiguously linked by means of Equation (16). The clean filter cloth exhibits a strong PD with about 10–15% of the filter area having a significantly higher permeability than the rest of the filter cloth.

FIG. 5 PD determined for the pressure drop rise shown in Figure 3. The shaded area corresponds to the integral mean value which is displayed as the dashed lined in addition.

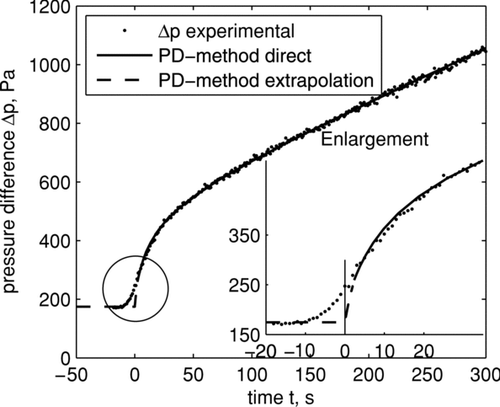
Figure 6 compares the measured and calculated pressure drop profiles. The solid black line is the computed output from the PD method indicating the range which was directly used as input data for the PD method. The initial phase, i.e., when the dust concentration in the filter housing is still increasing, is not used as input for the PD method, because that would violate the assumption of a constant solid concentration as required by Equation (5). In fact only a part of the pressure drop curve suffices, since the inverse problem is unambiguously determined as mentioned above.

FIG. 6 Pressure drop: experimental versus the PD method. The initial phase is enlarged. The solid curve shows the part which was directly used to determine the PD. The dashed curve shows the extrapolation of the PD method to the initial pressure drop value.

The shape of the PD in Figure 5, which is basically bimodal, can be interpreted in line with the results of Chen et al. (2001), who ascribe the initial pressure drop increase to an inhomogeneous porous structure of the filter medium. The voids on the surface would fill up initially, before a homogeneous cake build up proceeds. While Chen et al. (2001) explain their experimental results with a qualitative geometrical model of the filter surface, the PD method aims to give a direct quantification of the flow resistance of the filter medium relevant for the subsequent filtration. Of course, the result of the PD method, i.e., the resistance distribution, gives room for interpretation of the porous structure of the filter medium. The small area of 10–15% exhibiting high permeability can be pores that have a rather low flow resistance, but are rapidly filled with particles during the initial filtration period. The inherent irregularities of a porous medium have consequences on the upstream flow, Dufrêche et al. (2002). As particles follow the flow, an inhomogeneous filter cake is formed, but not in an attempt to strive for a geometrically homogeneous filter surface, as Chen et al. (2001) suggest, rather this is for a homogeneous flow situation. Both effects, the geometric and flow constraints, may be important and they are accounted for implicitly by the PD method.

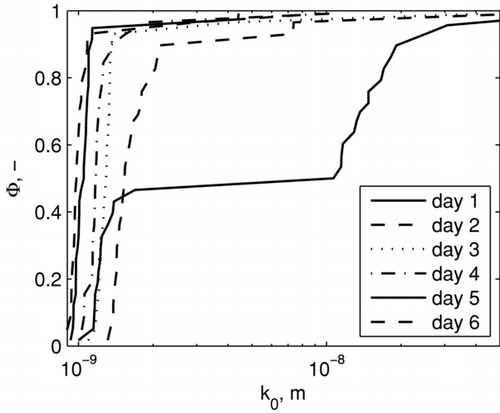
Filter cloth conditioning experiments in plant #2 lasted for 120 h and were conducted with an initially virgin cloth. Filter regeneration was accomplished by cleaning one bag with a reverse jet pulse at a preset cycle time of 300 seconds. Filtration was stopped once every day by switching off the dust feeder, but the gas flow was kept constant. The pressure drop profile during such a stop is exemplarily depicted in Figure 7 for the third experimental day during this 120 h period. The filter was thoroughly cleaned by a series of jet pulses in short succession until no change was observed in the residual pressure drop over the filter. The integral cloth permeability is determined from this residual pressure drop value. With the cleaning device disabled, a ramp test was carried out by engaging the dust feeder. Subsequently a pressure drop increase on the clean filter cloth was observed that clearly had a decreasing slope. The dust feeder was stopped again after about one hour and the filter bags were cleaned again to repeat the residual pressure drop value test. Eventually the normal filtration experiment with cleaning every 300 seconds was continued. The relatively large differences in the time scale when comparing Figure 3 and Figure 4 with Figure 7 must be attributed to significantly different experimental dust concentrations calculated from Equation (25). The integral permeability values corresponding to the residual pressure drop are displayed in Figure 8 for the entire experiment. These values are easily comparable to datasheets provided by a manufacturer and show a steady decrease during the conditioning period, which is leveling off at a certain value.

FIG. 7 Pressure drop profile during the residual pressure test on the third experimental day in plant #2.

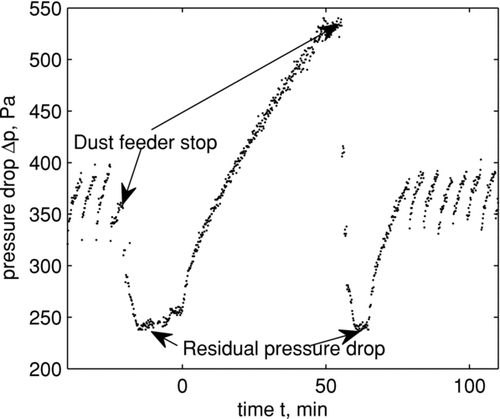
FIG. 8 Measured integral permeability values during filter cloth conditioning starting with the virgin cloth in plant #2.

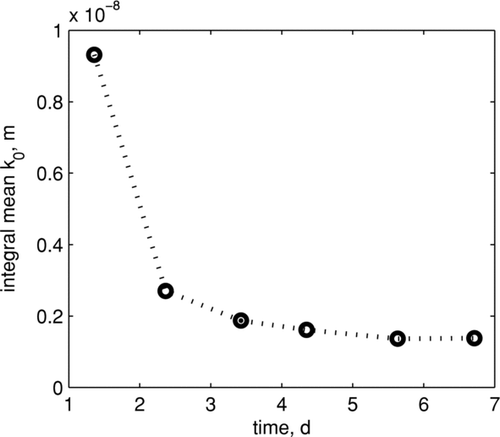
For each ramp test of the filter cloth conditioning experiment on plant #2 a PD is determined. The evolution mean permeability values of the clean cloth are presented in Figure 8 and show a steady decrease in the integral value. However, the PDs show quite a different picture. In Figure 9 one can see that a shift of the initial PD to lower levels is observed but also a significant shift of the jump on the ordinate is found. Thus not only a higher cloth pressure drop level must be expected after conditioning of the filter cloth, but also the filtration characteristics concerning the curvature of the pressure drop relation changes significantly. One particular feature is remarkable: the difference between the virgin filter cloth on day 1, i.e., a brand-new cloth without prior exposure to dust, and the other days. The PDs on the thoroughly cleaned filter cloth exhibit both, high absolute permeability values and an even step in the area distribution at about 50%. All successively determined PDs do not even come close to the values reached by the virgin material, indicating that even thorough filter cleaning cannot clean the filter medium completely. Here the change of a PD and thus the filtration characteristics of a filter cloth in operation can be seen, that cannot be derived from only the residual pressure drop levels when the bags are cleaned thoroughly.

FIG. 9 PDs computed for the pressure drop ramp tests during filter cloth conditioning on plant #2. The PDs are referenced to the actually measured integral value as shown by the corresponding measured points in Figure 8.

7. CONCLUSIONS AND OUTLOOK

A new method is proposed that allows transforming pressure drop profiles into permeability distributions of the filter media. The PD method is derived from an analytical filter model, which assumes cake filtration. The pressure drop–filtration velocity relation is described one dimensionally by Darcy's law. The filter cake is assumed to be incompressible and to have a constant specific flow resistance. The model is comprehensively deduced. Mathematically the unique equivalence of a pressure drop profile and a PD is shown. A direct independent experimental verification of the PD has not been possible which would require highly resolved velocity measurements in close proximity to the filter surface.

Clean filter clothes are found to exhibit a significant permeability profile. PDs are determined for experimental pressure drop data for two specific laboratory plants. However, pressure drop data from any filter plant that is covered by the basic flowsheet in Figure 2 can be used to determine a PD, since the method requires only standard measurements. Thus the PD method can be applied to the transient pressure drop data of industrial filter plants.

Violation of the assumption of an incompressible filter cake at all times, i.e., development of a compressible filter cake, would not necessarily become apparent when applying the PD method. The effect of a compressible cake would be lumped into the results of the PD unless information about the compressibility features of the filter cake is available additionally. Of course, if a relation is available that captures the dependency of the permeability and the filtration parameters, Equation (2) can be adjusted accordingly. Depending on the actual relation used in Equation (2), the subsequent deduction of the filter model will be altered. In general one cannot expect to obtain closed forms of the integral transformations as for the linear case. However, a closed form of the integral transformations is not required though it is desirable to apply the filter model. The resulting filter model would be in any case be severely complicated by the necessity to include the pressure drop in such a relation. As the uniqueness of the Stieltjes transform is even provided with a linear relation such as Equation (2) a nonlinear term should also lead to a uniquely decidable PD and thus the PD method can be based on a filter model that takes into account cake compression effects as well.

A filter medium that exhibits a permeability profile, i.e., it is not homogeneous with respect to permeability, leads to a fast pressure drop rise at the beginning of filtration. Consequently, the filtration performance of such an inhomogeneous filter cloth is reduced with respect to the pressure drop level and/or cycle time when compared with a homogeneous filter cloth having the same integral initial permeability. Thus, the PD gives a hint about the unused potential, i.e., the difference between a homogeneous permeability and an inhomogeneous distribution that can possibly be utilized by a different dust/filter medium combination.

Operating a filter exhibiting a strong PD at relatively low pressure drop levels is especially disadvantageous, since the slope of the pressure drop curve is steepest in this range. Hence, frequent filter cleaning is required to keep the desired pressure drop level, i.e., short cycle times evolve, and the flatter asymptotical pressure drop slope is hardly utilized. In addition, the achievable mean pressure drop level is relatively high, given the required cleaning frequency. The downside of such operation is filter medium wear due to excessive cleaning, solid breakthrough during cleaning and initial filtration, and excessive cleaning air consumption in the case of jet pulse cleaning.

As it is widely reported the performance of a filter depends upon the combination of the filter medium and the dust. This is accounted for by the PD method that gives a PD for exactly the combination of filter medium and dust. Consequently the PD could be different for the same filter medium but a different dust, which requires caution when trying to apply one PD to a different system.

The PD of a filter medium can change during filter operation. It is demonstrated that in a laboratory set-up this change of the PD can be observed and PDs determined from pressure drop data of industrial filter plants could be a useful tool to monitor the filtration characteristics over the life cycle of the filter bag.

NOTATION

A	=	location on the filter, m2
A*	=	dimensionless location on the filter
A dist	=	cumulative filter area, m2
A tot	=	total area of filter, m2
csol	=	solid concentration of raw gas reaching the filter, kg m3
k	=	permeability, m
k 0	=	permeability at the beginning of filtration, m
k c	=	permeability attributed to filter cake, m
m	=	number of nodes for the discretized PD, −
[mdot] c	=	dust mass flow to filter, kg s−1
p c	=	pre-factor in Equation (20), Pa m
s	=	filter state, m−2
t	=	time, s
t c	=	pre-factor in Equation (22), s m−1
[Vdot]	=	set value for the volumetric gas flow rate to filter, m3 s−1
[Vdot] exp	=	measured value for [Vdot], m3 s−1
u	=	abbreviation for k 0 − 2 (Chapter 3), m−2
v	=	filtration velocity, m s−1
z	=	cake mass loading per unit area, kg m−2

Greek letters

αm	=	specific cake resistance based on mass area load, m kg−1
Δ p	=	pressure drop across filter, Pa
η g	=	dynamic gas viscosity, Pa s
Φ	=	cumulative area distribution function of permeability, −

APPENDIX A: TIME TRANSFORMATION

The time transformation Equation (22) is obtained by pure mathematical manipulating the definition of filter state Equation (12). Derivation with respect to time yields:

Hereby the constants p _c and t _c , defined by Equations (19) and (21), respectively, are used to replace the coefficients that appear in Equation (12) originally. Rearranging Equation (A1) gives:

The pressure drop Δ p can be expressed by Equation (20):

Integration via s from zero to s yields:

By changing the order of integration on the left-hand side one obtains:

Evaluating the inner integral gives:

Using the boundaries of s gives:

which is equivalent to the time transformation Equation (22).

Acknowledgments

The authors thank Harald Hanche-Olsen from the Department of Mathematics at NTNU for invaluable hints concerning the mathematical background of the model, namely for noting that the present problem can be formulated as a Stieltjes transform. Financial support from the Austrian Science Foundation (FWF) under the project no. P16313-N07 and the Austrian Energy and Environment AG & Co KG is gratefully acknowledged.