Nonzero-Concentration Boundary Condition for Advection-Diffusion Aerosol-Transport Modeling

INTRODUCTION

This Brief Communication presents recent results related to advection-diffusion transport modeling of nanoparticle aerosols. While discussed elsewhere in detail (Gallis et al. 2008; Torczynski et al. 2008), these results are summarized briefly here for the convenience of Aerosol Science and Technology readers.

In aerosol-transport modeling, the particle concentration (number density in the gas) adjacent to a wall is almost universally taken to be zero (Friedlander 2000). This approximation is extremely good for commonly encountered aerosol particles in ambient air. However, for standardized nanoparticles with diameters of 20 nm now used in experiments (Kim et al. 2005), this approximation can become less accurate under certain circumstances (Gallis et al. 2008). Instead of vanishing at a wall, the concentration approaches a nonzero value proportional to the particle flux to the wall even when the probability that an impacting particle sticks is unity. This effect is significant only when the particle stopping distance based on the thermal velocity is comparable to the geometric length scale, which occurs for nanoparticle aerosols in microscale geometries at atmospheric pressure or in larger geometries at proportionally lower pressures.

GENERALIZED BOUNDARY CONDITION

In advection-diffusion modeling of aerosol particles with prescribed diameter and mass, the particle concentration n in the gas is governed by the following equation (Friedlander 2000):

Here, U is the particle drift velocity (set by balancing drag against external forces) and D is the particle diffusivity (set by gas and particle properties). Conventionally, the boundary condition at a wall is taken to be the zero-concentration condition (Friedlander 2000): n = 0 at a wall.

Through theoretical analysis based on the generalized Fokker-Planck equation and numerical simulation of particle Brownian motion using the Langevin equation, Gallis et al. (2008) show that n at a solid wall approaches a nonzero value proportional to the particle flux:

Here, c = (2k _B T/m)^1/2 is the most probable thermal speed of a particle of mass m in a gas of temperature T, and k _B = 1.380658 × 10⁻²³ J/K is the Boltzmann constant. The particle-flux coefficient f is an order-unity dimensionless quantity that depends on the sticking fraction s, the probability that an incident particle sticks to the wall, and the ratio Û = U/c, where U = U· [ncirc] and [ncirc] points into the wall and out of the gas. An approximate but reasonably accurate expression for f is determined (Gallis et al. 2008):

The particle-flux boundary condition is shown to behave correctly in all limiting regimes, including reducing to the zero-concentration boundary condition when the geometric length scale L is large compared to the thermal stopping distance ℓ = π^1/2 D/c = (π^1/2/2)cτ and the sticking fraction s is not small. Here, τ = m/β is the stopping time, and β is the linear drag coefficient.

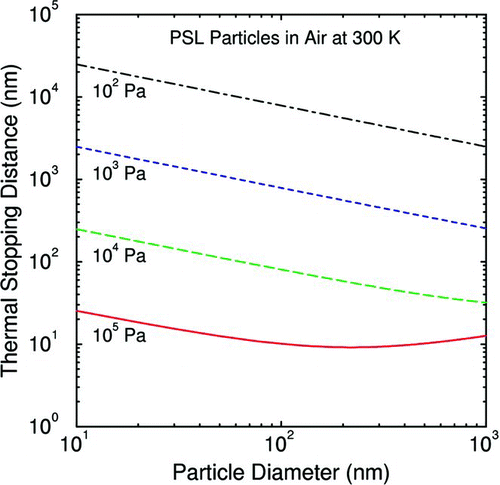
Figure 1 shows a plot of the thermal stopping distance vs. the particle diameter for PSL particles in air at 300 K from near-atmospheric to low pressures using the drag expression and parameters of Kim et al. (2005). Since the zero-concentration boundary condition applies when the geometric length scale is large compared to the thermal stopping distance (e.g., L ≥ 10²ℓ), departures from this boundary condition at near-atmospheric pressures are expected only in micron-scale geometries. As the pressure is reduced, the thermal stopping distance increases, and departures are expected in proportionally larger, but still small, geometries. As shown below, these departures are modest unless the sticking fraction becomes small.

FIG. 1 Thermal stopping distance of PSL particles in air. (Figure provided in color online.)

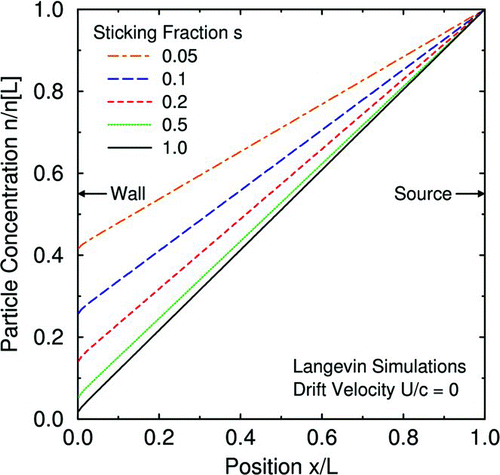
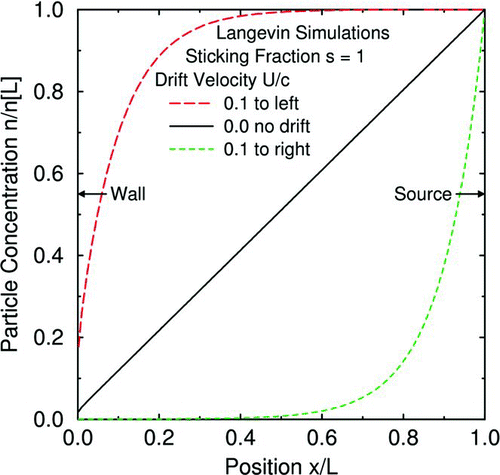
Figures 2–3 show examples of particle-concentration profiles with nonzero values adjacent to the wall determined by Langevin simulations (Gallis et al. 2008). PSL particles with a diameter of 20 nm are released from the source into a gap filled with air at 1 atm and 300 K (which yields a thermal stopping distance ℓ = 18 nm) and are allowed to drift and diffuse to a wall L = 1000 nm away. Figure 2 shows profiles for cases with zero drift velocity but various values of the sticking fraction s. As s is increased, the concentration at the wall decreases but does not become zero even when s = 1. As expected, these profiles vary linearly with position from the source to within a few thermal stopping distances of the wall. Figure 3 shows profiles for cases with unity sticking fraction but nonzero drift velocity (e.g., from gravity or thermophoresis). As also expected, a nonzero drift velocity produces an exponential profile. However, as with a zero drift velocity, the concentration adjacent to the wall is nonzero.

FIG. 2 Langevin simulations showing nonzero particle concentration adjacent to the wall: zero drift velocity and various sticking fractions. (Figure provided in color online.)

FIG. 3 Same as previous figure but with unity sticking fraction and various drift velocities. (Figure provided in color online.)

ADVECTION-DIFFUSION EXAMPLES

Two examples serve to illustrate the utility of the particle-flux boundary condition. In both of these situations, the advection-diffusion transport equation and the particle-flux boundary condition are used to determine the probability that particles are transported to a certain location.

In the first situation (Rader et al. 2002; Gallis et al. 2008), two infinite flat plates are separated by a distance L, the gap between the plates is filled with motionless uniform gas, and particles are placed at a distance 0 < H < L above the lower plate. The particles drift under the influence of an external force (e.g., gravity) and diffuse in a Brownian fashion until they deposit on one of the plates. Using Equations (1) and (2), the probabilities P and 1 − P that particles deposit on the upper (“2”) and lower (“1”) plates, are found, where the drift velocity U is taken to be positive when downward and the arrow denotes the zero-drift-velocity limit of U → 0:

If the thermal stopping distance vanishes so that ℓ/L → 0, the zero-drift-velocity probability reduces to P → H/L, an expression previously obtained using the zero-concentration boundary condition (Rader et al. 2002).

In the second situation (Torczynski et al. 2008), particle transport and deposition are considered in a long thin gap between parallel walls, through which gas flows at a fixed rate. Here, the coordinates x and y lie along and across the gap, respectively, and the following parameters are relevant: gap height H, mean gas velocity U along the gap (with a parabolic profile), particle diffusivity D, particle thermal speed c, and gravity (ignored here). Using Equations (1) and (2), a similarity solution is found for the particle concentration n in the gap:

Here, n _* is the particle-concentration scale value at x = 0, k is the normalized decay constant for n along the gap, f _* is the particle-flux parameter, Pe is the Peclet number, k ₀ and ñ ₀ apply when Pe = 0 (diffusion alone), k ₁ and ñ ₁ apply when Pe > 0 (advection-diffusion), and ₁ F ₁ is the confluent hypergeometric function. They also provide easily-evaluated approximations that agree closely with the above exact expressions:

The zero-concentration-boundary-condition expressions are recovered in the limit that f _* → ∞ .

CONCLUSIONS

A more general wall boundary condition has been recently derived for advection-diffusion modeling of aerosol transport. In this particle-flux boundary condition, the particle concentration in the gas does not approach zero as the wall is approached but rather approaches a value proportional to the particle flux to the wall. When the geometric length scale is large compared to the thermal stopping distance, this particle-flux boundary condition reduces to the almost universally used zero-concentration wall boundary condition. Nonzero concentration at walls can be significant for aerosols of standardized nanoparticles in microscale geometries at atmospheric pressure and in larger geometries at proportionally lower pressures. Generic transport and deposition probabilities for particles between two parallel walls have been derived using the particle-flux boundary condition.

Acknowledgments

This work was performed at Sandia National Laboratories. Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the United States Department of Energy's National Nuclear Security Administration under contract DE-AC04-94AL85000. The authors gratefully acknowledge financial support from Intel Corporation under CRADA SC93/01154 and technical interactions with Kevin J. Orvek, Intel contract monitor, David Y. H. Pui and Jing Wang, University of Minnesota, and Christof Asbach and Heinz Fissan, IUTA.