Abstract
In this study, we present three approaches to predict particle penetration coefficients through a single straight crack in building envelops. The three approaches are an analytical approach, an Eulerian approach, and a Lagrangian approach, respectively. The particle penetration coefficient through an idealized straight crack (smooth inner surfaces) and a strand board crack (rough inner surfaces) were modeled by the three presented approaches. The calculated results were compared with the literature results. The comparison shows that for the idealized smooth crack, the modeled results by the Eulerian approach match the experiments best for the entire range of particle sizes studied among the three approaches. The predicted results by the analytical approach also match the experiments reasonable well. Results modeled by the Lagrangian approach are less satisfied for fine particles (d p < 0.1 μm). Overall, all the three approaches agree well with the experiments for particle sizes ranging from 0.4–1.2 μm. For cracks with rough inner surfaces, the results agree better with the measurements for all the three approaches by adjusting the boundary conditions to incorporate the “intercept” effect of roughness on particle deposition in the cracks.
NOMENCLATURE
| a | = |
air exchange rate (h−1) |
| C | = |
concentration of the particle (number/cm3) |
| C c | = |
Cunningham correction factor |
| C cm | = |
flow rate-weighted average concentration at the outlet of the crack (number/cm3) |
| C max | = |
particle concentration at the centerline of the straight crack (number/cm3) |
| C(X z ,Y) | = |
particle concentration distribution at the outlet of the cracks (number/cm3) |
| C ∞ | = |
particle concentration outside the boundary layer (number/cm3) |
| d | = |
height of the crack (cm) |
| d p | = |
particle diameter (μ m) |
| D | = |
Brownian diffusivity of the particle (m2 s–1) |
|
| = |
Brownian motion (N) |
| F in | = |
infiltration factor |
|
| = |
additional acceleration (force/unit particle mass) term (N) |
| h | = |
vertical distance from the midline of the crack to the ceiling and floor (mm) |
| i | = |
a parameter to describe the direction of the wall surfaces, i.e., for an upward facing horizontal surface (floor), i = 1; for a downward facing horizontal surface (ceiling), i = −1; for a vertical surface, i = 0 |
| k | = |
particle decay rates (h–1) |
| k B | = |
Boltzmann constant; k B = 1.38 × 10–23 J/K |
| n | = |
vertical distance from the particle to the crack inner surfaces |
| N escape | = |
number of the escaped particles at the outlet |
| N total | = |
number of the total particles released at the crack inlet |
| P | = |
penetration coefficient |
| P d | = |
particle penetration coefficient due to Brownian diffusion alone |
| Pe | = |
Peclet number |
| P g | = |
particle penetration coefficient due to gravitational settling alone |
| P i | = |
particle penetration coefficient due to impaction alone |
| T | = |
absolute temperature of the air (K) |
| u | = |
airflow velocity in x direction (m s–1) |
| u m | = |
air average velocity (m s–1) |
| u max | = |
air velocity at the centerline of the straight crack (m s–1) |
|
| = |
velocity vector of fluid phase (m s–1) |
|
| = |
velocity vector of the particle (m s–1) |
| v | = |
airflow velocity in y direction (m s–1) |
| v d | = |
particle deposition velocity (m s–1) |
| v s | = |
gravitational settling velocity of particles (m s–1) |
| w | = |
airflow velocity in z direction (m s–1) |
| x | = |
horizontal axis |
| y | = |
absolute vertical distance from the ceiling or floor surface of the crack (mm) |
| y 0 | = |
height of the rough layer (μ m) |
| z | = |
flow path distance (or length) along the leakage path (cm) |
| Greek Symbols | = | |
| ε | = |
deposition ratio |
| λ | = |
the mean free length of the air molecule; λ = 0.0667 μm at a temperature of 20°C and atmospheric pressure |
| μ | = |
molecular dynamic viscosity of the fluid (g cm–1 s–1) |
| ρ | = |
fluid density (g cm–1) |
| ρ p | = |
density of the particle (g cm–1) |
| τ p | = |
particle relaxation time (s) |
1. INTRODUCTION
Recent epidemiological evidence has observed that ambient particle concentration is very closely associated with cardio-pulmonary morbidity and mortality and even premature death (CitationEPA 2005). Since most people spend much of their time indoors, human exposure to outdoor-originated particles may not equal to outdoor particle concentration levels. The elderly and infant, which are the most susceptible population groups, spend almost 100% of their time indoors. To accurately assess individual indoor exposure, it is important to distinguish the contribution from outdoor-origin fine particles, which penetrate indoors, to that of indoor-generated fine particles. This issue may be more important for those people who are living in high-rise residences in metropolitan cities. During summer time while air conditioning system is operating and winter time while the heating system is operating, windows are closed in most of the time. It results in very low air exchange rate so that infiltration becomes the most dominant pathways for ambient air entering residential places. The study by CitationZhu et al. (2005) also indicated that the penetration of particles may contribute dominantly for indoor particle concentration level for those buildings near highway.
There are mainly three methodologies to quantify the “effectiveness” of infiltration of particles: (1) indoor-to-outdoor concentration ratio (I/O); (2) infiltration factor; and (3) penetration coefficient. Among the three parameters, the most relevant parameter for the penetration mechanism through cracks is the penetration coefficient (or penetration factor) which is defined as a parameter to indicate the fractional penetration of particles from outdoors to indoors that is associated with infiltration airflow rate. Unlike the I/O ratio and infiltration factor, the third approach of penetration coefficient, avoids the interferential factors such as air exchange rate and particle decay rate, and thus it is a better measure to characterize the infiltration rate of particles.
There are three major deposition mechanisms controlling particle deposition when particle penetrating through cracks, i.e., gravitational setting, Brown diffusion, and inertial impaction. Based on the particle deposition mechanisms of gravitational settling, CitationFuchs (1964) applied a flow equation to derive the penetration coefficient for a channel flow, which can be expressed as:
CitationLicht (1980) proposed a similar method that calculated penetration coefficient by:
Based on the particle deposition mechanisms of gravitational setting and Brown diffusion, CitationTaulbee and Yu (1975) solved the particle transport equation for steady-state laminar flow in cracks to calculate the particle penetration coefficient:
Based on all the three deposition mechanisms, CitationLiu and Nazaroff (2001) developed a mathematical model to calculate the particle penetration coefficient through building cracks, as shown below:
Reviewing the particle penetration through building cracks, one can recognize that particle penetration can be determined directly by calculating the particle deposition onto the inner surfaces of the cracks of the building envelope. Experimental measurements are very scarce and the geometry studied were very simple (CitationLiu and Nazaroff 2003). Due to many plausible deposition mechanisms are involved, numerical modeling approach is always preferred to study particle penetration coefficient. In literature there are three popular mathematical approaches to calculate the particle penetration coefficient. In this work we presented and compared the results obtained from the three approaches based on an analytical, an Eulerian and a Lagrangian model.
The experiments of particle penetration coefficient through a two-dimensional crack measured by CitationLiu and Nazaroff (2003) under different conditions were employed to compare with the modeling results by the three approaches. The accuracy and performance of the three approaches were also discussed in details.
2. METHODOLOGY
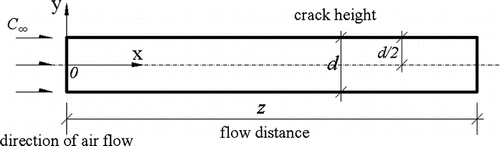
To compare the calculated results with the measured data by CitationLiu and Nazaroff (2003), the studied case was selected as the two dimensional straight crack which shown in .
2.1. Analytical Model
2.1.1. Particle Deposition in the Cracks
The airflow through the building envelope is usually laminar due to the small length scale and low air velocity (CitationLiu and Nazaroff 2003). Hence the particle deposition rate in cracks with smooth inner surfaces is mainly governed by two mechanisms: Brownian diffusion and gravitational settling. The analytical model is based on the understanding that there is a very thin particle concentration boundary layer submerged inside the airflow (momentum) boundary layer, and throughout the concentration boundary layer the particle flux, J, is constant and can be described by a modified form of Fick's law:
D, the Brownian diffusivity of the particle, can be calculated by:
The gravitational deposition velocity can be calculated by:
Let C ∞ as the particle concentration outside the boundary layer, the particle deposition velocity, v d , is calculated by the following equation:
There is no vertical surface for the two dimensional crack. For the idealized condition in which the inner wall surfaces of the crack are smooth, the boundary conditions for Equation (Equation11) are (referring to ):
It should be noted that n denotes the absolute normal distance from the ceiling or floor surface of the crack in Equation (Equation12). C max is the particle concentration at the centerline of the straight crack. The exact relationship between C max and C ∞ is difficult to determine, as it depends strongly on the particle size as well as the position in the axial direction of crack length. For simplifying the analytical calculation, we assume that the relationship between C max and C ∞ is similar to the relationship between u max and u m , i.e., u max = 3/2u m (CitationTaulbee and Yu 1975). Thus Equation (Equation12) can be rewritten as:
2.1.2. Calculation of Penetration Coefficient
After calculating the particle deposition velocity in the cracks, the penetration coefficient can be computed readily by using the following equation based on the previous analysis by CitationWu and Zhao (2007):
With known particle deposition velocity and using Equation (Equation16), we could compute the particle penetration coefficient for different particle diameters. For practical cases where the inner surfaces of the cracks are rough, the boundary conditions of Equation (Equation11) must be adjusted to incorporate the “intercept” effect of the surface roughness on particle deposition. According to the previous study by CitationZhao and Wu (2006), the boundary conditions shown in Equation (Equation12) should be modified as:
2.2. Eulerian Model
2.2.1. Modeling of Particle Mass Conservation Equation
The Eulerian model solves the particle mass conservation/transport equation numerically to predict the particle penetration coefficient directly. CitationZhao et al. (2009) concluded that in normal cases, (1) the drift flux caused by the momentum change rate per unit volume of particle phase has little effect on particle distribution for ultrafine particles (d p < 0.1 μ m); (2) the thermophoresis force may be larger than the gravitational force for particles with a diameter in the range of 0.01 to 0.1 μ m, but both forces are relatively small to affect the particle dispersion. Thus only the slip effect due to gravitational settling is included in the “drift flux” term. The particle mass transport equation models the settling effect by incorporating the “drift flux” term in the equation, as shown in following equation:
According to previous study by CitationTaulbee and Yu (1975), the effect of Brownian diffusion is negligible for Peclet number (Pe) > 100, where Pe denotes the ratio of the convection and diffusion and it is defined as:
Here two orientations are considered separately. In y-direction, l represents the crack height d. For cases considered in this study, the crack height is of the order of magnitude of 10–4 m (see ), thus combining particle diameters studied in the work, Pe in y direction is in the order of 102 or less and hence we need to consider Brownian diffusion and gravitational settling simultaneously. On the other hand, in the direction along the horizontal length of the crack, l indicates the crack length z. In this case Pe is large enough (in the order of 104) that we could ignore the effect of Brownian diffusion, and hence the equation above can be defined as
TABLE 1 The five studied cases
To facilitate the model development, Equation (Equation21) is normalized by the following dimensionless parameters which are defined as:
For a Poiseuille flow that works for the airflow through the straight cracks, the air velocity along the cracks can be calculated from an analytical solution of laminar airflow (CitationTaulbee and Yu 1975).
Equation (Equation20) could be rewritten as the following dimensionless form:
Equation (Equation29) was solved numerically by finite difference method (FDM). The numerical solution was solved with the assistance of the partial differential equations (PDE) function of the software MATLAB (CitationMathworks Inc. 2007). We performed the grid independence test by using the same mode with finer grids until the calculated results yielded small changes of the particle concentration. Grid convergence index (GCI), which is based on Richardson extrapolation method (CitationRichardson, 1910) and has been suggested by CitationRoache (1994), was calculated to show the relative error of grid independent test.
We tested three groups of grids (number of X grids × number of Y grids = 30 × 401, 40 × 501, 10 × 801, respectively). The values of GCI(C) were all less than 0.1% for the simulated cases, which shows that the grids are fine enough. Thus the grid 30 × 401 was selected. Other cases and particle sizes followed the similar rule and thus the procedure was not repeated here.
2.2.2. Calculation of the Penetration Coefficient
To calculate the particle concentration, we used the flow rate-weighted average concentration as the exit concentration as recommended by CitationMiddleman (1997). The concentration, C cm , is estimated as:
The particle penetration coefficient can be calculated by:
2.3. Lagrangian Model
2.3.1. Model for Fluid Phase
Particle motion results from various forces exerted by the airflow, so it is important to simulate the airflow field accurately. For this study, laminar airflow was modeled with computational fluid dynamics (CFD) tool. Air exchange/infiltration is driven by pressure difference between indoors and outdoors, thus the boundary conditions for the CFD simulation in this study are: defining the pressure difference at the inlet and outflow condition for the outlet of the cracks, respectively. The inner surfaces are stationary adiabatic walls.
We used FLUENT 6.2 CFD program to solve the governing equations for fluid flow (CitationFluent Inc., 2005). We conducted a grid independence test by calculating the same mode with finer grids until calculated results yielded only small changes during simulations. Again, the similar grid convergence index defined by Equations (Equation32)–(Equation34), GCI(u), was employed. The tested grid densities are 50 × 500 and 100 × 1000. The values of GCI(u) were all less than 5%, which show that the grids are fine enough. Thus the grid 50 × 500 was used for all simulations.
2.3.2. Particle Equation of Motion
The Lagrangian approach calculates the trajectory of each particle by integrating the force balance on each particle, which is written as
It is very flexible to incorporate different forces in Equation (Equation37). For the case studied, the drag force plays an important role according to the analysis by CitationZhao et al. (2004). The drag force follows the Stokes drag law for small Reynolds number (Re < 1) cases:
For fine particles that can penetrate through building envelopes, other forces such as Brownian motion should be considered, especially for ultrafine particles (CitationZhao et al. 2004). Therefore, the final form of the trajectory equation is:
When particles strike the wall, they will be trapped since they usually cannot accumulate enough rebound energy to overcome the adhesion force (CitationHinds 1982). When particles reach the crack outlet, they will escape and the trajectories calculation terminate. The boundary conditions for the particle phase modeling are: particles will be trapped when they reach the inner surfaces of the cracks or they will escape from the outlet. The particles are released at the crack inlet uniformly following the assumption by CitationFuchs (1964) and the initial velocity of the particles is set as zero as the inertia of studied particles is small enough to neglect the influence of initial velocity on the later trajectory.
We used FLUENT program to track the particle trajectories (CitationFluent Inc., 2005). We conducted a particle number independence test with different particle numbers: 1000, 5000, and 10,000. The differences between the results (penetration coefficient) by different particle numbers are less than 2% for each test, which shows that the particle numbers are sufficient. Thus, the particle number was set as 1000 for tracking.
It is a bit difficult to model the cases of cracks with rough inner surfaces by the Lagrangian model. Here we assumed that the particles trapped by the roughness of the inner surface and thus the particle tracks were terminated once they reached the effective roughness over the surfaces. By defining this intercept effect of the wall roughness, particle deposition was modeled. We set two imaginary planes as the virtual boundaries of the effective roughness, which were shifted a distance of the height of effective roughness from the ceiling and floor surface, respectively. When particles flow into the area limited by the imaginary planes, they were assumed to be trapped and the trajectories were terminated.
2.3.3. Calculation of Penetration Coefficient Based on Trajectories
It is easy to calculate the particle penetration coefficient based on the tracked trajectories:
3. CASES STUDY
3.1. Cases Description
The modeling configuration of crack is a single rectangular slot of uniform geometry as a surrogate of a leakage path in a building envelope. The measurement of particle penetration coefficient by Liu and Nazaroff was based on this configuration. The smallest dimension of the crack (known here as “crack height”) is denoted as d and the crack length is denoted as z. The crack pattern is illustrated in . Airflow can be represented as two dimensions, as the crack width is much larger than crack height. The airflow is driven by the pressure difference (ΔP) which was fixed at one of two values: 4 or 10 Pa. The crack length, the dimension parallel to the airflow direction, was 4.3 and 9.4 cm for idealized cracks, and 4.5 cm for the roughness cases. Various crack heights, perpendicular to the flow direction, were considered (d = 0.25 and 1.0 mm). Particles were assumed to be spherical with a density of 1 g/cm3 and with a broad range of particle diameters, 0.01 to 10 μ m. shows the details of the five studied cases of different conditions, which includes four cases with smooth inner surfaces and one case with rough inner surfaces of cracks. As it is the simplest among all, the analytical method in Equation (Equation4) (CitationLiu and Nazaroff 2001) was also included in the comparison.
3.2. Results
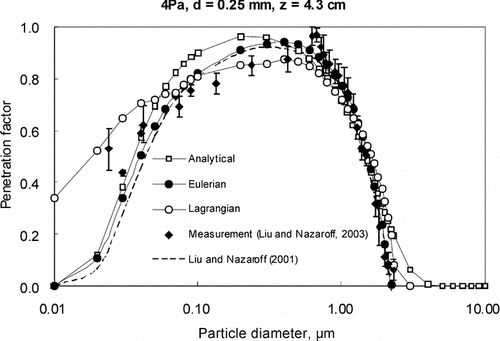
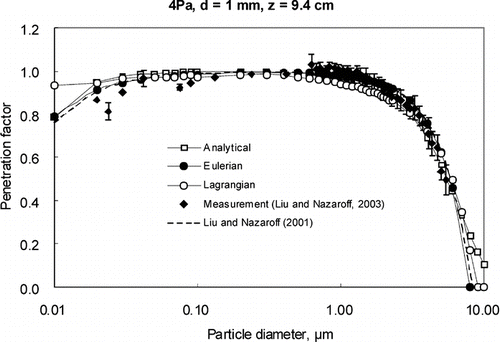
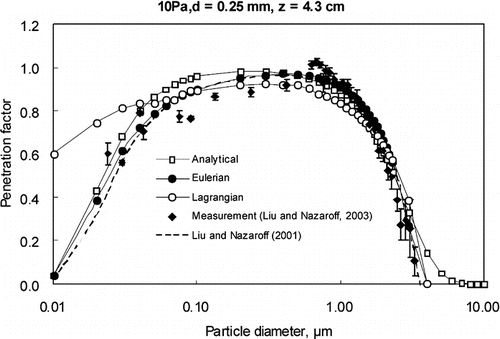
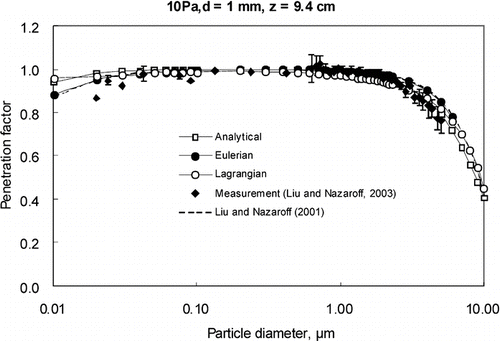
, , , present the prediction results of the three modeling approaches as well as the measured results and modeling results by CitationLiu and Nazaroff (2001) under four different conditions (i.e., Case 1, Case 2, Case 3, and Case 4).
For a given pressure difference, we observe that the penetration coefficient is almost unity for particles of 0.1–0.5 μ m when the crack height is 0.25 mm, and for particle of 0.02–7 μ m when the crack height is 1 mm. Particles outside of this size range present lower penetration coefficient as they are expected to deposit on crack surfaces by means of Brownian diffusion (for finer particles) or gravitational settling (for coarser particles). For crack height d = 1 mm, most of the particle penetration coefficients are greater than 0.9, while for d is smaller than 1 mm (d = 0.25 mm), penetration varies significantly. Compared the results under different crack lengths, we can see that penetration is significantly reduced in the longer cracks for many particle sizes. and present the predicted penetration for the straight-through cracks under various pressure difference, Δ P = 4 and 10 Pa, respectively. The results indicate that penetration coefficient increases under larger pressure difference. For instance, the penetration coefficient of 0.03 μ m particles with Δ P = 10 Pa is about 0.81, but only 0.65 with Δ P = 4 Pa. and also show similar observation that the penetration coefficient of 5 μ m particles with Δ P = 10 Pa is about 0.82, but only 0.63 with Δ P = 4 Pa. These results show that the influence of the key parameters, such as particle diameters, crack height and length and pressure difference on particle penetration coefficient were captured appropriately by the three approaches.
Inferring from the results, it could be found that the results predicted by the three approaches generally agree well with the experimental results within a certain range of particle sizes, while some of them show relative larger errors for particle sizes outside the range. Eulerian model satisfied best for all studied range of particle diameters among the three models. The results of the analytical method presented in this paper and the results of the simplest analytical method in Equation (Equation4) (CitationLiu and Nazaroff 2001) are very close to those of the Eulerian model. For coarse particles (d p > 1 μ m), gravitational settling is dominant for deposition; while Brownian diffusion controls the deposition for fine particles (d p < 0.1 μ m). The similarly in results are not surprising as these approaches incorporated the main deposition mechanisms when particles penetrating through a single straight crack. Nevertheless, we consider that the Eulerian approach is more flexible as it can incorporate different deposition mechanisms in cracks for different conditions. and indicate that the predicted results by the Lagrangian model agree worst for fine particles (d p < 0.1 μ m). The most plausible reason for the poor performance is that the Lagrangian approach models a weaker effect of the Brownian diffusion. To prove this, two typical analytical methods for modeling the effect of Brownian diffusion (CitationDe Marcus and Thomas 1952; CitationMartonen et al. 1996) were included in the comparison for fine particles, as shown in . The results show that only those modeled by the Lagrangian approach do not match the results of the two analytical methods. The Brownian force function in the original Lagrangian model (CitationLi and Ahmadi 1992) was replaced by the function suggested by CitationDe Marcus and Thomas (1952)in order to investigate the accuracy of the Brownian force in the original Lagrangian model. The function suggested by CitationDe Marcus and Thomas (1952) which represents the relationship between penetration factor and diffusion was transformed into the relationship between Brownian force and diffusion. Such modification was implemented in FLUENT. As can be seen in , the results of modified Lagrangian model also do not match the results of the measurements and the other models. The problem of Lagrangian model lies on the approach itself instead of the Brown force function. According to Fick's law, Brown diffusion depends on particle concentration gradient. However, the information of particle concentration gradient cannot be obtained when calculating the Brown force by Lagrangian approach. It should be pointed out that the calculation of particle trajectory does NOT depend on the particle concentration gradient, which may make the simulation of Brownian diffusion inaccurate. Similar conclusion was also reported by CitationRobinson et al. (1997) and they suggested that Fluent DPM was unable to model molecular diffusion. This preliminary analysis deserves to be further extended and studied.
FIG. 6 Comparison of different methods for modeling the effect of Brownian force for aluminum cracks for case 1 (fine particles).
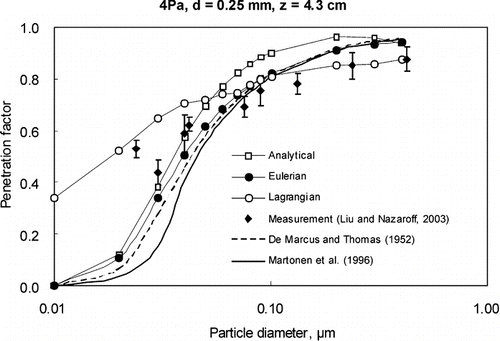
FIG. 7 Comparison of the results of modified Lagrangian model with other data for aluminum cracks for case 1 (fine particles).
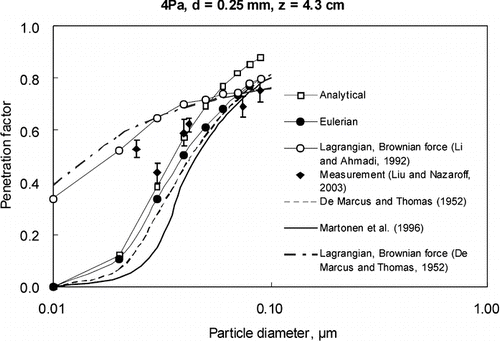
summarizes the comparisons of the three approaches for particles in different range of sizes, and it includes all the cases studied except for the case 5 where the inner surfaces of the crack are rough, and this case will be analyzed separately in the next paragraph. The analytical model costs minimum computing resources as it is an analytical expression of solving an ODE, while both the Eulerian and Lagrangian models need numerical simulation by discretizing the governing equations into algebraic equations. The Lagrangian model costs more computing resources than the Eulerian model as it resolves the air velocity distribution numerically, and the tracking of a large number of particle trajectories will also cost many resources.
TABLE 2 Summary of the performance of the presented three approaches for the eight smooth inner surfaces cases
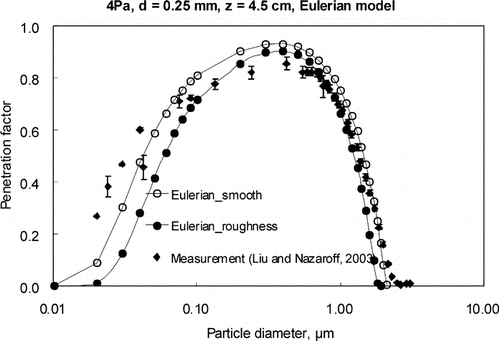
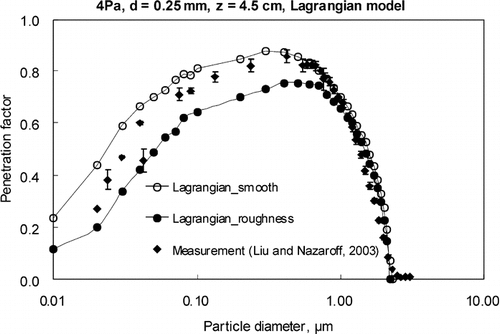
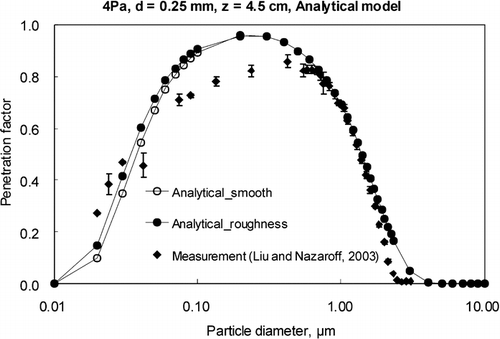
, , show the comparison of the presented three approaches with the measurement of strand board case (Case 5), respectively. As there is no information about the height of the effective roughness of the strand board (CitationLiu and Nazaroff 2003), we assumed this value instead of assigning to the models. After checking the relative error calculated by the equation shown in for different values of shifted distance, we found that shifted distance of 32 μ m for particle concentration boundary layer yielded satisfactory results. The calculation results of relative errors for using both the rough and smooth inner surfaces treatments for case 5 are listed in . From the results, we could find that after adjusting the boundary conditions to incorporate the “intercept” effect of roughness on particle deposition in the cracks, the results agree better with the measurements for all the three approaches. Similar adjustment was also reported in a previous study to account for the deposition boundary for sandpapers (CitationLai 2005). Thus, we could predict penetration coefficient better by including the approaches presented above. However, as the wall roughness is always irregular with complex texture in reality, it is hard to deduce a universal rule for the shifted distance of velocity boundary layer theoretically. Furthermore, the presence of roughness not only contributes the “intercept” effect, but also changes the boundary layer of the airflow over the surfaces. Therefore, the relative errors for the rough inner surfaces cases are still relative large, as shown in .
TABLE 3 Comparison of the relative errors of the presented three approaches by treating the inner surfaces as smooth or rough for case 5
FIG. 8 Comparison of analytical model predictions with experimental data for strand board cracks for case 5.
4. DISCUSSION
All of the three approaches assume that the crack configuration is straight-through. For real cracks, the irregularity of the crack shape may have a significant influence on the penetration coefficient. Thus, we have to set up a much more practical model, like a L-shaped model or a double-bend model measured by CitationLiu and Nazaroff (2003), as surrogates of leakage paths for building envelopes. In fact more experimental/measured data in practical conditions are needed to validate the models to cover a wider range of environmental conditions/parameters.
In reality the airflow from outdoor to indoor through the building cracks fluctuates due to the unsteady of the pressure difference created by the external wind pressure. The temperature gradient along the cracks may influence particle penetration, which may be expected a dominant factor during summer and winter seasons. The applicability of the presented approaches for such complicated cases needs further exploration.
Another limitation of the analysis is related to the assumption that particles are immediately removed once they deposit on crack surfaces. However, in real situations, deposited particles will accumulate inside cracks. The deposited particles are subject to resuspension when a burst of high differential pressure occurs. Particle resuspension is a more complicated scenario and it demands further study to advance our capability in predicting pollutant penetration.
5. CONCLUSION
We predicted the particle penetration coefficient through a straight crack in a building envelope by presenting three different approaches, an analytical approach, an Eulerian approach and a Lagrangian approach. The results were compared with the published measured data by CitationLiu and Nazaroff (2003). The conclusions drawn based on the presented results are as follows:
-
All the three models predicted particle penetration coefficient well for particles in the range of 0.4–1.2 μ m for the cases where the inner surfaces of the cracks are smooth, while the Eulerian model shows the best agreement with the measurements.
-
Both the results of the analytical method presented in this paper and the results of the simplest analytical method in Equation (Equation4) (CitationLiu and Nazaroff 2001) are very close to those prediction by Eulerian model.
-
The Lagrangian model cannot predict very well for particles smaller than 0.1 μ m as the Lagrangian approach models a weaker effect of the Brownian diffusion. To accurately model Brownian diffusion is critical and challenging for Lagrangian model.
-
For cracks with rough inner surfaces, the results agree better with the measurement data after adjusting the boundary conditions by shifting the inner surfaces a certain distance virtually, which is expected to incorporate the intercept effect of wall roughness on particle deposition.
This work was sponsored by the National Natural Science Foundation of China (Grant No. 50908127) and partially supported by a grant from City University of Hong Kong (7002378).
Notes
aThe computing time is based on the same personal computer with Intel® Core™ Duo CPU T2450 @ 2.00 GHz and RAM 1.0 GB DDR2.
bAveraged error is defined as:
cStandard deviation of the error is defined as:
σ = √∑(R
p
− 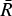 )2/N
p
)2/N
p
b ,
c The footnotes b and c are the same as shown in .
REFERENCES
- De Marcus , W. and Thomas , J. W. 1952 . Theory of a Diffusion Battery , Oak Ridge, TN : US Atomic Energy Commission, Oak Ridge National Laboratory .
- EPA . 2005 . Review of the National Ambient Air Quality Standards for Particulate Matter: Policy Assessment of Scientific and Technical Information OAQPS Staff Paper
- FLUENT Inc. 2005 . Fluent 6.2 User's Guide , Lebanon, NH : Fluent Inc. .
- Fuchs , N. A. 1964 . The Mechanics of Aerosols. , New York : Pergamon .
- Hinds , W. C. 1982 . Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles. , New York : Wiley .
- Lai , A. C. K. 2005 . Modeling Indoor Coarse Particle Deposition onto Smooth and Rough Vertical Surfaces . Atmos. Environ. , 39 : 3823 – 3830 .
- Li , A. and Ahmadi , G. 1992 . Dispersion and Deposition of Spherical Particles from Point Sources in a Turbulent Channel Flow . Aerosol Sci. Technol. , 16 : 209 – 226 .
- Licht , W. 1980 . Air Pollution Control Engineering. , New York : Marcel Dekker, Inc. .
- Liu , D. L. and Nazaroff , W. W. 2001 . Modeling Pollutant Penetration Across Building Envelopes . Atmos. Environ. , 35 : 4451 – 4462 .
- Liu , D. L. and Nazaroff , W. W. 2003 . Particle Penetration through Building Cracks . Aerosol Sci. Technol. , 37 : 565 – 573 .
- Martonen , T. , Zhang , Z. and Yang , Y. 1996 . Particle Diffusion with Entrance Effects in a Smooth-Walled Cylinder . J. Aerosol Sci. , 27 : 139 – 150 .
- Mathworks Inc. 2007 . MATLAB R2007a User's Guide Natick, MA
- Middleman , S . 1997 . An Introduction to Mass and Heat Transfer: Principles of Analysis and Design. , New York : John Wiley & Sons .
- Richardson , L. F. 1910 . The Approximate Arithmetical Solution by Finite Differences of Physical Problems Involving Differential Equations, with an Application to the Stresses in a Masonry Dam . Phil. Trans. Royal Soc. London , 210 ( A ) : 307 – 357 .
- Roache , P. J. 1994 . Perspective: A Method for Uniform Reporting of Grid Refinement Studies . ASME J. Fluids Engineer. , 116 : 405 – 413 .
- Robinson , R. J. , Snyder , P. and Oldham , M. J. 1997 . Comparison of Particle Tracking Algorithms in Commercial CFD Packages: Sedimentation and Diffusion . Inhal. Toxicol. , 19 : 517 – 531 .
- Taubee , D. B. and Yu , C. P. 1975 . Simultaneous Diffusion and Sedimentation of Aerosols in Channel Flows . J. Aerosol Sci. , 6 : 433 – 441 .
- Tian , L. , Zhang , G. , Lin , Y. , Yu , J. , Zhou , J. and Zhang , Q. 2009 . Mathematical Model of Particle Penetration Through Smooth/Rough Building Envelop Leakages . Build. Environ. , 44 : 1144 – 1149 .
- Wu , J. and Zhao , B. 2007 . Effect of Ventilation Duct as a Particle Filter . Build. Environ. , 42 : 2523 – 2529 .
- Zhao , B. , Chen , C. and Tan , Z. 2009 . Modeling of Ultrafine Particle Dispersion in Indoor Environments with an Improved Drift Flux Model . J. Aerosol Sci. , 40 : 29 – 43 .
- Zhao , B. and Wu , J. 2006 . Modeling Particle Deposition onto Rough Walls in Ventilation Duct . Atmos. Environ. , 40 : 6918 – 6927 .
- Zhao , B. , Zhang , Y. , Li , X. , Yang , X. and Huang , D. 2004 . Comparison of Indoor Aerosol Particle Concentration and Deposition in Different Ventilated Rooms by Numerical Method . Build. Environ. , 39 : 1 – 8 .
- Zhu , Y. , Hinds , W. C. , Krudysz , M. , Kuhn , T. , Froines , J. and Sioutas , C. 2005 . Penetration of Freeway Ultrafine Particles into Indoor Environments . J. Aerosol Sci. , 36 : 303 – 322 .