The Role of Error Covariances in Estimation of Aerosol Number Concentrations

Abstract

The evolution of error covariance and its impact in Kalman Filtering are examined. A synthetic aerosol size distribution and an associated error covariance matrix are used as an input for a tangent-linear box model simulating aerosol microphysics. The evolution of the error correlation structures are found to be robust with respect to changes in ambient vapor conditions and nucleation schemes. The near-diagonal error correlations evolve only modestly for particles larger than ∼20–30 nm, and the nucleation and condensation processes cause strong correlations between number density errors of small (below 10 nm) and large (above 100 nm) particles. The evolving error covariances significantly improve the estimation accuracy of the Kalman Filter in case of synthetic observations.

1. INTRODUCTION

Instruments for measuring aerosol microphysical properties, such as the Differential Mobility Particle Sizer (DMPS), provide indirect information of the aerosol population. Interpretation of the DMPS measurements in terms of aerosol size distribution is obtained by solving an inverse problem (e.g., Voutilainen 2001). For a single DMPS and one time instant, this is definitely an adequate procedure. In situ measurement time series, however, cover time intervals ranging from hours to years and the measurements are taken, for instance, during new particle formation events (e.g., Dal Maso et al. 2005). Moreover, the size distribution measurements are often complemented by additional instrumentation, such as a Hygroscopic Tandem DMA system (H-TDMA) or Aerosol Mass Spectrometer (AMS), both of which provide information on the particle chemical composition (Canagaratna et al. 2007; Swietlicki et al. 2008). Gas-phase measurements performed with, for example, a Proton Transfer Mass Spectrometer (PTR-MS) (de Gouw and Warneke 2007) can be further employed to complement measurements of aerosol microphysical properties. Simultaneous inversion of measurements made of different quantities at incoherent times and with different instruments with their specific error characteristics is challenging. More generally, tools for solving nonstationary inversion problems of multi-source data must be employed. Kalman filter (Kalman 1960) offers one option to advance toward estimation of the aerosol population properties, given multi-source aerosol measurements and an evolution model of aerosol microphysics.

The Kalman filter (KF) consists of two update steps: time evolution updating and observation updating. First, in the time evolution updating, the state (vector) of the aerosol population is evolved in time using a computational dynamical model. The model prediction is used as a prior estimate of the system state at the observation time. The prediction spans from the previous observation time to the current one. In our case, the model is an accurate evolution model of aerosol size distribution including all relevant microphysical processes. The error covariance matrix of the prior state estimate essentially tells how accurate the prior state is and how the errors are correlated between the state variables. On the diagonal of this matrix, there are the error variances of each prior state element. The off-diagonal elements express the error covariance between different prior state elements. This matrix is evolved in the time evolution updating according to the tangent-linear model dynamics. Then, in the observation updating, the prior state is updated with the observational information, according to the Bayes formula of conditional probability. The result is a posterior state estimate. The error covariance of the posterior state estimate is also updated, resulting in the estimate of the accuracy of the posterior state. Generally, the posterior state estimate is more accurate than the prior estimate due to the introduction of observational information, and thus the error covariance decreases at this step. Finally, these updating steps are repeated at later observation times. KF can thus be seen as a sequential application of the Bayesian estimation.

In aerosol physics, considerable effort has been devoted to improving aerosol microphysical models (e.g., Stier et al. 2005; Boy et al. 2006; Kokkola et al. 2008). These results are directly applicable in the time evolution updating of the system state in the KF. There is also emerging interest in the specification of error covariance for aerosol populations. Benedetti and Fisher (2007) developed a static description of the prior state error covariance for a global aerosol model for environmental prediction applications. The state evolution model (Morcrette et al. 2006) describes the aerosol mixing ratio in a three-dimensional grid. The error covariance matrix contains the error variance of the aerosol mixing ratio in each grid point, and their spatial (horizontal and vertical) covariance between different locations. Kahnert (2008) developed a static nonseparable spectral formulation of the aerosol background error covariance for a limited area atmospheric transport model (Robertson et al. 1999), based on the earlier work of Berre (2000), and illustrated the analysis increments obtained in a single observation experiment of aerosol backscatter coefficient using 3-dimensional variational data-assimilation technique. In this article, unlike in Benedetti and Fisher (2007), the aerosol model is quite comprehensive and a multi-variate error covariance is required among different aerosol species, size classes, and Fourier wave components of the spatial discretization.

In this article, the state evolution model is a size-segregated, zero-dimensional box model, and there are thus no spatial dimensions, nor spatial error covariance. The model is multivariate, where as the size distribution of the aerosol population is expressed by the number density for different size classes (or “bins”). There are thus correlations between the number density errors in different size bins. In contrast to the static prior error covariance formulations of, for example, Benedetti and Fisher (2007) and Kahnert (2008), temporal aspects of the multi-variate error covariance are emphasized. Generally, little is known of the tangent-linear evolution of error covariance in aerosol microphysics. This study is a preparation for approaching the multi-source aerosol microphysical measurement data from the non-stationary inversion problem point-of-view. First the tangent-linear evolution of the error covariance and then its impact in the context of Kalman filtering are studied.

2. METHODS AND MATERIALS

2.1. Extended Kalman Filter

The KF holds for linear problems. The evolution models usually considered in aerosol microphysics are non-linear, and a version of KF, called an Extended KF (EKF), can instead be applied. For a comprehensive textbook treatment of non-stationary inverse problems and Kalman filtering, we refer to Kaipio and Somersalo (2004). The motivation for using the EKF is to improve the time evolution updating by taking an advantage of an accurate non-linear evolution model. This model can be directly applied to the state (vector) update. Let x denote the state vector and M the non-linear computational evolution model. The time evolution updating for the state at time k+ 1 is obtained by

The KF assumes Gaussian error probability densities which remain Gaussian in linear transformations. For the error covariance (matrix) update in EKF, M cannot be directly applied. Instead, it is required that M is differentiable and a Jacobian of M, denoted by M, can be constructed. The time evolution updating of the error covariance at time k+ 1 reads

where C _k+1 is the error covariance of the state estimate x _k+1 prior to observation updating, and G _k+1 is the error covariance source term due to the state noise (such as numerical errors). In this article, it suffices to note that generally very little is known about G _k+1, and it is omitted. Instead, we attempt to generate a synthetic but justified C _k matrix, and apply the time evolution updating for the error covariance, according to

which is reorganized to the form

since C _k is symmetric and equals C ^T _k . This form is preferred as it allows employment of the tangent-linear model M twice, instead of M and its transpose.

Observation updating involves calculating the Kalman gain matrix, which contains the inverse of the sum of the observation and background error covariance matrices in observation space. Singular Value Decomposition (SVD), in which the matrix is decomposed in to eigenvectors and eigenvalues, was used to calculate the inverse matrix. If the covariance matrix is nonsingular, the inverse matrix provided by SVD exactly matches the correct inverse matrix. If the covariance matrix approaches singularity, SVD can be used to calculate a pseudo-inverse matrix by omitting the eigenvectors corresponding to very small eigenvalues, which is referred to as reducing the rank of the matrix.

A synthetic error covariance matrix C _k is used in this article. This is because there is no information available on how such an error covariance matrix might look like in practical applications, and the aim here is to obtain basic understanding of the error covariance evolution. Thus a simplified and smooth covariance structure will be studied here.

2.2. Evolution Model and Its Jacobian

In this article, the model M is the University of Helsinki Multi-component Aerosol model (UHMA) (Korhonen et al. 2004). It is a sectional box model that simulates the major known processes that affect the evolution of an atmospheric particle size distribution. Nucleation rate is calculated through the activation scheme (Sihto et al. 2006). The condensation is calculated with the adjusted Fuchs-Sutugin method (Fuchs and Sutugin 1971; Lehtinen and Kulmala 2003). The coagulation kernel is calculated through the Fuchs equation (Fuchs 1964). The deposition velocity is determined according to Rannik et al. (2003) and extrapolated to particles smaller than 10 nm. Here the model is discretized so that the size distribution is presented with 50 regularly spaced (in logarithmic sense) size bins. The particle diameter in the smallest (largest) size bin is chosen to be 0.66 nm (2 μm).

In data assimilation literature (Ide et al. 1997) the Jacobian M of the non-linear model M is called tangent-linear model: it is linear around the linearization state provided by the trajectory of the non-linear model integration (i.e., a sequence of model state vectors at different time steps). Here, the tangent-linear of the UHMA model (Viskari et al. 2008) is applied.

3. TANGENT-LINEAR EVOLUTION OF THE ERROR COVARIANCE

3.1. Initial State of the Aerosol Population and Its Error Covariance

One aim of this article is to examine the time evolution of the error covariance structures due to different aerosol dynamical processes. For the computer simulations, a suitable initial aerosol particle size distribution and an associated error covariance matrix is needed. For simplicity, a synthetic log-normal aerosol particle size distribution

is chosen, where N ₀ is the peak value for the particle number concentration (2.5 × 10⁸ 1/m³), r_i is the particle radius for the size bin i, r_peak is the peak of the distribution (40 nm), and w is the logarithm of the width of the distribution (2.6). A constant number concentration x_b (10⁴ 1/m³) is added in order to avoid the particle number concentration having very small values at the tails of the distribution as it can cause numerical problems in the evolution of the error covariance. The synthetic number concentration is an idealized size distribution but realistic enough both in magnitude and general shape for these simulations. Particles smaller than approximately 2–3 nm are below the detection limits of the current aerosol instruments (Kulmala et al. 2007). The synthetic number concentration in those size classes is retained here for simplicity and symmetry.

A simple error covariance matrix, a band matrix, will be used here. It is a sparse matrix, whose nonzero elements are confined to a diagonal band, comprising the main diagonal and one or more diagonals on either side. This means that errors in the state vector variables (here: aerosol model size bins) are correlated over a corresponding “distance.” The error covariance matrix associated to the synthetic size distribution is constructed as follows: The error variance σ ² _i of the number concentration in size bin i at the initial time (i.e., the diagonal elements of C _k ) is set to be proportional to the number concentration in the respective size bin through the formula

The synthetic size distribution and the associated error standard deviation are shown in Figure 1. Note that 10, 31.6, and 100 nm particle diameter corresponds to –8, –7.5, and –7, respectively, on the x-axis of Figure 1. The initial error covariance of the size distribution (i.e., the off-diagonal elements of C _k ) is constructed as follows: The error correlation between adjacent size bins i and j, cov _i,j , is set to 0.25. The error covariance between the size bins i and j is thus

FIG. 1 Initial size distribution (circles) and error standard deviation distribution (squares). On x-axis, 10-based logarithm of the particle diameter (m), on y-axis, number concentration (particles per cubic meter). On x-axis, 10 (100) nm particles correspond to –8 (–7).

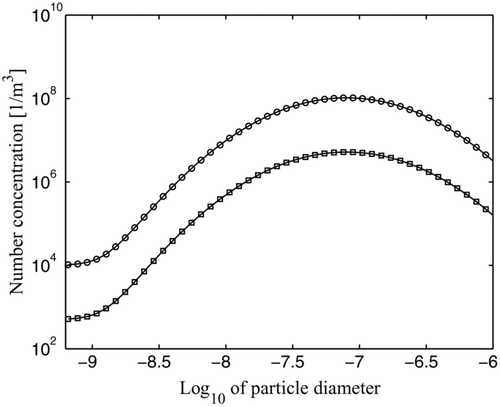
The resulting tri-diagonal error covariance structure is simplistic, but sufficient and convenient for the purposes of this study.

3.2. Simulation Details

In the experiments, there were two separate ambient vapors: sulphuric acid and an organic compound, which has a smaller density and a greater molar mass than the sulphuric acid. The vapor saturation concentration was set equal to zero for sulphuric acid and 10¹² 1/m³ for the organic compound (Kulmala et al. 1998; Kerminen et al. 2000; Anttila and Kerminen 2003). The production terms for both vapors were prescribed constants, with the organic compound having a slightly larger production term. The vapor sinks were determined by condensation, acting as a sink for both vapors, and nucleation, which acted as a sink for the sulphuric acid. The simulations were first performed with the ambient sulphuric acid vapor only, where the dry composition of the particles consisted solely of sulphuric acid and then repeated with the addition of the organic vapor, where 60% of the initial particle dry composition was sulphuric acid and the remaining 40% was the organic compound. The amount of water in particles was calculated through the particle dry composition. The organic compound was not tested separately as it would not effectively condense on the smallest particles due to its nonzero saturation vapor pressure, and consequently new particle formation would be effectively suppressed.

The time window for the simulation was chosen to be 1800 s (30 min). It is long enough for the effects of the aerosol dynamics to become clear in the covariance evolution, yet short enough to be within the validity of the tangent-linear hypothesis (Viskari et al. 2008). The ambient vapor concentration profile for sulphuric acid is illustrated in Figure 2.

3.3. Results and Analysis

The results at the end of the 30-min simulation period are illustrated by showing the evolved size distribution with the corresponding error standard deviation (Figure 3a), and the evolved error correlation matrix (Figure 3b). A correlation matrix, instead of the covariance matrix, is presented here to make the inter-comparison of different correlation structures easier. The evolved size distribution and its error standard deviation (Figure 3a) are dominated by newly formed particles (below 5 nm) and the peak of the initial size distribution (80–100 nm). Two significant correlation structures are visible in the error correlations (Figure 3b). There is a considerable negative error correlation (below −0.3) between large, ∼110–130 nm, and small particle sizes, and a very strong positive error correlation among particles smaller than 5 nm. The correlation mechanism is as follows: The new particle formation rate is proportional to the ambient sulphuric acid vapor concentration, and thus an error in the condensation sink value directly affects the new particle formation rate. A negative (positive) error in the size bin number concentration leads to a lower (higher) condensation sink and a higher (lower) ambient sulphuric acid vapor concentration, which in turn will increase (decrease) the new particle formation rate. This mechanism is stronger the larger the particle surface area is, and the most significant correlation will be with the particle sizes with the greatest combined surface area; for this particle size distribution, it is for particles between 100–140 nm. The condensation process creates an opposite correlation mechanism between small and large particles as the higher ambient vapor concentration also increases the condensational growth rate, which increases the particle flux to larger sizes and decreases the number concentration in the smaller particle sizes. Thus through the condensation process, a negative error in the large particle sizes creates a negative error in smaller particle sizes. In the particle size range ∼10–100 nm, the correlation structure becomes more complex due to the counteracting effects between incoming and outgoing particles in a particle bin, but the correlations are generally weak (less than 0.1) in this particle size range. With particles smaller than 10 nm, the correlation caused by the nucleation process is dominant, though the opposing correlation caused by the condensation process decreases it slightly.

FIG. 2 Ambient sulphuric acid vapor concentration profile over the simulation period. On x-axis, time (s), on y-axis, vapor concentration (molecules per cubic meter).

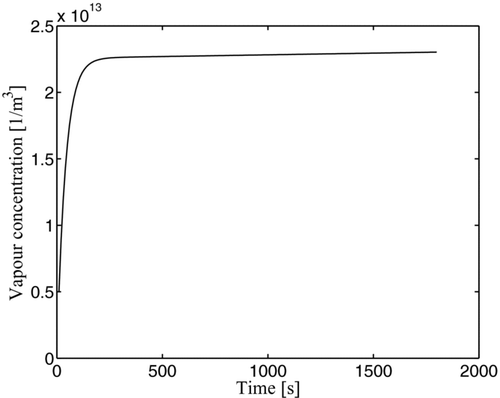
FIG. 3 (a) The particle size distribution (circles) and error standard deviation distribution (squares) after 1 800 s. On x-axis, 10-based logarithm of the particle diameter (m), on y-axis, number concentration (particles per cubic meter). (b) The corresponding error correlation structure. On x- and y-axis, 10-based logarithm of the particle diameter (m). Isolines represent correlation values of –0.3, –0.1, 0, +0.1, +0.3, and +0.5.

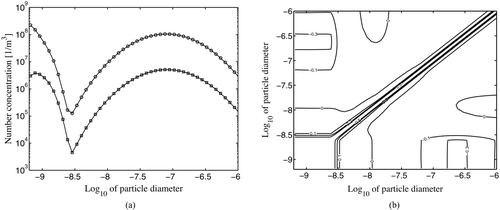
There is furthermore (Figure 3b) a clearly visible spreading of the error correlation near the diagonal of the matrix, which is more pronounced in the smaller particles sizes and decreased towards the larger particles. This is due to the rapid growth of the small particles, which tends to couple the errors in these particle sizes with the errors in smaller sizes. Here, the intensity of error coupling (i.e., correlation), depends on the proportion of shifted error in the particle number concentration to the larger particle size bin as compared to the error shifting out of it. As the particle sizes become larger, the condensational growth becomes weaker, and this proportion decreases, making the positive error coupling weaker. At the final time of the simulation, almost all particles smaller than 5 nm are newly formed. The error in their number concentration is almost solely due to the error in the ambient vapor concentration, which causes an error in the rate of nucleation, explaining the strong error correlation.

The sensitivity of the tangent-linear evolution for varying vapor profiles’ inclusion of an organic vapor and an alternative nucleation scheme was tested to assess the robustness of the previous findings. First, different sulphuric acid vapor profiles were utilized to understand the vapor production effects on the error correlation structures as both the nucleation and condensation processes are directly related to the gas-phase concentration of sulphuric acid. The main result (not shown) is that if the vapor production term is high enough, exact value dependent of the particle size distribution, opposing error correlations due to nucleation and condensation processes become as significant. In this situation, the correlation structure consists of small, intense dipoles of positive and negative correlations and the shape of the deviation distribution differs significantly from the particle size distribution for particles smaller than 10 nm.

Two alternative model formulations were also tested. First, the nucleation rate was calculated through the kinetic scheme (Sihto et al. 2006). Second, an ambient organic vapor was present in the system. In both cases, the particle number concentration and variances changed considerably (not shown), but the respective error correlation structures remained similar to those presented in Figure 3b. These results indicate that the error correlation evolution is not sensitive to these changes.

4. THE KALMAN FILTER APPLICATION

4.1. Experiment Details

The impact of the modelling accuracy of the error covariance on the Extended Kalman Filter (EKF) in recovering a synthetic particle size distribution is studied next. A so-called “identical twin” experiment setup was used. First, the evolution of the reference state (“truth”) is simulated over a 12-h time period using Equation (5) as the initial state. Synthetic observations of state variables are drawn from the reference state at 30-min intervals from 10 randomly selected size bins added with Gaussian noise. Both the size bins and the observation noise vary from one time interval to another. Next, an incorrect initial state (“prior state”) is evolved for 30 min, and a new state is estimated applying EKF with the 10 synthetic observations at the corresponding time. Time evolution and observational updating are sequentially repeated over the 12-h period. The observational and background error variances were set equal, equally weighting both information sources. The incorrect initial particle size distribution (“prior state”) is a sum of two log-normal distribution, with peaks of 10⁸ and 2*10⁸ 1/m³, peak radii 10 and 80 nm and widths 2.0 and 2.4, respectively. Initial particle size distributions are shown in Figure 4. The initial error covariance matrix is diagonal, with error standard deviations determined through Equation (6).

FIG. 4 The initial reference particle size distribution (circles) and the initial filtered size distribution (squares). On x-axis, 10-based logarithm of the particle diameter [m], on y-axis, number concentration [particles per cubic meter].

Three EKF experiments were performed. The first estimation with EKF was done with a static initial diagonal error covariance matrix (M replaced in Equation (4) by an identity). Second, the estimation was repeated with a fully evolving error covariance matrix starting from the diagonal matrix. Finally, the estimation was repeated with a reduced rank covariance matrix (rank 40 instead 50).

In order to assess estimation errors when applying different covariance matrices, the following error measure is introduced:

where x _r,i (t) and x _e,i( t) are the number concentrations of the reference and estimated size distributions, respectively, in size bin i at the time t.m is the total number of size bins. Although A is not unambiguous, it is practical in illustrating convergence of the estimation toward the “truth.”

4.2. Results and Analysis

The evolution of error measure A over time for the static covariance matrix, for the fully evolving error covariance matrix and the reduced error covariance evolution with the rank 40 are presented in Figure 5. The estimation error decreases with all error covariance matrices, which represents the convergence of the estimated state and “truth.” This is because the observational influence on the estimated state accumulates with the increased number of observational updates. As expected, EKF applying the fully evolving error covariance matrix decreases the estimation error faster than the one applying the static error covariance matrix and reaches the level of estimation error compatible with the observation noise. EKF proved to be sensitive to the reduction of the rank and produced negative particle number concentrations in case the rank was below 40.

FIG. 5 The evolution of SV over iteration loops. The values represent the static diagonal error covariance matrix (circles), the fully evolving error covariance matrix (squares), and the reduced error covariance matrix with the rank of 40 (diamonds). On x-axis, time [h], on y-axis, value of SV.

In all cases with an evolving error covariance matrix, there is a sudden increase in estimation error at 8.5 h. Figure 6 presents all size distributions after 8 h (Figure 6a) and after 8.5 h (Figure 6b). With the evolving error covariance there is an erroneous shift in the particle size distribution to larger concentrations for particles smaller than 10 nm and a smaller shift to smaller number concentrations for particles between 50–200 nm. This is due to a single observation in the smallest size bin which significantly overestimates the reference state number concentration. The large filter correction is due to significant error correlation between the smallest size bin and the size bins where the EKF seems to diverge from the “truth” (Figure 3b). Thus the explanation for this filter divergence is that the covariance structures spread the observation errors to quite distant size bins.

FIG. 6 The reference size distribution (circles), the size distribution filtered with the static diagonal error covariance matrix (squares), the size distribution filtered with the fully evolved error covariance matrix (diamonds), and the size distribution filtered with the reduced error covariance matrix (crosses) after (a) 8 and (b) 8.5 h. On x-axis, 10-based logarithm of the particle diameter (m), on y-axis, number concentration (particles per cubic meter).

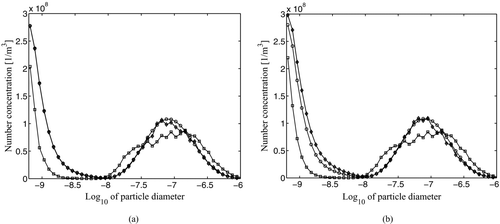
EKF was found to become unstable (not shown) if the particle number concentration changes several magnitudes over a narrow diameter range for particle smaller than 10 nm. In such cases, EKF has a tendency to produce negative number concentration estimates through the covariance terms. Both the nonlinearities in the model and the singularity of the covariance matrix are suspected to be behind this instability.

5. DISCUSSION AND CONCLUSIONS

The evolution of the error covariance of an aerosol particle size distribution in a size-segregated aerosol model was studied. The results show that the error correlation structure is dominated by the interacting nucleation and condensation processes and that the evolution of the error correlation is rather insensitive to changes in the nucleation scheme, production rate of gaseous sulphuric acid, and inclusion of a condensable organic compound. The strongest correlation patterns appeared between adjacent size bins and between the smallest particle sizes and the particles with the largest combined surface area.

The simulations were repeated with significantly different particle size distributions and error distributions, but the evolution of the error correlation structures generally remained remarkably similar. The evolved error correlation structures did differ, though, if the particle size distribution evolution caused the particle number concentration for particles smaller than 10 nm to change several magnitudes over a narrow diameter range. In such conditions, the nonlinear evolution becomes dominant for particles smaller than 10 nm. Consequently, the error correlation structure becomes very complicated and strongly dependent on the initial size distribution and its error standard deviation

The evolving error covariance matrix was applied in the Extended Kalman Filter (EKF). In an “identical twin” experiment, EKF was able to rather well recover a reference size distribution: after 10 observational updates, the estimation error decreased to one fifth of its initial value. It was discovered that EKF is sensitive to observation errors in certain particle sizes, which are strongly correlated with the errors in the rest of the particle size distribution. It was also determined that in distributions where the magnitude of the number concentrations change too steeply over a diameter range for particles smaller than 10 nm, the error covariance terms create a numerical instability and EKF can produce negative number concentrations.

Sensitivities observed in EKF estimations will require further testing in order to determine how significantly they affect the estimation accuracy. Overall the results can be interpreted as encouraging for future work on Kalman filtering applications using sectional aerosol models and real observations.

This research has been partially funded by the Academy of Finland research project 133142.