Using Statistical Regressions to Identify Factors Influencing PM_2.5 Concentrations: The Pittsburgh Supersite as a Case Study

Abstract

Using data from the Pittsburgh Air Quality Study, we find that temperature, relative humidity, their squared terms, and their interactions explain much of the variation in airborne concentrations of PM _2.5 in the city. Factors that do not appreciably influence the concentrations over a full year include wind direction, inverse mixing height, UV radiation, SO ₂ , O ₃ , and season of the year. Comparison with similar studies of PM _2.5 in other cities suggests that the relative importance of different factors can vary greatly. Temperature and relative humidity are important factors in both Pittsburgh and New York City, and synoptic scale meteorology influencing these two sites can explain much of the pattern in PM _2.5 concentrations which peak in the summer. However, PM _2.5 levels in other cities have different seasonal patterns and are affected by a number of other factors, and thus the results presented here cannot be generalized to other locations without additional study.

INTRODUCTION

The Pittsburgh Air Quality Study (PAQS) was a $7 million program funded by the U.S. Environmental Protection Agency and the U.S. Department of Energy. The main data collection effort was conducted at the Pittsburgh Supersite in Schenley Park, adjacent to the Carnegie Mellon University campus (Wittig et al. 2004). The overall goal of the study was to improve our understanding of the factors affecting concentrations of airborne particulate matter, especially PM_2.5, in eastern urban areas such as Pittsburgh. PM_2.5 is important because high concentrations have been associated with health effects, materials damage, ecosystem damage, and reduced visibility. PM_2.5 is also believed to contribute to climate change (Seinfeld and Pandis 2006).

In a previous paper (Chu et al. 2009), we describe a simple statistical procedure to identify specific sources that are likely contributing to PM_2.5 on days of elevated concentration. The procedure involves determining an effective wind direction over an averaging period that depends on estimated transport times, and examining patterns in wind direction frequency associated with periods of high PM_2.5 concentration.

We apply the method to days of high concentration in the PAQS dataset to reach the conclusion that a combination of elevated background PM_2.5 levels and local emissions from a few large sources in the Pittsburgh area causes exceedances of the National Ambient Air Quality Standard. It is likely that the background concentrations consist mostly of secondary particles created from gaseous precursors emitted from sources far upwind, while the local emissions are mostly primary particles.

Here we use the full PAQS dataset, which covers low as well as high PM_2.5 concentrations, to explore the importance of several explanatory variables, including temperature, relative humidity, wind direction (for windspeeds greater than 1 m/s), UV radiation, SO₂ concentration, O₃ concentration, mixing height, and season of the year, as well as interactions among some of these variables. The regressions and statistical tests are used to identify those variables that have a major affect on PM_2.5 concentrations as well as on changes in PM_2.5 concentration from one averaging period to the next.

EXPERIMENTAL METHODS

The PAQS dataset covers the period July 2001 to September 2002, although here we will use exactly one year of data starting September 1, 2001. The Supersite location was about six kilometers east of downtown Pittsburgh in Schenley Park, adjacent to the Carnegie Mellon University campus at one of the highest locations in the city. Although the site is in the middle of a high density urban area, there are no heavily traveled roads within a few hundred meters of the site. There are no major stationary sources within 2 km of the site except one source that has been shown statistically to have negligible influence (Chu et al. 2009). PM_2.5 was measured with a Rupprecht and Patashnick Model 1400A Tapered Element Oscillating Microbalance (TEOM), as described in Chu et al. (2009). Temperature and relative humidity were measured with a Campbell Scientific HMP45C Probe, while windspeed and wind direction data were obtained with a Met One 014A 3-cup anemometer and a Met One 024A wind vane, respectively. Ultraviolet radiation was measured with a Kipp & Zonen CUV3 UV Radiometer, which is sensitive over the entire range of UVA and UVB. SO₂ concentration was determined with an API model 100A Analyzer, and O₃ was measured with an API model 400A Analyzer. All of the data were obtained about 3 m above ground on the roof of a trailer positioned in the middle of a grassy field. Data have been combined to provide ten-minute average values throughout the study period for all of these instruments.

Balloon temperature measurements are taken at the Pittsburgh airport at 12:00 and 24:00 GMT (7 AM and 7 PM in Pittsburgh, Eastern Standard Time) and transformed into a vertical virtual potential temperature profile. To obtain the mixing height from the temperature profile, we used a variant of the Holzworth (1967) method applied to morning conditions, which intersects the measured virtual potential temperature with an offset line. Holzworth uses an offset line of 5°C added to the minimum surface temperature observed between 2 AM and 6 AM local standard time, “established arbitrarily to allow for urban-rural differences in morning surface temperatures and for some solar heating of the surface after sunrise” (Holzworth 1967, p. 1040).

Because we needed mixing height estimates at each hour, we chose to use data provided by the Rapid Update Cycle (RUC) model (Benjamin et. al. 2004), which estimates the temperature profile at a grid of points over the entire country. We used the closest grid point which is roughly 10 kilometers from the Pittsburgh airport. Since the airport is no longer entirely rural and RUC takes some ground heating into account, we used a maximum offset of 1.5°C (Benjamin, personal communication). The offset for each hour was taken to be proportional to the solar radiometer data, scaled to be 1.5°C at the solar zenith, with a minimum of 0.1°C. Values of mixing height lower than 100 m are set equal to 100 m to avoid singularities caused by ground level mixing height (infinite inverse mixing height) and to account for the fact that no emissions occur as low as ground level (z = 0). The explanatory variable used in the regressions is inverse mixing height, so the maximum value is 0.01 m^–1.

STATISTICAL METHODS

Linear regression assumes a dependent variable can be modeled by a linear combination of coefficients and explanatory variables (explanatory variables are also called independent variables in the regression, but they are not necessarily statistically independent):

where y = (y ₁, …, y _n ) is the vector of observations of the dependent variable, x _j = (x _1j , …, x _nj ) is the vector of observations of thej ^th explanatory variable, β _j are the coefficients, and ϵ _i are error terms. The task here is to find the values of β _j that provide the best fit to the data based on minimizing the least squares error.

The explanatory variables were chosen based on the data we had available from the supersite program. These variables included concentrations of SO₂ and O₃ as well as meteorological observations, so each x _j could be one of those variables or its transform. The dependent variable y could be the observed PM_2.5 concentration or alternatively the difference of two consecutive observed PM_2.5 concentrations. The former choice corresponds to building a model to explain the observed PM_2.5, and the latter corresponds to building a model to explain the change of the observed PM_2.5. We tried both models in our analysis.

For all the regressions presented here, there were 1,155 observations over one year. The limiting factor determining sample size was the number of 3-h time periods for which average values of all variables of interest were available.

RESULTS AND DISCUSSION

We start with Model 1, which predicts PM_2.5 concentration by explanatory variables x _j as listed in Table 1. The variables represented are:

• [SO₂]—SO₂ concentration; Temp—temperature; Humid—relative humidity

• [O₃]—O₃ concentration; UV—intensity of downwelling ultraviolet radiation; iMHc—inverse mixing height, corrected to a maximum 0.01 m⁻¹

• rSE, rS, rSW—fraction of time wind is from the direction southeast, south, and southwest

• fsummer—categorical variable denoting the influence of season, equal to 1 for Summer and 0 for the other seasons, where the seasons are defined by their calendar dates (Summer is June 21–September 21, etc.)

• ffall—same as fsummer but equal to 1 for Fall

• fwinter—same as fsummer but equal to 1 for Winter

• Intercept—the value of PM_2.5 concentration when all explanatory variables are zero, i.e., β₀ in Equation (1).

• There are a few points to note regarding these explanatory variables.

1. All the explanatory variables used in the regressions are 3-h averages, except for fsummer, ffall, and fwinter.

2. The directions for rSE, rS, and rSW are defined by potential local sources, where southeast corresponds to 112°–142°, south corresponds to 146°–201°, and southwest corresponds to 222°–254° (Chu et al. 2009).

3. The categorical variables fspring, fsummer, ffall, and fwinter account for the effect of season. By setting fspring = 0, we can interpret the coefficients β _fsummer , β _ffall , and β _fwinter as the difference in PM_2.5 concentration between spring and each of the other three seasons. This is done since the four categorical variables plus the intercept β ₀ are not linearly independent, and hence one variable must be eliminated to avoid a singularity in the solution. The values of the three coefficients are obtained by fitting the model, and they are interpreted as average values of the difference in concentration between each season and spring. These categorical variables have been included to determine whether the physically and chemically based variables in Table 1 successfully explain most of the variation in PM_2.5; the effects of the four seasons should be negligible, for example, if the variation in PM_2.5 is due entirely to changes in the variable Temperature.

TABLE 1 Results of the linear regression Model 1 for PM_2.5 concentration as the dependent variable. The symbols *, **, and § indicate significance at 0.05, 0.01, and 0.001 levels, respectively. The adjusted r² for this model is 0.59

Explanatory variable x	j Average value	j Estimate	j Standard dev.	j j	t value	Pr(> |t|)
Intercept	—	−12.6	1.57	−12.6	−8.05	2.1E-15§
[SO2]	10.5ppb	0.450	3.05E-02	4.73	14.73	< 2E-16§
Temp	14.1°C	0.449	4.93E-02	6.31	9.09	< 2E-16§
Humidity	59.0%	0.158	1.78E-02	9.32	8.87	< 2E-16§
fsummer	—	7.53	0.950	7.53	7.93	5.3E-15§
ffall	—	−0.267	0.768	−0.267	−0.35	0.73
fwinter	—	−1.28	0.780	−1.28	−1.64	0.10
iMHc	0.00587m^− 1	319	75.4	1.87	4.23	2.6E-05§
[O3]	29.7ppb	0.194	2.06E-02	5.76	9.44	< 2E-16§
UV	7.84watts/m^2	−0.247	3.93E-02	−1.94	−6.29	4.5E-10§
rSE	0.0847	8.41	1.24	0.712	6.80	1.7E-11§
rS	0.174	5.05	0.905	0.878	5.58	3.0E-08§
rSW	0.143	3.67	1.12	0.526	3.27	1.1E-3**

The estimated value of each coefficient _j in the table has units such that the product _{j j} has units of μ g/m³. The t value is the t-statistic for testing whether each coefficient is different from 0. The last column in the table shows Pr(> | t|), also known as the p-value, which is the probability of getting a value that is at least as extreme as the observed coefficient assuming the distribution of _j is centered at zero. The column _{j j} in the table includes values that are positive and negative, and the total average modeled concentration is the sum of all terms, which in this case is equal to 22.3 μ g/m³. Because the explanatory variables have a variety of units, the product _{j j} is particularly important. Traditionally significance levels (i.e., the p-values) for each explanatory variable are considered to represent its relative importance, but here most of the explanatory variables become important since the sample size is so large. Therefore we report the products to see which variables are important contributors to the PM_2.5 concentration on average.

Several results stand out from Table 1. Unlike results of our earlier work (Chu et al. 2009), the wind direction variables are not major contributors to predicting PM_2.5. The inverse mixing height is also unimportant. Results show that the most important explanatory variable is relative humidity, followed by the categorical variable summer. Compared to PM_2.5 concentrations in spring, the concentrations in summer are greater by about 1/3, the concentrations in fall are about the same as in spring, and the concentrations in winter are slightly smaller. From a physical viewpoint, one would expect that the concentrations are mostly affected by meteorological differences among the seasons; the fact that summer is one of the most important variables indicates that the regression has not captured the meteorological variables responsible for the seasonal differences. This suggests that Model 1 is too simple to explain the observed PM_2.5 levels. Thus we introduce Model 2, which includes higher order terms of some variables, e.g., squares of variables and interactions among variables that are expressed as products, to try to account for the differences between seasons. Results are shown in Table 2.

TABLE 2 Results of the linear regression Model 2 for PM_2.5 concentration as the dependent variable. The symbols *, **, and § indicate significance at 0.05, 0.01, and 0.001 levels, respectively. The adjusted r² for this model is 0.66.

Explanatory variable x	j Average value	j Estimate	j Standard dev.	j j	t value	Pr(> |t|)
Intercept	—	1.70	4.29	1.70	0.396	0.69
[SO2]	10.5ppb	0.589	0.220	6.19	2.678	7.5E-03**
Temp	14.1°C	−1.20	0.204	−16.9	−5.896	4.9E-09§
Humidity	59.0%	8.66E-02	0.104	5.11	0.831	0.41
[SO2]^2	180ppb^2	−8.14E-03	1.45E-03	−1.47	−5.616	2.5E-08§
Temp^2	294(°C)^2	4.02E-02	4.15E-03	11.8	9.700	< 2e-16§
Humid^2	3840(%)^2	−1.09E-03	7.03E-04	−4.19	−1.555	0.12
fsummer	—	2.70	0.973	2.70	2.773	5.7E-03**
ffall	—	−0.455	0.720	−0.455	−0.632	0.53
fwinter	—	−2.10	0.753	−2.10	−2.789	5.4E-03**
iMHc	0.00587m^− 1	353	69.2	2.07	5.105	3.9E-07§
[O3]	29.7ppb	0.101	2.44E-02	2.99	4.139	3.8E-05§
UV	7.84watts/m^2	−0.278	3.61E-02	−2.18	−7.692	3.1E-14§
rSE	0.0847	8.69	1.15	0.736	7.588	6.8E-14§
rS	0.174	4.29	0.838	0.745	5.114	3.7E-07§
rSW	0.143	1.73	1.04	0.247	1.664	9.6E-02
[SO2]× Temp	136ppb×°C	−5.00E-04	1.14E-02	−6.80E–02	−0.044	0.96
[SO2]× Humid	604ppb× %	−1.12E-04	3.04E-03	−6.73E–02	−0.037	0.97
Temp× Humid	776°C× %	1.12E-02	2.58E-03	8.66	4.317	1.7E-05§
[SO2]× Temp× Humid	7350 ppb×°C× %	2.25E-04	1.94E-04	1.65	1.158	0.25

The most important terms in the column of _{j j} are those for Temp, (Temp)², and Temp × Humidity. At the average values of the 16 explanatory variables, it is mainly these three variables that have an important effect on PM_2.5 concentration. The negative value of _{j j} for Temp would suggest an inverse relation between PM_2.5 concentration and temperature, but this is misleading. All terms containing temperature must be considered when examining the influence of temperature; when all five terms are considered together, the PM_2.5 concentration increases as the temperature increases, since the (Temp)² term becomes dominant at high temperature.

Care must be taken in interpreting the asterisks showing the significance of each independent variable. The last column suggests that the coefficient of iMHc is different from 0 with a probability of > 0.999. However, the value of _{j j} is only 2.07 while the sum of all terms is 17.2 μ g/m³. Compared to the contributions of Temp, Temp², and Temp × Humidity, the contribution of iMHc is quite small.

In checking the effects of an explanatory variable where there are higher order terms, it is necessary to include all terms containing that variable when considering its contribution. For example, the term Temp × Humidity has the third highest _{j j} value in Table 2 (after Temp and Temp²). Thus both Temp and Humidity are important variables despite the smaller values for Humidity and Humidity².

To further investigate the effects of temperature and relative humidity, we have run Model 3 including only the important explanatory variables in Model 2 along with the seasonal categorical variables. Results are shown in Table 3. The table shows that the seasonal terms are all negligible, indicating we have successfully explained most of the variation in PM_2.5 using physically meaningful variables. Although we only include the temperature and humidity terms in this model, along with associated quadratic terms, we are able to explain more than half (52%) of the variation in PM_2.5.

TABLE 3 Results of the linear regression Model 3 for PM_2.5 concentration as the dependent variable. The symbols *, **, and § indicate significance at 0.05, 0.01, and 0.001 levels, respectively. The adjusted r² for this model is 0.52.

Explanatory variable x	j Average value	j Estimate	j Standard dev.	j j	t value	Pr(> |t|)
Intercept	—	15.6	2.05	15.6	7.59	6.7e-14§
Temp	14.1°C	−1.59	0.176	−22.3	−9.03	< 2e-16§
Humidity	59.0%	−7.42E-02	2.83E-02	−4.38	−2.62	9.0E-3**
Temp^2	294(°C)^2	4.96E-02	3.83E-03	14.6	12.9	< 2e-16§
fsummer	—	1.83	1.10	1.83	1.67	0.096
ffall	—	−4.14E-02	0.814	−4.14E-02	−0.051	0.96
fwinter	—	−0.554	0.813	−0.554	−0.681	0.50
Temp× Humid	776°C× %	1.71E–02	1.81E–03	13.3	9.50	< 2e-16§

We have also run a model for the dependent variable y _i equal to the change in PM_2.5 concentration from one time period to the next, denoted by Δ PM_2.5. Results show that Humidity and Humidity² are the two most important explanatory variables in predicting Δ PM_2.5. However, this model is able to explain only a small percentage of the variation in Δ PM_2.5, as the adjusted value of r² is only 0.11.

Altogether, these results show that several variables expected to be important turned out not to be. The inverse mixing height was used in the model, mainly because we would expect PM_2.5 concentration to vary inversely with mixing height; as noted above it was of negligible significance in the regressions. Also of negligible significance were concentrations of SO₂ and O₃, wind direction, and intensity of ultraviolet radiation. Separate tests showed that day-of-week had little influence on PM_2.5 concentration, suggesting that vehicle emissions were not important.

Factor analysis by principal component extraction with varimax rotation was conducted with a more complete PAQS dataset by Millet et al. (2005). Their analysis showed that one of the factors was dominated by PM_2.5, and this factor had only a weak diurnal variation. On the basis of this analysis, which also included a number of individual volatile organic compounds, the authors concluded that automotive emissions were not important to the variability in PM_2.5 concentration, although local point source combustion had an effect and long range transport was a dominant factor influencing PM_2.5. The importance of long range transport on PM_2.5 during PAQS was also reported by Tang et al. (2004) based on measurements at several sites surrounding Pittsburgh. This hypothesis was further confirmed by Robinson et al. (2006) who considered the chemistry of organic aerosols to study the influence of oxidation during atmospheric transport on source apportionment modeling.

In addition, Zhou et al. (2004a) used Positive Matrix Factorization (PMF) with PAQS data for a five-week period in summer 2001 (no overlap with the present study). The input data included particle number and volume concentration by size as well as PM_2.5 mass, sulfate, and organic/elemental carbon, pollutant gases, and meteorology. The one factor dominated by PM_2.5 mass was attributed to long-range transport, and Fourier analysis showed no diurnal variation suggesting little influence of local traffic. However, using PMF with bulk chemical composition data over a five-day period in July 2001 (Zhou et al. 2004b; Zhou et al. 2005) and over 13 months (Pekney et al. 2006) during PAQS showed that the influence of local traffic on the measurement site could be discerned despite its lack of major influence on total PM_2.5.

Figure 1 shows the fitted values from Model 2 versus the observed data of a random sample (size = 100) from the PM_2.5 concentrations. Although the fit is reasonable, the influential factors in the model are not necessarily the cause of a high PM_2.5 concentration. Rather, the cause may be obscure.

FIG. 1 Fitted PM_2.5 vs. Observed PM_2.5. A random sample with size 100 is taken from all 3-h observations with valid observed data and fitted values. The length of error bars of the fitted values is set to the standard error from the linear regression.

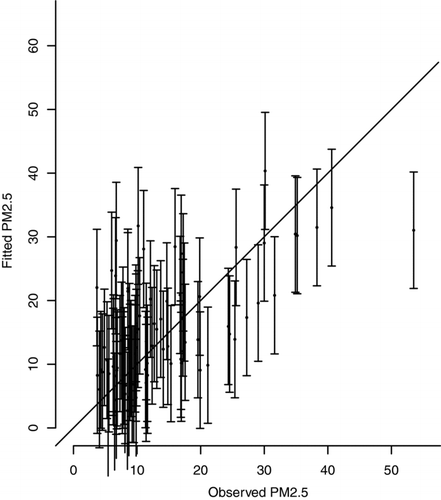
We also observe high correlations between some of the explanatory variables, e.g., temperature and relative humidity are highly correlated. This is somewhat consistent with the results that PM_2.5 is mostly influenced by temperature, squared temperature and temperature–humidity interaction, and Δ PM_2.5 is mostly influenced by humidity and humidity². Thus temperature and humidity are essentially one factor; PM_2.5 and Δ PM_2.5 are essentially associated with this one main factor.

The low r² value for the attempt to model Δ PM_2.5 suggests that we are not able to explain much of the change in PM_2.5 concentrations from one time period to the next. To explore these variations further, we have attempted to predict PM_2.5 concentrations using Model 4 which includes an autocorrelation structure, that is, the consecutive observations are not independent but correlated. Results are shown in Table 4.

TABLE 4 Results of the linear regression Model 4 for PM_2.5 concentration as the dependent variable with autocorrelated errors. The symbols *, **, and § indicate significance at 0.05, 0.01, and 0.001 levels, respectively. The adjusted r² equals 0.54, slightly lower than Model 2 without autocorrelation, but Model 2 incorrectly assumes independent errors. Model 4 gives an estimate for the first order autocorrelation coefficient of 0.77.

Explanatory variable x	j Average value	j Estimate	j Standard dev.	j j	t value	Pr(> |t|)
Intercept	—	6.87	4.11	6.87	1.67	9.45E-02
[SO2]	10.5ppb	0.293	0.153	3.08	1.91	5.62E-02
Temp	14.1°C	−1.57	0.246	−22.1	−6.39	< 3E-10§
Humidity	59.0%	0.122	8.67E-02	7.22	1.41	0.16
[SO2]^2	180ppb^2	−4.96E-03	8.90E-04	−0.893	−5.58	< 3E-8§
Temp^2	294(°C)^2	4.72E-02	5.16E-03	13.9	9.16	< 2E-16§
Humid^2	3840(%)^2	−1.32E-03	5.40E-04	−5.05	−2.45	1.46E-02*
fsummer	—	2.20	2.12	2.20	1.04	0.30
ffall	—	−0.915	1.98	−0.915	−0.462	0.64
fwinter	—	−1.86	1.89	−1.86	−0.985	0.32
iMHc	0.00587m^− 1	7.96	46.7	4.67E-02	0.170	0.86
[O3]	29.7ppb	−4.02E-02	1.99E-02	−1.19	−2.02	4.36E-02
UV	7.84watts/m^2	−6.84E-02	2.48E-02	−0.536	−2.76	5.80E-03**
rSE	0.0847	4.36	0.843	0.369	5.17	< 3E-7§
rS	0.174	3.17	0.612	0.552	5.18	< 3E-7§
rSW	0.143	1.52	0.760	0.217	2.00	4.61E-02*
[SO2] × Temp	136ppb×°C	2.52E-03	7.43E-03	0.343	0.339	0.73
[SO2] × Humid	604ppb× %	1.32E-03	2.11E-03	0.794	0.624	0.53
Temp× Humid	776°C× %	1.75E-02	2.47E-03	13.6	7.10	< 3E-12§
[SO2] × Temp× H	7350 ppb×°C× %	−9.62E-08	1.30E-04	−7.07E-04	−0.001	> 0.99

Results indicate that a model with 0.77 first order autocorrelation between residuals is a better fit to the data than Models 1–3 which assume the errors are independent. Thus the PM_2.5 concentration at any specified time is a very influential factor in predicting its value in the next time period. This also justifies averaging 10 min measurements to obtain 3-h average values as was done in our previous analysis (Chu et al. 2009), since PM_2.5 concentrations in this study generally did not change dramatically in the time scale of a few hours.

Table 4 shows that the explanatory variables Temp, (Temp)², and Temp × Humidity are the most important in explaining PM_2.5 concentration, as was true in Table 2. This is expected, as Model 4 is identical to Model 2 except for the addition of the autocorrelation structure. As we did with Model 3, we ran a reduced form of Model 4 with only temperature and humidity related terms as well as the categorical seasonal variables. Results of this reduced model were similar to those of Model 3 but with a first order autocorrelation coefficient of 0.79.

Although these results are interesting, we must acknowledge several limitations of the method. First and foremost, regressions can be influenced disproportionally by a small number of high valued points. Figure 1 shows that most measured concentrations are fairly low; the limited number of high concentration datapoints can thus play a major role in affecting the outcome. Second, these regressions assume linearity even though the actual relationships may be nonlinear. In addition, the assumption of normality of errors and independence of errors implied in the regressions may not be correct. Finally, we recognize that the existence of variables that explain much of the variation in PM_2.5 does not imply causality.

There are also limitations of the input data, which were subject to experimental error and represent conditions only at the measurement site. Meteorological data may vary over the region of PM_2.5 transport, which would not have been captured by the dataset.

Nevertheless, the results demonstrate that high temperatures and relative humidities in this region of eastern United States may be associated with high PM_2.5 concentrations to a greater extent than elevated concentrations of SO₂ or O₃ or high levels of UV. There does not appear to be an association between PM_2.5 and inverse mixing height. This may be useful information for air pollution control agencies tasked with predicting PM_2.5 episodes.

It is interesting to compare our results with PM_2.5 measurements in other cities. DeGaetano and Doherty (2004) report data from a network of 20 monitoring stations in New York City. Their analyses show that seasonal variability is similar to that in Pittsburgh: less than 20% of all morning hours in summer had average temperatures exceeding 29°C, yet more than half of the summer PM_2.5 concentrations above the 95th percentile occurred during those hours. There were no occurrences of 95th percentile concentrations when the temperature was below 21°C. High PM_2.5 concentrations were also associated with high humidity in their study. The annual maximum in PM_2.5 occurred in the summer as in our study.

Unlike Pittsburgh, however, strong diurnal and day-of-week variations were observed, with higher concentrations during the morning rush hour and in the afternoon and evening on weekdays, and lower concentrations on weekends, consistent with the influence of local traffic. The authors note that early morning atmospheric stability probably also contributed to the morning peak concentrations. The high summer PM_2.5 levels in New York were frequently associated with winds from the SW. Regional meteorology showed that these winds resulted from the presence of a high pressure center off the SE coast of the United States, indicating a westward displacement of the usual Bermuda High, and a low pressure center over northeastern Canada. Note that SW winds in New York are consistent with clockwise flow around the Bermuda High when the pressure center is located SE of the city. Spatial variations in concentration across the 20 urban sites were small. The authors conclude that regional meteorology and long-range transport dominate day-to-day changes in PM_2.5 concentration.

Regional meteorology and long-range transport are also important for the day-to-day variations in PM_2.5 in Pittsburgh. However, nearby sources SE of the city are also important, as shown by Millet et al. (2005) and Chu et al. (2009). Note that when winds are from the SE in Pittsburgh, this cannot be due to a displaced Bermuda High; if it were due to clockwise flow around a High, the pressure center would have to be NE of the city. Thus regional meteorology favoring high PM_2.5 concentrations in Pittsburgh is likely to be different from the regional meteorological conditions reported by DeGaetano and Doherty (2004) as sometimes responsible for high PM_2.5 in New York.

In contrast to Pittsburgh and New York City, Aldrin and Haff (2005) report on PM_2.5 concentrations at four locations in Oslo, Norway. Their results show essentially no correlation between temperature above 0°C and PM_2.5, and a strong inverse relation below freezing: PM_2.5 increases as temperature decreases below zero. This is attributed to wood burning during cold weather in the city. PM_2.5 concentrations increase only very weakly as relative humidity increases, although the concentration of coarse particles, PM₁₀ – PM_2.5, decreases sharply with a relative humidity increase.

There is almost no association between PM_2.5 concentrations in Oslo and the difference in temperature T(z = 25 m) − T(z = 2 m) which may be considered a proxy for mixing height. The authors also note that PM_2.5 concentration is positively correlated with automotive traffic in the vicinity of the four measurement sites, indicating the importance of local sources for these sites which were close to roads.

PM_2.5 concentrations in Oslo show an annual maximum in late March/early April rather than in summer as in Pittsburgh and New York. Berge et al. (2002) report that winter road maintenance and use of studded tires during periods of snow can contribute to airborne particle loadings in Oslo which may be occurring during this time period. In addition, the Joint Research Centre report on European aerosol (Putaud et al. 2003, p. 11) states that particulate matter in European cities can be strongly influenced by regional background concentrations. Note that the March/April time period is also the peak season for arctic haze (Heidam et al. 2004; Quinn et al. 2007). Thus large scale meteorology may be affecting the Oslo measurements but in a different way compared with the East Coast U.S. measurements.

Perez and Salini (2008) have developed predictive models for PM_2.5 concentration in Santiago, Chile. The models predict the concentration on the following day using data from 8:00 PM on the current day from four stations in the city. Based on comparing their model results with data, they report that the best variables to use in their predictive models are (1) 1-h average PM_2.5 concentrations at 7:00 PM and 8:00 PM on the current day, (2) average PM_2.5 concentrations over the previous 24 h determined at 8:00 PM on the current day, (3) the thermal amplitude (T _max – T _min ) for the city for the current day, (4) the predicted thermal amplitude for the following day, and (5) a predicted stability index for the following day, which ranges from highly stable and low mixing height to extremely unstable, e.g., for passage of a frontal system.

Their results show that unlike Pittsburgh or Oslo, high PM_2.5 concentrations are associated with greater atmospheric stability (low mixing height). The authors attribute this to the geography of Santiago, which is ringed by mountains preventing adequate ventilation of ground-level emissions when mixing height is low. The highest concentrations occur in the austral winter April–August, which is when mixing height is lowest.

Finally, it is of interest to consider the annual cycle of PM_2.5 concentrations in Los Angeles which is also ringed by mountains. Concentrations peak in November–December each year (South Coast Air Quality Management District 2007), probably due at least in part to the low mixing heights in winter. A secondary peak occurs in July, which is most likely indicative of rapid conversion of precursor gases to PM_2.5 during the high temperatures in summer.

We thus see that high PM_2.5 concentrations in Pittsburgh and New York appear to be influenced by regional meteorology and transport from upwind areas as well as by local sources. High concentrations in both cities are associated with high temperatures and relative humidities. A different situation exists in Oslo, where neither temperature nor relative humidity is strongly associated with PM_2.5 concentration. Regional meteorology appears to be important but in a different way. Both Santiago and Los Angeles are affected by high mountains, which prevent dispersion under certain conditions. PM_2.5 concentrations in these cities may be more influenced by the occurrence of low mixing height than in the other locations discussed.

These results can be reconciled with our previous work. The current study shows no effect of wind direction, even though local point sources to the S and SE of the monitoring site were shown to be important when including only exceedance days in the analysis (Chu et al. 2009). It is of interest that wind direction over the full year is correlated with temperature: higher temperatures are associated with winds from the S and SE. If wind direction is important for the overall dataset and correlates with high temperature (and relative humidity), then wind direction should show up as an important variable in winter. Therefore we ran another model with the fractional wind direction variables and the seasonal categorical variables to see if the wind direction is important in specific seasons. Results are similar to those in Model 2 in that wind direction is still not important and there are no important differences among the seasons. Thus we conclude that local point sources are not important in the overall dataset even though they are important on exceedance days.

It is also significant that PM_2.5 does not correlate with inverse mixing height in Pittsburgh, even though we might expect such a correlation. This result suggests that in the absence of mountains or other barriers to transport, factors affecting background concentrations such as regional meteorology will be more important than mixing height. Note that this finding is strictly applicable only to the set of data we analyzed and may not be more generally applicable. Nevertheless, we know that regional meteorology can cause major changes in background PM_2.5 concentration entering a city, and may be more important in influencing PM_2.5 than efforts such as reducing emissions locally. The location of Pittsburgh downwind of major sources in the Ohio Valley, and the location of New York City downwind of major sources to the west and southwest, suggests that a regional approach to PM_2.5 reduction is needed.

CONCLUSIONS

Data from September 1, 2001 to August 31, 2002 collected during the Pittsburgh Air Quality Study have been used with a linear regression model to identify factors that most influence concentrations of PM_2.5. Results show that temperature, relative humidity and their associated quadratic terms can explain much of the variation in PM_2.5, while wind direction, inverse mixing height, UV radiation, SO₂, O₃, and season of the year are not important. All of the data except inverse mixing height and season were 10-minute average values. Our previous work with this dataset but including only data for PM_2.5 exceedance days shows that wind direction is important, implicating local sources (Chu et al. 2009). We conclude that local sources influence PM_2.5 levels on the limited number of days of high concentration when the 24-h National Ambient Air Quality Standard for PM_2.5 is exceeded, but are less important than long-range transport in influencing PM_2.5 when examining a full year of data.

A limitation of the above regressions is that they assume the PM_2.5 concentration in one 10-min period is uncorrelated with the concentration in the next period. To assess this possibility, we ran the regression using an autocorrelation structure. Results showed that a better fit than the original model was obtained with 0.77 first order autocorrelation between residual errors (PM_2.5 observed minus PM_2.5 fitted). Temperature, relative humidity, and quadratic terms were still the most important factors explaining the variation in PM_2.5.

By comparing our results with those of studies in other cities, we note that in both Pittsburgh and New York City, much of the variation in PM_2.5 can be explained by measurements of temperature, and, to a lesser extent, relative humidity. Concentrations in both cities' peak in the summer. In contrast, concentrations of PM_2.5 in Oslo peak in March/April, with a different influence of temperature and smaller influence of relative humidity. In both Pittsburgh and Oslo, the atmospheric mixing height does not appear to have a major influence on the concentration. Finally, mixing height appears to be an important determinant in Los Angeles and in Santiago, Chile. Both of these cities are ringed by mountains. Overall we conclude that factors influencing PM_2.5 vary greatly from one city to another, especially for cities with different topographic characteristics and in different climate regimes, and thus conclusions based on data obtained at one location cannot be easily generalized to other locations.

We acknowledge the generous assistance of Stan Benjamin of the NOAA/ESRL Global Systems Division in obtaining the RUC data and assisting with interpretation, and that of Louis Giardano of the National Weather Service office in Pittsburgh for his assistance in estimating mixing heights. We also acknowledge the assistance of Xiting Yang, Anna Anselmi, and David Hwang in earlier versions of this work. This research was conducted as part of the Pittsburgh Air Quality Study that was supported by US Environmental Protection Agency under contract R82806101 and the US Department of Energy National Energy Technology Laboratory under contract DE-FC26-01NT41017. This article has not been subject to EPA's required peer and policy review, and therefore does not necessarily reflect the views of the Agency. No official endorsement should be inferred.