The Dynamic Shape Factor of Sodium Chloride Nanoparticles as Regulated by Drying Rate

Abstract

The influence of drying rate on the dynamic shape factor χ of NaCl particles was investigated. The drying rate at the efflorescence relative humidity (ERH) of 45% was controlled in a laminar flow tube and varied from 5.5 ± 0.9 to 101 ± 3 RH s^–1 at ERH, where RH represents one percent unit of relative humidity. Dry particles having mobility diameters of 23–84 nm were studied, corresponding to aqueous particles of 37–129 nm at the RH (57%) prior to drying. At each mobility diameter and drying rate, the critical supersaturation of cloud-condensation activation was also measured. The mobility diameter and the critical supersaturation were combined in an analysis to determine the value of χ. The measured values varied from 1.02 to 1.26. For fixed particle diameter the χ value decreased with increasing drying rate. For fixed drying rate, a maximum occurred in χ between 35- and 40-nm dry mobility diameter, with a lower χ for both smaller and larger particles. The results of this study, in conjunction with the introduced apparatus for obtaining quantified drying rates, can allow the continued development of a more detailed understanding of the morphology of submicron salt particles, with the potential for the follow-on development of quantitative modeling of evaporation and crystal growth at these dimensions.

1. INTRODUCTION

Many instruments classify particles by drag force (Baron and Willeke 2001). Examples include the differential mobility analyzer which classifies by electric mobility Z, impactors and cyclones which classify by aerodynamic diameter d _a , and several particle mass spectrometers which classify by vacuum aerodynamic diameter d _va . Instrument performance is typically defined for spherical particles, and the instruments include a dynamic shape factor χ in their performance equations to compensate for nonspherical particle geometries. The volume-equivalent dynamic shape factor of an aerosol particle is the ratio of the drag force on it to that on a spherical particle of identical volume (Davies 1979; Baron and Willeke 2001).

Various approaches exist for estimating the dynamic shape factor, ranging from calculation for perfect geometries such as cubes (Dahneke, 1973a, b, c) or spherical aggregates (Cheng et al. 1988; Kousaka et al. 1996) to measurement by combinations of techniques (Barbe-le Borgne et al. 1986; Brockmann and Rader 1990; Baron and Willeke 2001; Park et al. 2004; Zelenyuk et al. 2006; Kuwata and Kondo 2009). In the latter category, estimates of the volume-equivalent diameter can be obtained by microscopy, which can be combined with a measurement of the aerodynamic or mobility diameter to obtain the shape factor (Baron et al. 2001; Park et al. 2004). Another method for determining the shape factor is to measure separately the mobility and aerodynamic diameters (Katrib et al. 2005).

The dynamic shape factor of a particle is influenced by the conditions of aerosol production and subsequent processing. For example, pyrolytic or evaporative production of aerosol particles of metal oxides or noble metals, optionally followed by further thermal conditioning, can lead to a variety of morphologies (Kodas and Hampden-Smith 1999). Similarly, soot particles produced by open-flame synthesis, as well as diesel particles emitted by engine combustion, typically have a fractal backbone of black carbon spherules that can be coated by semivolatile organic material (Kittelson 1998; Park et al. 2004; Slowik et al. 2004; van Poppel et al. 2005; Adachi et al. 2007; Slowik et al. 2007). The extent and history of the organic coating can influence the dynamic shape factor.

For supermicron particles, the early seminal work of Charlesworth and Marshall (1960) as well as many later studies as reviewed in Lewis and Schwartz (2004) constitute a rich literature on the shapes of particles prepared by spray evaporation of aqueous NaCl and other salts. Systematic experimental measurements of how the drying rate influences the efflorescence and the morphology of nano-size salt particles, however, have not been described previously. Dry particle shape depends on the aqueous particle size and the rate of drying (Mikhailov et al. 2004; Biskos et al. 2006a; Rose et al. 2008; Mifflin et al. 2009; Mikhailov et al. 2009). For accurate prediction of shape, however, many factors must be taken into account including, at a minimum, coupling of mass transfer in the gas and solution phases, advancing crystal fronts, and local heating from latent heat release (Duffie and Marshall 1953; Leong 1987; Abramzon and Sirignano 1989; Yun and Kodas 1993; Walton 2000; Brenn et al. 2001). At present, detailed models cannot accurately describe these coupled process, and measurements of χ are therefore required.

The study described herein addresses the needs expressed above. Specifically, the dynamic shape factors of NaCl aerosol particles having dry mobility diameters less than 100 nm were obtained for a range of drying rates. A laminar-flow tube with a core wet-aerosol flow and an outer dry-air sheath flow was used. The drying rates were quantified on the basis of a diffusion calculation for this optimized geometry and flow regime. The rates were varied by adjusting the initial RH difference between the aerosol and sheath flows. The value of χ of the dry particles was obtained by using a differential mobility analyzer (DMA) to control the mobility diameter d _{m, + 1} ^dry (+1 charge) of the dry particles and by measuring the critical supersaturation S _c for cloud-condensation-nuclei (CCN) activation of the mobility-classified particles.

2. EXPERIMENTAL

The experimental strategy was to use a differential mobility analyzer (DMA) to select particles of mobility diameter d _{m, + 1} ^dry and to use a CCN counter (CCNC) to measure the activated fraction F _a at different setpoint supersaturations. This measurement was repeated at fixed supersaturation for multiple mobility diameters, and a CCN activation curve was thereby obtained. A schematic diagram of the experimental apparatus is shown in Figure 1. The following sections present the method of aerosol generation and preconditioning (§ 2.1), the design and operation of the horizontal laminar-flow tube (§ 2.2), the measurement of the CCN activation curve (§ 2.3), and the collection of transmission electron micrographs (§ 2.4).

FIG. 1 Schematic diagram of the experimental apparatus. (a) Aerosol generation by nebulization, adjustment of aerosol RH in Nafion 1 to high RH, drying of aerosol RH in the laminar-flow tube (see also panel b), selection of particle mobility diameter by nDMA, and measurement of activated CCN fraction. (b) Illustration of the drying of the aerosol flow by radial water-vapor diffusion into the sheath flow and the subsequent crystallization of the particles in the aerosol flow. The circles with solid dots represent spherical solution drops in a humid core flow, and the solid cubes represent the crystallized particles in a core flow. The dynamic shape factor of these cubes depends on the drying rate. Key: CCNC, cloud condensation nucleus counter; CPC, condensation particle counter; nDMA, nano differential mobility analyzer; MFC, mass flow controllers; PID, proportional integral derivative controller; PT, pressure transducer; RHS, relative humidity sensor.

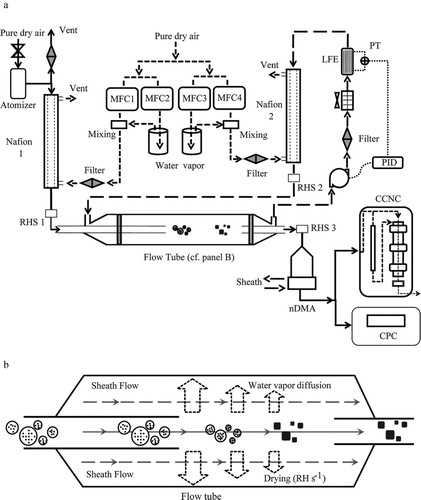
2.1. Aerosol Generation and Preconditioning

Polydisperse sodium chloride particles were aerosolized in pure air from aqueous solution (0.1 g L^–1) by nebulization (TSI Model 3076) (Liu and Lee 1975). The sodium chloride was high purity (J.T. Baker “Ultrex 100% pure”) and used as purchased. High-purity water was prepared by filtration, followed by ultraviolet irradiation and reverse osmosis (Barnstead Model D8971). After nebulization, the humid aerosol flowed at 3 L min^–1 through a Nafion conditioner (Permapure Model PD-50T) (Dick et al. 1995), in which the aerosol RH was adjusted to 57 ± 2%. The experiments were performed at room temperature (298 ± 1K). Under these conditions, the particles remained aqueous. A sensor mounted downstream of the conditioner verified the aerosol RH. As illustrated in Figure 1a, the RH in the drive flow of the Nafion conditioner was adjusted to 57% by use of two mass flow controllers to mix proportioned flows of dry air and air near water saturation. The latter was produced by bubbling pure air through water (18.3 MΩ cm) in a glass bubbler.

2.2. Aerosol Laminar-Flow Tube

As depicted in Figure 1b, the aerosol of polydisperse particles passed longitudinally as a core flow (0.8 L min^–1) within a sheath flow (11.2 L min^–1). Linear velocities of the two flows were the same, and laminar conditions were obtained, implying that water vapor was exchanged only by radial diffusion between the aerosol and the sheath volumes. The Pyrex flow tube was 1.2 m long and 4.5 cm (ID) in diameter. The injector for the aerosol flow (1.16 cm ID) was inserted 70 cm into the flow tube, thus allowing sufficient distance for the sheath flow to establish its steady-state flow profile. A collector (1.16 cm ID) of the aerosol flow was inserted 10 cm from the exit of the flow tube. The sheath and aerosol flows were thus exposed to one another for 40 cm, which was equivalent to 3.2 s for the flow rates used. Two flow-smoothing screens (700 mesh) were mounted in the sheath flow to maintain laminar flow, one located just prior to the point of aerosol injection and the other just after the point of aerosol collection. A red laser was used to confirm laminar flow by observing that the particles remained within the core volume along the length of the flow tube. The aerosol and sheath flows were regularly calibrated using Gilibrator bubble flow meters.

The aerosol flow was controlled downstream by the flow controllers installed in a condensation particle counter (CPC; TSI Model 3025; 0.3 L min^–1) and in a cloud condensation nuclei counter (Droplet Measurement Technologies, DMT Model CCN-2; 0.5 L min^–1) (Roberts and Nenes 2005; Lance et al. 2006; Rose et al. 2008). The balanced, recirculating sheath flow was controlled using the setup similar to that described in Biskos et al. (2006b). The flow passed through a Nafion conditioner for adjustment to the desired RH before recirculation into the flow tube.

The RH of the sheath inflow was conditioned between 6 and 40% (depending on the desired drying rate; cf. Table 1). The radial diffusion of water vapor from the aerosol to the sheath volume steadily reduced the aerosol RH along the longitudinal axis of the flow tube. When the RH of the aerosol flow dropped below the efflorescence relative humidity, the sodium chloride particles crystallized. Biskos et al. (2006a) showed that the ERH for NaCl particles having diameters of 20 nm and larger was 45%. The RH of the aerosol flow exiting the tube was monitored to verify that the value expected from calculation was obtained. Depending on the experiment (Table 1), this RH was between 11 and 41% RH.

TABLE 1 Calculated drying rates in the laminar-flow tube for experimental conditions 1 to 4 employed in this study. The initial aerosol RH (i.e., core flow) and the initial sheath RH (i.e., outer flow) of each experimental condition are shown. The final column shows the calculated average drying rate at an aerosol RH of 45% (i.e., the efflorescence RH of NaCl particles; cf. Equation (B4)). The drying rates are shown as open circles in panel d of Figure B1

	Experimental conditions
Experiment	Initial aerosol RH (%)	Initial sheath RH (%)	Initial Δ RH (%)	Calculated RH′ERH = 45%(RH s^–1)
1	57.2 ± 0.5	39.2 ± 1.0	18.0 ± 0.5	−5.5 ± 0.9
2	56.8 ± 0.8	27.6 ± 0.6	29.2 ± 0.3	−29.7 ± 0.7
3	57.5 ± 0.9	16.0 ± 0.4	41.5 ± 0.5	−58.4 ± 0.9
4	56.5 ± 1.1	6.4 ± 0.2	50.1 ± 0.8	−101 ± 3

2.3. CCN Activation Curve

The dried aerosol of polydisperse particles exiting the flow tube passed through a ²¹⁰Po bipolar charger (NRD Model P-2031) to establish an equilibrium charge distribution on the particles. The aerosol flow then passed through a nano differential mobility analyzer (nDMA, TSI Model 3085) set to select a monodisperse mobility diameter (+1 charge). Flow rates of 0.8 L min^–1 for the aerosol and 8 L min^–1 for the sheath were used. The RH of the sheath flow was maintained at 6% to avoid any shape reconstruction of particles inside nDMA. The flow of monodisperse aerosol particles was split into two subflows, the first (0.3 L min^–1) entering an ultrafine CPC and the second (0.5 L min^–1) entering a continuous-flow CCNC.

Inside the CCNC those particles having a sufficiently large solute mass activated at the set supersaturation (controlled by a temperature gradient in the instrument (Roberts and Nenes 2005)) to grow into droplets having diameters greater than one micrometer, which were detected by an optical particle counter. Supersaturations from 0.15 to 1.0% were investigated stepwise. The activated fraction at a set supersaturation and mobility diameter was determined as the ratio of the activated particle number concentration detected by the CCNC to the total particle number concentration detected by the CPC. During the experiments, the mobility diameter of the nDMA was scanned from 15 to 90 nm in steps of 2 to 5 nm for each supersaturation, and an activation curve over mobility diameter was thereby obtained. Each activation curve was fit with a sigmoid function, including a filter to omit the effect of multiply charged particles (King et al. 2007). The mobility-equivalent critical dry diameter was taken at F _a = 0.5. Raw data are plotted in Figure S1. For comparison, methods based on the sum of two cumulative Gaussian distribution functions (Rose et al. 2008) and on an inversion to take into account the DMA transfer function (Petters et al. 2007) were also used to analyze the data. Within experimental uncertainty, the three analyses yielded identical critical diameters. The dynamic shape factor was obtained from the equations as described in Appendix A.

Calibration of the supersaturation of the CCNC was performed using (NH₄)₂SO₄ particles for temperature gradients from 3.9 to 17.4 K (Shilling et al. 2007). The ammonium sulfate was purchased from EMD Chemical Inc. (> 99.5% purity). Aerosol particles, prepared by nebulization of aqueous solutions, were dried by dilution with particle-free dry air, followed by further drying in diffusion dryers. Our CCNC calibration using (NH₄)₂SO₄ particles was based on χ = 1.02, δ = 1, and the AP3 aqueous thermodynamic model of Rose et al. (2008), using the relations for water activity, surface tension, and density described therein. The studies in the literature concerning (NH₄)₂SO₄ particles converge on a dynamic shape factor of 1.02 ± 0.02 for a broad range of diameters and drying methods (Biskos et al. 2006b; Zelenyuk et al. 2006; Rose et al. 2008; Kuwata and Kondo 2009). Equation (A2) provides the parameterization of m _p ^dry[S _c ], and its inverse S _c [m _p ^dry] was used in the calibration, where m _p ^dry is the mass of a dry (NH₄)₂SO₄ particle.

2.4. Transmission Electron Microscopy

Dried particles were collected by redirecting the outflow from the nDMA (Figure 1) to a nanoparticle electrostatic precipitator (TSI model 3089) (Dixkens and Fissan 1999). The precipitator, which was operated at a flow rate of 0.8 L min^–1 and a collection voltage of 10 kV, collected positively charged particles for 30 min onto grids (Ted Pella Inc #1890; lacey-carbon Type-A, 300-mesh copper) for transmission electron microscopy (TEM). From collection through analysis, the ambient relative humidity was closely monitored and never exceeded 30%. This quality-assurance step was required because sodium chloride particles can reconstruct and change shape when water layers condense, even for RH values significantly below the deliquescence relative humidity (Kramer et al. 2000; Biskos et al. 2006a). The samples were maintained in airtight containers until the time of imaging. The relative humidity in the TEM laboratory was between 8 and 18% during all experiments, and the absolute humidity inside the microscope corresponded to vacuum conditions. TEM images were obtained using a Philips CM200 transmission electron microscope operated at 200 kV. A low-intensity electron beam was used to minimize any changes to the particles during imaging (Wise et al. 2005).

3. RESULTS

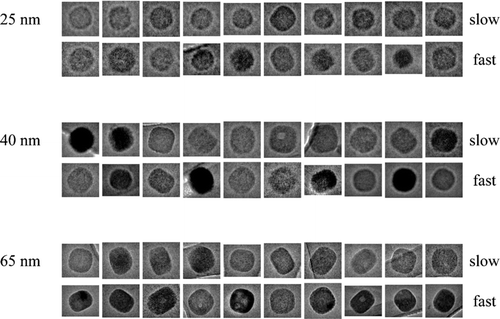
Figure 2 shows the transmission electron micrographs of particles collected for the fastest and slowest drying rates studied (i.e., experiments 1 and 4 of Table 1). The three rows in Figure 2 show particles collected for dry mobility diameters of 25, 40, and 65 nm, respectively. Drying in all three cases was initiated from aqueous particles of 57% RH, corresponding to initial aqueous diameters of 36 to 39, 58 to 63, and 95 to 102 nm, respectively, as calculated using the Aerosol Calculator (www.seas.harvard.edu/AerosolCalculator), for dynamic shape factors of the dry particles of 1.08 to 1.24. The images show that the particles tended toward sharper edges when dried slowly and softer edges when dried rapidly. The particles are more spherical at fast compared to slow drying. Although this trend is generally well known qualitatively, our present work provides quantitative results that fast and slow drying correspond, respectively, to 101 ± 3 and 5.5 ± 0.9 RH s^–1 for the particle sizes studied. The calculation of drying rate RH′_ERH at ERH is presented in Appendix B. The variability in the images confirms that the morphologies and hence the dynamic shape factors of NaCl particles are influenced by both drying rate and particle size.

FIG. 2 Transmission electron micrographs for NaCl particles prepared at different drying rates. Images are shown for particles collected by DMA classification at 25-, 40-, and 65-nm dry mobility diameter (+1 charge). Slow and fast drying refers to experiments 1 and 4 of Table 1 (i.e., 5.5 ± 0.9 and 101 ± 3 RH s^–1, respectively). Images within one diameter classification are on the same scale; images between diameter classifications are scaled for a common display size.

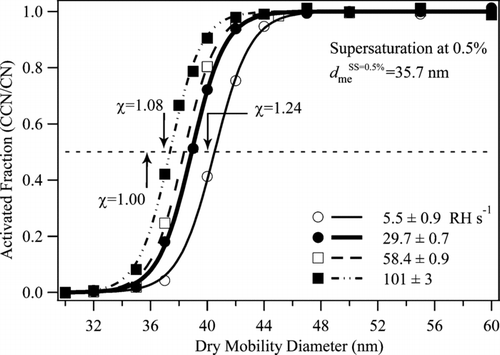
CCN activation curves, which represent the activated particle fraction for increasing mobility diameter, are shown in Figure 3 for NaCl particles prepared by drying aqueous particles at different rates and exposed to 0.5% supersaturation. Compared to the mass-equivalent diameter of 35.7 nm expected at this supersaturation, the measured mobility-equivalent critical diameters (i.e., the mobility diameter at 50% activated fraction) were higher, indicating nonspherical particles. For comparison, arrows in the figure mark the mobility-equivalent critical diameters expected for particles having χ of 1.00 (i.e., a sphere), of 1.08 (i.e., a cube in the continuum regime), and of 1.24 (i.e., a cube in the free-molecule regime) (DeCarlo et al. 2004; Biskos et al. 2006c). The measured activation curves straddle these values, with higher χ for slower RH′_ERH. The dynamic shape factors associated with the curves were obtained using Equation (A3). The values of χ are 1.26, 1.18, 1.15, and 1.09 for values of RH′_ERH of 5.5 ± 0.9, 29.7 ± 0.7, 58.4 ± 0.9, and 101 ± 3 RH s^–1, respectively, with drying initiated at 57% RH. Moreover, the width of the activation curves is equally narrow to that of the calibration (cf. Figure S2), indicating that for each experimental condition there is good homogeneity of shape factors in the population of NaCl particles. Simulations using the Aerosol Calculator set an upper limit of ± 0.02 on the heterogeneity in the χ values of the population because any larger variability would cause an observable increase in the width of the activation curve beyond that associated with the DMA transfer function alone.

FIG. 3 CCN activation curves at 0.5% supersaturation for NaCl particles for four different drying rates at ERH (cf. Table 1). The lines passing through the data are sigmoidal fits. The mobility-equivalent critical diameter is the intersection of a fit curve with the dashed line drawn at an activated fraction of 0.5. For comparison, the mass-equivalent critical diameter of a NaCl particle active at 0.5% supersaturation is 35.7 nm. Indicated by arrows are the mobility-equivalent critical diameters expected for NaCl particles having dynamic shape factors χ of 1.00, 1.08, and 1.24.

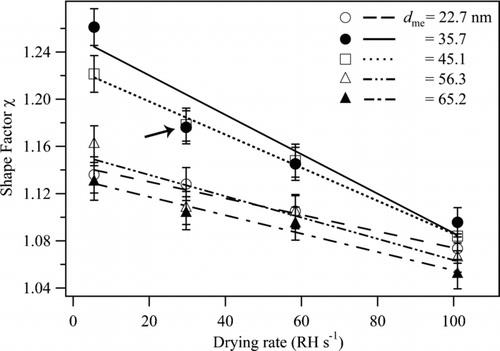
For each drying rate, activation curves were collected for supersaturations ranging from 0.15 to 1.0%. Figure 4 shows the results obtained for RH′_ERH of 29.7 ± 0.7 RH s^–1. For orientation, the thick solid lines in Figure 3 and Figure 4 represent the same data. By use of the approach described for the data of Figure 3, shape factors were obtained for the mobility-equivalent critical diameters of Figure 4. These shape factors for RH′_ERH of 29.7 ± 0.7 RH s^–1 are plotted in Figure 5 as the black circles. The other shape factors in Figure 5 were obtained from plots analogous to those of Figure 4 but for other drying rates. Selected size-dependent shape factors of Figure 5 are plotted for a complementary view in Figure 6 as drying-rate-dependent shape factors.

FIG. 4 CCN activation curves for supersaturations ranging from 0.15 to 1.0%. The drying rate is held constant at 29.7 ± 0.7 RH s^–1 at ERH. For orientation, the thick line in this figure is the same as shown in Figure 3.

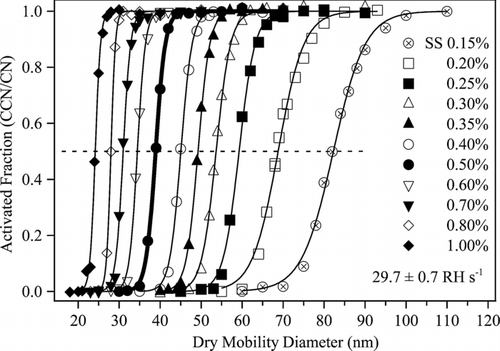
FIG. 5 (a) Dynamic shape factors χ of NaCl particles having dry mobility diameters from 23 to 84 nm and prepared by drying rates ranging from 5.5 ± 0.9 to 101 ± 3 RH s^–1at ERH (cf. Table 1). (b) Same as panel a but plotted as the inferred aqueous diameter prior to drying (i.e., by obtaining m _p ^dry from S _c and then d _ve ^aq from m _p ^dry for the initial RH values of Table 1). Uncertainty is based on the standard deviation of repeated measurements made on different days for nominally identical conditions (cf. Figure S3). Lines show the expected shape factors χ _c , χ _fm , and χ _t of cubes in the continuum, free-molecule, and transition regimes, respectively (DeCarlo et al. 2004; Biskos et al. 2006c). For orientation, the arrow marks the data point corresponding to the thick line shown in Figure 3 and Figure 4.

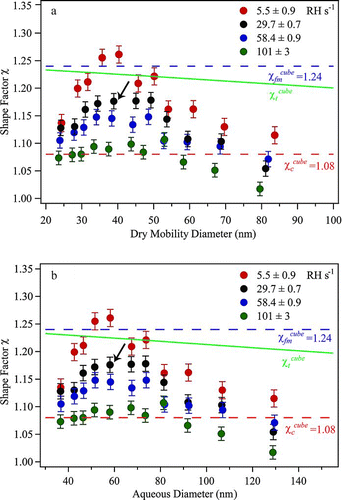
FIG. 6 Dynamic shape factors χ of NaCl particles for increasing drying rate at ERH. Results are shown for particles having mass-equivalent diameters ranging from 22.7 to 65.2 nm. The lines are not model fits but are drawn to aid the eye. Uncertainty on the data points is as described for Figure 5. For orientation, the arrow marks the data point corresponding to the thick line shown in Figure 3 and Figure 4.

The sensitivity of the values of χ shown in Figure 5 and Figure 6 to assumptions and uncertainties in the experimental methods and analysis can be considered. For example, a value of χ of 1.02 was used by us for the (NH₄)₂SO₄ particles in the calibration of S _c for the CCNC. Although this value is recommended, some previous work has suggested that the χ value of small (NH₄)₂SO₄ particles can vary between 1.00 and 1.04 (Biskos et al. 2006b; Zelenyuk et al. 2006; Rose et al. 2008; Kuwata and Kondo, 2009). CCNC calibration with a χ value of 1.00 or 1.04 for (NH₄)₂SO₄ calibration particles decrease or increase respectively, the determined values of χ for NaCl particles by 0.02. Regarding the porosity factor, our analysis assumed a δ value of 1. Equation (A3) shows that the term χ δ is lumped together, with a small additional correction in the numerator within the C _c term. The result is that an increase of δ to 1.01 shifts the χ value down by 0.02. The activation temperature within the CCNC, which compared to ambient is warmer by an unknown value of the order 3 to 6 K, represents another potential uncertainty because the calibration is influenced by temperature (cf. Equation (A1)) (Rose et al. 2008). For this reason, the coefficients of m _p ^dry[S _c ] for Equation (A2) include calibration at 298 and 304 K. Nevertheless, there is high co-variance between NaCl and (NH₄)₂SO₄ particles for the temperature sensitivity of the CCNC response, with the net result that there is a negligible influence on χ (< 10^–4) from temperature uncertainty. Although the combined uncertainties outlined in this paragraph can possibly systematically shift the quantitative values we report for χ of the NaCl particles, the qualitative trends with drying rate that we report are robust: (1) there is a maximum in the shape factor at 35–40 nm that falls off to smaller and larger diameters and (2) the shape factor decreases with faster drying rate.

Another possible influence on the results is impurities in the water because, although high-quality water was used in the experiments, all water contains solid residuals after evaporation (Biskos et al. 2006a). In this case, the nebulized NaCl aerosol particles likewise then have impurities at some level. We estimate a volume-based impurity level of less than 1 part in 10⁵ on the basis of the integrated volume of the aerosol impurities of the pure water (as measured by a scanning mobility particle analyzer) compared to the integrated volume of the nebulized polydisperse NaCl particles. The question is if the impurities, especially if surface active, are in large enough concentrations to influence the results. Biskos et al. (2006a) showed that the deliquescence, efflorescence, and hygroscopic growth factors of NaCl nanoparticles from 6 to 60 nm were identical within measurement for (a) particles prepared by the NaCl nebulization methods used in this study and (b) particles prepared by a water-free preparation method based on the vaporization-condensation of solid NaCl. These results of Biskos et al. (2006a) therefore suggest that the properties examined in this study also are not influenced by impurities; if they were, then the size-dependent shape factors should monotonically shift with particle diameter, in contradistinction to the observations of a maximum in Figure 5.

4. DISCUSSION

For NaCl particles in their idealized habit of cubes, the line χ _t ^cube of Figure 5 shows the expected value of the shape factor (i.e., corresponding to the size-dependent shape factor in the transition regime of the Knudsen number). In comparison, the actual measurements of the shape factors are largely bracketed by the values expected for a sphere (i.e., 1.00) and a cube (i.e., χ _t ^cube). Particles having shape factors less than χ _t ^cube are progressively more spherical than cubic. As clearly illustrated in Figure 5 and Figure 6, the dynamic shape factor of NaCl particles is a function of drying rate (§ 4.1) as well as particle size (§ 4.2).

4.1. Dependence of χ on Drying Rate

Extremes of drying rate and the associated effects on the morphology of crystallized particles can be considered (Duffie and Marshall 1953; Leong 1987; Abramzon and Sirignano 1989; Yun and Kodas 1993; Walton 2000; Brenn et al. 2001). Key concepts are (1) that the development of a morphology implies the diffusive movement of NaCl monomers and (2) that the diffusive movement of these monomers is facilitated by the water content of the particle. At one extreme of sufficiently rapid drying, water evaporation and hence removal from the particle is faster than NaCl monomers can move. In this case, the crystallizing solute does not have enough time to form a euhedral crystal, and the dry particles are locked into a morphology having rounded edges, approaching in a limit those of a sphere. At the other extreme of sufficiently slow drying, water removal is slower than the movement of NaCl monomers, and there is sufficient time for a local or global minimum of the Wulff shape to form on crystallization, corresponding to a cube in the case of NaCl (Adamson and Gast 1997).

For the experiments conducted herein, unknown a priori is whether the employed drying rates covered a sufficient range to approach either or both of the aforementioned extremes. However, the observations can be an a posteriori guide. Figure 6 shows that the range of drying rates employed (i.e., 5.5 ± 0.9 to 101 ± 3 RH s^–1) progressively decreases the value of the shape factor, in agreement with the general principles set out above. For particles having mass-equivalent dry diameters of 35.7 nm, the derived shape factor decreases from 1.26 for 5.5 ± 0.9 RH s^–1 to 1.09 for 101 ± 3 RH s^–1, indicating the transition from a cubic to a more spherical particle. Therefore, for this diameter, one extreme of fully sufficient slow drying was obtained for 5.5 ± 0.9 RH s^–1. Drying rates faster than 101 ± 3 RH s^–1, however, are required to achieve the other extreme of sufficiently fast to form perfect spheres. These results of inferred geometrical shape from the dynamic shape factor (i.e., cubes to spheres with increasing drying rate) are supported by the images shown in Figure 2 for the 40-nm particles. Figure 6 also shows, however, that for other particle sizes, a drying rate of 5.5 ± 0.9 RH s^–1 was insufficient to reach the extreme of sufficiently slow drying. For example, particles toward either limit of the size range studied (e.g., 22.7 and 65.2 nm in Figure 6) had shape factors of 1.13 at the slowest drying rate studied, indicating that they were far from cubic and that drying rates slower than 5.5 ± 0.9 RH s^–1 are needed to reach the extreme of sufficiently slow drying.

4.2. Dependence of χ on Particle Size

The dependence of the dynamic shape factor on particle size is shown in Figure 5 for different drying rates. The dynamic shape factor at all drying rates has a maximum value for a dry mobility diameter of 35–40 nm, falling off to lower values both for smaller and larger particles. For example, with a drying rate of 5.5 ± 0.9 RH s^–1, the maximum χ of 1.26 is observed around 40 nm, and decreases to 1.15 at 24 nm and 1.11 at 84 nm.

The key concepts introduced above can provide a qualitative explanation of the trend in dynamic shape factor with particle size. For particles sufficiently small, particle-phase diffusion of water to the surface of the evaporating particles has a small characteristic time, and all water can be removed almost immediately in a flash vaporization, shutting down the water-lubricated mobility μ of NaCl monomers along surfaces that is required to form euhedral shapes. The characteristic time of diffusive movement of monomers scales as L ²/D, where L is the length scale and D is the surface diffusion coefficient of NaCl monomers, which is proportional by the Einstein relation to their mobility μ. As a result of the flash vaporization, the time available for diffusive movement of NaCl monomers is short and insufficient for full euhedral growth as a cube. For progressively larger particles, the dominance of this timescale decreases because of the increasing characteristic time of particle-phase diffusion of water. At the other end of the size domain, however, for particles sufficiently large, the characteristic time given by L ²/D increases because the absolute length L that NaCl monomers must diffuse to transform a sphere into a cube increases. For particles represented by sufficiently large L, the characteristic time for particle-phase diffusion of water is shorter than that of euhedral growth, again resulting in particles that have at least partially spherical morphology. The combination of these two effects, one favoring more spherical particles at the small end of the size range and the other more spherical particles at the large end of the size range, can qualitatively explain the appearance of a maximum in the dynamic shape factor (i.e., indicative of more cubic particles) at an intermediate diameter for all drying rates (Figure 5).

4.3. Comparison to Literature

Previous studies, including their methods of drying, the particle size ranges employed, the analysis approach, and the reported shape factors, are summarized in Table 2. The table entries show that the shape factors reported in the literature vary from 1.00 to 1.40 for submicron NaCl particles. This range spans the values reported in the present study of 1.02 to 1.26. None of these studies, however, estimated the drying rate (i.e., RH s^–1) at ERH associated with their observations. Most of the studies also reported the final dry diameter rather than the initial aqueous diameter. The drying methods employed in these studies included (1) the mixing of the humid aerosol with dry air flow and (2) the passage of the aerosol through a dessicant-based diffusion dryer or a Nafion conditioner.

TABLE 2 Summary of the dynamic shape factors reported in the literature and those measured in this study for NaCl particles

Diameter (nm)	Drying method	Analysis approach	Shape factor	Source
120–560	Dried by diffusion dryer	f (d m , d va )	1.08 ± 0.04	Kelly and McMurry 1992
96	Dried by diffusion dryer	f (d m , g)	1.03–1.17	Kramer et al. 2000
99	First dried by diffusion dryer, then hydrated and dried again by mixing with dry air (ratio 10:1)	f (d m , g)	1.06	Mikhailov et al. 2004
201			1.07
6–60	Dried by mixing with dry air ^a /Hydrated and then dried in a Nafion conditioner ^b	f (d m , g)	1.22–1.24	Biskos et al. 2006c
100–300	First dried by two diffusion dryers and then by mixing with dry compressed air (ratio 50:1)	f (d m , d va )	1.02	Zelenyuk et al. 2006
200–800			1.06–1.17
200–700	Dried by mixing with dry air (ratio 50:1)		1.30–1.40
25–160 ^c	Dried by mixing with dry air (ratio 60∼ 15:1)	f (S c ^AS, S c ^SC)	1.00	Rose et al. 2008
30–130 ^c	Dried by diffusion dryer		1.08
50–150	Dried by two diffusion dryers	f (d m , m p )	1.05–1.14	Kuwata and Kondo 2009
23–84	Dried in flow tube with controlled and quantified drying rate of 5.5 ± 0.9 RH s^–1	f (d m , S c ^SC)	1.12–1.26 ^d	This study
	of 29.7 ± 0.7 RH s^–1		1.05–1.18
	of 58.4 ± 0.9 RH s^–1		1.07–1.15
	of 101 ± 3 RH s^–1		1.02–1.11
Legend: d a , aerodynamic diameter; d m , electric mobility diameter; d va , vacuum aerodynamic diameter; g, hygroscopic growth factor; m p , mass of particle; and S c , critical supersaturation of ammonium sulfate (AS) or sodium chloride (SC).

Given that the initial aqueous diameter, the initial RH, and the drying rate at ERH all influence the value of χ and that none of the literature studies reported these values, comparisons between our measurements and those in literature cannot be fully quantitative. Nevertheless, using conditions reported in several studies in conjunction with the equations in Appendix B, we can make some semi-quantitative comparisons in some cases. Zelenyuk et al. (2006) concluded that nearly spherical dry NaCl particles were produced from rapid drying (i.e., mixing wet and dry flows directly at a ratio of 1:50) whereas cubic NaCl particles were formed by slow drying with diffusion dryers. Although the particle sizes studied by Zelenyuk et al. (2006) were larger than those of our study, their results nevertheless support the same trends as ours showing the dependence of χ on drying rate. For the “slow drying” conditions of Zelenyuk et al. (2006), we estimate a drying rate of 45 RH s^–1 at efflorescence, with possible variation range of 30 to 60 RH s^–1 for the employed diffusion dryer (TSI Model 3062).

Rose et al. (2008) performed CCNC calibration experiments with both (NH₄)₂SO₄ and NaCl particles of 20- to 220-nm dry mobility diameter. In one set of experiments, the particles were dried by rapid dilution with air to below 15% RH. The cross-calibration between (NH₄)₂SO₄ and NaCl particles was good for χ = 1.00 using the same thermodynamic model as used herein (cf. figure 12a in Rose et al. 2008). This result is consistent with our results showing that χ approaches 1 for the fastest drying rates (Figure 5 and Figure 6). In another set of experiments, Rose et al. (2008) dried the aqueous particles using a silica gel diffusion drier. In this case, the calibration results of the two salts were self-consistent using χ = 1.08 for the NaCl particles (cf. figure 13 in Rose et al. 2008). Although a straight calibration line was used by Rose et al. (2008) for this case, re-analysis of the data shows that the residuals of the data compared to the line form a curve, implying a maximum value in the shape factor akin to our results in Figure 5. For example, the point at 0.25% supersaturation (corresponding approximately to 50-nm NaCl particles) in Rose et al. (2008) is above the line, suggesting χ > 1.08, whereas the points toward lower and upper end of the supersaturation ranges (corresponding approximately to 30- and 130-nm NaCl particles, respectively) lie below the line, suggesting χ < 1.08. The trend therefore shows a maximum in χ at an intermediate diameter, which is consistent with our trend showing the dependence of χ on particle size (Figure 5).

Kuwata and Kondo (2009) employed measurements of particle mobility diameter made with a DMA and of particle specific mass made by an aerosol particle mass analyzer (APM) to determine χ for 50- to 150-nm NaCl particles. Among runs, χ varied from 1.09 to 1.14 at the lower end of the size range. At the upper end, it varied from 1.04 to 1.10. TSI diffusion dryers were used, which we again estimate a drying rate of 30 to 60 RH s^–1. The results at the lower end of the size range investigated by Kuwata and Kondo (2009) can be compared to those at the upper end of our size range, and the agreement is good. Specifically, the values of 1.09 to 1.14 in Kuwata and Kondo (2009) can be compared to values of 1.05 to 1.15 shown in Figure 5 for 50- to 80-nm particles and drying rates of 29.7 ± 0.7 and 58.4 ± 0.9 RH s^–1.

5. CONCLUSIONS

This study presented experimental results showing the dependence of the dynamic shape factor χ of sub-100 nm NaCl particles on drying rate and particle size. Values of χ were determined from the mobility diameter measured by a DMA and the critical supersaturation determined by CCN analysis. The drying rate at efflorescence (45% RH), from an initial RH of 57% prior to drying, was quantified and varied from 5.5 ± 0.9 to 101 ± 3 RH s^–1. The results showed that the dynamic shape factor of NaCl particles can vary from values representing nearly cubic to almost spherical particles. Specifically, depending on particle size and drying rate, the value of χ ranged from 1.02 to 1.26. The value of χ decreased with increasing drying rate. High rates of drying (i.e., 101 ± 3 RH s^–1) caused rapid evaporation and crystallization, tending to favor a spherical shape. Slow rates of drying (i.e., 5.5 ± 0.9 RH s^–1) led to slower evaporation and crystallization, tending to favor cubic shapes. At fixed drying rate, particles having diameters of 35–40 nm had the highest χ values, which approached those theoretically expected for cubes. For both smaller and larger particles, the χ values decreased, eventually approaching values representing a spherical geometry. The dependence of χ on particle size can be attributed to the competing effects of the dominant characteristic times of particle-phase diffusion of water and diffusive movement of NaCl monomers, coupled to system size. The approach introduced herein for studying shape factors can allow the continued collection of data sets to underpin more detailed and quantitative theoretical developments of the connections among aqueous particle diameter, drying rate, and dry particle morphology.

The present study used a laminar aerosol flow tube having a dry sheath flow and a wet aerosol core flow to control the drying rate at ERH. The sheath flow extracting the water vapor was operated in continuous flow and continuously renewed the environment. Therefore, there was no influence of previous runs on a current set of measurements, and precise and reproducible drying rates were possible. This approach can be compared to complications that have arisen in earlier studies that have employed dessicant-based diffusion dryers. The drying capability can change with time, and differences among experimental runs with regard to the dynamic shape factor have been attributed to saturation and aging of the dessicant (Zelenyuk et al. 2006; Kuwata and Kondo 2009). The equations developed in Appendix B of this study lead to an estimate of a moderate drying rate between 30 to 60 RH s^–1 for the most commonly used configuration of a TSI diffusion dryer and typical flow rates through it.

The dynamic shape factor of NaCl aerosol particles having dry mobility diameters less than 100 nm (i.e., nanoparticles) has been an important source of uncertainty for the calibration of cloud condensation nuclei counters (CCNCs) (Kreidenweis et al. 2005; Shilling et al. 2007; Rose et al. 2008; Kuwata and Kondo 2009). The results herein provide quantitative descriptors of the factors affecting the χ value of NaCl particles and, in particular, emphasize the absolute requirement that detailed attention be given to aspects of particle generation and conditioning when carrying out CCN calibration for laboratory or field measurements.

APPENDIX A: Theory for χ = f(d _{m, + 1} ^dry, S _c )

The relationship of χ = f(d _{m, + 1} ^dry, S _c ) is derived, as follows. The dry solute mass m _p ^dry of a fully water-soluble salt particle is related to the critical supersaturation S _c of CCN activation by the Köhler model of Equation (A1). The notation S _c = S[w _t ]:max[f] of that equation reads that S _c is defined as the value of S at the point of maximum in the function f for the running variable w _t .

The terms of Equation (A1) include percent saturation S, solution water activity a _w , solution surface tension σ, solution partial molar volume of water V _m,w , universal gas constant R, absolute temperature T, aqueous particle diameter d _ve ^aq , solute weight fraction w _t , and solution density ρ _aq . The last line of Equation (A1) shows that the maximum depends on the independent parameter m _p ^dry. The other terms a _w , σ, V _m,w , and ρ _aq depend on the running variable w _t . For these terms, the AP3 model of Rose et al. (2008) provides the relations we use. The AP3 model and the Aerosol Calculator also used in this study have similar embedded thermodynamic values and give similar results.

Equation (A1) is solved by us for multiple values of m _p ^dryto obtain S _c . From a resulting lookup table of {S _c , m _p ^dry}, we construct a parameterization m _p ^dry[S _c ] for 0.1% < S _c < 2.0%:

The coefficients c _i are listed in Table A1 for sodium chloride and ammonium sulfate. The form of Equation (A2) is based on m _p ^dry∝ 1 / S _c ² for an infinitely dilute ideal solution, with an expected correction term of √S _c for nonideal solutions as described in equation A22 of Lewis (2008) and an additional empirical linear correction term of S _c .

TABLE A1 Coefficients of m _p ^dry[S _c ] for Equation (A2) that parameterize the dependence of dry particle mass m _p ^dry (kg) on critical supersaturation S _c (%) for sodium chloride and ammonium sulfate at 298 K and 304 K. For S _c ranging from 0.1 to 2.0%, the parameterization describes m _p ^drywithin a multiplicative factor of 1.003 compared to the original equation (i.e., Equation (A1)). The AP3 model of Rose et al. (2008) was used to generate the primary data used in the parameterization

	NaCl		(NH4)2SO4
Parameter	298 K	304 K	298 K	304 K
c 0	1.181 10^–20	1.112 10^–20	2.253 10^–20	2.122 10^–20
c 1	0.1182	0.1193	0.1184	0.1197
c 2	−0.0249	−0.0256	−0.0261	−0.0269

The value of χ is obtained from the following relationship (cf. equation 25 of DeCarlo et al. 2004):

where C _c is the Cunningham slip correction factor (Allen and Raabe 1985), ρ_dry is the dry material density, and δ is the porosity factor of the dry particle that satisfies d _ve ^dry = δ d _me ^dry for a volume-equivalent diameter d _ve and a mass-equivalent diameter d _me of the dry particle. For a nonporous particle, δ = 1; for a porous particle, δ > 1. The analysis herein assumes that δ = 1 unless stated otherwise. The factor χ has been defined both on volume-equivalent and mass-equivalent bases (Brockmann and Rader 1990; DeCarlo et al. 2004). Mass equivalency eliminates internal porosity in constructing the sphere whereas volume equivalency retains that porosity in the sphere. For nonporous particles, the two equivalent diameters are equal. In our application described herein, we follow the conventions described in DeCarlo et al. (2004), and we therefore employ the dynamic shape factor on a volume-equivalency basis. Equation (A3) shows that the value of S _c , in combination with the mobility diameter d _{m, + 1} ^dry classified using the DMA, is sufficient to obtain χ of nonporous NaCl particles, thereby defining the relationship of χ = f(d _{m, + 1} ^dry, S _c ).

For comparison, several studies in the literature have employed a hygroscopic tandem differential mobility analyzer (HTDMA) to obtain the dynamic shape factor (Kramer et al. 2000; Mikhailov et al. 2004; Biskos et al. 2006c). In this technique, the dry mobility diameter d _{m, + 1} ^dry of a salt particle and the mobility diameter d _{m, + 1} ^aq [RH] of its aqueous counterpart at elevated relative humidity are measured. At a fixed RH, there is a one-to-one relationship between the dry solute mass m _p ^dry of a fully soluble salt particle and the mobility diameter of its deliquesced aqueous counterpart, which we represent by the function m _p ^dry[d _{m, + 1} ^aq ;RH]. This relationship depends on the surface tension of the air-solution interface, the partial molar volume of water of the aqueous solution, the density of the aqueous solution, and the salt hygroscopicity (cf. equations 2a and 3 in Biskos et al. 2006c). The relationship does not depend on the dynamic shape factor χ or the porosity factor δ of the dry salt particle. The relationship for an HTDMA instrument, which measures d _{m, + 1} ^dry, RH, and d _{m, + 1} ^aq , can then be written as follows:

Equation (A3) for the DMA-CCNC and Equation (A4) for the HTDMA differ only in the primary measurement that is used to obtain m _p ^dry, which is a measurement of S _c in the former and of d _{m, + 1} ^aq in the latter.

APPENDIX B: DRYING RATE AT EFFLORESCENCE RELATIVE HUMIDITY

Achieving controlled and known drying rates is an experimental challenge. One method described in literature is the mixing of a humid aerosol flow with a flow of dry nitrogen or pure air. This approach should lead to rapid drying, but the reproducibility of the technique among laboratories or even among apparatus within the same laboratory depends on the specific aspects of the mixing tied to the apparatus and their operation. Moreover, the quantification of the drying rate (RH s^–1), including a possible heterogeneity of drying rates within the mixed aerosol, is completely uncertain, even the more so if the humid and dry flows are mixed turbulently by baffling or other flow constrictions as is commonly done. Another method is to flow the aerosol through a Nafion tube or through a dessicant dryer. Provided that the flow rates and the geometries are precisely stated, these methods should lead to reproducibility among experimenters, but the quantification of the drying rate, as required for theoretical studies, is still absent, and the ability to vary this rate is limited. In this study, a laminar-flow tube with a core wet-aerosol flow and an outer dry-air sheath flow was used. The drying rates at ERH were quantified on the basis of a diffusion calculation for this optimized geometry and flow regime.

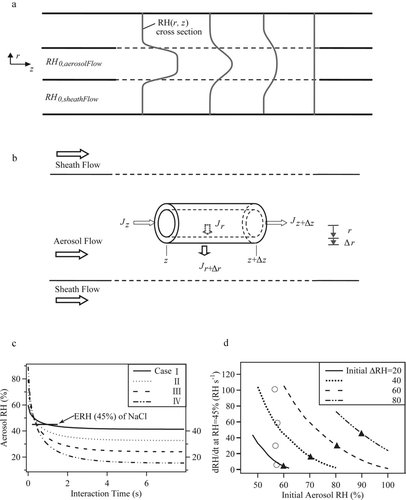
The geometry of the apparatus and its operation as relevant to the calculation of drying rate at ERH are depicted in Figure B1. For our experimental conditions, the Reynolds number of the flow in the tube was 370, corresponding to laminar motion. An inner core of wet aerosol particles flowing along the central longitudinal axis was surrounded by a dry outer sheath flow. For this setup, the dominant mechanism for water-vapor movement in the radial coordinate was diffusion, as described by Fick's law.

A quantitative model of these processes can be developed for the cylindrical geometry of the flow tube. In any infinitesimal cylindrical volume element at longitudinal coordinate z, radial coordinate r, and azimuthal coordinate θ (Figure B1), the general mass balance for water combined with Fick's law for diffusion is as follows (Cussler 1984):

where t is time, C ₀ is the vapor concentration of pure water, RH is the relative humidity, v _i is the advective flow velocity in direction i, and D is the diffusion coefficient of water in air. Conditions for the modeling include incompressible flow and constant temperature.

FIG. B1 Drying rate. (a) Depiction of the RH profiles in the inner and outer flows along the longitudinal axis of the flow tube. Flow is from left to right. The lighter solid lines represent the cross section of RH profile along the interaction distance and the dashed lines show the interaction area for inner and outer flows. (b) Depiction of a volume element for calculating the drying rate in the aerosol flow. (c) Calculated RH in the aerosol flow for increasing interaction time. Results are shown for the four model cases specified in Table B1. The interaction time can be related to the longitudinal position z in the flow tube by use of the linear flow velocity. The arrow indicates the ERH of NaCl particles (i.e., 45%). The slope of the curve at this point is the drying rate (RH s^–1) for an aerosol RH of 45%. (d) Drying rate (RH s^–1) at an aerosol RH of 45% for variable initial aerosol RH. Results are shown for several different initial Δ RH between the aerosol RH and the sheath RH. Lines show the ranges of drying rates that can be obtained by varying the initial RH but holding constant initial Δ RH. The solid triangles correspond to the four model case listed in Table B1, and the open circles indicate the calculated drying rates for the experimental conditions listed in Table 1.

For our experimental conditions, there is advection among volume elements only in z, implying v _r = v _θ = 0 and that z = v _z t. There is also azimuthal symmetry among the volume elements, meaning that ∂/∂ θ between elements is zero. Longitudinal diffusion among the elements (represented by ∂² RH/∂ z ²) is negligible for the residence time of our experimental setup. We seek the solution at steady state, and we can therefore omit terms of ∂/∂ t. The general governing differential equation (i.e., Equation (B1)) therefore reduces to the specific equation that must be satisfied by all volume elements in our experimental setup:

The experimental setup imposes several boundary conditions for the solution of Equation (B2). For RH(r, z), the conditions to satisfy are RH(r < r _aerosolFlow, 0) = RH _{0,aerosolFlow}, RH(r _aerosolFlow < r < r _sheathFlow, 0) = RH _0,sheathFlow (∂ RH/∂ r) _{r = 0} = 0 for all z, and (∂ RH/∂ r) _{r = r sheathFlow} = 0 for all z, where RH _{0,aerosolFlow} and RH _0,sheathFlow are the initial relative humidity in the inner and outer tubes, respectively, and the two flows come into first contact at z = 0.

The analytical solution of Equation (B2) for the stated boundary conditions and an approximation of a flat-flow profile is an infinite expansion, as follows:

where J ₀ and J ₁ are Bessel functions of the first kind and z _n = (r _sheathFlow ² v _z )/(Dα _n ²). The expansion is in the roots α _n of J′₀ (α _n ) = 0 (i.e., there is an infinite set of progressive roots). The first several of these roots are 3.8, 7.0, and 10.2, and they asymptotically approach (n + 1/4) π. The first term of Equation (B3) is the RH at long distance; the second term represents the evolution of RH from short to long distances. The evolution with distance is controlled by the decay constants z _n of the individual modes, the first several of which are 0.17, 0.051, and 0.024 m for the parameters of our experiment. The implication is that by approximately 0.1 m only the first few terms of Equation (B3) contribute appreciably to RH(r, z).

Modeling results are summarized in Table 1 and Table B1 as well as Figures B1. Parameter values for the modeling include v _z = 0.127 m s^–1, D = 2.56 × 10^–5 m² s^–1, r _aerosolFlow = 5.8 × 10^–3 m, and r _sheathFlow = 2.25 × 10^–2 m. The values of RH_0,sheathFlow and RH _{0,aerosolFlow} are listed in the tables. The analytical solutions obtained by Equation (B3) were compared to numerical solutions, and the agreement between the two approaches was good.

TABLE B1 Calculated drying rates in the laminar-flow tube for model cases I to IV. Each case corresponds to an initial aerosol RH and an initial sheath RH. The model is described by Equation (B3). Calculations are carried out for three interactions times (i.e., corresponding to three longitudinal positions). Shown in the table are the modeled aerosol RH at each interaction time and the average drying rate at that aerosol RH (Equation (B4)). The cases listed in the table correspond to those plotted in panel c of Figure B1

	Model conditions					Model results
Case	Initial aerosol RH (%)	Initial sheath RH (%)	Initial Δ RH (%)	Interaction time (s)	Longitudinal position (m)	Aerosol RH (%)	Sheath RH (%)	Δ RH (%)	(dRH/dt)Aerosol RH (RH s^− 1)
I	60	40	20	0	0	60.0	40.0	20.0	−8.5× 10^6
				0.96	0.121	45.0	41.0	4.0	−3.8
				7.94	1.000	41.3	41.3	0	0
II	70	30	40	0	0	70.0	30.0	40.0	−1.71× 10^7
				0.52	0.066	45.0	31.7	13.3	−16.6
				7.94	1.000	32.7	32.7	0	0
III	80	20	60	0	0	80.0	20.0	60.0	−2.56× 10^7
				0.43	0.054	45.0	22.4	22.6	−30.4
				7.94	1.000	24.0	24.0	0	0
IV	90	10	80	0	0	90.0	10.0	80.0	−3.42× 10^7
				0.39	0.049	45.0	13.1	31.9	−44.5
				7.94	1.000	15.4	15.3	0.1	−0.05

For our study, the key modeling endpoint is the drying rate at the longitudinal position at which particles crystallize. We calculate an average drying rate RH′_ERH in the aerosol flow at the efflorescence relative humidity, as follows:

where (∂ RH/∂ z)_ERH,r is evaluated at the position r that satisfies RH(r, z) = ERH. Table 1 lists RH′_ERH for the four different experimental conditions of this study.

In regard to the approximation of a flat-flow profile, the actual profile should approach parabolic by the end of the tube. Treatment of the flow transition, however, is not within the scope of our study. Nevertheless, the correction for a full treatment to the rate of radial diffusion of water vapor (i.e., drying rate) should be minor compared to the larger stepwise changes that occur for the different settings of the initial RH values in the inner and outer tubes (i.e., Table B1).

The results of model cases I through IV for different initial conditions of RH _0,sheathFlow and RH _{0,aerosolFlow} are presented in Table B1. The associated RH profiles are illustrated in Figure B1c by four lines, each representing the radially averaged RH _aerosolFlow(t; t = z/v _z ) of one of the model cases. As expected, RH _aerosolFlow decreases sharply at the beginning of the diffusive exchange with the drier air of RH _0,sheathFlow, and the highest instantaneous drying rates in the aerosol flow are obtained at time zero (cf. Table B1). Full homogenization between the aerosol and sheath flows is largely obtained in all four cases. The drying rates correspondingly decrease for increasing interaction time until falling to zero after full homogenization.

The average drying rate RH′_ERH at efflorescence is given by the slope of RH _aerosolFlow(t) at ERH. In Figure B1c, the intersections of the four lines for RH _aerosolFlow(t) with the inset horizontal line determine those time points. In Figure B1d, values of RH′_ERH as calculated by Equation (B4) are represented by lines of constant Δ RH for increasing RH _{0,aerosolFlow}, where Δ RH = (RH _{0,aerosolFlow}– RH _0,sheathFlow). Values of RH′_ERH for the model cases I to IV (i.e., the slopes of Figure B1c) are represented by the filled triangles along the lines. The results represented in Figure B1d indicate that the same value of RH′_ERH can be obtained with different combinations of conditions. For example, all four lines pass through a drying rate of 40 RH s^–1. Figure B1d also shows that, with Δ RH fixed, RH′_ERH decreases for increasing RH _{0,aerosolFlow}. In comparison, with RH _{0,aerosolFlow} fixed, RH′_ERH increases for increasing Δ RH. Open circles in Figure B1d show RH′_ERH for experiments 1 through 4 of this study, as summarized in Table 1. The rates range from 5.5 ± 0.9 to 101 ± 3 RH s^–1 for these experiments.

This material is based upon work supported by the Office of Science (BER), U.S. Department of Energy, Grant No. DE-FG02-08ER64529. The particle images were collected at the LeRoy Eyring Center for High Resolution Electron Microscopy within the Center for Solid State Science at Arizona State University. Zhe Wang was the recipient of a Chinese Government Scholarship for Postgraduates. E. Lewis was supported by the U.S. Department of Energy's Office of Science under Contract No. DE-AC02-98CH10886. We thank John Shilling and George Biskos for the valuable discussion.

[Supplementary materials are available for this article. Go to the publisher's online edition of Aerosol Science and Technology to view the free supplementary files.]

Notes

^a Particles generated by electrospray

^b Particles generated by vaporization-condensation

^c Diameters were approximately calculated from associated supersaturation in Rose et al. 2008

^d Range of values arises from the size dependence investigated from 23 to 84 nm