Transfer Functions and Penetrations of Five Differential Mobility Analyzers for Sub-2 nm Particle Classification

Abstract

The transfer functions and penetrations of five differential mobility analyzers (DMAs) for sub-2 nm particle classification were evaluated in this study. These DMAs include the TSI nanoDMA, the Caltech radial DMA (RDMA) and nanoRDMA, the Grimm nanoDMA, and the Karlsruhe-Vienna DMA. Measurements were done using tetra-alkyl ammonium ion standards with mobility diameters of 1.16, 1.47, and 1.70 nm. These monomobile ions were generated by electrospray followed by high resolution mobility classification. Measurements were focused at an aerosol-to-sheath flow ratio of 0.1. A data inversion routine was developed to obtain the true transfer function for each test DMA, and these measured transfer functions were compared with theory. DMA penetration efficiencies were also measured. An approximate model for diffusional deposition, based on the modified Gormley and Kennedy equation using an effective length, is given for each test DMA. These results quantitatively characterize the performance of the test DMAs in classifying sub-2 nm particles and can be readily used for DMA data inversion.

1. INTRODUCTION

The differential mobility analyzer (DMA) classifies particles according to their electrical mobility. The history of mobility analyzers can be traced back to measurements of atmospheric ions in the early 20th century (Flagan 1998). The DMA developed in the University of Minnesota Particle Technology Laboratory was a breakthrough both in terms of apparatus design (Liu and Pui 1974) and theory (Knutson and Whitby 1975). Similar to the instrument used by Hewitt (1957), this DMA has a coaxial cylinder arrangement with two inlets and two outlets. Since the mid 1970s, DMAs have been used routinely to produce aerosol standards of known size, concentration, and composition, to measure aerosol size distributions, and to measure aerosol properties with tandem measurement instrument systems (Park et al. 2008). The transfer function that was first derived by Knutson and Whitby (1975) was the key development in enabling quantitative applications of DMAs for such purposes. Over the past decades, several other types of DMAs have been developed and used in aerosol research, including the Vienna type (Winklmayr et al. 1991), the French radial type (RDMA, Mesbah 1994; Ooghe et al. 1994; Fissan et al. 1998), the Caltech radial type (Zhang et al. 1994, 1995; Brunelli et al. 2009), and the TSI nanoDMA (Chen et al. 1998). The performance of such DMAs in the 3 to 200 nm size range has been discussed in previous studies (Fissan et al. 1996; Birmili et al. 1997; Karlsson and Martinsson 2003). More recently, supercritical cylindrical DMAs that remain laminar in the classification region to Reynolds numbers much higher than 2000, and DMAs of unconventional geometries have been developed to improve the performance and were reviewed by Fernández de la Mora (2011).

FIG. 1 Experimental setup for generating monomobile ion standards and for testing DMA performances.

The classification of nanoparticles down to molecular dimensions is of special interest for current research. However, the transfer functions of most DMAs for sub-2 nm particle classification have not been systematically evaluated, largely due to the lack of suitable sub-2 nm particle standards. The tandem DMA (TDMA) method has often been used to evaluate DMA transfer functions (Stolzenburg and McMurry 1988; Fissan et al. 1996; Stratmann et al. 1997). In the 1–2 nm size range, diffusional broadening can significantly degrade the DMA resolution such that it is difficult to generate pseudo-monodisperse particles using a conventional DMA as the first DMA (Kousaka et al. 1986; Stolzenburg 1988). Recent developments in high-flow DMAs significantly improved the DMA resolution in the nanometer size range (Rosell-Llompart et al. 1996; Fernández de la Mora et al. 1998; Rosser and Fernández de la Mora 2005), and enabled the generation of molecular monodisperse mobility standards (tetra-alkyl ammonium ions) (Ude and Fernández de la Mora 2005). These monomobile ions, which have mobility diameters of 1–2 nm, have been used as size standards to test DMA resolution (Rosser and Fernández de la Mora 2005; Steiner et al. 2010), diffusional particle losses (Heim et al. 2010), and the transmission factors of mass spectrometers (Zhao et al. 2010). Another newly developed size standard is oven-generated fullerene (C₆₀) vapor. Monodisperse C₆₀ monomer has a geometrical size around 1 nm and has been used to test DMA performance (Tanaka and Takeuchi 2003; Iida et al. 2009).

In this study, the transfer functions and penetrations of five differential mobility analyzers for sub-2 nm particle classification were evaluated using tetra-alkyl ammonium ion standards. These DMAs included the TSI nanoDMA (Chen et al. 1998), the Caltech RDMA (Zhang et al. 1995) and nanoRDMA (Brunelli et al. 2009), the Grimm nanoDMA, and the Karlsruhe-Vienna DMA, an optimized version of the classical Vienna type DMA (Winklmayr et al. 1991; Heim et al. 2005). Calibration was performed using singly charged tetra-propyl ammonium (N⁺[C₃H₇]₄), tetra-heptyl ammonium (N⁺[C₇H₁₅]₄), and tetra-dodecyl ammonium (N⁺[C₁₂H₂₅]₄) ions with mobility diameters of 1.16, 1.47, and 1.70 nm, respectively. These monomobile ions were generated by electrospray and classified by the high resolution DMA (Fernández de la Mora et al. 1998; Ude and Fernández de la Mora 2005). Based on Stolzenburg's diffusive transfer function (Stolzenburg 1988; Stolzenburg and McMurry 2008), a data inversion routine was developed to obtain the true transfer function for each test DMA. In addition to transfer functions, we report the DMA penetration efficiencies.

2. EXPERIMENTS

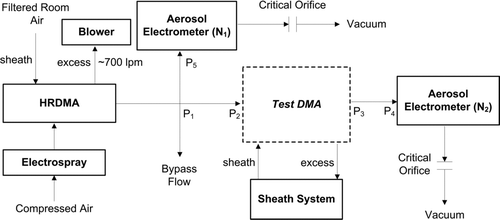
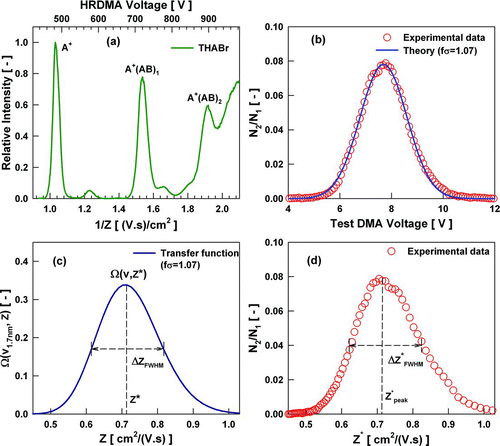
As shown in Figure 1, an electrospray was coupled to a high resolution differential mobility analyzer (HRDMA) to generate monodisperse size standards (tetra-alkyl ammonium ions). The electrospray system used here has been described in detail by Ude and Fernández de la Mora (2005). Particle-free compressed air was used as the carrier gas. The organic salts used to produce these ions (tetra-propyl ammonium iodide (TPAI, N[C₃H₇]₄I), tetra-heptyl ammonium bromide (THABr, N[C₇H₁₅]₄Br), and tetra-dodecyl ammonium bromide (TDDABr, N[C₁₂H₂₅]₄Br)) were dissolved in ultrapure methanol with low concentrations. All the chemicals were purchased and used as received from Sigma Aldrich. Rather than precisely controlling the salt concentrations (Ude and Fernández de la Mora 2005), serial dilutions were made to a solution of unknown concentration until the electrospray was stable and the peaks of monomer (A⁺; A denotes the tetra-alkyl ammonium) and dimer (A⁺(AB)₁; B denotes the halide) were somewhat higher than other peaks. Highly mobile positively charged ions generated by electrospray were then transported to a high-resolution differential mobility analyzer (Fernández de la Mora et al. 1998). An inverse mobility distribution of electrosprayed THABr ions measured by scanning HRDMA voltage while using an aerosol electrometer to measure the concentrations of mobility-classified ions is shown in Figure 2a. The HRDMA cleanly separates the monomer (A⁺), dimer (A⁺(AB)₁), and trimer (A⁺(AB)₂). The identities of these molecular ions have been confirmed by mass spectrometry (Ude and Fernández de la Mora 2005). Therefore, monodisperse molecular ions having known chemical structures (e.g., monomer or dimer) can be selected by fixing the HRDMA voltage at the value corresponding to the peak currents shown in Figure 2a. The electrical mobilities of electrosprayed tetra-alkyl ammonium ions have been studied extensively by Fernández de la Mora and coworkers. The equations used by Ude and Fernández de la Mora (2005) are used to convert their electrical mobilities to mobility diameters. The monomers of TPAI, THABr, and TDDABr have mobility diameters of 1.16, 1.47, and 1.70 nm, respectively. These ions were used in this study to test DMA performance. For some DMAs, the dimer and trimer of tetra-heptyl ammonium ions were also used. Their mobility diameters are 1.78 and 1.97 nm, respectively. For molecular ions and particles in this size range, mobility diameters differ from the estimated geometric diameters based upon their masses. Tammet (1995) discussed the theoretical relationships between these sizes. Ku and Fernández de la Mora (2009) carried out measurements and found that for particles with mobility diameters down to 1.6 nm, geometric diameters are 0.3 nm smaller than their mobility diameters. Recent tests show that to within 15%, the 0.3 nm correction applies to geometric diameter down to 0.68 nm (Larriba et al. 2011).

FIG. 2 (a) The measured inverse mobility distribution of electrosprayed THABr ions; (b) Example of measured concentration ratios and fitted N ₂/N ₁ values using Stolzenburg's diffusive transfer function. The TSI nanoDMA was operated at a flow ratio of 1.5/15 lpm while classifying 1.70 nm TDDABr monomer; (c) The transfer function of the TSI nanoDMA with a fixed DMA voltage for 1.70 nm TDDABr monomer; (d) Measured concentration ratios as a function of the centroid mobility (varying DMA voltage).

The selected monodisperse ions were then transported to the test DMAs to measure their transfer functions and penetrations. As shown in Figure 1, both the upstream ion concentration (N ₁) and the downstream ion concentration (N ₂) of the test DMAs were monitored by aerosol electrometers. The downstream to upstream electrometer ratios without the test DMA present were experimentally calibrated for every ion and flowrate combination to properly account for the difference in readings between two aerosol electrometers, and for the transport losses from the union cross (P ₁) to the test DMA inlet (P ₂), from the test DMA outlet (P ₃) to the downstream aerosol electrometer inlet (P ₄), from the union cross (P ₁) to the inlet (P ₅) of the upstream aerosol electrometer, and inside aerosol electrometers. The reported concentration ratios (N ₂/N ₁) account for these corrections. A bypass flow was used to adjust the aerosol outlet flowrate in the HRDMA. The concentration of monodisperse ions before the test DMAs was controlled by adjusting the electrospray operational conditions and the bypass flowrate. Measurements were made over a sufficient range of concentrations to confirm that data were not affected by space charge (Camata et al. 2001). During the DMA calibration, the voltage for the HRDMA was fixed and the voltage for the test DMA was scanned continuously. The DMA voltage was increased slowly to ensure pseudo-steady-state operation. A typical scan took approximately 15 min. Most measurements were done at an aerosol-to-sheath flow ratio of 0.1. Several other aerosol and sheath flow combinations were also examined. Balanced flows were used for all test DMAs, i.e., the aerosol inlet flowrate was equal to the aerosol sampling outlet flowrate. A closed-loop was used for DMA sheath and excess flows to ensure they were exactly equal (Rogak et al. 1993; Jokinen and Makela 1997).

TABLE 1 Geometry parameters and tested flow conditions for various DMAs

DMA type	Length/width (cm)	Inner radius (cm)	Outer radius (cm)	f factor	Flow ratios	Reference
TSI nanoDMA	4.987	0.937	1.905	0.716	1.5/15; 2/20	Chen et al. 1998
Grimm nanoDMA	1.3	1.3	2	0.81	2/21.9
Caltech RDMA	1	0.24	5	1	1.5/15; 2/20	Zhang et al. 1995
Caltech nanoRDMA	1	0.24	0.75	1	0.6/6; 1/10; 1.5/15; 0.6/10	Brunelli et al. 2009
Karlsruhe-Vienna DMA	2.5	2.29	3.3	0.838	6/61.4	Heim et al. 2005

The geometry parameters and the tested flowrates for each DMA are summarized in Table 1. Designs of the TSI nano- DMA, the Caltech RDMA and nanoRDMA are described in detail in the references given in Table 1. The description of the Karlsruhe-Vienna DMA and the Grimm nanoDMA are not readily available in literature. We discuss the difference between the Karlsruhe-Vienna DMA and the original Vienna DMA in Section 4.5. The Grimm nanoDMA is a commercial instrument, and we were unable to obtain a detailed description of its pertinent design features. The French radial DMA (Ooghe et al. 1994) was also tested. However, the use of a high voltage insulator inside this DMA causes high electrostatic transport losses, so that no ions were observed at the outlet. Such electrostatic losses have been reported previously with other DMAs and they become increasingly important as size decreases (Kousaka et al. 1986; Chen et al. 1998). Similar losses were observed for a copy of the Vienna type DMA (referred to as “DMA 1/40” in Winklmayr et al. 1991). The penetration through the Vienna type DMA was significantly improved by replacing the original insulator with a Delrin insulator, though the results of these two DMAs are not included in this study. The Grimm nanoDMA and the Karlsruhe-Vienna DMA were tested at the Karlsruhe Institute of Technology. The Caltech RDMA and nanoRDMA were evaluated at the University of Minnesota. The TSI nanoDMA was tested at both the University of Minnesota and Karlsruhe Institute of Technology.

Different versions of high-resolution differential mobility analyzers have been developed by Fernández de la Mora and coworkers. The HRDMA used in Minneapolis is also referred as the Herrmann DMA (Herrmann et al. 2000), while the HRDMA used in Karlsruhe is also referred as the Attoui DMA (Fernández de la Mora and Attoui 2007; Heim et al. 2010). Both HRDMAs were operated in an open-loop for sheath and excess flows and in a safe mode, i.e., the DMA outer electrode is grounded. The use of a “leaky” insulator (polyoxymethylene, Ensinger-HYDE, Germany) at the aerosol outlet facilitates the safe mode operation (Fernández de la Mora and Attoui 2007). This insulating material is slightly conductive which helps to dissipate the electric charges built up on the insulator surface due to charged particle depositions.

3. DATA INVERSION

The results of a typical measurement, where the TSI nano- DMA was operated at a flow ratio of 1.5/15 lpm while classifying 1.70 nm TDDABr monomer, are shown in Figure 2b. Since monodisperse particles were sent into the test DMA, the concentration ratio (N ₂/N ₁) can be written as,

where η_pen(d_p) is the penetration efficiency of particles of diameter d_p through the entrance and exit regions of the DMA and Ω(V,Z(d_p)) is the DMA transfer function. The transfer function is defined as the fraction of particles of electrical mobility Z(d_p) that penetrate through a DMA classifying region operated at voltage V. As shown in Figure 2c, the transfer function is characterized by two parameters: the height (Ω(V,Z*)) and the normalized full-width at half-maximum (NFWHM), or the resolution (R). The height of the transfer function is the penetration fraction of particles with the centroid electrical mobility (Z*), i.e., the mobility that corresponds to the DMA voltage V through the voltage-mobility equation (Knutson and Whitby 1975; Stolzenburg and McMurry 2008). The NFWHM of the transfer function is,

where ΔZ_FWHM is the transfer function width at half height (Figure 2c). The instrument mobility resolution is defined as the reciprocal of the NFWHM (Flagan 1999),

and is a figure of merit for DMA performance.

To measure the true DMA transfer function (Figure 2c), ideally one will fix the DMA voltage and send monodisperse particles of different sizes to the DMA to obtain Ω(V,Z(d_p )). Since it is impractical to generate many different monodisperse size standards under the narrow non-zero width of the transfer function, an alternative method is used—the particle size is fixed and the DMA voltage is scanned, as shown for example in Figure 2b. If the DMA transfer functions at different voltages are the same, the measured Ω at different voltages can be directly projected back to Figure 2c. Particle diffusion can broaden the DMA transfer function significantly when classifying sub-2 nm particles. The NFWHM of the DMA transfer function also becomes a function of the DMA voltage (the centroid mobility) due to diffusion. Therefore, the results obtained by measuring concentration ratios as a function of the test DMA voltage for monodisperse particles are not exactly equal to the transfer function, i.e., the diffusional broadening effect increases as the voltage is decreased in the course of the transfer function measurement. For all DMAs tested here, this effect was accounted for when inverting the data so that the transfer functions reported here correspond to the transfer function that would be measured at constant voltage if a sufficient range of calibration particles were available. The resolution of the Caltech nanoRDMA in the 1–2 nm size range was previously reported without considering this effect (Brunelli et al. 2009). In that earlier study, the resolution was estimated based on ΔZ*_FWHM and Z*_peak in Figure 2d.

In this study, a data inversion scheme was developed based on Stolzenburg's diffusive transfer function. Stolzenburg (1988) extended the non-diffusive transfer function developed by Knutson and Whitby (1975) to account for particle diffusion. A dimensionless diffusional broadening parameter, σ_theo , was defined and an expression for the diffusive transfer function was developed. This theory is described in detail elsewhere (Stolzenburg 1988; Flagan 1999; Stolzenburg and McMurry 2008) and is summarized in the Supplemental Information. In addition to particle diffusion, the transfer function might also be affected by instrument nonidealities, electrode imperfections and misalignments, and other factors that may influence the flow or electric fields (Stolzenburg 1988; Zhang and Flagan 1996; Chen and Pui 1997; Eichler et al. 1998; Karlsson and Martinsson 2003; Heim et al. 2005). To account for these potential effects, a multiplicative factor (f_σ ) is used and the broadening parameter in the diffusive transfer function is rewritten as,

If no other broadening exists, the factor (f_σ ) will be equal to unity. We assume that f_σ is constant across the narrow non-zero width of the transfer function. Particle diffusion will increase the transfer function NFWHM and decrease the height, subsequently lowering the peak value of N ₂/N ₁. The losses at the entrance and exit regions of the DMA will affect N ₂/N ₁ without changing the NFWHM (Martinsson et al. 2001). Therefore, two unknowns are needed to calculate the concentration ratio using Equation (1): f_σ and η_pen(d_p). A least squares fitting method was used to solve for these two unknowns by matching the theoretically predicted concentration ratios with the measured N ₂/N ₁. For the data shown in Figure 2b, the theoretical calculated concentration ratios agreed with the experimental data very well when f_σ is 1.07. The transfer function height (Ω(V,Z*)) and the penetration efficiency (η_pen ) were 33.8% and 23.1%, respectively. Their product is the peak value of N ₂/N ₁, 7.8% (Figure 2b). Another way to look at the additional broadening is to define it as σ_distor which can be estimated from (Stolzenburg 1988; Rosell-Llompart et al. 1996; Flagan 1999),

When comparing DMA performance, the migration Peclet number is often used (Zhang and Flagan 1996; Fissan et al. 1998; Flagan 1999; Karlsson and Martinsson 2003). It is defined as the ratio of the electrophoretic flux to the diffusive flux of particles during mobility classification. For each test DMA, the migration Peclet number allows the results obtained at different aerosol and sheath flowrates but the same aerosol-to-sheath ratio, β, to be conveniently presented on the same plot. In this study, we used the definition given by Flagan (1999),

where q is the charge carried by particles (one elementary charge for all ion standards used in this study), V is the DMA voltage, k is Boltzmann's constant, T is the absolute temperature, and f is a DMA geometry factor that accounts for the nonuniformity of the DMA electric field. For radial DMAs, this geometry factor is unity. For cylindrical DMAs, this geometry factor is,

where R ₁ and R ₂ are the inner radius and the outer radius of the DMA, respectively. The f factors for all test DMAs are summarized in Table 1.

TABLE 2 Estimated DMA transfer function parameters and effective lengths

DMA type	Dp (nm)	Flow ratio	σ*theo	fσ	σ*distor	Ω(V,Z*)	ηpen	NFWHM	R	Leff (m)
TSI nanoDMA	1.16	1.5/15	0.148	1.03	0.035	0.253	0.076	0.370	2.70	Inlet: 2.24 Outlet: 1.40
	1.47	1.5/15	0.119	0.98	-0.025	0.323	0.158	0.291	3.44
	1.70	1.5/15	0.103	1.07	0.040	0.338	0.231	0.277	3.61
	1.16	2/20	0.132	1.04	0.036	0.280	0.099	0.334	3.00
	1.47	2/20	0.103	0.98	-0.019	0.366	0.186	0.257	3.90
	1.70	2/20	0.088	0.98	-0.017	0.416	0.234	0.226	4.43
Grimm nanoDMA	1.47	2/21.9	0.068	1.01	0.012	0.465	0.066	0.185	5.41	3.87 (Qa = 2 lpm)
	1.78	2/21.9	0.056	0.98	-0.010	0.547	0.145	0.158	6.35
Caltech RDMA	1.47	1.5/15	0.151	1.34	0.134	0.194	0.109	0.481	2.08	1.99 (Qa = 1.5 and 2 lpm)
	1.70	1.5/15	0.129	1.42	0.130	0.212	0.196	0.439	2.28
	1.47	2/20	0.131	1.42	0.132	0.210	0.124	0.445	2.25
	1.70	2/20	0.112	1.58	0.137	0.219	0.221	0.425	2.35
Caltech nanoRDMA	1.16	0.6/6	0.081	0.95	-0.025	0.456	0.032	0.206	4.85	0.87 (Qa = 0.6,1, and 1.5 lpm)
	1.47	0.6/6	0.063	1.02	0.013	0.519	0.136	0.182	5.50
	1.70	0.6/6	0.054	1.09	0.023	0.553	0.286	0.171	5.86
	1.16	1/10	0.063	1.16	0.037	0.472	0.115	0.199	5.01
	1.47	1/10	0.049	1.21	0.033	0.553	0.258	0.171	5.86
	1.70	1/10	0.042	1.37	0.039	0.560	0.411	0.169	5.93
	1.16	1.5/15	0.051	1.38	0.049	0.486	0.169	0.194	5.16
	1.47	1.5/15	0.040	1.58	0.049	0.526	0.292	0.179	5.58
	1.70	1.5/15	0.034	1.84	0.053	0.528	0.376	0.179	5.60
	1.47	0.6/10	0.050	1.37	0.046	0.331	0.124	0.170	5.87
	1.70	0.6/10	0.042	1.44	0.044	0.363	0.279	0.155	6.44
Karlsruhe-Vienna DMA	1.47	6/61.4	0.059	1.22	0.041	0.476	0.056	0.193	5.17	11.53 (Qa = 6 lpm)
	1.78	6/61.4	0.048	1.07	0.018	0.594	0.123	0.156	6.43
	1.97	6/61.4	0.043	1.07	0.017	0.630	0.188	0.147	6.80
Note: σ*theo and σ*distor are σtheo and σdistor evaluated at the centroid electrical mobility (Z*), respectively; Qa is the aerosol inlet flow rate.

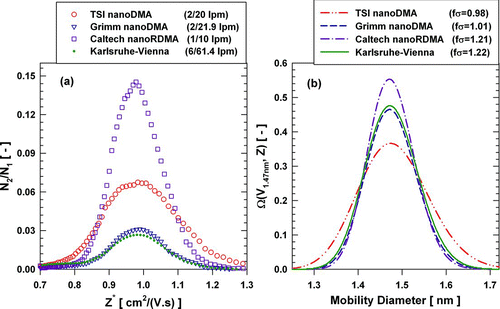
FIG. 3 Performances of four DMAs in classifying THABr monomer (1.47 nm): (a) measured concentration ratios by scanning the DMA voltage (varying centroid mobility); (b) the inverted transfer functions of four DMAs with a fixed DMA voltage for 1.47 nm THABr monomer. For the TSI nanoDMA, 15 lpm transport flow was used to reduce the losses through the entrance region (Chen et al. 1998).

The losses at the entrance and exit regions of the test DMAs were simulated using the laminar diffusional deposition model for cylindrical tubes, and an effective length, L_eff , for each test DMA is reported. Though these losses are probably more complicated (e.g., electrostatic deposition likely contributes to observed losses, and flow channels are not all cylindrical), it has been shown that the modified Gormley and Kennedy equation (Gormley and Kennedy 1949; Cheng 2002) provides a reasonable model for explaining size-dependent DMA penetration efficiencies (Reineking and Porstendorfer 1986; Karlsson and Martinsson 2003; Iida et al. 2006). More accurate estimation of the diffusion losses in DMA entrance and exit regions might be obtained by dividing them into different sections that are each analyzed using the approach originally developed for the corresponding heat transfer problem (Graetz 1885) and electrostatic deposition can also be included (Zhang and Flagan 1996; Karlsson and Martinsson 2003). However, the effective length approach is simpler and provides results that are more convenient to be included in DMA data inversion. The dimensionless deposition parameter, μ, can be written as,

where D is the diffusion coefficient of particles with diameter d_p and Q is the flow rate through the cylindrical tube. The penetration efficiency is given by (Cheng 2002),

An effective length can be derived by fitting the calculated penetration efficiencies using the above equations to the measured penetrations. A least squares method was used for the fitting.

The errors in determining the DMA transfer function (resolution/NFWHM and height) and penetration efficiency were estimated to be smaller than 7%. Uncertainties are due primarily to the uncertainties in DMA flowrates and particle concentration measurements. As shown in Figure 2b, the fitted concentration ratios mostly agree with the measured N ₂/N ₁ very well. Though it was not observed under the conditions shown in Figure 2b, an abnormal tail at higher voltage side (lower mobility) occurred under certain conditions for all test DMAs. This was also observed by Heim et al. (2010) in a TDMA experiment using THABr monomer and trimer, but not for the dimer. Their results for the monomer disagree with the proposed fragmentation and clustering hypothesis (Rosell-Llompart et al. 1996; Fernández de la Mora et al. 2005). The origin of this abnormal tail remains to be identified. Their N ₂/N ₁ values are often much smaller than the peak value. The abnormal tail was not included in the inversion fitting which may cause some additional uncertainty in the reported resolution and transmission.

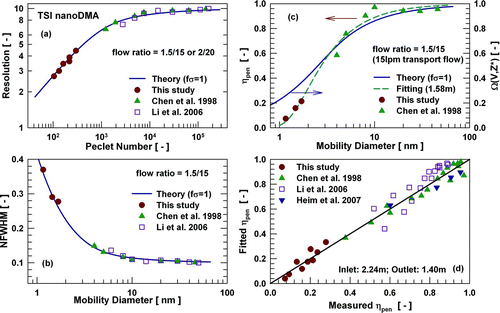
FIG. 4 TSI nanoDMA: (a) the resolution as a function of instrument Peclet number; (b) the NFWHM; (c) the height, and the penetration efficiency through DMA entrance and exit regions as a function of particle mobility diameter for the flow ratio of 1.5/15 lpm; (d) the measured penetration efficiency versus the fitted penetration efficiency.

4. RESULTS AND DISCUSSION

Estimated DMA transfer function parameters and effective lengths are summarized in Table 2. The performance of the TSI nanoDMA, the Grimm nanoDMA, the Caltech nanoRDMA, and the Karlsruhe-Vienna DMA in classifying 1.47 nm THABr monomer are shown in Figure 3. The measured transfer function of the Caltech RDMA was very broad and is therefore not included in Figure 3. Different flowrates were used for these DMAs, but the aerosol-to-sheath flow ratios were similar (∼0.1). In order to present the results from different DMAs in one graph, the corresponding centroid mobilities (Z*) rather than the test DMA voltages are used in Figure 3(a). The Caltech nanoRDMA has the highest peak N ₂/N ₁ value, followed by the TSI nanoDMA, the Grimm nanoDMA, and the Karlsruhe-Vienna DMA. Their inverted transfer functions, obtained by fixing voltage at a value corresponding to the centroid mobility diameter of 1.47 nm, are shown in Figure 3b. The resolution of the Caltech nanoRDMA was the best, followed by the Karlsruhe-Vienna DMA, the Grimm nanoDMA, and the TSI nanoDMA. Since the multiplicative factors (f_σ ) for both the TSI nanoDMA and the Grimm nanoDMA were close to unity, there was no additional broadening for these two DMAs. Both the Caltech nanoRDMA and the Karlsruhe-Vienna DMA had additional broadening under these conditions. The resolution and peak N ₂/N ₁ value of the Grimm nanoDMA were very close to those of the Karlsruhe-Vienna DMA.

The flowrates of a DMA are critical in determining its performance and different DMAs are designed to operate at different flowrates. Instrument characterization should be based on the optimum operation of each DMA such that a direct comparison of the different DMA performances is only suitable to a limited degree (Fissan et al. 1996; Birmili et al. 1997; Flagan 1999). In the following discussion, we focused on a comparison between the measured performances and the theoretical predictions for each test DMA.

4.1. TSI nanoDMA

Both the resolution and the penetration efficiency of the TSI nanoDMA are shown in Figure 4. Monodisperse ions with diameters of 1.16, 1.47, and 1.70 nm were tested using flow ratios of 1.5/15 and 2/20 lpm. In both cases, 15 lpm transport flow was used to reduce the losses through the nanoDMA entrance region (Chen et al. 1998). Literature data on the TSI nanoDMA performance in classifying particles larger than 3 nm are also included in Figure 4 (Chen et al. 1998; Li et al. 2006). As shown in Figure 4a and b, the experimentally determined resolution for this instrument agreed very well with its ideal resolution (f_σ = 1.0) in both diffusive and non-diffusive ranges. No additional broadening due, for example, to imperfections in flow profiles, electric fields, or machining tolerances, was observed under these conditions. At the test flowrates, the NFWHM of the TSI nanoDMA transfer function in classifying sub-2nm particles is 2∼4 times wider than the non-diffusive value (0.1).

Figure 4c shows the transfer function heights (Ω(V,Z*)) for classifying different sized particles at a flow ratio of 1.5/15 lpm and the penetration efficiencies (η_pen ) of sub-2 nm particles through the nanoDMA entrance and exit regions. Literature data for particles larger than 3 nm were also analyzed using the same method, i.e., by separating Ω(V,Z*) and η_pen . Together the penetration efficiencies for different sized particles were fitted with the modified Gormley and Kennedy equation. If the flowrate of 1.5 lpm was used (without considering the 15 lpm transport flow at the entrance region), the effective length of the TSI nanoDMA was found to be 1.58 m. As shown in Figure 4c, good agreement between the experimental data and the fitted penetrations is observed.

To include the transport flow, the entrance and exit regions can be fitted separately and two effective lengths will be reported. The flowrate through the first length (the entrance region) is then the aerosol flow plus the transport flow, while the flowrate through the second length (the exit region) is only the aerosol flow. Both results from this study and literature data were used for the fitting. There are total 45 data points and their information are summarized here—this study: 1.5 and 2 lpm (15 lpm transport flow), 1–2 nm; Chen et al. (1998): 1.5 lpm (with and without 15 lpm transport flow), 3–50 nm; Li et al. (2006): 0.75 and 1.5 lpm (no transport flow), 6–50 nm; Heim et al. (2007): 2 lpm (15 lpm transport flow), 3–10 nm. The effective lengths for the entrance and exit regions were found to be 2.24 and 1.40 m, respectively. As shown in Figure 4d, the fitted penetration efficiencies agree well with the measured ones.

FIG. 5 Caltech nanoRDMA: (a) the resolution as a function of instrument Peclet number; (b) the NFWHM; (c) the height, and the penetration efficiency as a function of particle mobility diameter for the flow ratio of 0.6/6 lpm.

4.2. Caltech nanoRDMA

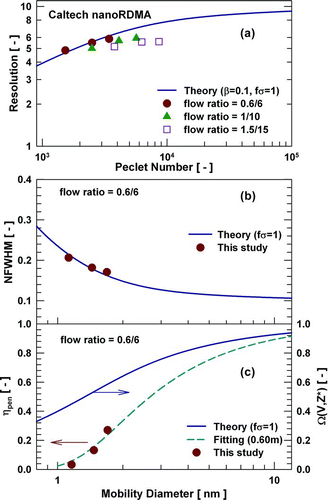
The results for the Caltech nanoRDMA are shown in Figure 5. Monomobile ions with mobility diameters of 1.16, 1.47, and 1.70 nm were tested using flow ratios of 0.6/6, 1/10, and 1.5/15 lpm. At the test flowrates, the NFWHM of the Caltech nanoRDMA transfer function in classifying sub-2 nm particles was equal to or less than 0.2 (relatively close to the non-diffusive value of 0.1). The measured resolution for this instrument agreed very well with its ideal resolution at the flow ratio of 0.6/6 lpm. However, the measured resolution fell below its ideal resolution at the flow ratio of 1/10 lpm and deviated further at higher flowrates (1.5/15 lpm). Its resolutions at the flow ratio of 0.6/10 lpm were also found to be lower than the ideal values, which is consistent to previous studies (Brunelli et al. 2009). As shown in Table 2, σ_distor increases with the increasing flowrate through the nanoRDMA. Additional tests indicated that turbulence occurred inside the nanoRDMA for a sheath flowrate of 18 lpm and particles were detected at the aerosol outlet when there was no voltage applied. Similar resolution degradation by flow effects was observed for the Caltech RDMA (Zhang and Flagan 1996) and was attributed to the flow disturbances near the entrance slot or at the classified aerosol exit. The shorter classification length of the nanoRDMA might cause additional non-uniformities in flow and electric field, e.g., in addition to the observed resolution degradation, as confirmed in this study, an empirical correction factor of 0.874 is needed for the conversion between the DMA voltage and the centroid mobility (Brunelli et al. 2009). Both the transfer function heights (Ω(V,Z*)) for classifying different sized particles and the penetration efficiencies (η_pen ) of sub-2 nm particles at a flow ratio of 0.6/6 lpm are shown in Figure 5c. The effective length of the Caltech nanoRDMA was found to be 0.60 m. If η_pen for all the tested flowrates (0.6, 1.0, and 1.5 lpm) were fitted together, the effective length was found to be 0.87 m.

4.3. Caltech RDMA

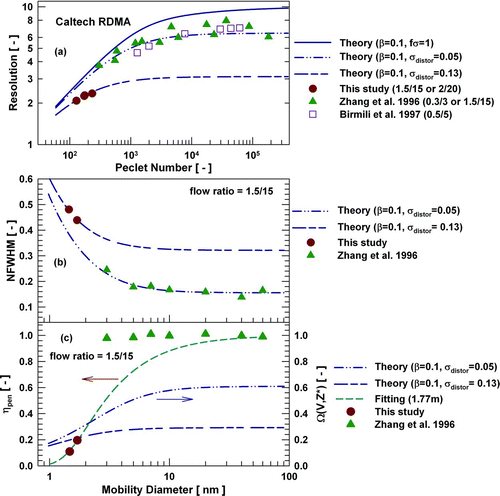
The results for the Caltech RDMA are shown in Figure 6. Monomobile ions with diameters of 1.47 and 1.70 nm were tested using flow ratios of 1.5/15 and 2/20 lpm. Literature data on the Caltech RDMA performance in classifying particles larger than 3 nm are also included in Figure 6 (Zhang and Flagan 1996; Birmili et al. 1997). As shown in Figure 6a and b, the measured Caltech RDMA resolution was lower than its ideal resolution in both diffusive and non-diffusive size ranges. By using a constant additional broadening (σ_distor = 0.05), theoretically calculated RDMA resolutions agreed very well with measured resolutions for particles larger than 3 nm, while σ_distor was estimated to be ∼0.13 for sub-2 nm classification. Again, flow disturbances inside the DMA might account for the observed resolution degradation for the Caltech RDMA.

The transfer function heights (Ω(V,Z*)) at σ_distor of 0.05 and 0.13 are shown in Figure 6c. The penetration efficiencies (η_pen ) for sub-2 nm particles and literature penetration efficiencies for large particles (Zhang and Flagan 1996) are also included in Figure 6c. For these literature data, η_pen and Ω(V,Z*) were already separated from each other. There was no single effective length to achieve good fitting with the penetration efficiencies of particles in the whole size range. When fitted separately, the effective length was found to be 1.77 m for sub-2 nm particles and less than 0.1 m for particles larger than 3 nm. If η_pen of sub-2 nm particles tested at all the flowrates (1.5 and 2 lpm) were fitted together, the effective length was found to be 1.99 m. Based on the same RDMA data set for large particles, an effective length of 0.083 m was reported by Karlsson and Martinsson (2003). It remains to be determined why the resolution/ NFWHM and penetration of RDMA is different for small particles (<2 nm) and for large particles (≥3 nm). This difference may indicate that different mechanisms, with different size-dependence, are responsible for losses in the two regimes, possibly electrophoretic and diffusive deposition (Kousaka et al. 1986; Zhang and Flagan 1996), but additional work would be required to resolve the cause for the variable loss rates. It has been observed that the performance of Vienna DMA copies can be different from one instrument to the next due to machining inconsistencies (Karlsson and Martinsson 2003). It remains to be tested whether this also contributes to the observed discrepancy for the RDMA.

FIG. 6 Caltech RDMA: (a) the resolution as a function of instrument Peclet number; (b) the NFWHM; (c) the height, and the penetration efficiency as a function of particle mobility diameter for the flow ratio of 1.5/15 lpm.

4.4. Grimm nanoDMA

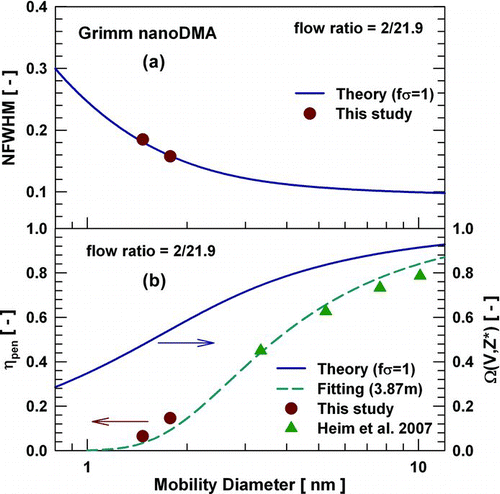
The results for the Grimm nanoDMA are shown in Figure 7. THABr monomer and dimer with diameters of 1.47 and 1.78 nm were tested using a flow ratio of 2/21.9 lpm. The measured Grimm nanoDMA resolutions agreed very well with its ideal resolutions for sub-2 nm particles and no additional broadening was observed under these conditions. The penetration efficiencies (η_pen ) of the Grimm nanoDMA were previously tested using particles larger than 3 nm (Heim et al. 2007). Together the penetration efficiencies for different sized particles were fitted with the modified Gormley and Kennedy equation. The effective length of the Grimm nanoDMA was found to be 3.87 m.

FIG. 7 Grimm nanoDMA: (a) the NFWHM, (b) the height, and the penetration efficiency as a function of particle mobility diameter for the flow ratio of 2/21.9 lpm.

4.5. Karlsruhe-Vienna DMA

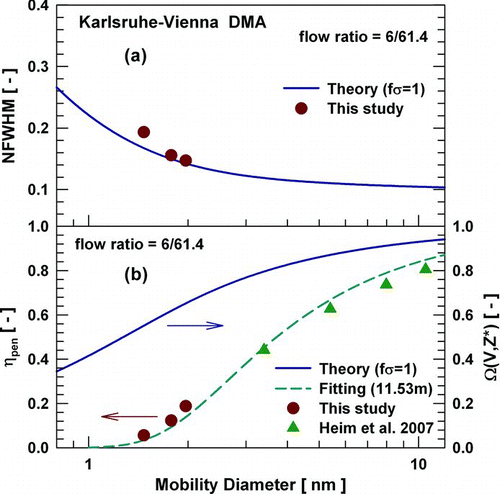
The results for the Karlsruhe-Vienna DMA are shown in Figure 8. THABr monomer, dimer, and trimer with diameters of 1.47, 1.78, and 1.97 nm were tested using a flow ratio of 6/61.4 lpm. The measured resolution for this DMA agreed very well with its ideal resolution for THABr dimer and trimer. For the 1.47 nm monomer, the measured transfer function was wider than the ideal transfer function and the multiplicative factor (f_σ ) was 1.22. This additional broadening is believed to be related to the abnormal tail that occurred at lower mobility side and was more severe for the Karlsruhe-Vienna DMA than other four test DMAs. By fitting the abnormal tail as a secondary peak and then excluding its contribution to the primary peak, f_σ for the THABr monomer was found to be 1.12, which is close to the values for the dimer and trimer, i.e., 1.07. Figure 8b shows both Ω(V,Z*) and η_pen at the flow ratio of 6/61.4 lpm. The penetration efficiencies of particles larger than 3 nm are also included (Heim et al. 2007). The effective length of the Karlsruhe-Vienna DMA was found to be 11.53 m. If the effect of the abnormal tail on η_pen was included, the effective length was found to be 11.04 m.

FIG. 8 Karlsruhe-Vienna DMA: (a) the NFWHM, (b) the height, and the penetration efficiency as a function of particle mobility diameter for the flow ratio of 6/61.4 lpm.

The Karlsruhe-Vienna DMA replaces the tangential flow arrangement in the original Vienna DMA (Winklmayr et al. 1991) with axisymmetric sheath inlet and excess outlet. The sheath flow is introduced into the center of a plenum chamber through a cylindrical tube. The flow is distributed radially via 40 holes around the circumference before entering the classification zone through a laminarization screen. To ensure flow uniformity, the excess outflow passes through 30 holes around the insulator circumference followed by four excess outlet ports. The tangential aerosol inlet used in Vienna type DMAs can cause asymmetric flow, and may result in DMA transfer function broadening (Heim et al. 2005). The DMA inlet blade was redesigned to increase the pressure drop through the annular gap in order to achieve a homogenous aerosol flow into the classifying region. The flow uniformity was confirmed even when the aerosol flowrate is as low as 0.3 lpm. In the aerosol outlet, a “leaky” insulator is used to prevent a penetration decrease over time due to the accumulation of charged particles on the insulator. The DMA classification length is 2.5 cm which can be easily extended to 6.5 cm by changing the inner electrode. Unlike previously tested Vienna DMA versions whose resolutions were found to be lower than ideal values (Fissan et al. 1996; Birmili et al. 1997), the resolution of the Karlsruhe-Vienna DMA is very close to theoretical values.

5. CONCLUSIONS

Transfer functions and penetrations for sub-2 nm particles were evaluated for five DMAs. The Caltech nanoRDMA shows the best resolution in this size range, followed by the Karlsruhe-Vienna DMA, the Grimm nanoDMA, the TSI nanoDMA, and the Caltech RDMA. The penetration efficiencies of each test DMA were fitted using the modified Gormley and Kennedy equation to determine an effective length. The effective lengths for the Caltech nanoRDMA, the Caltech RDMA, the TSI nano- DMA, the Grimm nanoDMA, and the Karlsruhe-Vienna DMA are 0.87, 1.99, 3.64, 3.87, and 11.53 m, respectively. The Caltech nanoRDMA shows the highest penetration efficiency. This study also demonstrates that Stolzenburg's diffusive transfer function accurately predicts transfer functions for particles down to the smallest tested size (1.16 nm). The resolutions of the TSI nanoDMA, the Grimm nanoDMA, the Caltech nanoRDMA (at low flow rates), and the Karlsruhe-Vienna DMA (for 1.78 and 1.97 nm particles) agree very well with the diffusive transfer function. Additional broadening was observed for the Caltech RDMA, the Caltech nanoRDMA (at high flow rates), and the Karlsruhe-Vienna DMA for 1.47 nm particles. Results are presented in a form that is useful for DMA data inversion.

Acknowledgments

This work was partially supported by a grant from the US NSF (ATM-0506674) and US DOE (DE-FG-02-05ER63997). JJ thanks Dr. Kenjiro Iida for his help on the data inversion program. A NSF graduate fellowship to NAB is gratefully acknowledged. We thank the two anonymous reviewers for helping to improve the clarity of our article.