The Mobility–Volume Relationship below 3.0 nm Examined by Tandem Mobility–Mass Measurement

Abstract

The validity of the Stokes-Millikan equation is examined in light of mass and mobility measurements of clusters of the ionic liquid 1-ethyl-3-methyl-imidazolium tetrafluoroborate (EMI-BF₄) in ambient air. The mobility diameter d_Z based on the measured mobility and the Stokes-Millikan law is compared with the volume diameter d_v , which generalizes the mass diameter for binary substances such as salts. d_v is based on the sum of anion and cation volumes in the cluster corrected for the void fraction of the bulk ionic liquid. For d_v > 1.5 nm, d _Z is within 1.4% of d_v + 0.3 nm. For smaller clusters 3.84 and 14.3% deviations are observed at d_v = 1.21 nm and 0.68 nm, respectively. These differences are smaller than expected due to a cancellation of competing effects. The increasing difference seen for d_v < 1.5 nm is due primarily to the interaction between the cluster and the dipole it induces in the gas molecules. Other potential sources of disagreement are non-globular cluster geometries, and departures of the cluster void fraction from the bulk value. These two effects are examined via molecular dynamics simulations, which confirm that the volume diameter concept is accurate for EMI-BF₄ nanodrops with d_v as small as 1.6 nm.

INTRODUCTION

There is a growing interest (Kulmala et al. 2005, 2007; McMurry et al. 2005; Eisele et al. 2006; Kuang et al. 2008; Winkler et al. 2008; Zhao et al. 2010) in the measurement of sub 3 nm diameter atmospheric aerosol particles, as evidenced by this special issue of Aerosol Science and Technology. The growth of such small particles into larger sizes, where they may act as cloud condensation nuclei, is an important but incompletely understood process. Unfortunately, commercial instruments used in the measurement of aerosol size distributions are usually not capable of detecting sub 3.0 nm particles (2.5 nm cutoff size in commercial condensation nucleus counters) with high efficiency (Stolzenburg and McMurry 1991). Studies of aerosol particles in this size range require the development of new instrumentation (Zhao et al. 2010) or improvements to existing measurement techniques (Iida et al. 2009). While existing size distribution measurement systems rely almost exclusively on electrical mobility measurements, e.g., a differential mobility analyzer (DMA) in series with a condensation nucleus counter (CNC), electrical mobility measurement alone may not be sufficient to fully understand the formation and growth of aerosol clusters (defined here as a small group of atoms or molecules). In general, only clusters which will grow further into larger particles are of atmospheric relevance, while many non-specific nanometer scale species in the atmosphere may be detected in DMA-CNC systems modified to function below 2.5 nm in size (McMurry et al. 2010). Measurements which allow for simultaneous determination of cluster size and chemical composition are thus most desirable for atmospheric aerosol cluster analysis. New instrumentation development also needs to be accompanied by fundamental studies of the mobility–size relationship for clusters, which is required to relate a cluster's measured electrical mobility to its size (diameter, volume, or mass). The Stokes-Millikan equation, used widely to infer aerosol particle sizes from electrical mobilities, is not necessarily valid for aerosol clusters (Tammet 1995).

Improved methods to examine aerosol clusters may find parallels with recently developed techniques in other subdisciplines. Like the atmosphere, biological fluids (e.g., protein plasma) are extremely complex and often require the use of tandem measurements, such as liquid chromatography–mass spectrometry for separation and detection of a representative fraction of the species present. Recently, tandem ion (electrical) mobility spectrometry–mass spectrometry instruments (IMS–MS) (Valentine et al. 2001; Tang et al. 2005; Taraszka et al. 2005; Bohrer et al. 2008; Isailovic et al. 2008) have been developed which are extremely powerful in their analytical capabilities, allowing for simultaneous determination of the electrical mobility and mass over charge ratio (m/z) of many species present in a complex mixture. Simultaneous electrical mobility and mass analysis of aerosol clusters would undoubtedly also aid in understanding atmospheric cluster formation and growth. However, the aforementioned studies of biological fluids have relied on complex homemade instruments, and have most often been limited to an m/z range of a few thousand Da. As an alternative, with an appropriate design, DMAs can be readily interfaced with many existing mass spectrometers having atmospheric pressure ion sources, including Time of Flight (ToF) instruments with unusually high m/z ranges. The recent commercial development of parallel plate DMAs having much higher ion/nanoparticle transmission efficiencies to the MS than conventional cylindrical DMAs offers some new opportunities not only for the analysis of biological systems, but also for simultaneous electrical mobility and mass measurement of atmospheric aerosol clusters. We have already used these high transmission DMA–MS instruments to study the properties of electrospray generated nanodrops (Hogan and Fernandez de la Mora 2009) and biomolecules (Hogan and Fernandez de la Mora 2010a; Hogan et al. 2010b). In this article, we extend these studies to aerosol clusters in the sub 3.0 nm size range in order to: (1) examine cluster mobility as a function of cluster structure, and (2) to demonstrate the capabilities of the new DMA–MS combination in aerosol cluster analysis. With simultaneously measured electrical mobilities and masses, we reexamine the validity of the Stokes-Millikan relationship for aerosol clusters by comparing mobility diameters to volume diameters. We confirm that the relationship is valid down to volume diameters of 1.5 nm (Ku and Fernandez de la Mora 2009). Below this size, Tammet (1995) has discussed several important sources of error in the Stokes-Millikan formula. We use numerical simulations to also examine critically the validity of the notions of mass or volume diameter at diameters below 1.7 nm. Finally, we discuss several potential advantages and difficulties of tandem DMA–MS for the measurement of atmospheric aerosols.

MATERIALS AND METHODS

Differential Mobility Analyzer–Mass Spectrometer Coupling

Cluster electrical mobility and mass measurements were made with a parallel-plate DMA (P4, SEADM, Boecillo, Spain) coupled to a QSTAR XL quadrupole-time-of-flight (qToF) mass spectrometer (MDS Sciex, Toronto, Canada). The mass/charge range of this instrument is 40,000 Da, corresponding to a diameter of 5.1 nm for a singly charged spherical particle with density ρ = 1g cm⁻³. Design features of parallel-plate DMAs, their transmission, resolving power (>50), and coupling to a mass spectrometer are described by Rus et al. (2010). Specific details on DMA–MS operation with a P4 DMA coupled to a QSTAR XL MS are described in several recent manuscripts (Hogan and Fernandez de la Mora 2009; Hogan and Fernandez de la Mora 2010a, 2010b; Hogan et al. 2010b). Here we note features of the DMA–MS combination relevant to its operation for the measurement of charged clusters and nanoparticles with characteristic sizes below 3.0 nm, as well as the operational parameters used in our cluster measurements.

FIG. 1 Schematic of parallel plate differential mobility analyzer P4 coupled to a QSTAR XL mass spectrometer. The DMA is operated with a small counterflow in the inlet, which makes it necessary to drive clusters into the DMA electrostatically, but also ensures that the recirculating sheath flow gas remains particle-free and of constant composition.

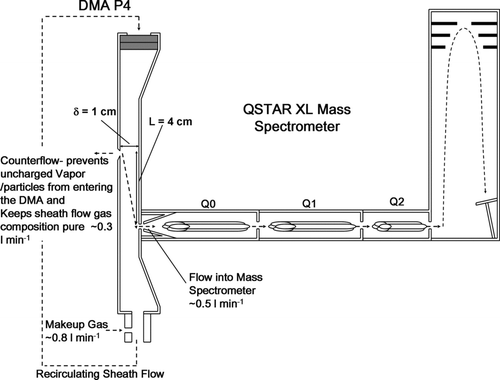
Figure 1 shows a schematic of the DMA–MS instrument. The DMA is operated at atmospheric pressure with a recirculating sheath flow of dry and filtered air or N₂, driven by a modified vacuum blower (operated for our experiments such that the sheath gas temperature was at ∼30°C). At the inlet of the parallel-plate DMA, a counterflow of ∼0.3 l min⁻¹ is utilized, which has several consequences. First, all charged clusters to be analyzed must be drawn into the DMA electrostatically. Second, uncharged clusters do not enter the DMA, which eliminates the need to use a filter in the sheath flow recirculation line. The counterflow also prevents humidity and other neutral vapors from entering into the DMA circuit, thus avoiding solvation of ions in the DMA (which could split each mobility peak into several peaks) as well as condensation on ions in the supersonic free jet leading to the vacuum system of the MS. In the case of volatile aerosol particles, the DMA may be maintained humid by using suction instead of counterflow, though this may create complications in the mass measurement. Some atmospheric pressure ionization–MS systems do ingest humid air, but this does not prevent aerosol evaporation because drying is typically substituted by substantial heating (also to prevent vapor condensation on the ions). Finally, the sheath flow gas composition in the DMA is not affected by the composition of the aerosol flow, which is advantageous for making precise mobility measurements in clean gas flows. The aerosol outlet acts as a critical orifice, allowing ∼0.5 l min⁻¹ (a flowrate specific to the QSTAR mass spectrometers) out of the DMA and into the MS. Clean and dry make-up gas is supplied continuously to the closed DMA circuit to provide the counterflow gas and replace the flow sampled into the MS. To transmit charged clusters of a prescribed electrical mobility, a voltage difference V_DMA, is applied across the DMA electrodes, with the upper electrode at a floating potential above the lower electrode (which has a fixed voltage applied to it as part of the ion focusing scheme in the MS inlet). The electrical mobility, Z, of the ions transmitted through the DMA may be determined from the equation:

where U is the sheath flow velocity, L is the DMA classification length (4 cm) and δ is the distance between electrodes (1 cm). Because of ambiguities in the measurement of the sheath flow velocity, U, the electrical mobility of transmitted ions is determined here by comparing the voltage applied across the DMA electrodes to the applied voltage necessary to transmit a calibrant ion of known mobility. The calibration procedure is described in further detail in the subsequent Charged Cluster and Calibrant Generation section.

Without careful design of the DMA–MS interface, poor cluster transmission precludes DMA–MS measurements on the time scale necessary for the study of atmospheric aerosol clusters (tens of minutes were required to measure a good single mass spectrum with a conventional cylindrical DMA operated at fixed voltage; Fernandez de la Mora et al. 2005). To ensure high cluster transmission efficiency from the DMA into the MS, each parallel plate DMA outlet is designed specifically to match the required flowrates and geometry of the accompanying MS (Rus et al. 2010), in this case the QSTAR XL. Electrical mobility classified clusters exit the DMA outlet and pass directly through the lens and skimmer system of the QSTAR XL, where the pressure is several torr. Clusters then enter a quadrupole ion guide (Q0), operated in radio frequency (RF) only mode, which transmits the ions efficiently in the axial direction, while the neutral gas expands radially. Charged clusters pass then through a small aperture into a second quadrupole (Q1), which can be operated such that only clusters of a prescribed mass to charge ratio m/z are transmitted to a collision cell (the final quadrupole Q2). However, for our experiments, Q1 was operated in RF only mode to transmit the full range of ions of interest. Like Q0, Q2 operates as an RF ion guide, but can also act as a collision cell, with collision gas driving fragmentation of mass-selected clusters from Q1. As we did not utilize Q1 for mass selection, we also did not use collision gas in Q2 in our cluster measurements. After passing through Q0–Q2, clusters enter the ToF tube, where m/z spectra are measured. For the measurement of tandem mass-mobility spectra, the DMA voltage is stepped in increments of 5–10 V, and at each fixed DMA voltage a mass spectrum is measured. A software package created by SEADM enables operation of the DMA and QSTAR without the need to manually change the DMA applied voltage or to manually start m/z data collection at each applied voltage. Data collection for one mass-mobility spectrum took ∼20 min for the spectra reported here, though spectra can be collected in as little as 10 minutes with adequate signal to noise (Hogan and Fernandez de la Mora 2010a).

Charged Cluster and Calibrant Generation

To examine the relationship between cluster size and cluster mobility, we generated clusters of the ionic liquid (IL) ethylmethylimidazolium⁺ (EMI⁺, cation mass of 111.2 Da) tetrafluoroborate⁻ (BF₄ ⁻, anion mass of 86.8 Da) by electrospraying a 10 mM solution of EMI-BF₄ in chromatography grade methanol. The choice of EMI-BF₄ responds to two considerations. First, IL clusters are generally expected to be almost involatile and close to spherical, at least for large enough clusters. Second, the small size of BF₄ ⁻ relative to most other ionic liquid anions permits obtaining an unusually large number of cluster sizes below 2 nm. These advantages were previously noted by Ku and Fernandez de la Mora (2009). However, the small mobility differences between adjacent peaks makes cluster identification difficult with a DMA alone, which led in their work to anomalous results for EMI-BF₄ clusters. Here we corroborate their suspicion that these anomalies were entirely due to incorrect composition assignment of some of their mobility peaks. All chemicals were purchased from Sigma-Aldrich. The electrospray source used is described in detail elsewhere (Hogan and Fernandez de la Mora 2009), and generated both singly charged and multiply charged clusters of the IL. The electrospray was operated in positive mode in the presence of CO₂, which aided in stabilizing the spray. The tip of the electrospray needle was positioned close (<1 mm) to the DMA inlet to maximize cluster transmission into the DMA. The IL measurements were made on a DMA-QSTAR XL at the Yale DMA-MS facility (New Haven, CT) with air as the sheath gas.

The electrospray source was also used to generate calibrant ions and set the electrical mobility scale in the DMA in lieu of direct measurement of the DMA sheath flowrate (∼1000 liters per minute). The calibrant was the (tetraheptylammonium⁺)₃ (bromide⁻)₂ cluster, which was produced by electrospraying 5 mM tetraheptylammonium bromide in methanol and has a mobility of 0.528 cm² V⁻¹ sec⁻¹ at 20°C in air (Ude and Fernandez de la Mora 2005). Since the DMA operates at roughly 30°C, the calibrant mobility was taken as 0.538 cm² V⁻¹ sec⁻¹, which is based on the assumption that it varies with temperature as a hard sphere. With the voltage required to transmit the calibrant cluster through the DMA known, the electrical mobilities of all measured ions were determined from the equation:

where Z_s and V _s are the electrical mobility of the standard and the voltage required to transmit the standard, respectively.

RESULTS AND DISCUSSION

Features in Tandem Mass-Mobility Spectra

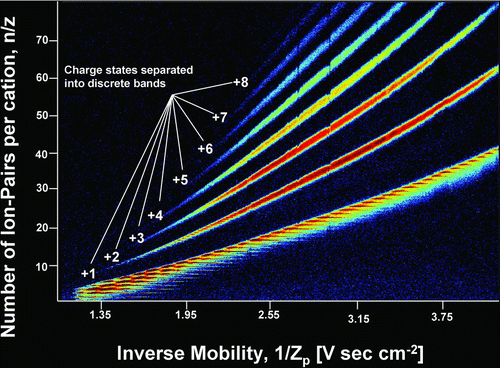
DMA–MS measurements produce two dimensional arrays of data, with ToF-measured signal intensity as a function of both the set electrical mobility in the DMA and the m/z inferred from the flight time in the MS. Such data are conveniently represented as contour plots, with parameters characterizing the measured electrical mobility and mass/charge represented on the x and y axes, respectively, and the measured signal intensity denoted with a false color scheme (with red as the most intense signal and blue as the least intense). Such contour plots are shown in Figures 2 and 3 for the measured EMI-BF₄ cluster data. Only signal corresponding to singly charged clusters is observable in Figure 2; multiply charged clusters were generated by the electrospray source and detected (Hogan and Fernandez de la Mora 2009) but the threshold signal intensity in Figure 2 is above the maximum signal intensity of the multiply charged clusters. For completeness the multiply charged clusters are shown in Figure 3. Here we focus mainly on the singly charged clusters, those most commonly observed in atmospheric aerosol cluster analysis. The distribution of multiply charged clusters characteristic of electrosprays is reported in our prior work (Hogan and Fernandez de la Mora 2009). All clusters observed here have the form (EMI-BF₄) _n (EMI⁺)_z, where n and z are the number of ion-pairs and excess cations in the cluster (z = 1 for the clusters in Figure 2). The horizontal (electrical mobility) scale used is the inverse mobility, 1/Z_p , which varies linearly with DMA voltage and for clusters of a given charge state z increases with increasing cluster size. The vertical (mass/charge) scale is represented as n/z, the number of ion-pairs (cation + anion, i.e., one ion-pair is one EMI⁺ and one BF₄ ⁻ together) per excess cation in the cluster, which, for the singly charged clusters, is simply the number of ion-pairs in the cluster. Each detected cluster is observed in the contour plot as a short line segment of high signal intensity. Line segments further to the right appear higher in the plot, as both the x and y variables increase with increasing cluster size. The smallest cluster visible in Figure 2 is the n = 1 cluster, with DMA-MS measurements on the n = 0 cluster (i.e., the EMI⁺ cation) made separately. The largest cluster visible in Figure 2 has n = 29, with the n = 30 cluster also discernable (though below the set plot threshold). We note that this is substantially larger than any other singly charged cluster observed in our previous work with EMI⁺ based IL clusters (Hogan and Fernandez de la Mora 2009) and even larger than singly charged clusters observed with a DMA where a radioactive source was used to charge-reduce clusters prior to DMA measurements (Ku and Fernandez de la Mora 2004). We attribute these anomalously large singly charged clusters to the presence of a mild electrical discharge in the electrospray source, which, although accidental, provided the opportunity to study the (EMI-BF₄) _n EMI⁺ series for n ranging from 0 up to 41.

FIG. 2 False color-scheme contour plot of the signal intensity of EMI-BF₄ clusters as a function of both the number of ion-pairs per cation in the cluster and the cluster inverse mobility. The “ladders” of line segments observed at discrete mobility are indicative of clusters undergoing neutral evaporation between the DMA and MS. The highest n/z cluster in each ladder has the correct mass at that mobility. Only singly charged clusters are shown in the plot.

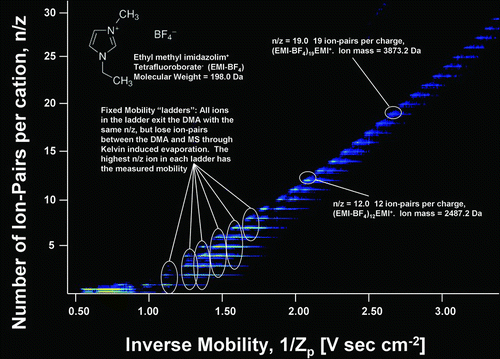
FIG. 3 False color-scheme contour plot of the signal intensity of EMI-BF₄ clusters as a function of both the number of ion-pairs per cation in the cluster and the cluster inverse mobility. The line segments of clusters with a given number of excess cations, z, are grouped into distinct bands in the contour plot, with the number of excess cations indicated for each band.

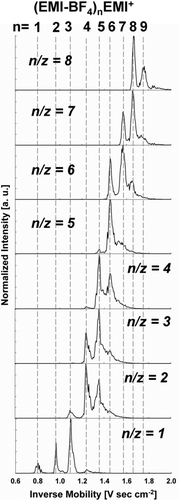
Before examining the size–mobility relationship for these clusters, we must note several other features characteristic of the contour plots. First, the line segments corresponding to detected clusters always extend in the direction of the mobility axis and are quite narrow in the n/z direction. This is because the resolution of the MS (∼10,000) is substantially higher than that of the DMA (slightly greater than 50), though the resolution of the parallel-plate DMA is much higher than in most DMAs in all size ranges. Second, the line segments in the contour plot have an appearance of increasing length along the inverse mobility axis at lower n/z. Examination of the mobility spectra at fixed n/z (shown for n/z = 1 to n/z = 8 in Figure 4) reveals that each line segment contains multiple peaks which are found at specific inverse mobility values, i.e., with specific applied voltages in the DMA, singly charged clusters of different n/z are detected in the mass spectrometer. Similar features in mobility–mass contour plots were found by Trimpin and Clemmer (2008) for salt clusters measured with a drift tube mobility spectrometer coupled to a mass spectrometer. We have interpreted the multiple n/z peaks present at single inverse mobility values as the result of neutral ion-pair evaporation (Hogan and Fernandez de la Mora 2010b), in this case EMI-BF₄ evaporation, from clusters as they travel between the DMA and the MS. For example, when the DMA is set to transmit clusters with an inverse mobility of 1.67 V s cm⁻², only ions with an n/z = 8, which correspondingly have an inverse mobility of 1.67 V s cm⁻² pass through the DMA. However, between the DMA and the ToF tube, the clusters receive sufficient internal energy for some of them to evaporate an ion-pair, going from n/z = 8 to n/z = 7, and others to evaporate two ion-pairs, leaving n/z = 6. Peaks with (1/Z, n/z) values (1.67, 6), (1.67, 7), and (1.67, 8) appear in the spectrum, though only the n/z = 8 clusters truly have an inverse mobility of 1.67 V s cm⁻². By accounting for the occurrence of neutral evaporation, the electrical mobility of all clusters can be inferred clearly from tandem mobility-mass measurements. For each mobility peak in Figure 4, the number of ion-pairs in the cluster which truly has that mobility is labeled. For the smallest clusters (e.g., n = 2 and n = 3) neutral evaporation proceeds so rapidly that when the DMA is set to transmit these clusters, they completely evaporate to smaller sizes before reaching the MS. However, their mobility information is preserved at the mass of the bare cation. As discussed by Hogan and Fernandez de la Mora (2010b), the size dependence of the evaporation rate is in qualitative agreement with the Kelvin effect (Friedlander 2000), i.e., the vapor pressure increases exponentially with decreasing cluster size. From the sharp mobility distributions, it is clear that the clusters do not undergo evaporation within the DMA. The observed evaporation is therefore not spontaneous; rather, it must be externally activated somewhere within the mass spectrometer. We have not studied this effect systematically, but have observed in some cases up to 6 ion pair losses. Since the heat of vaporization of one ion pair is typically between 1 and 2 eV, this succession requires some 10 eV of energy, which is more than the internal energy in the (CA)₁₀C⁺ cluster. An external source of energy is therefore required, which can only be provided by the radiofrequency (RF) field used in Q0 to focus the ions towards the axis (Hogan and Fernandez de la Mora 2010b). This field forces a fast radial oscillation of the clusters, leading to energetic inelastic collisions with the background gas, similar to the well-documented phenomenon of collision-induced dissociation (CID; Gross 2004) taking place in triple quadrupoles. Alternatively, the spatial gradient of the field may excite an internal oscillation of the IL nanodrops, which would be dissipated into heat by internal friction. We shall for lack of a more detailed understanding of the process refer to either of these phenomena as RF heating. This effect can in principle be controlled by decreasing the RF field, but at the expense of ion transmission. RF heating is therefore specific to the ion guide system present in our MS (as well as in most modern API–MS instruments), and is not in any way due to the DMA. The DMA simply enables the observation of decays that would normally go undetected in pure MS. It certainly warns against a risk far greater with labile atmospheric clusters (i.e., sulfuric acid clusters (Curtius et al. 2001), or other prenucleation clusters) than with the biological species typically studied by API–MS. Therefore, aerosol cluster measurement systems which rely on MS for detection and employ a multipole ion guide prior to mass analysis may overestimate the concentration of smaller clusters and underestimate the concentration of larger clusters (Eisele et al. 2006). Ion guides for labile cluster measurement need to be carefully designed and operated to preclude RF induced evaporation (Zhao et al. 2010). Electrical mobility separation upstream of the MS offers an approach to assess the importance of RF heating.

FIG. 4 Mass selected mobility spectra for singly charged clusters of n/z = 1.0 to n/z = 8.0. The multiple peaks observed in each spectrum are the result of ion-pair evaporation between the DMA and MS.

Size–Mobility Relation for Nanometer Particles

Much of our knowledge on the relationship between the diameter and the electrical mobility of spherical particles, large or small, is condensed into the so-called Stokes-Millikan Equation (3) (Davies 1945; Kim et al. 2005).

where K_n is the Knudsen number, λ the gas mean free path, d_p the particle diameter, e the elementary charge (1.6 × 10⁻¹⁹ C), μ the gas viscosity coefficient, m_g the molecular weight of the gas, k_B the Boltzmann constant (1.38 10⁻²³ J K⁻¹), T the gas temperature, and ρ the gas density. The values a = 1.257, b = 0.4, and c = 1.1 fit prior measurements well across a wide K_n range. For the clusters studied here, K_n > 56, and (3a) approaches closely the free molecule limit:

One first problem arising when attempting to apply Equation (3) to small nanometer particles is the ill defined nature of the notion of particle diameter. The mobility Z_p is however a measurable quantity, so, for a particle of given mobility Z_p , one may define the so-called mobility diameter d_Z such that the following identity is satisfied:

Tammet (1995) has analyzed some of the problems associated to the use of the Stokes-Millikan equation (3a–d) with nanometer particles. One of his corrections is to identify d_p in Equation (3a) or (3e) with the mass diameter (Equation (4b)) augmented with a quantity d_g (a function of temperature) to account for the effective diameter of the gas molecule:

where d_m is based on the actual mass m_p of the particle and the bulk density ρ_p of the material of which it is made (in our case the bulk density of EMI-BF₄).

For clusters with mass m_p comparable to that of the gas molecules, Equation (3e) cannot be correct, because two-body collisions are governed by the reduced mass mm_g/(m + m_g) rather than the mass m_g of one of the collision partners. Z_p cannot therefore be a function of only size as in Equation (3e), but the ratio Z_p /(1 + m_p/m_g )^1/2 can be, suggesting substituting Z_p in Equation (3) by Z_p* (Ku and Fernandez de la Mora 2009):

Neither this mass correction nor the replacement of d_p by d_m+d_g are rigorous in the continuum limit (K_n → 0), but this problem is irrelevant because the two corrections are imperceptible even at K_n = 1. Equations (3–5) therefore provide a first means to compare the Stokes-Millikan equation with cluster data: the experimental Z_p is divided by the factor (1 + m_p/m_g )^1/2 to provide the experimental Z_p*; the experimental m_p is converted into a mass diameter and augmented with d_g to provide a particle diameter d_p according to equation (4), and the corresponding experimental pair Z_p*(d_p ) is directly compared to the Z_SM (d_p ) curve. This approach was followed by Ku and Fernandez de la Mora (2009), who compiled a series of DMA and DMA–MS measurements for electrospray generated clusters of tetra-alkyl ammonium halides, ILs, and several other species. When choosing d_g = 0.3 nm at room temperature, they found excellent agreement between the measured Z_p /(1 + m_p/m_g )^1/2 and the theoretical Z_SM (d_m+d_g ) for almost all measured clusters with mass diameters >1.3 nm. These results validate the interpretation of the Stokes-Millikan equation according to Equations (4–5) for all but the smallest clusters. However, several unresolved issues remained. Some of the cluster masses in the prior data set (including in particular all for ILs) were not measured directly through a mass spectrometer, but inferred from the ordering of the mobility peaks in DMA measurements alone. As evidenced by miss-assignments of tetraheptylammonium bromide cluster masses in earlier tandem DMA measurements (Gamero-Castano and Fernandez de la Mora 2000), which were later corrected by DMA–MS measurements (Fernandez de la Mora et al. 2005), mass assignment without direct mass measurement is often risky. The need for direct mass measurement is confirmed by the disagreement found by Ku and Fernandez de la Mora (2009) for clusters of EMI-BF₄. They have also noted more subtle disagreements in mobilities reported for tetraheptylammonium bromide clusters, which they attribute to inaccurate mobility calibration. Mobility scale calibration issues have also been encountered (and approximately corrected) in prior DMA–MS work, due to lack of precise regulation of the pump driving the sheath gas flow (Hogan and Fernandez de la Mora 2009).

Not incorporated in Equations (3–5) are two other effects noted by Tammet: (1) the additional attraction between the charged cluster and the dipole it induces on the gas molecules (polarization effect; Mesleh et al. 1996), and (2) a proposed additional size dependence associated to the fact that collisions between the gas and large particles tend to be effectively diffuse while those with atoms and small molecules are specular and elastic. The latter effect alone leads to a 35.8% increase in the mobility as molecular dimensions are approached. Polarization has the opposite effect of decreasing mobility as the size shrinks. These effects have been discussed in earlier studies (Tammet 1995; Fernandez de la Mora et al. 1998; Friedlander 2000; Fernandez de la Mora et al. 2003; Li and Wang 2003, 2005) based on a few available data (Scheibel and Porstendorfer 1983; Kuga et al. 2001; Rudyak et al. 2002), to which high resolution DMAs and DMA-MS cluster data have been recently added. Because the corrections to Equation (3) required by these two additional effects remain unclear, the matter will not be further discussed here.

Another difficulty in comparing the Stokes-Millikan equation to cluster data is that the mass diameter requires the knowledge of a density as well as a mass. Use of the bulk density down to mass diameters of 2 nm may perhaps be justified for homogeneous materials. However, it is problematic for small clusters of structure (CA)_n(C⁺)_z, when the two different densities of the anion and the cation enter in variable proportions as (n + z)/n varies with the smallest clusters. This difficulty may be resolved by separate knowledge of the two ionic volumes V_a and V_c for the anion and the cation, corrected for the void volume fraction f_v defined in Equation (6a) for a cluster of known volume. In the bulk liquid f_v is a known quantity derivable from these ionic volumes, the corresponding ionic masses and the bulk density. This suggests interpreting Equation (6a) as a definition of the cluster volume (taking f_v as the bulk value), whence the associated definition of volume diameter (Equation (6b)) generalizes the mass diameter for the case of salts:

where z is the number of excess cations in the cluster. The ionic volumes and bulk volume fraction used to infer d_v from our data are given in Equations (6c–e), based on Larriba et al. 2008:

Both definitions, Equations (6b) and (4b), for d_v and d_m are meaningful only for large enough clusters, for which f_v and ρ_p approach the bulk value. At sufficiently small sizes the arrangement of molecules in the cluster will be size dependent, whereby f_v and ρ_p will differ from the bulk values and vary from one cluster to the other. In particular, f_v = 0 for the bare anion or cation (n = 0). The assumption of bulk packing is convenient, but it is not an essential limitation of the concepts of volume or mass diameters. All that is needed is a cluster volume V, which may in principle be determined directly based on molecular modeling. Finally, small ionic clusters with n = 1, 2, 3, cannot be spheroidal, not even for a substance that is liquid in the bulk (nor can non-ionic clusters with n = 2). It is therefore clear that the mobilities of the smallest clusters cannot be given by the Stokes-Millikan law, even in the absence of polarization effects or of a transition from diffuse to specular collisions.

Figure 5 shows the inverse of the square root of the quantity Z_p*/z = Z_p /[z(1 + m_g/m_p) ^1/2] versus the volume diameter (Equation (6b)) for singly and doubly charged EMI-BF₄ clusters. Also shown is the Stokes-Millikan equation (3a–d) with the identification d _p = d_v + 0.3 nm. Z_SM is computed for air, with μ = 1.82 × 10⁻⁵ Pa sec and λ = 70 nm. A horizontal line is additionally shown with the predicted Z_p*/z for point charges accounting for the polarization potential (i.e., the polarization limit), given by (Mason and McDaniel 1988; Tammet 1995):

where T∼303 K, P is the gas pressure (atmospheric), ϵ ₀ is the vacuum permittivity (8.854 × 10⁻¹² F m⁻¹), and α is the gas polarizability (∼1.7 × 10⁻³⁰ m³ for air). Tammet (1995) gives a slightly different value of 0.5105 for the numerical coefficient in Equation (7). The inferred mobility diameters, volume diameters and their percent difference are listed in Tables 1 and 2 for singly and doubly charged clusters, respectively. The Tables show also percent difference between the measured Z* and Z_SM(d_v + 0.3 nm). Analysis of the larger, multiply charged particles from the same data set will be presented elsewhere (Hogan et al. 2010a). The Table shows differences of less than 1.4% between d_v and d_Z for singly charged EMI-BF₄ clusters with n = 7 (d_Z = 1.55 nm) or larger. For n < 7, the diameter mismatch increases with decreasing size, reaching a maximum of 14.30% for the EMI⁺ cation. These data are in good agreement with the non-EMI-BF₄ data of Ku and Fernandez de la Mora (2009), and it appears that the anomalous EMI-BF₄ mobilities reported in that study were the result of an incorrect assignment of cluster masses. The mismatch between the measured and the Stokes-Millikan mobilities can be seen in magnified form in the mobility-based-density (Equation (8)) plotted in Figure 6 as a function of the number n of ion-pairs in the cluster:

FIG. 5 The inverse square root of Z_p */z as a function of the cube root of the cluster volume for singly (open symbols) and doubly charged (closed symbols) EMI-BF₄ clusters. Also shown are the predicted curves from the modified Stokes-Millikan equation (solid line) and the expected curve for a point charge accounting for the charge-induced dipole potential (dashed curve).

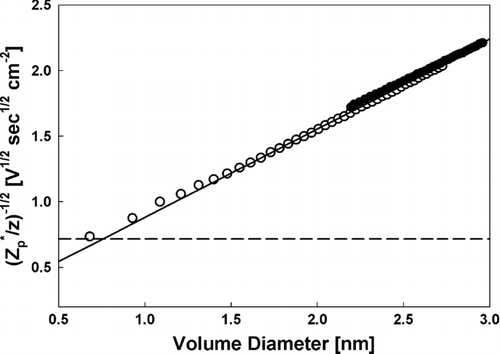
TABLE 1 Summary of the measured electrical mobilities, inferred mobility diameters (with the gas molecule diameter subtracted), inferred mass diameters, the percent difference in measured and predicted electrical mobilities (from the Stokes-Millikan equation), and the percent difference in mobility and mass diameters for the singly charged EMI-BF₄ clusters

Number of ion pairs	Mobility (cm^2 V^−1 sec^−1)	Mobility diameter (nm)	Volume diameter (nm)	% Difference in mobilities	% Difference in diameters
0	2.083	0.778	0.681	20.81	14.30
1	1.370	0.984	0.929	9.09	5.89
2	1.031	1.167	1.088	11.78	7.32
3	0.909	1.257	1.210	6.24	3.84
4	0.800	1.356	1.312	5.54	3.36
5	0.741	1.419	1.400	2.22	1.34
6	0.685	1.486	1.478	0.86	0.52
7	0.637	1.551	1.549	0.20	0.12
8	0.599	1.608	1.614	−0.60	−0.36
9	0.565	1.663	1.674	−1.03	−0.61
10	0.532	1.723	1.730	−0.65	−0.38
11	0.508	1.770	1.782	−1.13	−0.66
12	0.484	1.819	1.832	−1.16	−0.68
13	0.464	1.865	1.879	−1.29	−0.75
14	0.447	1.904	1.924	−1.74	−1.01
15	0.432	1.943	1.966	−2.05	−1.19
16	0.416	1.986	2.007	−1.85	−1.07
17	0.401	2.028	2.047	−1.58	−0.91
18	0.389	2.063	2.085	−1.84	−1.06
19	0.377	2.101	2.121	−1.65	−0.95
20	0.368	2.128	2.157	−2.31	−1.33
21	0.357	2.166	2.191	−2.01	−1.15
22	0.346	2.205	2.224	−1.52	−0.87
23	0.337	2.237	2.257	−1.50	−0.86
24	0.329	2.267	2.288	−1.61	−0.92
25	0.323	2.292	2.318	−1.99	−1.14
26	0.316	2.321	2.348	−2.02	−1.15
27	0.309	2.352	2.377	−1.86	−1.06
28	0.304	2.372	2.406	−2.43	−1.38
29	0.298	2.401	2.433	−2.36	−1.34
30	0.292	2.429	2.460	−2.27	−1.28
31	0.285	2.460	2.487	−1.89	−1.07
32	0.279	2.488	2.513	−1.77	−1.00
33	0.274	2.513	2.538	−1.77	−1.00
34	0.271	2.532	2.563	−2.14	−1.21
35	0.265	2.561	2.587	−1.84	−1.03
36	0.260	2.589	2.611	−1.53	−0.86
37	0.257	2.606	2.635	−1.97	−1.11
38	0.252	2.635	2.658	−1.51	−0.85
39	0.249	2.652	2.681	−1.91	−1.07
40	0.245	2.674	2.703	−1.92	−1.07
41	0.242	2.698	2.725	−1.79	−1.01

TABLE 2 Summary of the measured mobilities, inferred mobility diameters (with the gas molecule diameter subtracted), inferred mass diameters, the percent difference in measured and predicted electrical mobilities (from the Stokes-Millikan equation), and the percent difference in mobility and mass diameters for selected doubly charged EMI-BF₄ clusters

Number of ion pairs/excess cotions	Mobility (cm^2 V^−1 sec^−1)	Mobility diameter (nm)	Volume diameter (nm)	% Difference in mobilities	% Difference in diameters
10.5	0.678	2.231	2.213	1.48	0.84
11	0.661	2.264	2.245	1.48	0.84
11.5	0.648	2.288	2.277	0.88	0.50
12	0.632	2.321	2.308	0.97	0.55
12.5	0.617	2.352	2.338	1.09	0.62
13	0.606	2.376	2.367	0.65	0.36
13.5	0.596	2.399	2.396	0.25	0.14
14	0.583	2.430	2.424	0.46	0.26
14.5	0.570	2.460	2.451	0.69	0.39
15	0.564	2.475	2.478	−0.15	−0.08
15.5	0.553	2.502	2.504	−0.14	−0.08
16	0.543	2.528	2.529	−0.10	−0.06
16.5	0.533	2.553	2.554	−0.05	−0.03
17	0.526	2.572	2.579	−0.49	−0.28
17.5	0.515	2.604	2.603	0.10	0.05
18	0.510	2.619	2.627	−0.54	−0.30
18.5	0.502	2.640	2.650	−0.66	−0.37
19	0.494	2.665	2.673	−0.52	−0.29
19.5	0.487	2.686	2.695	−0.61	−0.34
20	0.480	2.707	2.717	−0.68	−0.38
20.5	0.475	2.724	2.739	−0.96	−0.54
21	0.465	2.755	2.761	−0.33	−0.19
21.5	0.461	2.769	2.782	−0.81	−0.45
22	0.455	2.789	2.802	−0.83	−0.46
22.5	0.448	2.813	2.823	−0.62	−0.35
23	0.443	2.830	2.843	−0.83	−0.46
23.5	0.439	2.843	2.863	−1.24	−0.69
24	0.434	2.863	2.883	−1.21	−0.67
24.5	0.429	2.883	2.902	−1.18	−0.65
25	0.423	2.903	2.921	−1.13	−0.63
25.5	0.420	2.916	2.940	−1.48	−0.82
26	0.413	2.942	2.959	−1.02	−0.57
26.5	0.410	2.955	2.977	−1.35	−0.75

FIG. 6 The mobility-based cluster density ρ_Z = m_p/volume as a function of the number of ion-pairs in the EMI-BF₄ clusters. Open Symbols: singly charged clusters; Closed Symbols: doubly charged. The horizontal dashed lines denote the expected densities based on cluster volumes accounting for the void volume fraction.

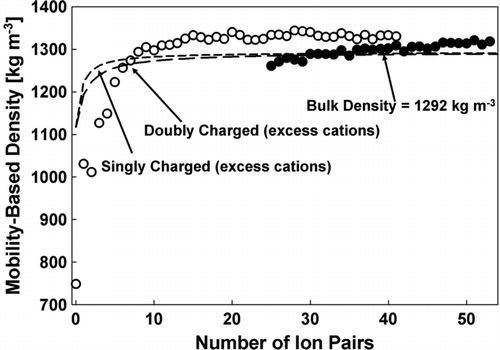
The dashed lines denote bulk density, based upon the cluster masses, volumes, and bulk void volume fraction (one excess cation for the singly charged and two for the doubly charged accounted for in calculating these curves). Except at relatively small n (n < 10), this theoretical reference shows a rather weak density variation with n. At large n, ρ_Z is in reasonable agreement with the bulk density, further demonstrating that the IL clusters are approximately spherical, with structures similar to those found in bulk ILs. The small excess density observed at larger sizes will be later rationalized as due to capillary compression of the nanodrop. The slight shift seen in ρ_Z from singly to doubly charged clusters of the same size cannot be attributed to the slight differences in anion and cation volumes, shown to be negligible in the dashed curves. These variations are therefore due to the different charge states, implying that small polarization effects are present even at n = 40. The importance of polarization effects is also evident in Figure 5 from the fact that the mobility of the EMI⁺ cation approaches the polarization limit. Furthermore, the polarization correction depends on a parameter that can be written as Z_p /Z_pol , and therefore increases with Z_p . This is also congruent with our finding (and that of Ku and Fernandez de la Mora 2009) that Z_p * drops below Z_M for mobilities exceeding 0.60 cm² V⁻¹ sec⁻¹, both for singly and doubly charged clusters (Tables 1 and 2). While the influence of polarization is not surprising, it is noteworthy that the deviation from the Stokes-Millikan equation is comparatively small, e.g., there is only a 3.84% difference in mass and mobility diameter for a cluster with a molecular weight of 705.2 Da.

In view of the importance of polarization effects at the smallest sizes, it is clear that one needs to correct for it before extracting quantitative size-dependent density or void fraction information from our data. This correction will be addressed in a future study (Fernandez-Garcia et al. 2010). In the mean time we use molecular dynamics (MD) simulations to examine qualitatively how the void fraction departs from its bulk value and how the shape ceases to be globular for ionic liquid clusters of decreasing sizes. These simulations will show that the cluster density should increase with decreasing size. The opposite trend seen in the data of Figure 6 is again clearly due to polarization effects, stressing further the need to correct for them in future work.

Molecular Dynamics Simulations of Cluster Size Density and Shape

The software used to minimize the energy of (EMI-BF₄) _n (EMI⁺) clusters with n = 1–11 was Chem3D, with the MM2 force field package (Allinger 1977). The cations and anions in each simulation were positioned randomly but close enough to each other for Coulombic attractions to be important, especially when dealing with cutoff distances. To begin each simulation, the energy-minimum configuration was found and MD simulations were subsequently run for an interval of 50–100 ps. The same software was used to calculate the solvent excluded volume of minimal energy clusters. Although no solvent was present in the molecular simulations, the solvent excluded volume was calculated as the volume delimited by the molecular surface described by the inward facing surface of a solvent probe (1.4A in radius) that is rolled along the Van der Waals (VdW) surface of the atoms. The molecular surface defined here is thus composed of two parts, the contact surface, which is formed by the contact point of the probe rolling over the VdW surface of any of the atoms in the molecule, plus what is known as the reentrant surface, which is the surface formed by the probe when it is in contact with more than one atom. This reentrant surface consists of, as defined by Richards (1977), the VdW surfaces connected by the envelope of the concave surfaces of the closest approaching sphere probe as it rolls over more than one atom. The solvent excluded volume is then simply equal to the ionic volumes (VdW volumes of the atoms) plus the interstitial volumes. Finally, the sum (n + z)V_c + nV_a of ionic volumes given by Chem3D was subtracted from the excluded volume to obtain the void volume, and from it the void fraction. Notice that the ionic volumes of Chem3D (110 and 41 A³ for EMI⁺ and BF₄ ⁻, respectively) are too small compared to those appearing in the literature (117 A³ or higher for EMI⁺ and 73 A³ for BF₄ ⁻; Allen 2002; Jenkins and Liebman 2005), and do not coincide with those given in (6c–e) and used for our own data analysis. Nonetheless, use of the ionic volumes from Chem3D is necessary for internal consistency within the Chem3D calculation. The densities reported in Table 3 were calculated using the anion and cation volumes reported by Larriba et al. (2008) and software calculated void fractions. This hybrid choice is justified by the unreasonable densities achieved using the ionic volumes and void fractions provided by Chem3D. For example, for n = 11, the density of the cluster is 1627 kg/m³ using 41 and 110 A³ for the cation and anion volumes and f_v = 0.239 (from Table 3), clearly too far from the bulk value. If 1600 kg/m⁻³ was taken to be approximately the bulk density, the resulting void fraction using ionic volumes reported by Larriba et al. (2008) would be 0.09, which would be impossible to reach without deforming the clusters. If Chem3D ionic volumes were used, the void fraction achieved when taking 1290 kg/m³ as the bulk density would be 0.41, which is incompatible with any reasonable extrapolation to high n of the f_v values from Chem3D. On the other hand, the void fractions computed by Chem3D are reasonable, and, when combined with sound ionic volumes, they yield realistic densities at large n.

TABLE 3 Void volume fractions and densities for IL clusters as determined from molecular dynamics simulations as well as resulting molecular structures. The various clusters are shown at different magnifications

Ion^d	Neutral molecules	Solvent excluded volume (A^3)	Void fraction^a	Spherical diameter^b (nm)	Density^c (kg/m^3)	MD structures
EMI^+	0	110.240	0.000	0.612	1538.23
BF4 ^−	0	41.351	0.000	0.499	2839.81
[EMIBF4]EMI^+	1	289.30 ± 5.65	0.095	0.863	1523.23
[EMIBF4]2EMI^+	2	477.43 ± 7.69	0.134	1.026	1488.08
[EMIBF4]3EMI^+	3	658.05 ± 8.57	0.141	1.145	1489.25
[EMIBF4]4EMI^+	4	871.57 ± 20.83	0.178	1.259	1433.58
[EMIBF4]5EMI^+	5	1077.55 ± 27.34	0.194	1.353	1409.59
[EMIBF4]6EMI^+	6	1288.48 ± 27.51	0.209	1.437	1387.93
[EMIBF4]7EMI^+	7	1504.10 ± 20.18	0.221	1.514	1368.07
[EMIBF4]11EMI^+	11	2335.73 ± 29.31	0.239	1.755	1342.30
^aCalculated using where Va, Vc , and Vexcvol are the volumes of anion, cation, and the solvent excluded volume given by Chem3D and stated in this table. The solvent excluded volume is calculated using a 0.14 nm probe radius.
^bThe Spherical diameter has been inferred from the density appearing on this table and not from the solvent excluded volume. See text for clarification.
^cCalculated using the Void Fraction from this table and cation and anion volumes from Larriba et al. (2008).
^dThe VdW atom radii used by Chem3D MM2 are 1.9 A^3 for Alkene C and 1.940 A^3 for Alkane C, 1.5 A^3 for H, 1.820 A^3 for N, 1.98 A^3 for B, and 1.650 A^3 for F.

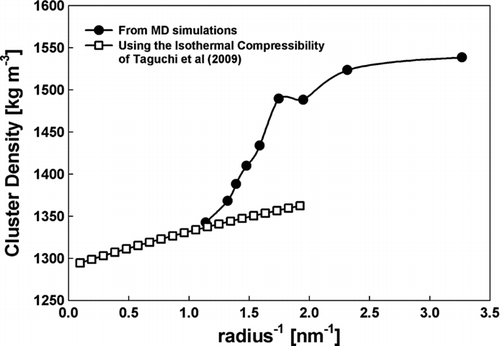
Several runs were made for each of the clusters, and the resulting solvent excluded volumes were averaged with a relative standard deviation (RSD) of 0.01–0.02 for most cases. This small RSD becomes a 5–10% variation when calculating the void fraction. The simulation density decreases as we increase the number of neutral molecules (from n = 0 to n = 11) starting at 1538 kg/m³ and reaching 1342 kg/m³ at n = 11 (1.755 nm in diameter), not far from the bulk density (1290 kg/m³ at room temperature). The discrepancy between these two density values for clusters close to 2 nm, apart from the already accepted ambiguity in molecular volumes, could in part be due to the capillary pressure which compresses the drop to hundreds of atmospheres, increasing therefore the density. Data on density versus pressure have been reported by Taguchi et al. (2009). Their experimental densities are represented in Figure 7 versus cluster curvature, where their pressure has been substituted by the capillary pressure 2γ/R based on the bulk surface tension of EMI-BF₄, γ = 0.052 N/mm. Interestingly, the two curves seem to extend each other continuously past n = 11, the largest value at which Chem3D is capable of providing excluded volume. This coincidence suggests that capillary compression is the main source of densification for clusters with n > 11, but smaller clusters compact even more strongly as a result of packing considerations.

FIG. 7 Density as a function of the curvature for clusters n = 1 to n = 11 based on the void fraction from MD simulations (line with circular markers). Also shown is the isothermal compressibility inferred for EMI-BF₄ from Taguchi et al. (2009) based on a bulk density of 1290 kg/m³ and a surface tension of 52 N/mm.

The calculation gave linear structures of alternating cations and anions for n = 3 and below, suggesting that the corresponding real structures are unlikely to be spheroidal. As the number of ion-pairs increased beyond n > 3, the energy minimized structures became more globular. The mobility of linear clusters would be lower than the mobility of spherical clusters of identical mass and charge (Ude et al. 2004; Trimpin and Clemmer 2008). MD-determined void volume fractions, densities and resulting structures are shown in Table 3 for the analyzed IL clusters. A clear decrease in the void fraction is found with decreased cluster size, with the n = 1 cluster having a void fraction of 0.10.

If the densification effect observed for clusters taking globular shapes (n > 3) are taken into account to define a more realistic cluster volume, the corresponding volume diameters would decrease. This would shift the data in Figure 5 even farther away from the Millikan curve, with differences between Stokes-Millikan and measured mobilities of 39.7% and 21.0% for the EMI⁺ and (EMI-BF₄)EMI⁺, respectively.

In spite of this densification effect and the other two effects noted by Tammet not included in the Stokes-Millikan equation, the DMA–MS measurements reported here strongly support the conclusions of Ku and Fernandez de la Mora (2009): For ionic liquid clusters with volume or mass diameters (based on bulk quantities) larger than 1.5 nm, the Stokes-Millikan relation based on d_v + 0.3 nm is surprisingly accurate in air at ambient conditions. The unexpectedly small disagreement between d _Z and d_v + 0.3 nm found at even smaller sizes is apparently due to a fortuitous cancelation of the contrary effects of polarization and densification.

Outlook for DMA–MS as a Technique for Atmospheric Cluster Analysis

At present we have used parallel-plate DMA–MS systems only for the analysis of electrospray generated clusters (Hogan and Fernandez de la Mora 2009; Hogan and Fernandez de la Mora 2010a, 2010b; Rus et al. 2010). However, with the success of IMS–MS in the analysis of complex polymeric and peptide mixtures (Valentine et al. 2001, 2009; Tang et al. 2005; Trimpin et al. 2007; Bohrer et al. 2008), we expect that DMA–MS systems will be used more widely for the analysis of atmospheric aerosol clusters. Tandem DMA–MS has been often used in aerosol studies primarily for analysis of the chemical constituents of individual particles (rather than for intact particle mass measurement as practiced here). Zhao et al. (2010) have used a cylindrical DMA to study the transmission of a special and singularly sensitive MS used for atmospheric cluster analysis. Given that parallel-plate DMAs have transmission efficiencies >50% for ∼1 nm particles (Rus et al. 2010), their use in series with the cluster-chemical ionization mass spectrometer (cluster-CIMS) of Zhao et al. (2010) would not only give cluster mobility and mass, but also a measure of the extent to which neutral evaporation occurs in the inlet of this mass spectrometer. Although parallel-plate DMA–MS systems are not limited in terms of the cluster charging scheme used, they have been optimized for electrospray generated clusters. Electrosprays may also be used to charge aerosol clusters indirectly through the collision of electrospray generated ions and neutral clusters (Tam and Hill 2004; Martinez-Lozano and Fernandez de la Mora 2008). The charging probability of most atmospheric pressure ionizers is small, 10⁻³–10⁻⁴ for vapors and presumably also for subnanometer particles (Fernandez de la Mora 2010). Note finally that the successful relation between mobility diameter and mass or volume diameter found here hinges on our measurement of both mobility and mass for unsolvated (dry) clusters. However, the mobility of atmospheric aerosols is often measured under humid atmospheric conditions, while their subsequent introduction into a mass spectrometer would tend to remove water or other volatile components, therefore distorting the relation found here between these two quantities.

CONCLUSIONS

We have generated a series of singly and multiply charged IL clusters by electrospray, and simultaneously measured their electrical mobilities and mass with a parallel plate DMA coupled to a mass spectrometer. From these measurements we conclude that:

1.	RF heating in the ion guide at the inlet of mass spectrometers leads to cluster evaporation even for nearly involatile substances. This demonstrates the need to carefully design MS inlets for the analysis of more volatile aerosol clusters.
2.	The measured mobility diameters of singly charged IL clusters composed of 7–41 ion pairs are in excellent agreement with their volume diameters augmented by 0.3 nm.
3.	For smaller clusters composed of 0 to 6 ion pairs, the main source of disagreement between mobility diameter and mass diameter is due to the interaction between the charge on the cluster and the dipole it induces on the neutral gas, which reduces the actual mobility below the Stokes-Millikan value. For the smallest cluster studied, the EMI+ cation, a maximum deviation of 14.3% is found.
4.	Molecular dynamics simulations of (EMI-BF4) n EMI+ clusters show that those with n > 3 are globular. These calculations reveal also substantial shifts in the cluster density (1292 to 1538 kg/m−3) in the range from n = 0 to n = ∞. Nontrivial density shifts are seen even at n = 11 (ρ = 1342 kg/m−3) and beyond, though in this range they appear to be due to capillary compression and to be predictable based on bulk compressibility data and capillary forces based on the bulk surface tension. This densification may conceivably be measured experimentally once polarization effects are accounted for.

Acknowledgments

We thank Alejandro Casado of SEADM and Bruce Thomson of MDS Sciex for the advice on the DMA-MS graphic software and the operation of the QStar. We are grateful to Dr. Dominic Goshtik of Applied Biosystems, and Gonzalo Fernandez de la Mora of SEADM for the loan of the MS and the DMA, respectively, and to the Yale Keck Biotechnology Center for hosting the tandem instrument.