The Mobility of Fractal Aggregates: A Review

Abstract

A review of the experimental and theoretical literature describing the mobility of fractal aggregates over the previous three decades is presented. Aggregates are those formed via both diffusion and reaction limited cluster-cluster aggregation processes, DLCA and RLCA, which form aggregates with fractal dimensions and prefactors of ca. 1.78 and 1.3 and 2.1 and 0.94, respectively. Emphasis is placed on DLCA aggregates. The entire Knudsen number range from continuum to free molecular is reviewed. The review finds a simple and general consensus description of mobility for the entire range.

1. INTRODUCTION

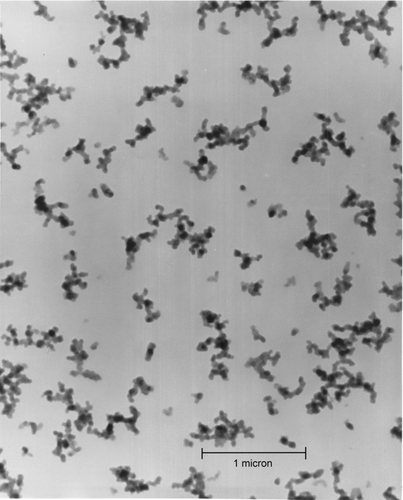
It is now well established that when solid particles come together via random aggregation processes they form aggregates with fractal morphology. As a consequence, fractal aggregates are common in aerosols and colloids in both our natural and technical environments. As such, we desire to know and quantify the physical properties of these particles. Figure 1 shows an electron micrograph of soot fractal aggregates collected from a flame. The particles appear complex, but fortunately we have the quantitative, fractal description of their morphology as a foundation for description of their other physical properties.

This review is concerned with the mobility of fractal aggregates in a medium. Mobility is a fundamental property that can be readily measured and that determines aggregate transport, dispersal, and the kinetics of their continued growth via aggregation. A considerable body of literature concerning fractal aggregate mobility has developed over the past three decades, but it appears that no review of this literature has been presented. A useful review would critically distill the data and theory to develop a single coherent and hopefully simple description of this phenomenon. It is our purpose here to present such a much needed review.

2. PRELIMINARIES

The mobility of fractal aggregates depends on a number of interweaving factors. There is the fractal nature of the aggregate and the fractal parameters that quantify this nature. There is the size of the aggregate as measured by a linear dimension such as a radius or a mass measure of size such as the number of primary particles or monomers that make up the aggregate. Note that as the monomer number falls to one, the aggregate is no longer fractal. Last but not least is the flow regime which is determined largely by the aggregate's linear size in comparison to the molecular mean free path of the molecules of the medium in which it is moving.

FIG. 1 Transmission electron micrograph of soot aggregate particles sampled thermophoretically from an ethylene/air laminar, diffusion flame.

2.1 Fractal Aggregates

Fractal aggregates are clusters of particles with a self-similar structure over a finite range of length scales. The particles composing the aggregates are called “primary particles” or “monomers.” Ideally they are spherical with point contacts and all the same size, but this description is an approximation. Regardless, we take them to be all the same size with a radius of a, and this sets the lower limit to the fractal scaling range. The upper limit is well described by the radius of gyration R_g which is a root mean square radius that quantifies the overall size of the aggregate. A consequence of self-similarity is that the number of primary particles N in the aggregates scales as a power law with the reduced size of the aggregate as

In Equation (1) D_f is the fractal dimension and k₀ is the scaling prefactor. Equation (1) may be considered as the defining relation for fractal aggregates (Sorensen 2001).

An important and well known way to mathematically describe the structure of condensed matter systems is the pair distribution function, g(r). Given a particle at any position, g(r)is the probability of finding another particle a distance r away. A second consequence of scale invariant, self-similarity is that the pair correlation function of the primary particles is a power law which can be expressed as

Here d is the spatial dimension. Equation (2) includes h(x), a so-called cutoff function that accounts for the fact that the aggregate exhibits finite extent. To preserve the power law, h(x) = 1 for x ≪ 1, and to cut off the power law, h(x) must decrease faster than any power law for x ≫ 1. A function that has proven adequate for this purpose is the stretched exponential

Various studies (Mountain and Mulholland 1988; Cai, Lu, and Sorensen 1995; Lattuada, Wu, and Morbidelli 2003b) have shown γ ∼ 2 to 2.5 for both DLCA and RLCA aggregates (see below).

Aerosol particles almost always aggregate via random Brownian motion; aggregates random walking, meeting, and sticking together. Such a process is called Diffusion Limited Cluster Aggregation, DLCA for short (Meakin 1983; Kolb et al. 1983). In three dimensional space DLCA leads to fractal aggregates with D_f = 1.78 ± 0.1 and k₀ = 1.3 ± 0.2. These numbers can be considered universal since results from a wealth of studies all concur. These studies include: experiments on both colloids and aerosols (Jullien and Botet 1987; Cai et al. 1995); simulations (Meakin 1988; Sorensen and Roberts 1997; Lattuada et al. 2003b; Pierce et al. 2006), which show an underappreciated anti-correlation between the fit values of D_f and k₀ (Sorensen and Roberts 1997); a simple analytical theory (Sorensen and Oh 1998) and recent work that has shown a correlation between the prefactor and the aggregate shape (Heinson, Sorensen, and Chakrabarti 2010). The prefactor k₀ for some combustion aerosols has been measured to be as large as 2.5 (Koylu and Faeth 1995), and this possible break from universality appears legitimate and warrants more attention. Moreover, work on some combustion aerosols has suggested D_f = 2.2 to 2.4, but we will demonstrate repeatedly below that this is a result of improper interpretation of mobility measurements. There also are situations where aggregates are found with larger fractal dimensions as a result of processes following the aggregation processes such as shear restructuring or cloud processing. More recently hybrid superaggregates with D_f = 1.8 on short length scales and D_f = 2.6 on larger length scales have been discovered (Sorensen et al. 2003; Kim et al. 2004, 2006). Regardless of these variants, here we will consider the canonical DLCA aggregates which represent the great majority.

In colloids the probability of cluster-cluster sticking upon meeting can be made very small and then a new type of aggregation ensues, Reaction Limited Cluster Aggregation, RLCA. Although RLCA is common in colloids, it seems not to have been observed in aerosols. RLCA leads to D_f = 2.05 to 2.15 with k₀ = 0.94 for the lower D_f value (Lattuada et al. 2003b).

The review below will concern both DLCA and RLCA aggregates with an emphasis on the former.

2.2 The Mobility Radius

The principle quantitative descriptor of mobility used in this review is the mobility radius. It is the mobility radius (or diameter) that can be precisely measured with a differential mobility analyzer (DMA) and hence is of great practical value. To define the mobility radius we first recognize that the drag force F_d on a particle in a medium moving with velocity v at low Reynolds number can be written as

where f is the drag coefficient. For a spherical particle the drag coefficient is a function of the particle radius, R

For a particle of arbitrary shape, we define the mobility radius R_m as that length which yields the correct drag coefficient with the same functionality, f(R), as for a spherical particle

Many authors use the term “mobility diameter” which is, of course, twice the mobility radius. We shall tend to use “radius” unless referring to work in which diameter values are given.

In this review we will describe the mobility radius in two ways. First, we will compare it to the foremost linear dimension measure of the aggregate size, the radius of gyration, with the ratio

Second, we will describe its functionality on aggregate mass with N, the number of primary particles (or monomers) in the aggregate, which is proportional to the actual mass. The functionalities are

and

We call D_m the mass-mobility scaling exponent, and x the mobility-mass scaling exponent. It quickly follows from Equations (8) and (9) that x = 1/D_m; hence the reciprocal nature of their names. Although Equations (8) and (9) are redundant, we will find it useful to look at the data both ways.

2.3 The Flow Regime

The functionality for the drag coefficient depends on the flow regime. The flow regime is determined by the Knudsen number, Kn, which is the ratio of the molecular mean free path to the particle radius (Friedlander 2000). The definition of the aggregate radius is somewhat problematic; possibilities include R_g, R_m, and the mass equivalent radius. Current usage favors R_m, but the exact value is of little consequence for quantification of the mobility radius.

In the continuum regime where Kn ≪ 1 the drag coefficient is given by the Stokes relation

where η is the shear viscosity of the medium.

In the free molecular regime where Kn ≫ 1, the Epstein equation holds

where ρ is the medium mass density, k_B is the Boltzmann constant, T the temperature, m the medium molecule mass and α is the accommodation coefficient (0 < α <1, typically α = 0.91).

Between these two limits lies the slip or transition regime, where ca. 0.1 < Kn < 10. Then

for all Kn where C(Kn) is the Cunningham slip correction factor which is a function of the Knudsen number Kn (Friedlander 2000).

A simple, general formula good for all Kn is the harmonic sum (Sorensen and Wang 2000)

This equation has Equations (10) and (11) as limits for small and large R_m, respectively, and is good to 10% or better compared to the standard slip formula, Equation (12), throughout the slip regime. Equation (13) and the slip correction Equation (12) are discussed further in Appendix A.

2.4 Size

Only in the limit N → ∞ can an aggregate truly be a fractal; all finite sized aggregates are, technically speaking, fractal-like. However, fractal-like aggregates of large N display properties similar enough to their pure fractal ideals to be called “fractal” by those of us with a practical bent. How large is large enough is an important issue for mobility that we will discuss below. Certainly an aggregate with N = 1, a single sphere, is not fractal, and we will demand that any proper formulation of fractal aggregate mobility must have the correct N = 1 limit. Furthermore, aggregates of two monomers, i.e., doublets with N = 2, have an exact morphology that allows for quantitative description. Hence we will likewise demand that any proper formulation of fractal aggregate mobility must have the correct N = 2 limit as well. An unambiguous shape description is not possible for aggregates with N = 3 or more; for example, if N = 3, the aggregate can be a linear rod or a triangle or some configuration in between these limits.

3. MOBILITY IN THE VARIOUS FLOW REGIMES

3.1 The Continuum Regime

In the continuum regime the medium is taken as infinitely divisible, hence it has no length scale. Moreover, if the fractal aggregate is asymptotically large, the primary particle size can be neglected relative to the overall size of the aggregate. Thus the only length scale involved in the aggregate mobility problem is the overall size of the aggregate, which is conveniently described by the radius of gyration R_g. Given this, the mobility size, which also has units of length, can only be proportional to the gyration radius. Thus we have

This is a transposition of Equation (7) where β is the ratio of the mobility and gyration radii of the aggregate. A constant ratio β would imply D_m = D_f.

Equation (14) holds for “asymptotically” large aggregates. The opposite limit is the single particle aggregate where N = 1. Then the “aggregate” is a single spherical particle with a mobility radius equal to the geometric radius R. For a sphere the radius of gyration is , thus in the single particle limit we must have

Chan and Dahneke (1981) and Dahneke (1982) first addressed the issue of drag for aggregates with a study of non-fractal, linear chains of spheres. These results have some bearing on the issue for fractals since, as the authors claimed, in the free molecular limit the results should apply to chains with occasional kinks and branches. Also, such chains represent fractal aggregates for N ≈ 3 or 4. In particular Dahneke (1982) presented a scheme to calculate the orientationally averaged drag on straight-chain aggregates of all sizes over the entire range of Knudsen numbers. In the continuum limit he did this by extrapolating the data in this limit of Horvath (1974) for straight chains with N = 2, 3, 4, 5 based on analytic expressions for prolate spheroids to arbitrary N. In the free molecular limit he used the Chan and Dahneke results for straight chains. He then developed an interpolation scheme based on the Cunningham correction factor to obtain the drag for arbitrary Kn. Thus all N and all Kn are covered for straight chains.

Figure 2 is a “working” graph that illustrates our picture of the mobility ratio β in the continuum regime as it evolves over the course of this review. We first plot the orientationally averaged data of Horvath as given by Dahneke. We see that β for the linear chains declines rapidly with increasing N. This is largely due to the rapid increase of R_g with N for the linear chains. Figure 3 plots these same data from the perspective of Equation (9). We find a rough power law with mobility-mass scaling exponent x = 0.52 for N = 1 to 5 and x = 0.56 for N = 1 to 10, the latter using the Dahneke extrapolation. These values imply D_m = 1.78 to 1.92, similar to the value of D_f for aggregates, not chains for which D_f = 1.0. This suggests that naïve use of the mass-mobility scaling relation for linear chains could be miss-interpreted as indication the aggregates have DLCA morphology. Also note that Figure 3 contains both continuum and free molecular results, and we find that the flow regimes are very similar for small N.

FIG. 2 Preliminary graph of the ratio the aggregate mobility radius to the radius of gyration, β = R_m/R_g, versus the number of monomers (primary particles) in the aggregate N in the continuum limit. Solid diamonds are exact values known for the N = 1 and 2 limits. Data include: open squares are the data of Horvath (1974) for linear chains, circle with X the data of Wiltzius (1987) for RLCA fractal aggregates, circles with plus sign are the data of Wang and Sorensen (1999) for both DLCA and RLCA fractal aggregates, square open diamond the data of Gwaze et al. (2006) for DLCA fractal aggregates. Theory includes: solid line Lattuada et al. (2003a), designated by LWM, for DLCA fractal aggregates, dashed dot line Lattuada et al. for RLCA fractal aggregates, medium dashed line Katzel et al. (2008), and long dashed lines “backbone” functionalities for DLCA fractal aggregates proposed in the text.

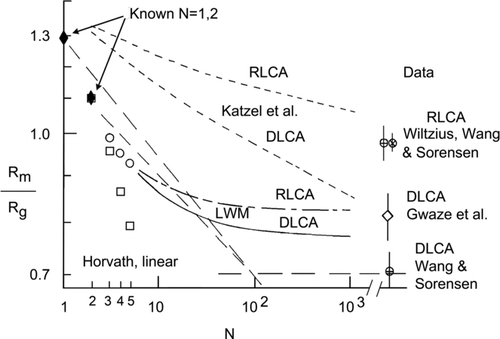
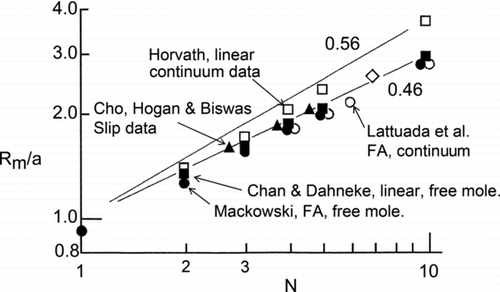
FIG. 3 Aggregate mobility radius normalized by the monomer (primary particle) radius, R_m/a, versus number of monomers in the aggregate, N. Open symbols designate continuum regime, closed free molecular regime. Data are open squares from Horvath (1974) for linear chains and closed triangles from Cho et al. (2007) for random aggregates. Theory includes: closed squares Chan and Dahneke (1981) for linear chains, closed circles Mackowski (2006) for DLCA fractal aggregates, open circles Lattuada et al. (2003a) for DLCA fractal aggregates, and open diamond Binder et al. for a compact seven-star. Lines represent power laws R_m = aN^x for x = 0.46 and 0.56.

Chen, Deutch, and Meakin (1985; 1987) first addressed the problem of fractal aggregate mobility by application of Kirkwood-Riseman formalism (Kirkwood and Riseman 1948). This method sums the forces on every primary particle in the aggregate which are due to the interaction of the flow with a given particle plus all the disturbances of the flow due to the other particles. The aggregates they considered were generated via Monte Carlo, cluster-cluster methods to yield both DLCA and RLCA clusters. The primary result of their work was verification of the proportionality between R_m and R_g expressed in Equation (14). Values of β = 0.875 and 0.97 were explicitly determined for DLCA and RLCA, respectively, for clusters in the size range N = 50 to 400.

Kirkwood-Riseman theory assumes the spheres that make up the aggregate are widely separated, which is a serious simplification. Despite this caveat, it has the advantage of a straightforward calculation of the coefficient β, viz.

Figure 4 shows values of β calculated using Equation (16) plotted versus the fractal dimension for a few different correlation function cutoffs (Equation (3)). For DLCA with D_f = 1.78 ± 0.05 and γ = 2 or slightly larger this graph suggests β values of roughly 0.68 to 0.78, the shaded zone on the graph. For RLCA with D_f = 2.15 ± 0.05 and again γ = 2 or slightly larger this graph suggests β values of roughly 0.83 to 0.91, also shaded in the figure.

FIG. 4 The ratio the fractal aggregate mobility radius to the radius of gyration, β = R_m/R_g, for large N in the continuum regime versus aggregate fractal dimension, D_f, calculated for three different density correlation function cutoffs using Equation (16). Cross-hatch regions represent reasonable DLCA and RLCA aggregate possibilities. Data included are: circle with X the data of Wiltzius (1987), circles with plus sign are the data of Wang and Sorensen (1999). Other theory includes: open circles, Rogak and Flagan (1990); open squares, Tandon and Rosner (1995).

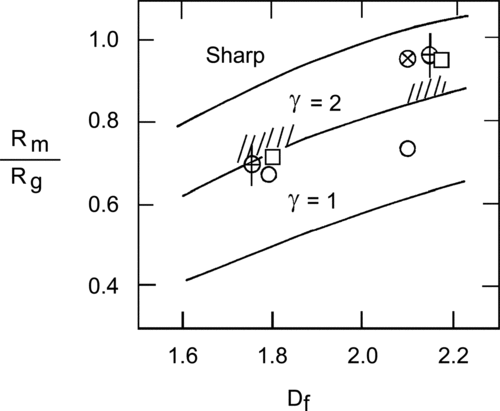
It appears that Wiltzius (1987) was the first to address the problem of fractal aggregate mobility experimentally. He studied a colloidal, RLCA system with D_f = 2.1 and used static light scattering to measure R_g and dynamic light scattering to measure R_m. A proper reanalysis of his results (Pusey et al. 1987) to account for the different moments of the size distribution of the aggregates measured by the two different light scattering techniques is needed. Use of this reanalysis with present day knowledge of the RLCA aggregate size distribution (Sorensen and Wang 1999) yields an experimental value of β = 0.97 ± 0.02, in very good agreement with the Chen, Meakin, and Deutch (1987) value. This experimental value is included in Figure 2.

Experimental work from this laboratory (Wang and Sorensen 1999) included both colloids and aerosols in the continuum regime. Similar to Wiltzius, both static and dynamic light scattering were used to determine the R_g and R_m, respectively. Proper corrections for aggregate polydispersity were carefully made. The colloid was composed of nearly monodisperse latex microspheres that were 28 nm in diameter in water destabilized by ionic salt addition. Both the DLCA and RLCA regimes were studied by using different salt concentrations. The measurements yielded fractal dimensions of D_f = 1.75 ± 0.10 and 2.15 ± 0.10, respectively. The aerosol was composed of TiO₂ particles ca. 35 ± 10 nm in diameter. These were allowed to aggregate in air via DLCA at a variety of background pressures from one atmosphere to 1/15 atmosphere to form large aggregates with D_f = 1.75. The smallest of these aggregates had R_g ≈ 700 nm which implies N ≈ 250.

For the colloid the DLCA yielded values of β = 0.71 ± 0.05 and the RLCA yielded β = 0.97 ± 0.05. Aerosols for Knudsen numbers in the range 0.02 < Kn < 0.30 yielded 0.70 ± 0.05. These experimental values are included in Figure 2. The β value increased to 0.75 ± 0.05 when 0.4 < Kn < 1.3, which is out of the continuum regime.

Wang and Sorensen continued their analysis by considering the theoretical work of others in the continuum regime. Rogak and Flagan (1990) simulated aggregates via an “expanded cube” procedure with selectable fractal dimension. They calculated β = 0.67 for such clusters when D_f = 1.79 and β = 0.73 when D_f = 2.1. Reanalysis of diffusivity calculations by Tandon and Rosner (1995) led to β = 0.71 and 0.95 for D_f = 1.8 and 2.18, respectively. These theoretical values are included in Figure 3.

To summarize the present review to this point, the experimental results are, for the most part, well supported by the various theories. We thus concur (for now) with the 1999 conclusion of Wang and Sorensen that for DLCA with D_f = 1.75, β = 0.70 ± 0.05, and for RLCA with D_f = 2.15, β = 0.97 ± 0.05 for asymptotically large fractal aggregates in the continuum regime.

We interrupt our historical review to heuristically develop the small N regime. Values of β for both aggregation mechanisms are less than one, whereas the N = 1 limit must have β = 1.29, Equation (15). Thus the question arises, how does β cross over from the asymptotic values to the N = 1 value? A suggestion follows if we relax rigor a bit and think in terms of orders of magnitude. We can argue that one order of magnitude in N is not likely asymptotic, two orders of magnitude to N ≈ 100 is likely close and three orders of magnitude to N ≈ 1000 is very probably in the asymptotically large N regime. With this we can propose a functionality for β similar to that sketched in our evolving Figure 2. Here are drawn the “backbone” curves of constant β = 0.7 at large N and a power law decline from the N = 1 value of β = 1.29 at small N to β = 0.7 at N = 100. “Large” and “small” are separated by N = 100. We pick a power law decline in the small N regime merely because nature often uses power law functionality, e.g., fractals. For DLCA to transform from β = 1.29 to β = 0.70 as N varies from N = 1 to N = 100 requires that

represent the small N backbone curve (A similar analysis for RLCA yields an exponent of –0.06). Wang and Sorensen proposed a similar crossover for the slip regime based on data from that regime, their figures 7 and 8 where β is plotted versus the Knudsen number. We will discuss this analysis extensively below. The known value for N = 2 doublets, 1.09 (Horvath 1974; Dahneke 1982: Kasper et al. 1985; Cheng et al. 1988; Kousaka et al. 1996, Zelenyuk et al. 2006) is also plotted in Figure 2 with the backbone behavior β = 1.18N^−0.11 for the region between N = 2 to 100 (wrong N = 1 limit but correct N = 2 limit). Katzel et al. (2008) calculated diffusional behavior for simulated aggregates with tunable fractal dimensions and found behavior qualitatively similar to Equation (17) but the decrease with increasing N continued up to and apparently beyond N = 1000, the largest size studied. However, the small N limit of this work is in error by as much as 20%, see Figure 2. Quite recently Al Zaitone et al. (2009) calculated a dependence that is well described by Equation (17) for simulated clusters with some sintering in the free molecular regime in the range N = 2 to 200.

We now continue with more work involving the continuum regime that mostly vindicates the backbone curves of Figure 2.

Filippov (2000) used numerical methods to integrate the interacting Stokesian dynamics of clusters of touching spheres. The aggregates he studied were computer generated and forced to have fractal dimensions of D_f = 1.0 (straight chains), 1.2 and 1.8, the latter of which equals that for DLCA. For D_f = 1.8 aggregates had prefactors of k₀ = 1.2, 1.3, and 2.3. It is important to point out that whereas these aggregates have D_f and k₀ values the same as or similar to aggregates made via a DLCA process, they might have structural difference from DLCA that in some unknown way affect the mobility. This work involved both continuum and slip regimes and was limited to N ≤ 100. For the DLCA-like aggregates (D_f = 1.8) in the continuum regime, β had values of about 0.95, 0.94, and 1.15 for k₀ = 1.2, 1.3, and 2.3, respectively, and a very slight decrease of about 7% as N varied from 7 to 100. These results do not support the backbone hypothesis in Figure 2 nor do they agree with the continuum regime measurements of Wang and Sorensen.

Lattuada, Wu, and Morbidelli (2003a) extended the Kirkwood-Risemann approach to fractal clusters composed of touching, spherical particles. They derived an analytical expression for the mobility radius for N ≥ 3 based on the particle-particle pair correlation function, a result analogous to Equation (16). The pair correlation function was determined in a companion paper (Lattuada et al. 2003b) which used a Monte Carlo simulation to create both DLCA and RLCA aggregates. These aggregates had D_f = 1.85 and k₀ = 1.17 for DLCA and D_f = 2.05 and k₀ = 0.94 for RLCA. Their results, figure 3 of their paper, are reproduced here in our evolving Figure 2.

Figure 2 shows that the Lattuada et al. (2003a) results are quite successful in that they support our physical intuition regarding small and large N regimes, the backbone curves in Figure 2, and a crossover between. The asymptotic values at large N are β = 0.765 and 0.831 for DLCA and RLCA, respectively. This is fairly good agreement with the experiments of Wang and Sorensen for DLCA but not so good for RLCA including Wiltzius's results. Figure 3 shows that the Lattuada et al. calculations for DLCA fractal aggregates fall ca. 15% below the Horvath data for continuum regime linear rods, but are only slightly below the calculations of Chan and Dahneke for free molecular regime linear rods.

There is a significant body of work that treats the fractal aggregate as a porous and permeable object to calculate the mobility radius (Adler 1987; Tandon and Rosner 1995; Veerapaneni and Wiesner 1996; Coelho, et al. 1997; Vanni 2000; Kim and Stolzenbach 2002; Lattuada, Wu, and Morbidelli 2004; Vainshtein, Shapiro, and Gutfinger 2004; Vainshtein and Shapiro 2005). These porous sphere models assume that the aggregate is spherical and require knowledge of the radial density distribution function from which the permeability is calculated. These models predict for DLCA aggregates in the continuum limit that the mobility radius scales with the number of monomers per aggregate with a mobility-mass exponent of approximately x ≈ 0.6 (Shapiro et al. 2004, 2005 and private communication; Lattuada et al. 2004). The ratio β = R_m/R_g is somewhat larger than unity for all sizes. This ratio would be smaller if the assumption of aggregate sphericity was relaxed (Shapiro, private communication). As the Knudsen number increases from zero to small values found for aerosols at atmospheric conditions, the ratio β shows a very strong functionality with N, falling from values greater than unity for small N, showing a minimum of ca. 0.3 near N = 10 and then rising to exceed unity at very large N. These behaviors are not consistent with the others portrayed in Figures 2 and 3.

Recently Binder et al. (2006) studied the application of Stokesian dynamics methods, exemplified by Filippov's work, and lattice Boltzmann methods for calculating mobility of fractal aggregates in the continuum regime. They considered the lattice Boltzmann method as the most rigorous. It involves a numerical solution to the entire flow field of the aggregate. Their paper compared the two methods for both accuracy and computational efficiency. Aggregates were either doublets, a compact star of seven primary spheres or DLCA simulated with Monte Carlo methods. The doublet result agreed with previous results. The compact, seven membered star result is plotted in Figure 3 and is very consistent with the other linear chain mobilities plotted there. This suggests that the shape is not particularly important in the small N limit. Fractal aggregates with D_f = 1.85 of size N = 16, 32, 64, and 128 were describe by R_m = 0.75aN^0.63. This can be converted to β with the aid of Equation (1), their value of and a reasonable guess at k₀ = 1.17 to yield β = 0.82N^0.09. This increasing function with N is opposite that expected from the data which led to Figure 2 and the Lattuada et al. result. However, we have replotted their data R_m versus N, log-log and find that the N = 128 point lies off a straight line, power law trend, and that its elimination from a fit to Equation (9) implies R_m = aN^0.55, consistent with the implication that β is constant in this regime.

We now summarize mobility for the continuum regime. This summary uses the judgment of the author to select results that are consistent with each other. A combination of theory and experiment (see also the discussion of Gwaze et al. (2006) who found an experimental value of β = 0.81 ± 0.07, below) suggests that asymptotically large DLCA fractal aggregates have a constant ratio β = 0.75 ± 0.05. Asymptotically large RLCA aggregates have β = 0.97 ± 0.05. Moreover there appears to be a crossover in functionality near N ≈ 100. Backbone functionalities for DLCA aggregates in the small and large N regimes are

Equation (18a) has the correct N = 1 and 2 limits; Equation (18b) yields β = 0.75 for fractal aggregates with D_f = 1.78 and k₀ = 1.3. Equations (18a) and (18b) crossover at N = 74 (This is not significantly different than 100 because the result depends sensitively on the difference in the exponents 0.56—0.46 = 0.10.)

3.2 The Free Molecular Regime

Since aggregates have two length scales, overall aggregate and primary particle sizes, the concepts of Knudsen number, which compares the particle size to the medium molecule mean free path, and the concomitant free molecular regime, can be ambiguous. In this work we shall use “free molecular” to mean that the mean free path is very large compared to the overall aggregate size. This is consistent with the use of the mobility radius for defining the Knudsen number of an aggregate as stated above.

The physics of the free molecular regime drag is straightforward enough to allow for reasonable physical, although not rigorous, arguments for the functionality of mobility radius on the number of primary particles in the aggregate. The physics is simply that the medium is not a medium at all but rather a collection of widely separated molecules traveling ballistically in straight lines that impart drag to any object by colliding with it. The probability of collision is proportional to the available geometric cross section of the object. This available geometric cross section is the projected area of the aggregate perpendicular to a molecule's linear path due to the relative velocity between the molecule and the aggregate averaged over all directions in space that the molecules may take. Thus the drag on a sphere is proportional to the square of the geometric radius, a², and the drag on an aggregate of N spherical particles of radius a is proportional to Na². Then the mobility radius is R_m = aN^0.5. This zeroth order result needs modification due to primary particle-particle screening or shadowing of the ballistic molecules. This would tend to make the functionality of the cluster projected area on N less than linear. These projected area arguments lead to a mobility radius given by

where the exponent x < 0.5 is, as first defined in Equation (9), the mobility-mass exponent. Note that Equation (19) has the correct N = 1 limit. As an example note that a dense aggregate with D_f = 3 would have x = 1/3. From this it is tempting to propose that for a fractal aggregate of arbitrary D_f, x = 1/D_f. This, however, will prove to be not true. The question is, what is x?

Meakin, Donn, and Mulholland (1989) created simulated aggregates with D_f = 1.8 and determined their projected area as a function of N. They found that the ratio of the projected area of the cluster, A_c, to the projected area of the primary particle, A_p, could be fit empirically to

The square root of this, which is proportional to the mobility radius, can be fit to the power law of Equation (9) with x = 0.455 for N = 1 to 100, x = 0.461 for N = 1 to 1000, and x = 0.462 for N = 10 to 1000.

Pierce, Chakrabarti and Sorensen (2006) studied the projected area of cluster-cluster aggregates formed from diffusive motion in the continuum with Stokes drag, diffusive motion in the free molecular regime with Epstein drag and cluster ballistic motion in the extreme free molecular regime. Aggregate sizes ranged from N = 10 to 300 and the fractal dimension for the Epstein regime aggregates was 1.80 to 1.82, depending on the method of analysis, with k₀ = 1.24. Aggregates formed via all schemes led to essentially the same mass-mobility exponent of x = 0.46 ± 0.002.

Recently, Al Zaitone, Schmid, and Peukert (2009) simulated aggregates with various degrees of sintering. Aggregate sizes ranged from N = 2 to 200. The free molecular mass-mobility exponent that can be inferred from their work is x = 0.46.

The first rigorous calculation of drag on an aggregate was done by Chan and Dahneke (1981) who considered linear chains of touching spherical particles in the free molecular regime. Their method was a Monte Carlo technique that determined the rate of momentum transfer, hence the drag force, due to molecular collisions with the aggregate. As mentioned above, they claimed that their results applied to chains with occasional kinks and branches so long as these perturbations on linearity did not introduce significant additional monomer-monomer screening effects. The result can be expressed as a mobility radius of the form

Results from Equation (21) are plotted in Figure 3 for the range N = 1 to 10. The approximate linearity of the results on this log-log plot implies that this formula can be recast very well in the form of the power law of Equation (9). We find the mobility-mass exponent x = 0.446 for the range N = 1 to 5 and 0.458 for the range N = 1 to 10. Thus, the exact numerical calculations of Chan and Dahneke are very consistent with the projected area concepts above. Moreover, they lead to essentially the same mobility-mass exponent.

Mackowski (2006) has presented an important paper which calculates the drag on fractal aggregates of spherical particles in the free molecular regime. His method followed the Monte Carlo approach of Chan and Dahneke to simulate the exchange of momentum and energy between the colliding molecules and the particles that make up the aggregate. Unlike that work, however, a slow moving flow condition was used which improved the accuracy and convergence of the method. The aggregates used were created via a sequential algorithm to produce synthetic cluster-cluster aggregates with predetermined D_f and k₀ in the ranges 1.7 to 2.0 and 0.7 to 2.0, respectively. We caution that there is as yet no certainty that such aggregates have morphology identical to canonical DLCA aggregates despite the similarity of D_f and k₀. His empirical fit to all his numerical results for N = 2 to 3000 is

These very general results yield a mobility-mass exponent of x = 0.47, quite consistent with all the results above. Results from Equation (22) are also plotted in Figure 3 for D_f = 1.78 and k₀ = 1.3. There it is seen that the Mackowski results are shifted down about 8% relative to Chan and Dahneke and the trend of Equation (19) with x = 0.46 because the prefactor of Equation (22) is 0.915 for these values of D_f and k₀.

Data for aggregate mobility deep in the free molecular regime are difficult to obtain because the mean free path in N₂ at STP is 66 nm and primary particles typically have radii of 15 nm or larger. Once an aggregate forms from these particles, the aggregate size is comparable to the mean fee path and hence in the slip regime. Wang and Sorensen (1999) tried using pressures down to 1/15 atmosphere where the mean free path is 990 nm but still the largest Knudsen number they achieve was 1.3.

It appears that the data set with the largest Knudsen numbers are those obtained by Cai and Sorensen (1994) who studied soot fractal aggregates in flames. Their flame environments were at atmospheric pressure but at elevated temperatures such that the mean free paths were ca. 330 nm to yield Kn in the range 4 to 16. Their method was the same as Wiltzius (1987), DLS was used to measure R_m and SLS was used to measure R_g. Proper analysis was used to deconvolute the effects of aggregate polydispersity. Scattering extinction measurements were performed to measure optically N and a (Sorensen et al. 1992). The soot was fractal with D_f = 1.79 ± 0.1 and N in the range 4 to 35. They found the ratio β was not constant but instead β ∼ N^−0.13. The exact dependence found is

with the error of 0.99 ± 0.08 and x = 0.43 ± 0.03. This result has both the correct N = 1 limit and very good agreement for the mobility-mass exponent with the theories above.

Cai and Sorensen interpreted their result as indicative of the importance of the projected area seen by the ballistic molecules of the medium for the effective drag and cited corroboration with Meakin, Donn, and Mulholland (1989), discussed above. They also likened the screening of ballistic molecules to the screening of electrons during TEM observation of fractal aggregates. TEM analysis finds that the projected area of the aggregate in the electron beam is sublinear with N, viz. ∼N^0.9, which is consistent with a mobility-mass exponent of 0.45.

For the free molecular regime, we again form a summary that uses the judgment of the author to select results that are consistent with each other. We find that the aggregate mobility in the free molecular regime is well described by mass-mobility and mobility-mass exponents of D_m = 2.17 ± 0.10 and x = 0.46 ± 0.02, respectively, for DLCA aggregates of all sizes N. We therefore write

Equation (24) has both the correct N = 1 and 2 limits. Now note the remarkable similarity between Equations (18a) and (24). We find that the mobility behavior in the continuum and free molecular flow regimes is, within a small uncertainty, the same in the small N regime. This appears to be a coincidence because the physics of mobility is different in the two flow regimes.

3.3 The Slip Regime

There have been numerous measurements of fractal aggregate mobility in the slip regime published in the aerosol literature. Many of these studies have found a power law relationship between the mobility radius and the number of primary particles in the aggregate in the form of the standard “fractal” equation, Equation (8) reproduced below

Moreover, many have called the exponent D_m the fractal dimension. Some workers have noted that D_m determined via Equation (8) does not equal the fractal dimension determined via other methods. We will show below that interpretation of D_m in Equation (8) as the fractal dimension is erroneous, misled by a subtle combination of the behavior of mobility in the slip regime and the small N limit.

Before we address the mobility aspects of Equation (8), it is important to recall the meaning of the fractal dimension in the defining relation, Equation (1). The fractal dimension quantifies the power law scaling of the mass of the aggregate, which is proportional to N, with a measure of its linear size. The radius of gyration, depending only on the spatial arrangement of the mass in the aggregate and nothing else, is an intrinsic quantity, hence it is a proper measurement of the linear size of the aggregate. The mobility radius, on the other hand, depends not only on the arrangement of the mass in the aggregate but also on features in its environment not intrinsic to the aggregate such as flow regime and aggregate alignment relative to the flow, and, therefore, is not a proper measure of linear size. This statement should not be taken to imply that the mobility radius is not a very useful and important quantity, but as we have seen above, it is not always directly proportional to R_g. Consequently, mobility radius should not be used to determine the fractal dimension without knowledge of how it is related to a true measure of linear size, such as the radius of gyration.

Measurements of mobility of aerosol fractal aggregates were pioneered by Schmidt-Ott (1988) who evaporated silver to create primary particles with a radius of 7.5 nm. These were allowed to aggregate, presumably via DLCA, and then their mobility size was measured with a differential mobility analyzer (DMA). After passing out of the DMA, the aggregates were sintered at elevated temperature to form compact aggregates which then passed through a second DMA to obtain the compact aggregate mobility size which is the geometric radius and directly related to the mass via a cubic scaling law. Both DMA's operated at ambient temperature and pressure. From these two measurements a mass-mobility description of the aggregates was obtained and fit to Equation (8) to yield D_m = 2.18. This was interpreted as the fractal dimension D_f of the aggregate.

Wang and Sorensen (1999) reanalyzed Schmidt-Ott's data assuming the aggregates were truly the result of DLCA and therefore had a fractal dimension of D_f = 1.75, not 2.18. Their conclusion was that the aggregates were in the small N regime where, as we have seen above for the continuum and free molecular regimes, R_m and R_g are not proportional. Then D_f of Equation (1) will not equal D_m of Equation (8). Figure 3 of Schmidt-Ott and the primary particle radius can be used to infer the number of primary particles in the clusters. The values range from N ≈ 2 to 37. This is well within the small N regime for the continuum flow, Figure 2 above, with the backbone behavior of Equation (17). If we take D_f = 1.75, then R_g ∼ N^0.57. Application of this with Equations (7) and (17) yields R_m ∼ N^0.44. This implies for the mass-mobility relation, Equation (8), D_m = 2.26, consistent with Schmidt-Ott's value. Reasoning in reverse, the Schmidt-Ott value D_m = 2.18 coupled with D_f = 1.75 imply the exponent in Equation (17) should be –0.11, the value obtained using the N = 2 limit, very reasonable for the physical argument given there.

Wang and Sorensen also reanalyzed the data of Rogak, Flagan, and Nguyen (1993). These workers used a tandem DMA, pre- and post-sintering method ala Schmidt-Ott with both TiO₂ and SiO₂ aerosols. By assuming these aggregates were the result of DLCA hence have D_f = 1.75, they showed that the exponent in Equation (17) would be –0.12 and D_m = 2.22.

Since 1999 there has been a plethora of measurements of aerosol fractal aggregate mobility all of which have been in the slip regime, typically with Kn < 1. Moreover, nearly all have involved aggregates that could be classified as small by our evolving point of view. We now review all these works with an eye towards a consistent interpretation involving both the proposition that all these aggregates are the result of DLCA, hence have a D_f of about 1.78, and that at least part of any given study involved aggregates in the small N regime. This latter point is particularly important for we have seen that the mobility behavior in the continuum and free molecular flow regimes is nearly the same for small N. Thus we expect that the slip flow regime, which resides between these two, will have the same behavior as well and that behavior is described by a mass-mobility exponent of D_m ≈ 2.2.

Cho, Hogan, and Biswas (2007) purposely studied aggregates with a small number of primary particles in the slip regime. Their method used nearly monodisperse polystyrene latex spheres with diameters of 55, 67, 76, and 99 nm obtained by spray drying colloids of these spheres. The method was essentially that of Schmidt-Ott. The mobility diameter of aggregates of N = 3, 4, and 5 of these primaries was measured with a DMA and then these were sintered in a furnace to create spheres. The mobility diameter of these sintered spheres was measured by a second DMA. The sintered sphere mobility diameter agreed very well with the diameter that can be calculated based on conservation of mass, the mass equivalent diameter. All the mobility diameters ranged from ca. 80 to 200 nm, hence given an ambient condition's air mean free path of 66nm the flow is in the transition regime with Kn = 0.66 to 1.65.

Cho et al. fit their results to a three parameter power law of the form of Equation (9) which found a mobility exponent of x = 0.426. This fit also found a slightly nonlinear dependence on primary particle diameter and had a bad N = 1 limit. We have refit the data to the simple Equation (9) including the N = 1 point as well. We find x = 0.44.

Park, Kittleson and McMurry (2004) studied diesel exhaust particles. Using TEM they compared aggregate length to projected area which can be related to total mass. This analysis yielded fractal dimensions of D_f = 1.61 and 1.75, depending on the details of the analysis. These values are consistent with DLCA. Using DMA and aerosol particle mass analyzer (APM) they obtained aggregate mass as a function of mobility diameter over the range 50 to 300 nm. This yielded a mass-mobility scaling exponent of D_m = 2.35. The primary particle mean diameter was 32 nm. We can use these values, assume R_m = 0.7R_g, k₀ = 1.3 and Equation (1) to estimate, very roughly, the N value in this size range to be ca. 5 to 110. This is within the small N regime as we have described above. Hence the large mobility-mass scaling exponent compared to the fractal dimension can be explained as due to a lack of proportionality between R_m and R_g in the small N regime. D_m = 2.35 can be inverted to yield a mobility-mass exponent of x = 0.426.

Maricq and Xu (2004) used a tandem DMA and an electrical low pressure impactor to compare aggregate effective density to mobility diameter for both premixed ethylene flames and diesel exhaust soot. In their review of the literature they point out the inconsistency of fractal dimensions measured via mobility analysis that tend to be larger than those measured via TEM analysis, exactly the problem addressed here. Ethylene flames yielded soot mobility diameters in the range 36 to 200 nm with an effective primary particle diameter of 16 to 26 nm depending on the height above the burner from which the soot was sampled. Measured density versus mobility diameter yielded mass-mobility scaling exponents of D_m = 2.1 to 2.2. Diesel exhaust yielded soot mobility diameters in the range 30 to 320 nm with an effective primary particle diameter of 16 to 25 nm. Density versus mobility diameter yielded D_m = 2.2 to 2.35. We can use these values, a fractal dimension of 1.78, a prefactor of k₀ = 1.3, β = 0.7, and Equation (1) to estimate the N values to be in the range ca. 4 to 350. That's over a decade within and half a decade out of the small N regime. According to the argument being presented here, the former smaller decade of size would see a scaling exponent of ca. 2.2; the latter half decade would see a scaling exponent of ca. 1.8. Close inspection of their figures plotting effective density versus mobility diameter shows that the slope of these double logarithmic plots is increasing with increasing mobility diameter. Since the slope is D-3 this implies D is decreasing with increasing mobility diameter, as we predict. If we regard the mass-mobility scaling exponents obtained by Maricq and Xu as showing the functionality of mobility in the small N limit as portrayed in Equation 8, then we obtain the mobility-mass exponent in the range x = 0.425 to 0.476.

De Carlo et al. (2004) and Slowik et al. (2004) presented back-to-back papers with an extensive review and study of the effects of particle morphology on density characterization and mobility. Following Wang and Sorensen (1999) and Baron, Sorensen, and Brockman (2001), they concurred that the mass-mobility scaling had two regimes depending on size and concluded that the crossover was at N = 60. However, they erroneously use the term “fractal dimension” to describe the power law scaling in each regime claiming that there are two distinct values of the fractal dimension and that it transitions smoothly between the two regimes. These conclusions are simply fixed by replacing “fractal dimension” by “mass-mobility scaling exponent.” Slowik et al. present data on soot extracted from a premixed propane “air” flame with mobility measured by a DMA and mass by an aerosol mass spectrometer.

Van Gulijk et al. (2004) confronted the reinterpretation of the Schmidt-Ott (1988) data by Wang and Sorensen (1999) by casting nebulous aspersions on the light scattering technique. This author could spend some time here demonstrating the reliability of light scattering for fractal aggregate measurements. Instead, we point out that Van Gulijk et al. failed to realize that Wang and Sorensen used the data of Schmidt-Ott (1988) and of Rogak, Flagan, and Nguyen (1993), neither of which used light scattering, to help uncover the problem that there is a small N limit in which the caution we are trying to convey exists. The different functionalities of the mobility radius depending on mass exist in non-light scattering data.

The experiments of Van Gulijk et al. studied soot from a diesel engine. A scanning mobility particle sizer measured the mobility diameter of the aggregates and an electrical low-pressure impactor measured the aerodynamic diameter. The data were obtained in the transition slip flow regime. The relationship between these diameters in the transition regime yielded a “fractal dimension,” based on the mass-mobility scaling relation, of 2.4. As we have seen, this is pretty typical for D_m in the small N regime. The primary particle diameters were 35 nm; the mobility diameters were in the range 75 to 280 nm. From this we can estimate, as described above, N ≈ 10 to 100, values that are within the small N regime. It is very interesting that even casual examination of the analysis presented in their figure 4, shows that the log-log plot of the five data points is not linear as expected for the simple power law expression for the analysis, their equation 24, which yielded “fractal dimension” of 2.4. In fact, the first two points have a stronger slope to imply a “fractal dimension” approaching 3, a reasonable value for an aggregate of only a few or less primary particles. Most interestingly, the last two points at the largest size have a slope of nearly zero, which by their equation 24 would imply a “fractal dimension” of 1.8. This is exactly what we expect as the mass-mobility scaling exponent becomes equal to the true fractal dimension as the aggregate size grows out of the small N limit! The data of Van Gulijk et al. (2004) support our argument.

Gwaze et al. (2006) studied fractal aggregates created from wood combustion under flaming conditions. The soot was size classified using a DMA to obtain aggregates with mobility radii of 100 to 396 nm. Subsequently these aggregates were collected via impaction on filter membranes for SEM analysis which yielded monomer size of 25.5 nm and fractal analysis that gave an average fractal dimension of D_f = 1.83. The scaling of the mobility radius with N had a mobility-mass exponent of x = 0.56 ± 0.04 which is equivalent to a mass-mobility scaling exponent of 1.79 consistent with the measured D_f. The measured number of primary particles for the range of mobility sizes studied ranged from ca. 23 to 420. Since some of this range is in the small N regime, it is somewhat surprising that the mobility scaling exponent compares so well to the fractal dimension. On the other hand a considerable part of the range is in the large N regime where the two exponents are equal. The aggregate R_g was also measured from the SEM images. This combined with the mobility led to a value of β = 0.81 ± 0.07 for the Knudsen range 0.17 to 0.5.

Scheckman et al. (2009) performed mass-mobility measurements on flame generated silica aggregates and found, what the arguments in this review would call, mass-mobility exponents D_m in the range 1.7 to 2.4, depending on flame conditions. Aggregate mobility radii ranged from 75 to 190 nm and primary particle radii ranged from 5 to 46 nm. Such radii and primary particle sizes imply monomer numbers, N, via Equation (1) in the approximate range of 10 to 1000; thus in our terminology both large and small aggregates. Of interest here is that aggregates with big primary particles, hence via Equation (1) small N for a given aggregate radius, showed large mass-mobility exponents, D_m > 1.7. On the other hand, aggregates with small primary particles, hence via Equation (1) large N for a given aggregate radius, showed smaller mass-mobility exponents, D_m = 1.7. In light of these data a reasonable interpretation is that all the aggregates where DLCA aggregates with D_f = 1.7. However, mass-mobility measurement yielded D_m = 1.7 only when flame conditions yielded primary particle sizes that were small enough to lead to aggregates with N > 100. When the flame conditions were such that primary particle sizes were large, aggregates with N < 100 appeared, and these showed D_m > 1.7 despite the fractal dimension still being 1.7.

Very recently, Shin et al. (2009, 2010) presented careful studies of the friction coefficient of silver aggregates in the slip regime. The methods involved using a DMA to select a mobility size and then an aerosol particle mass analyzer (APM) to measure the aggregate mass or a tandem DMA to measure mobility before and after aggregates sintering to spherical particles. The carrier gas was N₂ at ambient temperature. Primary particle sizes in the first study were 16 and 20 nm diameters for two different runs. Aggregate mass and primary particle size lead to primary particle number, which were in the range N = 40 to 600. In both studies TEM showed highly necked structures and analysis yielded fractal dimensions in the range D_f = 1.74 to 1.84, although there is some question whether these values should be scaled up by ca. 10% due to errors in interpreting 2d projections of the 3d aggregates. In the first study a mass-mobility comparison yielded an exponent of D_m = 2.10 ± 0.065 for mobility diameters ranging from 37 to 300 nm, hence Kn in the range 0.44 to 3.6. In the second study values of D_m = 2.172 ± 0.036 and 2.126 ± 0.061 were found for the DMA-APM and TDMA, respectively. All these values are consistent with the results discussed above.

In summary, in the slip, small N regime, the mass-mobility and mobility-mass exponents are well described by D_m = 2.22 ± 0.1 and x = 0.45 ± 0.02, respectively. These exponents are essentially equal to those found in both the continuum and free molecular regime. Interpretations that claim the fractal dimension equals the mobility-mass scaling exponent, i.e., that D_f = D_m, for small N slip are wrong. Whereas the literature offers examples of data sets that are in the slip regime at small N and transform into the continuum regime at large N, there appear to be no large N, slip regime data.

4. Overall Summary and Recommendations

4.1 Mobility

We now pull together and summarize all the results above, both experimental and theoretical, and make thoughtful conclusions for a best, general description of fractal aggregate mobility to date across the entire range of Knudsen numbers. It is important to stress that what follows is the author's best attempt for a distillation of the review above regarding functionality, numerical values, and error estimates for those values.

The general description for the mobility of DLCA fractal aggregates quantified by D_f = 1.78 and k₀ = 1.3 in the limits of Kn → 0 and Kn → ∞ is given by backbone Equations (18) and (24), respectively, which we reproduce here:

Continuum Regime,

Free Molecular Regime

The error in the exponents is estimated to be ±0.02. These results are displayed in Figure 5.

FIG. 5 General description of the mobility of fractal aggregates. Lower half shows the ratio of the aggregate mobility radius to the radius of gyration, β = R_m/R_g, versus the number of monomers (primary particles) in the aggregate, N. Filled narrow diamonds are exact results for N = 1 and 2. Solid line is for DLCA fractal aggregates in the continuum regime, long-short dashed line is for RLCA fractal aggregates in the continuum regime, long dashed line is for DLCA fractal aggregates in the free molecular regime. Upper half shows the ratio of the aggregate mobility radius to the monomer (primary particle) radius, R_m/a, versus the number of monomers in the aggregate, N. Solid line is for DLCA fractal aggregates in the continuum regime, long dashed line is for DLCA fractal aggregates in the free molecular regime. The lines overlap on this scale for N < 100. The slip regime is the cross hatched area bounded by the continuum and free molecular plots.

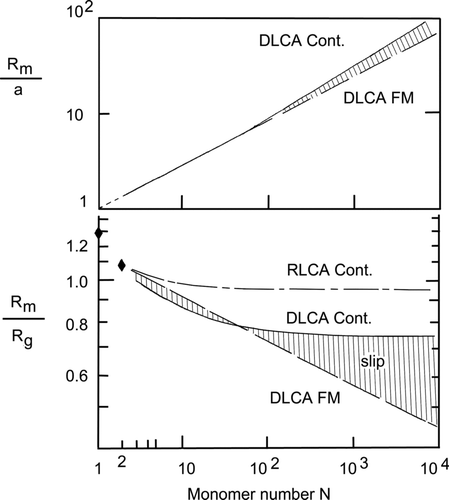
The lower half of Figure 5 shows a plot of the ratio of the mobility radius to the radius of gyration, β = R_m/R_g, versus the number of monomers (primary particles) in the aggregate, N, in both the continuum and free molecular regimes. This is a remake of and a replacement for our preliminary graph in Figure 2, based on our assessment of Figure 2. In Figure 5 we see that, in the continuum regime, the ratio β falls from known values at N = 1 and 2 to asymptotic values of 0.75 ± 0.05 and 0.97 ± 0.05, for DLCA and RLCA, respectively, as N goes to infinity. The small N (where β varies) to large N (where β is constant) crossover is near N ≈ 100. The free molecular regime result is shown only for DLCA aggregates. It is represented by Equation (24) divided by the solution of Equation (1) solved for R_g using k₀ = 1.3 and D_f = 1.78. Such a solution yields the correct value for R_g for N = 2, but not for N = 1. Thus the long dashed line representing this result limits to the correct N = 2 value.

The upper half of Figure 5 shows the mobility radius normalized by the primary particle radius, R_m/a, versus the number of monomers (primary particles) in the aggregate, N, for DLCA aggregates only. Slopes on this log-log graph are the mobility-mass exponent x. In the continuum regime for small N (N < 100) this graph displays the approximate power law where the mass-mobility exponent is x = 0.46 ± 0.02, Equation (18a). We stress that the functionality in this range of N is not exactly the backbone power law but rather the curving asymptotic approach similar to that calculated by Lattuada et al. (2003) and drawn for β in the lower half. However, experiment has shown that this curvature is hard to discern, the data are often well described by the power law, and the power law is very close to the curve. For large N (N > 100) the functionality crosses over to Equation (18b) with an exponent equal to the inverse of the fractal dimension.

The upper half of Figure 5 also shows R_m/a versus N in the free molecular for DLCA aggregates. Remarkably, the behavior in the free molecular regime for all N is essentially the same as the continuum regime behavior for small N.

By Equation (1), for a given N there is a uniquely specified R_g. Figure 5 shows that, for a given Knudsen number, a given N specifies a unique R_m. Thus there is a one-to-one correspondence between R_m and R_g for a given Knudsen number. On the other hand, a given cluster with N and R_g values can have different R_m values as the Knudsen number varies. This highlights, once again, the fact that R_m is not an intrinsic linear size measure.

We remark, that for DLCA aggregates in the free molecular regime, the results here imply β ∼ N ^−0.1. Thus β goes to 0 as N goes to ∞. This somewhat surprising result is a consequence of the decreasing density as the aggregate gets bigger. However, it does call into question the use of the mobility radius for defining the Knudsen number, an issue which will not be addressed here.

We will make the reasonable assumption that the slip regime lies between the two limits specified by Equations (18) and (24). With the help of either the lower or upper halves of Figure 5, it is not too difficult to picture what the functionalities of β or R_m/a are as Kn evolves from 0 to ∞. In the lower half plot, the continuum limit at N > 100 would rotate downward with increasing Kn until it met the free molecular limit drawn there, while for 2 < N < 100 the continuum curve would flatten slightly upward to meet the free molecular line. The picture is even simpler in the upper half, where for N > 100 the continuum limit straight line with slope 0.56 would rotate downward about the N = 100 point until it met the free molecular line with slope 0.46 with increasing Kn; there would be essentially no visible change for N < 100. These simple transformations describe the entire slip transition regime, i.e., the slip regime lies in the small regions between the continuum and free molecular plots in Figure 5.

This graphical picture of what happens in the slip regime for N > 100 can be expressed by an empirical formula

In Equation (25) the mobility-mass scaling exponent x is now a function of the Knudsen number. Note that Equation (25) has the proper limits at x = 0.46 and 0.56. Since the slip regime roughly spans 0.1 < Kn < 10, the extremes of which have x = 0.56 and 0.46, respectively, we can propose that x varies geometrically across that range. For example, one can propose x = 0.51Kn^0.043 in that range. It is hoped that someday data will be obtained in this regime to test this proposal.

FIG. 6 Dynamic Shape Factor of DLCA fractal aggregates for a variety of mobility radius Knudsen numbers as a function of the number of primary particles (monomers) in the aggregate.

4.2 The Dynamic Shape Factor

The dynamic shape factor of a particle can be defined as the ratio of the drag force on the particle divided by the drag force on the particle's volume equivalent sphere (Baron et al. 2001). Thus,

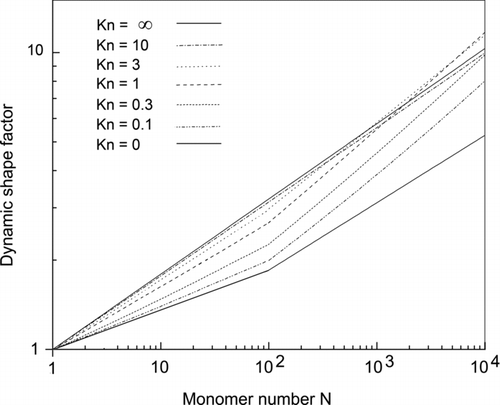
where R_ve = aN^0.33 is the volume equivalent sphere radius. With Equation (12) this becomes

where Kn_ve and Kn_m are the Knudsen numbers using the volume equivalent radius and the mobility radius, respectively.

With Equation (27), the dynamic shape factor can be calculated for a DLCA fractal aggregate with N < 100 using R_m = aN^0.46 [Equations (18a) and (24)] and for N > 100 using Equation (25). The results for a variety of mobility radius Knudsen numbers are given in Figure 6 (the constant A = 1.612, is explained in Appendix A). The nonmonotonic behavior with Kn_m for N > 1000 is due to the fact that at large N the ratio R_m/R_ve becomes so large that the quadratic functionality of the drag with linear size dominates even at small Kn_m.

5. Conclusion

Given the great abundance of DMA's in aerosol laboratories around the world, it seems reasonable to claim that mobility size, as described by the mobility radius R_m, is measured more than any other fractal aggregate size quantity. Moreover, mobility is an important physical quantity for any particle. This work attempts to relate this mobility size to intrinsic linear and mass sizes of the aggregate, R_g and N, respectively. The relation to mass is given succinctly in Equations (18) and (24), which are plotted in the upper half of Figure 5. The relation to R_g is plotted in the lower half of Figure 5 and is closely related to these equations and Equation (1). Figure 5 represents a distillation of the experimental and theoretical work on the mobility of fractal aggregates to date. It portrays an elegantly simple and comprehensive summary of how the fractal aggregate mobility is related to linear size R_g and mass N.

Acknowledgments

My work in this area has benefited from the pleasant and stimulating collaboration with my students J. Cai, N. Lu, G. M. Wang, C. Oh, T. Mokhtari, R. Dhaubhadel, C. Gerving, S. E. Gilbertson, D. Fry, F. Pierce and my colleague Amit Chakrabarti. This work has benefited from communications with G. Mulholland, W-G. Shin, S. Rogak, A. Filippov, J. Slowik, P. Gwaze, W. Peukert, M. Shapiro and P. McMurry. My work has been supported by the NSF and NASA.

APPENDIX A

Here we illustrate the usefulness of the harmonic sum, Equation (13), above, and reproduced here

as a general formula for the friction coefficient. The microscopic and macroscopic domains of a fluid are connected by the formula

The macroscopic quantities are η the shear viscosity and ρ the mass density of the fluid medium; the microscopic quantities are the mean thermal molecular velocity u = (8kT/πm)^1/2, where k_B is Boltzmann's constant, T the temperature, and m the medium molecular mass; and λ the medium molecule mean free path. The constant φ = 0.499 for elastic, hard sphere molecules. With this, the Epstein drag coefficient, Equation (11), can be written

Substitution of this along with the Stokes formula, Equation (10), into the harmonic sum formula with some minor algebra yields

where Kn = λ/R_m is the Knudsen number and A = 9φ/2(1 + απ/8). The constant can be evaluated for α = 1, a reasonable value, as A = 1.612.

With a constant A = 1.612, Sorensen and Wang (2000) demonstrated that the predicted value of the drag coefficient is accurate at the limits Kn = 0 and Kn ≫ 1, and is in error by as much as 10% too small near Kn = 0.5 relative to the standard Cunningham correction. The Cunningham correction would replace the constant A in Equation (A3) with

The constants α, β and γ are determined empirically by fitting to Millikan's data. Allen and Raabe (1982) give α = 1.155, β = 0.471, and γ = 0.596. However, the random error in the Millikan data are about 5%, which is half the discrepancy incurred by using the constant A. Moreover, as pointed out by Sorensen and Wang (2000), the 10% error is comparable to other uncertainties endemic in aerosol transport and kinetics studies. Hence use of Equation (A4) barely warrants the additional complexity.