A Numerical Model for Simulating the Motions of Ellipsoidal Fibers Suspended in Low Reynolds Number Shear Flows

Abstract

A computational model was developed to simulate the motions of ellipsoidal fibers suspended in viscous shear flows. The model incorporates drag, lift, gravity, and hydrodynamic torque acting on ellipsoidal particles. Two numerical experiments were conducted to test the accuracy of the model. First, a single fiber was subjected to a linear shear profile and allowed to rotate without translation. The model's predictions for the fiber rotational period were evaluated and were shown to match well with previously published theoretical and numerical values. Second, fibers were injected into a horizontal tube under different flow conditions and their motions were tracked. Inspection of individual fiber motion showed a tendency to remain aligned with the direction of bulk fluid flow. Fiber aspect ratio, injection location, and flow rate were shown to play important roles in the details of elongated particle motions. The predicted sedimentation efficiencies of fibers matched well with the previously published works. On the basis of the computational model results, an empirical expression for the sedimentation rate of fibers in a horizontal tube with circular cross-section was proposed.

1. INTRODUCTION

Prevalence of fibrous materials in construction and industrial processes, coupled with their link to toxicity in humans, has led to recent efforts being directed toward a better understanding of fiber transport mechanisms. The anisotropic shape of a fiber makes the physics of transport through fluids markedly different from that of a sphere. Drag on a slender elongated body changes with orientation that plays an important role in computing their trajectories.

In one of the first attempts to describe the motion of a nonspherical particle, Jeffrey (1922) examined an ellipsoidal fiber subjected to a linear shear flow field. While macroscopic linear shear flow is an idealization, a sufficiently small fiber suspended in viscous flows is exposed to velocity gradients that can be locally approximated as linear. Additionally, Jeffrey (1922) showed that the rotations of these elongated fibers are periodic and the period of rotation is a function of their aspect ratio and the flow shear rate, when the effects of inertia are neglected. The expressions derived for the coupled translational and rotational motions of fibers by Jeffrey (1922) have been widely accepted and used.

Chen and Yu (1991) solved for the specific case of ellipsoidal fibers suspended in a horizontal circular cross-section, straight tube under laminar flow conditions. They presented correlations for fiber sedimentation with aspect ratio and flow rate. Fan and Ahmadi (1995) developed a model for ellipsoidal fiber transport and deposition in the sublayer region of turbulent channel flows. They used Euler's quaternions for describing the kinematics of ellipsoidal fibers. A deposition criterion was also developed taking into account the orientation of the ellipsoid with respect to the wall. They suggested an expression for the deposition rate as a function of an effective dimensionless particle relaxation time.

Asgharian and Anjilvel (1995a) developed a series of direct equations for the angular acceleration of Euler's angles. They demonstrated that the resulting equations could simulate the period predicted in Jeffrey (1922) for ellipsoidal fibers not experiencing significant inertial effects. As inertia became more significant the period first shortened before reaching a critical inertia that slowed their rotations.

An application of these equations to track fibers in airways was presented by Asgharian and Anjilvel (1995b). They examined a straight pulmonary branch with circular cross-section and length to radius ratio of 3:1. A parabolic flow profile was assumed. After examining deposition behavior for several orientations of the branch, they suggested an expression for deposition as a function of tilt angle, fiber aspect ratio, and particle relaxation time.

Typically, in an attempt to characterize the motion of an irregular shaped body, an equivalent sphere diameter is introduced. In the specific case of the motion of a rigid ellipsoid, a uniform distribution of the fiber's orientation in the flow field is implied by averaging the mobility of the ellipsoid in the three dimensions. Many such formulations have been suggested and utilized in the literature. Stober (1972) proposed the calculation of an aerodynamic diameter (d_ae ) for a prolate spheroid based on a dynamic shape factor, k, that takes into account all possible orientations of the particle with respect to the flow direction. That is, a unique d_ae for when the fiber is aligned with the flow, perpendicular to the flow, or randomly distributed in the flow.

Shapiro and Goldenberg (1993) proposed characterization of an ellipsoid's motion with a particle relaxation time dependent on the averaged mobility dyadic and the assumption of isotropic orientation in the flow. Similarly, Fan and Ahmadi (1995) suggested an equivalent Stokes diameter based on the averaged translational dyadic.

Wang et al. (2008) derived several expressions for the aerodynamic diameter of an ellipsoid when it is aligned with the flow (d_{ae ,∥}), normal to the flow (d _ae,⊥), and randomly distributed within the flow (d_{ae ,R} ). They used the “point force approximation” technique explained in Clift et al. (1978). This technique uses a polynomial approximation for the distributed force along the ellipsoid's axes.

Many commercial CFD software packages have the ability to track a second phase in general flow fields. One such example is the Discrete Phase Model (DPM) in the commercial package ANSYS FLUENT. The DPM is a Lagrangian particle tracking algorithm. Particle geometries are assumed spherical and tracked individually with forces acting at its center. Drag is dynamic and dependent on particle Reynolds number. Contact with a surface is assumed once the distance between the center of mass and a boundary becomes less or equal to the radius of the sphere.

This work used the existing infrastructure of the FLUENT DPM as the foundation for a numerical model for tracking ellipsoidal fibers in general laminar shear flows. A series of User Defined Functions (UDF) were incorporated to alter the behavior of the particles from that of a sphere to that of an ellipsoid. The dynamic Reynolds dependent drag was expanded to include a dynamic shape factor. Equations of rotational motions were solved to predict the instantaneous orientation of the ellipsoid at each time step.

The computational model was shown to simulate the period theoretically predicted by Jeffrey (1922) and simulated by Asgharian and Anjilvel (1995a) when an ellipsoidal fiber was subjected to a linear shear with their translation suppressed. The flow field inside a horizontal pipe with circular cross-section was evaluated numerically with ANSYS FLUENT. Spherical and ellipsoidal fibers were tracked in the simulated flow field. Sedimentation rates for ellipsoidal fibers agreed favorably with the experimental findings and that of equivalent sphere diameter particles as defined by Fan and Ahmadi (1995). The sedimentation rates for ellipsoidal fibers under various conditions studied all collapsed onto a single curve and an empirical, expression was proposed when plotted against the parameter suggested by Asgharian and Anjilvel (1995b).

2. INCOMPRESSIBLE FLOW EQUATIONS

The conservation of mass and momentum equations for steady, laminar, incompressible flows are defined as follows.

In Equations (1) and (2) u is the three-dimensional (3D) fluid velocity vector, ρ is the constant density of the fluid, and ν is the constant kinematic viscosity.

The commercial package ANSYS FLUENT was used to numerically solve Equations (1) and (2). ANSYS FLUENT employs a finite volume algorithm. Discretization of the conservation equations was performed with the upwind scheme to a second order accuracy, pressure-velocity coupling was performed with the SIMPLE scheme, and derivatives were computed via the Green-Gauss Node Based method (ANSYS FLUENT, Fluent User's Manual, 2007).

3. LAGRANGIAN PARTICLE TRACKING

3.1 Spherical Particles

A direct Lagrangian approach was used to track individual particles in dilute concentrations. For spherical particles, position and velocity were obtained by integrating the following equations of motion.

Here, x represents the three coordinates of the particle position vector and v is the 3D particle velocity vector.

The terms on the right-hand side of Equation (4) represent the drag, lift, and acceleration of gravity per unit mass. Drag is dynamic and dependent on particle Reynolds number and defined as (Hinds 1982)

In Equation (5) C_D is the drag coefficient, Re _p is the particle Reynolds number, u—v is the difference between particle and fluid velocities also known as slip velocity, and τ is the particle relaxation time that can be defined as

Here S is the solid-to-fluid density ratio, d is the diameter of the particle, ν is the kinematic viscosity of the fluid, and C_C is the Cunningham slip correction factor that can be defined as follows.

Here λ is the mean free path of the fluid.

Saffman (1965) provided an expression for the shear-induced lift on a small sphere to be given as

In Equation (8) K = 2.594 is the constant coefficient of Saffman lift force and d_ij is the components of the deformation rate tensor.

3.2. Ellipsoidal Fibers

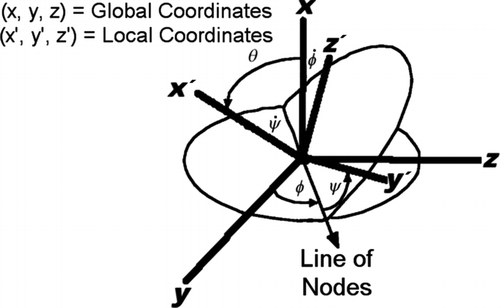
Before discussing the motion of a fiber, it is imperative to introduce two independent coordinate systems as shown in Figure 1. The global coordinate system (x, y, z) is fixed in space while the local coordinate system (x′, y′, z′) is fixed on the fiber and will translate and rotate with the fiber. Orientation of the local coordinate system and thereby the fiber with respect to the global coordinate system is defined in terms of three angles (φ, θ, ψ) known as Euler's angles. Figure 1 shows how the two coordinate systems are related by Euler's angles. The rotational motion of the fiber can now be derived from the time rate of change in the Euler angles.

FIG. 1 Relationship between local and global reference frames.

The equations of translational and rotational motions of rigid fibers are coupled and are given as

Equation (9) describes the translational motion and is similar to that of a sphere. The forces on the right-hand side of Equation (9) are hydrodynamic drag (F_D ), shear-induced lift (F_L ), and gravity. Equation (10) describes the rotational motion of the fiber that is generated by the hydrodynamic torque (T_h ) exerted on a fiber.

The hydrodynamic drag is a dynamic function dependent on the orientation of the fiber and its Reynolds number. It can be defined mathematically as

Here d is the cross-sectional diameter or minor axis of the fiber and K is the translational dyadic, sometimes referred to as the resistance tensor, and its elements are defined in the particle reference frame as follows (Asgharian and Anjilvel 1995a).

Here β is the major axis-to-minor axis aspect ratio, and the components are placed along the diagonal of the translational dyadic as follows.

K′ can be transposed into the global frame (i.e., K) with the basis transformation as shown

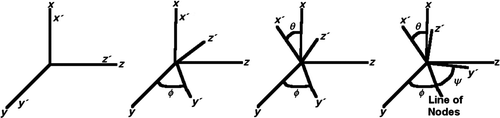
In Equation (14), A is the direction cosine matrix (DCM). The DCM is obtained by multiplying three matrices representing three consecutive rotations about an axis. For the purposes of this formulation an x-y-x convention was assumed. The three consecutive rotations are sketched in Figure 2. With this convention the total rotation of the ellipsoid is represented by a rotation of φ about the x-axis in the initial frame, followed by a rotation θ about an intermediate y-axis (line of nodes), finishing with a rotation of ψ about the x′-axis in the final reference frame. The DCM is then written in Equation (15) for the x-y-x convention (Goldstein 1980; Hughes 1986). That is,

The DCM, A, depends on fiber orientation. To determine orientation, the rotational motion must be analyzed. The hydrodynamic torques are given by

FIG. 2 Intermediate rotations that make a single fiber rotation with the x-y-x convention.

In Equations (16)–(18), ω_i is the components of angular velocity; η, ξ, and ζ are the components of vorticity; d_ij is the components of the deformation rate tensor; and α ₀ and γ ₀ are dimensionless constants. The vorticity and deformation rate quantities are defined in the global frame as

The fluid angular velocity components are

Equations (19)–(27) can be transformed into the particle frame, as needed, by Equation (14). The angular velocity components were defined in the particle frame by Asgharian and

Anjilvel (1995a) to be

The moment of inertia tensor is

with components along the and transverse to the fiber polar axis being

And the dimensionless parameters α ₀ and γ ₀ were defined by Asgharian and Anjilvel (1995a) to be

After substituting Equations (19)–(35) into Equations (16)–(18) and considerable simplification, the angular acceleration components can be expressed as follows.

For an ellipsoid of revolution suspended in a simple shear flow, the shear-induced lift can be expressed as follows.

In Equation (39), L is the lift coefficient matrix described by Fan and Ahmadi (1995) as

FIG. 3 2D illustration of the location of the interception point on an ellipsoid.

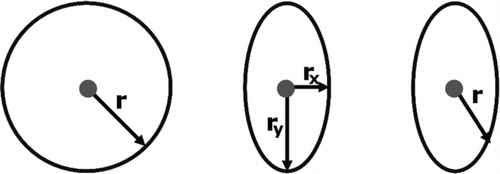
Determining interception between an ellipsoid and a plane is both a function of the ellipsoid's orientation and the distance from the plane. The distance is defined by the radius vector in the particle frame. Figure 3 shows a two-dimensional sketch defining the radius vector. To determine the radius vector first, define a unit vector pointing out from the center of mass of the fiber. This vector will sit on a unit sphere about the center of mass. If this vector is scaled by the semiminor and semimajor axes of the ellipsoid, the vector will point from the center of mass to a point on the ellipsoid surface. The point at which the vector meets the ellipsoid surface is the interception point. If the unit vector is taken to be the inverse of the unit normal of the plane and the distance between the plane and the center of mass of the fiber is less or equal to the magnitude of the radius vector, the fiber will intercept the plane (i.e., deposition has occurred).

4. MODEL IMPLEMENTATION

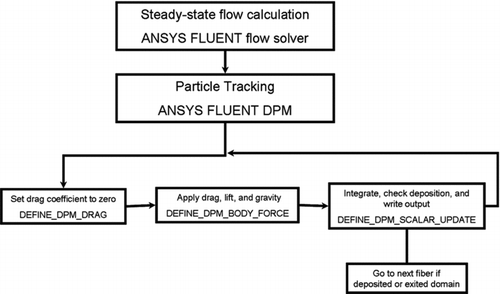
A series of three UDF's were developed for ANSYS FLUENT to perform the calculations of fiber motion. Figure 4 shows a flow chart of the process from flow solution to fiber trajectory. Because of the one-way coupling assumption fiber tracking could be treated as a postprocessing step. The flow field need not to be updated after trajectory iterations.

FIG. 4 Flow chart of the process by which fiber trajectories were computed.

The ANSYS FLUENT default drag coefficient assumes that the particle is spherical. This was set to zero so a nonscalar drag could be applied. This was done by returning 0.0 with the DEFINE_DPM_DRAG macro. This macro was called once per iteration.

Drag was applied as a 3D body force. The results of Equation (11) were returned componentwise from the DEFINE_DPM_BODY_FORCE macro. This macro was called once per component per iteration.

The DEFINE_DPM_SCALAR_UPDATE macro was used for a number of bookkeeping items. Equations (36)–(38) were integrated to update the Euler angles at every iteration. This update was necessary to provide the appropriate orientation for Equation (11). Within this same macro the distance from a wall boundary was checked if the fiber was located in a cell that touched a wall boundary and position, velocity, and orientation were written to an output file. This macro was called once per iteration.

5. ROTATIONAL MOTION

To validate the computation of rotational motion in this model, a series of simulations were performed that subjected an ellipsoidal fiber to a simple shear flow. Particular attention was given to the examination of the predicted rotational periods of the ellipsoids and their comparison against the theoretical model of Jeffrey (1922) and the simulations of Asgharian and Anjilvel (1995a). The results of these simulations are presented in this section.

To establish a linear shear flow, a 3D configuration between two parallel plates shown schematically in Figure 5 was prepared in GAMBIT for use in ANSYS FLUENT. The domain was 2 mm tall (y-direction), 2 mm wide (x-direction), and 5 mm long (z-direction). The sides of the channel that are in the yz-plane were modeled with a specified shear of zero. Velocity values were extrapolated from within the domain to the exit plane that was held at a constant static pressure. A linear shear velocity profile was applied to the inlet surface. The top wall was set to translate with constant velocity equal to the maximum value along the inlet profile, while the bottom wall remains stationary. The no-slip boundary condition was imposed on the top moving wall and stationary bottom wall. Steady state flow fields for different top wall velocities were evaluated.

FIG. 5 Translating flat plate over a stationary flat plate to induce a linear velocity profile in the interspatial air.

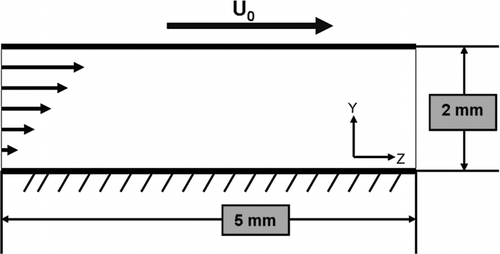
The velocity of the top wall (U ₀) was varied from 0.02 to 2 cm/s to examine the effects of shear rate on fiber rotational period. A single ellipsoidal fiber was placed at the center of the channel for different generated steady simple shear flow fields. The fiber was allowed to rotate, but the drag, lift, and gravitational sedimentation were set to zero to prevent translation. Three aspect ratios of 5, 10, and 15 were examined. The mass of the fiber was varied by examining a range of diameters from 1 to 100 μm and densities from 1 to 10 g/cm³.

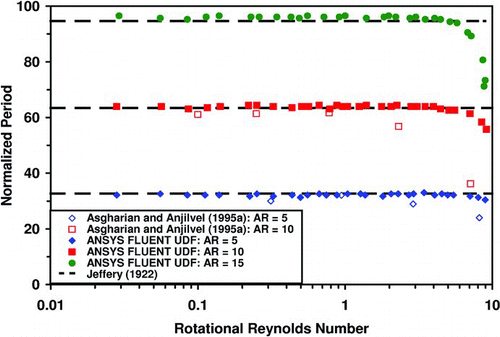
Jeffrey (1922) analyzed the motion of an ellipsoidal fiber under a constant velocity gradient condition. He showed that under this condition the rotational period was scaled with the velocity gradient. This resulted in a dimensionless period (T*) that was shown to vary with the fiber aspect ratio. This period was presented as

Using a computational model, Asgharian and Anjilvel (1995a) showed fibers with negligible inertia to rotate with the period predicted by Equation (41). They defined a rotational Reynolds number to account for the particle cross-sectional diameter (d), density (ρ), fluid dynamic viscosity (μ), and magnitude of the constant velocity gradient (G). That is,

Figure 6 shows the present simulated rotational period of the particle as a function of the rotational Reynolds number. Also shown are the predicted period given by Equation (41) and the earlier simulations of Asgharian and Anjilvel (1995a). Simulations performed with the ANSYS-FLUENT UDF developed here agreed quite well with the independent code developed by Asgharian and Anjilvel (1995a) and the theoretical values of Jeffrey (1922) for the range of interest. Both sets of simulated data show a decrease in rotational period at the higher end of rotational Reynolds number. Asgharian and Anjilvel (1995a) explained this to be an effect of inertia. They also showed that if the rotational Reynolds number were increased further the period would reach a minimum then increase in the limit that the rotational Reynolds number becomes very large.

FIG. 6 Simulated rotational period as a function of Rotational Reynolds number at 3 aspect ratios.

Given the close agreement of the simulated rotational period to the theoretical period and the similar trends published in Asgharian and Anjilvel (1995a), it can be concluded that the developed model can accurately predict the rotational motion of an ellipsoid suspended in linear shear flows.

6. MOTIONS OF A FIBER IN A VISCOUS FLUID

The anisotropic shape of a fiber will cause motions that markedly depart from that of a sphere when released in a moving viscous fluid. Fluid vorticity acts on the elongated body causing the fiber to tumble as it translates. This section discusses the motions of a fiber when released in the center plane of a horizontal tube with circular cross-section.

A horizontal tube geometry was prepared and meshed in GAMBIT for use in ANSYS FLUENT. The tube was 792 mm long with an inner diameter of 4.05 mm. The walls of the tube were taken to be rigid and smooth with a no-slip boundary condition. Two flow rates corresponding to Reynolds numbers of 150 and 450 were examined where Re = U ₀ d/ν. A schematic diagram of the computational domain is shown in Figure 7.

FIG. 7 Horizontal tube with circular cross-section; parabolic velocity profile imposed at the inlet surface.

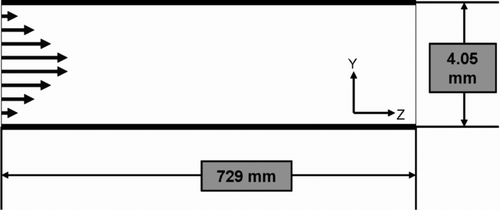
FIG. 8 Axial velocity contours along the center plane of the horizontal tube; Re = 150 (top) and Re = 450 (bottom).

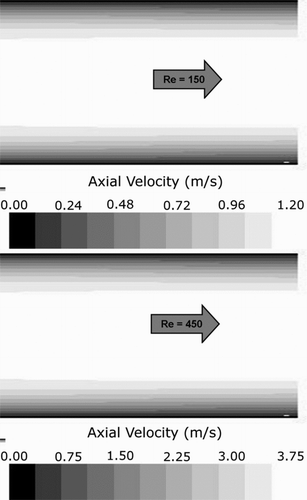
A parabolic velocity profile was imposed at the inlet surface and the outlet was maintained at a constant 0 Pa static gage pressure. Flow field variables were solved numerically within the domain using the ANSYS FLUENT code (Fluent User's Manual, 2007). Figure 8 shows contours of axial velocity along the center plane of the tube. Consistent with typical pipe flow, the axial velocity reaches a peak at the center and decays with the square of the radius to zero at the walls.

FIG. 9 Direction cosines as a function of time for a fiber with aspect ratio of 5 released a half radius above and a half radius below the center line in the center plane of the tube with Re = 150.

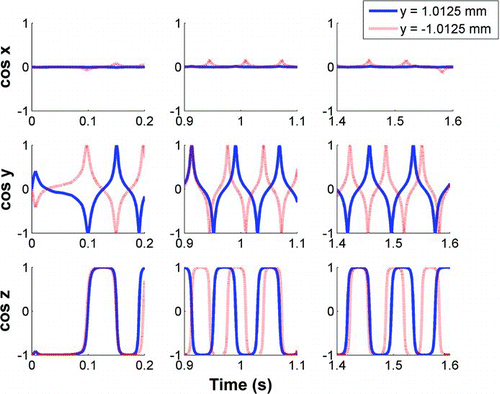
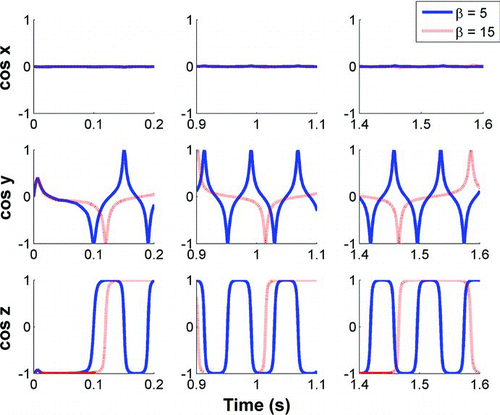
FIG. 10 Direction cosines as a function of time for a fiber with aspect ratio of 5 and aspect ratio 15 released a half radius above the center line in the center plane of the tube with Re = 150.

Three numerical experiments were conducted to examine the motions of individual fibers. The results of these experiments are shown in Figures 9–11. In each experiment, two fibers were released in the center plane of the tube. The two fibers were used to vary in injection location, aspect ratio, and flow rate. Direction cosines, as functions of time, were used to record the motions of the fibers (Figures 9–11). The three direction cosines for the fiber are the cosine of the angle made between the fiber's semimajor axis and the x-axis, y-axis, and z-axis, respectively. A cosine of zero indicated that the fiber was perpendicular to the axis, while a cosine of one indicated that the fiber was parallel with the axis.

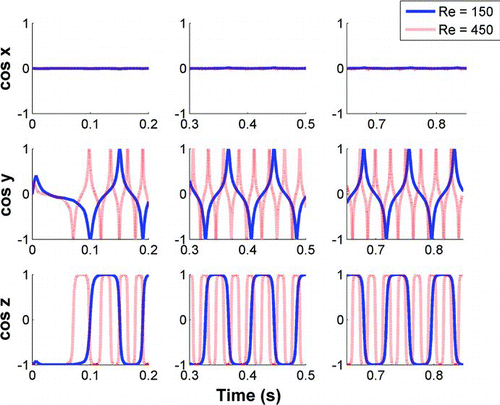
FIG. 11 Direction cosines as a function of time for a fiber with aspect ratio of 5 released a half radius above the center line in the center plane of the tube with Re = 150 and Re = 450.

In general, the fibers tended to remain parallel with the direction of flow (i.e., x and y direction cosines were nearly zero with z-direction cosines nearly ±1 in Figures 9–11). Rotations happened suddenly. This can be observed in Figures 9–11 by the sudden switch from 1 to −1 (or −1 to 1) in z-direction cosines and the sharp spikes to ±1 in y-direction cosines. This indicates that once enough torque was present to perturb the fiber off of the initially assumed equilibrium state, the fiber was destabilized, rotated 180°, and a new quasi-equilibrium was achieved. Since the center plane of the tube was normal to the x-axis, the x-direction cosines remained zero for each of the experiments conducted.

Figure 9 shows the direction cosines of two fibers released in the center plane of the tube. One was released a half radius above the center and the other was released a half radius below the center. The fibers are initially rotated in opposite directions because the direction of the shear gradients are opposite above and below the center of the tube. Time between rotations was very similar for the two fibers. As time progressed, however, the effect of gravity was observed. The fiber released above the center was pulled toward the center by gravity, into smaller shear gradients. This caused the time between rotations to lengthen. Conversely, the fiber released below the center was pulled away from the center by gravity, into larger velocity gradients. This caused the time between rotations to shorten. Both y and z direction cosines show a small phase shift in Figure 9 as time progresses.

The effect of aspect ratio was examined by releasing fibers with aspect ratio of 5 and 15 a half radius above the center into the flow field with Re = 150. The direction cosines of these fibers as they translate along the center plane of the tube are shown in Figure 10. More torque was required to rotate the larger fiber. This is why Figure 10 shows a longer time for the fiber with aspect ratio 15 to rotate than the fiber with aspect ratio 5.

Figure 11 shows the direction cosines of a fiber with aspect ratio 5 released a half radius above the center under flow conditions of Re = 150 and Re = 450. The fiber released into the flow field with Re = 450 rotated more frequently. This is due to the larger shear gradients present in the faster moving flow.

7. DEPOSITION IN A HORIZONTAL TUBE

When injected to a moving, bounded flow field in the presence of gravity, a small ellipsoidal fiber will translate and either escape the domain or deposit on the tube wall. To validate the accuracy of the developed model under these conditions, sedimentation rate in the horizontal tube domain was computed. Rates of gravitational sedimentation were compared with the earlier work of Asgharian and Anjilvel (1995b). These results are presented in this section.

To examine the deposition rate of fibers in the horizontal tube configuration discussed above a lattice of equal-spaced fibrous particles was released at the inlet surface with random orientations. This resulted in the release of 6375 particles per trial. Each particle was tracked individually, and trials were conducted for diameter 0.5, 1, 1.5, and 2 μm with aspect ratio ranging from 4 to 24. The same procedure was repeated for spheres with the equivalent diameter computed with the suggested approach of Fan and Ahmadi (1995). They suggested the equivalent diameter of a fiber to be

FIG. 12 Sedimentation efficiency as a function of aspect ratio for ellipsoidal fibers and equivalent sphere diameter particles as computed by Equation (43).

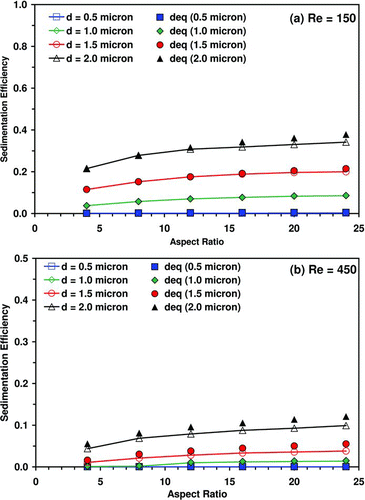
Figure 12 shows the sedimentation rate as a function of aspect ratio for ellipsoidal fibers released in the horizontal tube setup. Also shown in Figure 12 are sedimentation efficiencies for equivalent sphere particles, the diameter of which are computed by Equation (43). Favorable agreement was observed for fibers and equivalent spheres. Sedimentation increased with aspect ratio. This was due to the fact that fiber mass increased with aspect ratio. Minor differences were observed between fibers and equivalent spheres at higher aspect ratios. This could indicate that Equation (43) is appropriate for certain sized fibers but not for all. Sedimentation was also seen to decrease with increasing Reynolds number. This is due to the reduced residence time with higher flow rate.

TABLE 1 Coefficients for Equation (23) (Asgharian and Anjilvel 1995b)

N	cn
0	−0.844
1	14.400
2	−22.409
3	16.586
4	−5.669
5	0.726

Asgharian and Anjilvel (1995b) showed fiber sedimentation in a straight circular airway to vary with dimensionless relaxation, fiber aspect ratio, and inclination angle of the airway. They proposed the following relationship

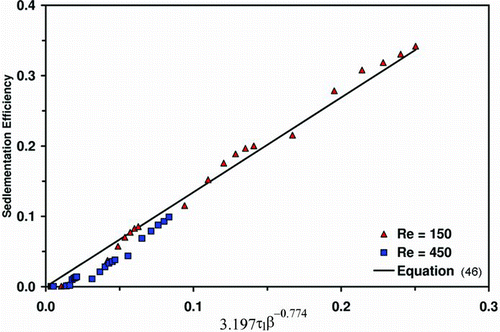
In Equation (44), c_n are constants defined in Table 1, α is the inclination angle of the tube, and τ ₁ is the dimensionless relaxation defined as

Here U is a characteristic velocity. All of the simulations conducted here were done with the tube in a horizontal alignment (α = π/2).

Figure 13 shows the simulated sedimentation efficiency of fibers in the horizontal tube across all aspect ratios and fiber diameters under flow rates with Re = 150 and Re = 450. The simulation data collapse approximately onto a single curve that can be curve fitted with the following simple expression:

FIG. 13 Sedimentation efficiency as a function of aspect ratio and particle relaxation time.

Close agreement with the earlier prediction of Asgharian and Anjilvel (1995b) indicates that the proposed augmentation to the ANSYS FLUENT DPM is capable of accurately predicting the transport and sedimentation of ellipsoidal fibers.

8. CONCLUSIONS

A computational model for simulating the rotational and translational motions of an ellipsoidal fiber was developed. Two shear flow conditions were simulated to validate the model. First, a single particle was subjected to a constant linear shear flow and allowed to rotate without translation. The model was shown to simulate a rotational period similar to the predicted period of Jeffrey (1922) and the simulations of Asgharian and Anjilvel (1995a). Next, flow through a horizontal straight pipe was numerically simulated. Ellipsoidal fibers were injected into the resulting steady flow fields, and the motions and sedimentation were evaluated. The following conclusions may be drawn from the results presented here:

•	Normalized rotational period of an ellipsoidal fiber was a function of its aspect ratio and the developed model was able to accurately predict the period.
•	Gravity was able to shift the path of fibers enough to alter the period with which they rotated while translating through the horizontal tube.
•	Sedimentation rate of fibers increased with aspect ratio and relaxation time but decreased with flow rate.
•	The developed empirical curve fit model given by Equation (46) is suitable for predicting the sedimentation rate of fibers in a circular tube.
•	The developed model was able to accurately predict the translation, rotation, and sedimentation of ellipsoidal fibers in laminar viscous shear flows.

Nomenclature

Latin Symbols	=
a	=	Semiminor axis of an ellipsoid
a+	=	Dimensionless semiminor axis of an ellipsoid
A	=	Direction cosine matrix
b	=	Semimajor axis of an ellipsoid
b+	=	Dimensionless semimajor axis of an ellipsoid
cn	=	Constant coefficients in Equation (23)
CD	=	Drag coefficient
dae	=	Aerodynamic diameter (m)
dev	=	Diameter of an equivalent volume sphere (m)
df	=	Fiber cross-sectional diameter (m)
dij	=	Deformation rate tensor
Eff	=	Sedimentation efficiency
f d	=	Drag force on a sphere per unit mass
f l	=	Lift force on a sphere per unit mass
FD	=	Drag force on an ellipsoid
FL	=	Lift force on an ellipsoid
G	=	Magnitude of linear velocity gradient
g	=	Gravitational acceleration (m/s2)
IM	=	Moment of inertia tensor
K	=	Saffman lift force = 2.594
K	=	Translational dyadic
m	=	Mass of fluid (kg)
mp	=	Mass of particle (kg)
Re	=	Fluid Reynolds number
Re p	=	Particle Reynolds number
Re R	=	Rotational Reynolds number
S	=	Solid-to-gas density ratio
T*	=	Normalized rotational period
Th	=	Hydrodynamic torque
t	=	Time (s)
u	=	Local fluid velocity (m/s)
U	=	Characteristic velocity (m/s)
U 0	=	Velocity of translating plate (m/s)
v	=	Instantaneous particle velocity (m/s)
x, y, z	=	Position coordinates of particle center of mass (m)
Greek Symbols	=
α	=	Inclination angle
α 0	=	Dimensionless parameter
β	=	Aspect ratio
δ	=	Distance of fiber center of mass from a wall (m)
ϕ, θ, ψ	=	Euler angles (rad)
γ 0	=	Dimensionless parameter
η, ξ, ζ	=	Vorticity components
κ	=	Dynamic shape factor
κ ∥	=	parallel to a wall
κ⊥	=	normal to a wall
κR	=	randomly oriented
μ	=	Dynamic viscosity (kg/m/s)
ν	=	Kinematic viscosity (m2/s)
ρ	=	Fluid density
ρp	=	Particle density
ρf	=	Particle density
ρ H2O	=	Density of water
τ	=	Particle relaxation time (s)
τ +	=	Dimensionless particle relaxation time
τ 1	=	Ratio of particle relaxation time
ω	=	Angular velocity (rad/s)

Acknowledgments

The financial support of the National Institute for Occupational Safety and Health (NIOSH) through Grant R01 OH003900 and the Environmental Protection Agency (EPA) under grant 916716 is gratefully acknowledged.

This work has not been subjected to either Agency's required peer or policy review and therefore does not necessarily reflect the views of the agencies and no official endorsement shall be inferred.