Thermophoresis of a Spherical Particle: Reassessment, Clarification, and New Analysis

Abstract

The thermophoretic force acting on a spherical particle depends on the Knudsen number and the particle-to-gas thermal conductivity ratio, and it can be estimated using various analytical and numerical methods for solving the Boltzmann equation. A substantial body of experimental data also exists. Nevertheless, the situation is not as clear as it might be and this article assesses the current predictive capabilities. First, some issues of nondimensionalization and data presentation are discussed. Then, the Grad 13-moment (G13) method of solution is examined in detail, and it is shown how the method generates a hierarchy of expressions for the thermophoretic force at low Knudsen number including all the well-known results. The non-Navier–Stokes–Fourier thermal stress and pressure-driven heat flux and their relation to the phenomenon of reversed thermophoresis are discussed. Theories of thermophoresis at arbitrary Knudsen number are then examined and it emerges that there are essentially only two theories extant. The available experimental measurements of the thermophoretic force and velocity are compared with these theories. Finally, it is shown that the G13 solution can be adapted to provide an interpolation formula for the transition regime, which gives a good approximation for practical calculations and is quantitatively very different from the commonly used prescription.

1. INTRODUCTION

Small particles suspended in a gas with a nonuniform temperature field experience a force whose direction is usually opposite to that of the local temperature gradient (i.e., from hot to cold). The phenomenon is known as thermophoresis and was first described by Tyndall (1870) who noticed the formation in a dusty atmosphere of a dust-free zone near a heated surface. Shortly afterward, Maxwell (1879) postulated a theory of gaseous thermal creep at a flat solid surface along which there was a temperature variation. Half a century later Epstein (1929) incorporated Maxwell's work into a theory for the thermophoretic force experienced by a spherical particle in a gas with a temperature gradient.

In the second half of the twentieth century, there were major theoretical and experimental advances and two central issues emerged. One was the problem of modeling the thermophoretic force for particles so small that the surrounding gas could no longer be treated as a continuum, and the second was the effect of the thermal conductivity of the particle itself.

The noncontinuum regimes are characterized by the particle Knudsen number Kn, defined here as the ratio of the mean free path of a gas molecule to the radius of the particle. Theories were readily forthcoming from Epstein (1929) for the continuum regime (Kn ≪ 1), Brock (1962) for the slip-flow regime (Kn ∼ 0.1), and Waldmann (1959) for the free-molecule regime (Kn ≫1). Unsurprisingly, however, the transition regime proved much more difficult to model. For practical calculations, Talbot et al. (1980) proposed an interpolation formula that has been widely used in many applications. However, there is now evidence to suggest that it may be quite seriously deficient in the slip-flow and transition regimes.

The evidence comes from theoretical studies of the effect of the particle thermal conductivity on the thermophoretic force. When the particle-to-gas thermal conductivity ratio is high, the thermal creep velocity tends to zero (because the particle is at near-uniform temperature) and a higher-order effect known as the thermal stress slip flow takes precedence. This results in a force whose direction is the same as that of the temperature gradient (i.e., from cold to hot). “Reversed” thermophoresis was first predicted by Dwyer (1967) but it has never been demonstrated experimentally. More recent theoretical work by Beresnev and Chernyak (1995) suggests that the effect may not be as pronounced as previously suspected.

Although accurate measurements of the thermophoretic force on a particle are difficult to obtain, a substantial body of experimental data is now available in the literature. Unfortunately, the accuracy of the data and the range of Knudsen number embraced are insufficient to provide confirmation of any of the theories. A number of review articles have also been published (Talbot et al. 1980; Bakanov 1991; Zheng 2002) but the situation is still not as clear as it might be. The purpose of this article is therefore to supply clarification, physical insight, and an improved theoretical basis for calculations. We start with some dimensional analysis that, although fundamental, has not appeared in the literature before.

2. GENERAL CONSIDERATIONS

2.1. Dimensionless Forms for the Thermophoretic Force and Velocity

Consider a monatomic perfect gas of infinite extent flowing with uniform velocity U ₀=U ₀ e _z , where e _z is a unit vector in the z-direction. In the gas, there is a uniform temperature gradient ∇T ₀=G ₀ e _z . A spherical particle of radius a is placed in the gas and is held stationary with its center at a point where the undisturbed temperature, pressure, density, mean free path, dynamic viscosity, and thermal conductivity are T ₀, p ₀, ρ ₀, l ₀, μ ₀, and k ₀ respectively. We define the mean free path via the kinetic theory expression:

but note that several alternative definitions have been used and it is important to apply the relevant conversion factors where necessary. For a monatomic gas, k ₀ and μ ₀ are related by

where R is the gas constant per unit mass. Equation (2) is consistent with a Prandtl number of 2/3 and a specific heat ratio of γ = 5/3.

Under the conditions defined earlier, experimental observations show that a force F=F e _z acts on the particle. Assuming that F depends on the variables a, G ₀, U ₀, T ₀, ρ ₀, l ₀, μ ₀, k ₀, and the particle thermal conductivity k_p , dimensional reasoning shows that

We define the flow Reynolds number by Re=aρ₀|U ₀|/μ₀, the Knudsen number by , and the conductivity ratio by Λ=k_p /k ₀. The group a|G ₀|/T ₀ does not have a name, so we shall call it the “Epstein number” Ep in honor of Paul Epstein who was the first to publish a theory for the thermophoretic force on a spherical particle. We now assume that Ep and Re are sufficiently small that the force is linearly dependent on them and write

where and . The terms on the right are the signed magnitudes of dimensionless thermophoretic force F _T and viscous drag F _D .

The linear approximation of Equation (4) is only acceptable if Ep ≪ 1 and Re ≪ 1. This may seem like a serious constraint but it is rarely so in practice. Consider, for example, the fairly extreme case of 5 μm radius particles entrained in the boundary layer of an air-cooled turbine blade of a jet engine. Here, the gas temperature may drop from a free-stream value of 1800 K to a blade surface temperature of 1100 K in a distance of around 2 mm. On the basis of the mean temperature, Ep = 5×10⁻⁶×(1800−1100)/(2×10⁻³×1450)=0.0012.

In the continuum limit Kn→0, Epstein showed that Φ is independent of Kn and is a negative function of Λ. In this limit, Equation (4) asserts that F _T and F _D are proportional to a and that F _T is negative (i.e., the direction of the thermophoretic force is opposite to that of the temperature gradient). In the free-molecule limit Kn→∞, experiments and theory show that F _T and F _D are directly proportional to a ² and F _T is again negative. Equation (4) then asserts that, in this limit, Φ and Ψ must vary with Kn ⁻¹. For Kn→∞, it is also found that Φ is independent of Λ. It is the form of Φ in the transition regime about which there is uncertainty, and this is particularly so for high values of Λ where Φ may possibly change sign.

The signed magnitude of the thermophoretic velocity U _T is defined as the value of U ₀ such that the total force on the particle is zero. From Equation (4), we obtain, in dimensionless form,

The thermophoretic velocity is not as fundamental a quantity as the thermophoretic force because it requires knowledge of the function Ψ. In passing, we note that thermal polarization (i.e., the differential heating of a moving particle due to the drag force) has only a tiny effect in the context of thermophoresis and we shall ignore it (Beresnev et al. 1990).

2.2. Presentational Issues

In published work, it is customary to present the thermophoretic force data in a dimensional form by plotting −F _T/a ² G ₀ against Kn for various parametric values of Λ. This method of presentation stems from the way in which experiments are normally conducted with varying temperature gradient but near constant values of T ₀. From the kinetic theory, the mean free path l ₀ is inversely proportional to the density and hence the product l ₀ ρ ₀ is independent of p ₀ at constant T ₀. The viscosity μ ₀ is also almost independent of p ₀. From Equation (4), we have

which shows that if a is varied but Kn is held constant by adjusting the pressure, −F _T/a ² G ₀ should remain constant. Hence, if the data are plotted as −F _T/a ² G ₀ against Kn, all points should fall on a single curve irrespective of the particle radius a (for a fixed value of Λ).

If, as noted earlier, Φ varies with Kn ⁻¹ as Kn→∞ and is also independent of Λ in this limit, Equation (6) shows that curves for different Λ should converge on a single value of −F _T/a ² G ₀ as Kn→∞. This is a useful test for experimental data. However, Equation (6) also shows that the values of −F _T/a ² G ₀ for different Λ all approach zero as Kn→0. This is because the product ΦKn tends to zero, even though Φ itself does not. Because of this behavior, the all-important way in which the curves for different Λ approach zero is obscured because the method of plotting makes it difficult to distinguish between them. This problem is evident in the vast majority of published articles. We avoid it here by focusing on the dimensionless function Φ rather than the dimensional group −F _T/a ² G ₀.

2.3. Accommodation Coefficients

The thermophoretic force depends on the mode of interaction of gas molecules with the particle. This complex phenomenon is normally modeled (following Maxwell) by assuming that a fraction α of incident molecules is reflected diffusely while a fraction (1−α) is reflected specularly. Different values α _m and α _e can be used for momentum and energy transfer so that the (positive) reflected momentum and energy fluxes and are given by

where and are the (positive) incident tangential momentum and kinetic energy fluxes, and is the (positive) reflected energy flux if the molecules were to achieve thermal equilibrium with the surface.

As defined, α _m and α _e lie between 0 and 1, and it is very difficult to predict or measure their actual values because these depend not only on the particle material and the gas molecules but also on the state of the surface. As it seems invidious to draw conclusions about the correctness of a theory by arbitrarily adjusting the accommodation coefficients to give a good match with experimental data, we shall always set α _m = α _e = 1. Indeed, most estimates of the coefficients tend to be fairly close to unity except for specially prepared surfaces. The reader is, of course, at liberty to use different values if he or she feels they are justified.

Some kinetic theorists are of the opinion that the Maxwell type of boundary condition is not a good physical model but the alternatives (Sone 2002) require the specification of a “scattering kernel,” which is quite unknown. Solid boundaries in the kinetic theory pose difficult problems because the true physical boundary condition involves a discontinuity between the incident molecular flux and the reflected (half Maxwellian) flux, whereas the field equations in their linearized form are continuous. Methods to overcome this difficulty have been proposed (Ivchenko et al. 2007) but they have yet to be applied to thermophoresis.

2.4. Thermal Creep, Velocity Slip, and Temperature Jump

Thermal creep occurs when there is a temperature variation along the particle surface. Under continuum flow conditions, there is an identical temperature variation in the adjacent gas layer (because the surface temperature jump tends to zero in the continuum limit). If the particle is stationary, the gas moves along the surface toward the hot region with a thermal creep velocity ΔU_tc given in dimensionless form by

where ∂T/∂s is the gas temperature gradient along the surface and ΔU_tc depends on the particle conductivity; as Λ→∞, the particle temperature becomes uniform and ΔU_tc →0. Using a simple kinetic theory, Maxwell found the value of the thermal creep coefficient K_tc to be 0.75, but more accurate values are now available based on the solutions of various model Boltzmann equations. Sharipov (2004) has collated the published data and cites values in the range 1.02–1.18 depending on the molecular collision model used in the calculations. A “working average” value is therefore around K_tc ≅ 1.10.

The surface velocity slip ΔU_slip is given by

where ∂u/∂n is the gradient of streamwise velocity normal to the surface. Using a simple kinetic theory, Maxwell obtained a value of  A_m = 1.0 but Sharipov (2004) cites more accurate values in the range 1.11–1.15 depending on the molecular collision model. ¹ A working average value is thus around A_m ≅ 1.13.

Table 1 Theoretical expressions for the functions Φ and Ψ. The current best estimates of the thermal creep, velocity slip, and temperature jump coefficients are K_tc = 1.10, C_m =1.13(2−α _m )/α _m , and C_e =2.17(2−α _e )/α _e

Authors and range of validity	Φ (Kn, Λ)	Ψ (Kn)
Kn → 0 (Epstein (1929) and Stokes (1851))		6π
(Brock (1962) and Bassett (1888))
(Waldmann (1959) and Epstein (1924))

The surface particle-to-gas temperature jump ΔT_jump is given by

where ∂T/∂n is the gas temperature gradient normal to the surface. For a monatomic gas, Maxwell obtained a value of A_e = 15/8 = 1.875 but Sharipov (2004) cites values in the range 2.13–2.21. A working average value is thus around A_e ≅ 2.17.

It is important to note that, unlike ΔU_slip and ΔT_jump , ΔU_tc does not tend to zero in the continuum limit.

3. EARLY ANALYTICAL THEORIES

Epstein (1929) attempted to derive an expression for the thermophoretic force in the continuum and slip-flow regimes and was the first to identify the importance of Λ at low Kn. However, Brock (1962) found that he had used an incorrect slip-flow boundary condition and had also (though unimportantly) neglected the convection terms in the energy equation. Correcting the boundary condition, Brock arrived at an expression that reduced to Epstein's as Kn→0. Both Epstein and Brock used Maxwell's value of K_tc = 0.75, and Brock also used the values of A_m and A_e accepted at the time. Hence, when assessing their results, it is important to substitute the more recent values. Brock also derived a slip-flow drag expression identical to the one obtained by Bassett (1888). These results are given in Table 1.

For the free-molecule regime (Kn ≫ 1), Waldmann (1959) derived an expression for the thermophoretic force that is still considered to be very reliable. He also derived an expression for the free-molecule drag force on a sphere, although the same result had been obtained much earlier by Epstein (1924). Their results are also given in Table 1.

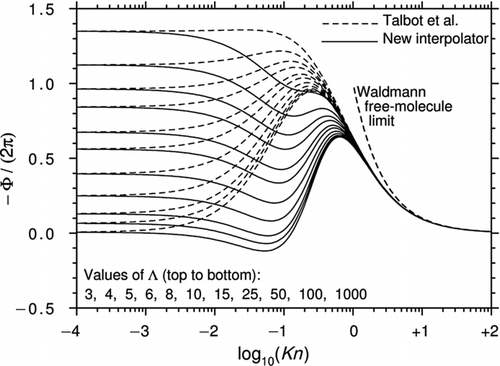
Brock's theory was only intended to model the slip-flow regime, but Talbot et al. (1980) noticed that by slightly adjusting the coefficients K_tc and C_m , the equation provided a good approximation to Waldmann's expression in the limit Kn→∞ (it is given exactly if K_tc = C_m ). It also gave values for transitional Knudsen numbers, which, at the time, seemed reasonable. This prescription has been widely used ever since. Figure 1 shows how Φ varies with Kn and Λ for the Talbot et al. prescription with α _m =α _e =1.

Figure 1 Curves of −Φ/(2π) plotted against log₁₀(Kn) for various Λ using the interpolation formula of Talbot et al. (1980) with α_m = α_e = 1. All curves asymptote to Epstein's continuum limit as Kn→0.

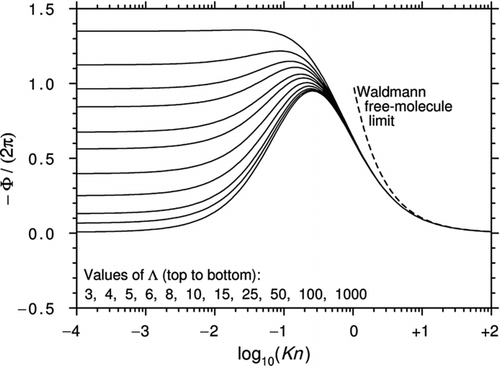
The curves in Figure 1 seem plausible but it is important to remember that the Talbot et al. prescription is not based on physical principles. Indeed, a number of studies have suggested that at high Λ and low Kn, the direction of the thermophoretic force may actually be reversed. Reversed thermophoresis was first predicted by Dwyer (1967) and Sone (1972) but it has never been demonstrated experimentally.

Briefly, when Λ ≫ 1, the particle temperature is almost uniform and Maxwell's thermal creep flow is negligible. Then, the thermal stress slip flow, a higher-order effect sometimes known as the “second mechanism of thermophoresis,” determines the flow field and the force on the particle is in the opposite direction (i.e., from cold to hot).

Most calculations that predict reversed thermophoresis are complex solutions of model Boltzmann equations but Dwyer's theory is based on the Grad 13-moment (G13) method and has an explicit solution. Nevertheless, the result is seldom if ever used, probably because the analysis is quite difficult to follow and there was no attempt to clean it up. However, it would be wrong to ignore the theory. Recently, Struchtrup (2005) has clarified the status of the G13 method and its application provides a crucial extension to Brock's theory. Using a more transparent approach, we now consider in detail the solution based on the G13 method.

4. SOLUTION USING THE G13 METHOD

4.1. Governing Equations

Consider a monatomic perfect gas and let f=f(c_i , x_i , t) be the molecular velocity distribution function dependent on the molecular velocity c_i , the position vector x_i , and the time t. In cartesian tensor notation with the summation convention, the Boltzmann equation is given by

where S is the source term due to collisions. If m is the mass of a molecule and d c is a volume element in velocity space, f is defined such that the local density is given by

where the integration is taken over the whole of velocity space. The mean velocity u_i is then defined by

The peculiar velocity is defined by C_i =c_i −u_i and the temperature T is given by

where θ=RT. The pressure tensor P_ij is defined by

and the scalar pressure p is one third of its trace,

The trace-free part of the pressure tensor (which Struchtrup calls the stress tensor) is

where δ _ij is the unit tensor. Finally, the heat flux vector q_i is defined by

The 13 moment equations are obtained from Equation (11) by successively multiplying by m, mc_i , mc ²/2, mc_ic_j , and mc ² c_i /2, integrating over velocity space and identifying the macroscopic terms defined in Equations (12). This gives a mass conservation equation, three component equations for momentum conservation, one for energy conservation, five evolution equations for the independent components of the stress tensor, and three for the components of the heat flux vector. The procedure, assumptions, and range of applicability are discussed in Struchtrup (2005), where the resulting equations are labeled (6.4), (6.13), and (6.14). In terms of p rather than ρ, the full set for a monatomic gas (γ = 5/3) is

where D/Dt=∂/∂t+u_k ∂/∂x_k . In Equation (13d), there are three symmetric, traceless tensors denoted by an angular bracket shorthand notation. When written out in full, these are given by

where w_i stands for u_i or q_i and

Equations (13) have been derived using the so-called ellipsoidal statistical Bhatnager, Gross, Krook model (ES-BGK) model for the source term S in Equation (11). This model is discussed in Struchtrup (2005) and results in the factor of 2/3 appearing on the right-hand side of Equation (13e). If the original BGK model (Gross and Jackson 1959) is used, an incorrect factor of unity is obtained.

In recent years, the G13 method has been extended by “regularizing” the closure conditions (Struchtrup 2005). The regularized 13-moment (R13) method can capture, at least partially, Knudsen layers adjacent to solid surfaces. The G13 equations cannot do this and hence Knudsen layers appear as discontinuous jumps. However, as the R13 equations are much more complex to solve than the G13 equations, we shall not use them here.

We now nondimensionalize and linearize Equations (13). For the reference length, we use the particle radius a and for the reference velocity, we take our cue from Equation (8) and define u_ref =μ₀|G ₀|/(ρ₀ T ₀). It is now clear that the Epstein number Ep=a|G ₀|/T ₀= aρ₀ u_ref /μ₀ represents the Reynolds number of the thermally driven flow. We also define and . Denoting dimensionless variables by a caret, we have

Details of the nondimensionalization and linearization are given in Appendix 1, where it is shown that for Kn < 1 the only requirement for linearization is Ep≪1. The G13 equations are accurate to Kn ² (Struchtrup 2005), so we might expect a linearized analysis to be valid for . In dimensionless form, the linearized equations are

Equations (14a)–(14c) are simply the mass, momentum, and energy conservation equations for low Reynolds number continuum flows. The final terms of Equations (14d) and (14e) represent respectively the thermal stress and the pressure-driven heat flux and these do not appear in the Navier–Stokes–Fourier (NSF) formulation. The form of the thermal stress is better appreciated by substituting Equation (14d) into Equation (14e) to give (in dimensional form)

At this point, we mention a theory of thermophoresis by Cha and McCoy (1974). These authors based their analysis on the linearized Burnett equations, which are identical to Equations (14). However, Cha and McCoy made the drastic assumption that the “the suspended particle does not substantially distort the temperature distribution in the gas” and hence the temperature varies only in the direction of the background temperature gradient. They then solved for this temperature distribution and calculated the force on the sphere as if it were entirely due to the thermal stress. It will emerge later that this reasoning is fundamentally incorrect.

4.2. Solution of the Equations

Substituting Equation (14d) into Equation (14b), differentiating with respect to x_i and using Equations (14a) and (14c), we obtain (switching to vector notation)

where is ∇ based on dimensionless lengths. Differentiating Equation (14e) with respect to x_i and using Equations (14c) and (15a) gives

Differentiating Equation (14e) twice with respect to x_k and using Equations (15a) and (15b) gives

Substituting Equation (14d) into Equation (14b) and using Equations (14a), (14c), and (15c) gives

The thermal stress completely disappears from the equation of motion, although it is still present in Equation (14f) for the stress tensor.

We solve Equations (15) in the (r, θ, φ) spherical polar coordinate system shown in Figure 2. The imposed temperature gradient is in the z-direction (z=rcos θ, G ₀=dT ₀/dz) and for generality, we include an imposed free-stream velocity U ₀ also in the z-direction. The problem exhibits axial symmetry about the z-axis (∂/∂φ=0).

Figure 2 The spherical polar (r, θ, φ) coordinate system used for the G13 analysis. There is axial symmetry around the z-axis (∂/∂φ=0).

In dimensionless form, the far-field boundary conditions are

and the condition of zero normal velocity at the surface of the sphere is

The solution of Equations (15a) and (15d) is the same as that for Stokes flow around a sphere and is given in many fluid mechanics textbooks. The velocity and pressure fields are

where B_p is a dimensionless constant. The solution of Equation (14b) is also easily obtained as

where B_t is another dimensionless constant. The components of the heat flux vector are found by substituting Equations (17) into Equation (14e) written in spherical polar form:

where . The nonzero components of the stress tensor are found by substituting Equations (16) and (18) into Equation (14d) written in spherical polars:

4.3. Conservation of Energy at the Particle Surface

Equating the radial energy fluxes in the particle and gas at the surface,

where T_p and k_p are the particle temperature and thermal conductivity. Nondimensionally,

where Λ=k_p /k ₀. The final term can be neglected as we are assuming Ep≪1. The particle temperature deviation satisfies Laplace's equation. The solution is

where D_t is a dimensionless constant. Substituting Equations (18a) and (21) into Equation (20) gives

4.4. The Force on the Particle

From the geometry of Figure 2,

where , σ _rr , and σ _rθ are evaluated at r = a. Nondimensionalizing,

where , , and are evaluated at . Substituting Equations (17), (20a), and (20c) gives

This equation is deceptive because it suggests that the imposed free-stream velocity does not contribute to the force. We shall find, however, that the expression for B_p obtained using the surface boundary conditions derived later includes a contribution from U ₀.

4.5. The Surface Boundary Conditions

The most crucial part of the theory is the specification of the surface boundary conditions, introduced earlier as Equations (7). In order to evaluate the fluxes, we take the velocity distribution function f at the surface as the G13 distribution, Equation (6.11) of Struchtrup (2005),

where p, ρ, θ = RT, q_i , and σ_ij are the local values. The distribution function for molecules reflected diffusely from the surface is assumed to be

where θ_p = RT_p and ρ_s is found from the condition that the number flux of incident and reflected molecules must be equal.

The specification of the surface boundary conditions involves calculating the fluxes in Equations (7) using the distribution functions of Equations (24) and (25), and then linearizing. The procedure is outlined in Appendix 2. The final linearized equations in dimensionless form are

where all quantities are evaluated at . We now introduce the creep, slip, and jump coefficients from Equations (7)–(9) and write Equations (26) in the form

We now substitute Equations (16), (17), (18), (19), and (21) with into Equations (27). Collecting terms and including Equation (22), we obtain

where the definition has been used to eliminate B_t in Equation (28b). Equations (28) provide three equations for the three unknown constants B_p , B_q , and D_t , which specify the pressure, temperature, velocity, stress, and heat flux fields via Equations (16) through Equation (19). Knowing B_p , the force on the sphere can be found from Equation (23).

From Equations (26), we can see that the G13 analysis generates the classical values of the thermal creep, velocity slip, and temperature jump coefficients originally obtained by Maxwell, specifically K_tc =3/4, A_m =1, and A_e =15/8. The thermal creep coefficient in particular has a strong effect on the magnitude of the thermophoretic force, and it will be seen later that with the Maxwell value, the force tends to be underpredicted. As noted in Section 2.4, however, more accurate solutions of the kinetic equations for the classical problems of thermal creep, velocity slip, and temperature jump suggest that the real values of the coefficients are around K_tc =1.10, A_m =1.13, and A_e =2.17. In order to improve numerical accuracy, it is therefore proposed that these, rather than the Maxwell values, be substituted into the solution when calculating the thermophoretic force.

Clearly, this procedure introduces an inconsistency into the analysis that requires justification. The Maxwell values arise specifically because of the form of the G13 velocity distribution function f_{G 13} for incident molecules given by Equation (24). The G13 equations cannot capture the structure of the Knudsen layer however, and the real distribution function for incident molecules at the surface is different from the f_{G 13} distribution. The rationale for using the three non-Maxwell coefficients is that the real distribution, were it known, would generate these values. In other words, the effect of the real Knudsen layer is modeled in the G13 analysis by modifying the boundary conditions.

Purists, of course, will argue that the G13 solution should simply be abandoned in favor of a direct solution of the Boltzmann equation or one of its models. As we shall see, however, the direct solutions available lack consistency, so this is far from being a clear cut decision. In any case, the G13 solution has many advantages over the more complex kinetic methods because it is straightforward in application, gives good physical understanding, and leads to explicit analytical solutions, which are easy to interpret. Rather than relinquishing these assets, we shall therefore retain the basic form of the solution but draw on the more accurate creep, slip, and jump analyses by appropriating the values of the three coefficients. The success of this procedure will be judged by comparison with the direct solutions and with experimental measurements.

4.6. A Hierarchy of Solutions

Rather than deriving the full solution of Equations (28) outright, we shall examine the hierarchy of solutions generated by systematically retaining the terms of increasing powers of Kn.

We start by setting Kn = 0 in Equations (28). Using Equations (23) and (2), we then obtain

Comparison with Table 1 shows that Equation (29a) is Epstein's result, while Equation (29b) gives the Stokes drag law. We note that thermal creep survives in this limit, although velocity slip and temperature jump disappear.

Retaining the terms of order Kn leads to Brock's expression. Brock was aware of the temperature-driven part of the thermal stress in Equation (14f) and showed, quite correctly, that when this is integrated over the surface, it gives no net contribution to the thermophoretic force. He therefore ignored it in his analysis. However, what Brock failed to appreciate was that the thermal stress also enters in the final term of the boundary condition Equation (27a), where it has a strong effect on the surface slip velocity. This effect does not disappear on integration.

We first adopt Brock's assumption, which is equivalent to neglecting the term in Equation (28a). From Equations (23) and (2), we then obtain

Comparison with Table 1 shows that these are indeed Brock's expressions. It will be noted that Φ is always negative and hence Brock's equation cannot predict reversed thermophoresis.

Figure 3 Curves of −Φ/(2π) plotted against log₁₀(Kn) for various Λ using Equation (31a) (Brock's theory plus the temperature-driven part of the thermal stress). Reversed thermophoresis at high Λ is evident but the behavior at high Kn is nonphysical.

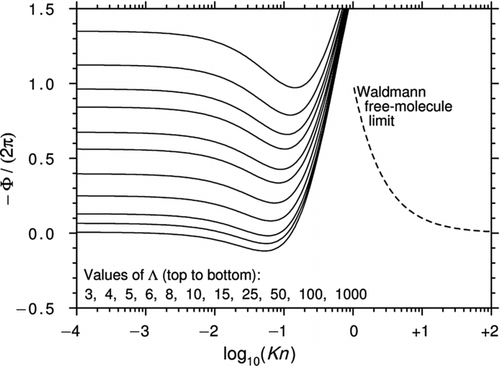
If we now include the term in Equation (28a), the expressions for Φ and Ψ become

This comparatively modest correction makes a most significant difference because Φ now changes sign at sufficiently large Λ, thus demonstrating reversed thermophoresis; see Figure 3. The figure also shows that, unsurprisingly, Equation (31a) behaves nonphysically at high Kn.

In Dwyer's solution, both temperature-driven thermal stress and pressure-driven heat transfer were included. However, although Dwyer included the pressure-driven heat flux correctly in his equivalent of Equation (27a), he encountered difficulty with his equivalent of Equation (27b). The problem seems to have been overcome by neglecting the pressure-driven heat flux in the term and omitting the term entirely.

Examination of Figures 1–4 in Dwyer's article shows that his calculations overshoot Waldmann's result and eventually decay according to Φ ∼ Kn ⁻² as Kn→∞. This is in contrast to Waldmann's results of Φ ∼ Kn ⁻¹ in the limit Kn→∞. Interestingly, this behavior was criticized by Brock in the discussion to the article, drawing a reply from the author attempting to justify the clearly erroneous results. But in any case, the dispute was academic. First, had Dwyer included the pressure-driven heat flux term in the term of Equation (27b), he would have found, through a fortuitous cancellation of two Kn ⁴ terms, that Φ asymptoted to Kn ⁻¹ (albeit with quite the wrong coefficient to match Waldmann's result). Second, and far more importantly, the G13 equations cannot be justified for Kn > ∼0.2.

Figure 4 Curves of −Φ/(2π) plotted against log₁₀(Kn) for various Λ using Equation (32a) (Dwyer's theory with the pressure-driven heat flux included correctly). For Kn < 0.2, the curves are almost identical to those of Figure 3 but the behavior at high Kn is nonphysical.

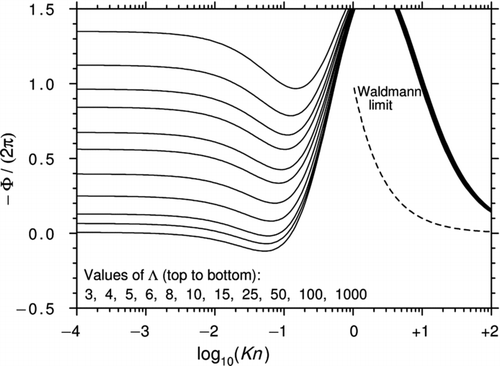
Rather than pursuing Dwyer's approximations any further, it seems more profitable to present the full solution to Equations (28) and then discuss the implications. Accordingly, we eliminate B_q in favor of D_t using Equation (28c) and then solve for B_p and D_t . Using Equations (23) and (2), we obtain

A comparison of Equations (31a) and (32a) shows that for Kn < 0.1, the terms involving have little effect. As Kn increases, these terms start to dominate but, as noted earlier, the theory cannot be justified for Kn > ∼0.2. Indeed, it is not even certain that the modifications in Equation (32a) are to be trusted in any range. Previously, it was mentioned that Struchtrup (2005) had improved the G13 system of equations by “regularizing” the closure conditions to produce the R13 system. A solution based on this system is not yet available but an examination of the equations shows that extra terms of order Kn ² will be generated, which may affect the solution. In the opinion of the author, it is best to disregard Equations (32) and revert to the algebraically simpler Equations (31), at least until an R13 solution becomes available.

Figure 4 is a plot of −Φ/(2π) against log₁₀(Kn) for selected values of Λ calculated from Equation (32a). The curves have been extended into the high Kn region for illustrative purposes only. For Kn < 0.2, the differences between Figures 3 and 4 are comparatively minor for all values of Λ.

5. THERMOPHORESIS AT HIGH KNUDSEN NUMBERS

5.1. Free-Molecule Thermophoresis

We now turn our attention to thermophoresis at high Kn and start by considering Waldmann's free-molecule analysis. When calculating the mass, momentum, and energy fluxes incident on the particle, Waldmann assumed that the molecular velocity distribution function f_U was the same as the Chapman–Enskog first approximation for the undisturbed gas:

where c is the absolute molecular velocity and q ₀=−k ₀∇T ₀. For the reflected molecules, Waldmann assumed that a fraction α of the incident molecules was reflected diffusely with complete thermal accommodation and a fraction (1−α) was reflected specularly. His expression for Φ then followed as

which is independent of α and Λ. Equation (34) is pleasingly simple and compact but there are assumptions in its derivation, which are seldom noted and which need to be considered.

The main assumption is that the particle behaves as a perfect thermal conductor (Λ→∞) and hence the particle temperature is uniform. This constraint can be removed by solving Laplace's equation for the particle temperature field and coupling the solution to the gas phase equations. Without going into details, the result for a monatomic gas is

For Λ > 0, Equation (35) tends to Equation (34) as , but for a truly nonconducting particle (Λ = 0),

which for α=1 is about 50% larger than Waldmann's result.

Ivchenko and Yalamov (1970) assumed that all incident molecules were reflected diffusely with an energy accommodation coefficient α _e . Repeating the analysis with this model gives

For a truly nonconducting particle (Λ = 0),

which is the same as Equation (36) for α=1. However, as for any Λ > 0,

The term involving 5π/32 = 0.491 agrees exactly with the second term in Equation (22) of Ivchenko and Yalamov and if α _e =1, the Waldmann result is recovered.

The conclusion is that different models give different results but Waldmann's expression is likely to be reliable for most situations where the accommodation coefficients are near unity. This conclusion is corroborated by the numerical calculations of Gallis et al. (2004) who studied free-molecule thermophoresis using the Direct Simulation Monte Carlo (DSMC) method of Bird (1994). The work of Gallis et al. is very thorough and confirms that, unless high accuracy is required, Waldmann's expression should suffice.

5.2. The Near-Free-Molecule Regime

There have been attempts by Brock (1967) and Ivchenko and Yalamov (1970) to find analytical solutions, which show how the thermophoretic force approaches the free-molecule limit. However, as will be shown later, Brock's result is incorrect.

Both methods start from the original BGK approximation to the Boltzmann equation:

where τ₀=μ₀/p ₀ and f_M is the Maxwell distribution function based on the local values of density ρ, mean velocity u_i , and temperature T corresponding to the actual distribution function f. In linearized form,  f_M can be written as

where ω and τ are defined by ρ=ρ₀(1+ω) and T=T ₀(1+τ).

Both Brock and Ivchenko and Yalamov obtained a solution to Equation (40) by expanding f in powers of . As an approximation, they set u_i , ω, and τ in Equation (41) equal to the values corresponding to the local free-molecule distribution f_FM (which, it is important to appreciate, is not the same as the far-field distribution f_U ). 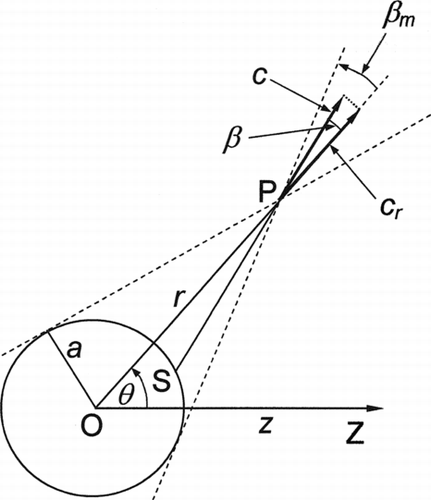The main problem, therefore, is to obtain an expression for f_FM at a general point P; see Figure 5.

Figure 5 Diagram to illustrate the calculation of the free-molecule distribution function f_FM .

In free-molecule flow, intermolecular collisions are ignored, so the distribution function at P involves two groups of molecules. One group has velocity vectors that lie outside the cone defined by the angle β=β _m in Figure 5. These molecules come directly from the far field and have the distribution f_U of Equation (33). The other group has velocity vectors that lie within the cone and these molecules have all been reflected from the surface of the sphere.

Ivchenko and Yalamov (1970) assumed that all incident molecules were reflected diffusely with an energy accommodation coefficient α _e . It is then straightforward to find the two parts of F_FM , and the local values of ω, u_i , and τ can be obtained from the relevant moments of the distribution. For the special case α _e =1, the results are

Equations (42) agree with Equations (18) and (19) of Ivchenko and Yalamov for α _e =1 when the rigid elastic sphere expressions for their coefficient a ₁ and the mean free path λ are used.

Brock assumed that a fraction α of the incident molecules was reflected diffusely with complete thermal accommodation and a fraction (1−α) was reflected specularly. The calculation of the distribution function for the reflected molecules is then much more complicated as those molecules specularly reflected from the point S on the sphere in Figure 5 have an angle of incidence dependent on the position of S.

Few details are given in Brock's article and it is very difficult to construct the intermediate steps of his analysis. However, a detailed examination does indicate that although Brock obtained the correct expression for ω (for α = 1), his expression for τ was probably

rather than the correct version given in Equation (42). Further examination also shows that Brock made a second error when integrating his Equation (14) from the surface to the far field. To do this, he expanded the exponential in the integrand as a series, integrated the first term and ignored the others. Unfortunately, however, all terms other than the first diverge. The correct approach is to continually integrate by parts as this generates the required convergent series in .

We therefore conclude that Brock's expression for the thermophoretic force is incorrect but that given by Ivchenko and Yalamov is probably reliable. We therefore concentrate on the latter, which, for α _e =1, can be written with our definition of Kn as

The accuracy of this expression will be examined later.

6. THEORIES FOR THE TRANSITION REGIME

Equation (43) gives some information as to how the thermophoretic force approaches the free-molecule limit but it gives no clue as to the behavior in the central transition regime. For this, it is necessary to resort to numerical solutions of the Boltzmann equation itself. In practice, this is never done and a simpler model Boltzmann equation is always used as the starting point. The simplest model available is the original BGK equation, Equation (40).

6.1. Solutions of the Original BGK Equation

Solutions of the original BGK equation of varying complexity have been published by Gorelov (1976), Sone and Aoki (1981, 1983), Yamamoto and Ishihara (1988), Loyalka (1992), and Takata et al. (1993). All these articles involve very difficult mathematics that is only accessible to those expert in advanced methods of the kinetic theory.

Gorelov (1976) solved an integral form of the linearized BGK equation by the method of successive approximation. He presented graphs of the thermophoretic force for Λ = 5 and 500, but it is difficult to make a comparison with other results because his mean free path seems to be based on a nonstandard expression, which may be erroneous.

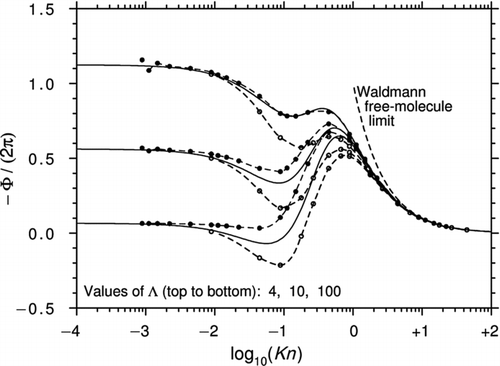
In their 1981 article, Sone and Aoki found an asymptotic solution of the linearized BGK equation for Λ→∞ and Kn ≪ 1 (note that their definition of the mean free path differs from Equation (1) by a factor 4/π). In their 1983 article, the same authors used a quite different approach to calculate the force at arbitrary Kn. To do this, they exploited the axisymmetry of the problem to separate the spherical polar form of the BGK equation into two equations: one involving cosθ terms only and the other sinθ (Figure 5). This procedure is straightforward but the resulting solution is not. Sone and Aoki conceded that “the analysis includes very lengthy manipulation” and they gave only a brief outline of the method that involves integrating along the characteristics and finding an approximate solution using a variational approach.

Figure 6 shows the results from Figures 1 and 2 of the 1983 article, converted to the present notation. Also shown is a graph from Yamamoto and Ishihara (1988) for Λ→∞. These authors solved exactly the same equation as Sone and Aoki by a different method and the fact that the two curves agree so closely gives confidence that the mathematical procedures were reliable. The solution of Ivchenko and Yalamov, Equation (43) with Λ→∞, is also plotted in Figure 6. Remarkably, this is consistent with the other calculations for values of Kn as low as 1.0 despite the fact that Equation (43) is accurate only to the first order in .

Figure 6 Curves of −Φ/(2π) plotted against log₁₀(Kn) for a perfect thermally conducting sphere (Λ→∞). The calculations are from Sone and Aoki (1981, 1983) and Yamamoto and Ishihara (1988). Also shown is Equation (43) from Ivchenko and Yalamov, the first-order correction in

to Waldmann's free-molecule expression.

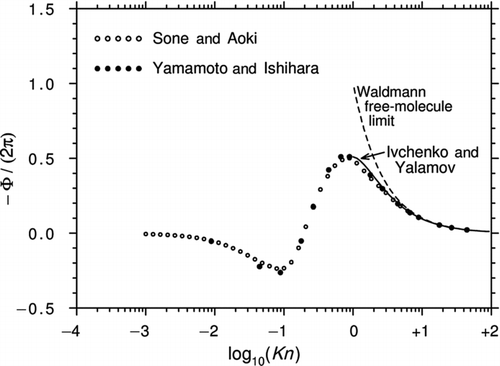
The comparison of Figure 6 with the results of the G13 method for high Λ (Figures 3 and 4) shows that the shape of the curves in the slip and lower transition regimes is similar but the region of reversed thermophoresis in Figure 6 is substantially larger. This may be because the original BGK equation yields a Prandtl number of unity, whereas the G13 solution is based on the ES-BGK equation that gives the correct Prandtl number of 2/3 for a monatomic gas.

In the article by Yamamoto and Ishihara mentioned earlier, the authors solved the Stokes equations for flow around a sphere in a uniform flow with a temperature gradient (exactly as in the G13 analysis). This far-field solution was then matched to a solution of the BGK equation for the kinetic region adjacent to the sphere. The expression for Φ extracted from Equation (41) of Yamamoto and Ishihara and valid for arbitrary Kn is

The constants are given for sixteen discrete values of K in Tables 1 and 2 of the original article.

Table 2 Published experimental data for the thermophoretic force

Authors and source	Particle and gas	Λ	Kn
Saxton and Ranz (1952), Figure 3	Castor oil in air	9.5	0.05–0.12
Schmitt (1959), Figure 6	Silicone oil in air	7.5	0.11–2.00
Schadt and Cadle (1961), Figure 1b	TCP in air	10	0.14–0.76
Schadt and Cadle (1961), Figure 2b	NaCl in air	322	0.20–1.49
Schadt and Cadle (1961), Figure 3	Hg in air	581	0.45–3.60
Jacobsen and Brock (1965), Figures 4 and 5	NaCl in Ar	300	0.06–0.67
Tong (1975), Figure 6	Al in He	1519	0.01–0.32
Davis and Adair (1975), Figure 5	Cork in Ar	2.5	0.05–1.80
Li and Davis (1995a), Figure 11 (0905b)	PSL in air	5.4	0.06–5.00
Li and Davis (1995a), Figure 8 (0501a)	DOP in air	6	0.06–1.55
Li and Davis (1995a), Figure 10 (0510d)	DOP in air	6	0.05–5.00
Li and Davis (1995a), Figure 12 (0927b)	Glass in air	40	0.10–5.00
Li and Davis (1995a), Figure 12 (0726a)	Ni in air	4700	0.09–5.00
Li and Davis (1995b), Figure 6	PSL in CO2	10	0.10–3.50
Li and Davis (1995b), Figure 6	DOP in CO2	12	0.05–4.20
Li and Davis (1995b), Figure 6	Glass in CO2	75	0.12–4.00
Li and Davis (1995b), Figure 10	DOP in He	0.8	0.10–1.90

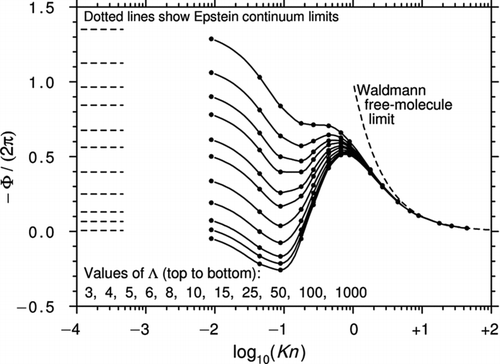
Figure 7 shows the curves of −Φ/(2π) plotted against log₁₀(Kn) for various values of Λ. Although not obvious from Equation (44), the curves asymptote to the correct Epstein continuum limits. However, a comparison with Figures 3 and 4 shows that the Yamamoto and Ishihara theory tends to predict a deeper “depression” than the G13 solution in the transition region. As noted earlier, this may be because the calculations were based on the original BGK equation.

Figure 7 Curves of −Φ/(2π) plotted against log₁₀(Kn) for various Λ from Yamamoto and Ishihara (1988). The black circles are calculated from Equation (44) and Tables 1 and 2 of the original article. Also shown are the Epstein continuum limits.

There are two other published solutions of the linearized BGK equation. Loyalka (1992) solved the equation numerically for Λ = 10 and 100 and obtained good agreement with the Yamamoto and Ishihara solutions at five discrete values of Kn. Takata et al. (1993) noted that the solution for arbitrary Λ could be expressed as a linear combination of the solution for Λ→∞ and that for a spherical particle with a given axisymmetric and sinusoidally varying surface temperature immersed in an infinite expanse of gas at temperature T ₀ and pressure p ₀. They obtained numerical solutions in close agreement with those of Yamamoto and Ishihara for Λ = 1, 10, 100, and ∞.

6.2. Solutions of Improved Model Boltzmann Equations

All the calculations discussed earlier are based on the original BGK equation with its questionable physical modeling of the collision term. To address this issue, Beresnev and Chernyak (1995) worked with the S model of Shakhov (1968), a generalization that yields 13 correct moments of the distribution function and the correct Prandtl number of 2/3.

Beresnev and Chernyak integrated the S-model equation along the characteristics to give a set of four integral moment equations. These were then solved by successive approximation. In the present notation, the expression for Φ obtained from Equations (20), (21), and (25) of the original article and valid for arbitrary Kn and accommodation coefficients α _m =α _e =1 is

The constants are given for twenty-four discrete values of the Knudsen number for a Prandtl number of 2/3 in Table 1 of the Beresnev and Chernyak article.

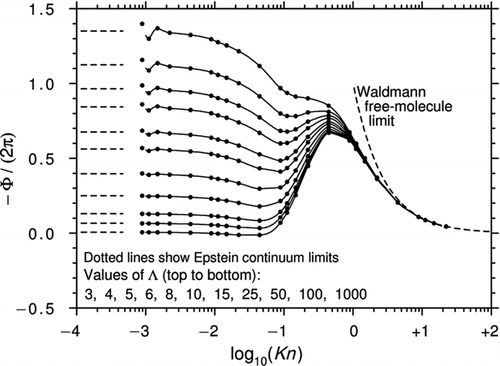
Figure 8 shows the curves of −Φ/(2π) calculated from Equation (45) and plotted against log₁₀(Kn) for various values of Λ. The region of reversed thermophoresis has all but disappeared and is only just present for the highest value of Λ = 1000. The peak values in the transition region are also substantially higher than those of Figure 7.

Figure 8 Curves of −Φ/(2π) plotted against log₁₀(Kn) for various Λ from Beresnev and Chernyak (1995). The black circles are calculated from Equation (45) and Table 1 of Beresnev and Chernyak. Also shown are the Epstein continuum limits.

Loyalka (1992) expanded the collision kernel of the linearized Boltzmann equation in spherical harmonics, and for a hard-sphere gas, solved the resulting equations numerically for Λ = 10 and 100. Unfortunately, because of high computing requirements, results for only 5 points in the upper transition regime were presented. In this region, the thermophoretic force was found to be about 5% lower than that calculated for the original BGK equation (whereas the Beresnev and Chernyak values are 20%–30% higher). The significance of this finding is not clear because of the different molecular collision models used.

6.3. Summary of the Transition Regime Theories

The earlier discussion has shown that there are really only two theories extant for transition regime thermophoresis despite the rather large number of published articles. On the basis of the original BGK equation, the work of Yamamoto and Ishihara (1988) effectively embodies the results of Gorelov (1976), Sone and Aoki (1981, 1983), Loyalka (1992), and Takata et al. (1993). A better model equation is the Shakhov S-model extension used by Beresnev and Chernyak (1995). A comparison of Figures 7 and 8 shows that with the latter theory, reversed thermophoresis has all but disappeared. It is clear, however, that neither of these models lead to a definitive solution at arbitrary Kn and Λ. Theoretical considerations tend to favor the Beresnev and Chernyak solution as it is based on a more reliable model kinetic equation.

7. EXPERIMENTAL MEASUREMENTS OF THE THERMOPHORETIC FORCE

Although it is very difficult to make accurate measurements of thermophoretic effects, a substantial body of experimental data is available in the literature. Most of the measurements of the thermophoretic force are listed in Table 2. Generally, authors have presented their data as plots of −F_T /a ² G ₀ against Kn. As discussed in Section 2.2, the problem with this method of presentation is that −F_T /a ² G ₀ tends to zero as Kn tends to zero, whereas the function Φ tends to a nonzero limiting value. Hence, in order to apply a more sensitive test when comparing with theoretical calculations, values of Φ were obtained from the published data, usually by making hand measurements from the graphs followed by processing of the data. In assessing the data, comparisons will be made with the theories of Yamamoto and Ishihara (Y&I) and Beresnev and Chernyak (B&C).

At this point, it is relevant to mention the problem of polyatomic gases. All the theories described earlier have assumed that the carrier gas is monatomic but many of the experimental measurements involve diatomic (air, N₂, H₂) or even triatomic (CO₂) gases. The effect of the gas molecular structure on the thermophoretic force represents a very difficult problem and no rigorous theory has yet appeared in the literature. The usual recommendation, following Waldmann (1959), is that the “translational” component of the thermal conductivity (rather than the full value that includes energy transport due to the rotational and vibrational contributions) should be used in all calculations. This recommendation has been corroborated by the DSMC calculations of Gallis et al. (2004). Accordingly, the values of the thermal conductivity ratio Λ were calculated using the translational thermal conductivity evaluated from tabulated viscosity data and Equation (2).

7.1. Comparison of the Thermophoretic Force Data with Theory

Saxton and Ranz (1952) used a Millikan cell to measure the thermophoretic force on oil droplets in air. Unfortunately, their diagrams are of poor quality and it is very difficult to identify the plotted points. Also, the range of Knudsen number covered is very limited.

Schmitt (1959) also used a Millikan cell. Figure 6 of his article shows the data for silicone oil droplets in argon (Ar) (Λ = 7.5) and this was reproduced as Figure 3 in Waldmann and Schmitt (1966). Figure 9a shows the resulting plot of −Φ/(2π) against log₁₀(Kn). There is good agreement with the predictions of the B&C theory apart from the data point at Kn = 0.06.

Figure 9 The thermophoretic force data of (a) Schmitt (1959); (b) Schadt and Cadle (1961); (c) Jacobsen and Brock (1965); (d), (e), and (f) Li and Davis (1995a, 1995b). Theoretical predictions for the corresponding values of Λ: Beresnev and Chernyak (solid lines), Yamamoto and Ishihara (dotted lines).

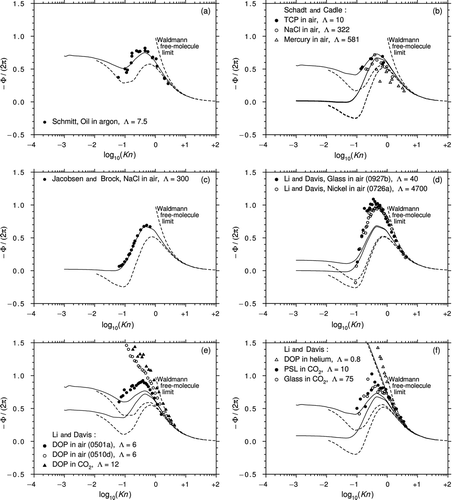
Schadt and Cadle (1961) used a Millikan cell to measure the thermophoretic force in air on tricresyl phosphate (TCP) droplets, single crystals of sodium chloride (NaCl), and mercury (Hg) droplets (Λ = 10, 322, and 581). In their article, they stated that the NaCl crystals were cubical in shape and so comparison with a theory that assumes the particle to be spherical is dubious. Figure 9b shows that the TCP and NaCl data fit the B&C curves rather well but the mercury data exhibit considerable scatter and the fit is poor. It is also noticeable that the B&C and Y&I predictions for Λ = 322 and 581 are almost identical, whereas the NaCl and mercury data show quite large differences.

Jacobsen and Brock (1965) studied spherical NaCl particles in Ar (Λ = 300) using a Millikan cell. Figure 9c shows that the data are extremely self-consistent with little scatter and the agreement with the B&C theory is remarkable. There is quite a strong indication that reversed thermophoresis does not occur at this value of Λ.

Table 3 Published experimental data for the thermophoretic velocity

Authors and source	Particle and gas	Λ	Kn
Rosenblatt and LaMer (1946), Table III	TCP in air	10	0.05–1.50
Schmitt (1959), Figure 5	Oil in Ar, N2, CO2, H2	various	0.16–2.65
Prodi et al. (1979), Table 3	NaCl in air	309	0.08–0.64
Toda et al. (1998), Table 1	PMMA in air	7.9	0.004–0.027
Toda et al. (1998), Table 1	SiO2 in air	74	0.004–0.14
Santachiara et al. (2002), Figure 2	Wax in air	4.6	0.10–0.61
Santachiara et al. (2002), Figure 5	PSL in air	5.4	0.10–0.33
Santachiara et al. (2002), Figure 4	NaCl in air	309	0.14–0.56
Santachiara et al. (2002), Figure 2	Ag in air	22530	0.22–0.71
Prodi et al. (2006), Figure 2	Paraffin, wax, NaCl in air	various	0.04–0.90
Prodi et al. (2007), Figures 2 and 3	Paraffin in He, N2, Ar, Xe	various	0.05–0.90
Sagot et al. (2009), Figure 11	Vegetable oil in air	10	0.02–3.0

Tong (1975) measured the thermophoretic force by suspending macroscopic aluminum spheres of radii 1−3 mm by a thin cord in a vacuum chamber containing helium (He) (Λ = 1520). However, for reasons that are not clear, the analysis of the data gives values of Φ very much greater than those predicted by either of the two theories.

L. A. Davis and Adair (1975) measured the thermophoretic force on a cork sphere of radius 6.3 mm suspended in a number of different gases in a vacuum chamber. Their main interest was to investigate the effect of the proximity of the plates producing the temperature gradient and their data is not directly applicable to the present discussion.

Li and E. J. Davis (1995a) used electrodynamic levitation in a Millikan cell to measure the thermophoretic force in air on polystyrene latex (PSL) spheres, dioctyl phthalate (DOP) droplets, and glass and nickel spheres (Λ = 5.4, 6.0, 40, and 4700). The results for glass and nickel spheres are shown in Figure 9d, where it can be seen that the data points fall well above the B&C curves. Figure 9e shows datasets 0501a and 0510d for DOP droplets. The points for dataset 0501a are about 20% greater than the predictions of the B&C theory but otherwise agree qualitatively. However, dataset 0510d does not even show qualitative agreement, and the data seem to be more representative of a value of Λ of around unity.

Li and E. J. Davis (1995b) studied DOP droplets in He and carbon dioxide (CO₂) (Λ = 0.8 and 12) and PSL and glass spheres in CO₂ (Λ = 10 and 75). Figure 9e shows that the dataset for DOP droplets in CO₂ displays a similar trend to that of dataset 0510d and is more representative of a Λ value of about unity. In Figure 9f, it can be seen that the data for PSL and glass spheres in CO₂, and DOP droplets in He, are all in reasonable agreement with the B&C theory.

7.2. Summary of the Thermophoretic Force Data

Taken overall, the six graphs comprising Figure 9 give a strong visual impression of the quality of the thermophoretic force data and the predictive capabilities of the two theories.

With the exception of the Schadt and Cadle mercury in air data, the early experiments show good consistency and close agreement with the B&C theory. The later work by Li and E. J. Davis is impressive and extensive but the data must be evaluated objectively and three important points should be noted. First, almost all the data points fall above the B&C predictions in the transition regime. Second, the anomalous behavior of two of the DOP datasets is worrying. Third, the fact that the Φ values for the high Λ datasets exceed those, at the same Knudsen numbers, for the low Λ datasets is not predicted by any theory.

All the datasets asymptote with good accuracy to the Waldmann limit at high Kn. Unfortunately, however, none extends to sufficiently low Kn to validate Epstein's continuum theory. This problem has been emphasized previously by Bakanov (1991).

8. EXPERIMENTAL MEASUREMENTS OF THE THERMOPHORETIC VELOCITY

We now turn to the experimental measurements of thermophoretic velocity U _T , most of which are listed in Table 3. In order to calculate the values of the function Φ from measurements of U _T using Equation (5), we have used Millikan's celebrated interpolation expression for the drag function Ψ. With the updated constants recommended by Allen and Raabe (1982), this is

8.1. Comparison of the Thermophoretic Velocity Data with Theory

Rosenblatt and LaMer (1946) used a Millikan cell to study TCP droplets in air (Λ = 10). In processing the data, it was found that the Φ values were about ten times greater than those predicted by the B&C theory. This discrepancy may originate from a scale error in one of the tables in the article and if the values are reduced by a factor of 10, the agreement with the B&C theory is very good. However, given the uncertainty, we shall not consider this data further.

Schmitt (1959) measured the thermophoretic velocity of oil droplets in hydrogen (H₂), nitrogen (N₂), Ar, and CO₂ (Λ = 1.0, 7.3, 8.8, and 13.5). These measurements were reproduced as Figures 4 and 5 in Waldmann and Schmitt (1966). The H₂ dataset is particularly interesting because the value of Λ is very low. Figure 10a shows the processed data for Ar and H₂. The data points for CO₂ and N₂ are similar to those for Ar and are not shown. The agreement with the B&C theory is generally good.

Figure 10 The thermophoretic velocity data of (a) Schmitt (1959), (b) and (c) Santachiara et al. (2002), (d) Prodi et al. (2007), and (e) Sagot et al. (2009). Theoretical predictions for the corresponding values of Λ: Beresnev and Chernyak (solid lines), Yamamoto and Ishihara (dotted lines).

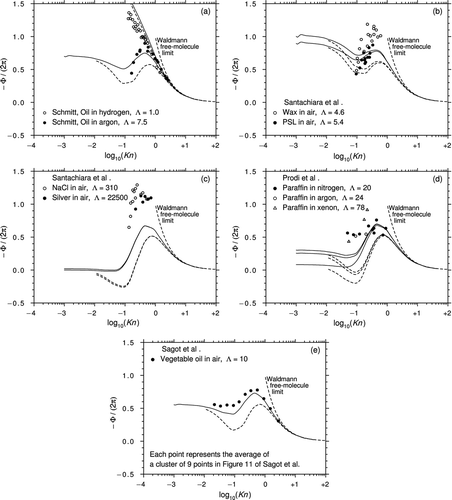
Prodi et al. (1979) studied NaCl particles in air (Λ = 310). The air passed in laminar flow along a channel between walls maintained at different temperatures and the cross-stream temperature gradient propelled the particles in a direction transverse to the flow. As the same apparatus was used more than 20 years later in a far more extensive series of tests, we shall defer discussion until later.

Toda et al. (1998) measured the thermophoretic velocity of PMMA and SiO₂ particles in air. To eliminate the effects of gravity, they performed the tests in the “drop-tower” facility of the Japan Microgravity Centre. In processing the data, it was found that the measurements were significantly different from any other published results. The reason for this is not clear.

Santachiara et al. (2002) resurrected the channel flow apparatus of Prodi et al. (1979) and measured the thermophoretic velocity in air of carnauba wax particles, PSL spheres, and NaCl and silver particles (Λ = 4.6, 5.4, 310, and 22,500). The processed data are shown in Figures 10b and c. Clearly, there is considerable scatter and the agreement with the theory is poor.

Prodi et al. (2006, 2007) measured the thermophoretic velocity in two microgravity situations. To do this, they mounted their apparatus in an Airbus 300, which then undertook a series of parabolic-arc flights and they also used the free-fall “drop-tower” at Bremen. In the experiments, they used several different particle materials (paraffin, carnauba wax, and NaCl) and gases (air, N₂, He, Ar, and xenon (Xe)). Unfortunately, the results of these ambitious and (no doubt) very expensive tests were inconclusive. First, there are very few data points for many of the particle–gas combinations and, second, the data exhibited considerable scatter. Figure 10d shows the processed data for paraffin droplets in N₂, Ar, and Xe (Λ = 20, 24, and 78) from Prodi et al. (2007). It is difficult to draw conclusions but the data does tend to favor the B&C theory (although the deviation at lower Kn is considerable).

Sagot et al. (2009) measured the thermophoretic velocity of vegetable oil droplets in air (Λ = 10). The air passed in laminar flow along an annular gap between walls maintained at different, but almost constant, temperatures and the cross-stream temperature gradient, which hardly varied along the duct, propelled the particles in a direction transverse to the flow. This so-called 3T configuration generated extremely consistent measurements of what Sagot et al. refer to as the thermophoretic diffusion coefficient K_th (or Φ/Ψ in our notation) over an exceptionally wide range of Knudsen number from 0.02 to 3.0. Figure 10e shows that the processed data are in quite good agreement with the B&C theory. It is also the only data that extend to sufficiently low Knudsen numbers to provide verification of Epstein's result in the continuum limit. From the description in the original article, it is clear that the measurements were performed very carefully indeed and this is, therefore, an extremely valuable dataset.

8.2. Summary of the Thermophoretic Velocity Data

The measurements of Schmitt complement the thermophoretic force data and provide corroborating evidence in favor of the B&C theory, the data for oil droplets in H₂ being especially interesting. The experiments of Santachiara et al. (2002) suggest that the peak values of Φ are much higher than the predictions of the B&C theory and that there is little difference between low and high values of Λ in the (fairly small) range covered. Conversely, the few microgravity experiments of Prodi et al. tend to favor the B&C theory. However, the data scatter in Figures 10b–d is substantial and any conclusions drawn are very tentative. Conversely, the data of Sagot et al. (2009) shown in Figure 10e are very consistent and show good agreement with the B&C theory right down to Epstein's result in the continuum limit.

9. AN INTERPOLATION FORMULA FOR PRACTICAL CALCULATIONS

The theories of Beresnev and Chernyak and Yamamoto and Ishihara are somewhat inconvenient for practical calculations because the constants required for evaluating Equations (44) and (45) are presented in the form of look-up tables of discrete values. On the other hand, the G13 analytical solution is only valid for the range Kn < ∼0.2. It is therefore of interest (and in the spirit of Talbot and his co-workers) to construct an interpolation formula linking the G13 solution with Waldmann's free-molecule expression. In Section 4.6, it was explained why the corrected Brock expression of Equation (31a) is to be preferred to the ostensibly more rigorous corrected Dwyer expression of Equation (32a). Accordingly, we work with Equation (31a) and note that Φ tends to −6π as Kn→∞. This suggests the interpolating prescription

Equation (47) is Equation (31a) with a factor inserted in the denominator so that Waldmann's result, Equation (34), is obtained exactly for Kn→∞. The Millikan-style exponential term provides flexibility and a choice of 0.5 for the interpolation constant C_int seems to be about optimal. Figure 11 shows curves of −Φ/(2π) calculated from Equation (47) and plotted against log₁₀(Kn) for three values of Λ. Also shown are the predictions of Y&I and B&C. There are substantial differences between these two theories, and Equation (47) may thus provide a reasonable working compromise, biased toward the B&C theory, which is probably the more reliable.

Figure 11 Curves of −Φ/(2π) plotted against log₁₀(Kn) for various Λ. The white circles are from Yamamoto and Ishihara (1988), the black circles are from Beresnev and Chernyak (1995), and the solid lines are from the interpolation formula Equation (47) with C_int = 0.5.

Figure 12 shows a more extensive plot of Equation (47). A comparison with Figures 3 and 4 confirms that the regions of reversed thermophoresis are almost identical [Equation (47) deviates from Equation (31a) by less than 5% for Kn < 0.2]. However, as also shown in Figure 12, there are very large differences between Equation (47) and the Talbot et al. (1980) prescription.

Figure 12 Curves of −Φ/(2π) plotted against log₁₀(Kn) for various Λ using the interpolation formula Equation (47) with C_int = 0.5. For Kn < 0.2, the curves are almost identical to those of Figures 3 and 4. For comparison, the Talbot et al. (1980) prescription is also plotted.

10. CONCLUSIONS

In order to calculate the thermophoretic force at arbitrary Kn, it is necessary to solve the Boltzmann equation or one of its model forms with the appropriate boundary conditions. The solutions of Yamamoto and Ishihara and Beresnev and Chernyak embody all other approaches to date. Y&I used the original BGK equation, whereas B&C started with the S-model extension. There are substantial differences between the two solutions; Y&I predict a significant region of reversed thermophoresis while B&C do not. On theoretical grounds, it is expected that the B&C theory with its superior model of the collision term should give more accurate results.

The G13 method can only be justified for Kn < 0.2 but it has the advantage of transparency. The inclusion of the temperature-driven part of the thermal stress in the surface boundary condition allows the prediction of reversed thermophoresis, the extent of the region falling somewhere between the B&C and Y&I predictions.

The G13 solution can be extended by the addition of a Millikan-type interpolation factor to give an approximate analytical expression for the thermophoretic force at arbitrary Kn. The expression asymptotes to Waldmann's result at high Kn and gives values that lie between the B&C and Y&I predictions in the transition regime, tending to favor the B&C theory. The new interpolator should provide an improvement over the formula of Talbot et al. (1980).

There is a large body of experimental data on the thermophoretic force and velocity in the literature. Compared with the theoretical predictions of B&C and Y&I, the bulk of this data favors the former rather than the latter. The use of a wide range of gases has not proved particularly informative except for the use of H₂ and He, which allows measurements to be made at very low values of Λ. In general, the B&C theory agrees well with the older measurements but underpredicts the newer, some of which display considerable scatter. Exceptionally, the recent data of Sagot et al. (2009) show excellent consistency in the range 0.02 < Kn < 3.0 and favor the B&C theory, albeit for one value of Λ.

The experimental data cover a limited range of Knudsen number. At the upper end, most measurements approach the Waldmann free-molecule limit with remarkable consistency. At the lower end, there are few measurements for Kn < 0.1 where the thermophoretic force is small and difficult to measure. In many articles, there is discussion on whether or not certain experimental data provide a good fit to Epstein's theory. Such a comparison is inappropriate as, apart from the measurements of Sagot et al. (2009), there are simply no data available to allow conclusions to be drawn.

Future studies might usefully concentrate on (i) obtaining a solution to a more exact model of the Boltzmann equation, (ii) solving the R13-moment equations in order to study reversed thermophoresis in greater detail, and (iii) establishing a data bank of accurate measurements in the range Kn < 0.1. As this study has shown, there is little point in producing large quantities of transition regime data of dubious accuracy using unnecessarily sophisticated techniques. When all is said and done, the Millikan cell does a rather good job!

NOMENCLATURE*

a	=	Particle radius
Cm Ce	=	Velocity slip and temperature jump coefficients
C Ci	=	Molecular peculiar velocity
c ci	=	Molecular absolute velocity
e	=	Unit vector
Ep	=	Epstein number (a|G 0|/T 0)
F D F T	=	Viscous and thermophoretic forces on a particle
f	=	Molecular velocity distribution function
G 0	=	Scalar temperature gradient in the absence of the particle (dT 0/dz)
k 0 kp	=	Gas and particle thermal conductivities
Ktc	=	Thermal creep coefficient
Kn	=	Knudsen number (l 0/a)
l 0	=	Molecular mean free path
m	=	Mass of a molecule
Pij	=	Pressure tensor
p	=	Pressure and pressure deviation (p−p 0)
Re	=	Flow Reynolds number (aρ0|U 0|/μ0)
q qi	=	Heat flux vector
T	=	Temperature and temperature deviation (T−T 0)
U T	=	Thermophoretic velocity
u ui	=	Mean molecular velocity
α m α e	=	Momentum and energy accommodation coefficients
Φ	=	Function of Kn and Λ defined by Equation (4)
Λ	=	Particle-to-gas thermal conductivity ratio (kp /k 0)
μ 0	=	Dynamic viscosity
ψ	=	Function of Kn defined by Equation (4)
ρ	=	Density and density deviation (ρ−ρ0)
σij	=	Stress tensor (trace-free part of Pij )
θ	=	Temperature in energy units (RT)

Subscripts

0	=	Gas conditions at the center of the particle in its absence
p	=	Particle
ˆ	=	Denotes a dimensionless variable

Acknowledgments

The author wishes to thank Dr. David Healy, formerly of the Cambridge University Engineering Department, for introducing him to the theory of thermophoresis and for computerizing some of the experimental datasets.

Notes

Sharipov uses a different definition of the mean free path from our Equation (1) and his velocity slip and temperature jump (but not thermal creep) coefficients need to be multiplied by a factor of .

APPENDIX 1

Nondimensionalization and Linearization of the G13 Equations

Using the definitions of , , and the dimensionless variables given in the main text, together with Equation (2) and the definitions (we assume G ₀ > 0) and , we obtain the exact nondimensionalized version of Equations (13) as follows:

We also have

All dimensionless variables and gradients are O(1). Hence, if Kn < 1, the condition Ep ≪ 1 gives the linearized Equations (14) in the main text.

APPENDIX 2

Derivation of the G13 Surface Boundary Conditions

A local cartesian (not polar) coordinate system in velocity space (C_r , C _θ, C _φ) is set up at the point (a, θ, φ) on the surface of the sphere. Here, Equation (24) takes the specific form

Equations (A2.1) and (25) are substituted into Equations (12) in order to calculate the total, incident, and diffuse reflected fluxes of mass, momentum, and energy. In performing the integrations, it is best to work in a spherical polar system in velocity space (C, β, γ) defined by the transformation equations C_r =Ccos β, C _θ=Csin βcos γ, and C _φ=Csin βsin γ.

Given this admittedly rudimentary information, the reader will spend many happy hours armed with tables of integrals trying to derive the three boundary conditions. As experienced practitioners know, this is one of the inescapable joys of the kinetic theory. Eventually, the following equations for the conservation of mass, momentum, and energy will be obtained:

All quantities are evaluated at r=a and the relevant value of θ. Nondimensionalizing gives

Using Equations (A1.1f) with the condition Ep ≪ 1 gives the linearized Equations (26) in the main text.