Abstract
A numerical model for the simulation of aerosol flows via an Eulerian–Eulerian, one-way coupled, two-phase flow description is presented. An in-house computational fluid dynamics code is used to simulate the gaseous (continuous) phase, whereas a modified convective diffusion equation models particle transport. The convective diffusion equation, which includes inertial, gravitational, and diffusive particle transport, is solved by computational fluid dynamics techniques. The model is validated by comparing the calculated laminar fluid flow and particle deposition fractions to analytical and experimentally studied aerosol flows in a laminar flow 90° bend of circular cross section available in the literature. Model predictions are also compared with numerical predictions of Eulerian-Lagrangian models. Particle concentration profiles at different cross sections are calculated, and deposition sites on the wall boundary are indicated. For the range of studied particle diameters, the Eulerian–Eulerian model predicts deposition fractions satisfactorily, being in good agreement with the experimental data.
LIST OF SYMBOLS
| Latin | = | |
| c | = |
particle concentration |
| Cc | = |
Cunningham slip correction factor |
|
| = |
gravitational settling velocity vector |
| De | = |
Dean number |
| dp | = |
particle diameter |
| dt | = |
tube diameter |
| Fr | = |
Froude number |
|
| = |
gravity vector |
| Jc | = |
convective flux |
| Jd | = |
diffusive flux |
|
| = |
Cartesian basis vectors |
| k | = |
gravitational settling parameter |
| L | = |
tube length |
|
| = |
normal to the surface unit vector |
| p | = |
fluid pressure |
| Pe | = |
Peclet number |
| Peth | = |
thermal Peclet number |
| Rb | = |
bend radius |
| Re | = |
Reynolds number |
| Ro | = |
bend curvature ratio |
| rt | = |
tube radius |
|
| = |
surface area vector |
| St | = |
Stokes number |
| T | = |
temperature |
| T | = |
time |
|
| = |
fluid velocity vector |
| u, ν, w | = |
Cartesian components of fluid velocity |
|
| = |
particle velocity vector |
| Greek | = | |
| ϵ | = |
relative error |
| ϵ RMS | = |
root-mean-square of the relative error |
| η | = |
deposition fraction |
| μ f | = |
fluid dynamic viscosity |
| ρ f | = |
fluid density |
| ρ p | = |
particle density |
| τ ij | = |
components of the stress tensor |
| τ p | = |
particle relaxation time |
| dΩ | = |
elemental volume |
| Subscripts | = | |
| f | = |
fluid |
| m | = |
mean |
| p | = |
particle |
| T | = |
tube |
| w | = |
wall |
ABBREVIATIONS
| CDS | = |
central differences discretization |
| CFD | = |
computational fluid dynamics |
| CVs | = |
computational volumes |
| PBE | = |
population balance equation |
| UDS | = |
upwind discretization scheme |
INTRODUCTION
Particle deposition in bends is an important removal mechanism in many industrial and biological aerosol processes. Sampling and transport of particles in high-purity gas streams, synthesis and processing of materials using aerosol routes, as well as flow characterization techniques based on aerosol diagnostics are few examples of industrial processes in which particle losses may affect the desired output. The deposition of inhaled particles on human airways, inhaled either from ambient air or as medicinal drugs, is a process important for biological and health effects. In all these processes, particle transport in bends, and specifically particle deposition, plays a significant role.
The most extensive experimental study of particle deposition in a 90° bend of circular cross section up to now has been conducted by Pui et al. (Citation1987). Measurements were performed for both laminar and turbulent flows using monodisperse aerosol populations. The bends were of different tube diameters dt (or radii rt ) and the bend curvature ratios Ro , defined as Ro =Rb /rt with Rb the bend radius, varied from 5.6 to 7.
Numerical investigations of particle deposition due to the fluid-inertia-induced secondary flow have also been carried out. The Lagrangian description of the particulate phase, whereby the particle equations of motion are solved to determine the deposition efficiency [either numerically Breuer et al. (Citation2006), Crane and Evans (Citation1977), Tsai and Pui (Citation1990), or analytically Cheng and Wang (1975, 1981)], is the most frequent choice because it provides a convenient and easy method to treat inertial effects. However, the determination of some average quantities, for example, the local particle concentration field (Slater and Young Citation2001) or the mean interphase momentum transfer (Garg et al. Citation2009), can be particularly difficult. A large number of particle trajectories have to be calculated to minimize statistical error (Desjardins et al. Citation2008), rendering the Lagrangian approach computationally inefficient. The control of the numerical error associated with Lagrangian-Eulerian simulations becomes more important for highly nonuniform spatial distributions of particles as the number of simulated particles in a grid cell decreases; accordingly, the statistical error, which is inversely proportional to the square root of the number of particles per cell, increases. Recent advances in numerical implementations of Lagrangian-Eulerian method have addressed this issue by introducing improved error estimators to obtain numerically convergent simulations (Garg et al. Citation2009).
A distinct advantage of the Lagrangian approach is that it easily captures particle trajectory crossings for finite inertia (finite Stokes number) particles, namely, cases in which the particle velocity distribution is not unimodal and a finite probability exists that particles at the same location have different velocities. Such situations may occur when two particle jets cross, when a particle jet impinges on a surface and it rebounds, or for finite Stokes number particle flows in Taylor–Green vortices. A recently proposed quadrature-based Eulerian moment closure was shown to predict accurately flows with particle-crossing trajectories (Desjardins et al. Citation2008).
Notable alternatives to the Eulerian-Lagrangian calculations are the works of Armand et al. (Citation1998) and Lawson et al. (Citation2006). The latter attempted to calculate the particle concentration in a bend by a full Lagrangian method (Healy and Young Citation2005). Accordingly, the particle concentration was determined by calculating the deformation (dilation or compression) of an infinitesimal rectangular volume along the trajectory of a single particle. The former proposed and validated, in both laminar and turbulent regimes, a Eulerian approach that included inertial particle drift in a two-fluid model. The particle velocity was determined by solving numerically the coupled dispersed-phase mass and momentum equations.
The particle population balance equation (PBE) in a Eulerian description examines aerosol processes (e.g., transport, nucleation, growth, and coagulation) in a fixed elemental volume: diffusion, thus, is treated directly and particle concentration is calculated in a straightforward manner. However, inertial effects cannot be easily included in the standard form of PBE. Here, an approximate expression for the particle velocity is used to incorporate inertial effects in a Eulerian formalism.
This Eulerian approach offers significant advantages over two fluid models that do not decouple the mass and momentum conservation equations of the dispersed phase. First, the numerical solution of the particle momentum equation is not required to determine the particle velocity field, as the momentum equation has been solved perturbatively. As a result, the particle velocity is expressed solely in terms of the fluid velocity and its spatial derivatives (in steady state). Moreover, it can be used for small particle diameters where the particle equations of motion in a Lagrangian approach become numerically stiff. Finally, it is more accurate than passive tracer models as it can take into account simultaneous diffusive and inertial particle transport.
Efforts along this direction have already been made for submicrometer particles. Longest and Oldham (Citation2008) developed an Eulerian–Eulerian model to predict particle deposition in a laminar-bifurcating flow system for cases in which diffusion and inertia are important for particle deposition. They extended the drift flux approach with near-wall corrections to account for particle deceleration between the nearest control volume center and the wall surface. Xi and Longest (Citation2008a) extended this Eulerian–Eulerian model to also account for aerosol dispersion in both turbulent and unsteady flows, and they applied the model to predict deposition in a realistic model of the tracheobronchial airways. Moreover, Xi and Longest (Citation2008b) applied the Eulerian–Eulerian model to predict particle deposition due to inertia, diffusion, and turbulent dispersion in a complex model of the nasal cavity. Similarly, Zhao et al. (Citation2009) presented a generalized drift-flux model for turbulent flows of ultrafine particles in indoor environments. These studies also reported particle concentration and deposition profiles.
In this work, we use a similar Eulerian–Eulerian description of a dilute dispersed flow in the limit of low mass loading and low volume fractions. One-way coupling of the dispersed phase is considered, whereby the dispersed-phase motion is affected by the continuous phase, but not vice versa. In the Eulerian description of the dispersed phase, we approximate the particle velocity in the mass conservation equation of the dispersed (particulate) phase, or equivalently the PBE, by an expression obtained in the limit of low particle relaxation time. The particle velocity is decomposed into a diffusive term, which depends on the particle concentration gradient, and a convective term, independent of particle concentration. The convective particle velocity becomes the fluid velocity corrected by the inertial drift (or slip) and the gravitational settling velocities, thereby introducing particle inertial and gravitational effects in the Eulerian form of the PBE. The main goal of the present work is to study the validity of the particle velocity approximation for higher particle relaxation times. In order to do so, the simple bend geometry and laminar flow field were chosen and we focused on coarse particles (5 μm⩽dp ⩽20 μm), where inertial effects are important and gravity may not be neglected a priori.
The modified PBE is solved numerically in three dimensions using computational fluid dynamics (CFD) techniques. Particle concentration is obtained by imposing the commonly used condition of totally absorbing wall (zero particle concentration at the wall). The particle deposition flux is calculated as the sum of a convective and diffusive flux. The numerical results of the Eulerian fluid particle model are compared with benchmark solutions available in literature.
MODEL DESCRIPTION
Continuous Phase: Numerical Method
The in-house CFD code developed by Neofytou and Tsangaris (Citation2006) is used to solve the Navier–Stokes equations for the three-dimensional incompressible flow field of the carrier fluid. The mass continuity equation in integral form is
In the above equations, ![]() is the fluid velocity, p is the pressure, ρ
f
is the fluid density, τ
ij
is the components of the stress tensor,
is the fluid velocity, p is the pressure, ρ
f
is the fluid density, τ
ij
is the components of the stress tensor, ![]() is the elemental surface with
is the elemental surface with ![]() as the normal to the surface unit vector, dΩ is the elemental volume, and
as the normal to the surface unit vector, dΩ is the elemental volume, and ![]() are the Cartesian basis vectors.
are the Cartesian basis vectors.
The code uses the SIMPLE scheme incorporated in a finite volume method with a collocated arrangement of variables, and it enables multiblock computations. The discretization of the convection terms is performed using the QUICK difference scheme of the third order. A solution is reached assuming Newtonian fluid, laminar flow, constant fluid properties, and one-way coupling, i.e., the influence of the particulate phase on the hydrodynamic field of the carrier fluid is considered negligible. A parabolic velocity profile at the inlet was chosen, and a no-slip fluid velocity condition was imposed at the wall boundaries.
Dispersed Phase: Governing Equations
The general form of the PBE for a monodisperse particle population in a flowing fluid is
Here, we focus on the transport of a population of particles, i.e., the PBE is examined neglecting the internal processes of the right-hand side of EquationEquation (3). The mass conservation equation under steady-state conditions becomes
The effect of inertia on Brownian diffusive transport in isothermal aerosol flows under steady-state conditions was considered by Fernandez de la Mora and Rosner (Citation1982). Stokes’ drag was assumed (particle Reynolds number much smaller than unity) and the particle density was taken to be much higher than the carrier-flow density. They solved the particle momentum equation for the particle velocity to the first order in the particle relaxation time τ p (the inverse of Stokes friction coefficient per unit mass):
The particle velocity is, thus, decomposed into two parts: a diffusive part, dependent only on the particle concentration gradient, and a convective part ![]() , independent of particle concentration. In particular, the convective particle velocity
, independent of particle concentration. In particular, the convective particle velocity
The low-τ p expansion of the particle velocity decouples the mass and momentum conservation equations for the dispersed phase. Therefore, the dispersed-phase mass conservation, EquationEquation (4), takes the form of a modified steady-state convective diffusion equation:
EquationEquation (11) incorporates the effects of particle convection, inertia, and diffusion in an Eulerian formalism to the first order in the particle relaxation time. In the dimensionless and integral form, it becomes (to simplify notation, we retain the same variables to denote dimensionless quantities)
The modified convective diffusion equation written in the form of EquationEquation (13) resembles the usual convective diffusion equation and, thus, it can be numerically treated similarly.
Dispersed Phase: Boundary Conditions
At the inlet, a plug concentration particle profile was used (inlet concentration of unity in the dimensionless form). The particle concentration wall boundary condition was the usual condition of a totally absorbing wall:
Moreover, there is a finite nonzero particle convective velocity just before the wall, due to the external forces [EquationEquation (10)], resulting in a (dimensionless) convective flux, Jc | w , which can be written as
Longest and collaborators (Longest and Oldham Citation2008; Xi and Longest Citation2008a, 2008b) used EquationEquation (17) to calculate the deposition fraction of inertial particles as the sum of a convective and a diffusive term. Furthermore, they analyzed two other alternatives to specify the convective flux at the wall. They found that a velocity correction based on a subgrid Lagrangian solution improved numerical predictions for the local and regional deposition fractions of fine respiratory aerosols. We do not expect that this correction would modify significantly our deposition fraction results because we simulate high inertia particles (high Stokes number particles), whose velocity responds slowly to changes of the fluid velocity. Their velocity at the center of the computational grid closest to the wall persists for a longer time than that of fine aerosol particles (dp ⩽1 μm). More importantly, in our simulations gravity, a body force independent of the fluid velocity acts on these particles.
The modified convection–diffusion equation, EquationEquation (11) or (12), was obtained from the leading-order correction of the particle velocity in terms of the particle relaxation time (in a low Stokes number expansion). It arises from a perturbative solution of the particle-phase momentum conservation equation. Consequently, it captures the leading-order effect of particle inertia on the usual convective diffusion equation, and hence, it becomes important when both inertial and diffusive particle transport occur simultaneously [for an analysis of the low Stokes number expansion in a simple shear flow, and the decoupling of the two continuum conservation equations, see Drossinos and Reeks (Citation2005)]. In the following section, the modified convective diffusion equation will be used to model deposition of nonzero, finite Stokes number particles in a laminar flow bend.
Furthermore, the range of validity of the low Stokes number expansion has not been specified. Ferry and Balachandar (Citation2001) investigated the range and in particular the uniqueness of the Eulerian particle velocity field as a function of τ p , in the absence of diffusion and with elastic particle rebound at the walls. Although they derived an inequality specifying how small τ p should be, they ascertained the accuracy of the expansion through a comparison of the particle velocity obtained by Lagrangian particle tracking and the Eulerian method truncated at various orders (zeroth, first, and second) in a turbulent channel flow. They found that for small τ p (specifically, when the particle response time normalized by the fluid time scale is less than unity), the first-order approximation gave a significant improvement over the zeroth-order term, but the second-order correction did not lead to further improvements. In this work, where in addition, a concentration boundary layer exists and particles diffuse, the validity of the approximation is ascertained by comparing our results with experimental data and previous simulations.
Dispersed Phase: Numerical Solution
Once the fluid velocity ![]() is numerically obtained, the convective particle velocity
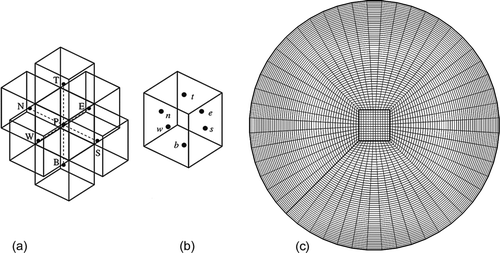
is numerically obtained, the convective particle velocity ![]() is calculated using EquationEquation (10). The modified convection–diffusion equation is subsequently solved in three dimensions using a finite volume method with a collocated arrangement of variables, a numerical scheme analogous to that used for the carrier fluid flow. The convective-velocity term is treated by a deferred-correction approach to avoid a direct application of high-order schemes that would result in big computational molecules (Ferziger and Peric Citation2002). Thus, the convective term is discretized into an implicit part in which a first-order upwind scheme (UDS) is used, and an explicit part composed of the difference between the UDS and the second-order central difference scheme (CDS). Once the iterations converge, the lower-order scheme (UDS) cancels out and the obtained solution corresponds to the higher-order scheme (CDS). The second-order CDS is preferred for the diffusive term. The topology of the grid (Neofytou and Tsangaris Citation2006) and the control volume are shown in .
is calculated using EquationEquation (10). The modified convection–diffusion equation is subsequently solved in three dimensions using a finite volume method with a collocated arrangement of variables, a numerical scheme analogous to that used for the carrier fluid flow. The convective-velocity term is treated by a deferred-correction approach to avoid a direct application of high-order schemes that would result in big computational molecules (Ferziger and Peric Citation2002). Thus, the convective term is discretized into an implicit part in which a first-order upwind scheme (UDS) is used, and an explicit part composed of the difference between the UDS and the second-order central difference scheme (CDS). Once the iterations converge, the lower-order scheme (UDS) cancels out and the obtained solution corresponds to the higher-order scheme (CDS). The second-order CDS is preferred for the diffusive term. The topology of the grid (Neofytou and Tsangaris Citation2006) and the control volume are shown in .
The discretized form of EquationEquation (12) applied on a computational cell leads to the following algebraic equation:
Dispersed Phase: Bend Geometry and Computational Grid
Deposition of a monodisperse aerosol population in a 90° bend of circular cross section was simulated adopting the geometry proposed by Pui et al. (Citation1987) and Breuer et al. (Citation2006). The main geometrical features of the bend are shown in . Two linear sections, the first horizontal of length dt
at the bend inlet and the second vertical of length 2dt
at its exit, are introduced to ensure that the fluid flow in the bend is not disturbed by the inlet and outlet conditions. The diameter of a cross section of the tube at the symmetry plane is denoted as A-A, whereas the diameter of a cross section of the tube perpendicular to the symmetry plane is denoted as B-B. Given this geometry, the flow Reynolds number is Re=ρ
f
υ
o
dt
/μ
f
and the flow Dean number is ![]() . Note that the bend radius Rb
depends on the scale used to render lengths dimensionless, whereas the bend curvature ratio Ro
(=Rb
/rt
) does not.
. Note that the bend radius Rb
depends on the scale used to render lengths dimensionless, whereas the bend curvature ratio Ro
(=Rb
/rt
) does not.
FIG. 2 (a) Geometry (Rb =2.85, Ro =5.7): A-A is the diameter of the cross section at the symmetry plane and B-B is the diameter perpendicular to it; (b) orientation of the bends for Re=100 (left) and Re=1000 (right) and the corresponding gravity vectors.
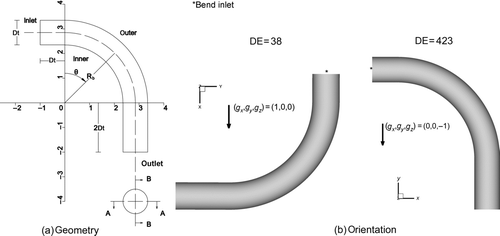
On the basis of the description of the experimental setup of Pui et al. (Citation1987), the orientation in three-dimensional space of the tubes for Re=100 and Re=1000 are shown in . The unit gravity vectors in each case are also noted in this figure. For the case Re=100, a vertical inlet section was used in the experimental setup to minimize particle settling in this section.
The computations were performed using a grid based on an O-type multiblock structure to avoid singularities imposed by a polar grid. The outer block is nearly polar, enclosing the square inner block as shown in . The grid is refined in the vicinity of the wall to capture in detail the concentration boundary layer, a region important for the calculation of particle deposition. The resolution of the grid is about 1.46×106 computational volumes (CVs), consisting of about 6500 grid points in every cross section and 225 grid points in the direction of the flow.
Grid independence of the solution was tested using different grid densities. The root mean square of the relative error of the particle concentration for various grid densities is shown in . The root mean square is defined as ![]() , where ϵ
i
=|(c
i,coarse
−c
i,fine
)/c
i,fine
| is the relative error and N is the number of points used (here 300 from different regions of the computational domain). shows that a further increase in the CVs of the chosen grid by 20% changes the concentration by less than 0.5%.
, where ϵ
i
=|(c
i,coarse
−c
i,fine
)/c
i,fine
| is the relative error and N is the number of points used (here 300 from different regions of the computational domain). shows that a further increase in the CVs of the chosen grid by 20% changes the concentration by less than 0.5%.
TABLE 1 A measure of grid convergence: the root mean square error of particle concentration, ε RMS , for different coarse and fine grid densities
RESULTS AND DISCUSSION
Fluid Flow
FIG. 3 Axial velocity profiles at θ = 0° (inlet), θ = 45°, and θ = 90° (exit) cross sections along the diameters A-A (left) and B-B (right). (a) De=38, and (b) De=419. Results of this study are in black, and those of Tsai and Pui (Citation1990) are in gray.
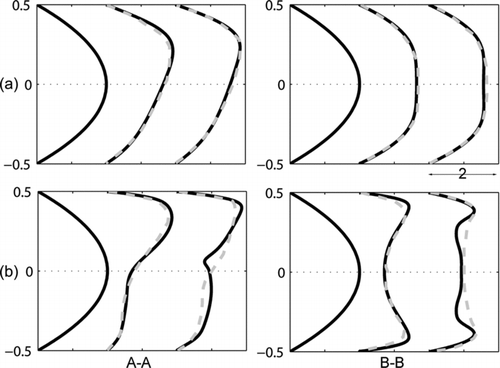
FIG. 4 Secondary flow streamlines and contours of constant axial velocity at θ=45° (top) and θ=90° (bottom) cross sections for De=38 (left) and De=423 (right).

The validity of the calculated flow field is ascertained by simulating two flows with Re=100, Ro =7 (De=38) and Re=1000, Ro =5.7 (De=419). Results are shown in . The axial velocity profiles along the diameters A-A in the symmetry plane (left column) are skewed toward the outer bend wall due to the centrifugal forces exerted on the fluid. The axial velocity profiles along the diameters B-B, which are perpendicular to the symmetry plane (right column), are deformed but remain symmetric with respect to the symmetry plane of the bend. The deformation of the axial velocity profiles along the diameters A-A shifts toward the outer boundary wall of the bend with increasing Dean number. These results are in good agreement with the numerical solution of Tsai and Pui (Citation1990).
The secondary flow streamlines and contours of constant axial fluid velocity are shown in at angles θ=45° and θ=90° along the bend for Dean numbers De=38 (left column) and De=423 (right column). The streamlines of the low Dean number secondary flow show the formation of a pair of symmetric, counter-rotating vortices, the centers of which are slightly displaced toward the outer bend wall at both angles. The main feature of the flow is the formation of an inviscid rotational core surrounded by a thin boundary layer. The peak of the axial fluid velocity is located closer to the outer wall. Our results are similar to those obtained by Pui et al. (1987) for intermediate Dean numbers (17⩽De⩽370).
The secondary flow streamlines for De=423 at 45° also show two main, symmetric counter-rotating vortices, but their centers are displaced toward the inner bend wall and they are skewed with respect to the symmetry plane. In addition, increased centrifugal forces lead to increased fluid flow toward the outer wall; the boundary layer of the secondary flow gets thinner near the outer wall and thicker near the inner wall. At θ=90°, three vortices and their symmetric with respect to the A-A diameter, are formed and the peak of the axial fluid velocity shifts further toward the outer wall. These results are in agreement with both the theoretical descriptions of Pui et al. (Citation1987) for large Dean numbers (De⩾370) and the numerical simulations of Breuer et al. (Citation2006).
Passive Tracer (Graetz-Nusselt Problem)
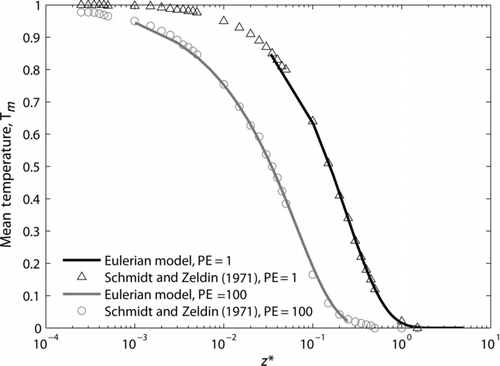
The numerical discretization of the diffusive term is validated by solving the usual convective diffusion problem for a passive tracer. Given the similarities of heat and mass transfer, we simulated the Graetz-Nusselt problem (Shah and London Citation1978). Assuming a hydrodynamically developed fluid flow and a thermally developing temperature field, the following (dimensionless) equation was solved for a straight circular duct:
FIG. 5 Mixing temperature in a straight duct of circular cross section for different Peclet numbers.
Inertial Particles: Deposition Fraction
The fraction of the deposited particles in a duct, η, is calculated by
Inertial Particles: Gravitational Settling
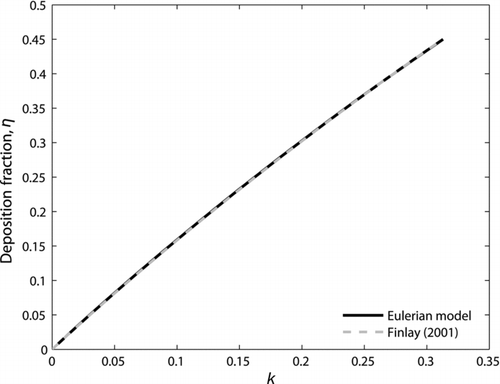
In order to verify the gravitational term in the presented model, the problem of particle deposition in a straight horizontal tube under the sole influence of gravity is simulated. Finlay (Citation2001) presented an analytical solution for the gravitational settling of particles in each generation of the human lung, assuming tubular geometry and Poiseuille fluid flow. For the case of the trachea (tube diameter dt =0.018 m, length L=0.125 m, and mean inlet velocity υ o =1.166 m/s), the results of the Eulerian model agree with the analytical solution, as shown in . The parameter k in the figure is defined by
Inertial Particles: Bend Deposition
The inertial term in the Eulerian–Eulerian model is validated by comparing the calculated particle deposition fractions with previous theoretical calculations and experimental results. Simulations were performed for both analytical and experimental flow fields.
TABLE 2 Fluid and particle properties used in the simulations
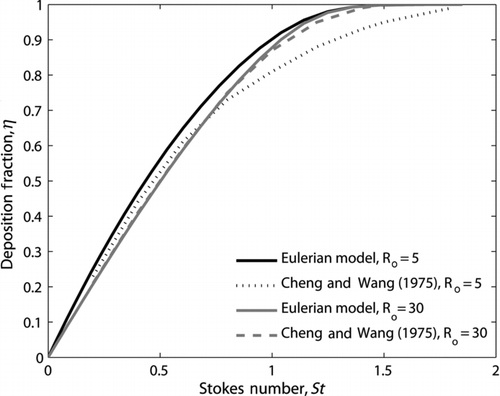
Deposition calculations without gravitational settling were performed for two bend curvature ratios (Ro =5 and 30) with the ideal flow field without secondary flow used by Cheng and Wang (1975); calculated deposition fractions are compared with their analytical results in . The predictions of the Eulerian model agree with the analytical solution at low Stokes numbers, whereas they diverge at high Stokes numbers and at the low bend curvature ratio. The disagreement at high Stokes numbers is not unexpected because the model is based on a low Stokes number expansion. The difference is at maximum 10%, tending to zero with increasing bend curvature, i.e., as particle inertial effects become weaker.
FIG. 7 Deposition fraction—comparison with analytical results of Cheng and Wang (Citation1975).
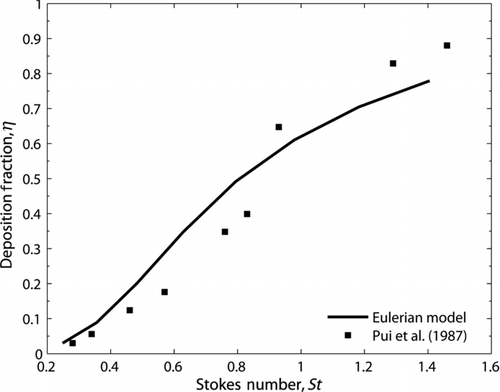
Simulations were also performed for experimental flows taking into account both gravitational and inertial effects and using the parameters shown in . Numerical simulations of aerosol flows for two Dean numbers (De=38 and 423) are compared to the experimental results of Pui et al. (Citation1987), who used oleic acid aerosol particles of varying diameters from 5 to 20 μm, as well as with the Lagrangian simulations of Tsai and Pui (Citation1990).
The Eulerian model predicts well the deposition fraction with respect to experimental data of Pui et al. (Citation1987) for both De=38 and De=423, as shown in Figures and respectively.
FIG. 9 Deposition fraction for De=423—comparison with experimental measurements and numerical simulations.
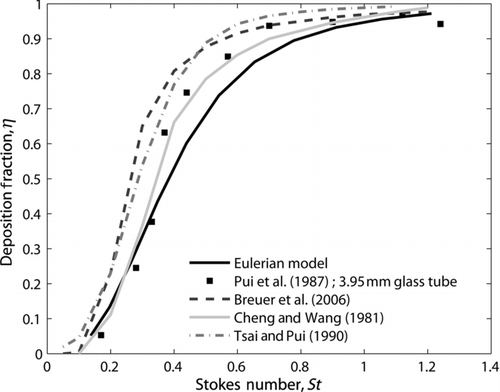
FIG. 10 Particle concentration at θ=45° (top row) and θ=90° (bottom row) cross sections along the bend. (a) De=38 (first two columns) and (b) De=423 (last two columns).

These experiments have been used repeatedly for the validation of deposition efficiency calculations via Lagrangian simulations of the particulate phase for the De=423 case. The results of some of these simulations (Cheng and Wang Citation1981; Breuer et al. Citation2006) are compared with ours in , allowing a direct comparison of Eulerian and Lagrangian methods. The deposition fractions calculated using the Eulerian model differ from the results of Cheng and Wang (Citation1981) (who performed Lagrangian simulations with the analytical fluid flow proposed by Mori and Nakayama [Citation1965]) by less than 10%. However, the difference is up to 30% with the numerical results of Tsai and Pui (Citation1990) and Breuer et al. (Citation2006), who solved numerically for the flow field and used a different friction law. It should be noted that the aforementioned Lagrangian simulations do not take into account gravity. However, we found that gravity is not important compared to the inertial effects in this particular geometry.
Inertial Particles: Particle Concentration Profiles
One of the most appealing features of the Eulerian approach is that it allows an easy calculation of particle concentration profiles. The spatial distribution of particle concentration is presented in at the θ=45° and θ=90° cross sections along the bend for De=38 and St=0.36 (first column) and 1.18 (second column), and De=423 and St=0.35 (third column) and 1.21 (fourth column). The color scale was chosen to vary from 0 (light) to 15 (dark) to visualize the main features of the concentration profiles as maximum particle concentrations of approximately 570 (De=38) to 1100 (De=423) were calculated. For the low Dean number flow, lower Stokes number particles (St=0.36) follow the fluid streamlines and the main features of the secondary fluid flow can be recognized. Deposition is negligible, although there is significant particle accumulation close to the bend walls. With increasing Stokes number, and consequently inertial effects, bend deposition increases, the secondary flow persists, and particles accumulate closer to the walls. Nevertheless, particle trajectories do not deviate significantly from the gas streamlines. For the higher Stokes number (St=1.18), the particle concentration field is qualitatively different from the fluid velocity field because inertial effects dominate, almost no particles exit the bend, and the deposition fraction tends to unity. The large particle-free regions in make evident the difficulty to compute particle concentrations via traditional numerical implementations of Lagrangian particle tracking: a very dense particle injection grid would be required to capture the small regions, where the particle concentration is low. As mentioned in the Introduction section, for highly inhomogeneous spatial particle distributions, an improved numerical scheme, such as suggested by Garg et al. (Citation2009), should be used in the Lagrangian simulations. These trends become more prominent for De=423 because the fluid flow is more intense.
Inertial Particles: Deposition Sites
The location of particle deposition in terms of the particle concentration at the wall boundary is shown in for De=38 (top) and De=423 (bottom): the particle concentration at the computational wall boundary cell is shown. Deposition sites are shown for low and high Stokes numbers, and the bend is presented for both the inner and outer sides. For both Dean numbers and for low Stokes numbers (St=0.36 and St=0.35), significant deposition occurs toward the exit of the bend, as well as at the last straight portion of the tube. As a result of the secondary flow, a substantial amount of particles deposits on the bend side walls, in addition to those deposited on the outer wall. For high Stokes numbers (St=1.18 and St=1.21), deposition occurs closer to the bend inlet, and particles deposit mostly on the outer walls. Thus, the particle-free zone of the bend walls at the inner side is wider in this case. The aforementioned trends are particularly obvious for the higher Dean number flow. They are in agreement with both the experimental observations of Pui et al. (Citation1987) and the calculations of Breuer et al. (Citation2006). Moreover, a comparison of the two subfigures (a) and (b) confirms that the effect of particle inertia is considerably more intense at higher Dean numbers.
CONCLUSIONS
An Eulerian–Eulerian model was developed to simulate steady-state aerosol flows and to calculate particle deposition fractions. Particle transport due to gravity, diffusion, and inertia was incorporated in the Eulerian description of the particulate phase by adding a Stokes-number-dependent, first-order correction to the particle velocity field. Under steady-state conditions, the inertial drift correction depends only on the fluid velocity and its derivatives allowing its evaluation from the fluid velocity field without solving an additional equation, the particulate-phase momentum equation. Particle deposition was calculated from the sum of the diffusive and convective fluxes at the wall.
The Eulerian–Eulerian model was validated against analytical, numerical, and experimental results on inertia-induced particle deposition efficiencies in a 90o laminar flow bend of circular cross section. In particular, model predictions for low Stokes numbers agreed with the analytical results of Cheng and Wang (Citation1975), who used an ideal fluid flow without the secondary flow, slightly overestimating deposition at high Stokes numbers. Maximum difference was about 10% for the smallest bend curvature ratio, tending to zero as the curvature ratio increases, and therefore sufficiently accurate for practical purposes. Comparison of the Eulerian model with experimental data was very good for both low and high Dean number flows (De=38 and De=423). However, the model underestimated deposition with respect to numerical predictions of Eulerian-Lagrangian models. Profiles of particle concentration were calculated and sites of particle deposition along the bend were indicated.
Acknowledgments
Y. Drossinos thanks Sandy Lawson for many useful and critical discussions on the motion of particles in bends and on Lagrangian particle tracking.
REFERENCES
- Armand , P. , Bouland , D. , Pourprix , M. and Vendel , J. 1998 . Two Fluid Modeling of Aerosol Transport in Laminar and Turbulent Flows . J. Aerosol Sci. , 29 : 961 – 983 .
- Breuer , M. , Baytekin , H. T. and Matida , E. A. 2006 . Prediction of Aerosol Deposition in 90o Bends Using LES and an Efficient Lagrangian Tracking Method . J. Aerosol Sci. , 37 : 1407 – 1428 .
- Cheng , Y.-S. and Wang , C.-S. 1975 . Inertial Deposition of Particles in a Bend . J. Aerosol Sci. , 6 : 139 – 145 .
- Cheng , Y. S. and Wang , C. S. 1981 . Motion of Particles in Bends of Circular Pipes . Atmos. Environ. , 15 : 301 – 306 .
- Crane , R. I. and Evans , R. L. 1977 . Inertial Deposition of Particles in a Bent Pipe . J. Aerosol Sci. , 8 : 161 – 170 .
- Desjardins , O. , Fox , R. and Villedieu , P. 2008 . A Quadrature-Based Moment Method for Dilute Fluid-Particle Flows . J. Comput. Phys. , 227 : 2514
- Drossinos , Y. and Housiadas , C. 2006 . Aerosol Flows, in Multiphase Flow Handbook , Boca Raton, FL : Taylor & Francis . C. T. Crowe, ed., (Chap. 6)
- Drossinos , Y. and Reeks , M. W. 2005 . Brownian Motion of Finite-Inertia Particles in a Simple Shear Flow . Phys. Rev. E , 71 : 031113
- Fernandez de la Mora , J. and Rosner , D. E. 1982 . Effects of Inertia on the Diffusional Deposition of Small Particles to Spheres and Cylinders at Low Reynolds Numbers . J. Fluid Mech. , 125 : 379 – 395 .
- Ferry , J. and Balachandar , S. 2001 . A Fast Eulerian Method for Disperse Two-Phase Flow . Int. J. Multiphase Flow , 27 : 1199 – 1226 .
- Ferziger , J. H. and Peric , M. 2002 . Computational Methods for Fluid Dynamics (3rd ed.) , Berlin : Springer .
- Finlay , W. H. 2001 . The Mechanics of Inhaled Pharmaceutical Aerosols. An Introduction , London : Academic Press .
- Garg , R. , Narayanan , C. and Subramaniam , S. 2009 . A Numerically Convergent Lagrangian-Eulerian Simulation Method for Dispersed Two-Phase Flows . Int. J. Multiphase Flow , 35 : 376
- Healy , D. P. and Young , J. B. 2005 . Full Lagrangian Methods for Calculating Particle Concentration Fields in Dilute Gas-Particle Flows . Proc. R. Soc. A , 461 : 2197
- Lawson , J. A. , Reeks , M. W. , Potts , I. and Drossinos , Y. 2006 . “ On the Motion of Particles in a Laminar Flow Bend, ” . In Proceedings of the 7th International Aerosol Conference , Edited by: Biswas , P. , Chen , D. R. and Hering , S. 622 Saint Paul, MN : American Association for Aerosol Research .
- Longest , P. W. and Oldham , M. J. 2008 . Numerical and Experimental Deposition of Fine Respiratory Aerosols: Development of a Two-Phase Drift Flux Model with Near-Wall Velocity Corrections . J. Aerosol Sci. , 39 : 48 – 70 .
- Mori , Y. and Nakayama , W. 1965 . Study on Forced Convective Heat Transfer . Int. J. Heat Mass. Transf. , 8 : 67 – 82 .
- Neofytou , P. and Tsangaris , S. 2006 . Flow Effects of Blood Constitutive Equations in 3D Models of Vascular Anomalies . Int. J. Numer. Meth. Fluid , 51 : 489 – 510 .
- Pui , D. Y. H. , Romay-Novas , F. and Liu , B. Y. H. 1987 . Experimental Study of Particle Deposition in Bends of Circular Cross Section . Aerosol Sci. Technol. , 7 : 300 – 315 .
- Schmidt , F. W. and Zeldin , B. 1971 . Laminar Heat Transfer in the Entrance Region of Ducts . Appl. Sci. Res. , 23 : 73 – 94 .
- Shah , R. K. and London , A. L. 1978 . Laminar Flow Forced Convection in Ducts New York, NY : Academic Press, .
- Slater , S. A. and Young , J. B. 2001 . The Calculation of Inertial Particle Transport in Dilute Gas-Particle Flows . Int. J. Multiphase Flow , 27 : 61 – 87 .
- Tsai , C.-J. and Pui , D. Y. H. 1990 . Numerical Study of Particle Deposition in Bends of a Circular Cross-Section-Laminar Flow Regime . Aerosol Sci. Technol. , 12 : 813 – 831 .
- Xi , J. and Longest , P. 2008a . Evaluation of a Drift Flux Model for Simulating Submicrometer Aerosol Dynamics in Human Upper Tracheobronchial Airways . Ann. Biomed. Eng. , 36 : 1714 – 1734 .
- Xi , J. and Longest , P. 2008b . Numerical Predictions of Submicrometer Aerosol Deposition in the Nasal Cavity Using a Novel Drift Flux Approach . Int. J. Heat Mass. Transf. , 51 : 5562 – 5577 .
- Zhao , B. , Chen , C. and Tan , Z. 2009 . Modeling of Ultrafine Particle Dispersion in Indoor Environments with an Improved Drift Flux Model . J. Aerosol Sci. , 40 : 29 – 43 .