The Structure of Agglomerates Consisting of Polydisperse Particles

Abstract

Agglomeration is encountered in many natural or industrial processes, like growth of aerosol particles in the atmosphere and during material synthesis or even flocculation of suspensions, granulation, crystallization, and with colloidal particle processing. These particles collide by different mechanisms and stick together forming irregular or fractal-like agglomerates. Typically, the structure of these agglomerates is characterized with the fractal dimension, D_f , and pre-exponential factor, k_n , of simulated agglomerates of monodisperse primary particles (PP) for ballistic or diffusion-limited particle–cluster and cluster–cluster collision mechanisms. Here, the effect of PP polydispersity on D_f and k_n is investigated with agglomerates consisting of 16-1024 PP with closely controlled size distribution (geometric standard deviation, σ_g = 1–3). These simulations are in excellent agreement with the classic structure (D_f and k_n ) of agglomerates consisting of monodisperse PPs made by four different collision mechanisms as well as with agglomerates of bi-, tridisperse, and normally distributed PPs. Broadening the PP size distribution of agglomerates decreases monotonically their D_f , and for sufficiently broad PP distributions (σ_g > 2.5) the D_f reaches about 1.5 and k_n about 1 regardless of the collision mechanism. Furthermore, with increasing PP polydispersity, the corresponding projected area exponent, D_α , and pre-exponential factor, k_a , decrease monotonically from their standard values for agglomerates with monodisperse PPs. So D_f as well as D_α and k_a can be an indication for PP polydispersity in mass mobility and light scattering measurements if the dominant agglomeration mechanism is known, like diffusion-limited and/or ballistic cluster–cluster coagulation in aerosols.

Copyright 2012 American Association for Aerosol Research

INTRODUCTION

Significant advances have been made in agglomerate characterization by employing the so-called fractal theory and relating agglomerate structure to its generation pattern through the fractal dimension, D_f . For example, agglomerates made by diffusion-limited cluster–cluster agglomeration (DLCA) have D_f = 1.78 (Jullien et al. 1984), or by diffusion-limited particle–cluster agglomeration (DLA) have D_f = 2.5 (Tolman and Meakin 1989), ballistic cluster–cluster agglomeration (BCCA) have D_f = 1.90 (Meakin and Jullien 1988), and ballistic particle–cluster agglomeration (BPCA) have D_f = 3.0 (Ball and Witten 1984) as were summarized for aerosols by Schaefer and Hurd (1990). These D_f values have become the standard in agglomerate (physically bound particles) and even aggregate (chemically- or sinter-bound particles) characterization despite the fact that such particles may not fully obey fractal theory but are sufficiently close to it to be called fractal-like.

This concept has served well the process design of a wide spectrum of filamentary particles (carbon black, nickel, and fumed silica), made up mostly by aerosol coagulation. In fact, a number of characterization techniques and process design concepts have been developed capitalizing on these D_f values to extract other particle properties (e.g., collision diameter, primary particle size) and design reactors for manufacturing such particles. They are characterized by a power law relating the number of primary particles in an agglomerate to primary particle radius and radius of gyration or collision radius. For example, in aerosol reactor design, the coagulation rate of spherical particles is corrected to that of fractal-like ones in the free molecular (Matsoukas and Friedlander 1991) and continuum (Oh and Sorensen 1997) regimes by introducing the radius of gyration and D_f in their collision area term (Mountain et al. 1986).

What might have been overlooked in characterization and simulations of fractal-like particles is that the above D_f values have been developed for agglomerates of monodisperse primary particles. Notable exceptions come from Tence et al. (1986) and Bushell and Amal (1998) who had examined the effect of primary particle polydispersity on agglomerate structure and scattering behavior. They numerically generated BCCA and DLCA agglomerates having Gaussian-distributed (Tence et al. 1986) and mono-, bi-, and tridisperse (Bushell and Amal 1998) primary particles and found no effect on D_f for their employed polydispersities.

For coagulating aerosols, however, this needs to be carefully examined, as Brownian coagulation-driven particle formation leads to polydisperse particles. Their distribution, even at a single streamline is, at best, as narrow as that given by the self-preserving theory, e.g., having geometric standard deviation, σ_g , of about 1.45 (Landgrebe and Pratsinis 1989). When agglomerates are made in aerosol reactors at different (e.g., radial) residence time distributions and collected, typically, by filtration, much broader size distributions can be obtained. Agglomerates with quite polydisperse primary particle size distribution are obtained during gas-to-particle conversion or when primary particles with different residence time histories are mixed. So, the common extraction of D_f by microscopic counting of such agglomerates and primary particles may not necessarily lead to an accurate assessment of their formation pathway as has been proposed by Schaefer and Hurd (1990). Similarly, the use of D_f in designing aerosol synthesis of such particles needs to account for agglomerates of polydisperse primary particles.

Here, fractal-like agglomerates consisting of 16, 64, 256, 512, and 1024 primary particles having closely controlled size distributions are generated by DLA, DLCA, BCCA, and BPCA. So, the employed primary particle radii are lognormally distributed with geometric standard deviation σ_g ranging from 1 (monodisperse) to 3 and the structure characteristics (D_f and pre-exponential factor k_n ) of such agglomerates are calculated by fractal theory for these collision mechanisms and compared to the literature at limiting cases. Furthermore, the projected area exponent and pre-exponential factor that are used in aerosol characterization by mass-mobility measurements are obtained as a function of primary particle polydispersity.

Theory

Agglomerates grown by particle collisions exhibit a power law scaling between number of primary particles, n_p , and radius of gyration, r_g (Mandelbrot 1982):

where the exponent D_f is the fractal dimension, r_p the monodisperse or geometric mean, primary particle radius, k_n, a prefactor, and the radius of gyration is:

with m_i being the mass and x_i the distance of primary particle i to the agglomerate center of mass. For agglomerates of polydisperse primary particles, the equivalent monodisperse or surface area mean primary particle radius r_va and number n_va are commonly determined by the (total) agglomerate volume v and surface area a:

This corresponds to the average primary particle radius determined experimentally by nitrogen adsorption, r _BET, and small-angle X-ray scattering (SAXS), r_VS (Hyeon-Lee et al. 1998). The r_va is equal to r_p for agglomerates of monodisperse spherical primary particles.

The projected agglomerate area a_a onto a plane is also related to n_p by a power law (Medalia 1967):

where a_p is the projected area of a primary particle and D_α and k_a are the power law exponent and prefactor, respectively. The projected area is an important agglomerate property as it can be used to define the agglomerate mobility diameter, d_m , in the free molecular regime (Meakin 1988):

This holds well even in the transition regime up to Knudsen number Kn = 0.28 (Rogak et al. 1993). Equations (5) and (6) are used to characterize agglomerates by mass-mobility measurements (Park et al. 2003).

FIG. 1 Agglomerates consisting of 1024 monodisperse primary particles made by (a) diffusion-limited (DLCA) and (b) ballistic cluster–cluster (BCCA) agglomeration as well as by (c) diffusion-limited (DLA) and (d) ballistic particle–cluster (BPCA) agglomeration. These agglomerates have D_f = 1.79, 1.89, 2.25, and 2.81 identical to those calculated by Botet et al. (1982), Tence et al. (1986), Witten and Sander (1981), and Sutherland (1966), respectively.

The a_a is calculated by Monte Carlo integration (Meakin 1988) and averaged over 50 homogeneously distributed random angles for each agglomerate. The D_f and k_n as well as D_α and k_a are obtained by ensemble averaging over agglomerates of different n_p (Eggersdorfer et al. 2010) and similarly to the evaluation of experiments (Sorensen et al. 1992). The D_f or D_α is determined from the slope of r_g or a_a versus the n_p or n_va in a double logarithmic plot, while the intersection with the y-axis is the logarithm of the prefactor k_n or k_a , respectively (Medalia 1967; Forrest and Witten 1979).

RESULTS AND DISCUSSION

Validation

One hundred agglomerates of each number (n_p = 16-1024) and polydispersity (σ_g = 1–3) of primary particles (PP) are generated by DLA (Witten and Sander 1981), DLCA (Botet et al. 1984), BCCA (Tence et al. 1986), and BPCA (Sutherland 1966) to determine D_f and k_n by Equation (1) and D_α and k_a by Equation (5). Figure 1 shows typical images of agglomerates made with monodisperse primary particles (σ_g = 1) for DLA, DLCA, BCCA, and BPCA similar to Schaefer and Hurd (1990). These agglomerates have D_f = 1.79 ± 0.03 (DLCA), 1.89 ± 0.03 (BCCA), 2.25 ± 0.02 (DLA), and 2.81 ± 0.03 (BPCA). The DLCA and BCCA values are in excellent agreement with Jullien et al. (1984) and Tence et al. (1986). The D_f of DLA and BPCA are slightly smaller than their asymptotic limits of 2.5 and 3 by Tolman and Meakin (1989) and Ball and Witten (1984), respectively. This is a finite size effect, as the D_f of small agglomerates is always lower than their asymptotic D_f (Meakin 1999). k_n = 1.40 ± 0.12 for monodisperse DLCA agglomerates (Table 1) is consistent with Sorensen and Roberts (1997). The BCCA, DLA, and BPCA agglomerates of monodisperse primary particles have k_n = 1.36 ± 0.1, 0.86 ± 0.04, and 0.46 ± 0.03 (Table 1, actual n_p and r_p ).

TABLE 1 The prefactor k_n and fractal dimension D_f of agglomerates made by DLCA, BCCA, DLA, and BPCA as obtained using the actual PP number n_p and radius r_p are compared to k_n and D_f obtained assuming monodisperse PPs of equivalent average number n_va and radius r_va (Equations (3) and (4))

	Actual np and rp		Mondisperse assumption, nva and rva (Equations (3) and (4))
σg	Df	kn	Df	kn
	DLCA
1.00	1.79 ± 0.03	1.40 ± 0.12	1.79 ± 0.03	1.40 ± 0.12
1.45	1.77 ± 0.03	1.23 ± 0.11	1.79 ± 0.03	1.42 ± 0.11
2.00	1.68 ± 0.03	0.98 ± 0.11	1.74 ± 0.03	1.53 ± 0.11
2.50	1.57 ± 0.04	0.90 ± 0.13	1.68 ± 0.04	1.66 ± 0.11
3.00	1.48 ± 0.04	0.77 ± 0.13	1.60 ± 0.04	1.80 ± 0.11
σg	BCCA
1.00	1.89 ± 0.03	1.36 ± 0.10	1.89 ± 0.03	1.36 ± 0.10
1.45	1.85 ± 0.03	1.25 ± 0.11	1.86 ± 0.03	1.49 ± 0.11
2.00	1.74 ± 0.04	1.09 ± 0.12	1.75 ± 0.03	2.04 ± 0.14
2.50	1.62 ± 0.04	1.06 ± 0.15	1.53 ± 0.04	3.01 ± 0.19
3.00	1.52 ± 0.04	1.00 ± 0.16	1.36 ± 0.04	3.62 ± 0.20
σg	DLA
1.00	2.25 ± 0.02	0.86 ± 0.04	2.25 ± 0.02	0.86 ± 0.04
1.45	2.21 ± 0.03	0.63 ± 0.05	2.21 ± 0.03	0.83 ± 0.05
2.00	1.91 ± 0.05	0.64 ± 0.10	1.91 ± 0.05	1.23 ± 0.10
2.50	1.71 ± 0.06	0.63 ± 0.13	1.71 ± 0.06	1.50 ± 0.13
3.00	1.51 ± 0.05	0.82 ± 0.17	1.51 ± 0.05	2.31 ± 0.2
σg	BPCA
1.00	2.81 ± 0.03	0.46 ± 0.03	2.81 ± 0.03	0.46 ± 0.03
1.45	2.62 ± 0.04	0.41 ± 0.04	2.70 ± 0.04	0.55 ± 0.04
2.00	2.12 ± 0.05	0.51 ± 0.08	2.26 ± 0.05	1.17 ± 0.11
2.50	1.80 ± 0.06	0.61 ± 0.14	1.93 ± 0.06	1.76 ± 0.17
3.00	1.57 ± 0.06	0.75 ± 0.17	1.58 ± 0.06	2.56 ± 0.21

Agglomerates with bi- and tridisperse primary particles were made also by DLCA to compare to Bushell and Amal (1998). These agglomerates consist of primary particles of two and three distinct diameters, respectively. Their bidisperse agglomerates with a PP radius ratio of 3:1, and about 4% of the large particles were calculated here to have D_f = 1.79 ± 0.03. Similarly their tridisperse PP radius ratio of 5:3:1 with distributions of 1:18:81% and PP radius ratio of 5:2:1 with distributions of 10:60:30% were calculated here to have D_f = 1.77 ± 0.03 and 1.79 ± 0.03, respectively. All were in excellent agreement with Bushell and Amal (1998) who had reported D_f = 1.78 ± 0.03. Tence et al. (1986) obtained by BCCA agglomerates of primary particles having a Gaussian-like distribution (n = 2 and β = 5) that corresponds to a σ _g = 1.35. The present simulations with primary particles having this σ _g resulted in agglomerates that had a D_f = 1.91 ± 0.05, which is quite close to that of 1.89 ± 0.03 (Tence et al. 1986). These results validate the employed algorithms to address the structure of agglomerates having arbitrarily broad distributions of primary particles.

FIG. 2 Snapshot of 100 agglomerates made by diffusion-limited cluster–cluster agglomeration (DLCA) consisting of 512 primary particles with a lognormal size distribution with geometric standard deviation σ_g = 2.

Effect of Primary Particle Polydispersity on Fractal Dimension and Prefactor

The primary particles are lognormally distributed with a geometric standard deviation σ_g = 1–3. Figure 2 shows a TEM-like image of 100 DLCA agglomerates consisting of 512 PPs with σ_g = 2.

Figure 3 shows close-up snapshots of randomly chosen agglomerates consisting of 1024 PPs of σ_g = 2 and 3 made by DLCA, BCCA, DLA, and BPCA along with the corresponding D_f . The broader the PP size distribution and thus the larger the difference between PPs, the stringier and more open are the agglomerates having a lower D_f than the benchmark agglomerates of monodisperse PPs (Figure 1). At σ_g = 3, all agglomerates look similar somehow, regardless of the collision mechanism.

Figure 4a quantifies these pictures by showing the D_f of agglomerates as a function of their constituent PP size distribution from σ_g = 1 (monodisperse) to 3 for DLCA (circles), BCCA (squares), DLA (triangles), and BPCA (diamonds). D_f decreases with increasing σ_g and for σ_g = 3 the different collision mechanisms converge to nearly the same D_f ≈ 1.5. Clearly, the presence of various primary particle sizes results in more open agglomerate structures. The more polydisperse are the PPs, the more open space they leave between them within an agglomerate.

FIG. 3 Agglomerates of polydisperse primary particles having geometric standard deviation σ_g = 2.0 (left column) and 3.0 (right column) made by diffusion-limited (DLCA) and ballistic cluster–cluster agglomeration (BCCA) as well as by diffusion-limited (DLA) and ballistic particle–cluster agglomeration (BPCA). The structure of agglomerates consisting of very polydisperse (σ_g = 3) particles is quite similar (D_f = 1.48 – 1.57) indicating that their polydispersity essentially “washes out” differences in agglomeration mechanisms.

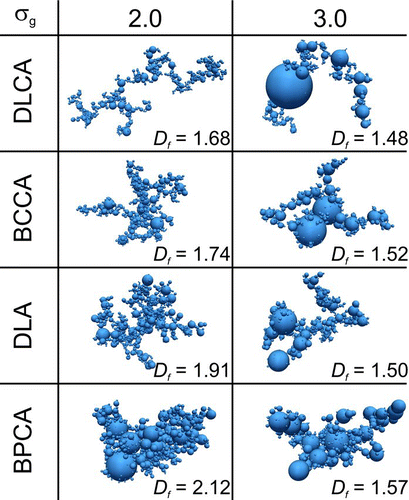
Polydispersity adds another element of disorder when uniform primary particles are replaced with nonuniform ones. As the motion of particles or clusters is independent from each other, their arrival or sticking point upon collision is fixed. Take, for example, particle–cluster agglomeration. The trajectory of the particle till its collision with a cluster is determined by its mobility diameter. As individual polydisperse PPs arrive at the cluster, more irregular and open structures are developed than with uniform PPs. As a result, the compact agglomerate structures made by DLA and BPCA of monodisperse PPs with D_f of 2.25 and 2.81, respectively, are affected most dramatically by the PP polydispersity (Figure 4a). Similar concepts apply to cluster–cluster agglomeration. The larger particles contribute much more to r_g than the smaller ones since r_g is calculated with the mass-weighted mean square displacement (Equation (2)). So D_f is very sensitive to PP polydispersity. The differences between particle masses increase for increasing σ_g so that at high polydispersities fewer particles effectively contribute to D_f . This results in D_f = 1 in the limit of two effective particles as r_g represents the high-order moments of the distribution (square root of the ratio between 2nd and 0th moment of mass-based distribution).

FIG. 4 The asymptotic (a) fractal dimension D_f and (b) prefactor k_n of 500 agglomerates as a function of the geometric standard deviation, σ_g , of their primary particles (PP) for different collision or agglomeration mechanisms. At σ_g = 1 (monodisperse PP), the classic D_f of the corresponding structures is obtained. With increasing σ_g , the D_f decreases gradually reaching asymptotically ≈ 1.5 (a) and k_n ≈ 1 (b) at σ_g = 3, nearly independent of the agglomeration mechanism.

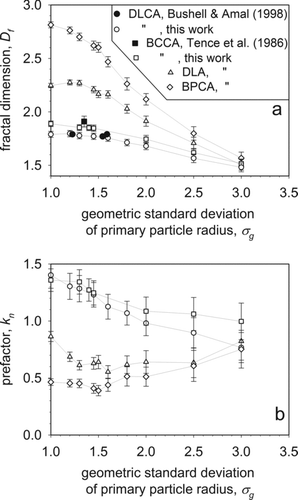
Figure 4a shows also the DLCA simulations (filled circles) of bi- and tridisperse PPs by Bushell and Amal (1998) as well as the BCCA ones (filled square) of Tence et al. (1986). Clearly, both studies had been carried out with relatively narrow PP-size distributions to observe any reduction of D_f by the polydispersity of primary particles seen here. This monotonic reduction of D_f with increasing σ_g can be used to determine the effect of PP polydispersity on the structure of agglomerates by all four collision mechanisms.

Figure 4b shows the prefactor k_n for the agglomerates made here as a function of PP σ_g also. While D_f decreases monotonically for increasing σ_g , regardless of collision mechanism, not all k_n exhibit such a monotonic behavior. Nevertheless, all reach a k_n ≈ 1 for very broad PP polydispersities (σ_g > 2.5). For DLCA and BCCA particles, k_n decreases continuously with increasing PP polydispersity, while for both DLA and BPCA k_n reaches a minimum here at σ_g = 1.6 and 1.5, respectively.

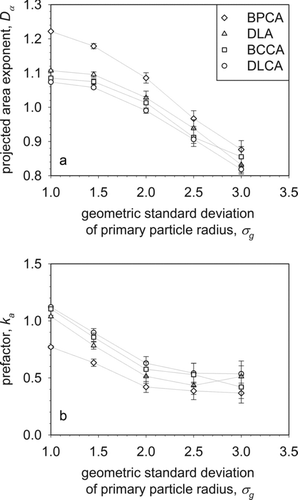
FIG. 5 The projected area exponent D_α (a) and prefactor k_a (b) of DLCA (circles), BCCA (squares), DLA (triangles), and BPCA (diamonds) agglomerates as a function of the geometric standard deviation σ_g of their constituent primary particles. D_α and k_a decrease monotonically for increasing σ_g regardless of the agglomerate generation mechanism.

For σ_g = 1.45, the standard deviation of the self-preserving size distribution (SPSD) obtained by Brownian coagulation that corresponds best to DLCA, both D_f and k_n are within the error bars of agglomerates with monodisperse PPs and thus indistinguishable from each other. This indicates that PP polydispersity may not affect the structure of DLCA agglomerates made by aerosol coagulation on a single process streamline or residence time history. When, however, such particles are collected from a filter where particles of various residence time (and even temperature) histories are arriving, there would be a significant effect depending on their actual polydispersity. In practical systems, the primary particle size distribution is often unknown and for simplicity assumed to be monodisperse.

Table 1 compares the D_f and k_n determined with the actual r_p and n_p to that determined by the assumption of an average PP size of polydisperse (σ_g = 1–3) PPs using r_va and n_va as might be determined by microscopic counting, nitrogen adsorption, or SAXS. For all agglomeration mechanisms, the D_f is not affected by more than 10%. In contrast, the k_n is overestimated significantly when assuming all primaries to have the same size for all collision mechanisms (Table 1, last column).

FIG. 6 The fractal dimension D_f versus projected area exponent 2D_α for DLCA (circles), BCCA (squares), DLA (triangles), and BPCA (diamonds) agglomerates and σ_g = 1–3. The broken line corresponds to D_f = 2D_α . For cluster–cluster agglomerates, 2D_α is always larger than D_f , while particle–cluster agglomerates have a transition at D_f ≈ 2.1 between σ_g = 1.5 and 2.

Effect of Primary Particle Polydispersity on Projected Surface Area and Mass-Mobility Characterization

The projected surface area a_a of agglomerates controls the mass and heat transfer, e.g., the collision frequency with particles much smaller than the gas mean free path and thus the mobility of agglomerates in the free molecular and transition regime (Meakin 1988; Rogak et al. 1993). For DLCA agglomerates of monodisperse PPs, D_α = 1.08 ± 0.002 in Equation (5), which is consistent with Pierce et al. (2006). Similar to D_f , the D_α decreases with increasing σ_g (Figure 5a). The a_a depends on the square of PP radius. So, the largest PPs dominate while the smallest PPs hardly contribute to a_a . Agglomerates of the same mean PP radius but broader σ_g also have a larger a_a and, in turn, a reduced D_α regardless of the collision mechanism.

Figure 5b shows the prefactor k_a of Equation (5) as a function of σ_g . The k_a decreases until σ_g = 2.0 and levels off for higher polydispersities. Though even for σ_g = 3.0, where D_f and k_n are nearly independent of the collision mechanism indicating a similar mass distribution of the agglomerates, D_α and k_a differ for the four collision types. The DLCA particles have always the largest k_a and smallest D_α , since their most open structure results in primary particles that are less shielded by neighbors compared to BCCA, DLA, and BPCA agglomerates (Figure 1 and 3). For all collision mechanisms, the monotonic dependence of D_α and k_a on σ_g can be used to extract the effect of PP polydispersity of agglomerates by mass-mobility measurements as with D_f (Figure 4a).

As two measures of fractal dimension are available for these agglomerates of various PP polydispersities and collision mechanisms, it is worth comparing them. So, Figure 6 shows the D_f versus 2D_α by combining Figures 4a and 5a. For both diffusion-limited and ballistic cluster–cluster agglomeration, the r_g -based D_f is smaller than the r_m -based 2D_α regardless of PP polydispersity, with r_m = d_m /2. This is not surprising as DLCA and BPCA agglomerates have a D_f < 2 and very open chain-like structures even for a monodisperse PP-size distribution, so always r_m < r_g (Sorensen 2011) and D_f < 2D_a . Particle–cluster agglomerates (triangles & diamonds), however, are rather compact at σ_g < 2 with D_f > 2 (Figure 4a), so D_f > 2D_α . Both BPCA and DLA agglomerates of monodisperse PPs have r_m > r_g similar to that of a sphere with (Hiemenz 1986). With increasing PP polydispersity, however, the particle–cluster agglomerates become more open so and exhibit a transition at D_f ≈ 2.1 from D_f > 2D_α to D_f < 2D_α (between σ_g = 1.5 and 2 in Figures 4a and 5a) as their r_m < r_g . For D_f > 2, the projected areas are compact objects with screening of individual PP while for D_f < 2 almost all PPs are accessible (Mulholland et al. 1988). So the polydispersity of PPs affects most dramatically the structure of particle–cluster agglomeration made by both diffusion-limited and ballistic collisions.

CONCLUSIONS

Agglomerates consisting of polydisperse primary particles were generated by DLCA, BCCA, DLA, and BPCA. The effect of primary particle size distribution on resulting agglomerate fractal dimension D_f and prefactor k_n , projected area exponent D_α , and prefactor k_a was investigated. Asymptotic D_f and k_n values were obtained for agglomerates of primary particles having geometric standard deviation σ_g ranging from 1.0 to 3.0. These simulations were in agreement with the literature for fractal agglomerates of monodisperse primary particles and even with limited studies of fractal-like particles containing Gaussian-like, bi- and tridisperse primary particles.

It was discovered that polydisperse primary particles result in more open agglomerate structures with lower D_f , D_α, and k_a than the classic with monodisperse PPs. This is most notable for particle–cluster (up to 50% reduction) and to a lesser extent for cluster–cluster (up to 20% reduction) ballistic and diffusion-limited collision-generated agglomerates. Furthermore, it was shown that the assumption of an average primary particle size, which is commonly applied in particle characterization, hardly affects D_f but significantly overestimates k_n for polydisperse PPs for all collision mechanisms. Most remarkably, for processes generating agglomerates by a known collision mechanism, a D_f , D_α , or k_a smaller than the benchmark values of agglomerates consisting of monodisperse PPs might be an indication for agglomerates of polydisperse primary particles.

Acknowledgments

This research was funded by ETH Research Grant (ETHIIRA) ETH-11 09-1 and the European Research Council.