Particle Size Distributions following Condensational Growth in Continuous Flow Aerosol Reactors as Derived from Residence Time Distributions: Theoretical Development and Application to Secondary Organic Aerosol

Abstract

Condensational growth in continuous flow reactors, such as continuously mixed flow reactors (CMFRs) and flow tube reactors, is widely employed in the field of aerosol science and technology to produce particles for industrial use and scientific research. The development of analytical equations for the number-diameter distribution n(d) of the particles in the outflow from these reactors is advantageous both for the inversion of data sets to obtain thermodynamic and kinetic parameters as well as for the rational design of experiments. In this study, equations are derived that relate the number-diameter distribution n(d) to the probability density function p(t) of particle residence time. Specifically, the condensational growth rate is used to derive n(d) based on p(t). Analytical equations are developed for CMFRs, laminar-flow reactors, and dispersive plug-flow reactors, with a focus on CMFRs. The CMFR equation accurately describes data sets collected for α-pinene and β-caryophyllene ozonolysis in the Harvard Environmental Chamber (HEC). The interpretation is that condensational growth can be considered as the principal mechanism for change in particle diameter in these experiments.

Copyright 2012 American Association for Aerosol Research

1. INTRODUCTION

Continuous flow reactors have been employed widely in various areas of aerosol science and technology, including industrial particle generation (Pratsinis 1998), materials science (Chiang and Sankaran 2009), and aerosol chemistry (Martin and Han 2000; Katrib et al. 2004). These reactors, operated under conditions of balanced and steady inflows and outflows, include continuously mixed chambers as well as flow-tube reactors. Of particular recent interest, these types of reactors have been used for atmospherically related studies of secondary organic material (SOM) (Kleindienst et al. 1999; VanReken et al. 2006; Shilling et al. 2008; Wex et al. 2009; Ezell et al. 2010; Lambe et al. 2011; Vesterinen et al. 2011). Continuously mixed flow reactors (CMFRs) can be used for stable sampling over long time periods, and this capability permits quantitative measurements of SOM particle properties at concentrations as low as those that occur in the atmosphere.

TABLE 1 Definitions and equations for f(d,t), N_T , n(d), and p(t)

Quantity	Symbol	Units	Equation
Distribution function of particle number concentration	f(d,t)	particles m^−3 m^−1 s^−1	n/a	(T1)
Total particle number concentration	NT	particles m^−3		(T2)
Number-diameter distribution	n(d)	particles m^−3 m^−1	n(d)=∫limits ^∞ 0 f(d, t)dt	(T3)
Probability density function of particle residence time	p(t)	particles s^−1	p(t)=N ^−1 T ∫limits ^∞ 0 f(d, t)dd	(T4)

Theories of the particle number-diameter distribution n(d) in the reactor outflow can allow for the derivation from experimental data of several different chemical kinetic and thermodynamic parameters. Furthermore, controlling and predicting the number-diameter distributions in the reactor is important for the effective design of experiments. For these reasons, several different theoretical approaches have been developed to calculate n(d) in continuous flow reactors. These approaches have considered in various ways the processes of nucleation, coagulation, and condensational growth of the particles. The approaches have included both analytical (Crump and Seinfeld 1980; Seinfeld et al. 2003) and numerical (Kodas and Friedlander 1988; Verheggen and Mozurkewich 2006; Vesterinen et al. 2011) solutions to the General Dynamic Equation (Friedlander 2000). Modal aerosol dynamics models have also been developed (Whitby and McMurry 1997). The formulation presented by Seinfeld et al. (2003) has been particularly successful in application to the data sets of several recent CMFR SOM studies (King et al. 2009; Smith et al. 2011).

In the case of condensational growth, a governing principle of continuous flow reactors is that particles grow during their residence time, meaning that young particles are small and old particles are large. For this reason, the number-diameter distribution n(d) of the particle population in the reactor outflow is tightly coupled to the probability density function p(t) of particle residence time t (Dragoescu and Friedlander 1989). For instance, a tightly distributed p(t) is recommended for the production of monodisperse particles in continuous flow reactors (Pratsinis et al. 1986; Kodas and Friedlander 1988). The distribution p(t) can be calculated for ideal reactors or alternatively measured for real reactors (Davis and Davis 2003), including aerosol particle reactors (Lambe et al. 2011).

In the present study, we develop a theoretical framework that directly connects n(d) to p(t) using the condensational growth rate of the particles. Formulations are presented for CMFRs, laminar-flow reactors, plug-flow reactors of variable dispersion, and reactors of arbitrary p(t). The main focus is on the condensational growth of particles for a CMFR in which secondary organic aerosol is produced. The developed equations are relatively simple mathematically and computationally yet are shown to accurately model the number-diameter distributions measured for α-pinene and β-caryophyllene ozonolysis in the Harvard Environmental Chamber (HEC).

2. THEORY

2.1. Definitions

A reactor of the laminar, plug, or continuously mixed type has a mean particle residence time τ (Appendix A and Supplemental Information). Particle diameter increases by condensational growth that takes place in the reactor. The seed particle number concentration is sufficiently high such that there is no significant new particle formation by nucleation yet sufficiently low that particle–particle coagulation is not important. For these conditions, the distribution function f(d,t) of particle number concentration in the reactor outflow is bivariate in particle diameter d and particle residence time t. From f(d,t), the total particle number concentration N_T , the number–diameter distribution function n(d), and the probability density function p(t) of particle residence time can be obtained. The equations are listed in Table 1.

The seed particle population has a number-diameter distribution n*₀(d) in the inflow to the reactor and a distribution n ₀(d) in the outflow from the reactor. For any finite wall-loss rate in the reactor, n*₀(d)>n ₀(d). In the absence of condensational growth in the reactor, n(d)=n ₀(d), meaning that the subscript 0 represents the case of a condensational growth rate of zero. When condensational growth does occur, n(d)≠n ₀(d), and in this case n ₀(d) represents the number-diameter distribution of the cores inside the core-shell particles in the reactor outflow.

Without loss of generality, under the condition that no particle–particle coagulation occurs the number-diameter distribution n ₀(d) can be taken as a delta function of concentration N_T at diameter d ₀. For clarity to the reader, “d ₀” is appended to the terms f(d,t;d ₀), n(d;d ₀), and p(t;d ₀) to denote that these quantities are associated with a seed distribution represented by a delta function. Any cut in d or t across f(d,t;d ₀) is also a delta function whereas n(d;d ₀) and p(t;d ₀) are broad functions because they are associated with integration across t or d, respectively (Table 1). The representation of the seed distribution by a delta function generalizes to the case of a polydisperse seed distribution in analogy to the method of lines for solution to partial differential equations (Schiesser 1993). That is, for the polydisperse distribution, particles of one diameter grow independently of particles of other diameters. A solution obtained for f(d,t;d ₀) can be generalized to the polydisperse case of f(d,t) by typical methods, such as taking a discretized sum or alternatively setting up a continuous integration (Appendix B).

In a full treatment that includes transient conditions, the form of f(d,t;d ₀) is f(d,t;d ₀,t*), indicating the dependency on seed particle distribution as well as the absolute time t* since the experiment was begun. For our application, we assume that f(d,t;d ₀,t*) has reached a non-oscillatory steady state so that t* is omitted as a variable for the remainder of this study's analysis (Friedlander 1983; Seinfeld et al. 2003).

As an informative example related to the definitions introduced in this section, Figure 1 shows (a) a contour plot of a typical f(d,t) representing polydisperse seed particles in the outflow from a CMFR and (b) a line plot of a typical f(d,t;d ₀) representing monodisperse seed particles.

FIG. 1 Density plots of particle number concentration for the bivariate distribution function f(d,t) of particle diameter d and particle residence time t for condensational growth (Equation (8)) in a CMFR. The method to evaluate f(d,t) is provided in the Supplemental Information. The inset plot to the bottom of the abscissa axis shows the number-diameter distribution n(d) obtained by Equation (T3). The inset plot to the left of the ordinate axis shows the probability density function p(t) obtained by Equation (T4). Cases are shown for (a) a contour plot of f(d,t) for polydisperse seed particles and (b) a line plot of f(d,t;d ₀) for monodisperse seed particles. For the polydisperse case, the number-diameter distribution n ₀(d) of the core seed particles is represented by the dashed line. (Color figure available online.)

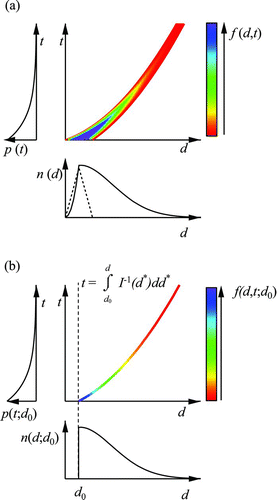
Apparent in Figure 1a is a ridge of higher values of f(d,t) along a path of d–t coordinates. In Figure 1b, this ridge coalesces into a curve that is color-coded by decreasing values of f(d,t;d ₀) for increasing t. The d–t curvature apparent in the plane projection of both Figures 1a and b is explained by the feature of condensational growth for a single-condensable species that for d > d ₀ (Seinfeld and Pandis 2006). Below the d-axis of both Figures 1a and b are plots of n(d) obtained by Equation (T3). These plots show that particles having long residence times grow to large diameters. Correspondingly, their number concentrations decrease because of the low probability of survival to long residence times, both because of CMFR outflow and wall loss. The dashed line in Figure 1a shows for reference the distribution n ₀(d) of the cores. To the left of the t-axis in Figures 1a and b are plots of p(t) obtained by Equation (T4). Poisson statistics governs whether a particle stays in a CMFR or instead is lost in the chamber outflow or to the walls (Koch 1999). The resulting p(t) is an exponential distribution (Davis and Davis 2003), as represented in the figure.

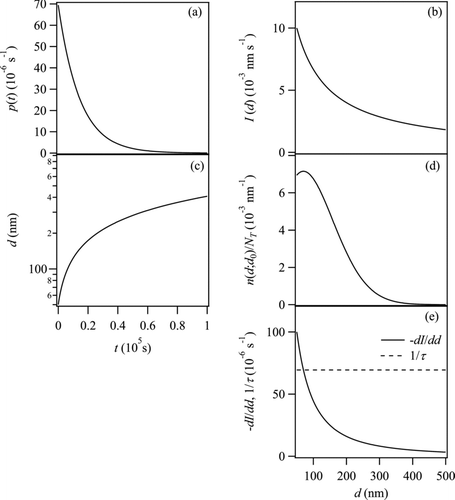
FIG. 2 Diagnostic plots of some key quantities affecting the number-diameter distribution n(d;d ₀) for condensational growth in a CMFR. (a) Probability density function p(t) of particle residence time in the CMFR outflow. (b) Dependence of particle growth rate I(d) on particle diameter. (c) Dependence of particle diameter d on particle residence time. (d) Example of a number-diameter distribution n(d;d ₀) that is normalized to total particle number concentration N_T . (e) Dependence of the first derivative of particle growth rate with respect to diameter on diameter (Equation (6)). For comparison, the inverse of the mean residence time is also plotted. Parameter values used in plots: {τ, β, λ, d ₀} = {14,400 s, 1 nm² s⁻¹, 50 nm, 50 nm}.

2.2. General Equation for Particle Growth in Flow Reactors

The distribution function f(d,t;d ₀) depends both on the seed particle diameter d ₀ and the particle growth rate I(d). Although Figure 1 is prepared specifically for a CMFR, the statement of a dependence of f(d,t;d ₀) both on d ₀ and I(d) generalizes to other types of continuous flow reactors, too. The growth rate term I(d) represents the change dd/dt of particle diameter with time. It depends on particle diameter and is positive for particle growth (Seinfeld et al. 2003). For the boundary condition of {d, t} = {d ₀, 0}, the relationship between particle residence time t and particle diameter d within the reactor is given as follows:

for a dummy variable of integration d*. This equation calculates the residence time that is required for a particle to grow from an initial diameter d ₀ to a diameter d.

Given that I(d) is positive, Equation (1) is sufficient to demonstrate that t(d;d ₀) is a monotonic function. In this case, the rule for variable transformation of probability density functions holds, as follows (Koch 1999):

for n(d;d ₀) and p(t;d ₀) that characterize the reactor outflow. This equation is a statement of conservation of particle number concentration for corresponding intervals of dt and dd.

Rearrangement of Equation (2) and substitution with the derivative form of Equation (1) then leads to the following relationship:

This equation represents n(d;d ₀) for d ≥ d ₀, which otherwise evaluates to zero. The distribution function n(d;d ₀) is on a linear scale (i.e., dN/dd) but as desired can be transformed to a logarithmic scale (i.e., dN/dlog₁₀ d) by standard methods (Seinfeld and Pandis 2006). An alternate version of Equation (3) that incorporates a polydisperse distribution n ₀(d) for the seed particles, rather than a singular diameter d ₀, is provided in Appendix B.

Equations (1)–(3) are mathematically valid for any type of continuous flow reactor so long as the basic underlying assumptions are met. The reactor should be at steady state, and there should be a uniform spatial distribution of condensing compounds, implying that I(d) should be independent of t. Particle–particle coagulation should be absent, and particle–phase reactions that can change particle diameter should not occur. The probability density function p(t;d ₀) of particle residence time in the reactor outflow should be known a priori either by theoretical or empirical methods.

2.3. Specific Equation for Particle Growth in a CMFR

The probability density function p(t;d ₀) of particle residence time for a CMFR at steady state and having a mean particle residence time τ is given by the following equation (Figure 2a) (Danckwerts 1953):

This equation assumes a diameter-independent wall loss rate (Supplemental Information). An implication of this assumption is that n ₀(d) does not change even as n(d) does change for different growth rates I(d) (Supplemental Information).

Substitution of Equation (4) into Equation (3) leads to the following equation:

Equation (5) is the specific equation for particle growth in a CMFR and applies for d ≥ d ₀. Equations for plug-flow and laminar-flow reactors are presented in Appendix A.

An interesting characteristic of Equation (5) for typical condensational growth in a CMFR is that its shape can bifurcate between one of monotonic descent for d > d ₀ or one of a maximum at some d > d ₀. The factors governing this bifurcation can be analyzed by taking the derivative of the Equation (5), as follows:

in which the prime symbol is used to represent a derivative with respect to d. Given that the first and third terms of Equation (6) are necessarily positive, the sign of n′(d;d ₀) is equal to the sign of −(1+τI'(d)). Therefore, n′(d;d ₀) is negative for I'(d)>−τ⁻¹ and positive for the opposite case (Figures 2d and e). The term I(d) goes as d ⁻¹ for typical condensational growth (Seinfeld and Pandis 2006). In this case, the left-hand term I′(d) of the inequality is negative and the second derivative I′′(d) is positive, meaning that I'(d)>−τ⁻¹ becomes true for some sufficiently large d. The implications are that n′(d;d ₀) is positive for sufficiently small d, that n′(d;d ₀) is zero corresponding to a maximum in n(d;d ₀) for some critical diameter d ^† satisfying I'(d†)=−τ⁻¹, and that n′(d;d ₀) is negative for d > d ^†. In the case that d ₀ ≥ d ^†, n(d;d ₀) monotonically descends for increasing d because Equation (6) for n(d;d ₀) is applied only for d ≥ d ₀. In the case that d ₀ < d ^†, n(d;d ₀) goes through a maximum at d = d ^†. The physical explanation for the maximum is that the tendency for particle number concentration to consolidate in d-space because I′(d) < 0 and thereby to elevate number concentration is eventually countervailed by the tendency of longer-lived particles (which also are of increasingly larger diameters) to progressively lose concentration because of wall loss and CMFR outflow.

2.4. Equation for Secondary Organic Aerosol Particle Growth in a CMFR

Within a secondary organic aerosol, the condensation of organic molecules from the gas phase to particle surfaces is at least one principal mechanism for the increase of particle diameter with time (Seinfeld et al. 2003; Chan et al. 2007). The formulation of Seinfeld et al. (2003) is used by us for the diameter-dependent particle growth rate I(d), as follows:

to describe the condensation of different compounds i, each of mean free path λ_i in the gas phase. The term β_i is proportional to the difference between the partial pressure p_i in the reactor of compound i and its vapor pressure p ⁰ _i in the particle phase. The formulation of Equation (7) is based on a continuum growth rate law that is corrected by a noncontinuum factor g_i (λ_i ,d) and that assumes a molecular accommodation coefficient of unity: I_i (d) = β_i g_i (λ_i ,d)/d and g_i (λ_i ,d) = (1 + λ_i /d)⁻¹.

The oxidation of even a single volatile organic compound (VOC) can produce myriad compounds (Chen et al. 2011), and the vapor pressures among these different product compounds can vary by many orders of magnitude (McFiggans et al. 2010). The governing equation for λ_i in air for an organic molecule of relative molecular mass m_i and an air-organic collision diameter σ_i follows a proportionality relationship: (Kauzmann 1966). For m_i > m _air and our estimate that m_i and σ_i vary by factors of 4 and 2, respectively, as upper limits within the family of expected organic products, we conclude that the variability in the mean free paths of typical condensing organic products is significantly less than a single order of magnitude. Therefore, as a simplification, our further analysis uses a common λ in place of λ_i for all condensing organic molecules. Equation (7) is then written as follows (Figures 2b and c).

Substitution of Equation (8) into Equation (5) followed by evaluation of the integral leads to a form of n(d;d ₀) that is defined by known or measurable parameters and is applicable to particle diameter growth in a secondary organic aerosol for a CMFR, as follows:

Evaluation of I'(d†)=−τ⁻¹ yields so that n(d;d ₀) descends monotonically for and has a maximum otherwise. In the case that there is a maximum, its position is shifted to larger diameters both for longer particle residence times and faster particle growth rates. A version of Equation (9) that accounts for polydispersity in seed particle diameters is presented in Appendix B.

Alternatives to Equation (9) that do not assume a single value for all λ_i are presented in Supplemental Information. As shown there, the case of assuming a single-product, meaning i∈{1}, results in a mathematical formulation identical to Equation (9). The two-product model, meaning i∈{1, 2} for λ ₁ and λ ₂, results in an equation that has many more terms and that is the same after manipulation to the result presented by Seinfeld et al. (2003) (Supplemental Information).

The plots shown in Figure 3 represent the sensitivity of n(d;d ₀) of Equation (9) to the variation of its parameters, including the gas-phase concentration parameter β, the particle mean residence time τ, the gas-phase mean free path λ, and the seed particle diameter d ₀.

FIG. 3 Parameter sensitivity of the number-diameter distribution n(d;d ₀) for condensational growth in a CMFR (Equation (9)). Panels (a) through (d) respectively show the effects on n(d;d ₀) of individually varying β, τ, λ, and d ₀. Base-case parameter values are as listed for Figure 2. (Color figure available online.)

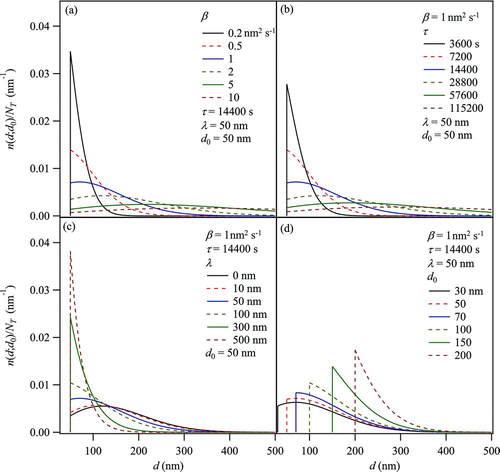
The values selected as a base case include τ = 14,400 s, β = 1 nm² s⁻¹, λ = 50 nm, and d ₀ = 50 nm; these values are representative of some of the observations for α-pinene ozonolysis. Figure 3a shows that higher concentrations of condensable compounds in the gas phase, corresponding to increasing β values, shift the distribution n(d;d ₀) to larger diameters. Longer particle residence times similarly shift n(d;d ₀) to larger diameters (Figure 3b). The physical explanations are that greater β favors growth to larger diameters within the available particle residence time while greater τ provides more time prior to outflow from the CMFR for the particles to grow. Moreover, Equation (9) shows that the product βτ consistently occurs together as a lumped term, which explains the identical variational behavior apparent in Figures 3a and b.

TABLE 2 Summary of the data sets used in this study.

			Inflow			Outflow
Exp
Label	Date	Compound	[VOC] (ppbv)	(nm)	(nm)	[O3] (ppbv)	NT (# cm^−3)	M org (μg m^−3)
a	Dec 2009	α-pinene	8	30 ± 1	43 ± 1	50	2000	1.4
b	Dec 2009	α-pinene	80	30 ± 1	43 ± 1	50	1000	37
c	Dec 2010	α-pinene	8	76 ± 2	112 ± 3	50	2000	3.3
d	Mar 2011	α-pinene	190	70 ± 2	101 ± 3	300	4400	60*
e	Dec 2010	α-pinene	16	46 ± 2	67 ± 2	50	2800	8.2
f	Dec 2010	α-pinene	16	76 ± 2	112 ± 3	50	2300	8.2
g	May 2009	β-caryophyllene	1.6	50 ± 2	72 ± 2	50	2700	0.4
h	May 2009	β-caryophyllene	13	50 ± 2	72 ± 2	100	4100	11
Note: Experiment labels correspond to the panels of Figure 4. The term [VOC] is the concentration of the reactant compound in the inflow to the CMFR. Terms and are the mode diameters of the +1 and +2 charged seed particles, respectively. Uncertainty is estimated based on calibration with polystyrene latex particle size standards (Duke Scientific Corporation, CA). The terms [O3] and NT are the ozone concentration and the total particle number concentration in the CMFR outflow, respectively. Organic particle mass concentrations M org in the chamber outflow were measured using an Aerodyne Aerosol Mass Spectrometer (AMS) (DeCarlo et al. 2006), except for the case denoted by the asterisk for which an SMPS measurement was used. The mean residence time of inert species was 12,240 s for the α-pinene experiments and 12,960 s for the β-caryophyllene experiments

Figure 3c shows the sensitivity of the distribution n(d;d ₀) to the gas-phase mean free path λ of the condensing organic molecules. The Knudsen number of the condensing organic molecules, which is calculated as 2λ/d, is the key governing quantity for the effects seen in Figure 3c. In the continuum regime of K_n < 0.1, the correction factor g_i (λ_i ,d) evaluates to approximately unity, and the growth rate I(d) is therefore insensitive to K_n (Seinfeld and Pandis 2006). In the free-molecule regime of K_n > 10, however, g_i (λ_i ,d) decreases as approximately K_n ⁻¹, implying that I(d) likewise decreases. The trends apparent in the sensitivity study represented by Figure 3c can then be explained. For small K_n (i.e., λ ≪ d), there is little sensitivity of n(d;d ₀) to λ. This result likewise follows from the appearance of λ only in the terms (d ₀ + λ) and (d + λ) of Equation (9). For larger K_n (i.e., 2λ/d > 1), the regime of condensational growth shifts to the transition region and even nearly into the free-molecule region for the largest investigated λ values. The growth rate I(d) significantly decreases as the Knudsen number passes from the continuum, to the transition, and finally to the free-molecule regime (Seinfeld and Pandis 2006). The distribution n(d;d ₀) correspondingly shifts to smaller diameters for these step changes in Knudsen regimes. Figure 3c shows that the changes can be large enough to bifurcate from a distribution having a local maximum to one characterized by monotonic descent.

Figure 3d demonstrates how the seed particle diameter d ₀ affects the distribution n(d;d ₀). The pattern is a shift in the cut-on diameter (i.e., d ₀) without a change in the shape of n(d;d ₀) for d > d ₀, meaning that the ratio of each curve to another is a flat line for d > d ₀ (not shown). The scale changes apparent in Figure 3d arise because the shift in cut-on diameter to larger values requires a corresponding increase in the scaling factor to conserve N_T among all curves. This result can be demonstrated by re-writing Equation (9) as follows:

The bracketed first term is the scaling factor that depends on d ₀ but not d. The bracketed second term is the shape of n(d;d ₀), representing the dependency on d and showing an independence from d ₀. This equation also demonstrates that, unlike in the case of d ₀, the other three parameters β, τ, and λ cannot be separately isolated with respect to an influence on scaling or shape.

3. DATA SETS

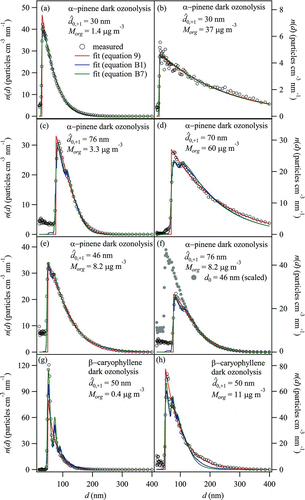
Number-diameter distributions n(d) were collected during α-pinene and β-caryophyllene ozonolysis experiments carried out in the HEC (Shilling et al. 2008; King et al. 2009). The primary data, including detailed descriptions of the experimental protocols, were reported in Kuwata et al. (2011) and Chen et al. (2012) for α-pinene and β-caryophyllene, respectively. Table 2 summarizes the reaction conditions for each experiment selected for analysis in the present study. The table entries show that the diameter of the primary mode of the seed particles varied from 30 to 76 nm and that the organic particle mass concentration ranged from 1 to 60 μg m⁻³. Increased particle growth rates I(d) were associated with higher mass concentrations (Figure 4).

FIG. 4 Number-diameter distributions n(d) measured in the outflow from the Harvard Environmental Chamber (HEC) for (a–f) α-pinene and (g–h) β-caryophyllene ozonolysis. The distributions were measured at steady state and averaged for 4–12 h (Figure S3). The conditions of each experiment are listed in Table 2. In each panel, the optimized model fit n(d) is shown for a seed particle distribution described by a delta function (Equation (9)), for the measured seed particle distribution (Equation (B1)), and for a seed particle distribution described by an analytic Gaussian function (Equation (B7)). For these equations, Table 3 lists the values of the optimized parameters that were obtained. In the case of panels c and e, n(d) > 0 for small diameters because new particle formation was occurring concurrently with condensational growth. (Color figure available online.)

A brief description of the experimental protocols is as follows. The chamber consisted of a 4.7 m³ Teflon bag housing in a temperature-controlled environment. The major inflow into the bag was purified air of 40% relative humidity. Minor inflows included ozone, the reactant terpene of interest (i.e., α-pinene or β-caryophyllene), a radical scavenger, and (NH₄)₂SO₄ seed particles. The radical scavenger was 2-butanol in the case of α-pinene ozonolysis and cyclohexane in the case of β-caryophyllene ozonolysis. The radical scavengers quickly reacted with hydroxyl radicals that were produced as by-products of ozonolysis, and this scavenging thus prevented hydroxylation reactions of the terpenes and their products (Keywood et al. 2004). The total inflow to the bag corresponded to a mean gas residence time of 3.4 h (12,240 s; α-pinene) or 3.6 h (12,960 s; β-caryophyllene). The ozone concentration and the relative humidity in the bag outflow were continuously monitored and maintained at stable values in the bag by feedback conditioning of the respective inflows. Either α-pinene or β-caryophyllene was supplied from a syringe pump to a heated flask, which was swept out by pure air to provide a continuous supply of the precursor into the bag. The syringe was filled with a liquid solution of either α-pinene in 2-butanol (1:600 v/v) or β-caryophyllene in cyclohexane (1:2500 v/v). The syringe injection rate controlled the reactant terpene concentration in the inflow to the bag and thus ultimately the organic particle mass concentration M _org in the outflow from the bag (Table 2). Seed particles were produced using an atomizer to aerosolize an aqueous solution of (NH₄)₂SO₄, which was varied from 0.1–0.5 g L⁻¹ depending on the seed particle diameter desired for an experiment. Following drying and charge neutralization, the seed particles were classified by a differential mobility analyzer (DMA). The setpoint of the electric mobility diameter (+1 electrical charge) ranged from 30 to 76 nm for the presented experiments (Table 2).

The polydisperse particle number-diameter distributions n(d) in the bag outflow were measured using a scanning mobility particle sizer (SMPS) (Wang and Flagan 1990). The SMPS consisted of a DMA (TSI model 3081) and a condensation particle counter (CPC, TSI model 3776). The quasi-monodisperse particle number-diameter distributions n*₀(d) of the seed particles present in the bag inflow were also measured using the SMPS. The inversion of the SMPS data to obtain n*₀(d) was based on a tandem DMA configuration to account for the narrow dispersion of n*₀(d) after the first DMA. The iterative inversion algorithm used a kernel function that took into account both the DMA transfer function and the particle charging efficiency (Knutson and Whitby 1975; Markowski 1987; Wiedensohler 1988). The smoothing parameter of the Markowski algorithm was reduced by us from 0.25 to 0.025 to represent the narrowly dispersed n*₀(d) that exited the first DMA.

4. RESULTS AND DISCUSSION

The number-diameter distributions n(d) collected for α-pinene and β-caryophyllene ozonolysis are shown in Figure 4. The distributions shift to larger diameters for increasing M _org. Higher M_org are associated with higher partial pressures of precursor compounds and hence oxidation products. As discussed in Seinfeld et al. (2003), the β term of particle growth rates (Equation (8)) is proportional to the difference between the partial pressure and the vapor pressure of condensable compounds. Therefore, for all other factors held constant, higher partial pressures lead to faster growth rates and hence to shifts in n(d) to larger d.

The number-diameter distributions of Figure 4 were analyzed for a distribution n ₀(d) of seed particle cores described by a delta function (Equation (9)), for one discretized using the measured polydisperse distribution (Equation (B1)), and for one represented by an analytical Gaussian approximation (Equation (B7)). Comparison of these lines to the data shows that all three models describe the data sets reasonably well (Figure 4). For large d, the three models provide similar results because the value of d ₀ and the form of n ₀(d) do not affect the tails of the distribution to a great extent (Equation (B2)). The implication of the successful model-data comparison is that the assumptions employed in deriving the employed equations are reasonable, at least for α-pinene and β-caryophyllene ozonolysis.

For d in the vicinity of d ₀, increased accuracy between the model and the data can be obtained by employing more detailed treatments of the seed particle distribution. Representation of the distribution by a delta function accounts neither for the presence of multiply charged seed particles at diameters larger than d ₀ nor the finite width of the transfer function of the DMA. These limitations are most significant in the cases of low M _org and large d ₀ (Figure 4g). For many applications, however, these cases are not important, and in these circumstances Equation (9) is acceptably accurate for describing n(d).

One prediction of this equation is that the shape, though not the scaling, of n(d;d ₀) is independent of d ₀ for d > d ₀ (Equation (10)). The distributions of Figures 4e and f provide a test of this prediction. The mode diameter of the seed particle distribution was increased from 46 to 76 nm by adjusting the DMA setpoint while leaving unchanged other conditions in the HEC. Total particle number concentration N_T increased from 2300 to 2800 cm⁻³ with the change in setpoint diameter. This small difference reduced the possibility of significant changes in the condensation process. The data of Figures 4e and f confirm the prediction that the shape of n(d;d ₀) is independent of d ₀ when other factors are held constant.

TABLE 3 Optimized parameter values that were obtained for Equations (9), (B1), and (B7) for the data sets of Figure 4.

	Delta function		Polydisperse discretized bins		Gaussian function
Exp
Label	λ/β (s nm^−1)	λ (nm)	λ/β (s nm^−1)	λ (nm)	λ/β (s nm^−1)	λ (nm)
a	260	>50 (250)	230	>60 (127)	250	>80 (225)
b	53	>650 (NA)	55	>1000 (NA)	56	>600 (NA)
c	48	>10 (20)	32	>4 (10)	30	>2600 (NA)
d	70	>400 (NA)	95	>5000 (NA)	95	>1000 (NA)
e	120	>30 (125)	180	>200 (690)	200	>500 (NA)
f	68	>15 (56)	120	>80 (110)	140	>60 (169)
g	760	>650 (NA)	1500	>100 (NA)	400	>0 (16)
h	220	>200 (NA)	510	>1000 (NA)	530	>1000 (NA)
Note: The optimization was carried out in Mathematica (version 8, Wolfram Research, Inc.). The entries in Table 3 list the value of the lumped parameter λ/β along with the constraint of applicability, meaning a minimum value of λ. For some entries, there is an optimized value of λ that corresponds to a weak local minimum (i.e., the chi-square test is not satisfied for the optimized value). The optimized value of λ/β varies by up to ±10% as λ varies (Figure S1), and the values listed in this table correspond either to (1) the best fit value of λ when such exists or (2) λ = 10^4 nm otherwise.

The optimized values that parameterize the lines of Figure 4 are listed in Table 3. For the collected data sets, the optimized values of λ and β strongly co-vary as a ratio λ/β for any value of λ above a threshold value. Even in the case of a local minimum in λ, the minimum is shallow and the chi-square test is not satisfied (Figure S1). For some experiments, however, the threshold values of λ listed in Table 3 are too large to be considered physically reasonable (e.g., greater than 400 nm). These cases correspond to experiments of relatively high organic mass concentrations and have size distributions that tail to large particle diameters. For these tails, the assumption made of a size-independent wall-loss rate, which underpins the derivation of the probability density function p(t;d ₀) of particle residence time expressed by Equation (4), is not accurate (McMurry and Grosjean 1985). The term λ can therefore be considered as a parameter that is based on mean free path but in some cases includes other compensations, such as diameter-dependent wall-loss corrections. For instance, decreased wall-loss rates for larger particles can significantly decrease the threshold value of λ, but a numerical discretized model would be required for implimentation of this approach, rather than a closed form analytical equation like Equation (9).

The number-diameter distribution equations developed herein should be applicable only when condensational growth is the dominant mechanism for changes in particle diameter. These equations successfully describe the data sets recorded for α-pinene and β-caryophyllene ozonolysis. By comparison, the equations do not successfully describe data sets recorded for isoprene and toluene photooxidation (Figure S2), suggesting that the diameter growth for these systems is also affected by additional processes. Chan et al. (2007) developed quantitative models of SOM production for several different general mechanisms, such as particle-phase reactions including oligomerization, evaporation of semivolatile species following particle-phase chemical reactions, or photolysis. Chen et al. (2011b) compared modeled to measured O:C and H:C ratios and suggested that particle-phase reactions of hydroperoxides could be important for reducing model-measurements gaps. The analysis presented herein could be adapted in the future for inclusion of these processes by modification of I(d). To that purpose, Equation (1) would be used to relate the particle-phase chemical processes (i.e., that would be expressed in a kinetic framework of a time variable) to an expression for I(d). This result for I(d) would then be used in Equation (3) to formulate n(d).

In summary, this study developed a general equation to describe the particle size distribution that results from condensational growth in continuous flow reactors. The probability density function of particle residence time and the size-dependent particle growth rate were used in conjunction to formulate a general expression for the particle size distribution in the reactor outflow. Analytical equations were developed for CMFRs, laminar-flow reactors, and dispersive plug-flow reactors. The presentation of results focused on the condensational growth of SOM particles inside CMFRs. Analytical equations were presented for seed particle size distributions described by delta functions, Gaussian functions, and discretized bins. Data sets collected for α-pinene and β-caryophyllene ozonolysis could be accurately modeled for the most part by all of these equations, including the simplest one based on a seed particle size distribution described by a single delta function. By contrast, data sets collected for isoprene and toluene photooxidation could not be successfully fit by any of these equations. The implication could be that, in the case of ozonolysis, the rate of particle growth was largely governed by the steady condensation of reaction products from the gas phase to the particle surfaces whereas, in the case of photo-oxidation, the rate of particle growth was significantly influenced by particle-phase chemistry and subsequent diameter changes that occurred on a timescale that was of the same order as the particle residence time in the reactor.

APPENDIX A

Equations for Plug-flow and Laminar-flow Reactors

Plug-flow reactor. The probability density function p(t;d ₀) of particle residence time t in the outflow from a plug-flow reactor (PFR) having a mean particle residence time τ is given by the following equation (Davis and Davis 2003):

in which the Peclet number Pe quantifies the relative importance of longitudinal dispersion. The mean particle residence time is calculated as τ = V/Q for reactor volume V and flow Q, meaning that our analysis corresponds to cases that do not have significant particle wall loss. The Peclet number is the ratio of the characteristic time for particle dispersion along the length of the longitudinal axis to the mean particle residence time in the reactor. For ideal PFR operation, the design goal is Pe → ∞. Particle dispersion, which decreases Pe, can occur by mechanisms of diffusion as well as by turbulence. In the latter case, Equation (A1) also represents a first-order description for a turbulent-flow reactor. For practical application, the Peclet number is calculated as uL/D for reactor linear velocity u, reactor length L, and dispersion coefficient D. The derivation of Equation (A1) assumes that Pe is constant within the reactor, yet the diameter is increasing during particle residence in the PFR. The implication is that the dispersion coefficient must not vary with particle diameter for use of the presented equation.

Substitution of Equation (A1) into Equation (3) leads to the following result:

The term ξ is recognized as the particle residence time t required to grow from an initial particle diameter d ₀ to an outflow diameter d [Equation (1)]. Equation (A2) describes particle growth by gas-to-particle condensation in a PFR and gives the number-diameter distribution in the outflow from the PFR. The equation is applicable for a PFR in which the rate of condensational growth I(d) is independent of longitudinal or radial position, such as can occur in the case of excess concentration of condensable species or the case of in situ production of the condensable species.

In the limit of approaching a PFR having no dispersion, meaning that Pe → ∞ and thus σ ² → 0 for all particle diameters, Equation (A2) conforms to the definition of the Dirac delta function, as follows (Fitts 1999):

The implication of this equation is that no broadening of n(d) occurs for an ideal PFR. The particles in the outflow have some uniform diameter d _out that satisfies Equation (1) for t = ξ. The outflow diameter d _out of the particles satisfies the following equation:

Under the condition that Equation (8) holds for the condensational growth of particles in a secondary organic aerosol, meaning I(d) = β/(d + λ), we can further write:

for a dispersive reactor. For a non-dispersive PFR, this equation simplifies to the following:

The term d_out evaluates to for use in this equation.

Laminar-flow reactor. The probability density function p(t;d ₀) of particle residence time t in the outflow from a laminar-flow reactor (LFR) having a mean particle residence time τ is given by the following equation (Fogler 2005):

Particles in the center streamline pass through the reactor in a time period of τ/2 whereas particles near the walls take several multiples of τ to pass through the reactor. The mean particle residence time is calculated as τ = V/Q, implying absences in our treatment of significant particle wall loss as well as of significant radial diffusion of the particles across streamlines.

Substitution of Equation (A7) into Equation (3) leads to the following result:

This equation represents n(d; d ₀) for d ≥ d _min, which otherwise evaluates to zero. The term d _min is the smallest diameter particle that exits the LFR, which is the one that moves along the center streamline and has residence time τ/2. It satisfies Equation (A4) for d _min = d _out and t = τ/2. For applicability of Equation (A8), the same restrictions hold on I(d) as were discussed for Equation (A2). Equation (A8) describes the number-diameter distribution in the LFR outflow for particle growth by gas-to-particle condensation.

Under the condition that Equation (8) holds for the condensational growth of particles in a secondary organic aerosol, we can further develop Equation (A8) as follows:

The term d_min evaluates to for this case.

APPENDIX B

Equation for n(d) for Polydisperse Seed Particles

Discretization approach. A number-diameter distribution n ₀(d) for the seed particles, alternatively described as cores for the core-shell particles in the outflow from the reactor, can be discretized into j monodisperse bins of monotonically increasing diameters {d _0,1, d _0,2, …, d _0,j } and corresponding number concentrations {N ₁, N ₂, … N_j }. The relationship holds that N_T = Σ _jN_j . Following from Equation (9), we write the number-diameter distribution n(d) for condensational growth on the seed particles, as follows:

The integer k is the count of entries in {d _0,1, d _0,2, …, d _0,k } that satisfy d _0,j ≤ d, meaning that k is an integer function of d. In the case of k = 0, n(d) evaluates as zero.

The polydisperse case of Equation (B1) gives the same result as the monodisperse approximation represented by Equation (9) in the limit of large d such that (d _0,j + λ)² / (d + λ)² → 0 for all j. The equation for this case is as follows:

For accuracy, the polydisperse equation should be employed in cases for which the variance of the distribution n ₀(d) is on the same order of or larger than the variance of the distribution n(d).

Continuous function. In the case that the distribution n ₀(d) can be represented as a continuous function, the outflow distribution is bivariate in d and d ₀ and is written as n(d,d ₀) so as to distinguish from n(d;d ₀). The bivariate distribution n(d,d ₀) has units of particles m⁻³ m⁻¹ m⁻¹ and can be mapped to f(d,t) by using Equation (1) (not shown herein). The distribution n(d) for the condensationally grown particles is written as follows for n ₀(d) represented by a continuous distribution:

for which the second line follows by adapting Equations (1)–(3) to a continuous distribution. For the condensational growth of particles in a secondary organic aerosol within a CMFR, Equation (B3) is developed further as follows:

by using a version of Equation (9) that is adapted to a continuous distribution n ₀(d).

For many chamber experiments, such as those described in this study, prior to entering the chamber polydisperse seed particles are classified in electric mobility by passage through a DMA (Knutson and Whitby 1975). The resulting particle population in the chamber inflow is described by n*₀(d), which is related to n ₀(d) by taking into account particle wall loss in the reactor (Supplemental Information). The distribution n ₀(d) includes multiply charged particles that are approximately monodisperse in electric mobility. In diameter space, the number-diameter distribution of this particle population is acceptably approximated as a sum of normal distributions, as follows:

Each charge q contributes one mode to n ₀(d). A mode centered at diameter has a variance σ² _q and a total concentration N_q . The relationship holds that N_T = Σ _qN_q . The variance depends in large part on the relative flows of the sheath and sample flows in the DMA as well as the mode diameter. As a practical procedure, the transfer function for each q should be separately calculated in diameter space by standard methods and then empirically fit to obtain σ² _q . Although the upper limit of Equation (B5) is represented as infinity for completeness, in practice |q|∈{+1, +2, +3} is sufficient.

Substitution of Equation (B5) into Equation (B3) leads to the following equation:

Evaluation of the integral yields the following result:

in which γ ₀ = βτ, γ _q =βτ−σ² _q , , z(x ₁, x ₂, x ₃)=(x ₁−x ₃)+x ₂(λ+x ₃), and z(x ₁)=z(x ₁, 1, 0)=x ₁+λ. Equation (B7) describes the number-diameter distribution in the CMFR outflow for particle growth by gas-to-particle condensation on to the surfaces of DMA-classified seed particles.

Acknowledgments

This study was supported by the Office of Science (BES), U.S. Department of Energy, Grant no. DE-FG02–08ER64529. Mikinori Kuwata was supported by the Japan Society for the Promotion of Science (JSPS) postdoctoral fellowship for research abroad. We acknowledge Q. Chen and Y.J. Li for providing the published experimental data for the β-caryophyllene ozonolysis experiments and A. Bateman for the unpublished data for the toluene photo-oxidation experiments. Y. Liu, M.L. Smith, and S. R. Zorn are appreciated for useful discussion and assistance with the α-pinene ozonolysis and isoprene photooxidation experiments.

[Supplemental files are available for this article. Please go to the publisher's website for Aerosol Science and Technology to view the free supplementary files.]