The Multiple Monodisperse Outlet Differential Mobility Analyzer: Derivation of Its Transfer Function and Resolution

Abstract

Conventional differential mobility analyzers (DMAs) for classification of aerosol particles have one polydisperse-particle inlet and one monodisperse-particle outlet. As a result, when they are used as particle classifiers in aerosol mobility spectrometers, it is needed to scan through different operating conditions, thereby requiring a significant amount of time (i.e., of the order of a minute) for a single mobility distribution measurement. DMAs with multiple outlets can significantly reduce this scanning time because particles of different mobilities can be classified and detected simultaneously. In addition, depending on the relative location of the first and the last outlet from the inlet, one can increase the dynamic mobility range of the selected particles in a single particle mobility distribution measurement. In this article, we derive analytical expressions for estimating the transfer function and the resolution of DMAs with multiple monodisperse outlets. Starting with the simple consideration of nondiffusing particles, we extend our analysis for diffusing particles and provide expressions of different complexity and accuracy. The theoretical framework provided in this article can be employed to optimize the design of DMAs with more than one monodisperse-particle outlet, and to analyze the measurements when such DMAs are used in aerosol mobility spectrometers.

Copyright 2012 American Association for Aerosol Research

1. INTRODUCTION

Differential mobility analyzers (DMAs) are widely used in aerosol research as a tool for sizing and for producing monodisperse airborne particles having diameters in the submicron and nanometer range (Flagan 1998; McMurry 2000; Biskos et al. 2008). In view of improving several aspects of their performance (e.g., particle size range, resolution, etc.), several DMA designs have been proposed over the last decades (Liu and Pui 1974; Knutson and Whitby 1975; Pourprix and Daval 1990; Pourprix 1994; Zhang et al. 1995; Fissan et al. 1996; Zhang and Flagan 1996; Brunelli et al. 2009; Santos et al. 2009). The most popular DMA design employs two coaxial cylindrical electrodes between which an annular flow carries the sample particles in a particle-free sheath flow (Liu and Pui 1974; Knutson and Whitby 1975). Applying a potential difference between the two cylindrical electrodes, the charged particles migrate from one electrode to the other so that only particles having mobilities within a very narrow range can exit through the monodisperse-particle outlet.

Conventional DMAs employ one monodisperse-particle outlet. As a result, particles having mobilities only within a specific narrow range can be classified for each combination of operating conditions (i.e., flows and applied voltage between the two electrodes). This, however, poses the limitation that when DMAs are used as particle classifiers in aerosol mobility spectrometers, it is required to scan through different operating conditions, thereby requiring a significant amount of time (from 30 s up to a few minutes depending on the required accuracy of the measurement) for a single mobility distribution measurement (Wang and Flagan 1990; Endo et al. 1997). In addition, because the flow field is usually kept constant and only the electric field is altered in order to classify particles of different mobility, the dynamic size range of conventional DMAs can typically span over one order of magnitude (McMurry 2000). DMAs with multiple outlets on the other hand can significantly reduce the scanning time when used as classifiers in mobility spectrometers because particles of different mobilities can be selected and detected simultaneously. Depending on the relative distances of the first and the last outlet from the inlet, one can also increase the dynamic mobility range of the selected particles in a single measurement.

To measure particles having diameters from one and up to a few hundred nanometers, Seol et al. (2002) designed an adjustable-length DMA. Working in the same direction, Takeuchi et al. (2005) proposed a dual-type DMA that employs two cylindrical, coaxial classifiers. The sample flow in the dual-type DMA is split into two parts before passing through either one of two classifiers that select particles having mobilities of different ranges. In an attempt to make a DMA that could scan faster through the instrument's channels, Chen et al. (2007) built and tested a classifier having three monodisperse-particle outlets. The performance of this DMA has only been determined experimentally and numerically (Li 2006), and to the best of our knowledge, there is still lack of a theoretical model for predicting its behavior.

The performance of DMAs can be fully described by their transfer function (Knutson and Whitby 1975; Hoppel 1978; Haaf 1980; Kousaka et al. 1986; Stolzenburg 1988; Rosell-Llompart et al. 1996). Knutson and Whitby (1975) provided a derivation of the transfer function for an ideal DMA and showed that this has a triangular shape, if the polydisperse-particle sample inlet flow and monodisperse-particle exit flow rates are equal (i.e., balanced flows), or a trapezoidal shape, if the flows are not perfectly balanced. Motion of particles in the nanometer size range within the DMA is also affected by the Brownian motion of the particles, resulting in a Gaussian-shape transfer function (Tammet 1970; Kousaka et al. 1985, 1986; Stolzenburg 1988; Rosell-Llompart et al. 1996; Stratmann et al. 1997; Hagwood et al. 1999; de la Mora 2002).

In this article, we derive the transfer function of the Multiple Monodisperse Outlet DMA (MMO-DMA), and the formula for determining the resolution of each outlet. Using the approach followed by Knutson and Whitby (1975) and Stolzenburg (1988) for the conventional DMA, we first derive the transfer function of the MMO-DMA for nondiffusing particles, and then extend it to include particle diffusivity. Considering that the transfer function of the MMO-DMA can be approximated by a Gaussian distribution, we also derive the diffusion-limited resolution of each outlet using the approach proposed by Flagan (1999).

2. DERIVATION OF THE MMO-DMA TRANSFER FUNCTION

In this section, we employ the theoretical approach proposed by Stolzenburg (1988) to derive the transfer function of cylindrical DMAs with multiple monodisperse-particle outlets. Considering that the flow field is axisymmetric and steady (Figure 1a), and that the air flow is laminar and incompressible, we can define the flow stream function as

Assuming also that the space charge and image charges are negligible, we can further define the axisymmetric and steady electric flux function as

In Equations (1) and (2), u is the flow velocity and E is the electric field strength, whereas r and z denote the radial and axial components, respectively.

FIG. 1 Schematic diagram of the MMO-DMA showing (a) the flows associated with each monodisperse-particle outlet, (b) the fluid and electric field streamlines, and (c) the particle streamlines. Key: Q_a is the polydisperse aerosol inlet flow rate, Q_sh is the sheath air flow rate,

is the sample flow rate of the ith monodisperse-particle outlet,

is the excess flow rate after the ith monodisperse-particle outlet,

is the sheath air flow rate before the ith monodisperse-particle outlet, and R ₁ and R ₂ are the outer and the inner radii of the MMO-DMA, respectively.

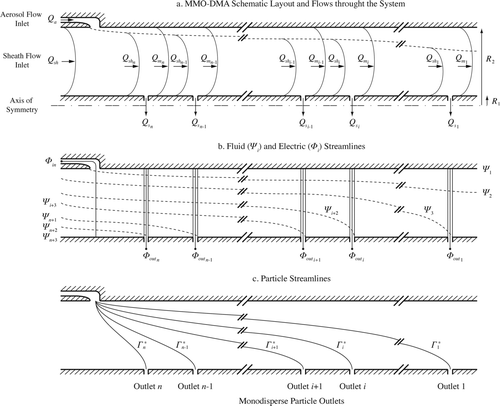
As shown in Figure 1b, streamlines and bound the aerosol inlet flow, whereas and bound the monodisperse-particle sample flow of the ith exit. If the positive z direction is taken to be in the same direction as the flow, then by definition . Based on these characteristic stream functions, one can determine the following volumetric flow rates:

Here Q_a is the incoming polydisperse-particle sample flow rate and is the sample flow rate of the ith outlet, whereas and are the sheath and the excess air flow rates just before and just after the ith outlet, respectively. The total flow through the DMA is

where Q_sh is the initial sheath air flow (Figure 1a). The following relations for the flow rates also hold:

and

where n is the number of the monodisperse-particle sample outlets of the MMO-DMA.

The electric field is zero and is uniform deep inside the aerosol inlet and the exit channels, having values and , respectively. The electric flux corresponding to the ith monodisperse-particle exit is the difference between these two values and also a function of the electric field (Equation (2)). The axial and radial components of the electric field along the classification column are respectively given by

and

Here R ₁ and R ₂ are the radii of the central rod and the outer electrode, respectively, and V is the signed potential difference between the inner and outer electrodes. The integration limits in Equation (2) are the positions r and z of the particles at the midpoint locations of the entrance and the ith exit slit, which are spaced at a distance L_i apart. Thus,

Our objective now is to estimate the probability of any particle entering the DMA to exit through the ith monodisperse-particle exit. Considering that the values of the stream function at the entrance and the exit are and , respectively, we can write and .

Defining to be the probability of a particle entering the classifier on a streamline between and , and to be the probability of a particle that enters the classifier on streamline to exit on a streamline between and , the transfer function of the ith exit of the MMO-DMA can be expressed as

Assuming that there is no variation in aerosol concentration across the inlet channel, the particles can enter the classifier in any streamline between and with equal probability so that we can write

To determine , we need to know the velocity υ of the particles at any point within the DMA. If we assume that particle inertia is negligible, this is given by

where bold letters indicate vectors. In Equation (15), is the electrical mobility of the particle carrying charge q and having diffusion coefficient D at a temperature T (k is the Boltzmann constant). The function can be determined by the stream function and the electric flux function, which can be combined to form the particle stream function (Stolzenburg 1988), defined as

Here υ _r and υ _z are the radial and axial particle velocity components, respectively. In fact, depends on the difference between the entering and the exiting particle streamline . For a particle that enters on particle stream function , successfully traverses the classifier and exits on particle stream function , this difference can be written as

where and . For the conventional DMA with one monodisperse-particle outlet, Knutson and Whitby (1975) and Stolzenburg (1988) showed that , or , along the deterministic trajectory of a nondiffusing particle. Extending this for the MMO-DMA, we can write that , or .

When particle diffusivity is taken into account (Section 2.2), and therefore the estimation of particle deviations from their deterministic streamlines is required. In this case, one needs to calculate the associated particle streamline standard deviation, , which in turn depends on the gradient of given by

Here e _r and e _z are the unit vectors in the radial and the axial direction, respectively (Stolzenburg 1988). We can derive an expression for with or without considering particle diffusivity, and by plugging it in Equation (13), we can obtain the exact transfer functions for the respective cases. Considering that the flow is laminar and without disturbances along the column (especially upstream and downstream of each monodisperse-particle outlet), Sections 2.1 and 2.2 that follow provide the derivation of and from that the transfer function of the MMO-DMA for nondiffusing and diffusing particles, respectively. If the effect of potential disturbances resulted from the formation of recirculation zones around each outlet need to be considered, one has to employ a numerical model, which is beyond the scope of the present work.

2. 1 The MMO-DMA Transfer Function for Nondiffusing Particles

If we assume that the diffusivity of the particles is negligible, their motion is completely determined by Equation (15). In this case, remains constant along the path of the particles, and thus, (Riley et al. 2009). Consequently, , and thus, from Equation (17) we obtain

In this case, the probability function can be expressed as

where δ _D is the Dirac delta function. Substituting Equation (20), along with f_in given by Equation (14), in Equation (13) and integrating (Supplemental Information Part A) yields the transfer function of the ith exit of the MMO-DMA for nondiffusing particles:

Key flow streamlines are those associated with the centroid points at the aerosol inlet and the monodisperse-particle outlets of the MMO-DMA, respectively, defined as

and

From Equations (22) and (23), we can also define

which is the change in flow stream function experienced by a particle traversing the classifier along particle streamline from to . Combining Equation (24) with Equations (12) and (17), one can predict the midpoint electrical mobility , i.e., the electrical mobility of the particles traversing from the midpoint of the inlet to the midpoint of the ith exit when particle diffusivity is considered negligible (i.e., ), by

The midpoint electrical mobility for each monodisperse-particle outlet can be used to define the dimensionless particle electrical mobility:

We can further define the following dimensionless flow parameters that correspond to the ith exit:

and

Using Equations (3)–(6) and the definitions given by Equations (24)–(28), the transfer function for nondiffusing particles (Equation (21)) can be written in dimensionless form as (Supplemental Information Part A)

Equation (29) is similar to that derived by Stolzenburg (1988) for the single monodisperse-particle outlet DMA, with the difference that all the nondimensional variables correspond to the ith exit as described by Equations (26)–(28).

2. 2 The MMO-DMA Transfer Function for Diffusing Particles

Small particles traversing the DMA column on a given particle streamline, defined by Equation (16), deviate from their paths as a result of Brownian motion. The relative importance of particle migration and diffusion can be expressed in terms of the migration Peclét number defined by (Flagan 1999)

Here υ _E is the electrophoretic migration velocity of the particles, and b=R ₂−R ₁ is the radial distance between the two coaxial electrodes. The electrophoretic velocity of the particles is proportional to their electrical mobility and the electric field strength that varies only in the radial direction (Equation (11)). The particle diffusion coefficient D is also proportional to the electrical mobility such that, for singly charged particles, the Peclét number has no explicit dependence on particle size but is proportional to the classification voltage V.

Because diffusion across even a small fraction of the aerosol inlet flow can substantially distort the transfer function, it is sufficient to consider small deviations from the starting particle stream function (Zhang and Flagan 1996). Stolzenburg (1988) modeled the diffusive departure of the particles from their streamline in the cylindrical DMA using a local orthogonal curvilinear coordinate system based on streamwise and cross-stream coordinates. To do so, he defined s as the distance traversed by the particle along the particle streamline, and x as the perpendicular distance of the particle from . Because typical particle convective Peclét numbers are large for sub-10-nm particles, it is sufficient to consider only cross-stream diffusion (x-direction) and to neglect diffusion in the streamwise direction. It is also assumed that the cross-stream shear does not affect cross-stream diffusion as streamwise flow does not affect the distance of the diffusing particle from the nondiffusing particle streamline, and that the particle losses to the walls of the classifier column are negligible. The root-mean-square displacement of the particles from the mean trajectory increases with increasing the time the particles spend in the DMA according to (Hinds 1999)

The distribution of the deviation of the particles about their mean trajectory can be approximated with a Gaussian distribution having standard deviation σ _x =<x_rms >.

When diffusion is significant, motion of the particles cannot be completely determined by Equation (15) that gives the mean velocity of the particle moving on well-defined stream functions as described by Equation (16). In other words, is no longer constant along a particle path when particle Brownian motion is significant. To derive the transfer function of the DMA in this case, we need to determine the probability distribution for when the particle reaches the vicinity of the monodisperse-particle outlet slit.

The deterministic velocity of the particles within the DMA can be expressed as

where r and υ are vectors representing the particle position (relative to the origin) and velocity, respectively, and and represent the particle velocity components. In a conventional DMA, the developing probability distribution for the perpendicular distance x of a particle from its deterministic streamline is Gaussian having a peak value at x = 0 and a standard deviation σ _x . This deviation changes with time according to Equation (31), and thus, we can write

Following Stolzenburg's analysis, for small deviations, can be approximated by a first-order Taylor series:

The difficulty in estimating (x) is in determining the slope of the equation above, which can be expressed as . At x=0, however, , whereas and are perpendicular to the particle streamline. Using Equation (18), we can therefore estimate the rate of change in with respect to x, and thus obtain (Riley et al. 2009)

Equation (34) can now be written as

where r and υ are evaluated at x=0. The probability distribution in x can then be transformed to a Gaussian distribution in centered at and having a standard deviation

In the absence of diffusion, the particles move along fixed particle streamlines (i.e., remains constant), so that the distribution of as a whole and in particular remain constant. In calculating the change in from Equation (37), we need to consider only the differentials resulting from diffusion, and therefore, using Equation (33), we can obtain

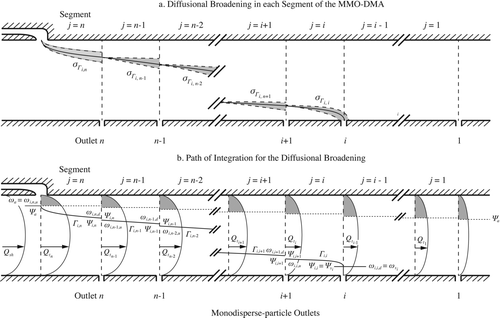
For the case of the MMO-DMA, the variance of the distance of the particles about the trajectory that leads to the ith monodisperse-particle outlet increases as the particles traverse each segment of the DMA. The segments of the MMO-DMA are the sections between successive outlets so that the jth MMO-DMA segment is defined as the section between the j + 1 and the jth sample outlets (Figure 2a). In the case of the nth sample outlet, i.e., the one closest to the aerosol inlet, the corresponding MMO-DMA segment is that between the aerosol inlet and the nth sample outlet. As the total flow rate through the MMO-DMA column decreases by after the particles pass each outlet, the contribution to diffusional broadening must be calculated separately for each segment. Thus, the diffusional broadening along the whole path of the particles traveling along the ith particle streamline can be expressed as

Here, denotes the contribution to the diffusional broadening of the particles classified through the ith monodisperse-particle outlet when traversing the jth segment of the MMO-DMA on the particle streamline leading to the ith monodisperse-particle outlet. This can be estimated by integrating Equation (38) along the part of the particle streamline in that segment (Figure 2a):

The probability of a particle that has entered the classifier on particle streamline to arrive at the ith exit on a particle streamline between and is

Using this probability for and , we can derive the transfer probability distribution function of a diffusing particle for the ith exit as

In order to estimate by Equation (42), and from that to obtain the transfer function of the ith monodisperse-particle exit using Equation (13), we need to estimate and from that .

FIG. 2 Schematic diagram of the MMO-DMA showing (a) the individual segments of the column, and the associated diffusional broadening parameters for the particles exiting through the ith outlet (note that the total broadening is the sum of the spreading parameters in each segment given by Equation (39)), and (b) the integration path along the particle streamline with the associated steps over each monodisperse-particle outlet. Key: ω _i,j,u and ω _i,j,d are the dimensionless radial positions of a particle classified through the ith outlet when it enters and exits, respectively, the jth segment, and

is the total flow rate at the jth segment.

2.2.1 The Dimensionless Diffusional Broadening Parameter

For the calculation of using Equation (40), all paths of integration _in can be approximated by the centroid particle streamline for each segment corresponding to and . This approximation allows us to write

where .

We can define the dimensionless diffusional spread parameter that characterizes the broadening of the transfer function in the jth segment for the ith monodisperse-particle outlet of the MMO-DMA as

where

is the total flow within the jth segment as depicted in Figure 2b. Correspondingly, we also define the total dimensionless spread parameter that characterizes the broadening of the transfer function for the ith monodisperse-particle outlet as

Note that is the mean change in stream function for particles going from the aerosol inlet to the ith monodisperse-particle outlet, while is the standard deviation of the particle and fluid stream functions ( is fixed) in going this same distance. Thus, σ _i is a true relative standard deviation due to diffusion in both stream function and electrical mobility (Equation (25)).

To evaluate , we need to estimate the velocity υ of the particles within the DMA. The axial component of the particle velocity υ _z is determined by fluid convection, and the average axial fluid velocity in the jth segment is given by

The magnitude of the radial component of the velocity υ _r of a particle having electrical mobility estimated at the outer wall (i.e., r=R ₂) is the same for all segments and is given by

For particles traveling on streamline , the transit time through the classifier (i.e., the time in which a particle covers the distance from R ₂ to R ₁) can be approximated by

For convenience, we define the dimensionless variables

and

so that

We can further define the dimensionless diffusion coefficient corresponding to the particles that exit through the ith outlet as

The inverse of this parameter is analogous to the migration Peclét number as defined by Flagan (1999). Evaluating Equation (30) for particles having electrical mobility , we substitute v_E with given by Equation (48) and use the corresponding particle diffusivity given by . The migration Peclét number associated with the ith exit is then

The nondimensional form of Equation (43) now becomes

Using the geometric parameter

the dimensionless diffusional broadening parameter can be written as

where

is a unique geometric- and flow-condition-dependent parameter for each combination of aerosol exit i and segment j.

2.2.2 The Path of Integration for the Diffusional Broadening Parameter

In order to calculate the integral in the G _i,j factor, it is necessary to determine the path of integration and the velocity along that path. To do that, we must make some simplifying approximations about the flow field in the MMO-DMA in order to obtain an analytical solution for the integral. Following Stolzenburg and McMurry (2008), we assume that the axial flow profile is static within each segment, either flat or fully developed. Thus, all radial flows are confined to the boundaries between the segments at the midlines of the aerosol entrance and exit slits. At these boundaries, the axial flow is assumed to make an instantaneous transition from the upstream profile to the downstream profile. A nondiffusing particle following a fluid streamline at this transition will make an instantaneous radial jump inward as shown in Figure 2b, which is assumed to have negligible contribution to the integral (Supplemental Information Part B).

The path of integration is simply the trajectory of a nondiffusing particle, having centroid electrical mobility , that begins on the inlet centroid streamline . The condition fixes the ratio of flow crossed along the trajectory to the electric flux crossed, or simply the distance z, down the MMO-DMA column. This is exemplified by Equation (25) for the end point of the trajectory where the ratio is a constant, independent of position. Thus, if Q _i,a is the flow bounded by and the value of the stream function at any position (r, z) along the trajectory, then

Using the known axial flow profile and the total flow at any axial distance z, Q_i,a can be related to a radial position, thereby completely determining the trajectory. To this end, let Q_i be the flow between the trajectory at z and the outer wall at R ₂. Then,

The total flow at z is just , where L _j+1<z<L_j . The ratio is then the flow fraction between the particle trajectory at (r, z) and the outer wall at R ₂. This flow fraction is given by the integral (Stolzenburg 1988; Stolzenburg and McMurry 2008)

where is the dimensionless axial velocity profile. Here,

is a dimensionless radial position variable. The upstream and downstream end points (ω, z) of the trajectory through segment j are then given by (ω _i,j,u , L _j+1) and (ω _i,j,d , L_j ), respectively, where

and

All that remains to complete the determination of the trajectory and path of integration is to define the dimensionless axial flow profile f _γ(ω).

For the case of plug flow (Stolzenburg 1988), f _γ(ω)≡1 and the flow fraction is

For the case of Poiseuille or fully developed flow, the dimensionless velocity is (Bird et al. 2007)

where

In this case, the flow fraction equals to (Stolzenburg 1988)

2.2.3 Evaluation of the Diffusional Broadening Parameter

With the path of integration determined, we now turn our attention to the integrand of the diffusional broadening parameter. As already mentioned, the velocity υ of the particles at any point within the DMA is given by Equation (15), i.e., υ = u +Z_p E . Consistent with our approximation of the flow field in the previous section, we assume that there is no radial component of the air velocity within the segments (this is a good assumption if one ignores the flow patterns in the vicinity of the aerosol inlet and exit slits). The radial particle velocity component is then

Assuming also that E_z =0 everywhere within the DMA column (again, this is a valid assumption if one ignores the regions close to the aerosol inlet and exit slits), the axial component of particle velocity is

The dimensionless particle velocity can then be expanded as

Considering now that

we obtain

Substituting Equations (69)–(71) into Equation (57) yields

which can be rewritten as

From Equations (47), (48), and (55), we obtain

The G_i,j factor can now be written as

where

and

as defined by Stolzenburg (1988). For plug flow, Stolzenburg (1988) calculated

and for Poiseuille flow,

Finally, we can write the dimensionless diffusional broadening parameter in several different forms:

where

and and σ* _i are, respectively, and σ _i evaluated for particles having electrical mobility . Note that the former depend only on instrument parameters while the latter depend on particle size as well.

2.2.4 Derivation of the Transfer Function for Diffusing Particles

The transfer function of the ith exit of the MMO-DMA for diffusing particles is given by Equation (13), which, using Equations (14) and (42), yields (Supplemental Information Part C)

Here ϵ is the integral of the error function defined as

where the standard error function is given by

Using the dimensionless variables defined by Equations (26)–(28) and (46), the transfer function of the ith exit of the MMO-DMA for diffusing particles can be re-expressed as (Supplemental Information Part C)

Predictions using the diffusing transfer function given by Equation (84) are in good agreement with the measurements provided by Chen et al. (2007), for the specific design they proposed. The details of this comparison are presented in Giamarelou et al. (2012).

3. RESOLUTION OF THE MMO-DMA

According to Zhang and Flagan (1996), the resolution of a DMA is the ratio of the mobility corresponding to the peak of the transfer function Z* _p to the full width of the mobility transfer function at its half maximum (FWHM), . The limiting resolution for DMAs with a single monodisperse-particle outlet is that predicted using the nondiffusive transfer function to estimate ΔZ_FWHM (Knutson and Whitby 1975). Because the larger particles are classified at higher voltages applied between the two electrodes, the limiting resolution (i.e., ignoring particle diffusivity) is obtained under these conditions and can be expressed as . For balanced flows (i.e., δ=0), the limiting resolution is reduced to . By analogy, the resolution of the ith exit of the MMO-DMA can be calculated as

and for balanced flows, i.e., when the sample flow rate of the ith exit is equal to the aerosol flow rate δ _i =0 or , as

The resolution of each DMA channel can be evaluated by using numerical values of its transfer function. When particle diffusivity is taken into account, the spread of the transfer function, and thus the resolution of the DMA, depends on the particle migration Peclét number through σ, and on the flow ratios β and δ. Flagan (1999) showed that for small particles, the resolution is proportional to the square root of the applied voltage. Downard et al. (2011) extended this approach for the opposed migration aerosol classifiers (OMACs) and the inclined grid mobility analyzers (IGMAs), and showed that at low voltages both these instruments exhibit better resolution compared with that of the DMA. Using their approach, we derive here a general expression for estimating the resolution of the ith exit of the MMO-DMA for given operating conditions.

Since the introduction of the closed loop sheath flow system (Kousaka et al. 1985), it is more common to operate the DMA with balanced flows, which for the case of the MMO-DMA means that . Operationally, the closed loop would work more conveniently with , but for comparison with previous works for the conventional DMA, we will consider the case of here. In this case, the dimensionless diffusional transfer function for the ith outlet (Equation (84)), can be written as

To simplify the calculations and without loss of generality, we proceed by defining the dimensionless mobility

and the dimensionless variance

After substituting Equations (88) and (89) into Equation (87) and rearranging, the dimensionless transfer function becomes

For convenience, we further define

so that Equation (90) can be simplified to

The fraction within braces on the right side is a central difference approximation of the second derivative of the integrated error function υϵ, which is equal to .

Following Flagan (1999), we now consider the situation β² _i ≪σ² _i ≪1. The first condition indicates that the width of the transfer function is dominated by the effect of diffusion over the base width determined by the flow ratio. The second condition indicates that the diffusion-broadened width is still small compared with the peak, , such that relative variation of is small within the width, and can be approximated as constant. This also means that the transfer function is still relatively symmetric about the peak. Both of these conditions are necessary and sufficient to accept the central difference approximation above as reasonably accurate.

Under these conditions, the behavior of the transfer function for diffusing particles can be estimated by

so that the transfer function of the ith exit can be expressed as

Using Equations (91), (88), (89), and (86) and rearranging, we obtain

In a similar manner, we obtain that for nonbalanced flows

As shown in Equation (95), the transfer function of the ith exit of the MMO-DMA reduces to a Gaussian distribution with standard deviation σ _i . In this case, the position of the peak corresponds to the centroid electrical mobility, i.e., , and the FWHM is related to the standard deviation by (Taylor 1997). Based on the definition of Zhang and Flagan (1996), i.e., , the resolution of the ith exit of the MMO-DMA, estimated by using the approximate diffusional transfer function (Equation (95)), can be expressed as

To derive Equation (97), we have used Equations (54) and (79). Note that Equation (57) differs from the expression given by Flagan (1999; Equation (57)) in that he incorporates the extra factor of (1−R ₁/R ₂) into the definition of G_i . Beginning with Equation (54) and expressing the particle migration Peclét number as a function of the applied voltage between the two electrodes,

the diffusion-limited resolution becomes

where f . It should be noted that depends on the geometry of the MMO-DMA and on the operating conditions. Under the assumption that the particles entering the DMA are singly charged, and that the operating temperature is ambient (i.e., T = 298 K), , where e is the elementary charge. In a similar manner with the single monodisperse-particle outlet DMA (Flagan 1999), the diffusion-limited resolution becomes

The smallest particle sizes that can be accurately classified with DMAs are affected by particle diffusion. The extent to which particle diffusion can affect the performance of a DMA can be characterized by the diffusion-onset voltage , which can be estimated by the intersection of and (Flagan 1999). Below this voltage, the classification resolution of a DMA is significantly reduced by particle diffusivity (Seol et al. 2002). As a result, when equating Equation (86) with Equation (100) for balanced flows, the diffusion-onset voltage for the ith exit of a cylindrical MMO-DMA becomes

To obtain an expression that describes the variation of the resolution with voltage over the entire operating range, we will need to evaluate certain moments of the transfer function. For an ideal DMA, Stolzenburg (1988) calculated the variance of the nondiffusing transfer function as . For the case of the MMO-DMA, the variance of the ith exit is given by

so that can be written as

When particle diffusivity becomes important, Stolzenburg (1988) and Stolzenburg and McMurry (2008) showed that for the diffusing transfer function, the corresponding moment for the conventional DMA becomes , which for the case of the MMO-DMA can be written in the form

Following Flagan (1999), we replace with in Equation (103) and apply it over the entire range of σ _i , thus obtaining

Equally valid would be to replace σ* _i with in Equation (97) to give

The leading numerical factors of these two formulations differ only by 4%. But clearly, there is too much dependence on the flow asymmetry parameter δ_i in Equation (105) in the diffusion-limited regime. For 0⩽δ _i <1, the factor in the parentheses of Equation (105) can range from 1 up to , a 30% possible variation. This degree of variation with δ_i is not present in Equation (106) in the diffusion-limited regime where σ*² _i ≫β² _i . Similarly, Equation (106) is off by the same factor in the nondiffusing limit. Thus, neither approach yields a valid approximation for the resolution of the DMA over the entire range of σ_i when unbalanced flows are considered.

For the case of balanced flows, i.e., δ_i = 0,

is a good approximation to within 4% in the diffusion-limited regime and is exact in the nondiffusing limit. Here,

To maximize the resolution of the MMO-DMA, σ*² _i should be minimized. For a given geometry, i.e., for fixed γ values, and flow rate ratios β _i  and δ _i , σ*² _i decreases continuously with increasing or voltage, corresponding to a decreasing length or increasing sheath flow. For conventional DMAs, one seeks to minimize the effect of particle diffusivity by optimizing the distance between aerosol inlet and monodisperse-particle outlet (i.e., by setting the term according to Rosell-Llompart et al. [1996] and de la Mora [2010, personal communication, 15 November, 2010], or the term according to Flagan [1999], close to unity). For the MMO-DMA, such an optimization is appropriate only for the nth monodisperse-particle outlet, for which one can use the approaches proposed for the conventional DMAs.

4. CONCLUSIONS

In this article, we derive an analytical expression for the transfer function of a cylindrical DMA with multiple monodisperse outlets (namely an MMO-DMA) using the same approach followed by Stolzenburg (1988) for the conventional DMA. We first derive the transfer function for each monodisperse-particle outlet without taking into account particle diffusivity (Equation (29)), and then extend our analysis to derive the transfer function for diffusing particles (Equation (84)). The derived MMO-DMA transfer functions differ from the conventional DMA transfer function (Stolzenburg 1988) in that every individual channel has an associated sheath flow rate (Equation (5)) and excess flow rate Q_mi (Equation (6)) as shown in Figure 1a.

By analogy to the conventional DMA, the limiting resolution of the ith monodisperse-particle outlet of the MMO-DMA for nondiffusing particles can be determined by and for balanced flows by , where β_i and δ_i are nondimensional flow parameters corresponding to each outlet (cf. Equations 27 and 28, respectively). In the diffusion-limited regime, assuming that the transfer function of the MMO-DMA is Gaussian, we derive the diffusion-limited resolution for each outlet (Equations (97), (99), and (100)), using the approach followed by Flagan (1999) and Downard et al. (2011). Combining the two limiting cases (i.e., for nondiffusing and for diffusing particles), we further derive an approximate resolution (Equations (107) and (108)) for balanced flows only, which can be applied over the entire range of particle mobilities and diffusional broadening parameters.

NOMENCLATURE

b	=	radial distance between the two coaxial electrodes
D	=	diffusion coefficient
	=	dimensionless diffusion coefficient
e	=	charge of the electron
E	=	electric field vector
E r	=	radial component of the electric field
E z	=	axial component of the electric field
e r	=	unit vector in the radial direction
e z	=	unit vector in the axial direction
erf (x)	=	error function
F γ	=	flow fraction
f	=	geometric parameter
f in	=	probability of a particle entering the DMA on a specific streamline
	=	probability of a particle exiting the DMA at the ith monodisperse-particle outlet
f γ	=	dimensionless velocity profile
G i	=	geometric and flow parameter for the ith monodisperse-particle outlet
I γ(ω)	=	geometric integral parameter
k	=	Boltzmann constant
L i	=	distance between the middle of the aerosol flow inlet and the middle of the ith sample outlet
n	=	number of monodisperse-particle outlets
P e	=	Péclet number
q	=	particle charge
Q a	=	aerosol flow rate
	=	excess flow rate after the ith monodisperse-particle outlet
	=	sample flow rate of the ith monodisperse-particle outlet
Q sh	=	sheath air flow rate
	=	sheath air flow before the ith monodisperse-particle outlet
Q t	=	total flow rate
	=	total flow rate corresponding to the ith segment
r	=	position vector
r	=	radial position
	=	dimensionless radial position
R 1	=	inner radius
R 2	=	outer radius
	=	resolution
	=	resolution when considering nondiffusing particles (conventional DMA)
	=	resolution of the ith outlet of the MMO-DMA when considering nondiffusing particles
	=	limiting resolution
	=	resolution of the ith outlet of the MMO-DMA using the approximate diffusional transfer function
	=	approximate resolution of the ith outlet of the MMO-DMA
s	=	distance along the particle streamline
S 2 d	=	variance of transfer function
T	=	temperature
t	=	time
	=	dimensionless time of the particles traveling to the ith sample outlet of the MMO-DMA
	=	electrophoretic migration velocity of at R 2
U j	=	average flow velocity of the jth MMO-DMA segment
u	=	flow velocity vector
u r	=	radial velocity component of the flow
u z	=	axial velocity component of the flow
υ	=	particle speed
υ	=	particle velocity vector
	=	dimensionless particle velocity in the jth MMO-DMA segment
υ r	=	radial particle velocity component
υ z	=	axial particle velocity component
υ E	=	electrophoretic migration velocity
V	=	applied voltage
	=	diffusion-onset voltage
x	=	perpendicular distance from particle streamline in
z	=	axial position
Z p	=	particle electrical mobility
	=	centroid particle electrical mobility corresponding to the ith outlet
	=	dimensionless electrical mobility corresponding to the ith outlet

Greek Letters

β i	=	dimensionless flow ratio corresponding to the ith outlet
γ	=	geometric parameter
	=	particle stream function
δ i	=	dimensionless flow ratio corresponding to the ith outlet
δ D	=	Dirac delta function
∇	=	gradient operator
ϵ(x)	=	integral of the error function
ζ i	=	dimensionless mobility
σ i	=	dimensionless total diffusional broadening parameter of particles exiting through the ith outlet
σ i,j	=	dimensionless diffusional broadening parameter within the jth MMO-DMA segment of particles exiting through the ith outlet
σ* i	=	dimensionless diffusional broadening parameter of particles with centroid electrical mobility corresponding to the ith outlet
	=	total diffusional broadening of particles exiting through the ith outlet
	=	diffusional broadening parameter within the jth MMO-DMA segment of particles exiting through the ith outlet
	=	diffusional broadening parameter around particle streamline
σ x	=	standard deviation in the direction perpendicular to the particle streamline
τ i	=	characteristic transit time through the MMO-DMA for particle having mobility
	=	flow stream function
	=	electric flux function
ω	=	dimensionless radial position
Ω	=	transfer function
	=	transfer function of the ith monodisperse-particle outlet for nondiffusing particles
	=	transfer function of the ith monodisperse-particle outlet for diffusing particles

Acknowledgments

We thank Loukas Vitiniotis, Dias Haralambopoulos, and Michiel Kreutzer for the constructive discussions on various parts of our article. MG also thanks Andy Downard for sharing his theoretical and experimental results.

[Supplementary materials are available for this article. Go to the publisher's online edition of Aerosol Science and Technology to view the free supplementary files.]