The Effect of Orientation on the Mobility and Dynamic Shape Factor of Charged Axially Symmetric Particles in an Electric Field

Abstract

The mobility of a nonspherical particle is a function of both particle shape and orientation. Thus, unlike spherical particles, the mobility, through its orientation, depends on the magnitude of the electric field. In this work, we develop a general theory, based on an extension of the work of Happel and Brenner (1965), for the orientation-averaged mobility applicable to any axially symmetric particle for which the friction tensor and the polarization energy are known. By using a Boltzmann probability distribution for the orientation, we employ a tensor formulation for computing the orientation-averaged mobility rather than a scalar analysis previously employed by Kim et al. (2007) for nanowires. The resulting equation for the average electrical mobility is much simpler than the expression based on the scalar approach, and can be applied to any axially symmetric structures such as rods, ellipsoids, and touching spheres. The theory is applied to the specific case of nanowires and the experimental results on the mobility of carbon nanotubes (CNT). A set of working formulas of additional mobility expressions for nanorods and prolate spheroids in the free molecular, continuum, and transition regimes are also presented. Finally, we examine the expression of dynamic shape factor common in the literature, and propose a clearer definition based on the tensor approach. Mathematica codes for the electrical mobility evaluations for five cases are provided in the Supplemental Information.

Copyright 2012 American Association for Aerosol Research

1. INTRODUCTION

The differential mobility analyzer (DMA) is widely used for measuring the size distribution of nanoparticles in the aerosol phase (Kim et al. 2007; Li et al. 2011a, b). For a spherical particle, the electrical mobility diameter is equivalent to its geometric diameter. However, for nonspherical particles, the measured electrical mobility diameter is that for a sphere of equivalent mobility. This can be complex, because the mobility becomes a function of particle shape and orientation. The orientation and thus mobility, in turn, depend on the magnitude of the electric field, which poses an additional complexity to predicting the mobility.

There have been several studies on the effect of the electric field on the orientation of nonspherical particles, whose mobility diameter is less than 0.5 μm. The most widely studied particles are doublets of polystyrene latex (PSL) spheres with primary sphere sizes in the range of 100 nm to 400 m (Kousaka et al. 1996; Zelenyuk and Imre 2007). Shin et al. (2010) studied the alignment of silver agglomerates with up to about 1000 primary spheres of diameter ∼20 nm. Several investigators have observed alignment in nanowires including Moisala et al. (2005) for single-walled carbon nanotubes (SWCNTs), Song et al. (2005) for electrospray-generated gold nanorod particles, and Kim et al. (2007) for multiwalled CNTs.

The focus of this article is on the development of a general theory to compute the electrical mobility of axially symmetric particles, which includes doublets of spheres and nanowires. Kim et al. (2007) developed a theory for calculating the orientation-averaged mobility of charged nanowires in an electric field based on a Boltzmann probability distribution for nanowire orientation. As an application of this theory, the lengths of monodisperse carbon nanowires were expressed as a function of the mobility diameter of the nanowires. However, there are some issues in Kim et al.'s approach. First, Kim et al. calculated the orientation-averaged mobility by using the friction coefficient expressed in the scalar form, which more rigorously should be expressed in a general tensor form. Second, the polarization energy for an ellipsoid particle was a factor of “2π” higher than the correct value.

In this work, we develop a more robust theory of orientation-averaged mobility using the tensor form of drag force and the general expression for the polarization energy for an axially symmetric particle. We compare the results of our theory with the experimental mobility data for CNTs in Kim et al.'s (2007) study. While our validation is based on experimental data for nanowires, our theory is generally applicable to any axially symmetric particle for which the friction tensor and the polarization energy are known, and is an extension of the Happel and Brenner (1965) theory for the sedimentation of nonskew objects to include a Boltzmann probability distribution for the orientation. We also discuss the expression of dynamic shape factor common in the literature, and propose a clearer definition.

2. THEORY

2.1. Orientation-Averaged Mobility for Axially Symmetric Particles

The mobility of a charged particle within a DMA is determined through a balance of the electrostatic (F_e ) and drag force (F _drag) along the electric field direction (radial for a cylindrical DMA). In a cylindrical DMA, for example, both the magnitude and direction of electric field vary radially. However, so long as the characteristic time for a particle to reach its asymptotic drift velocity is small compared with the time over which there is a significant change in the electric field, we can assume that the particle follows the varying electric field instantaneously.

For axially symmetric particles, the drag force is (Happel and Brenner 1965)

where is the friction coefficient tensor and is the drift velocity of the particle. The particle will be undergoing Brownian rotation. We assume that the Brownian rotation is slow compared with the translational relaxation time, which is valid for particles in the continuum regime, most particles in the transition regime, and high aspect ratio particles in the free molecular regime. The detailed discussion will be described in a separate manuscript. For this quasi-equilibrium, the drag force is balanced by the electric force

where q is the free charge on the particle. Multiplying both sides of Equation (2) by ,

The quantity is expressed in terms of the body-fixed coordinate system () parallel to the three principal axes of the particle, and the direction of the electric field is expressed in terms of the unit vectors fixed in space (). The unit vector is chosen along the electric field direction (radial) and is chosen parallel to the axis of an axially symmetric particle. The angle between and is θ.

Then the tensor can be expressed as the dyadic products of the unit vector:

where K ₁, K ₂, and K ₃ are the three principal components. Since is a diagonal matrix, the inverse of is easily computed:

From Equations (3), (5), and (6), one obtains

For axially symmetric particles, K ₁=K ₂=K _⊥, where K _⊥ is the principal component of the friction coefficient tensor perpendicular to the axial direction, and K ₃=K _∥, where K _∥ is the component parallel to the axial direction. In general, the drift velocity, , of nonspherical particles is orientation dependent so that there will be components other than in the direction (the electric field direction).

For a particle population, the axial orientation of particles will show a distribution. If the particles are small enough, over the time scale of interest, the rotational Brownian motion will result in a steady-state distribution of the orientation, i.e., Boltzmann angular distribution.

The orientation-averaged velocity is expressed in terms of the Euler angles θ, φ, ψ, which relate body-fixed coordinate system () to the space-fixed coordinates () (Goldstein et al. 2002), and the orientational probability function f(θ):

where the integration for ψ and φ are from 0 to 2π and for θ is from 0 to π. This method applies to nonspherical particles with orientation probability dependent on only θ. Expressing the unit vector dyadic products in Equation (7) in terms of the Euler angles, for an axially symmetric particle, one obtains the following expression for the average drift velocity:

where

and

We note that the average velocity has only a single component in the direction (the electric field direction).

If we define the average electrical mobility as , then a general expression for the average electrical mobility is

Equation (11) provides a general expression for the average mobility of axisymmetric particles, whose evaluation requires a knowledge of K _⊥ and K _∥, which depend on drag model specific to the geometry of interest (e.g., ellipsoid, rod, doublets of spheres), and the orientation average value <cos²θ>. The calculation of (K _⊥, K _∥) and <cos²θ> is discussed in the following sections (Sections 2.2 and 2.3). In what follows, we evaluate and validate Equation (11) for a nanowire based on prior experimental measurements on carbon nanotubes (CNTs; Kim et al. 2007), and then extend the analysis to other axisymmetric shapes.

The expression of electrical mobility mentioned earlier is also related to the definition of dynamic shape factor for nonspherical particles, which is discussed in Section 3.3.

2.2. Drag Force, F _drag, and Expression of K _⊥ and K _∥

The values of K _⊥ and K _∥ depend on the expression of drag force in Equation (1), which is dependent on particle shape and the flow regime appropriate for the particle.

In this work, we focus on the example of nanowires, for which we have experimental results for comparison. We will also compare our new result with the work of Kim et al. (2007).

2.2.1. Nanorod in Free Molecular Regime

In the free molecular regime, the drag force for a cylindrical particle (length L_f , diameter d_f ) with hemispherical ends was developed by Dahneke (1973b),

where η is the gas viscosity, λ is the mean free path of gas, f is the momentum accommodation coefficient, and β ₁ is the aspect ratio for rod defined by L_f /d_f . For parallel and perpendicular orientations, Equation (1) is simplified to F _∥=K _∥ V _∥ and F _⊥=K _⊥ V _⊥, while F _∥ and F _⊥ can be obtained from Equation (12) with θ = 0 and θ = π/2, respectively. Then,

and

2.2.2. Other Expressions for K _⊥ and K _∥

Expressions for K _⊥ and K _∥ for nanorods and prolate spheroids in the free molecular, continuum, and transition regimes are given in the Appendix (Section A1), and can be applied to obtain the mobility through Equation (11).

2.3. Orientation Distribution f(θ) and Expression of <cos²θ>

The probability that the angle between the axis of an axially symmetric particle and the electric field direction lies in the interval (θ, θ + dθ) due to Brownian motion, following Boltzmann's law (Fuchs 1964),

where ∫^π ₀ f(θ)sin θdθ=1, and U is the interaction energy between the particle and the external electric field. The interaction energy may be from a permanent dipole (Fredericq and Houssier 1973), a free charge on the particle, or an induced dipole due to polarization. In this work, we only consider the energy from the free charge and the energy due to polarization. Energies are expressed in SI units.

2.3.1. Evaluation of the Interaction Energy, U, for Various Situations

2.3.1.1 Interaction energy from the free charge The interaction energy from the free charge depends on where the charge is located on the particle. For example, the free charge may stay at the ends of the particle, or be uniformly distributed along the entire surface. In this work, we only provide the expressions of interaction energy from the free charge for conducting nanorod and conducting prolate spheroid.

•	Conducting nanorod

For conducting nanorod, using the same assumption as in Kim et al. (2007) that the free charge can immediately respond and freely move along the CNT surface to the end of the nanowire closest to the lowest voltage electrode, we obtain the electric energy from free charge q (θ = π/2 as the reference position), which can be represented as

•	Conducting prolate spheroid

The electric energy can be obtained from (16) by replacing L_f with the major axis 2a.

2.3.1.2 Interaction energy from an induced dipole for an axially symmetric particle The polarization energy for a particle with polarizability is given by (Böttcher and Belle 1973)

For an axially symmetric particle, Equation (17) becomes

where α_⊥ is the principal component of polarizability perpendicular to the axial direction and α_∥ is the component parallel to the axial direction. For the orientational probability governed by Boltzmann's law, only the relative energy based on angle is relevant, so any term in the energy expression not related to angle can be neglected. Thus, Equation (18) can be expressed as

2.3.1.3 Interaction energy from the free charge and an induced dipole for a nanorod or prolate spheroid assuming a conducting surface From Equations (16) and (19), the total energy is given by

where l = L_f for nanorod and l = 2a for prolate spheroid.

We approximate the polarization energy of a nanorod with that of a prolate spheroid with the same volume and the same aspect ratio as the rod. For a prolate spheroid with relative permittivity ϵ _k , aspect ratio β ₂ (major semiaxis a; minor semiaxis b; β ₂ = a/b) and volume v, the two principal components of polarizability α_∥ and α_⊥ are expressed in the Appendix (Section A2). There is an error in the expression of the polarization energy for an ellipsoid in Kim et al. (2007). Their value is a factor of 2π times larger than the correct value given here. A similar factor error also occurs in Fuchs (1964), where a 1/4π factor is missing for the polarization energy for an ellipsoid in Gaussian units.

2.3.2. Evaluation of <cos²θ >

Using Equations (10), (15), and (20), we calculate <cos²θ > for four cases.

2.3.2.1 Fully random When the electric field goes to zero, the orientation of particles is random and <cos²θ > = 1/3.

2.3.2.2 Fully aligned When the electric field goes to infinity, the particles are fully aligned and <cos²θ > = 1.

2.3.2.3 Free charge and induced dipole orientation for a nanorod or prolate spheroid assuming a conducting surface Assuming that the free charge can immediately respond, and freely move along the surface of a particle to the end of the axially symmetric particle closest to the lowest voltage electrode, and the total interaction energy follows Equation (20), then

where x = cosθ,

for nanorod and for prolate spheroid,

and , the imaginary error function.

2.3.2.4 Pure induced dipole orientation for an axially symmetric particle If we only consider the induced dipole energy,

2.4. Voltage–Shape Information Relationship in a DMA Measurement (Step Mode)

A knowledge of the orientation-averaged mobility, e.g., Equation (11), can be used to determine the voltage at which an axially symmetric particle can be detected in a DMA measurement. Following Kim et al. (2007), the detection voltage (V_e ) and shape information (hidden in orientation-averaged mobility ) relationship can be obtained as

where

	rin is the radius of inner electrode of DMA,
	rout is the radius of outer electrode of DMA,
	Qsh is the sheath flow rate,
	Qa is the aerosol flow rate,
	Ld is the length of DMA electrode,

and

The averaged mobility, , which is a function of electric field and contains the shape information, is given by Equation (11) for axially symmetric particles such as a nanowire.

The derivation of Equation (23) is given in the Appendix (Section A3).

2.5. Evaluation of Mobility for Special Cases

Equation (11), given again next, is the general form for the orientation-averaged mobility:

There are several advantages of this formulation over our previous analysis (Kim et al. 2007):

•	We employ a more rigorous evaluation of the friction coefficient by using a tensor form.
•	We are now able to find a closed-form expression that is much easier to evaluate.
•	Equation (11) is a general expression that can be applied to any axially symmetric shape, such as an ellipsoid or a doublet of spheres, assuming that one has expressions for K ⊥ and K ∥, and the interaction energy.

In the following, we provide six cases of mobility evaluation for nanorod and prolate spheroids using Equation (11). The <cos²θ> in Equation (11) can be evaluated based on Equation (10) generally, and for four specific conditions, it is given in Section 2.3.2. Note that the polarization energy for an ellipsoid contained in the expression for <cos²θ> corrects for the 2π error in Kim et al. (2007). The cases are as follows:

1.	Case 1: Nanowire with semispherical ends in free molecular regime: For the specifics of a nanowire with semispherical ends, the averaged electrical mobility in the free molecular regime is evaluated based on Equation (11), where K ⊥ and K ∥ are given in Equations (13) and (14).
2.	Case 2: Nanowire with flat ends in free molecular regime: The expressions of K ⊥ and K ∥ required in Equation (11) are given in the Appendix in Equations (A1) and (A2).
3.	Case 3: Prolate spheroids in free molecular regime: The expressions of K ⊥ and K ∥ are given in the Appendix in Equations (A3) and (A4).
4.	Case 4: Slender rod in continuum regime: The expressions of K ⊥ and K ∥ are given in the Appendix in Equations (A5) and (A6).
5.	Case 5: Prolate spheroids in continuum regime: The expressions of K ⊥ and K ∥ are given in the Appendix in Equations (A7) and (A8).
6.	Case 6: Slender rod and prolate spheroids in transition regime: The mobility expressions for nanorods and prolate spheroids in the transition regime can be evaluated based on Equation (11) and the expressions of K ⊥ and K ∥ are given in the Appendix (Section A1.3).

The Mathematica codes for the electrical mobility evaluations for the above five cases (Cases 1–5) are provided in the Supplemental Information.

3. RESULTS AND DISCUSSIONS

In this section, we compare the results for the electrical mobility of nanowires as a function of electric field with our previous theoretical treatment as well as with experiments on the mobility of CNTs (Kim et al. 2007). We use the same values as in Kim et al. for the relative permittivity of CNT, ϵ _k = ∞, and the momentum accommodation f = 0.9. At the end of this section, we also discuss the expression of dynamic shape factor common in the literature, and propose a clearer definition and an effective dynamic shape factor for a particle population.

3.1. Electrical Mobility as a Function of Applied Electric Field

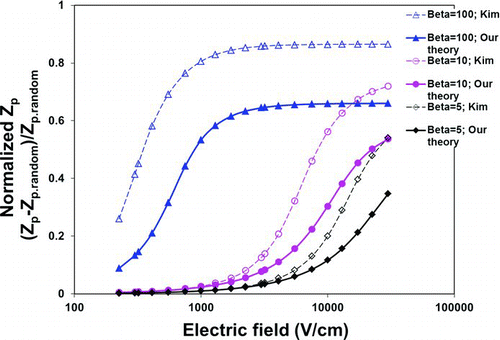
In Figure 1, we plot normalized (relative to random orientation) electrical mobility versus applied electric field for a wide range of aspect ratios, β, with diameter d_f = 15 nm in the free molecular regime based on our theory (Case 1 in Section 2.5) and using our previous formulation (Kim et al. 2007). At low field strengths, the thermal energy dominates the aligning energy, and Brownian dynamics result in a random orientation. As the electric field increases, the wire will tend to align resulting in a larger electrical mobility. Both theories show a clear increase in mobility observed with increasing field strength for all βs and the onset of alignment occurring at lower field strength with increasing β. However, in all cases, the normalized electrical mobility based on Kim et al. (2007) is substantially higher. This discrepancy of asymptotic behavior at high field is due to the scalar form of the friction coefficient used in Kim et al.'s theory instead of a general tensor form used here.

FIG. 1 Theoretical calculations of our theory and Kim et al.'s theory on the effect of the electric field on the scaled mobility, (Z_p – Z_{p ,random})/Z_p ,_random, for nanowires with diameter d_f = 15 nm and various aspect ratios in the free molecular regime (30,000 v/cm is the air breakdown limit). (Color figure available online.)

3.2. Experimental Validation

In the work of Kim et al. (2007), CNTs were generated with a fixed diameter d_f = 15 nm and a wide range of lengths from 50 to 2000 nm. The CNTs were size selected by a DMA and counted by a condensation particle counter (CPC). The size-selecting voltages of DMA (detection voltage, V_e ) were chosen in a range from 465 to 4962 volts, with the corresponding equivalent spherical diameters (D_m ) from 50 to 150 nm. The selected CNTs were also electrostatically deposited after the DMA and their lengths were measured by transmission electron microscopy (TEM) analysis.

The predicted length of those selected CNTs can be calculated based on Equation (23) and the averaged mobility given in Case 1 for the free molecular regime or in Case 6 for the transition regime. Equation (23) provides the relationship between the detection voltage (V_e ) and the length of nanowire for given diameter (d_f ), which is hidden in the expression of average electrical mobility provided in Case 1 or in Case 6. In Figure 2, we plot the theoretically predicted nanowire length using our theory in both free molecular and transition regimes assuming that a nanowire is randomly rotating, fully aligned, and aligned by combined energy (free charge + polarization), as a function of experimentally measured electrical mobility diameter (D_m ), which is basically derived from the detection voltage V_e by assuming spherical particles.

FIG. 2 Comparison of theoretically predicted nanowire length: curves are for nanowires randomly rotating, fully aligned, and aligned by combined energy (i.e., free charge + polarization), respectively, with the lengths measured by TEM analysis in Kim et al. (2007), as a function of electrical mobility diameter measured with DMA. The drag force expressions of rod in both free molecular and transition regimes are used. (Color figure available online.)

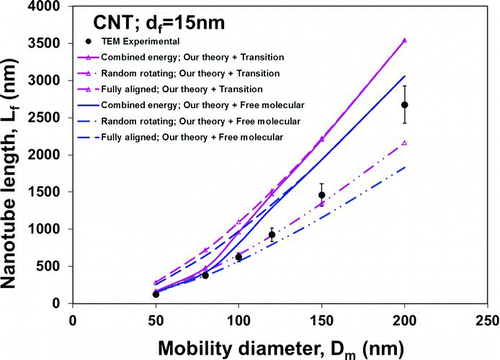
The predicted lengths of CNT calculated earlier are compared with the lengths measured by TEM analysis in Kim et al. (2007) in the same figure. It is seen that the TEM experimental results fall between the two limiting cases of random rotation and fully aligned using Dahneke's free molecular expression of drag force, and fall slightly lower than for random rotation at small nanowire lengths using Dahneke's transition expression of drag force. The experimental data match the predicted behavior of a randomly aligned nanowire for low mobility diameters, and then tends toward the curve corresponding to the totally aligned nanowires for the largest diameters. The data qualitatively follow the predicted trends; however, there is a slight discrepancy at small lengths using the transition drag force expression and a discrepancy at large nanowire lengths in both regimes. These discrepancies likely result from kinks and bends in the nanotubes, while the theory assumes a perfect rod-like structure.

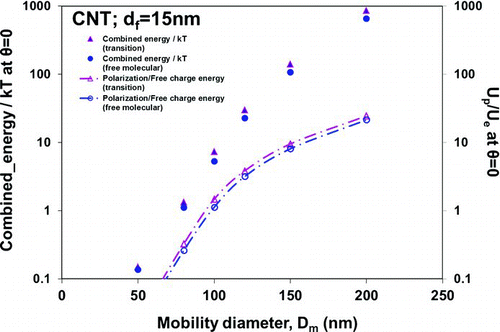
Figure 3 presents the relative combined electrical energy (i.e., free charge + polarization) in Equation (20) at θ = 0 to thermal energy as a function of experimentally measured electrical mobility diameter (D_m ). In the same figure, we draw the dipole polarization energy (U_p ) normalized by the energy from free charge (U_e ) at θ = 0. It is seen that, for a mobility diameter of 100 nm and larger, the aligning energy dominates thermal energy. Also, for a mobility diameter of 100 nm and larger, polarization energy starts to dominate the energy from free charge, which means that orientation due to polarization is the dominant effect.

FIG. 3 The relative combined electrical energy (i.e., free charge + polarization) in Equation (20) at θ = 0 to thermal energy is shown as a function of experimentally measured electrical mobility diameter (D_m ). At each points, the dipole polarization energy (U_p ) normalized by the energy from free charge (U_e ) at θ = 0 is plotted. The drag force expressions of rod in both free molecular and transition regimes are used in computing the aspect ratios. (Color figure available online.)

3.3. Defining the Dynamic Shape Factor

In this section, we review the expression for the dynamic shape factor found in the literature and suggest an alternative definition. We also propose an effective dynamic shape factor for a particle population.

For an axisymmetric particle, we can rewrite the drift velocity, , in Equation (7) in terms of the Euler angles θ, φ, ψ:

where

In general, the drift velocity, , of nonspherical particles is orientation dependent so that there will be components other than in the direction (external force direction). For example, V_d,i and V_d,j are not generally equal to 0 in Equations (25) and (26) for an axisymmetric particle.

The widely used definition of dynamic shape factor, χ, is that it is the ratio of the actual drag force of the nonspherical particle to the drag force of a sphere having the same volume and velocity as the nonspherical particle, as shown in Figure 4 (Cheng et al. 1988; Cheng 1991; Hinds 1999):

where d_e is the equivalent volume diameter and C_c is the slip correction factor.

FIG. 4 Direction of drag force and velocity for a nonspherical particle and reference sphere used in the definition of dynamic shape factor are shown. The drift velocity of the nonspherical particle has components other than just the direction of the external force. The left side of this figure shows the basis of the widely used shape factor, while the right side shows the basis of our proposed definition of dynamic shape factor. (Color figure available online.)

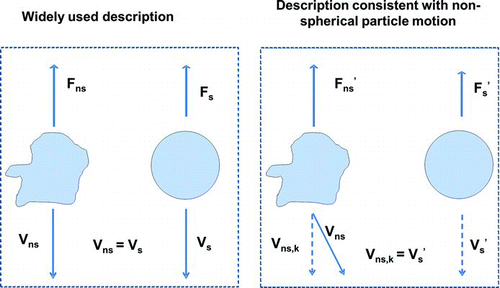
Unfortunately, this definition assumes that the drift velocity of the nonsphere is equivalent to a sphere, and can be treated as a scalar. However, as we showed earlier, for nonspherical particles, the drift velocity is a vector and has components other than just the direction of the external force.

To correct this inconsistency, we propose replacing V_d in Equation (28) with V_d,k , which is the drift velocity component along the external force direction, as shown in Figure 4. Then the corresponding dynamic shape factor, χ′(θ), is defined as

i.e., χ′(θ), is defined as the ratio of the actual drag force of the nonspherical particle to the drag force of a sphere having the same volume as the nonsphere and the particle velocity, which equals the drift velocity component along the external force direction of the nonsphere.

For the polar axis of an axisymmetric particle making a fixed angle, θ, with the direction of electric field, using Equations (27) and (29) and considering (1) and F _drag=qE, we obtain

where χ′_∥ is the dynamic shape factor when particle travels parallel to the axial direction, and χ′_⊥ is the dynamic shape factor when particle travels perpendicular to the axial direction. We note here that χ′_∥=χ_∥ and χ′_⊥=χ_⊥ because when θ = 0 and π/2, based on Equations (25) and (26), V_d,i and V_d,j vanish, and only a single component V_d,k exists. In this case, Equation (28) is equivalent to Equation (29). This approach removes the ambiguity in the value of the drift velocity found in previous studies (Cheng et al. 1988; Cheng 1991; Song et al. 2005).

For axisymmetric particles with a distribution of orientations, f(θ), the average velocity has only a single component in the external force direction. In this case, we can define an effective dynamic shape factor, χ_eff , based on orientation-averaged velocity as

Using Equations (31) and (9) and considering (1) and , we obtain

For applications where the particles are small, the Brownian rotation will rapidly approach the Boltzmann distribution. This is the case discussed in detail earlier for the nanowires.

In some applications, one is interested in the behavior of a system of randomly oriented particles. For random orientation, Equation (32) becomes

which is widely reported (Happel and Brenner 1965; Dahneke 1973a; Cheng et al. 1988; Cheng 1991; Song et al. 2005). The dynamic shape factor for random orientation given by Fuchs (1964), which differs from Equation (33), is slightly in error as was previously pointed out by Dahneke (1973a).

A general relationship between the average electrical mobility, , and the effective dynamic shape factor can also be obtained by using Equation (31) and:

For the case of a Boltzmann distribution, f(θ) will be a function of the field strength and will affect the values of both χ _eff and .

4. CONCLUSIONS

The approach of Happel and Brenner (1965) for computing the average drift velocity for randomly oriented axially symmetric particles has been extended to include a Boltzmann probability distribution based on the orientation energy of the particle. This theory uses a tensor formulation for computing the orientation average mobility rather than a scalar analysis previously employed by Kim et al. (2007) The resulting equation for the average electrical mobility is much simpler than the expression based on the scalar approach, and can be applied to other axially symmetric structures such as ellipsoids and touching spheres, provided that the friction tensor and the orientation energy are known.

The theory was applied to the specific case of nanowires, and the results are compared with the experimental results on CNTs in Kim et al. (2007). Based on the tensor approach, we have reevaluated the derivation of the dynamic shape factor to clarify its meaning. Finally, we provide in the Supplemental Information a set of programming codes for electrical mobility evaluation for some specific cases.

APPENDIX

A1. EXPRESSIONS FOR K _∥ AND K _⊥

The calculation of the average electrical mobility in Equation (11) requires a knowledge of K _∥ and K _⊥, which depend on the expression of drag force. In this appendix, we provide some specific examples.

A1.1 In Free Molecular Regime

A1.1.1 Nanorod

In the free molecular regime, K _∥ and K _⊥ for a cylindrical particle (length L_f , diameter d_f , aspect ratio β ₁ = L_f /d_f ) with hemispherical ends are given in Equations (13) and (14).

For a cylindrical particle with flat ends (Dahneke 1973b), we obtain

A1.1.2 Prolate Spheroids

For a prolate spheroid with semipolar axis, a, and semiequatorial axis, b, based on the drag force for a prolate spheroid in the free molecular regime (Dahneke 1973b), we obtain

where

A1.2 In Continuum Regime

A1.2.1 Nanorod

In the continuum regime, for slender cylinders (length L_f , diameter d_f , β ₁ = L_f /d_f >> 1) (Batchelor 1970), the components of friction coefficient parallel and perpendicular to the radial moving direction are

where ϵ=1/ln(2β₁).

and

where ϵ=1/ln(2β₁).

A1.2.2 Prolate Spheroids

With semipolar axis, a, semiequatorial axis, b, and aspect ratio, β ₂ = a/b (Dahneke 1973a),

and

where γ=(β² ₂−1)^1/2.

A1.3 Transition Regime

For spherical particles in the transition regime, the drag force in the continuum regime is reduced due to fluid molecular slipping along the particle surface, and the Stokes equation is modified by the Cunningham slip correction factor C_c :

where d_p is the diameter of spherical particle, and A ₁ = 1.142, A ₂ = 0.558, and A ₃ = 0.999 were given by Allen and Raabe (1985) at room temperature and atmosphere pressure.

Similarly, for a nonspherical particle, Dahneke (1973c) proposed an adjusted spherical diameter to calculate the drag force in the transition regime:

where d_a is the adjusted spherical diameter defined as Equation (A11) matches asymptotically the drag forces given in both free molecular and continuum equations when 2λ/d_a goes to either infinity or zero, that is (Cheng 1991),

Once the drag force in the transition regime is known by Equation (A11), K _⊥ and K _∥ can be obtained with θ = π/2 and 0, respectively.

A2. EXPRESSION OF TWO PRINCIPAL COMPONENTS OF POLARIZABILITY, α_∥ AND α_⊥, OF PROLATE SPHERICAL PARTICLES

We approximate the polarization energy of a nanorod with that of a prolate spheroid with the same volume and the same aspect ratio as the rod. For a prolate spheroid with relative permittivity ϵ _k , aspect ratio β ₂ (major semiaxis a, minor semiaxis b, β ₂ = a/b), and volume v, the two principal components of polarizability are defined as (Böttcher and Belle 1973; Sihvola 1999, 2007)

and

where ϵ ₀ is the permittivity of free space,

For a slender cylinder, ζ₁ is approximated to ln(2β₂)/β² ₂ and ζ₂ approximated to 0.5.

A3. VOLTAGE–SHAPE INFORMATION RELATIONSHIP FOR AXISYMMETRIC PARTICLES IN A DMA MEASUREMENT

A knowledge of the orientation-averaged mobility, e.g., Equation (11), can be used to determine the DMA precipitation time (t_p ), the time for the axisymmetric particles to travel from the location of inlet slit to the location of outlet slit. Following Kim et al. (2007), the precipitation time is

where

	rin is the radius of inner electrode of DMA,
	rout is the radius of outer electrode of DMA,
	Qsh is the sheath flow rate,
	Qa is the aerosol flow rate, and
	⟨Vr ⟩ is the drift velocity of the particle in the radial direction.

Since for axisymmetric particles and the radial dependence of the electric field in a cylindrical DMA, , where V_e is the detection voltage in the DMA measurement, Equation (A17) becomes

where and .

And the flow transit time in DMA is

A particle is detected when its precipitation time, t_p , is equal to the flow transit time, t_f , in the DMA. By equating Equations (A18) and (A19), the detection voltage (V_e ) and shape information (hidden in ) relationship can be obtained as

where the averaged mobility, which is a function of electric field and contains the shape information, is given by Equation (11) for axially symmetric particles such as a nanowire.

Acknowledgments

[Supplementary materials are available for this article. Go to the publisher's online edition of Aerosol Science and Technology to view the free supplementary files.]