Determination of the Scalar Friction Factor for Nonspherical Particles and Aggregates Across the Entire Knudsen Number Range by Direct Simulation Monte Carlo (DSMC)

Abstract

The friction factor of an aerosol particle depends upon the Knudsen number (Kn), as gas molecule–particle momentum transfer occurs in the transition regime. For spheres, the friction factor can be calculated using the Stokes–Millikan equation (with the slip correction factor). However, a suitable friction factor relationship remains sought-after for nonspherical particles. We use direct simulation Monte Carlo (DSMC) to evaluate an algebraic expression for the transition regime friction factor that is intended for application to arbitrarily shaped particles. The tested friction factor expression is derived from dimensional analysis and is analogous to Dahneke's adjusted sphere expression. In applying this expression to nonspherical objects, we argue for the use of two previously developed drag approximations in the continuum (Kn → 0) and free molecular (Kn → ∞) regimes: the Hubbard–Douglas approximation and the projected area (PA) approximation, respectively. These approximations lead to two calculable geometric parameters for any particle: the Smoluchowski radius, R _S, and the projected area, PA. Dimensional analysis reveals that Kn should be calculated with PA/πR _S as the normalizing length scale, and with Kn defined in this manner, traditional relationships for the slip correction factor should apply for arbitrarily shaped particles. Furthermore, with this expression, Kn-dependent parameters, such as the dynamic shape factor, are readily calculable for nonspherical objects. DSMC calculations of the orientationally averaged drag on spheres and test aggregates (dimers, and open and dense 20-mers) in the range Kn = 0.05–10 provide strong support for the proposed method for friction factor calculation in the transition regime. Experimental measurements of the drag on aggregates composed of 2–5 primary particles further agree well with DSMC results, with differences of less than 10% typically between theoretical predictions, numerical calculations, and experimental measurements.

Copyright 2012 American Association for Aerosol Research

1. INTRODUCTION

In aerosols, low-speed drag forces are ubiquitous, and these forces affect particle inertial, diffusive, and electrostatic motion. For a particle moving at a small Reynolds number and rotating slowly relative to a background fluid, the drag force, , can be written as

where is the fluid velocity vector, is the particle velocity vector, and f is the scalar friction factor (rather than the friction tensor; Peters 1999), which is a function of both the particle and the fluid properties. Because of the linear relationship between the drag force and the scalar friction factor, the friction factor strongly governs the behavior of aerosol particles. For a spherical particle with a radius a _p, which is significantly larger than the hard sphere mean free path of the gas molecules λ ¹ (Fuchs and Stechkina 1962), Stokes’ law applies and the friction factor is expressed as

where the subscript “Cont” denotes the continuum limit and μ is the gas dynamic viscosity. Conversely, when a _p is substantially smaller than λ (but still significantly larger than the gas molecule radius), particle–gas molecule momentum transfer is a free molecular process, with the friction factor in a hard-sphere gas given as (Epstein 1924; Tammet 1995):

where “FM” denotes the free molecular limit, ξ is the dimensionless momentum scattering coefficient (Hogan and Fernandez de la Mora 2011), and with a number of experimental measurements (Eglin 1923; Rader 1990; J. H. Kim et al. 2005; Ku and de la Mora 2009; Larriba et al. 2011), dating back to the work of Millikan (1923), revealing ξ ≈ 1.36.

Between these two limiting cases, f is a function of the ratio λ/a _p (the momentum transfer Knudsen number, Kn) and can be calculated for spheres with the semi-empirical Stokes–Millikan equation:

where C_C (Kn) is the Cunningham slip correction factor, commonly written as:

with empirically determined constants A ₁, A ₂, and A ₃. As Kn → 0, the Stokes–Millikan equation converges to (2) and similarly, converges to (3) as Kn → ∞. In the intermediate Kn range (the momentum transfer transition regime), measurements (Eglin 1923; Rader 1990) confirm the Stokes–Millikan equation's validity for spherical particles, with the values of A ₁ = 1.257, A ₂ = 0.4, and A ₃ = 1.1 given by Davies (1945) in good agreement with most experimental data. A number of theoretical studies of the drag on a spherical particle at intermediate Kn, both via the Boltzmann transport equation (Cercignani and Pagani 1968; Cercignani et al. 1968; Phillips 1975; Takata et al. 1993) and via Fuchs' flux matching theory (Fuchs and Stechkina 1962), also agree well with Equation (4).

Scalar friction factor calculation for spheres across the entire Kn range at low Re and low Ma (Mach number) appears extremely reliable via the Stokes–Millikan equation. Meanwhile, over the past several decades, there has been considerable interest in the physical characterization of nonspherical aerosol particles. In particular, there has been an emphasis on quasi-fractal aggregates, i.e., entities composed of a number of point contacting or partially coalesced primary spheres, where the number of primary spheres per entity exhibits a power law relationship with the entity's radius of gyration (Rogak et al. 1993; Weber et al. 1996; Scheckman et al. 2009; Sorensen 2011). Such nonspherical particles and aggregates also frequently lie within the momentum transfer transition regime, with their friction factors dependent upon Kn (Wang and Sorensen 1999). An expression similar to the Stokes–Millikan equation, yet applicable to particles of all shapes, is thus highly desirable. However, with few exceptions (Pich 1969; Dahneke 1982; Filippov 2000; Vainshtein and Shapiro 2005; Gmachowski 2010), scalar friction factor expressions for nonspherical objects have been proposed solely for either the Kn → 0 (continuum) or Kn → ∞ (free molecular) limits. To our knowledge, only Dahneke has presented a complete approach (termed the adjusted sphere approach) to friction factor calculation for nonspherical bodies in the transition regime (Dahneke 1973a–c), and despite some experimental support (Cheng et al. 1988; Rogak et al. 1993), present characterization techniques for nonspherical particles and aggregates do not make use of Dahneke's method. Instead, most recent analyses rely on simplified models of particle geometry, such as the “loose agglomerate model” (Lall and Friedlander 2006; Wang et al. 2010) for aggregates, or the approximation that high aspect ratio bodies can be modeled as prolate spheroids in the free molecular limit (S. H. Kim et al. 2007). It is thus clear that further investigation into the friction factor for nonspherical particles and aggregates in the continuum, free molecular, and, most importantly, the transition regime is warranted. The goal of this study is to propose and numerically test a simple algebraic expression for the orientationally averaged scalar friction factor of an arbitrarily shaped aerosol particle, which is moving relative to a background gas at low speed, across the entire Kn range. The proposed expression is applicable to both spheres, for which it converges to the Stokes–Millikan equation, and nonspherical entities, for which it takes as inputs two clearly defined particle geometric descriptors. In the sections that follow, theoretical justification for the use of these geometric descriptors, which define the effective particle size (orientationally averaged) in the continuum and free molecular regimes, respectively, is first given. Standard dimensional analysis is then used to predict a functional form for the friction factor of an arbitrarily shaped particle in the momentum transfer transition regime, and it is shown that this functional form coincides with Dahneke's adjusted sphere model (which was originally proposed without this supporting analysis). The proposed transition regime friction factor relation is tested via direct simulation Monte Carlo (DSMC) (Bird 1994; Chun and Koch 2005; Prasanth and Kakkassery 2006) for the drag force on quasi-fractal aggregates at various Kn values, for which the calculation methodology and results are also described in detail. Finally, the implications of the proposed functional form for the transition regime friction factor are discussed with regard to both theoretical and experimental studies of nonspherical particles and aggregates in aerosols.

2. THEORETICAL AND NUMERICAL METHODS

2.1. Continuum Regime

Similar to Stokes’ law for spheres, for nonspherical particles, we write the continuum regime, orientationally averaged scalar friction factor as

where R _H is the nonspherical particle hydrodynamic radius (Chen et al. 1988; Hubbard and Douglas 1993). A correctly determined R _H not only satisfies Equation (5) but is also a geometric descriptor of the particle, i.e., R _H is not dependent on fluid properties/system conditions. While for a number of common shapes, R _H values are given by Dahneke (1973a), as noted in the Introduction, most prior research efforts have been devoted to R _H calculation for quasi-fractal aggregates. For example, Chen and coworkers (Chen, Deutch et al. 1984; Chen, Weakliem et al. 1988) applied the theories of Kirkwood and Riseman (1948) for R _H prediction under these circumstances. Binder et al. (2006) employed accelerated Stokesian dynamics (Brady and Sierou 2001) for R _H calculation. Rosner and coworkers (Tandon and Rosner 1995; Garcia-Ybarra et al. 2006) have modeled aggregates as porous spheres where the permeability, and hence the friction factor, relates to the aggregate geometry. Each of these prior approaches, however, is limited to the analysis of entities composed of spherical subunits. Moreover, porous sphere models apply only for sufficiently dense aggregates with a large number of primary particles, and Kirkwood–Riseman calculations are only valid for objects for which there is minimal hydrodynamic shielding between primary spheres (Sorensen 2011). A simple approach is alternatively desired to estimate the hydrodynamic radius, with minimal limitations on particle shape.

Related to the issue of R _H determination is the calculation of the Smoluchowski radius, R _S (Gopalakrishnan et al. 2011), also commonly referred to as the capacity. R _S is defined such that the collision kernel, β, between the particle and a point mass of diffusivity D in the continuum regime is expressed as β = 4πDR _S. Like R _H, R _S depends solely on the geometry of the particle; hence, it is the mass transfer analog of R _H. Algorithms have been developed for R _S calculation that are relatively simple to implement and are not limited to particles of a particular shape or class of shapes (Northrup et al. 1984; Northrup et al. 1986; Zhou et al. 1994; Given et al. 1997). Focusing on drag determination for polymer chains in a solvent, Hubbard and Douglas (1993) put forth the approximation R _H ≈ R _S. Considering shapes for which R _H is known and linear chains of spheres with minimal shielding (applicable to the Kirkwood–Riseman theory), it is found that this approximation holds within several percentage points (Douglas et al. 1994) if both orientationally averaged R _S and R _H are considered. Independent of Hubbard and Douglas, Isella and Drossinos (2011) have also found that R _S and R _H are typically within 1% of one another (without orientational averaging) for linear aggregates of up to eight primary particles. Given the establishment of this approximation in polymer and colloid science, it is thus reasonable to propose its use for aerosol particles as well, and we do so here without further justification. A computationally efficient algorithm for orientationally averaged R _S calculation, employed in subsequent calculations, is described in the supplemental information of Gopalakrishnan et al. (2011), which is applicable to particles of any possible shape. We refer readers to this document for details as well as to the work of Hubbard, Douglas, and coworkers on the continuum regime scalar friction factor (Hubbard and Douglas 1993; Douglas et al. 1994; Zhou et al. 1994; Given et al. 1997).

2.2. Free Molecular Regime

Analogous to Equation (3), which applies specifically for spheres, the orientationally averaged scalar friction factor for an arbitrarily shaped particle in the momentum transfer free molecular regime (also referred as “Epstein's regime”) is given by the following equation (Mason and McDaniel 1988; Li and Wang 2003):

where Ω is the collision cross-section/momentum scattering cross-section for the particle (also orientationally averaged to account for particle rotation). Unlike R _H and R _S, Ω is not strictly a geometric descriptor of a particle, even in the absence of potential interactions with the surrounding gas molecules; rather, the collision cross-section depends upon both the particle size and the physics of particle–gas molecule collisions (Epstein 1924; Tammet 1995; Fernandez de la Mora 2002). Despite this complexity and the additional complexities of nonspherical geometries, calculation methods for Ω are well established, with calculations for model aggregates (Chan and Dahneke 1981; Meakin et al. 1989; Nakamura et al. 1994; Nakamura and Hidaka 1998; Mackowski 2006) as well as all-atom models of gas-phase macromolecules and molecular clusters (Shvartsburg and Jarrold 1996; Shvartsburg et al. 2007; Bleiholder et al. 2011) employed in a number of studies. All such calculations involve determination of the total amount of momentum exchanged between gas molecules and particles upon collision or close approach, for which a model of gas molecule reflection after collision is required. In large part, for evaluation of the collision cross-section of aggregates, where the base unit is a sphere with molecular-scale surface roughness, diffuse collisions have been considered. In diffuse collisions, the collision angle is sampled randomly and the gas molecule kinetic energy after collision is typically resampled from a Maxwell–Boltzmann distribution. Conversely, in Ω calculations for molecular clusters, where the base units are the individual atoms of the entity, specular collisions with deterministic reflection angles have been used in models. Although there are clear differences in the scattering models that have been employed, both types of calculations consistently reveal that the collision cross-section for a sufficiently large entity in the gas phase can be approximated as Ω ≈ ξPA, where PA is the orientationally averaged projected area for the entity of interest (Hogan and Fernandez de la Mora 2011; Hogan et al. 2011). Depending on the nature of energy exchange between gas molecule and particle upon collision, ξ = 1.30−1.39 for collisions that are largely diffuse (Epstein 1924), with most experiments consistent with ξ = 1.36 (Millikan 1923; Allen and Raabe 1985; Cai and Sorensen 1994; Larriba et al. 2011). While the approximation Ω ≈ ξPA, which we henceforth refer to as the PA approximation, is by no means theoretically rigorous, we propose that it will be reasonably accurate for particles of all shapes, provided that molecular-scale roughness and the physics of particle–gas molecule collisions do lead to apparently diffuse collisions (i.e., most of the time, incident gas molecules depart from the particle surface at angles that are nearly independent of the incident collision angle).

FIG. 1 Values of Ω/PA for quasi-fractal aggregates as determined from a 91% diffuse-angle/9% specular angle gas molecule collision model (closed symbols) as well as a 100% specular gas molecule collision model (open symbols). Quasi-fractal aggregates are generated using a modified cluster–cluster aggregation model with the noted D _f and N _prim, and with k _f = 1.3. For each shown result point, Ω calculations are performed on a single generated aggregate with momentum transfer from 5 × 10⁵ incident gas molecules to the aggregate for three perpendicular orientations. The resulting symmetric drag tensor from these calculations is diagonalized, and from the eigenvalues of the diagonalized tensor, the friction factor is calculated. The primary sphere radius in each aggregate is of arbitrary unit value, and each gas molecule is modeled as a sphere with a radius 1% that of the primary sphere radius. Orientationally averaged project areas (PA) are determined by the Monte Carlo method described in Gopalakrishnan et al. (2011). (Color figure available online.)

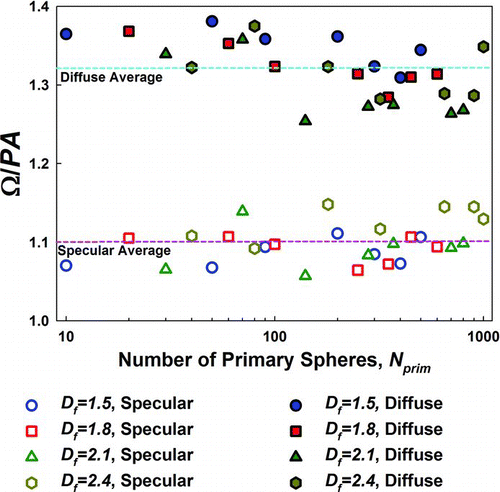
Use of the PA approximation drastically simplifies friction factor calculations in the free molecular regime, as algorithms for orientationally averaged projected area calculation are simpler and faster than hard-sphere scattering calculations of Ω (Shvartsburg et al. 2007; Bleiholder et al. 2011). Further support for implementation of the PA approximation is shown in Figure 1, which is a plot of the calculated ratio Ω/PA = ξ as a function of the number of primary spheres in quasi-fractal aggregates, obeying the relation (N _prim = number of primary spheres, k _f = pre-exponential factor, R _g = radius of gyration, a _prim = primary particle radius, and D _f = fractal dimension). For these calculations, aggregates are produced using a cluster–cluster aggregation algorithm described by Filippov et al. (2000), with point contacts between primary spheres. PA calculations are performed using the algorithm described by Gopalakrishnan et al. (2011). For Ω calculation, a 91% diffuse-angle/9% specular angle scattering model based on the work of Mackowski (2006) and a 100% specular scattering model (Shvartsburg and Jarrold 1996) are both employed. With application of the diffuse model to a sphere, scattering calculations reveal ξ = 1.36, in agreement with the analytical value obtained under these circumstances (Epstein 1924). Specular scattering calculations with a sphere lead to ξ = 1.00, which is also in agreement with the specular analytical value. In both diffuse-angle and specular scattering calculation procedures, multiple collision of a gas molecule with a particle are accounted for; i.e., after colliding with the particle, the gas molecule may recollide with the same particle if the angle at which it leaves the particle surface leads it to do so. Considering all examined particles, ξ takes on a value of 1.32 ± 0.04 with predominantly diffuse-angle scattering and 1.10 ± 0.03 with purely specular scattering. For both examined sets, there is only a small dependency of ξ on aggregate morphology, slightly decreasing for diffuse-angle scattering and slightly increasing for specular scattering with increasing N _prim, which was also observed by Meakin et al. (1989) when using similar calculation procedures. In spite of this small N _prim dependency, the fact that the ξ is roughly constant for diffuse-angle scattering (presumably the more appropriate scattering model for aerosol particles) provides theoretical support for the use of the PA approximation. Subsequently, the PA approximation is employed here with ξ = 1.36.

2.3. Transition Regime

From the Hubbard–Douglas and PA approximations, we find that the relevant size scales for calculation of friction factors are R _s and PA in the continuum and free molecular regimes, respectively. We now use dimensional analysis to find an appropriate definition of Kn for an arbitrarily shaped particle, as well as an appropriate functional relationship to describe the transition regime friction factor. We assume that only parameters found in either the continuum or free molecular friction factor relations can influence drag in the transition regime; hence, we nondimensionalize (Buckingham 1914, 1915) the parameters, f, μ, R _s, λ, and PA. Only two fundamental dimensions are required to describe this system (mass per time and length), leading to the dimensionless ratios:

No clear definition of Kn arises from this dimensional analysis, as R _s can be alternatively used as a nonrepeating variable, changing Equations (7a) and (7b). It is clear, however, that as any appropriate definition of Kn approaches zero, ζ must also approach zero, Θ must approach unity, and χ remains constant. In addition, as Kn → ∞, Equation (6) must hold valid, which, with the PA approximation, requires that Θ → 0.6035ζ⁻¹χ⁻¹, ζ →∞, and χ again remains constant. Noting these limiting functional forms for Θ and building on recent success in the analysis of mass transfer in the transition regime (Gopalakrishnan et al. 2011), wherein the relevant length scale for the diffusive Knudsen number (Kn _D) was found to be PA/πR _s for all examined values of χ, we propose similarly that an appropriate definition of Kn is

The use of Equation (7d) would eliminate the parameters ζ and χ (provided their influence on the friction factor is always coupled), leaving the friction factor relationship described dimensionlessly by the function Θ(Kn). For Θ(Kn) to apply for all shapes, it must certainly apply for spheres, which leads to

where C _C is again the Cunningham slip correction factor (Equation (4b)), which is now applied to particles of arbitrary shape with known R _s and PA.

The definition of Kn as the product of ζ and χ coincides with Dahneke's proposed equivalent sphere method, provided the expressions listed here for the friction factor in the continuum and free molecular regimes are equivalent to those given by Dahneke. In the continuum regime, Dahneke (1973a) expresses the scalar friction factor of an arbitrarily shaped particle as

where the subscript D denotes Dahneke's model, c ₀ is a dimensionless constant, and L _C is a characteristic length scale for the object in question, often taken as its length in the equatorial plane. For both Equations (5) and (8a) to hold valid with the Hubbard–Douglas Approximation, 6πR_s = c ₀ L _C. In the free molecular regime, Dahneke (1973b) writes the scalar friction factor for an arbitrarily shaped object as

where c* is a second dimensionless constant. With the PA approximation assumed valid, from Equations (6) and (8b), the relation c*L _C ² = 2.67ξPA is recovered. Dahneke (1973c) then defines the transition regime friction factor as

where R _Adj is the adjusted sphere radius, i.e., the radius of a sphere having the same slip correction factor as the nonspherical body under examination. For Equations (8a) and (8b) to hold valid in the limits where λ/R _Adj → 0 and λ/R _Adj → ∞, R _Adj = 1.657(c*/c ₀)L_C = PA/(πR _s) must hold true. Therefore, λ/R _Adj = Kn, and Equation (8c) is simply the predicted form Θ(Kn) expressed dimensionally, using a specific functional form for the slip correction factor (4b).

FIG. 2 Images of the test aggregates used in DSMC. The reported R_S and PA values, calculated using the Hubbard–Douglas and PA approximations, respectively, are normalized with respect to a primary particle radius of 1.0 (arbitrary units). (Color figure available online.)

2.4. Direct Simulation Monte Carlo (DSMC)

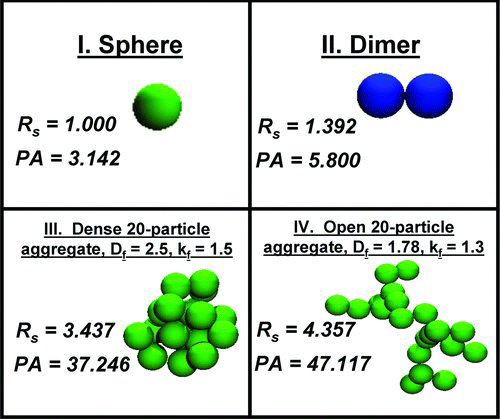
Although Dahneke's adjusted sphere model and the friction factor expression deriving from the dimensional analysis converge, further examination of the function form of Θ(Kn) is necessary. For this purpose, we employ DSMC for the flow field around model structures of spheres, point-contacting dimers, and two model quasi-fractal aggregates. Digital images of these objects as well as their R _s and PA values (calculated using the algorithms described in Gopalakrishnan et al. 2011) are provided in Figure 2. Although the denser aggregate has χ = 1.00 (which is common for particles with little-to-no apparent aspect ratio), the more open quasi-fractal aggregate has χ = 1.26, which is slightly greater than the χ value for a linear aggregate composed of five primary particles (χ = 1.22). Therefore, the calculations here effectively test the validity of the proposed friction factor relation for particles with aspect ratios up to ∼5. The DSMC procedure is described in detail below. The goal of each calculation is to extract an orientationally averaged value of Θ for a prescribed value of Kn. We directly compare calculated values of Θ⁻¹ (which should be equivalent to the slip correction factor C _C) to Equation (4b). While a number of other authors have put forth values for A ₁, A ₂, and A ₃, some with a slightly modified definition of λ (Allen and Raabe 1982, 1985; Buckley and Loyalka 1989; Rader 1990; J. H. Kim et al. 2005), we find that these alternatives lead to similar results as Davies’ (1945) coefficients; thus, comparison with alternative coefficients is not warranted. Of a different functional form than Equation (4b), we also compare DSMC calculations to the function proposed by Phillips (1975) for diffuse-angle scattering:

and the functional form:

which was originally put forward by Annis et al. (1972) based on the assumption 1/f = 1/f _cont + 1/f _FM across the entire Kn range. While used infrequently shortly after its original presentation, Equation (9b) has more recently been supported by Sorensen and coworkers (Sorensen and Wang 2000; Wang and Sorensen 2001; Pierce et al. 2006; Sorensen 2011) in the analysis of quasi-fractal aggregates due to the simplicity of this functional form as compared with competing relations, hence its inclusion in our comparison.

DSMC is a stochastic particle method used to simulate the Boltzmann equation. As a result, DSMC provides an accurate model across the entire Kn range; however, it is most useful for simulating gas flows in the transition regime (0.01 < Kn < 10). DSMC tracks a large number of simulation “particles” (distinct from the examined aggregates shown in Figure 2, which serve as boundaries in DSMC) through a computational grid allowing for gas-phase and gas-surface collisions, where each simulation particle represents a large number (W _p) of real gas molecules. Simulation particles are translated in straight lines along their molecular velocity vectors for a short time step (Δt ≈ τ _c/4), after which, collisions with neighboring particles located in the same computational cell (Δx ≈ λ/2) are performed stochastically. Here, τ _c is the local mean collision time, and λ is the local mean free path; thus, the restrictions on Δt and Δx enable the decoupling of movement and collision processes to be accurate for dilute gases. For steady-state flows, only a relatively small number of particles are required per cell (N _p ≈ 20) (Bird 1994) to maintain accurate collision rate statistics. However, for low-speed flows where thermal velocities are much larger than the bulk flow velocity, a large number of sampling time steps are required after the simulation reaches a steady state to reduce statistical scatter in macroscopic flow and surface properties of interest. DSMC requires the specification of collision cross-sections to determine particle collision rates, and these cross-sections are rigorously linked to the coefficient of viscosity through the Chapman–Enskog theory (Chapman and Cowling 1970; Bird 1994). Therefore, the viscosity (μ) of the simulated gas is precisely defined, and results can be scaled by μ, λ, and, ultimately, by Kn (varied in this work by varying the primary particle size in the examined particles, while μ and λ are kept constant).

We obtain DSMC solutions using the molecular gas dynamic simulator (MGDS) code (Gao et al. 2011) for a flow of gas around the aforementioned aggregate particles, as well as single spheres. The free-stream conditions in all simulations correspond to a diatomic gas of pure nitrogen (N₂) at temperature T = 300 K, pressure p = 1 atm, and velocity V = 5 m/s. The density is determined through the ideal gas law, p = ρ _gas RT, where R is the specific gas constant for N₂. DSMC employs the variable hard-sphere (VHS) model, which models the collision cross-section as σ_VHS∝σ_HS/g ^2(ω−1/2). Here, σ_HS=πd ² _ref is the hard-sphere cross-section, g is the relative collision velocity, and ω determines the power law temperature dependence of the viscosity. Upon substitution of the VHS cross-section into the Chapman–Enskog first approximation to the viscosity coefficient (Chapman and Cowling 1970), the following viscosity law is obtained for the DSMC simulations (Bird 1994):

where m is the mass of an N₂ molecule, and k is the Boltzmann constant. The DSMC parameters for N₂ are specified as ω = 0.74, T _ref = 273 K, and d _ref = 4.17 × 10⁻¹⁰ m (Bird 1994). This results in a simulation viscosity of μ = 1.78 × 10⁻⁵ kg/m/s at T = 300 K that closely matches the accepted value for molecular nitrogen gas (Hirschfelder et al. 1954). To be consistent with the scaling parameters used in the accompanying friction factor theory, we characterize the flow condition by the ratio μ/(0.499ρ _gas c), which is precisely defined for the simulated gas (c is the mean thermal speed of the gas). This ratio is referred to as the hard-sphere mean free path, i.e., λ ≡ μ/(0.499ρ _gas c), which is the scaling parameter used to define Kn for both the theoretical and the numerical results of this work.

In all simulations, the computational grid is uniform and Cartesian (since λ remains essentially constant). Tested aggregate geometries are represented by triangulated spheres, as is depicted in Figure 3. The triangulated spheres do not intersect with each other, yet their surfaces are sufficiently close so as to emulate point contacts. The MGDS DSMC code is equipped with cut-volume algorithms (Zhang and Schwartzentruber 2011) that sort arbitrary triangulated surface elements into Cartesian cells for surface collision detection and with algorithms that compute the flow volume of “cut-cells” next to complex surface geometries. For the complex 3D geometries considered, this approach requires far less user time than generating a body-fitted flow field grid. When simulation particles collide with triangulated surface elements, the particles undergo diffuse reflection (random angle of reflection) and full thermal accommodation. Specifically, the velocities and rotational energies of reflected molecules are drawn from Maxwell–Boltzmann distributions corresponding to the wall temperature, which is set as T _w = 300 K for all cases.

FIG. 3 Uniform Cartesian flow field grid and triangulated surface geometry cut from the Cartesian grid for the dense 20-particle aggregate described in Figure 2. (Color figure available online.)

The drag forces on aggregate surfaces in DSMC are not computed using pressure distributions or shear stresses determined from velocity gradients; rather, the force exerted on a triangulated surface element by the gas is simply the average momentum transferred to the surface element by the colliding particles per unit time. The total force in a given principal direction (x, y, or z) is then determined by summing the average momentum transfer over all surface elements. Under the investigated low-velocity, room-temperature conditions, statistical fluctuations lead to large scatter in DSMC solutions; thus, it is important to quantify the variance in the computed average drag force. The average force components per unit area (Fx _s,i , Fy _s,i, Fz _s,i , in the x, y, and z directions, respectively) due to the number of collisions with the aggregate (wall collisions, denoted as N _w,s,i , with a single surface element i of area A_i , during a sampling time interval t _s = MΔt) are computed by the relations:

where v ^inc _x,y,z,p and v ^reflect _x,y,z,p are the incoming and reflected velocity components of particle p, respectively, and t _S is some number (M) of DSMC time steps (each taking time Δt). Since we are interested in the drag force (i.e., in the x-coordinate direction, the direction of incoming flow), the overall average drag force acting on the entire surface during this sampling time interval is

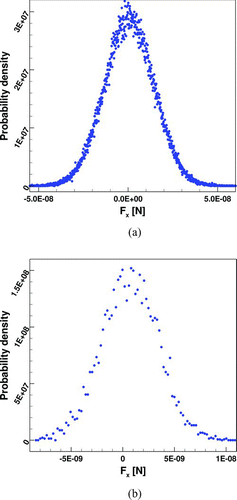
Therefore, constitutes the average force on the entire surface computed for a single sample. Lift forces (perpendicular to the flow) can be similarly extracted from DSMC, but are not considered here. For the case where M = 1 (i.e., the instantaneous forces computed during a single DSMC time step), the probability distribution function of instantaneous forces in the x-direction on a dimer is plotted in Figure 4a. A total of 130,000 discrete time steps are used to obtain these distributions. It is evident from this figure that the average forces computed for small samples (M = 1) follow a normal distribution, with a standard deviation substantially larger than the mean of the distribution. This confirms that for low velocities at room temperature, fluctuations are considerable and must be accounted for proper inference of the drag force on a particle.

FIG. 4 (a) The probability distribution function of instantaneous drag force computed for the dimer at Kn = 0.15 and an angle of 30° (N _tot = 130,000, M = 1, N _s = 130,000). F_x is the total drag force acting on the dimer. (b) The probability distribution function of sampled drag force computed for the dimer at Kn = 0.15 and an angle of 30° (N _tot = 130,000, M = 20, N_s = 6500). F_x is the total drag force acting on the dimer. (Color figure available online.)

If N _tot time steps are examined via DSMC method, then these can be binned into N _s = N _tot/M distinct samples, and the average force over all such samples is determined by

The variance of the distribution of these sampled forces can then be computed as:

For example, the distribution of sampled forces on the dimer for M = 20 (thus N _s = 6500 sampling intervals, in contrast with the M = 1, N _s = 130,000 case shown in Figure 4a), is shown in Figure 4b. The distribution of the sample averages for N _s = 6500 is observed to also follow a normal distribution, and although not shown, if plotted for various sample sizes (various M values), the distributions obtained are always Gaussian. This implies that all samples (of any M) are statistically independent; thus, it follows that the standard deviation (σ) of the average itself ( in Equation (13)) can be estimated by

where σ remains approximately constant for any binning (any M and corresponding N _s). Reported error bars in the DSMC results derive from the standard deviation of determined with N _s ranging between 50 and 200. The calculated relative statistical errors of the simulations are compared with the theoretical expression for relative expected error obtained by Hadjiconstantinou et al. (2003), which applies in the continuum regime. Overall, the relative statistical errors of the simulations we report in this article are found to be consistent with the theoretical expressions, generally within a factor of 2.

In addition to concern over the statistical dispersion in results, for low-speed flow computations, the influence of boundary conditions on the computed result must also be carefully investigated. Typical subsonic outflow boundary conditions combine extrapolated flow properties from within the computational domain with a specified back-pressure, thereby determining the upstream-moving characteristic required as a boundary condition in subsonic flows. However, using extrapolated macroscopic flow properties in DSMC is problematic due to the high scatter, which would result in numerically fluctuating outflow boundary conditions. We instead impose far-field inflow boundary conditions, wherein particles fluxing through all boundaries in the DSMC simulations are drawn from Maxwell–Boltzmann distributions at the inflow conditions (u, T, p). If the boundaries are located sufficiently far from the test aggregate boundary, where the streamlines have recovered to their free-stream values, these boundary conditions should physically represent the flow about the particle, and, numerically, the solution should be independent of the boundary locations.

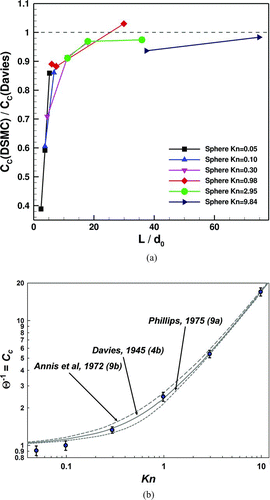
To understand the numerical and physical accuracy of far-field inflow boundary conditions, simulations employing different domain sizes are conducted for flow over a single sphere, where theoretical and experimental results regarding the drag force are available for comparison. The comparisons are then used to select proper domain sizes for the remaining simulations. Figure 5a displays the ratio of the slip correction factors calculated from DSMC, C _C(DSMC), to those predicted by Davies, C _C(Davies), as a function of the simulation domain side length. When the domain size is sufficiently large compared with the diameter of the sphere, the computed slip correction factor is in excellent agreement with the expected slip correction factor, with differences of 4% or less between calculations and predictions for all Kn ≥ 0.3. However, as Kn decreases, the absolute domain size (as opposed to the normalized domain size) required to predict an accurate slip correction factor increases, which leads to a systematic underestimation in the slip correction factor (overestimation in the drag force) for the domain sizes used for Kn close to 0.1 and smaller. Larger domain sizes than the largest ones employed here become practically unfeasible with our current DSMC algorithms, requiring exceedingly long computation times (computation time is noted at the end of this section) for statistical convergence to stable probability distribution functions for the drag force. We therefore anticipate that with DSMC, it is possible to accurately determine the slip correction factor for Kn ≥ 0.3, but we note that because of the finite simulation domains employed, underestimation in C _C prediction is expected, particularly at lower Kn. Based on this sensitivity analysis with spheres, the domain side lengths used for all simulations are listed in Table 1, and the slip correction factor for spheres as a function of Kn is shown in Figure 5b, using the Table 1 domain side lengths. Again, in this figure, good agreement is observed between Equation (4) predicted slip correction values and simulations for Kn ≥ 0.3, and reasonable agreement is found with the slightly different predictions of Equations (9a) and (9b), the alternative functional forms for the slip correction factor.

FIG. 5 (a) The ratio of the slip correction factor predicted by DSMC compared with Davies’ predicted slip correction factor for spheres, as a function of computational domain size and Kn. The domain side length is normalized by the diameter of the sphere, d₀. (b) The inferred slip correction factor on a sphere from DSMC as compared with predictions from previously developed slip correction factor relationships. The error bars displayed derive from the estimate of the standard deviation on the drag force, which is described in the text. (Color figure available online.)

Finally, at each examined Kn, DSMC is performed at four different orientations relative to the incoming flow velocity for dimers and at 12 different orientations for both the dense and open test aggregates. Specifically, the dimer is held at angles of 0⁰, 30⁰, 60⁰, and 90⁰ relative to the incoming gas flow for calculations, while each aggregate is examined with four randomly selected sets of completely orthogonal orientations (leading to 12 total orientations). Values of Θ for each Kn are calculated using the equation:

where F _Stokes=3πμVd ₀,, V=5m/s (the free stream velocity employed), and F _DSMC is the orientationally averaged drag force calculated by DSMC. In total, the results presented in the subsequent section consist of approximately 200 distinct simulations. Each simulation is obtained on a single processor in an average time period of approximately one week; thus, the computational time required for this study is ∼1400 CPU days.

3. RESULTS AND DISCUSSION

3.1. Flow Visualization

In addition to providing a measure of the orientationally averaged drag force on nonspherical particles, DSMC is uniquely able to predict the flow field around nonspherical aerosol particles in the momentum transfer transition regime. Figure 6 shows four contour plots of the x-direction velocity averaged over a large number of sampling time steps after reaching steady state on the dense test aggregate for four selected Kn, oriented such that the flow moves from left to right in the figure. Also shown via color contours are the x-direction stresses (P_x , due to both normal and shear stresses) on the aggregate surface. In each case, numeric fluctuations in the velocity are evident both close to the particle surface and out in the free stream region. Close to the aggregate, modulations in x-direction velocity are brought about by gas molecule (simulation particle) reflection at the particle surface, while out in the free stream, fluctuations are inherently present due to the thermal energy present in the flow, as well as the statistical nature of DSMC. Only at extremely high values of the ratio ϑ _gas = mU² /kT (where m is the gas molecule mass, U is the gas bulk velocity, and kT is the thermal energy) will fluctuations disappear in flows, and similarly, these fluctuations will lead to random diffusive particle motion (Chandrasekhar 1943), which strongly influences particle behavior except in circumstances where the ratio ϑ _p = m _p U² /kT (where m _p is the mass of a particle) is sufficiently large.

TABLE 1 Computational domain sizes normalized by particle size, for each simulated geometry and Knudsen number. d ₀ = 2PA/πR _S

N = 1 single sphere
Knudsen number	0.05	0.10	0.30	0.98	2.95	9.84
Domain side length/d 0	5.24	7.48	17.95	29.92	35.91	74.8
N = 2 dimer
Knudsen number	0.15	0.49	1.38	1.97
Domain side length/d 0	9.62	21.4	47.9	57
N = 20 dense aggregates
Knudsen number	0.10	0.30	0.79	0.98	1.97	3.94	6.89
Domain side length/d 0	6.01	10.14	15.02	15.02	30.03	45.05	57.82
N = 20 open aggregates
Knudsen number	0.20	1.67	2.46	2.95	4.92	7.87	9.84
Domain side length/d 0	7.68	15.07	22.16	26.59	44.32	52	59.09

3.2. DSMC-Calculated Slip Correction Factors

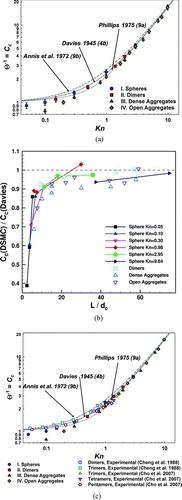
The calculated slip correction factors for spheres and all test aggregates are shown in Figure 7a as a function of Kn, which is calculated from Equation (7d) using the normalized values from Figure 2 and the primary particle radius employed in each calculation. Also shown are the expected slip correction factor–Knudsen number curves from Equations (4), (9a), and (9b). Two conclusions can be immediately drawn from this figure: (1) As anticipated, there is considerable deviation from predicted curves for Kn < 0.3 (between 10 and 30% when compared with all three curves), which arises from the need to use unfeasibly large simulation domains to examine these cases. Small deviations from predictions appear at high Kn as well, though not nearly as pronounced as is found at Kn < 0.3. (2) All calculated slip correction values appear to collapse to a single Θ(Kn) curve, with differences between results with dimers, dense aggregates, and open aggregates not evident. This is made clearer in Figure 7b, which is an analogous plot to Figure 5abut displays the ratio of the DSMC-inferred slip correction factors to those predicted by Davies (1945) for all examined particles. Irrespective of particle morphology, all inferred slip correction factor values collapse to nearly the same curve. DSMC thus provide strong support for the argument that Θ(Kn) is a shape-independent relation that describes the low-Re, low-Ma, orientationally averaged drag force on arbitrarily shaped particles. Further, as Kn is calculated for each aggregate using both the Hubbard–Douglas and the PA approximations, DMSC provide support for the use of these algorithms for determination of the Knudsen number length scale for arbitrarily shaped particles. The better agreement found between with the predictions of Philips (1975) and aggregate calculations, however, cannot be taken as proof that this function is more reliable than the relation provided by Davies (1945), as finite domain sizes in DSMC invariably lead to slight underestimation of the slip correction factor (note the log-scale plot magnifies differences between calculations and predictions near Kn = 1.0 and reduces differences in the high and low Kn limits). Future calculations will be necessary to better refine the functional form of Θ(Kn).

FIG. 6 Contour plots of the x-direction (horizontal) component of the gas flow velocity (V_X ) averaged over a large number of sampling time steps around the dense 20-mer test aggregate at selected Kn. The free-stream velocity of the gas is 5.0 m/s in the x-direction, which moves from left to right, while the aggregate is held fixed. Also shown in the contour plot (on the aggregate surface) are the x-direction stresses (P_X ) on the aggregate. (Color figure available online.)

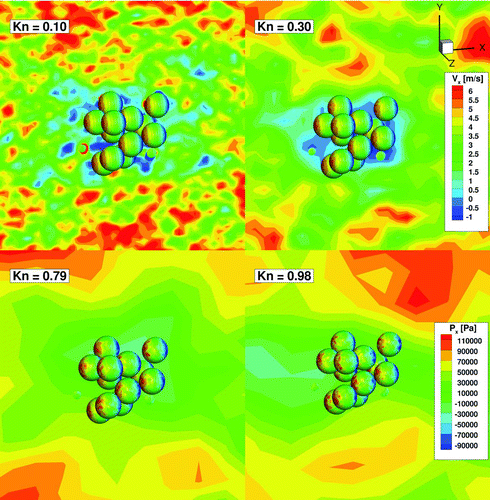
FIG. 7a (a) The inferred slip correction factor on spheres and all test aggregates from DSMC as compared to predictions from previously developed slip correction factor relationships. The error bars displayed derive from the estimate of the standard deviation on the drag force, which is described in the text. (b) The ratio of slip correction factor predicted by DSMC compared with Davies’ predicted slip correction factor for spheres and aggregates, as a function of computational domain size and Kn. The domain side length is normalized by d₀, which is defined in the Table 1 caption for nonspherical particles. (c) Slip correction factors inferred from all DSMC results as well as those measured experimentally by Cheng et al. (1988) and Cho et al. (2007) for nonspherical particles of well-described geometry. (Color figure available online.)

3.3. Comparison with Experimental Data

Unfortunately, most prior experimental measurements do not permit comparison with the predicted Θ(Kn) curve, as to compute Kn, two size descriptors for a particle are needed, and in most examinations of nonspherical particles, these size descriptors have not been reliably calculated. There are, nonetheless, several instances where friction factor measurements have been made on nonspherical particles of near-unambiguous structure, enabling R _S and PA calculation. These include the linear dimers and assumed linear trimers examined by Cheng et al. (1988) using a Millikan cell, and the maximally packed trimers, tetramers, and pentamers measured by Cho et al. (2007) using tandem differential mobility analysis. The inferred Θ⁻¹ values as a function of Kn (again calculated using R _S and PA for each structure) for these data are shown in Figure 7c, alongside DSMC results. The experimental data are in good agreement with both DSMC calculations and predicted curves, also within 10% of the Davies (1945) curve, providing further support for the universality of the Θ(Kn) relationship. We must note, however, that the χ values for aggregates measured in both studies are relatively close to unity, and more critical examination of the proposed Θ(Kn) will require experimental measurement of the orientationally averaged drag force on higher aspect ratio (higher χ) entities.

3.4. Implications for Experimental Measurements of Nonspherical Particles

Provided that the Θ(Kn) does indeed hold valid for arbitrarily shaped particles, in experimental measurement of the drag force on nonspherical particles (e.g., through mobility analysis, diffusion batteries, impaction, etc.), it is important to note that in general πR _S ² ≠ PA unless the particle has an aspect ratio of unity when comparing any perpendicular end-to-end lengths. The main implication of this inequality is that, as noted by Sorensen (2011), inference of a single length scale or shape parameter from measurements is not necessarily sufficient to describe particle size, particularly if the measurement is made in the momentum transfer transition regime. As an example, the dynamic shape factor κ is often calculated through the relationship:

where R _V is radius of a sphere of equivalent volume to the particle under examination. With the exception of a sphere, the relation PA/πR _S = R _V does not hold valid, and rather than a single number, particles of a given geometry will have a unique κ(Kn) curve (Scheckman et al. 2009), with unique Kn → 0 and Kn → ∞ limits.

Unlike the conclusions of Sorensen (2011), however, we do note that R _S and PA themselves are geometric descriptors for any particle and do not depend on the properties of the surrounding gas; i.e., at Kn → 0 and Kn → ∞, the effective radius of a particle with regard to momentum transfer (the mobility radius, R _m) does not vary with Knudsen number (dR _m/dKn → 0 in these limits). Furthermore, with these two parameters inferred, the friction factor can be calculated for an arbitrarily shaped particle at any Kn. Taking this conclusion in combination with the results of Gopalakrishnan et al. (2011), where it is shown that vapor molecule uptake by arbitrarily shaped particles also depends on R _S and PA, as well as with the experimental measurements of mass and momentum transfer rates of Rogak et al. (1991), there is now strong justification that mass transfer and momentum transfer of vapor and gas molecules to particles of arbitrary shape are linked; measurement of drag forces on particles enables prediction of the condensation rates onto particles, and vice versa, irrespective of particle shape. Finally, with the known links between conductive energy transfer and diffusive mass transfer in both the continuum and free molecular limits, we suggest that R _S and PA are the appropriate size scales for heat conduction between gas molecules and particles in the Kn → 0 and Kn → ∞ limits, respectively, with Kn again defined by Equation (7d).

4. CONCLUSIONS

A combined approach is used to systematically examine low-Re, low-Ma drag forces on arbitrarily shaped aerosol particles in the momentum transfer transition regime. Two approximations are first invoked to define appropriate size descriptors for arbitrarily shaped particles in the continuum and free molecular limits. Dimensional analysis then reveals a suitable functional form for both the Knudsen number, Kn, and the dimensionless friction factor Θ(Kn), which describes orientationally averaged drag across the entire Kn range. The parameterization of Θ(Kn) coincides with Dahneke's adjusted sphere approach and is tested via DSMC on model aggregates composed of point-contacting primary spheres. Based on this study, we draw the following conclusions:

1.	The Hubbard–Douglas and PA approximations can be used to reasonably estimate the necessary length scales to describe gas molecule–particle momentum transfer in the continuum and free molecular limits, respectively.
2.	Despite significant statistical dispersion in the results for the drag force on aerosol particles moving at low speed, predictions of the slip correction factor (Θ−1) for both spherical and nonspherical particles can be extracted from DSMC for comparison with predictions based on prior work.
3.	DSMC in large part, supports the universality of the proposed Θ(Kn) relationship, although present limits on precision and accuracy prevent determination of the most appropriate functional form of Θ(Kn). Nonetheless, the use of any previously proposed functional form of the slip correction factor should provide reasonably accurate predictions of the drag on an arbitrarily shaped aerosol particle, provided the correct definitions of Θ and Kn are employed.
4.	Many parameters used to quantify particle shape, including aerodynamic diameter and dynamic shape factor, are Kn-dependent outside the Kn → 0 and Kn → ∞ limits. Using the friction factor expression examined here, these parameters can be calculated for any well-described geometry at any Kn. Moreover, in lieu of inference of Kn-dependent parameters, momentum-transfer-based measurements (e.g., differential mobility analysis) can be used for inference of R S and PA (though we note that this will require the use of tandem measurement schemes; Park et al. 2008).
5.	The application of DSMC to the examination of particle-laden and nanoscale systems is relatively new (Filippov and Rosner 2000; Gallis et al. 2002; Chun and Koch 2005; Ramanathan et al. 2010; Volkov 2011) and can open new avenues of theoretical investigation into transition regime mass, momentum, and energy transfer to aerosol particles. We note that the simulations presented were serial (single-processor) computations; hence, much more extensive DSMC studies could be performed in the future on large parallel-computing clusters, enabling simulation of the drag on a larger number of aerosol particles of greater morphological complexity. Not accounted for in this study, but of interest in future studies of aerosol particle transport, are the viscous interactions arising between particles during close approach in the momentum transfer transition regime (Gopinath and Koch 1999); higher-Re, higher-Ma influences (Moshfegh et al. 2010); and the influence of particle rotation (Loyalka and Griffin 1994; Peters 1999) on drag.

Acknowledgments

We thank the Minnesota Supercomputing Institute (MSI) for providing the high-performance computing hardware used in some of the reported calculations. Partial support for this work was provided by the Division of Chemistry, National Science Foundation (grant no. NSF-CHE-1011810) and by the University of Minnesota Center for Filtration Research.

Notes

In this study, λ is defined exactly by the equation μ = 0.499λρ_gasc, where ρ_gas is the mass density of the gas and c is the gas mean thermal speed.