Experimental Study of Impulse Resuspension with Laser Doppler Vibrometry

Abstract

Particle resuspension due to mechanical impulse was studied for spherical polymethylmethacrylate (pmma) particles ranging from 1.7 to 14.4 μm in diameter on titanium dioxide (TiO₂) and silicon dioxide (SiO₂) wafers. Dry powders were dispersed, electrostatically neutralized, and allowed to deposit under the influence of gravity. Contaminated surfaces were then mechanically excited with a 5 MHz piezoelectric transducer where surface accelerations (∼10⁶ m/s²) and resuspension ratios were quantified with laser Doppler vibrometry (LDV) and digital microscopy, respectively. For TiO₂, experiments were performed over a broad range of relative humidity (25 to 95%) to assess the effects of capillary condensation. Resuspension was a monotonically decreasing function of relative humidity. Existing theories were used to separate data into two adhesion regimes based on capillary bridge formation: van der Waals (vdW) and capillary dominated adhesion. For relative humidity above 60%, resuspension forces were nondimensionalized by the theoretical capillary force. Resuspension data for all particle sizes and relative humidity were described by a single sigmoid function dependent on the dimensionless resuspension force. Below 60% relative humidity, resuspension forces were nondimensionalized by the vdW force calculated with Johnson–Kendall–Roberts adhesion theory. The experimental work of adhesion (pmma-TiO₂) was optimized such that the dimensionless resuspension curves, for capillary and vdW forces, had equivalent dimensionless resuspension forces at 50% resuspension. The calculated value, 0.047 J/m², was within the range of values expected from other published works. Resuspension was not observed for particles on SiO₂ substrates. This result was attributed to electrostatic surface charge patches where particle charge and surface resistivities were measured to analyze the relative influence of electrostatic adhesion forces.

Copyright 2012 American Association for Aerosol Research

1. INTRODUCTION

Adhesive behavior of particles on surfaces has received much attention due to the possibility of resuspension and desired control over it. Accurate characterization of the fundamental forces of adhesion, the effects of surface and particle heterogeneity, and environmental factors like relative humidity are critical to predicting aerosol fate in response to external forces like those created by aerodynamic flows. These effects influence many applications, such as resuspension in indoor environments (Thatcher and Layton 1995; Mukai et al. 2009), controlling the effects of surface cleaning procedures (Ziskind et al. 2002), and the development of trace detection technologies (Fletcher et al. 2008). The focus of this work is accurate characterization of adhesive forces which underpin the development of particle resuspension models, ensemble particle behavior in response to impulse forces, and the effects of capillary condensation.

Past experimental works on adhesion force characterization can broadly be classified into two categories: contact and noncontact methods. Atomic force microscopy is the primary contact method used to measure particle adhesion forces (Butt et al. 2005). The popularity of AFM arises from its high force resolution, repeatability, and a broad range of control over removal force magnitude. Gotzinger and Peukert (2004) used AFM to characterize adhesion force probability distributions for van der Waals (vdW) interactions where forces are distributed due to particle and surface roughness, and surface heterogeneity. The works of Ata et al. (2002), Rabinovich et al. (2002), Jones et al. (2002), Paajanen et al. (2006), and Farshchi-Tabrizi et al. (2008) employed AFM to illustrate several key features of capillary adhesion: the smallest scales of surface roughness govern adhesive interactions, the critical value of relative humidity at which the onset of capillary forces occurs is largely dependent on this roughness length scale, and multiple contact models can be used to represent contact geometries on the nanoscale and achieve better representation of experimentally measured values. A good review of multiple contact models, and experimental adhesion studies, can be found in Prokopovich and Starov (2011).

Although AFM provides highly accurate data, noncontact methods can provide better overall insight into adhesion through observations of statistically representative numbers of particles with randomly distributed orientations and locations (Ding 2008). Centrifugal and vibrational methods utilize surface accelerations and particle inertia to engender particle removal. Thus, noncontact methods are often limited to particles larger than 1 to 2 μm due to limitations on equipment used to accelerate surfaces (e.g., rotational speed and vibrational frequency). Soltani and Ahmadi (1994) review experimental works based on substrate accelerations and develop an analytical theory of detachment which includes normal and rolling modes. Busnaina and Elsawy (2000) and Salazar-Banda et al. (2007) used the centrifugal technique to study particle adhesion due to capillary condensation and particle shape, respectively. And several works provide comparisons of AFM and centrifugal techniques (Mizes et al. 2000; Zhou et al. 2003). Of the inertial detachment mechanisms, centrifugal techniques typically seek to avoid impulse forces by slowly equilibrating the rotational speed. Conversely, vibratory techniques create large, impulsive forces.

Mullins et al. (1992) used a sonicator-optical particle counter technique to study the effects of particle geometry on adhesion. Hein et al. (2002) improved the accuracy of this technique by coupling the piezoelectric transducer with laser Doppler vibrometry (LDV). This allowed them to make direct measurements of surface accelerations rather than having to assume an impulse frequency and displacement magnitude of their piezoelectric crystal. More recently, Murthy-Peri and Cetinkaya (2005) have used the piezoelectric-LDV technique to study individual particle-substrate adhesive bonds due to vdW forces. Their noncontact measurement of differential oscillatory motion was used to calculate experimental works of adhesion although they did not characterize ensemble particle behavior. This work utilizes the piezoelectric-LDV technique to analyze the effects of capillary and vdW adhesion force probability distributions on microparticle resuspension due to impulse forces.

2. EXPERIMENT

2.1. Wafer Preparation and Characterization

Silicon semiconductor wafers were selected as substrate materials with and without a 3000 Å thick titanium (Ti) coating deposited by physical vapor deposition (International Wafer Service, Colfax, CA, USA). Wafers were diced into 12.5 mm square substrates on a dicing saw after being coated with photoresist to prevent contamination during the dicing procedure. After dicing, the substrates were cleaned with the following process to remove photoresist and other organic species: 1 min oxygen plasma ashing, acetone wash, isopropanol wash, N₂ drying, and another min of oxygen plasma. Substrates were then vacuum bagged until needed for experiments to prevent contamination.

A stylus profilometer (P-15, KLA-Tencor, Milpitas, CA, USA) was used to quantify surface roughness on each of the wafers. A contact angle meter (CAM100, KSV Instruments, Monroe, CT, USA) was also used to quantify macroscopic contact angles on each of the surfaces by imaging a sessile drop and curve fitting to the Young–Laplace equation. Lastly, to assess the effects of static charge dissipation, sheet resistivity measurements were made with a four-point probe (Prometrix VersaProbe VP10e, KLA-Tencor) and used to calculate bulk resistivities of each surface material.

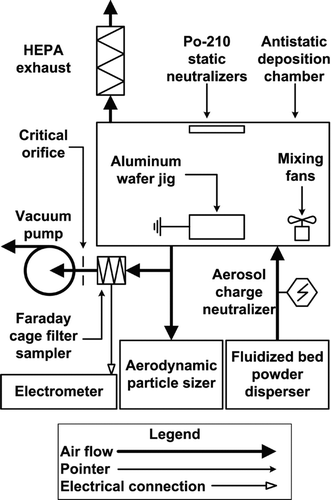
FIG. 1 Deposition chamber schematic. Dry powder pmma particles were dispersed, electrostatically neutralized, and deposited on test wafers. Aerosol concentration and aerodynamic particle size were measured directly with an APS. Average electrostatic charge per particle was measured with a Faraday cage filter sampler and electrometer.

2.2. Particle Deposition

A particle deposition chamber was constructed out of antistatic PVC with dimensions of 0.9 m × 0.3 m × 0.45 m (length × width × height). The setup is shown in Figure 1. Polydisperse polymer microspheres (pmma) were dispersed into the deposition chamber with a fluidized bed powder disperser. The following nominal manufacturer specified particle diameters were used: 3.4, 6.5, 9.9, and 14.8 μm where particle density was 1.2 g/cm³ (Bangs Laboratories, product number BB01N). It should be noted that Bangs Laboratories specifies the 3.4, 9.9, and 14.8 μm microspheres as having size ranges within 10–15% of the mean diameter. However, the 6.5 μm microspheres are specified as having a size range between 3–10 μm. The former are, therefore, considered quasi-monodisperse and the latter are considered polydisperse. The reason for this difference is that quasi-monodisperse and polydisperse microspheres are produced by different manufacturing processes.

A single point bipolar corona ionizer (Haug, Williamsville, NY, USA) was installed at the outlet of the fluidized bed to electrostatically neutralize 9.9 and 14.8 μm particles. The setup was changed to utilize a 10 mCi krypton-85 neutralizer (TSI 3077A) for 3.4 and 6.5 μm particles since the corona electrode became coated with particles over time and could have adversely affected neutralization. Aerosols were fed into the deposition chamber where two 0.12 W electronics cooling fans were used to mix the aerosol and obtain steady-state conditions. Particles were deposited under the influence of gravity onto sets of 25 wafer pieces fixed to an electrically grounded aluminum wafer jig. Two 500 μCi polonium-210 antistatic strips were also installed inside the chamber facing the wafer jig to further reduce electrostatic effects.

Aerosol size distributions were sampled from the chamber with an aerodynamic particle sizer (APS). Measurements were taken once per minute over the duration of particle deposition (15–90 min). Size measurements were used to specify physical diameters of deposited particles and also calibrate length scales from microscope images to be described below. By adopting the well-mixed gravitational settling model (Hinds 1999), aerosol number concentrations and mean diameters were used to calculate the total deposition time required to obtain an approximate surface area coverage of 5–10%. Deposited particles were primarily in the form of monomers. The gravitational settling model was less accurate for particles smaller than approximately 10 μm where turbulent diffusion could have played a more significant role in the deposition process. Microscope images were used as a preliminary tool to determine the optimal deposition time for each particle size.

Average particle charge within the chamber was measured with a custom built Faraday cage filter sampler. A 25 mm fiberglass filter was housed inside the Faraday cage and the current between the filter holder and shielding housing was measured with a Keithley model 6517a electrometer. The entire filter sampler was placed inside a grounded stainless steel enclosure to minimize the effects of external fields on the low-level current measurements. Noise levels were reduced to less than 0.01 pA with current measurements on the order of 10–20 pA. Air was drawn through the filter with a vacuum pump where the flow was regulated with a 10 Lpm critical orifice. Steady-state particle concentrations were obtained within the chamber over a specified deposition period by venting the chamber to atmosphere through a HEPA capsule filter.

FIG. 2 Particle resuspension test schematic. Particle contaminated substrates were vibrated with an ultrasonic transducer within a humidity controlled chamber. Particle resuspension was recorded with a high speed camera through a bright field microscope. Surface vibrations were measured directly with LDV.

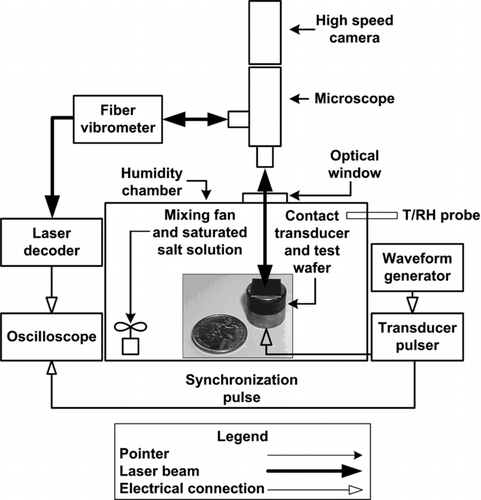
TABLE 1 Saturated salt solutions, and respective theoretical relative humidity conditions at saturation, used to vary capillary condensation during experiments. Saturation conditions were taken from Rockland (1960)

Saturated salt solution	Theoretical relative humidity (%)
None (ambient air)	25
Sodium bromide (NaBr)	57
Sodium chloride (NaCl)	75
Potassium Chloride (KCl)	90
Potassium Sulfate (K2SO4)	97

2.3. Particle Adhesion

Microscopy, high speed imaging, and LDV were used to characterize particle resuspension due to surface excitation. Figure 2 shows the LDV-microscope setup. Particle contaminated wafers were mechanically coupled to a 5 MHz ultrasonic contact transducer with ultrasonic couplant gel. The wafer and transducer were housed inside a 20 cm cubic acrylic enclosure used as a humidity chamber. An antireflective optical window was placed in the top face of the enclosure to allow for laser penetration and bright field microscopy. Humidities were controlled with saturated salt solutions and moderate convective mixing with a 0.12 W electronics fan. The saturated salts listed in Table 1, and the theoretical relative humidity at saturation, were used to vary capillary condensation and adhesion. A duct style temperature-relative humidity probe was used to measure air conditions within the chamber. Relative humidity was allowed to equilibrate within the chamber for 10 min prior to substrate excitation. This time scale was considered sufficient given the theoretical equilibrium capillary condensation time scale of several μs (Butt and Kappl 2009).

A Staveley NDT Workstation 2000 was used to electrically excite the 5 MHz ultrasonic contact transducer. The frequency of the transducer was fixed by the properties of the piezoelectric crystal. Surface displacements were varied over a range of 10–60 nm by controlling the excitation voltage (100–300 V) and damping resistance (50–200 Ω) settings. The contact transducer was pulsed at a repetition rate between 100 Hz and 10 kHz by synchronizing the pulser with a square wave generator. The surface displacement response frequencies of other contact transducers (e.g., 3.5, 10, and 15 MHz) were also measured. Surface displacement response frequencies did not match manufacturer specificied piezoelectric crystal resonance frequencies. Rather, mechanical vibration frequencies between 2.5 ± 1 MHz were observed. This could have been the result of inefficient electro-mechanical coupling of the piezoelectric crystal and pulser, or inefficient mechanical coupling between the transducer and contaminated wafer. Another potential explanation for the lack of linearity between piezoelectric and mechanical vibrational frequencies is that the nominal vibrational frequency of 2.5 MHz is a resonant frequency of the transducer-couplant-wafer system. This illustrates the uncertainties which arise from using piezoelectric transducers for particle resuspension experiments. The theoretical surface acceleration of a piezoelectric crystal is given by a=ω²δ where a, ω, and δ are the surface acceleration, circular frequency, and surface displacement of the piezoelectric crystal (Rimai and Quesnel 2001). Using this assumption to calculate surface acceleration gives rise to large experimental uncertainties due to the following: manufacturers rarely have accurate data on the magnitudes of piezoelectric surface displacements, surface vibrational frequencies are not necessarily equal to the frequency of the piezoelectric, and mechanical coupling of the wafer-transducer was difficult to repeat with less than 25% error in this work. The key to eliminating these uncertainties is making direct measurements of surface accelerations with LDV.

A Polytec OFV-552 fiber vibrometer and OFV-5000/DD-300 laser decoder were used to directly measure surface dynamics of contaminated wafers while observing particle resuspension. LDV uses interferometry and the Doppler effect to measure surface displacements and velocities through comparison of the incident and reflected laser beams. The laser decoder used in this work had temporal resolution adequate for measuring vibrations up to 20 MHz in frequency. The laser decoder outputs a voltage signal proportional to the displacement where a 2 GHz oscilloscope was used to acquire voltage measurements. Transducer pulses and oscilloscope measurements were timed according to the synchronization pulse of the Staveley pulser unit. A Phantom V310 high speed camera was used to record particle resuspension through an Olympus bright field microscope. In this setup, the laser beam traverses the objective lens enabling measurements of surface displacement in the microscope field of view. Image resolution was 800 × 600 pixels with frame capture rates ranging from 100–400 frames per second. Post-processing of video files and images was performed in MATLAB with image processing and computer vision toolboxes.

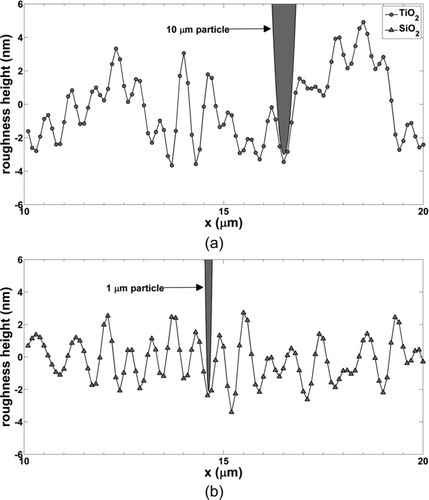
FIG. 3 Surface roughness height (nm) vs. stylus profilometer linear scan distance, x (μm), for (a) TiO₂, and (b) SiO₂ wafer surfaces where 10 and 1 μm particles are drawn for TiO₂ and SiO₂ scans, respectively. Peak-to-peak distance is one the order of 1 μm, thus, particles effectively interact with a molecularly smooth surface rather than multiple surface asperities.

3. DATA

3.1. Wafer Surface Roughness, Contact Angle, and Electrical Resistivity

Results of surface roughness measurements are shown in Figures 3a and b for TiO₂ and SiO₂ wafers. Roughness measurements were taken over a scan length of 100 μm, with a horizontal resolution of 0.1 μm, to capture variations in roughness elements with low and high spatial frequencies. For other studies, low spatial frequency height variations may affect aerodynamic resuspension by shielding particles from turbulent bursts into the laminar boundary layer. In this study, we are primarily interested in roughness heights over horizontal length scales of a single particle diameter. This determines the effective separation distance which governs effective works of adhesion and geometries over which capillary adhesion occurs. Figure 3a shows the TiO₂ wafer where the RMS roughness is 2.5 ± 0.7 nm, and Figure 3b shows the SiO₂ wafer where the RMS roughness is 1.5 ± 0.3 nm. Greater roughness for the TiO₂ surface could be a result of the Ti vapor deposition process or a consequence of greater roughness of the underlying silicon substrate. Particles of 10 and 1 μm diameter are drawn in Figures 3a and b, respectively, where the vertical and horizontal scales are on the order of surface roughness length (nm) and particle diameter (μm), respectively. Peak-to-peak distance is on the order of 1 μm. These drawings illustrate that particles lie in between asperity peaks where the standard approximation for molecularly smooth surface roughness, 0.4 nm, was used (Israelachvili 2011). Multiasperity contact models (Rabinovich et al. 2002; Prokopovich and Starov 2011) would be appropriate if the peak-to-peak distance were less than approximately 100 nm.

Three contact angle measurements (with water) were made for each wafer type. Contact angles, θ, for TiO₂ and SiO₂ were 61 ± 6° and 36 ± 2°, respectively. As was expected, the SiO₂ wafer was more hydrophobic than the TiO₂ surface. Surface resistivity measurements were also made to assess static charge dissipation. Bulk resistivities for TiO₂ and SiO₂ were 6·10⁻⁵ ± 3·10⁻⁵ Ω cm and 3·10⁻² ± 1.5·10⁻² Ω cm, respectively. The electrical conductivity of TiO₂ is significantly higher (three orders of magnitude) and is thus expected to dissipate static charge more readily than SiO₂.

3.2. Particle Size Distributions

Particle size and concentration data from the APS were averaged over the deposition period and fit with the lognormal distribution (John 2001):

where N, d_g , and σ _g are the number of concentration (#/cm³), geometric mean particle diameter (μm), and geometric standard deviation. Aerodynamic particle diameters, d _ae, were converted to mean physical diameters, d_p , with the following relation

where ρ _p is the true particle density (1.2 g/cm³) and ρ₀ is unit density (1 g/cm³). Particle concentrations were normalized and plotted in Figure 4 for each of the dry powders dispersed with the fluidized bed. Particle size distributions with geometric mean physical diameters of 14.4, 9.1, and 1.7 μm were quasi-monodisperse (defined here as σ _g ≤ 1.05).

FIG. 4 Normalized particle size distributions measured with the APS and converted to physical diameter, d_p .

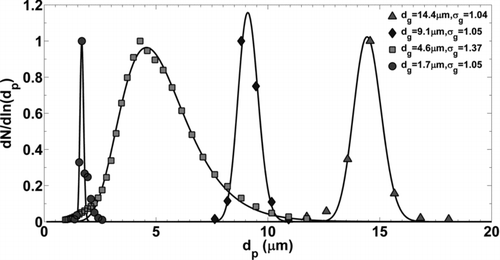
Microscope length scales were set for each experiment by analyzing 25 wafers immediately after deposition, before impulse excitation, and quantifying imaged particle size distributions. A digital microscope image is shown in Figure 5 where the wafer was contaminated with 14.4 μm particles and the approximate surface area coverage is 10%. Each field of view contained approximately 200–300 individual particles. Histograms of imaged particle area were converted to lognormal distributions and compared to distributions measured with the APS. The average geometric mean diameter (pixels) was then used to calibrate the image length scale (μm/pixel). Geometric standard deviations of imaged particle size (pixels) were in good agreement with lognormal distributions measured with the APS (within 3%).

FIG. 5 Digital microscope image of test substrate contaminated with 14.4 μm pmma microspheres. Surface area coverage is approximately 10% where only monomers were included in the analysis of microparticle resuspension.

The spread of the distribution with d_g = 4.6 μm was much larger, comparatively, σ _g = 1.37. As previously mentioned, this dry powder was produced with a different manufacturing process with respect to the quasi-monodisperse powders. Experiments conducted with this set of particles were not considered monodisperse in subsequent analysis. As an approximation to a well-mixed chamber, deposition flux was considered proportional to settling velocity and aerosol concentration. In other words, more large particles will deposit over time and should be accounted for when comparing lognormal size distributions from the APS and microscope images. The APS number distribution was, therefore, weighted by the terminal settling velocity and compared to the imaged particle size distribution to obtain a more accurate calibration length scale. Particle removal analysis was then performed by discretizing the imaged particles into three size bins with a width of approximately 1.5 μm instead of associating all particles with the geometric mean diameter of the lognormal distribution.

3.3. Electrostatic Particle Charge

The average electrostatic particle charge in the deposition chamber was calculated from measurements of the total aerosol concentration and electrical current passing through the Faraday cage filter sampler. The average number of charges per particle, N, is given by

where I is the measured current across the Faraday cage filter sampler measured with the electrometer, C_T , is the total aerosol concentration measured with the APS, Q, is the volumetric flow rate through the filter, and e is the charge of a single electron, 1.6 × 10⁻¹⁹ C. Preliminary measurements showed no ion production in the absence of aerosol generation; excess electrical charges resided solely on the particles as the result of triboelectrification within the fluidized bed. For triboelectrification, charge magnitude is highly dependent on the contacting materials, thus, data presented here are specific to the combination of bronze beads and pmma powder.

FIG. 6 Average charge per particle, n (electrons), calculated from APS measurements of deposition chamber particle concentration and electrometer measurements of Faraday cage filter current. Error bars represent standard deviations from current measurements. Data were fit with a d_p ² power law function.

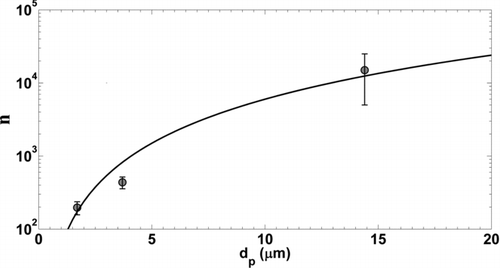
Figure 6 shows the average charge as a function of particle diameter. Approximately, 200, 440, and 15,000 charges were carried by particles with physical diameters of 1.7, 4.6, and 14.4 μm, respectively. Data were fit with a d_p ² charging law where surface area is a key parameter in particle contact charging. Johnston et al. (1987) measured the electrostatic charge of quartz particles dispersed through the fluidized bed and found the charging power law exponent to be on the order of 1.9 where the mean charge on a 7.5 μm particle was 1500 electrons. Forsyth et al. (1998) later measured the charge of alumina and Arizona road dust aerosols generated with the fluidized bed. They found the charging power law exponent to be on the order of one for particles smaller than approximately 2.5 μm. The number of elementary charges was similar to values measured here for 1.7 and 4.6 μm particles (∼100). A modest number of charges per particle were observed at 14.4 μm considering the relationships given by Forsyth et al. However, surface charge densities measured by Akande and Lowell (1987) suggest a 14.4 μm pmma particle could attain a particle charge of approximately 35,000 electrons when triboelectrically charged by gold.

The radioactive neutralizer used in this study (255 mL volume) did not provide sufficient residence time for electrostatic charge neutralization given the large air flow rates from the fluidized bed (30 SLPM). Similarly, particles exposed to bipolar ions from the Haug single point ionizer had residence times on the order of 0.1 s and retained significant charge. An analysis based on the work of Liu and Pui (1974) suggests the residence time would need to be on the order of 2 s for effective charge neutralization.

3.4. Wafer Surface Dynamics

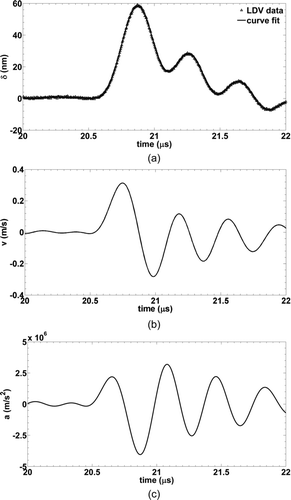
Figures 7a–c show surface displacement, velocity, and acceleration of a contaminated wafer at the maximum transducer excitation voltage of 300 V. Figure 7a shows the measured displacement along with a Fourier series curve fit. The maximum displacement is approximately 60 nm with a peak-to-peak period of 0.43 μs and a corresponding frequency of 2.3 MHz. At this point, the wafer undergoes its largest negative acceleration (downward) of approximately 3 × 10⁶ m/s². The particle resuspension force, F _resuspension, at this point is equal to the particle mass, m_p , times surface acceleration, a.

All resuspension forces presented in this work will be calculated based on the force experienced during the maximum negative acceleration. The local minima and maxima observed after the initial impulse are not characteristics of the piezoelectric crystal, rather, are a consequence of damping within the gel couplant layer in between the face of the piezoelectric and the substrate. LDV measurements at the face of the piezoelectric crystal do not show these subsequent oscillations. The displacement curve returns to zero approximately 5 μs after the initial pulse. The duty cycle ranged from 0.005–5% over the range of pulse repetition rates tested here (100 Hz–10 kHz). Resuspension forces were a series of impulses rather than a periodic vibration with fixed frequency. Duty cycle did not affect particle resuspension. Particles which detached did so within the first several pulses; there was no observed time dependence. This type of resuspension mechanism (impulse) is thereby distinguished from aerodynamic resuspension where turbulent phenomena add a stochastic component resulting in time dependence and additional experimental uncertainty.

FIG. 7 (a) Wafer surface displacement (nm) measured with LDV and curve fit, (b) calculated surface velocity (m/s), and (c) calculated surface acceleration (m/s²) for 5 MHz contact transducer pulsed at maximum power (300 V).

3.5. Particle Adhesion and Resuspension

Image processing algorithms were used to determine the number of particles resuspended from the surface as a consequence of impulse forces. Particles not existing as isolated monomers were not included in this analysis, for example, doublets and triplets were not counted in the resuspension percentage since no simple theory exists to describe adhesive behavior of cohesively bonded particles. Computational algorithms can be used to examine the effects of cohesion on particle adhesion (Marshall 2009); however, these were beyond the scope of this work.

Butt and Kappl (2009) provides a review of capillary condensation and its dependence on relative humidity. The capillary adhesion force is given by

where R_p is the particle radius, θ _p is the particle–water contact angle taken to be approximately 70° (CHEMnetBASE, CRC Press), θ _s is the measured surface–water contact angle, and D is the separation distance between the particle and surface (0.4 nm). The Kelvin radius, r, is given by

where λ _k is the kelvin length scale of water at 25°C (0.52 nm), and P/P ₀ is the ratio of the actual partial pressure of water vapor in the air to the saturation vapor pressure, or relative humidity. In the limit of P/P ₀→1, and contact angles of 0°, Equation (5) reduces to F _cap=2πγd_p . For experiments with relative humidity less than 60%, the term in brackets in Equation (5) becomes negative indicating that capillary condensation is not sufficient to bridge the gap between the particle and substrate (Rabinovich et al. 2002). In this case, we attribute adhesion to vdW interactions rather than capillary condensation. Where capillary condensation is assumed, we attribute adhesion entirely to capillary forces since interfacial energies (vdW) are reduced significantly (∼10×) when liquid is present in the interface (Israelachvili 2011). The vdW forces may contribute to overall adhesion outside the zone of capillary condensation although their contribution is likely to be small relative to capillary forces.

Equation (4) was normalized by Equation (5) to give the dimensionless resuspension-capillary force, F*_cap=F _resuspension/F _cap. The percentage of particles resuspended from the surface was plotted in Figure 8 as a function of the normalized resuspension force for all particle sizes tested on TiO₂ where relative humidity was greater than 60%. Wafers contaminated with 1.7 μm particles showed no signs of resuspension at any level of transducer excitation and are not plotted. Resuspension forces vary to the third order of particle diameter (inertial acceleration) and therefore decay quickly to a level at which they are insignificant with respect to capillary forces. In Figure 8, particle diameters of 2.6, 3.2, 4.0, 4.9, and 5.4 μm came from the lognormal distribution of particles with d_g = 4.6 μm and σ _g = 1.37. Two sets of tests (25 wafers each) were performed yielding slightly different deposited particle size distributions and discretized particle diameters. There is a dependence of the normalized detachment force on particle diameter since resuspension forces are dependent on particle mass. Surface accelerations could be experimentally varied by a factor of 6 which is not sufficient to span the entire dimensionless force spectrum with a single transducer.

FIG. 8 Percent microparticle resuspension from TiO₂ surface as a function of the resuspension force normalized by the theoretical capillary force, Equation (5), for data above 60% relative humidity. A sigmoid function was used to fit the linearized data set and find the mean response and 95% prediction interval bounds. Vertical error bars (±5%) are due to image processing and particle counting. Horizontal error bars were calculated with the Kline–McClintock equation from uncertainties in parameters used to calculate the capillary force.

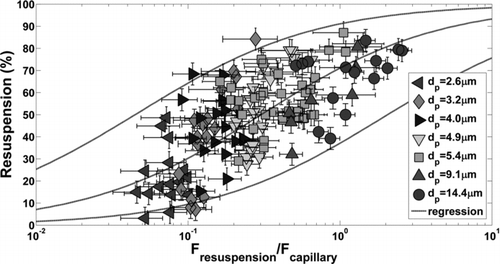
Data in Figure 8 were fitted with a sigmoid function which gives proper asymptotic behavior with respect to the normalized resuspension force. No particle resuspension is expected for negligible values of resuspension forces and complete resuspension is expected for large values of F*_cap. The resuspension ratio was fitted with the following equation:

Equation (7) was linearized and least squares regression was performed to determine the mean response and 95% prediction intervals shown. The empirical constants in Equation (7) were b _cap=0.30 and c _cap=0.75. The 95% prediction interval limit width is approximately 45% resuspension and is attributed to surface heterogeneity. The spread observed here agrees conceptually with the existence of adhesion force probability distributions measured by AFM.

Vertical error bars in Figure 8 represent ±5% resuspension uncertainty associated with counting particles before and after surface excitation. At the initial counts of approximately 200 particles, this error is equivalent to miscounting ±10 particles due to image processing techniques and particles which agglomerate on the surface after excitation. Horizontal error bars represent a more significant challenge due to the parameters included in the theoretical capillary force, Equation (5). The Kline and McClintock equation (1953) was used to estimate uncertainty in F*_cap for the following parametric uncertainties: θ _p ±5°, θ _s ±5°, D±0.1 nm, P/P ₀±0.02, and R_p ±0.5 μm. The resulting uncertainty in the dimensionless force is approximately 30–50%.

Below 60% humidity, capillary bridges are not expected to form. Adhesion is attributed to the vdW force in this region. The vdW force originates from intermolecular interactions where instantaneous electrical dipoles polarize adjacent molecules thereby creating an adhesive force. For compliant particles (e.g., soft and elastic), forces are strong enough to cause particle deformation ultimately resulting in a condition where the interfacial energy and elastic stored energy of the particle are in equilibrium. This theory was first described by Johnson et al. (1971) where a macroscopic parameter called the work of adhesion, W_A , is used to quantify the net force between a particle and surface. Johnson–Kendall–Roberts theory is adopted here to describe the adhesion of pmma particles to TiO₂ substrates.

Work of adhesion is proportional to surface energy, and in most cases, is determined experimentally due to the complexities of calculating intermolecular forces. The surface energy of pmma, SiO₂, and TiO₂ are all of similar magnitude, 0.050 ± 0.025 J/m² (Chehimi et al. 2003) where specific combinations, for example, pmma-TiO₂, are typically measured. The intervening medium also plays a pivotal role in determining intermolecular forces where vdW forces are reduced when water is present at the interface. The reader is referred to Israelachvili (2011) for a comprehensive description of surface energies and JKR theory.

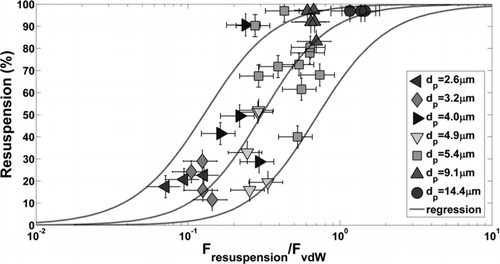
In our analysis of vdW forces, we assume the dimensionless resuspension force which causes 50% resuspension is independent of the underlying adhesion mechanism. Thus, the midpoint of the empirical fit from Figure 8, F*_cap=0.3, determines the dimensionless resuspension-vdW force at 50% resuspension (F*_vdW=0.3). This assumption specifies the experimental work of adhesion for pmma-TiO₂ data, 0.047 J/m², and is within the range of expected values. Murthy-Peri and Cetinkaya (2005) present data for other polymer-metal pairs where works of adhesion are approximately 0.020–0.150 J/m² for polystyrene latex spheres on copper, silicon, aluminum, and tantalum surfaces. Percent resuspension is plotted against the dimensionless resuspension-vdW force in Figure 9 for experimental data where the relative humidity was below 60%. The slope of the empirical fit, Equation (7), was optimized to best fit the data where the empirical constants were b _vdw=0.30 and c _vdw=2.0.

FIG. 9 Percent microparticle resuspension from TiO₂ surface as a function of the resuspension force normalized by vdW force (JKR), Equation (8), for experimental data below 60% relative humidity. The theoretical work of adhesion was optimized so that the midpoints of the regression curves (50% resuspension) for F*_vdw and F*_cap were equivalent. Vertical error bars (±5%) are due to image processing and particle counting. Horizontal error bars (±30%) were specified according to estimated uncertainty in the experimental work of adhesion.

Particles of all sizes remained adhered to the SiO₂ surface regardless of excitation force. This behavior was attributed to electrostatic effects, and more specifically surface charge patches, since the effective interfacial energies of pmma-SiO₂ and pmma-TiO₂ are expected to be of similar magnitude but surface conductivity is three orders of magnitude higher for TiO₂. More analysis is provided below.

4. DISCUSSION

With respect to Figure 8, percent resuspension has a more modest slope than expected. At F*_cap values of 0.1, 1.0, and 10.0, average resuspension is approximately 30, 70, and 90%, respectively. According to the mean response, nonzero resuspension would be observed at dimensionless forces as small as 0.01 and incomplete resuspension (<100%) would occur for dimensionless forces on the order of 100. A steeper curve could be drawn within the prediction interval bounds which would be more intuitive, however, the gradual change in resuspension could also be a true effect of capillary condensation. Values on the abscissa are subject to uncertainty due to the assumed parameters in Equation 5. Here, we assume the macroscopic sessile-drop contact angle measured on the surface is the same as the microscopic contact angle in the particle–surface interstitial region. We also assume that the macroscopic contact angle on bulk pmma (70°) is the same as on the surface of a microparticle. These uncertainties mean that the mean response curve could be shifted such that percent resuspension at a dimensionless force of 0.5 is 50%. However, experimental validation of the parameters used to determine the capillary force is difficult due to the length scales of interest (sub-nm). With respect to Figure 9, the vdW correlation has a distinctly steeper slope than the capillary correlation. Since the vdW data set is relatively small with respect to capillary adhesion, more measurements should be taken in the vdW regime to clarify if a more gradual change in resuspension is a true effect of capillary adhesion.

An unexpected result of this work was the observation of anomalously large adhesive forces for pmma-SiO₂. The work of adhesion between pmma-SiO₂ should be on the same order of pmma-TiO₂ judging from the interfacial energies of SiO₂ and TiO₂. If electrostatic forces were not significant, we would expect similar resuspension for the SiO₂ system since surface roughness is similar for both surfaces. Complete adhesion for pmma-SiO₂ indicates some other force is responsible. An analysis of image forces is traditional where the adhesion force is given by

where ϵ₀ is the absolute permittivity of free space (8.854 × 10⁻¹² C²/Nm²) and Q is particle charge (C). Data from Figure 6 were used to calculate theoretical image forces for particles studied here. Electrostatic forces are less than 1 nN and are several orders of magnitude smaller than the respective vdW force. We should also point out that the concept of an image force is physically incorrect since each of these substrates is nonconducting below the first few nm of the surface. Electrostatics is thereby assumed to be a surface phenomenon. The measured conductivity of TiO₂ is three orders of magnitude higher than SiO₂. This supports the hypothesis that electrostatic charge initially present at the particle–surface interface is more likely to redistribute on the TiO₂ wafer. Conversely, SiO₂ is relatively nonconductive and we hypothesize that initial particle charge in the interfacial region was concentrated into surface charge patches. Our hypothesis agrees qualitatively with the works of Pollock et al. (1995) and Hays (1995) who suggest electrostatic charge patches may be responsible for adhesive forces which are one to two orders of magnitude larger than what might be expected for uniformly distributed charge. Since pmma-SiO₂ adhesion forces were outside the range of achievable impulse resuspension forces, future studies are recommended to clarify this result.

5. SUMMARY

LDV and digital microscopy were used to characterize impulse resuspension of pmma microparticles from SiO₂ and TiO₂ substrates. Particles from 1.7 to 14.4 μm in diameter were dispersed as aerosols, electrostatically neutralized, and allowed to deposit on 12.5 mm substrates. Substrates were then mechanically coupled to a 5 MHz contact transducer within a humidity-controlled chamber. High speed imaging was used to observe particle resuspension while making in-situ LDV measurements of surface displacement. Surface accelerations were then calculated and used to correlate resuspension ratios with impulse resuspension forces. This technique provides a direct measurement of resuspension forces in a noncontact manner thereby allowing statistically significant numbers of particles to be studied simultaneously in contrast to AFM. For TiO₂ surfaces, resuspension was a monotonically decreasing function of relative humidity. Existing theories suggested capillary condensation was unlikely to bridge the interstitial region for relative humidity below 60% (Rabinovich et al. 2002). This value of relative humidity is specific to pmma-TiO₂ at a separation distance of 0.4 nm although it is qualitatively consistent with other works which observe the existence of a critical vapor pressure at the onset of capillary condensation. Experimental data were thereby separated into two adhesion regimes based on relative humidity: vdW (<60%) and capillary (>60%) dominated adhesion. Resuspension forces were nondimensionalized by their respective adhesion forces. Capillary adhesion data were fitted with a sigmoid function representing percent resuspension as a function of the dimensionless resuspension force. Prediction interval bounds (95%) showed a spread of ±20% resuspension with respect to mean resuspension. This variability was attributed to surface heterogeneity. Data in the vdW adhesion regime were nondimensionalized by the JKR adhesion force. To do so, the work of adhesion was optimized such that the midpoints of the vdW and capillary resuspension curves (50% resuspension) occurred at equivalent dimensionless forces. This assumes the dimensionless force at 50% resuspension is independent of the underlying adhesion mechanism. An optimized value of 0.047 J/m² fell within the range of expected values (0.02–0.150 J/m²) for similar materials characterized in other works (Murthy–Peri and Cetinkaya 2005). Complete adhesion was observed on SiO₂ surfaces. Particle charge and surface resistivity measurements support the hypothesis that electrostatic surface charge patches were responsible for anomalously large adhesive forces relative to TiO₂.

Acknowledgments

This work was funded through Sandia National Laboratories, Laboratory Directed Research and Development (LDRD) Early Career R&D program.Sandia National Laboratories is a multiprogram laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the U.S. Department of Energy's National Nuclear Security Administration under contract DE-AC04–94AL85000.